引言

波浪是时刻存在于海-气界面的一种运动形态, 被视为时空尺度较小的海洋过程。在旋转的海洋中, 由于波浪运动的持续性, 即使考虑很小的粘性, 波浪也会存在大尺度效应, 波浪的大尺度效应主要表现在三方面:波浪对大洋环流的驱动作用^[1-2]、波浪对Ekman层能量的输入^[3-5]及波浪输运对大洋热量再分配的影响^[6-9]。

20世纪90年代研究发现, 南大洋内存在时间尺度为年际尺度的向东传播的距平信号, 称此低频信号为南极绕极波(ACW)。南极绕极波的信号存在于南极绕极流区域的海表面压强(SLP)、经向风应力(MWS)、海表面温度(SST)和海冰覆盖(SIE)距平场中, 此距平信号表现了明显的向东传播的特征, 具有4~5 a的周期, 并且需要8~10 a的时间绕纬圈一周^[10]。随后的研究显示, 波浪与ACW信号具有显著的一致性, 同样保持周期性的由西向东的传播特征^[9]。但是, 与ACW中的SLP、MWS、SST及SIE变量不同, 自西向东传播的波浪遇到澳大利亚和南美洲大陆的阻挡后, 会向东北方向转折形成涌浪并且在大洋东岸堆积向赤道方向传输。Chen et al.^[11]通过分析卫星资料发现大洋东边界涌浪强化的事实, 即“涌浪池”的存在。Deng et al.^[12]进一步证明了南大洋的风浪遇陆地阻隔而形成大洋东岸的涌浪是“涌浪池”的主要源头。可见, 大洋东岸的涌浪是连接南大洋与东赤道太平洋的重要动力过程。

赤道东太平洋海温异常(ENSO)是地球系统中最为重要的一种海气相互作用现象, 它对全球大气海洋动力过程有重要的影响。因此, ENSO一直是国际大气和海洋学研究的热点课题之一。除了热带西太平洋通过纬向过程对ENSO产生重要影响外, 许多研究发现, 高纬度地区大气和海洋的异常信号也可以通过经向过程影响热带海洋^[13-15]。本文企图建立大洋东岸的高纬度到低纬度之间的桥梁, 将波浪过程对该方面的相关研究成果进行简要概述及回顾, 说明南大洋海域的波浪通过经向过程对ENSO影响的物理过程及可能的动力机制。

1 涌浪的东向强化

图 1给出了多年月平均全球波浪在不同季节的周期分布。1月, 波浪平均周期分布的最突出特点是出现东向强化的现象, 波浪在太平洋及北大西洋的东边界平均周期普遍较大。4月, 北半球波浪的平均周期减小普遍小于10 s, 而在几乎覆盖整个南半球的区域均大于10 s。到7月, 南半球的波浪平均周期继续增大, 最大值出现在澳大利亚西北沿岸, 约在14 s。10月, 波浪的平均周期呈现出东传的现象, 南印度洋的平均周期减小, 而南太平洋的平均周期增大, 由于东传现象及陆地的影响, 此时, 整个太平洋东岸的平均周期均增大。值得注意的是, 虽然波浪的平均周期随季节不同变化较大, 但是在南太平洋的东岸, 波浪的平均周期几乎全年都在10 s以上, 说明南半球大洋东岸海域主要以涌浪为主并且以秋季和冬季最强。

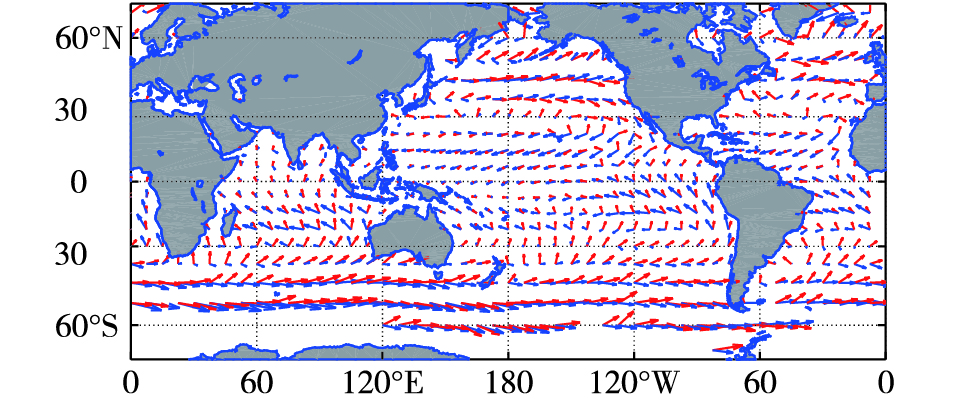
在实际大洋中一般很难定义某时某地的海浪输运风浪或涌浪, 但是当涌浪占优时波向和风向会存在较大的偏差。图 2给出了全球平均风速方向(蓝色箭头)和波向(红色箭头)空间分布, 可以看出, 大洋东岸的风向和波向存在较大的差异, 说明这一海域涌浪占优, 这也印证了大洋东岸涌浪强化的事实。

以上数据分析结果显示出南半球涌浪存在明显的涌浪东向强化现象, Chen et al.^[11]通过分析卫星资料发现大洋东边界涌浪强化的事实, 即赤道东太平洋“涌浪池”的存在。随后的研究工作也进一步证明了南大洋的风浪遇陆地阻隔而形成大洋东岸的涌浪是“涌浪池”的主要源头。

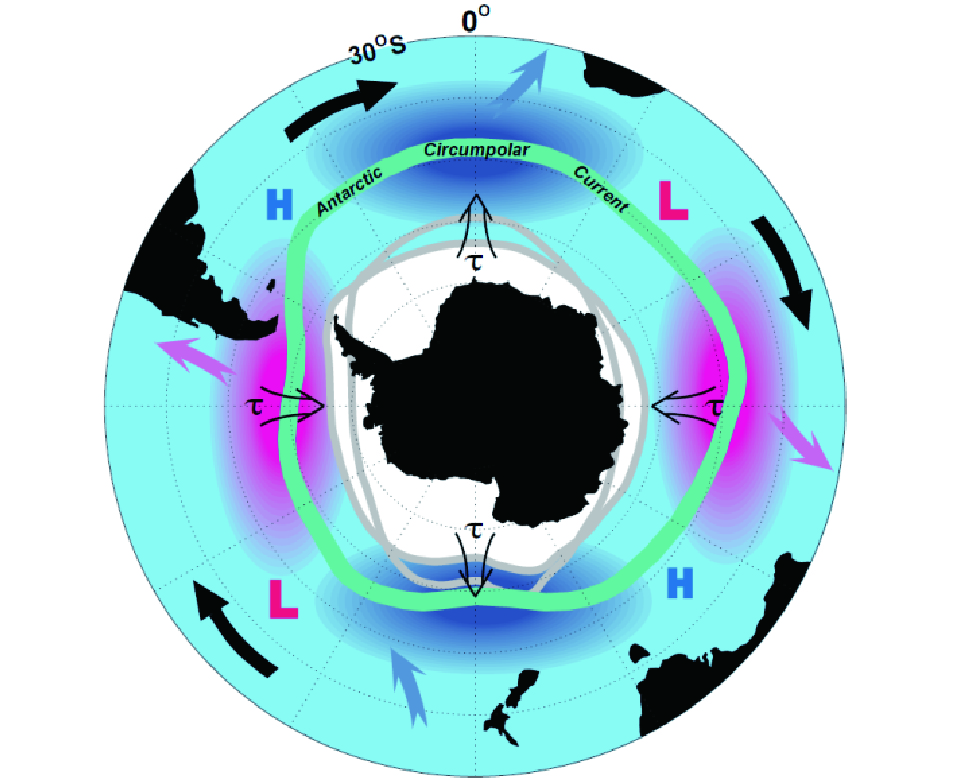
2 从波浪中发现绕极波

南大洋在全球范围内的气候异常传递方面扮演非常重要的角色。近年科研工作者对于南大洋的研究过程中发现, 南大洋内存在时间尺度为年际尺度的向东传播的距平信号, 称此低频信号为南极绕极波(ACW)(图 3)。南极绕极波的信号存在于南极绕极流区域的海表面压强(SLP)、经向风应力(MWS)、海表面温度(SST)和海冰覆盖(SIE)距平场中, 此距平信号表现了明显的向东传播的特征, 具有4~5 a的周期, 并且需要8~10 a的时间绕纬圈一周。ACW的存在对于南半球的高纬度区域气旋的数量和分布特征具有一定的影响^[16-17], 而充分成长的海表面波浪要素与风速具有直接的联系^[18], 因此, 南极绕极流区域的海表面波浪场与ACW之间必然会存在一定的联系。

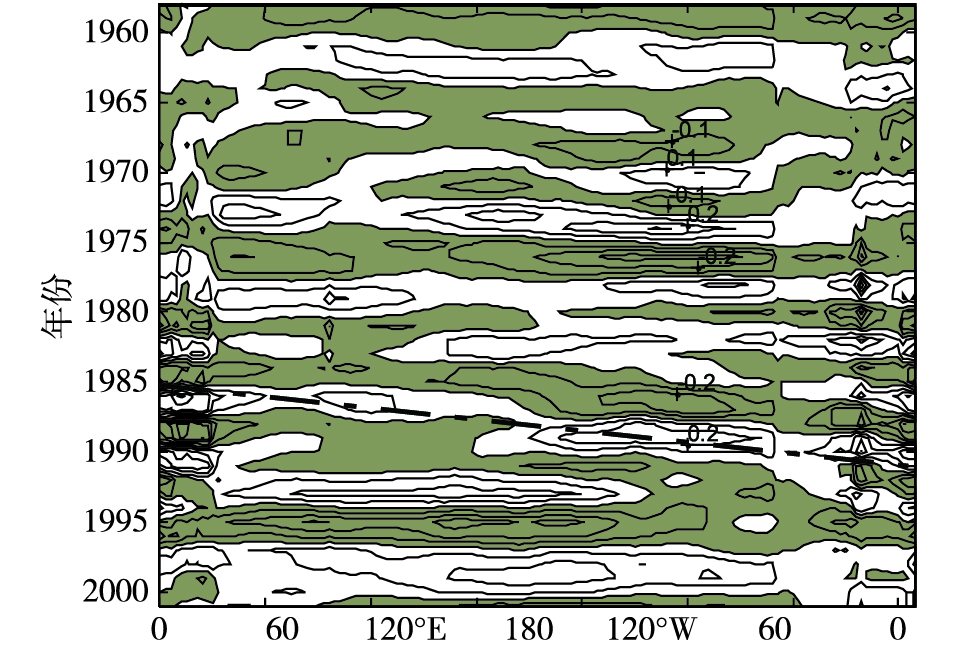
图 4和图 5给出了有效波高(significant wave height, SWH)距平的时间-经度图, 在图中SWH年距平表现了明显的4~5 a周期性, 并且在1985—1995年时间段内表现了明显的向东传播的特征。1985—1995年时间段内这一传播信号的一个独立位相需要8 a左右的时间绕纬圈一周, 并且在全球内表现为两个首尾相连的波长。虽然在1985—1995年时间段以外SWH距平信号的传播性并不明显, 但1985—1995年时间段内SWH距平的低频特征与White and Peterson^[10]给出的ACW定义较为一致。南极绕极流区域海表面压强SLP, 海表面温度SST和海冰覆盖SIE场中的ACW信号已经被前人的研究工作所证明^[19], 并且指出ACW的信号只有在1985—1994年时间段内较为明显, 此时间段之前或者之后, ACW信号的传播性均不明显。另一方面, 海洋中的动量和热量主要来源为风和太阳辐射, 而波浪能量主要来源于风, 波浪信号与ACW中的风信号直接相关。以上两方面皆证明了SWH距平中的低频信号与SLP、SST和SIE中的ACW信号具有显著的一致性^[9]。

存在于ACW中波浪信号, 一部分自西向东绕地球传播, 一部分在传播过程中遇到澳大利亚和南美洲大陆的阻挡后, 向东北方向转折形成涌浪并且在大洋东岸堆积向赤道方向传输。

至此, 我们发现两个观测事实, 即存在于绕极波中的波浪信号和大洋东岸的涌浪强化, 大洋东岸的涌浪是由绕极流区传播而来, 同时涌浪携带着输运和冷水。因此, 大洋涌浪东边界强化的发现为波浪产生的输运存在向赤道的分量提供了一个有力的证据, 该证据不仅隐含了大洋东边界的波浪输运对海洋表层输运有贡献, 而且还启示我们进一步思考波浪是否会对大洋东岸SST有影响, 是否会在大洋东岸建立高纬度和低纬度之间的桥梁。

3 从波浪到厄尔尼诺

在南、北中高纬度海域, 常年盛行西风, 风力强劲, 风速大, 特别是南半球, 各大洋东西贯通, 提供了较长的风区, 更有利于波浪的增大, 波浪常年保持自西向东的较大输运量。由上述的分析可以看出, 波浪离开绕极流区变成涌浪向低纬度大洋东岸传播, 大洋东岸的涌浪在向低纬度传播过程中携带大量的冷水, 而这一过程必然会对赤道东太平洋SST异常产生一定的影响。

3.1 波浪对海表面温度(SST)影响的理论分析

当波浪受地球自转的影响, 会产生作用于水体下方的科氏-斯托克斯力(CSF), 从而导致难以置信的事实:小尺度的波浪现象也会产生大尺度效应。McWilliams and Restrepo^[1]从理论上对波浪影响海洋环流进行了证明, 分别将Stokes漂诱导的涡度力, Stokes漂物质输运等波浪特征作为边界条件加入到海平面, 压强和垂向流速计算的动力学机制中, 对经典环流理论进行修正, 并指出在较大的水平尺度上, 海洋中存在的表面重力波对Sverdrup输运具有非常重要的贡献, 并且在中高纬度区域波浪诱导的输运与风生环流输运能够达到同等的量级。Lane et al.^[20]从动力学上将波浪与流建立了相关关系, 认为波浪对平均流的影响主要表现为Stokes漂的质量输运以及涡度力等动量影响的作用。对于水体示踪物的平流输运, 波浪输运与平均流具有同等作用。

上层海洋温度变化方程^[21]为:

$ \begin{align} & \frac{\partial \bar{T}}{\partial t}=\frac{{{Q}_{0}}-{{Q}_{-h}}}{\rho {{c}_{p}}}-\left[ \overline{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {V}}}\cdot \nabla \bar{T}+\nabla \cdot \left( \int_{-h}^{0}{{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {V}}}^{\prime }}}{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {T}}}^{\prime }}\text{d}z \right) \right]- \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{\bar{T}-{{T}_{-h}}}{h}{{w}_{e}} \\ \end{align} $

(1)

其中T为温度, w为垂向流速, Q为垂向热通量(为辐射通量与扩散热通量之和), ρc_p为单位体积海水的热容量, c_p为海水的比热容, -h深度以上海洋平均温度和水平速度为T_a和V_a, T′和${{{\vec{V}}}^{\prime }}$分别表示温度、水平速度相对于平均量的偏差, 也可以称作为扰动项, w_e为穿越等h面的垂向速度。方程左边一项表示海洋-h深度以上海水平均温度随时间的变化率; 方程右侧第一项为上层海洋净热通量对于温度的影响; 右侧第二项表示温度的平流输运作用的影响; 右边第三项为垂直卷挟作用的影响。但上述温度变化方程中忽略了波浪输运项, 同时在温度平流变化项中只考虑平均流的贡献亦是有所欠缺的, 所以在混合层温度方程平流输运项中加入波浪输运的影响是合理且必要的。

在温度平流变化项中加入Stokes漂影响, 主要是对于热输送项进行修正, 则修正形式的SST方程为:

$ \begin{align} & \frac{\partial \bar{T}}{\partial t}=\frac{{{Q}_{0}}-{{Q}_{-h}}}{\rho {{c}_{p}}h}-\overline{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {V}}}\cdot \nabla \bar{T}-\overline{{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {V}}}_{s}}}\cdot \nabla \bar{T}-\nabla \cdot \\ & \ \ \ \ \ \ \ \left( \int_{-h}^{0}{\left( {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {V}}}^{\prime }}+\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {V}_{s}^{\prime } \right)}{{T}^{\prime }}\text{d}z \right)-\frac{\bar{T}-{{T}_{-h}}}{h}{{w}_{e}} \\ \end{align} $

(2)

其中

$ \begin{align} & \overline{{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {V}}}_{s}}}=\frac{1}{{{d}_{s}}}\int_{-{{d}_{s}}}^{0}{{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {V}}}_{s}}}\text{d}z \\ & \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {V}_{s}^{\prime }={{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {V}}}_{s}}-\overline{{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {V}}}_{s}}} \\ \end{align} $

$\overline{{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {V}}}_{s}}}$为波浪输运在其影响深度上的平均流速, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {V}_{s}^{\prime }$为相对平均流速的扰动项, d_s为波浪输运有效影响深度。

需要指出, 当选取h为混合层深度时, 由于混合层内的流速梯度以及温度梯度均较小, 因此方程(2)中右侧第四项(主要由平均流流速, 波浪输运流速和温度的扰动量贡献)为小量, 为了简化计算的复杂性, 在进行定量计算的过程中将此项忽略掉。所以式(2)右侧第三项即为浪致水平输运对混合层平均温度变化的贡献项。

首先对影响SST变化的几个物理量进行量纲分析, 其中T_q、T_c、T_s和T_w分别为:热通量项, 海洋平均流热输送项, 浪致热输运项, 以及垂直卷挟项对SST变化的贡献。各物理量的量级由以下表达式给出:

$ \begin{align} & {{T}_{q}}=\frac{{{Q}_{0}}-{{Q}_{-h}}}{\rho {{C}_{p}}h}=O\left( \frac{Q}{\rho {{C}_{p}}H} \right) \\ & {{T}_{c}}=\overline{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {V}}}\cdot \nabla \bar{T}=O\left( \frac{\bar{U}\overline{T}}{L} \right) \\ & {{T}_{s}}=\overline{{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {V}}}_{s}}}\cdot \nabla \bar{T}=O\left( \frac{{{{\bar{U}}}_{s}}\bar{T}}{L} \right) \\ & {{T}_{w}}=\frac{\bar{T}-{{T}_{-h}}}{h}{{w}_{e}}=O\left( \frac{\bar{T}W}{H} \right) \\ \end{align} $

(3)

其中, ${\bar{U}}$为混合层内平均流流速的量级, ${{{\bar{U}}}_{s}}$为Stokes深度内平均Stokes漂流流速的量级, $\overline{T}$为混合层平均温度的量级, W为穿越等h面的垂向流速量级, L为水平距离的量级, H为混合层深度的量级。

对于中高纬度区域(30~80°N, 30~80°S), 海洋上层热通量量级Q为10 W/m², 混合层深度量级H为10 m, 混合层内平均流流速量级${\bar{U}}$为0.01 m/s, 混合层内Stokes漂流速量级${{{\bar{U}}}_{s}}$为0.01 m/s, 混合层平均温度 量级为10 ℃, 水平距离尺度量级L为10⁵ m, 穿越等h面速度量级W为10^-5 m/s。将以上个各物理量的量级值代入到公式(3)中可以得到南北半球中高纬度区域各物理量的量级, 单位为℃/s, 量值分别为:

$ \begin{align} & {{T}_{q}}=1\times {{10}^{-6}} \\ & {{T}_{c}}=1\times {{10}^{-6}} \\ & {{T}_{s}}=1\times {{10}^{-6}} \\ & {{T}_{w}}=1\times {{10}^{-5}} \\ \end{align} $

(4)

对于低纬度区域(30°S~30°N), 海洋上层热通量量级Q为10 W/m², 混合层深度量级H为10 m, 混合层内平均流流速量级${\bar{U}}$为0.01 m/s, 混合层内Stokes漂流速量级${{{\bar{U}}}_{s}}$为0.001 m/s, 混合层平均温度 量级为10 ℃, 水平距离尺度量级L为10⁵ m, 穿越等h面速度量级W为10^-5 m/s。将上述各个物理量的量级值代入到公式(3)中可以得到低纬度区域各物理量的量级, 单位为℃/s, 量值分别为:

$ \begin{align} & {{T}_{q}}=1\times {{10}^{-6}} \\ & {{T}_{c}}=1\times {{10}^{-6}} \\ & {{T}_{s}}=1\times {{10}^{-7}} \\ & {{T}_{w}}=1\times {{10}^{-5}} \\ \end{align} $

(5)

虽然在低纬度区域, 波浪的平流热输送作用相对较弱, 甚至可以作为小量忽略, 但是波浪所诱导的平流热输运作用在南北半球中高纬度区域对混合层温度变化的贡献是非常显著的, 能够与上层海洋平均流的平流热输运贡献, 热通量项的贡献达到同等量级, 说明了波浪对混合层温度变化过程的重要性。

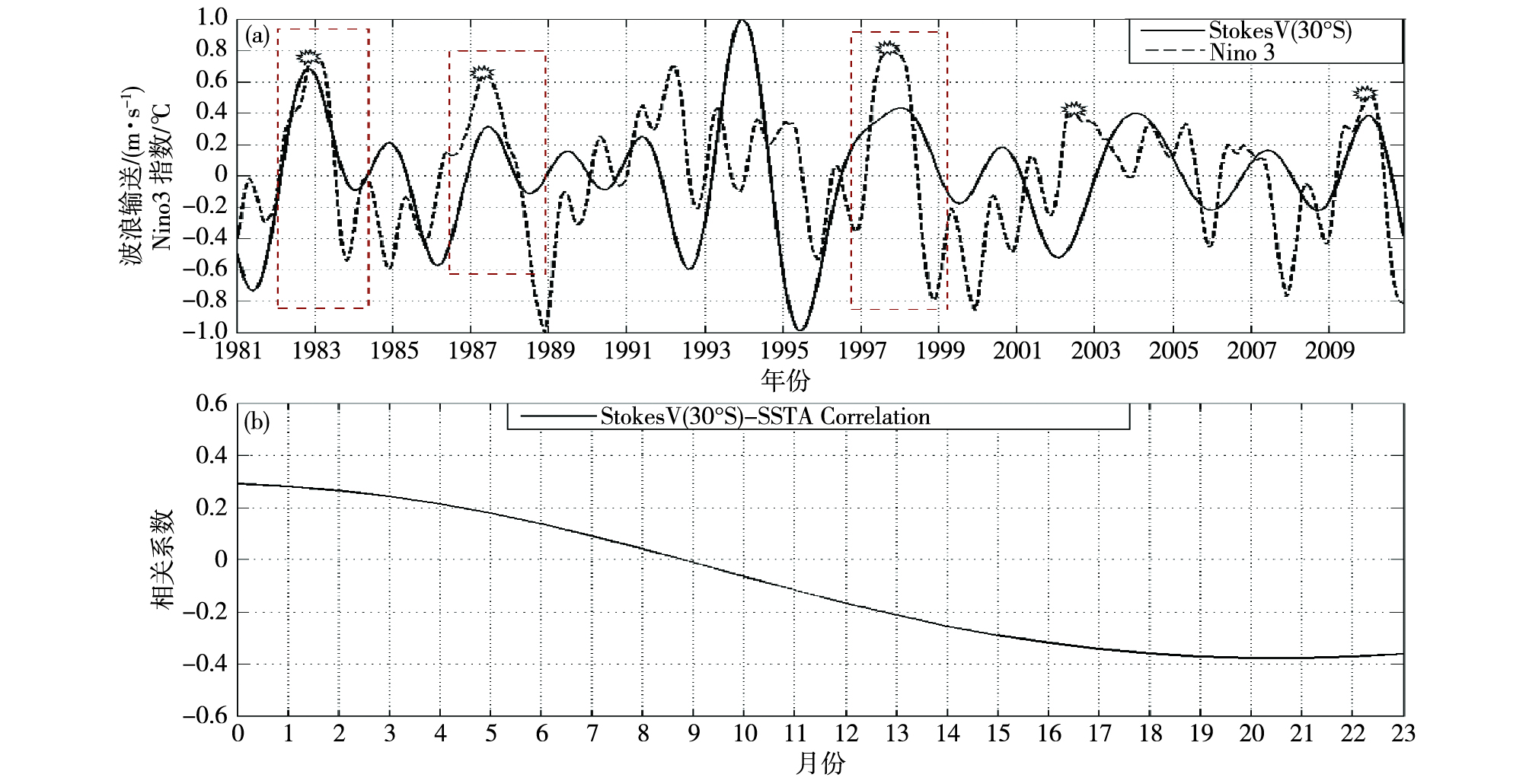
3.2 波浪对SST影响的定性计算

选取30°S断面, 计算南—北向波浪输运量, 图 6a给出了南—北向波浪输运的时间序列与Nino3指数的变化关系。由图可知, 1983、1987、1997及2009年赤道东太平洋SST正异常达到较大振幅(大于0.5 ℃), 即发生厄尔尼诺事件。SST正异常达到较大振幅之前, 北向的波浪输运都有明显的减小, 即波浪由绕极流海域携带到赤道海域的冷水减少。图 6b给出了波浪输运与Nino3指数的相关系数的时间序列, 在Nino3指数滞后一年半左右的时间时, 二者负相关系数最大, 约为-0.4^[22]。

虽然相关系数的大小可以更直观地看出波浪输运量与SST异常的相关关系, 但针对赤道东太平洋SST异常的特殊过程而言, 波浪输运的贡献可能大于-0.4的相关, 这一特点可以从二者时间序列上明显看出:在Nino3指数振幅较大的几个年份(厄尔尼诺年), 波浪输运量的振荡较剧烈, 且二者的变化特征相吻合, 而在一般的年份内, 二者没有明显的相关关系。

4 讨论

海表面波浪的存在对于上层海洋具有不可忽视的影响, 其影响不仅体现在海气界面上的小尺度过程, 同时, 海表面波浪因其诱导输运的存在, 对于上层海洋的大尺度过程也具有不可忽视的影响。特别是绕极流海域存在全球最大的波浪输运量以及南半球波浪输运的东向强化特征, 使其成为连接高纬度和低纬度动力过程之间的桥梁。本文的研究成果对于波浪在上层海洋中的作用提供了更全面的认识, 对于波浪的大尺度效应的研究具有非常重要的意义。

水体输运的变化是影响赤道东太平洋SST异常的原因之一。Alexander and Scott^[23]利用海-气耦合模式中的混合层方程中加入Ekman热量输运项, 并设置若干组对比实验验证其对ENSO事件发生的影响, 结果显示, 包含Ekman热量输运项的实验中, 赤道太平洋的温度异常区域放大了1/3。Brown and Fedorov^[24]估算了跨密输运对热带太平洋暖水团体积变化及对ENSO事件的影响, 其中总的水平输运包括地转流和Ekman输运, 研究发现1994—1995年弱的厄尔尼诺和1997—1998年强的厄尔尼诺年之间的暖水积累主要是由于南向水体输运的减小和东向水体输运的增加。但以往的研究工作中并未包含波浪诱导的水体输运部分, 由本文的分析可知, 沿赤道由西向东的波浪输运的暖水与大洋东岸北向的波浪输运的冷水与赤道东太平洋的SST异常存在密切的关系, 具体主要表现厄尔尼诺事件发生前, 冷水输运量减小, 并且考虑到波浪在大洋东岸独特的输运特征, 我们猜想波浪诱导的经向输运也是引起赤道东太平洋SST异常变化的重要部分。

基于本文的分析与讨论, 我们提出两点思考:在大洋西边界, 西边界流是联系高纬度和低纬度的重要通道; 在大洋东边界, 涌浪也是联系高纬度和低纬度的通道, 而波浪过程所起的作用及大小是怎样的?White等从ACC区的SST、SLP、MWS异常中发现了绕极波(ACW)。我们从ACC区风对Ekman层的能量输入和波浪对Ekman层的能量输入中也发现了ACW。ACW是连接三大洋的纽带, 对气候变化有非常重要的作用, 波浪是否会对气候变化有潜在的重要作用?为进一步深入研究以上几个问题, 未来工作中, 我们将利用海浪-海流-大气耦合模式, 考虑波浪的大尺度效应, 探究波浪在大气海洋动力过程中的重要作用。