2. 中国华阴兵器试验中心,陕西 华阴 714200;
3. 海军海洋水文气象中心,北京 100071
2. Huayin Weapon Test Center of China, Huayin 714200, China;
3. Navy Hydrometeorological Center, Beijing 100071, China
海面风场是海洋上层运动的主要动力来源,它与海洋中绝大多数的物理过程密切相关,是研究海洋动力环境的重要参数,在海洋灾害监测、海洋资源的开发利用等方面亦具有重要意义[1],海面风场的探测已成为当前海洋学研究中的一个热点。利用卫星遥感手段进行海洋观测的技术已经趋于成熟,尤其是海面风场的观测[2]。星载合成孔径雷达(synthetic aperture radar,SAR)具有全天时、全天候、高分辨率(数十米至数米)等特点,尤其适用于海岸带和岛屿区的观测,可以弥补散射计、微波辐射计等载荷在海面风场探测方面的不足[3-4]。相对于其他探测海面风场的卫星载荷,SAR具备反演获取高精度海面风场的特点,拥有广阔的应用前景[5]。与微波散射计不同,星载合成孔径雷达仅能单视角方向对海观测,因此海面风场反演需先获得风向再反演风速,其风向获取依赖于图像风条纹或外部风向,其中外部风向的时空分辨率不易与SAR风场匹配,而基于风条纹的风向反演方法精度高,但统计表明仅有44%左右的SAR图像包含风条纹信息[6-7];全极化SAR能够独立反演海面风场,但对交叉极化弱信号的绝对辐射定标要求较高,在具体工程实现方面存在较大困难[8],限制了SAR海面风场反演的业务化应用。
许多研究证明多源数据的融合有利于提高气象、海洋等产品的探测精度,探索将SAR探测资料反演的海面风场数据与其他风场资料进行融合,有望提高风速和风向精度[9]。目前,已有学者对微波散射计、微波辐射计和微波高度计海面风场资料进行了融合研究,但针对SAR数据与其他风场资料融合的相关研究较少。Anctil et al.[10]对高度计风速与大西洋船测风场进行了资料融合,Chin et al.[11]采用结合多分辨率分析的插值方法将ERS-1卫星散射计风场数据与欧洲中期天气预报中心模式风场数据进行融合,Atlas et al.[12]通过变分方法融合辐射计资料SSM/I海面风速、常规观测和欧洲中期天气预报中心分析值,生成了变分分析风场,美国国家大气研究中心(NCAR)数据支持部门(DSS)开发了QuikSCAT散射计观测值和NCEP再分析资料的融合产品QSCAT-NCEP混合风场资料[13],但针对SAR数据与其他风场资料融合的相关研究较少。
本文开展基于星载SAR数据与模式资料的海面风场变分融合方法研究,利用小波分析的时-频局部化特性,反演出风条纹区域高精度的风向和风速,并通过变分方法与数值预报模式风场进行融合,获得分析风场。分别仿真研究模式风场存在误差和SAR后向散射截面存在误差两种情况下的结果,对比融合得到的分析风场与理想风场的误差,结果表明两种情况下均是变分融合的结果更接近于理想风场,尤其在风条纹区域更为明显;选取ENVISAT/ASAR数据与欧洲中期天气预报中心模式风场资料进行海面风场的变分融合试验,结果表明融合后的海面风场结果较模式风场更加接近浮标观测结果。仿真分析与试验结果均表明,文章提出的基于星载SAR数据与模式资料的海面风场变分融合方法能够有效提高海面模式风场的精度。
1 变分融合方法 1.1 基于小波的SAR海面风场反演方法小波分析因其出色的时-频局部化特性被誉为信号处理中的“数学显微镜”[14]。通过理论分析和实际的反演试验,Mexican-hat小波在SAR海面风场反演方面取得了较好的效果[15-16]。二维Mexican-hat小波具有较好的时域和频域局部化能力及信号能量集中特性,对于信噪比较高、风条纹清晰的SAR图像,该方法能够获取较高的海面风向反演精度[17]。在空间-频率域,二维Mexican-hat小波变换可表示为:
| $ \mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_{H}(\mathit{\boldsymbol{k}})=(\mathit{\boldsymbol{k}}\cdot \mathit{\boldsymbol{k}}){{\text{e}}^{\left( \frac{1}{2(\mathit{\boldsymbol{k}}\cdot \mathit{\boldsymbol{k}})} \right)}} $ | (1) |
式中: k表示二维空间-频率域的变量;·表示向量内积。
Mexican-hat小波法反演风向的过程是首先对SAR图像进行二维连续Mexican-hat小波变换,获取不同尺度下的小波能量谱图像,提取风条纹信息。然后对能量谱图像进行二维FFT变换,计算SAR图像中风条纹的波数谱。最后将二维波数谱峰值的连线做垂线,对其进行风向去模糊后得到海面风向[18]。针对Mexican-hat小波法反演风向存在的风向180°模糊问题,采用数值预报模式风向对其进行去除。文献[19]的研究表明,在二维连续小波分解尺度为8时,海面风向反演获取的效果较好。
Hersbach et al.[20]经大量试验建立了SAR后向散射截面与海面风场之间关系的CMOD地球物理模型:
| $ \begin{align} & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{\sigma }^{0}}(V,\theta ,\varphi )= \\ & {{B}_{0}}(V,\theta ){{\left( 1+{{B}_{1}}(V,\theta )\cos \varphi +{{B}_{2}}(V,\theta )\cos 2\varphi \right)}^{\alpha }} \\ \end{align} $ | (2) |
其中B0、B1、B2是风速V和入射角θ的函数,φ为风向,α为常数。将反演出的风向作为地球物理模型函数的相对风向输入,同时输入定标后的后向散射系数和入射角,通过迭代计算得到相应的海面风速,最终获得SAR反演海面风场信息。
1.2 变分融合本文采用变分方法对SAR风场与模式风场进行融合。首先,将SAR海面风场矢量(观测风场)与模式风场矢量(背景风场)分解为经向分量U和纬向分量V(即水平与垂直分量),分别利用Kriging插值法将分解的背景风场插值到SAR风场所在区域上得到SAR风速观测算子H[21],然后利用变分融合方法求解分析风场。
假定Vi为背景风场中第i个点的风速(i=1, 2, …, N),
| $ \begin{array}{*{35}{l}} \overline{\mathit{\boldsymbol{Y}}}={{\left( {{{\bar{V}}}_{1}}, {{{\bar{V}}}_{2}}, \cdots , {{{\bar{V}}}_{k}} \right)}^{\text{T}}} \\ \overline{\mathit{\boldsymbol{X}}}={{\left( {{V}_{1}}, {{V}_{2}}, \cdots , {{V}_{N}} \right)}^{\text{T}}} \\ \end{array} $ |
则:
| $ \overline{\mathit{\boldsymbol{Y}}}=\mathit{\boldsymbol{HX}} $ |
观测算子H可表示为:
| $ \mathit{\boldsymbol{H}}={{\left( h_{i}^{k} \right)}_{K\times N}} $ |
贡献权重hik由以下Kriging方程组得到:
| $ \begin{align} & \left( \begin{matrix} h_{1}^{k} \\ \vdots \\ h_{n}^{k} \\ \mu \\ \end{matrix} \right)={{\left( \begin{matrix} c\left( {{x}_{1}},{{x}_{1}} \right) & \cdots & c\left( {{x}_{1}},{{x}_{1}} \right) & 1 \\ \vdots & \ddots & \vdots & 1 \\ c\left( {{x}_{1}},{{x}_{1}} \right) & \cdots & c\left( {{x}_{1}},{{x}_{1}} \right) & 1 \\ 1 & \cdots & 1 & 0 \\ \end{matrix} \right)}^{-1}}\times \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left( \begin{matrix} c\left( {{x}_{1}},{{x}^{k}} \right) \\ \vdots \\ c\left( {{x}_{n}},{{x}^{k}} \right) \\ 1 \\ \end{matrix} \right) \\ \end{align}$ |
这里μ为极小化处理时的拉格朗日乘子,c(xi, xj)为背景风场中网格点xi与xj之间的协方差函数,xk为观测风场区域上的插值点。本文采用指数型插值函数:
| $ c(L)=\left\{ \begin{array}{*{35}{l}} 0(L=0) \\ {{C}_{0}}+{{C}_{1}}\left( 1-\exp \left( \frac{-3L}{\text{a}} \right) \right)(L>0) \\ \end{array} \right. $ |
其中,L为插值点与观测点之间的距离,C0、C1、a均为常数。
观测风场与背景风场采用二维变分(2D-Var)的方法进行融合计算,其在数学上可以描述为使如下定义的目标函数最小:
| $ J=J_{q}+J_{m} $ | (3) |
其中,观测风场的目标函数Jq和背景风场的目标函数Jm定义如下:
| $ \begin{align} & {{J}_{q}}=\frac{1}{2}{{\left( \mathit{\boldsymbol{HU}}-{{\mathit{\boldsymbol{U}}}_{q}} \right)}^{\text{T}}}\mathit{\boldsymbol{Q}}_{u}^{-1}\left( \mathit{\boldsymbol{HU}}-{{\mathit{\boldsymbol{U}}}_{q}} \right)+ \\ & \ \ \ \ \ \ \ \frac{1}{2}{{\left( \mathit{\boldsymbol{HV}}-{{\mathit{\boldsymbol{V}}}_{q}} \right)}^{\text{T}}}\mathit{\boldsymbol{Q}}_{v}^{-1}\left( \mathit{\boldsymbol{HV}}-{{\mathit{\boldsymbol{V}}}_{q}} \right) \\ \end{align} $ | (4) |
| $ \begin{align} & {{J}_{m}}=\frac{1}{2}{{\left( \mathit{\boldsymbol{U}}-{{\mathit{\boldsymbol{U}}}_{m}} \right)}^{\text{T}}}\mathit{\boldsymbol{M}}_{u}^{-1}\left( \mathit{\boldsymbol{U}}-{{\mathit{\boldsymbol{U}}}_{m}} \right)+ \\ & \ \ \ \ \ \ \ \frac{1}{2}{{\left( \mathit{\boldsymbol{V}}-{{\mathit{\boldsymbol{V}}}_{m}} \right)}^{\text{T}}}\mathit{\boldsymbol{M}}_{v}^{-1}\left( \mathit{\boldsymbol{V}}-{{\mathit{\boldsymbol{V}}}_{m}} \right) \\ \end{align} $ | (5) |
其中,U和V分别是融合得到的经向风速和纬向风速(即分析风速),q和m代表观测风场和背景风场,Q和M分别是观测风场和背景风场的误差协方差矩阵。将(4)和(5)式带入(3)式可得:
| $ \mathit{\boldsymbol{U}}={{\left[ \mathit{\boldsymbol{H}}_{q}^{\text{T}}\mathit{\boldsymbol{Q}}_{u}^{-1}{{\mathit{\boldsymbol{H}}}_{q}}+\mathit{\boldsymbol{M}}_{u}^{-1} \right]}^{-1}}\left[ \mathit{\boldsymbol{H}}_{q}^{T}\mathit{\boldsymbol{Q}}_{u}^{-1}{{\mathit{\boldsymbol{U}}}_{q}}+\mathit{\boldsymbol{M}}_{u}^{-1}{{\mathit{\boldsymbol{U}}}_{m}} \right] $ | (6) |
| $ \mathit{\boldsymbol{V}}={{\left[ \mathit{\boldsymbol{H}}_{q}^{T}\mathit{\boldsymbol{Q}}_{v}^{-1}{{\mathit{\boldsymbol{H}}}_{q}}+\mathit{\boldsymbol{M}}_{v}^{-1} \right]}^{-1}}\left[ \mathit{\boldsymbol{H}}_{q}^{T}\mathit{\boldsymbol{Q}}_{v}^{-1}{{\mathit{\boldsymbol{V}}}_{q}}+\mathit{\boldsymbol{M}}_{v}^{-1}{{\mathit{\boldsymbol{V}}}_{m}} \right] $ | (7) |
利用最优化算法求解(6)和(7)式便可得出融合后的分析风速。
1.3 海面风场变分融合流程本文提出的基于星载SAR数据与模式资料的海面风场变分融合方法,首先在SAR影像线性纹理特征明显的区域(风条纹区域)采用二维连续小波变换提取风条纹信息,但是存在180°的风向模糊问题,对此可以利用模式资料的风向对其进行风向去模糊得到SAR海面风向[22]。然后将反演出的风向作为相对风向输入地球物理模型函数进一步求解SAR海面风速,并将风速分解为经向分量和纬向分量。利用Kriging插值法将分解的背景风场插值到SAR风场所在区域上得到SAR风速观测算子,构建SAR风速与背景风速融合的代价泛函,最后通过变分方法求解分析风速得出融合结果。具体反演流程如图 1所示。

|
图 1 海面风场的变分融合流程图 Fig.1 Flow chart of variational fusion of sea surface wind field |
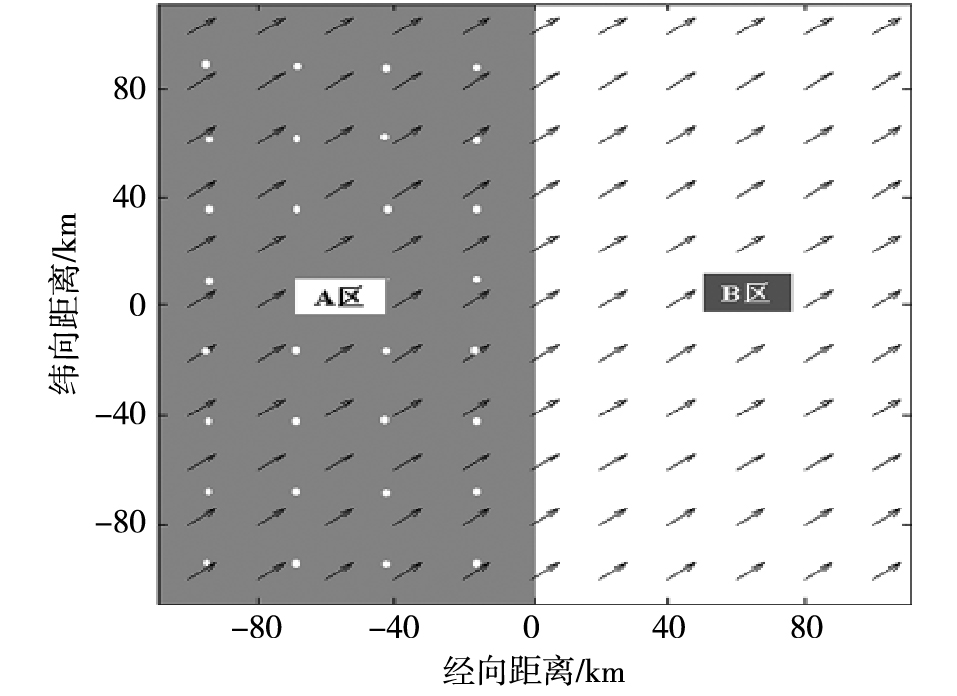
为深入地分析融合效果,考查误差对融合结果的影响,引入随机扰动,分别针对模式风场存在误差、SAR风场无误差和SAR后向散射截面存在误差、模式风场无误差两种情况,对变分融合结果进行敏感性分析,将变分融合后的分析风场与理想风场进行比对,验证变分方法融合SAR风场和模式风场的有效性。仿真模拟的SAR风场区域及理想风场探测点位置如图 2所示,图中黑色箭头代表理想风场,白点代表SAR风场坐标位置,理想风场经向分量ui=8 m·s-1、纬向分量vi=6 m·s-1,分辨率为20 km。左侧灰色区域为A区,表示SAR风场覆盖区域。利用Kriging插值方法将理想风场插值到A区上构造理想SAR风场,分辨率为30 km。灰色区域右侧的区域为B区(参考区域),将参考区上的融合结果与A区的融合结果进行比对,以考察SAR风场覆盖区域和非SAR风场覆盖区域的融合效果,这主要是考虑到并非SAR图像上都存在风条纹,在实际应用中SAR图像中仅部分区域包含风条纹。整体风场的经向距离取值范围为[-100 km,100 km],纬向距离取值范围为[-100 km,100 km]。
|
图 2 模拟的背景风速探测点位置和SAR风场反演区域 Fig.2 Location of detection point of simulated background wind speed and retrieval area of SAR wind field |
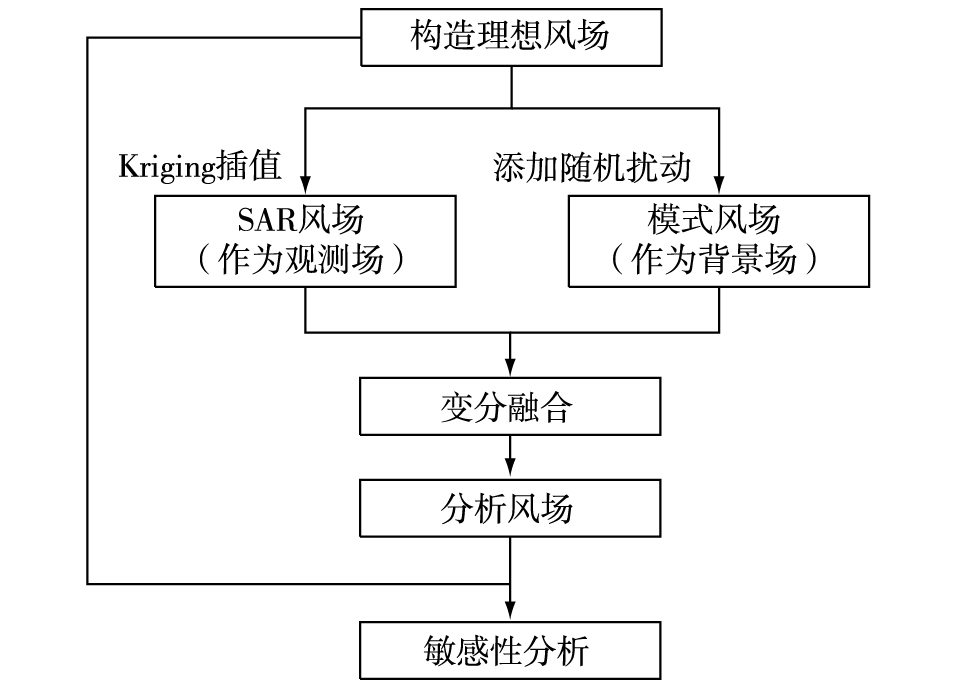
当理想风场的风速为10 m·s-1左右时,背景风场的风速均方根误差一般不超过1 m·s-1。由于选取的理想风场的风速均为中等风速(10 m·s-1),所以对该理想风场添加ε=1 m·s-1的随机误差(记ε为最大扰动振幅),进而得到扰动风场。将扰动风场作为背景场,然后引入模拟的SAR风场,经过变分融合得到分析风场,具体研究流程如图 3所示。
|
图 3 背景风场存在误差时的研究流程图 Fig.3 Research flow chart of background wind field with error |
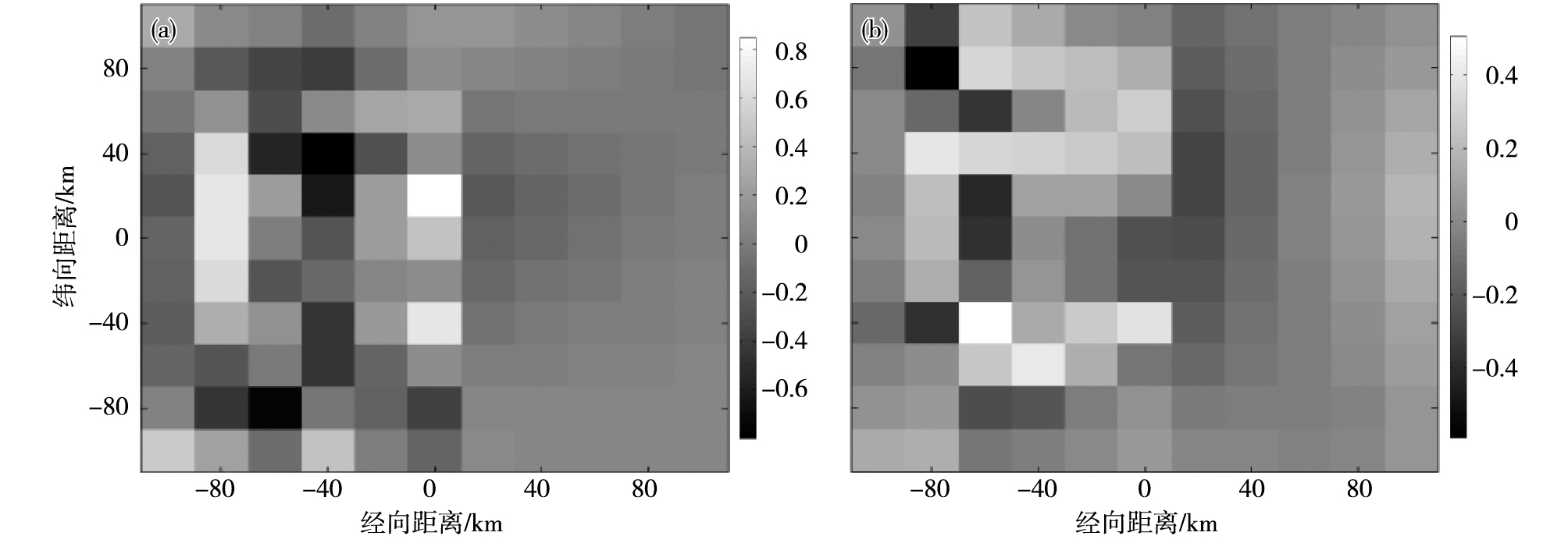
利用Kriging插值计算得到的理想SAR风速为10 m·s-1,背景风速最小为9.15 m·s-1,最大为10.94 m·s-1。通过比对融合后的分析风场与模式风场的差值(图 4)可知,SAR风场覆盖的A区域融合后分析风场的变化较为明显,而融合后B区域的分析风场相较于背景模式风场变化不大。经计算得出的A区域的分析风速在9.63~10.57 m·s-1之间振荡,扰动明显得到了抑制,即采用变分方法融合SAR风场与模式风场是有效的。
|
图 4 融合后的分析风场与模式风场的误差(a.经向分量U,b.纬向分量V) Fig.4 Error of analysis wind field and model wind field after fusion(a.meridional component U, b.zonal component V) |
为考察本文方法在不同扰动强度、不同区域内的融合效果,采用文献[23]的方法,针对融合结果对整体以及A区和B区的风场进行敏感性试验分析。取ε=0.5、1.0、2.0 m·s-1,分别将背景以及分析风场和理想风场进行对比,计算得到各自对应的均方根误差,结果如表 1-3所示,其中ebu为背景风场在经向分量上的均方根误差,ebv为背景风场在纬向分量上的均方根误差,eau为分析风场在经向分量上的均方根误差,eav为分析风场在纬向分量上的均方根误差。综合分析表 1-3可知,随着ε的减小,分析风场的均方根误差随之减小。当ε=0.5、1.0、2.0 m·s-1时,分析风场在经向分量和纬向分量方向上的均方根误差均比背景风场在经向分量和纬向分量方向上的均方根误差小,说明基于星载SAR数据与模式资料的变分融合方法对模式数据有积极效应。由于B区背景风场距离SAR风场区域较远,不能使SAR风速对背景风场产生有效影响,因此,对于均方根误差,背景和分析风场的结果几乎相同,结果如表 3所示;A区中SAR风场覆盖的背景风场受到较大的影响,从均方根误差来看,分析风场均明显小于背景风场(表 2),融合效果明显,这些与图 4所得结果一致。统计表明:在A区,利用SAR风场与背景风场进行变分融合后,背景风场的均方根误差能够降低17%左右。整体风场在经向和纬向分量上的均方根误差介于A区与B区风场在经向和纬向分量上的均方根误差之间。由此可知,采用本文的方法进行风场融合是有效的。
|
|
表 1 不同振幅扰动下整体区域背景风场和分析风场相对理想风场的均方根误差 Table 1 Root mean square error of overall regional background wind field and analysis wind field compared to ideal wind field under different amplitude disturbances |
|
|
表 2 不同振幅扰动下A区背景风场和分析风场相对理想风场的均方根误差 Table 2 Root mean square error of background wind field in area A and analysis wind field compared to ideal wind field under different amplitude disturbances |
|
|
表 3 不同振幅扰动下B区背景风场和分析风场相对理想风场的均方根误差 Table 3 Root mean square error of background wind field in area B and analysis wind field compared to ideal wind field under different amplitude disturbances |
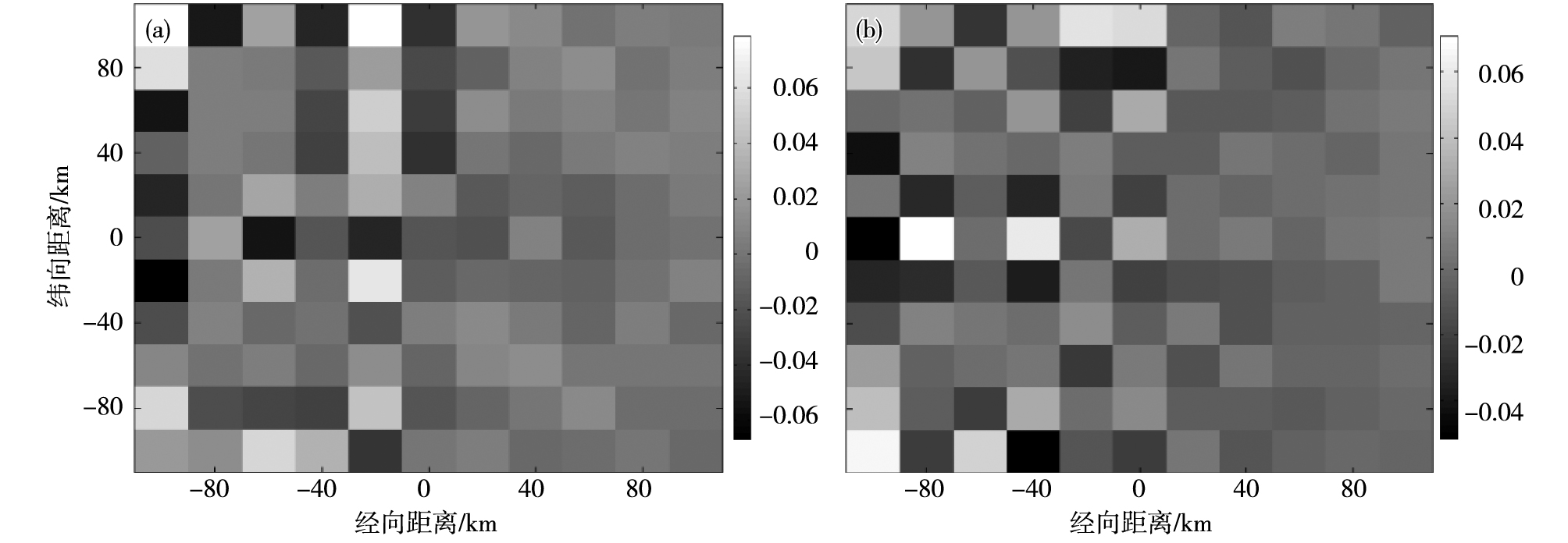
下面针对SAR后向散射截面存在误差的情况,对变分融合结果进行敏感性分析,具体研究流程如图 5所示。对理想的SAR后向散射截面σi添加随机扰动得到加扰动的SAR后向散射截面σ0。Freeman初步给出了SAR反演海面风场、海浪等海洋环境要素时的辐射定标精度,认为SAR探测风速的误差小于20%时,其绝对定标精度、相对定标精度均为1 dB[24]。当风速为10 m·s-1时,假定入射角为30°,相对风向为90°,代入地球物理模型求得σi=-11.8 dB,对σi添加最大为1 dB的扰动,反演的SAR风速与背景风速之差最大值可达2.3 m·s-1,统计得到SAR风速的均方根误差为1.06 m·s-1。假设对背景风场不作扰动,即(ub, vb = ui, vi),在这种情况下利用变分方法进行风场融合后,通过比对分析风场与理想风场的误差(图 6)可知,分析风场由于计入SAR后向散射截面随机扰动而有小幅度扰动,但不明显,其原因是在变分方法中分析风场中的信息只有15%左右来自观测场的贡献,其余85%左右来自背景场的贡献[25]。SAR后向散射截面受扰动后,针对整体风场以及A区风场和B区风场,计算各个风场经向分量和纬向分量相对于理想风场经向分量和纬向分量的均方根误差,所得结果如表 4所示。由表 4可知,当SAR后向散射截面存在误差时,覆盖区域的均方根误差稍大一些,远离覆盖区域的均方根误差稍小一些,整体的风速误差仅在厘米每秒级。

|
图 5 SAR后向散射截面存在误差时的研究流程图 Fig.5 Research flow chart of SAR backward scattering cross section with error |
|
图 6 融合后的分析风场与理想风场的误差(a.经向分量U,b.纬向分量V) Fig.6 Error of analysis wind field and ideal wind field after fusion(a.meridional component U, b.zonal component V) |
|
|
表 4 σi受扰动下背景风场和分析风场相对理想风场的均方根误差 Table 4 Root mean square error of background wind field and analysis wind field compared to ideal wind field under σi disturbed |
本文采用的SAR数据是两轨ENVISAT/ASAR的宽幅成像模式垂直极化数据;采用的背景风场数据是与SAR数据时空匹配的欧洲中期天气预报中心再分析资料;浮标数据为NDBC(National Data Buoy Center)数据,其观测高度为海表面5 m,通过风场剖面能量法则将浮标风速转化为海表面10 m等效风速。
3.2 结果分析首先在SAR影像纹理特征明显区域采用二维小波法反演海面风向,利用CMOD_IFR2模型求解海面风速并分解为经向分量和纬向分量。以图 8中第一轨SAR图像浮白框区域SAR子图像(图 7a)为例,说明基于Mexican-hat小波变换的海面风场反演过程,先对SAR图像进行二维连续小波变换获得小波能量谱,再对其进行二维FFT变换计算风条纹的波数谱,波数谱峰值连线(实线)的垂线(虚线)就是所求风向(图 7b)。但图 7b中所得风向存在180°模糊,将模式风向作为比对去模糊风向。根据模式风向判断,2011年5月24日08时左右探测区域为东南风,去除西北向的模糊风向,可得风向的反演结果为101.1°,结合地球物理模型函数求解出海面风速为12.2 m·s-1。

|
图 7 小波法反演的SAR子图像(a)和风向(b) Fig.7 SAR sub image(a) and wind direction(b) inversed by the wavelet method |

|
图 8 SAR反演风场和数值预报模式风场 Fig.8 Wind field retrieval results of SAR and wind field of numerical forecasting model |
图 8为第一轨SAR数据反演风场和2011年5月24日06时欧洲中期天气预报中心再分析风场资料的探测点位置及浮标位置图。图中箭头方向代表风向,箭头长度代表风速。SAR资料探测时间为2011年5月24日07:52。白色箭头代表SAR风场,经纬网格点分辨率为0.3°×0.3°;黑色箭头代表模式风场,经纬网格点分辨率为0.25°×0.25°;白点代表浮标位置,浮标号为46078,观测时间为07:50。计算风条纹区域SAR反演风向和风速并分解为经向分量和纬向分量,以此作为观测风场,并以模式风场作为背景场,经过变分融合得到分析风场,如图 9所示,图中箭头方向表示风向,箭头长度表示风速,图中左上角为风速标尺,标尺长度代表风速为10 m·s-1。

|
图 9 变分融合后的分析风场 Fig.9 Analysis wind field after variational fusion |
图 10中SAR数据探测时间为2011年8月23日20:55,与之时空匹配的2011年8月23日18时欧洲中期天气预报中心再分析风场资料的探测点位置及浮标位置如图所示,浮标号为46075,观测时间为20:50。图 11为经过变分融合得到的分析风场。

|
图 10 SAR反演风场和数值预报模式风场 Fig.10 Wind field retrieval results of SAR and wind field of numerical forecasting model |

|
图 11 变分融合后的分析风场 Fig.11 Analysis wind field after variational fusion |
由图 11可知,变分融合后的分析风场与模式风场的趋势基本保持一致,将浮标点附近的SAR反演风速、分析风速和模式风速同浮标探测值进行比对分析,结果如表 5所示。
|
|
表 5 浮标点附近的SAR反演风速、分析风速和模式风速 Table 5 SAR retrieval wind speed, analysis wind speed and model wind speed near the buoy |
由表 5可以看出,SAR反演风速与浮标风速最为接近,模式风速与之相比误差较大。这一方面是由于基于小波的SAR反演风场具有精度高、误差小的特点,另一方面SAR图像探测时间与浮标探测时间几乎相同,而模式风场的探测时间与浮标观测时间相差较多,其中浮标2处的模式风速与浮标观测值相比误差很大,这可能与模式风速探测时间同浮标观测时间相差近3 h有关。通过变分融合得到的分析风速较模式风速更加靠近浮标风速,其中浮标1处的分析风速与浮标观测值十分接近,浮标2处的分析风速相较于模式风速也得到改善,证明本文提出的风场融合方法有效。
4 小结本文提出的基于星载SAR数据与模式资料的海面风场变分融合方法,主要是利用SAR反演海面风场精度高、区域广的特点,通过小波变换法提取较高精度的风条纹风向,结合地球物理模型函数反演风速并分解为经向分量和纬向分量,以数值预报模式资料作为背景风场,构建变分融合的代价泛函,最后利用变分方法求解分析风场,实现合成孔径雷达数据反演海面风场与数值预报模式风场资料的融合,以期提高区域性海面模式风场的整体精度。仿真研究表明,在背景模式风场存在误差、SAR反演风场无误差的情况下,SAR风场对背景风场的调整有积极作用,能够使背景风场的均方根误差降低17%左右,远离SAR风场覆盖区域效果次之。在SAR后向散射截面存在扰动、背景模式风场无误差的情况下,融合后的分析风场受扰动的幅度较小,说明在一定的辐射定标精度内SAR后向散射截面误差对风场融合结果的影响相对较小,利用本文方法融合的风场具有较强的抗噪性。但该方法需要SAR图像中存在一定区域的风条纹信息,以便提取较高精度的风条纹风向及风速信息与背景风场进行融合,进而提升海面风场融合的整体精度。
| [1] |
Shimada T, Sawada M, Sha W, et al. Low-level easterly winds blowing through the Tsugaru Strait, Japan. Part Ⅰ: Case study and statistical characteristics based on observations[J]. Mon Wea Rev, 2010, 138(10): 3806-3821. DOI:10.1175/2010MWR3354.1 |
| [2] |
Sheng Z. The estimation of lower refractivity uncertainty from radar sea clutter using the Bayesian-MCMC method[J]. Chin Phys B, 2013, 22(2): 580-585. |
| [3] |
Liang Z. New GMF+RAIN model based on rain rate and application in typhoon wind retrieval[J]. Acta Phys Sinica, 2010, 59(10): 7478-7490. |
| [4] |
Martin S. An introduction to ocean remote sensing[M]. Cambridge: Cambridge University Press, 2014: 401-435.
|
| [5] |
Portabella M, Stoffelen A, Johannessen J A. Toward an optimal inversion method for synthetic aperture radar wind retrieval[J]. J Geophys Res, 2002, 107(C8): 1-13. |
| [6] |
Apel J R. An improved model of the ocean surface wave vector spectrum and its effects on radar backscatter[J]. J Geophys Res, 1994, 99(C8): 16269-16291. DOI:10.1029/94JC00846 |
| [7] |
Attema E P W, Duchossois G, Kohlhammer G. ERS-1/2 SAR land applications: Overview and main results[C]// Geoscience and remote sensing symposium proceedings, 1998. IGARSS'98. 1998 IEEE International. 1998: 1796-1798.
|
| [8] |
Zhang B, Perrie W, Vachon P W, et al. Ocean vector winds retrieval from C-Band fully polarimetric SAR measurements[J]. IEEE Trans Geosci Remote Sens, 2012, 50(11): 4252-4261. DOI:10.1109/TGRS.2012.2194157 |
| [9] |
Grody N C, Weng F. Microwave emission and scattering from deserts: Theory compared with satellite measurements[J]. IEEE Trans Geosci Remote Sens, 2008, 46(2): 361-375. DOI:10.1109/TGRS.2007.909920 |
| [10] |
Anctil F, Donelan M A, Forristall G Z, et al. Deep-water field evaluation of the NDBC-SWADE 3-m discus directional buoy[J]. J Atmos Oceanic Technol, 1993, 10(1): 97. DOI:10.1175/1520-0426(1993)010<0097:DWFEOT>2.0.CO;2 |
| [11] |
Chin T M, Milliff R F, Large W G. Basin-scale, high-wavenumber sea surface wind fields from a multiresolution analysis of scatterometer data[J]. J Atmos Oceanic Technol, 1998, 15(3): 741. DOI:10.1175/1520-0426(1998)015<0741:BSHWSS>2.0.CO;2 |
| [12] |
Atlas R, Hoffman R N, Ardizzone J, et al. A new cross-calibrated, multi-satellite ocean surface wind product[C]// Geoscience and Remote Sensing Symposium, 2008. IGARSS 2008. IEEE International. 2008: I-106-I-109.
|
| [13] |
Grody N C, Weng F. Microwave emission and scattering from deserts: Theory compared with satellite measurements[J]. IEEE Trans Geosci Remote Sens, 2008, 46(2): 361-375. DOI:10.1109/TGRS.2007.909920 |
| [14] |
张日伟, 严卫, 艾未华, 等. 基于Gabor小波变换的机载SAR海面风向反演方法[J]. 微波学报, 2011, 27(5): 79-83. |
| [15] |
孔毅, 赵现斌, 艾未华, 等. 基于墨西哥帽小波变换的机载SAR海面风场反演[J]. 解放军理工大学学报(自然科学版), 2011, 12(3): 301-306. |
| [16] |
Leite G C, Ushizima D M, Medeiros F N, et al. Wavelet analysis for wind fields estimation.[J]. Sensors, 2010, 10(6): 5994-6016. DOI:10.3390/s100605994 |
| [17] |
Ai W H. Ocean surface wind direction retrieval from multi-polarization airborne SAR based on wavelet[J]. Acta Phys Sinica, 2012, 61(14): 321-328. |
| [18] |
程玉鑫, 艾未华, 孔毅, 等. 基于影像纹理特征和外部风向的星载SAR海面风场反演研究[J]. 海洋科学, 2015, 39(12): 157-164. DOI:10.11759/hykx20141027002 |
| [19] |
艾未华, 孔毅, 赵现斌. 基于小波的多极化机载合成孔径雷达海面风向反演[J]. 物理学报, 2012, 61(14): 465-473. |
| [20] |
Hersbach H, Stoffelen A, Haan S D. An improved C-band scatterometer ocean geophysical model function: CMOD5[J]. J Geophys Res Oceans, 2007, 112(C3): 225-237. |
| [21] |
Jiang Z H. A new approach to adjusting sea surface wind using altimeter wind data by variational regularization method[J]. Acta Phys Sinica, 2010, 59(12): 8968-8977. |
| [22] |
张毅, 蒋兴伟, 林明森, 等. 合成孔径雷达海面风场反演研究进展[J]. 遥感技术与应用, 2010, 25(3): 423-429. |
| [23] |
姜祝辉, 黄思训, 杜华栋, 等. 利用变分结合正则化方法对高度计风速资料调整海面风场的研究[J]. 物理学报, 2010, 59(12): 8968-8977. DOI:10.7498/aps.59.8968 |
| [24] |
Freeman A. SAR calibration: An overview[J]. IEEE Trans Geosci Remote Sens, 1992, 30(6): 1107-1121. DOI:10.1109/36.193786 |
| [25] |
Comstock K K, Wood R, Yuter S E, et al. Reflectivity and rain rate in and below drizzling stratocumulus[J]. Quart J Roy Meteor Soc, 2004, 130(603): 2891-2918. DOI:10.1256/qj.03.187 |
 2017, Vol. 37
2017, Vol. 37


