风廓线雷达能够对大气垂直方向上的风场进行实时监测,连续获取测站上空高时空分辨率的垂直风廓线资料,可以有效补充探空数据的不足[1-3]。虽然风廓线雷达是为晴空设计的,但在降水时段,其观测的垂直速度值是垂直风速和降水粒子垂直下降速度的复合值,而且在很大程度上反映的是后者。高时空分辨率的观测资料能够很好地监测低空急流的出现[4],因此,可以利用垂直速度出现的高度、速度值、时空变化特征等辅助判断降雨的开始、结束时间及降雨的强度,甚至还可以利用降雨前后的垂直速度变化情况,设置不同高度层、不同季节的垂直速度阈值,用以辅助预报暴雨等灾害性天气的发生。王令等[5]在对北京风廓线雷达垂直速度应用的研究中发现,晴空、降水以及不同相态、不同强度的降水在发生时垂直速度有着明显不同的变化范围,晴空时垂直速度在-1.0~0.7 m·s-1之间,毛毛雨、小雨、暴雨和冰雹发生时垂直速度变化范围分别为0.8~2.0 m·s-1、2.1~4.0 m·s-1、4.1~8.0 m·s-1以及≥8.1 m·s-1。胡明宝等[6]认为晴天时风廓线雷达垂直速度在1.0 m·s-1以下,在低层连续数个高度层的垂直速度都大于4.0 m·s-1时,可以判定地面有降雨发生。古月和王令[7]针对北京延庆风廓线雷达资料的应用研究指出垂直速度小于1.0 m·s-1时基本无降水,在1.0~4.0 m·s-1之间时,降水量变化不大,大于4.0 m·s-1时,降水强度随垂直速度的增大呈波动增强的趋势。本文以济南为例,采用2014年风廓线雷达数据和地面降雨资料对垂直速度和地面降雨的关系进行了研究和探讨。
1 资料和研究方法 1.1 资料来源本文所用垂直速度来自济南(章丘)风廓线雷达站数据产品ROBS、OOBS文件,测站位于(117°33′E,36°41′N),海拔高度为121.8 m。雷达型号为CLC-11-D型固定式边界层风廓线雷达,主要技术指标为:时间分辨率≤6 min,最低探测高度≤100 m、最高探测高度≥3 km,高、低模式分辨率分别为60/120 m、30/60 m,垂直速度测量范围±20 m·s-1,风速测量精度≤1.5 m·s-1(RMS),径向速度分辨率≤0.2 m·s-1。垂直速度数据均经过一致性平均质量控制、时空连续性检验。
所采用的地面降雨量数据来自章丘国家基本气象站分钟降雨记录,观测场经纬度、海拔高度均与风廓线雷达一致。分钟降雨数据观测仪器2014年10月30日前为双翻斗遥测雨量传感器(SL3-1型,测量精度0.1 mm),之后为称重降水传感器(DSC1型,测量精度0.1 mm)。所使用的降雨分钟数据已通过自动质量控制和人工审核。
垂直速度有下沉速度和上升速度,定义下沉速度为正,上升速度为负。在进行降雨过程垂直速度时空分布分析时,采用自100~2 980 m各观测高度层的逐6 min垂直速度数据;在进行降雨量-垂直速度相关分析时,考虑数据质量、近地面层干扰和天气预报使用习惯,选取风廓线雷达距地面280 m、925 hPa(高度为700~900 m)、850 hPa(高度为1 400~1 600 m)和700 hPa(高度为2 900~3 100 m)[8-9]的垂直速度信息,时间分辨率为1 h和6 min,详见表 1。
|
|
表 1 资料(2014年)详细信息表 Table 1 Detailed information of data (2014) |
多项式分布是最常用的拟合曲线分布形式之一,属于一元高阶非线性分布,能够逼近任意连续可到母体[10]。根据高等数学理论,若连续函数f(x)在x=x0的某一邻域内具有直到(n+1)阶的导数,则函数f(x)在x=x0处可展开为n阶的Taylor级数形式[11]:
| $ \begin{align} & f(x)=f\left( {{x}_{0}} \right)+{{f}^{\prime }}\left( {{x}_{0}} \right)\left( x-{{x}_{0}} \right)+\frac{{{f}^{\prime \prime }}\left( {{x}_{0}} \right)}{2!}{{\left( x-{{x}_{0}} \right)}^{2}}+ \\ & \ldots +\frac{{{f}^{(n)}}\left( {{x}_{0}} \right)}{n!}{{\left( x-{{x}_{0}} \right)}^{n}}+\frac{{{f}^{(n+1)}}(\xi )}{(n+1)!}{{\left( x-{{x}_{0}} \right)}^{n+1}} \\ \end{align} $ | (1) |
其中ξ是x与x0之间的某个值。这说明任意连续的在x=x0邻域内具有(n+1)阶导数的函数均可以简化为多项式函数表达式形式:
| $ y=\beta_{0}+\beta_{1} x+\beta_{2} x^{2}+\cdots+\beta_{p} x^{p}+\varepsilon $ | (2) |
多项式拟合是对统计数据的普适拟合方法,适用于任意母体规律存在的样本数据回归分析过程[10-11]。
观测数据总的离差平方和可分解为回归平方和与残差平方和两部分,残差平方和表征着拟合值与估计值之间的偏离程度,若回归方程能够完全拟合观测数据,则残差平方和为零。因此,残差平方和在总离差中所占比重越小,说明拟合效果越好,回归方程越逼近母体分布函数[10]。采用R检验方法,又称拟合优度检验,对回归方程的显著性进行检验,R为复相关系数,R2称为方程的确定性系数:
| $ {{R}^{2}}=\frac{\sum\limits_{i=1}^{n}{{{\left( {{{\hat{y}}}_{i}}-\bar{y} \right)}^{2}}}}{\sum\limits_{i=1}^{n}{{{\left( {{y}_{i}}-\bar{y} \right)}^{2}}}}=1-\frac{\sum\limits_{i=1}^{n}{{{\left( {{y}_{i}}-{{{\hat{y}}}_{i}} \right)}^{2}}}}{\sum\limits_{i=1}^{n}{{{\left( {{{\hat{y}}}_{i}}-\bar{y} \right)}^{2}}}} $ | (3) |
式中:y为实际降水量;
| $ R_{\text{ajusted}}^{2}=1-\left(1-R^{2}\right) \times \frac{n-1}{n-p-1} $ | (4) |
式中:n表示样本个数;p表示自变量数目。
在确定拟合函数前,首先对观测数据散点分布图进行观察,并用不同数学函数形式进行拟合,对比确定性系数的大小,发现四次多项式拟合曲线更为符合实际数据分布特征,最终确定采用四次多项式拟合方法计算280 m、700 m、1 420 m、2 980 m高度层2014年小时垂直速度序列与小时降雨量序列的回归方程,方程各项回归系数及拟合优度参数采用Matlab数值计算分析软件中曲线拟合工具进行计算。
2 垂直速度与降雨量的统计关系分析 2.1 垂直速度-降雨量回归分析图 1a-d给出了2014年章丘站280 m、700 m、1 420 m、2 980 m高度层垂直速度与小时雨量散点及四次多项式拟合曲线图。由图中可以看出,在4个高度层小时垂直速度与降雨量都存在显著的正相关关系。表 2中列出了2014年四季及全年小时降雨量与垂直速度的四次多项式回归方程和方程拟合优度检验参数,方程回归系数均通过了95%的信度检验。
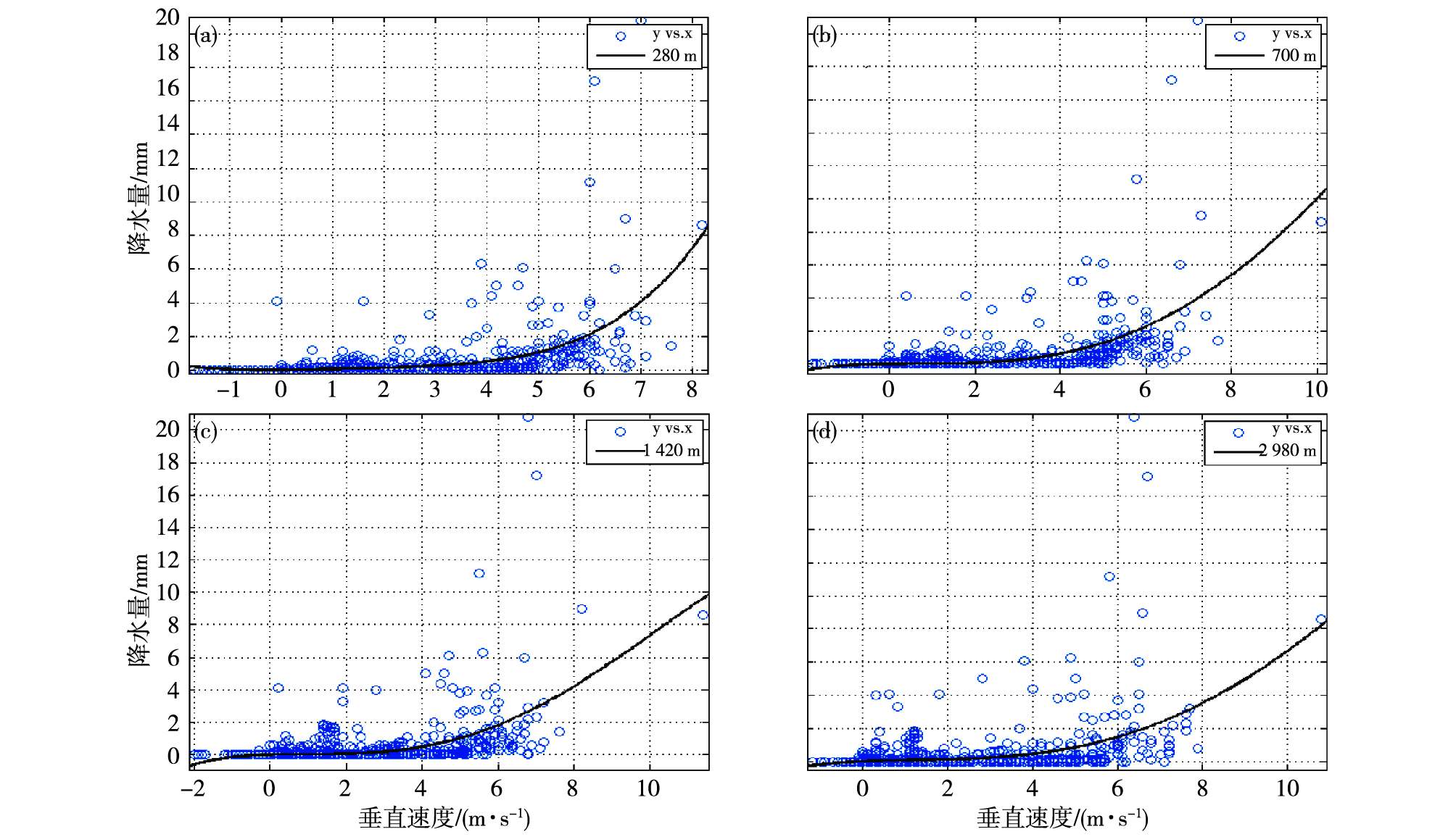
|
图 1 280 m (a)、700 m (b)、1 420 m (c)、2 980 m (d)小时垂直速度与降雨量多项式回归拟合图 Fig.1 Hourly vertical velocity and rainfall polynomial regression fitting chart at 280 m (a), 700 m (b), 1 420 m (c), and 2 980 m (d) |
|
|
表 2 2014年四季及全年小时降雨量与垂直速度多项式回归拟合结果 Table 2 Seasonal and annual rainfall and vertical velocity polynomial regression fitting results in 2014 |
由表 2中修正确定性系数值可知,从季节上来看,冬季小时降雨量与垂直速度回归方程拟合优度最高,280 m方程修正确定性系数达到0.611 5;其次是秋季和春季,综合分析各高度层结果,夏季方程拟合结果最差,修正确定性系数在0.242 8~0.376 8之间。从各高度层拟合结果分析,280 m方程修正确定性系数在0.265 9~0.611 5之间;700 m在0.365 5~0.589 9之间;1 420 m和2 980 m的方程修正确定性系数范围分别为0.304 7~0.494 1和0.238 9~0.487 4;总体来看风廓线雷达垂直速度能够反映雨滴的下落速度特征,700 m高度层垂直速度与小时雨量回归方程拟合优度较高。有研究成果[7]显示高层的垂直速度比低层的垂直速度更能反映降水特征,本文研究的结果与前述结论并不完全一致。
从小时雨强与垂直速度的关系上来看,当垂直速度小于1.0 m·s-1时,基本无降雨发生;垂直速度在1.0~4.0 m·s-1之间时,小时降雨强度基本在4 mm以下。当垂直速度大于4.0 m·s-1时,降雨强度随垂直速度的增大而增强趋势明显。从拟合曲线形状可见,风廓线雷达探测的垂直速度与降雨强度并非简单的线性关系,当垂直速度大于4.0 m·s-1的临界值时,降雨强度随垂直速度的增大而迅速增强,这与胡明宝等[6]、古月和王令[7]以及陈楠等[12]学者之前研究结果相一致。
2.2 降雨和无降雨时段小时垂直速度分布对降雨时段和无降雨时段的小时垂直速度数据绘制箱形图,进一步观察各高度层小时垂直速度的分布情况。如图 2所示,非降雨时段各个高度层的小时垂直速度分布特征较为一致,分布区间集中,5%~95%分位的数据基本在-0.5~1.0 m·s-1之间;25%~75%分位的数据700 m高度层分布最为集中,基本在0 m·s-1左右。降雨时段,280 m小时垂直速度分布最为集中,5%~95%分位的数据分布区间为0.8~6.7 m·s-1,25%~75%分位的数据基本分布在1.8~5.1 m·s-1之间;其他三个高度层5%~95%分位的数据分布特征较为接近,在0.2~6.8 m·s-1之间;700 m和2 980 m高度层25%分位数据较之1 420 m略低,在1.0 m·s-1左右。综合本研究中各个高度层的数据分布情况以及结合文献中学者的研究基础可以发现,可将1.0 m·s-1作为降雨发生的参考判定指标,1.0~4.0 m·s-1之间时,降雨量变化不大,当垂直速度大于4.0 m·s-1降雨强度明显增强。
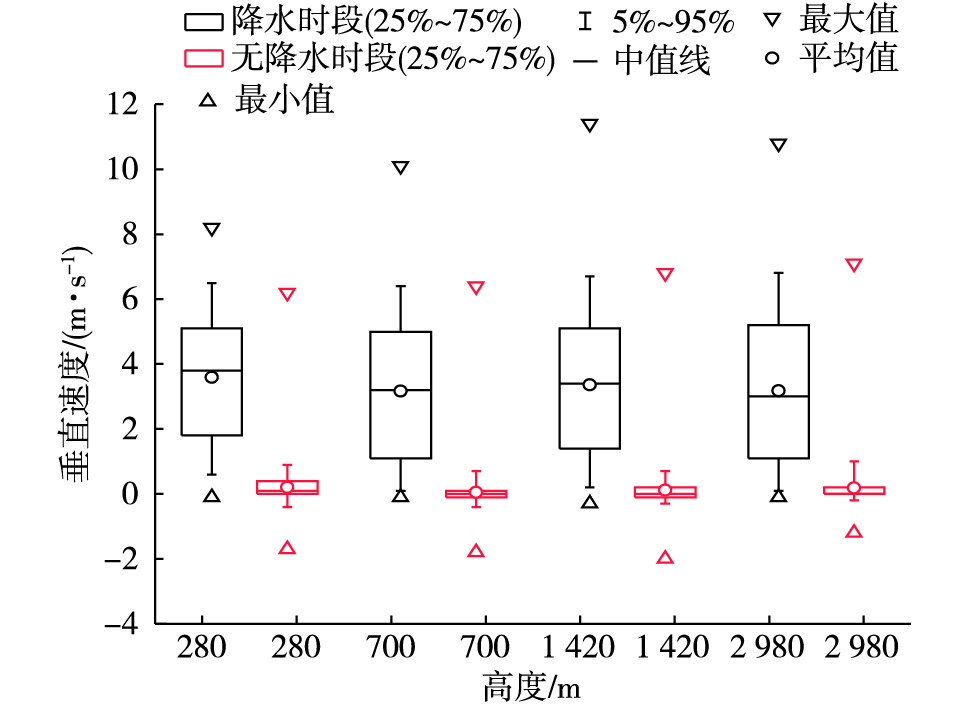
|
图 2 降雨和无降雨时段小时垂直速度(单位:m·s-1)分布 Fig.2 Vertical velocity (units:m·s-1) distribution during raining and non-raining period |
由于风廓线雷达小时垂直速度是该小时内各个6 min垂直速度的一致性平均值,故小时垂直速度变化与6 min垂直速度变化特征并不完全一致。时间分辨率更高的6 min数据更完善地记录了垂直速度的实际变化,从而使得降雨开始阶段的垂直速度由小到大的过程更加明晰。6 min数据相较小时数据而言在时间轴坐标上有明显的提前量,这使得6 min垂直速度变化特征在用于判断降雨起止时间时更有优势,可见高时间分辨率的风廓线雷达垂直速度数据对于降雨过程的短临预报更有指示意义。在强度方面,尽管降雨量是一定时间段内的累加值而垂直速度是瞬时值,二者之间并非简单的线性关系,但特定的垂直速度阈值对降雨强度的预报仍然具有参考价值。根据上节的分析,本文在进行个例分析时,将以垂直速度1.0 m·s-1作为场次降雨过程垂直速度指示降雨开始时刻的阈值。
利用四季个例场次降雨过程时段风廓线雷达各高度层探测数据绘制小时垂直速度随高度时间变化剖面图,用以初步判断各高度层垂直速度变化与降雨时段对应关系。正垂直速度表征了降水粒子的下落速度及降水粒子密度,接地的下沉气流速度越大降水越强,大速度的下沉气流维持时间越长降水越强[13]。对280 m、700 m、1 420 m、2 980 m共4个特征高度层,利用风廓线雷达逐6 min垂直速度数据及相同时间分辨率地面降雨量资料绘制四季个例场次降雨过程时段垂直速度与降雨量关系,对不同季节降雨过程垂直速度与降雨量对应规律进行细致分析。
3.1 春季降雨过程分析分析本次过程的背景可知,2014年4月25—26日,受切变线和地面倒槽共同影响,山东地区自西向东出现了一次大范围强降雨过程。从25日海平面气压场分析,除半岛东部以外的山东大部地区处在地面倒槽的控制之下,降雨明显时段为25日23时—26日09时,以稳定性降雨为主。由小时垂直速度随高度时间变化剖面图(图 3)可见,各高度层小时垂直速度指示的降雨时段与地面降雨记录时段一致性很高。结合分析6 min垂直速度与降雨量关系(图 4)可知,2 980 m高度垂直速度相对低层较小,分析原因春季降雨云层的主要高度可能低于该高度层,融化层附近冰晶粒子还没有完全融化,冰晶落入融化层后开始融化,密度变大,下降速度增大;而冰晶粒子经过融化层后完全融为水滴,致使下降速度增大到一定范围后趋于稳定[9, 14],该层垂直速度指示地面降雨略差,但可预先指示空中降雨。1 420 m高度垂直速度起伏变化最大,尤其在05—07时、09—12时,可能指示空中降雨而未达地面的情形,故该层对于指示空中和地面降雨均有一定意义;700 m和280 m高度垂直速度变化基本一致,仅在06时左右略有差别,以此两高度指示地面降雨相对稳定。
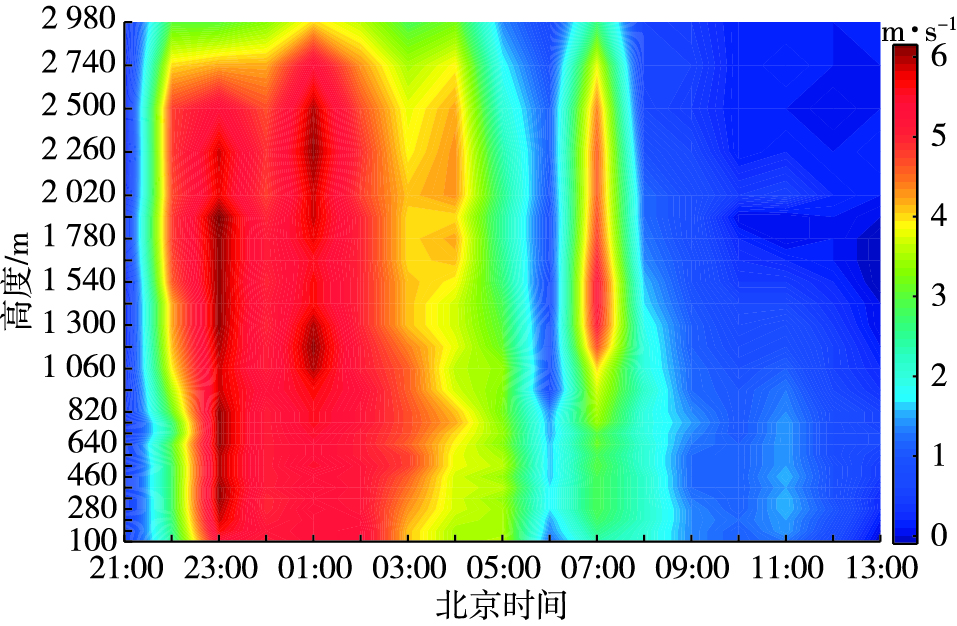
|
图 3 春季降雨过程小时垂直速度(单位:m·s-1)随高度时间变化剖面图 Fig.3 The height-time cross section of hourly vertical velocity (units:m·s-1) of a spring rainfall |

|
图 4 春季降雨过程6 min垂直速度与降雨量关系 Fig.4 Relationship of 6-min vertical velocity and precipitation variation during a spring rainfall |
在本例中,降雨开始前各高度层垂直速度迅速增大,若以垂直速度大于1.0 m·s-1作为阈值预报地面降雨,则随高度层的升高预报提前量有增大趋势,1 420 m和2 980 m高度层可提前1 h 48 min指示降雨开始(表 3)。在指示地面降雨过程结束方面,当垂直速度小于1.0 m·s-1时,降雨过程出现明显的中断,但无法判断是否结束。在中断期间前1 420 m和2 980 m垂直速度明显小于1.0 m·s-1,但较低的两个高度层依然大于阈值,若以280 m和700 m垂直速度小于1.0 m·s-1参考判定降雨结束,280 m高度层可提前1 h 18 min,700 m高度层可提前1 h 42 min。在反映整个过程降雨强度的波动方面700 m和1 420 m垂直速度对细部过程反映最为清晰,地面6 min降雨量大于0.2 mm的时段这两层的垂直速度均大于4.0 m·s-1,且较之地面观测降雨开始时间均有一定的提前量。
|
|
表 3 春季降雨过程垂直速度表征降雨起(≥1.0 m·s-1)止(<1.0 m·s-1)时间及地面记录 Table 3 Precipitation start (≥1.0 m·s-1) and end (< 1.0 m·s-1) time of a spring rainfall indicated by vertical velocity and ground record |
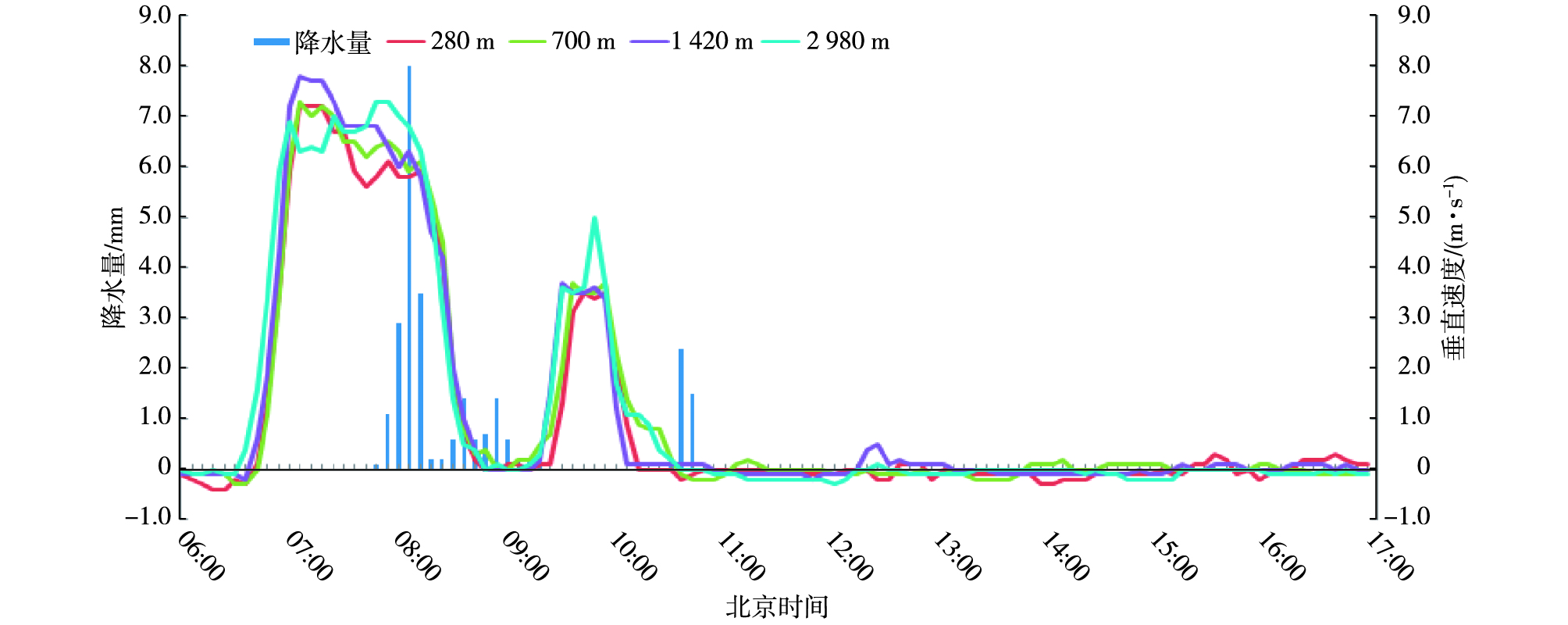
2014年8月5日,受切变线影响,山东大部地区出现降雨。5日08时,低层切变线压在山东与河北的交界处,降雨主要集中在5日08—11时,基本以稳定性降雨为主。具体分析济南个例降雨过程发现,此次过程降雨开始于8月5日07时48分,最后降雨记录出现在16时48分,降雨量为0.1 mm,然而10时48分至16时42分均无降雨,故分析时将过程结束时间截止到10时42分。
过程中出现大于1 h的降雨间隔,故在表 4、表 5中对两段降雨开始结束时间进行分别统计。由小时垂直速度随高度时间变化剖面图(图 5)可见,本例中各高度层垂直速度值变化规律一致性较好,夏季降雨云层的主要高度可能远高于2 980 m高度层,可预先指示空中降雨,但应进一步研究提高指示高度。结合分析6 min垂直速度与降雨量关系(图 6)可知,降雨开始前各高度层垂直速度迅速增大,若以垂直速度大于1.0 m·s-1作为阈值指示地面降雨,各高度层可提前1 h左右指示降雨开始。若以垂直速度小于1.0 m·s-1参考判定地面降雨结束时间,则各高度层对降雨中断的预判可提前42 min(表 4),对最终降雨结束的预判提前量在30 min左右。在反映整个过程降雨强度的波动方面,各高度层对细部过程反映较为一致。在第一段降雨过程中地面6 min降雨量大于0.2 mm的时段各层的垂直速度均大于4.0 m·s-1且有与指示降雨开始相近似的提前量,在第二段持续时间为12 min,强度在0.2~2.4 mm/(6 min)的降雨过程中,280 m、700 m和1 420 m高度层垂直速度范围在1.3~3.7 m·s-1之间,2 980 m高度层垂直速度最大达到5 m·s-1(表 5)。
|
|
表 4 夏季降雨过程垂直速度表征降雨起(≥ 1.0 m·s-1)止(<1.0 m·s-1)时间及地面记录(过程1) Table 4 Precipitation start (≥ 1.0 m·s-1) and end (< 1.0 m·s-1) time of a summer rainfall indicated by vertical velocity and ground record (Process 1) |
|
|
表 5 夏季降雨过程垂直速度表征降雨起(≥1.0 m·s-1)止(<1.0 m·s-1)时间及地面记录(过程2) Table 5 Precipitation start (≥ 1.0 m·s-1) and end (< 1.0 m·s-1) time of a summer rainfall indicated by vertical velocity and ground record (Process 2) |
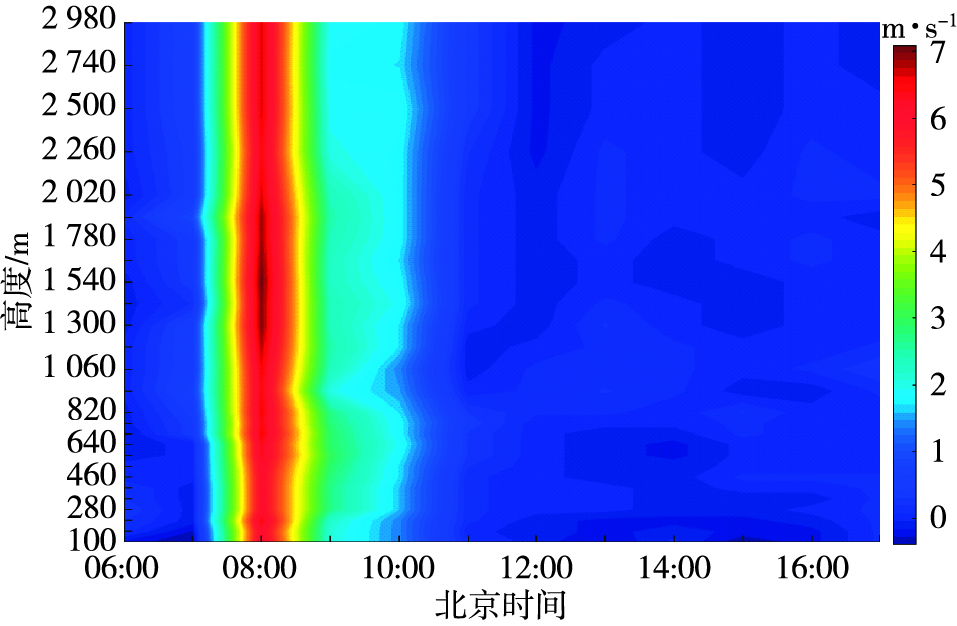
|
图 5 夏季降雨过程小时垂直速度(单位:m·s-1)随高度时间变化剖面图 Fig.5 The height-time cross section of hourly vertical velocity (units:m·s-1) of a summer rainfall |
|
图 6 夏季降雨过程6 min垂直速度与降雨量关系 Fig.6 Relationship of 6-min vertical velocity and precipitation variation during a summer rainfall |
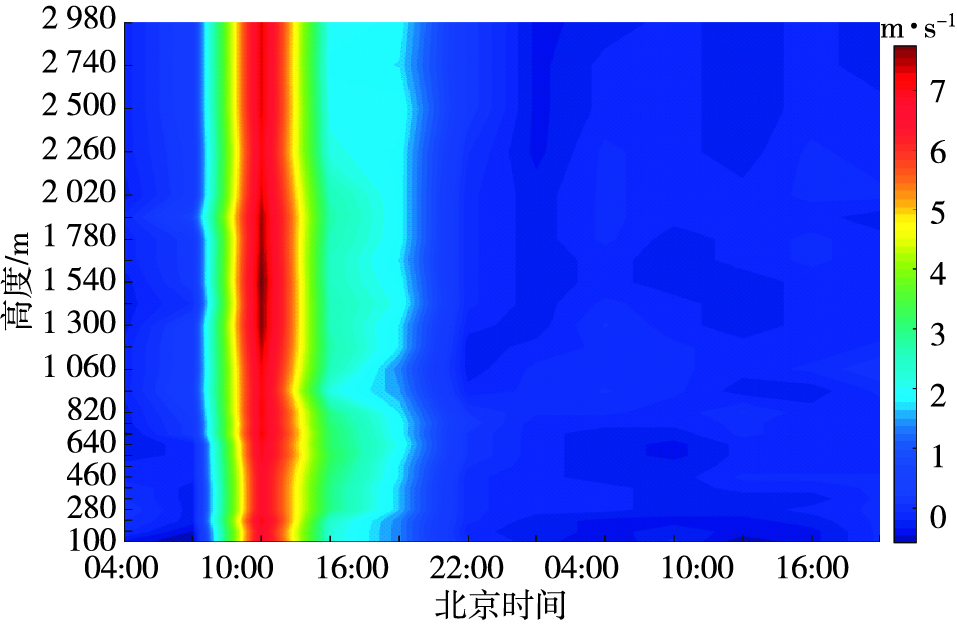
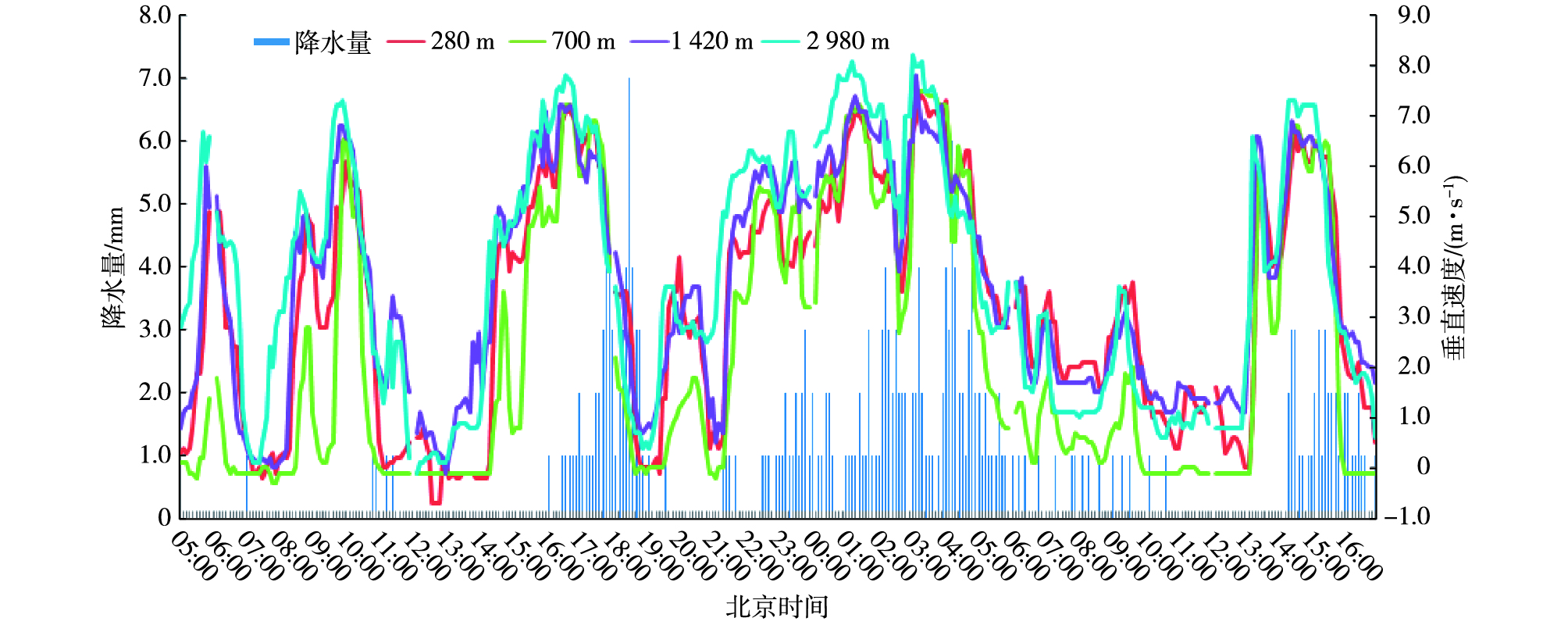
2014年9月16—17日,受低槽冷锋和切变线影响,山东地区出现明显降雨,降雨持续时间较长,降雨量比较大。高空处于偏西气流中,地面为冷高压控制,是山东秋季回流降雨的一种形势,属于混合型降雨。本次济南站降雨持续时间较长,从小时垂直速度随高度时间变化剖面图(图 7)上可以清晰地看到各个高度层的小时垂直速度变化与降雨时段对应均较为一致。分析6 min垂直速度与降雨量关系(图 8)可知,本例中,各高度层垂直速度值和变化规律一致性较好,但在变化幅度上700 m高度层与其他层垂直速度变化有一定的差别。降雨开始前各高度层垂直速度迅速增大,若以垂直速度大于1.0 m·s-1作为阈值指示地面降雨开始,各高度层提前量均在1 h以上,除700 m外,存在随高度层的升高指示提前量增大的趋势,2 980 m高度层可提前2 h 6 min指示降雨开始(表 6)。本次降雨过程中存在多个大于1 h的降雨中断,各高度层垂直速度均出现提前下降至阈值以下的情况,对于降雨结束的指示提前量1 h左右。在反映整个过程降雨强度的波动方面,700 m高度层对细部过程的反映明显优于其他层,降雨过程中地面6 min降雨量大于0.2 mm的时段垂直速度均大于4.0 m·s-1且有1 h左右的提前量。
|
图 7 秋季降雨过程小时垂直速度(单位:m·s-1)随高度时间变化剖面图 Fig.7 The height-time cross section of hourly vertical velocity (units:m·s-1) of a autumn rainfall |
|
图 8 秋季降雨过程6 min垂直速度与降雨量关系 Fig.8 Relationship of 6-min vertical velocity and precipitation variation during a autumn rainfall |
|
|
表 6 秋季降雨过程垂直速度表征降雨起(≥1.0 m·s-1)止(<1.0 m·s-1)时间及地面记录 Table 6 Precipitation start (≥1.0 m·s-1) and end (< 1.0 m·s-1) time of an autumn rainfall indicated by vertical velocity and ground record |
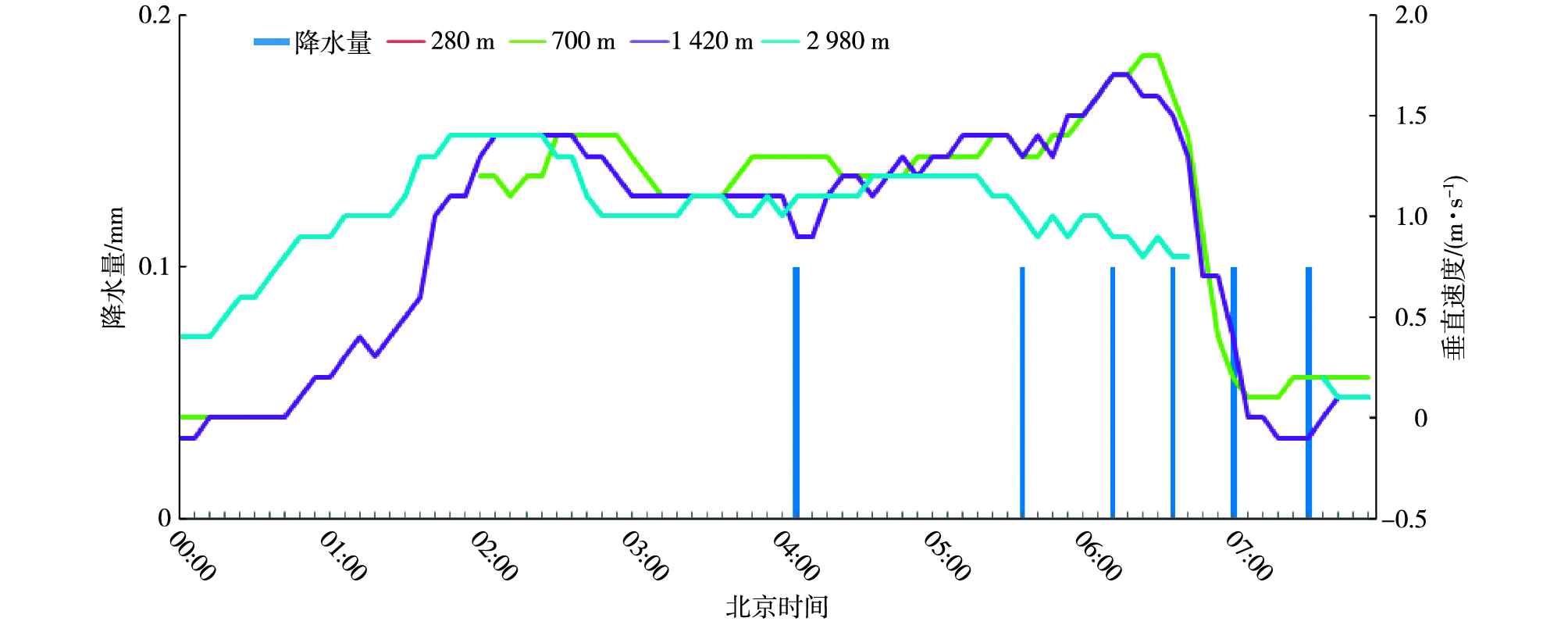
由于冬季过程12月10日00—02时多个高度层存在小时垂直速度数据缺测问题,故无法绘制小时垂直速度随高度时间变化剖面图。分析本次个例降雨过程背景可知,2014年12月10日01—17时,受低槽冷锋影响,除鲁西北的西部和半岛北部的部分地区外,山东其他大部地区共89个站出现雨夹雪天气。9日20时,500 hPa高空在河套地区存在一浅槽,700 hPa高空槽比较明显,此时处于山西与河北交界处,地面有冷锋配合。由6 min垂直速度与降雨量关系(图 9)可见,冬季个例降雨垂直速度特征与春、夏、秋季个例显著不同,过程中各高度层垂直速度均小于2.0 m·s-1。以垂直速度大于1 m·s-1指示降雨开始,280 m和700 m在02时之前数据缺测,02时垂直速度已大于阈值故按02:00记可提前2 h 6 min指示降雨开始;1 420 m和2 980 m高度层可分别提前2 h 24 min和2 h 36 min指示降雨开始。以垂直速度小于1.0 m·s-1指示降雨结束,2 980 m高度层降雨结束前出现数据缺测,其他高度层的预报提前量在48 min左右(表 7)。在反映整个过程降雨强度的波动方面,各高度层对细部过程均不明显,整个降雨过程中垂直速度变化幅度较小,在1.0~2.0 m·s-1之间。
|
图 9 冬季降雨过程6 min垂直速度与降雨量关系 Fig.9 Relationship of 6-min vertical velocity and precipitation variation during a winter rainfall |
|
|
表 7 冬季降雨过程垂直速度表征降雨起(≥1.0 m·s-1)止(<1.0 m·s-1)时间及地面记录 Table 7 Precipitation start (≥1.0 m·s-1) and end (< 1.0 m·s-1) time of a winter rainfall indicated by vertical velocity and ground record |
1) 对济南固定式边界层风廓线雷达垂直速度-降雨量回归分析表明,垂直速度能够反映雨滴的下落速度特征,综合各个高度层来看,700 m高度层垂直速度与小时雨量回归方程拟合优度较为稳定,其他高度层在不同季节拟合优度差别略大。
2) 对场次降雨过程垂直速度-降雨量关系分析表明,尽管垂直速度的大小并不能完全定量的预报降雨强度,但对于整个过程的雨强波动变化仍有着明显的指示性作用。700 m高度层垂直速度对于降雨的预报指示效果最为稳定。
垂直速度对降水的指示性可用于灾害性天气,如暴雨、冰雹、降雪等的预警及临近预报,本研究只考虑了降雨过程。垂直速度阈值对冬季降雨的指示性(雨量、高度),与春、夏、秋季呈现明显不同的特征,具体变化原因可能是受降水相态、降水类型、气温、湿度、湍流等影响。冬季降水包括雨、雨夹雪、雪、冰粒、冻雨等多种相态且降水过程有时存在相态的数次复杂变化 ,本研究只考虑了降雨过程。此外,垂直速度并非是判别降雨与否的唯一指标,杨馨蕊等[16]采用组合识别方法分别建立降雨与垂直径向速度和信噪比相关关系的判别函数,以及降雨与垂直径向速度和谱宽的判别函数,判别较为准确。因此针对不同相态、不同类型的降水的垂直速度阈值确定以及利用风廓线雷达探测资料多产品指标进行组合识别应用于降雨预报是下一步深入研究的方向。
| [1] |
吴志根. 边界层风廓线雷达在降水时段中的在线分析应用研究[J]. 气象, 2012, 38(6): 758-763. |
| [2] |
董保举, 刘劲松, 高月忠. 基于风廓线雷达资料的暴雨天气过程分析[J]. 气象科技, 2009, 37(4): 411-414. DOI:10.3969/j.issn.1671-6345.2009.04.005 |
| [3] |
翟亮. 北京奥运期间一次暴雨过程风廓线资料特征[J]. 气象, 2008, 34(S1): 26-31. DOI:10.7519/j.issn.1000-0526.2008.S1.004 |
| [4] |
古红萍, 马舒庆, 王迎春, 等. 边界层风廓线雷达资料在北京夏季强降雨天气分析中的应用[J]. 气象科技, 2008, 36(3): 300-302. DOI:10.3969/j.issn.1671-6345.2008.03.009 |
| [5] |
王令, 王国荣, 古月, 等. 风廓线雷达垂直径向速度应用初探[J]. 气象, 2014, 40(3): 290-296. |
| [6] |
胡明宝, 李妙英, 陈楠. 风廓线雷达测量垂直风速的应用研究[C]//第八届长三角气象科技发展论坛论文集. 杭州: 浙江省气象学会, 2011.
|
| [7] |
古月, 王令. 风廓线雷达探测垂直风速与夏季降雨之间的关系研究[C]//中国气象学会. 第三十届中国气象学会年会论文集. 北京: 气象出版社, 2013.
|
| [8] |
吴蕾, 董丽萍, 王令, 等. 风廓线雷达在强降水监测预警中的应用研究[J]. 南京大学学报(自然科学), 2014, 50(6): 865-872. |
| [9] |
董丽萍, 吴蕾, 王令, 等. 风廓线雷达组网资料初步对比分析[J]. 气象, 2014, 40(9): 1145-1151. |
| [10] |
高正明, 赵娟, 贺升平. 多项式回归分析及回归方程的显著性检验[C]//中国核科学技术进展报告(第二卷)——2011年学术年会论文集第4册(核材料分卷, 同位素分离分卷, 核化学与放射化学分卷). 北京: 中国原子能出版社, 2011.
|
| [11] |
同济大学数学教研室. 高等数学[M]. 北京: 高等教育出版社, 1986: 174-208.
|
| [12] |
陈楠, 胡明宝, 徐芬, 等. 基于边界层风廓线雷达资料的春季对流云降雨特征分析[C]//中国气象学会. 第二十八届中国气象学会年会论文集. 北京: 气象出版社, 2011.
|
| [13] |
周莉蓉, 施娟, 朱斌. 风廓线雷达产品在强降雨短临预报中的初步应用[J]. 高原山地气象研究, 2012, 32(4): 27-30. DOI:10.3969/j.issn.1674-2184.2012.04.005 |
| [14] |
黄钰, 阮征, 葛润生, 等. 2010年夏季北京零度层亮带特征统计[J]. 气象, 2013, 39(6): 704-709. DOI:10.3969/j.issn.1001-7313.2013.06.007 |
| [15] |
杨成芳, 刘畅, 郭俊建, 等. 山东相态逆转降雪天气的特征与预报[J]. 海洋气象学报, 2017, 37(1): 73-83. |
| [16] |
杨馨蕊, 马舒庆, 吴蕾. UHF风廓线雷达降水数据判别方法的比较与评价[J]. 大气科学学报, 2010, 33(5): 576-581. DOI:10.3969/j.issn.1674-7097.2010.05.009 |
 2017, Vol. 37
2017, Vol. 37

