大气边界层(atmospheric boundary layer,ABL)是直接受地球表面影响的那部分对流层,它对地面作用响应的时间尺度约为1 h或者更小,受地球表面热力和动力的影响,ABL内各种气象要素的日变化和垂直梯度较大[1]。人类大部分生产生活过程是在大气边界层中进行的,人类活动产生的污染物也主要存在于该层大气,因此大气边界层的环境问题直接影响到人类的健康和生存[2]。通常与大气发生物质能量交换的下垫面可分为海洋和陆地两部分,在海洋上方的大气边界层即为海洋大气边界层(marine atmospheric boundary layer,MABL)。
大气边界层高度主要受湍流和垂直运动过程的影响[3]。国内对于陆地上边界层高度的时空变化及边界层对大气污染物浓度和扩散的影响研究较多[4-9],而对海洋大气边界层以及天气过程对边界层的影响研究较为匮乏。海洋上,由于海水上层强烈混合使海面温度日变化很小,此外,海水热容量大,海面温度日变化不明显,MABL厚度变化十分缓慢,主要由天气、中尺度垂直运动和不同气团平流引起[1]。国外对于海洋大气边界层的研究较多,Tanimoto et al.[10]分析梅雨锋穿过黑潮延伸体时MABL结构的变化发现,梅雨锋和黑潮延伸体海洋锋的相对位置变化会影响穿过黑潮延伸体的风向,导致海面气象结构和表面湍流热通量发生巨大变化,并与深层对流和海雾及低云形成潜在的反馈。Kim and Yum[11]利用探空资料研究不同边界层类型下海雾的季节发生频率,发现海气温差(气温-海表温度)为较大负值的较冷月份容易形成对流边界层;而较暖月份容易形成稳定边界层,低层的暖平流增加了海雾的发生频率,常见海雾及低层层云的发生。
海气界面稳定度通常用海气温差来表征,海气温差越大,海气界面稳定度越小,研究发现海气温差越大,对流活动越强,边界层高度越高[12-13]。近海面大气边界层的静力稳定度与海表面风场及降水之间存在密切联系,研究[14-15]表明,东海黑潮及黑潮延伸体区域的海洋锋与近海面风速之间存在明显的正相关,暖(冷)舌下对应高(低)风速,海洋锋暖侧存在海表面风辐合,出现深层对流,在垂直方向上超出海洋大气边界层,频繁发生积云对流,降水强度和高度增大,这与Minobe et al.[16-17]发现湾流区域的暖海表对夏季降水的影响是一致的。这种同相关系与传统的强风速冷却海表温度的观点恰好相反,表明了海洋对大气的影响。
目前,国内外对于天气过程对海洋大气边界层结构影响的研究较少,其中锋面过程是对边界层影响的重要天气现象,分析锋面过程对边界层结构的影响机制具有非常重要的意义。本文利用GPS探空资料和ERA-Interim再分析资料,分析一次冷空气过程对黄东海区域海洋大气边界层结构的影响,深入理解冷锋过程对海洋大气边界层的影响机制,为海洋大气相互作用研究提供依据。
1 观测与数据 1.1 资料介绍本文使用的资料是欧洲中期天气预报中心(European Center for Medium-Range Weather Forecasts,ECMWF)提供的ERA-Interim再分析数据集和黄海及东海北部观测的探空数据。
1.1.1 再分析数据本文使用的ERA-Interim数据有1979—2015年与探空观测数据同时刻、同经纬度的0.125°×0.125°的海表温度和海面2 m气温,时间分辨率为3 h;2016年11月7—10日海表温度、气温、位势和风场,时间分辨率为6 h,空间分辨率为0.25°×0.25°。
1.1.2 探空数据探空系统的温度传感器的测量范围为-90~+40 ℃,精度为±0.3 ℃,分辨率为0.01 ℃,响应时间小于2 s;风速和风向测量范围分别为0~100 m·s-1和0°~360°,精度分别为±0.3 m·s-1和±3°,分辨率分别为0.01 m·s-1和0.1°,响应时间均小于1 s;相对湿度的测量范围为0~100%,精度为±3%,分辨率为0.1%;气压利用大气静力学方程和湿空气气体状态方程,通过迭代法计算,其精度从海面至500 hPa为±1.5 hPa,500 hPa以上为±0.7 hPa,分辨率为0.01 hPa。
探空系统的观测频率为1 Hz,因此观测所得原始探空数据的时间间隔为1 s。原始探空数据首先经过由北京长峰微电科技有限公司提供的GPSTK数据接收软件初步处理进行数据自动质量控制,包括异常值的剔除、数据的平滑控制、圆锥摆运动的滤除,之后再对数据进行人工质量控制,包括阈值控制和内部一致性控制。
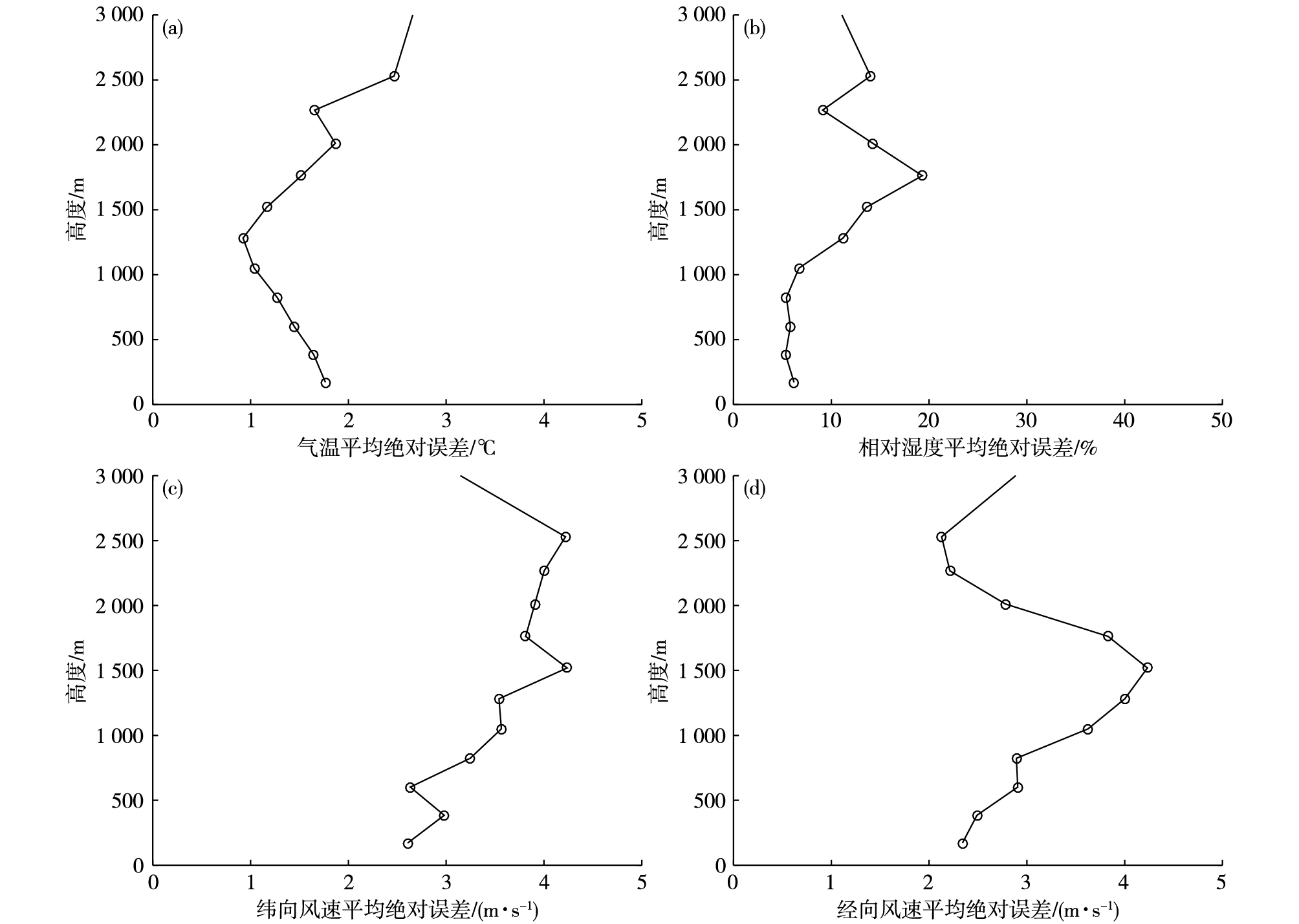
探空数据是在风力较大的冷空气过程下观测所得,GPS探空气球相对施放位置的纬向漂移不超过0.15°经度,经向漂移不超过0.07°纬度,而探空观测站位之间的纬向间距最小为0.33°经度,经向间距最小为2.52°纬度,因此每组探空数据能够代表各观测站位上空的气象情况进行分析(图略)。图 1为14组探空数据的气温、相对湿度和风速廓线,由图 1a可以看出,3 000 m以内气温垂直廓线受海面气温的影响较大,整体气温随高度而减小的趋势一致,平均气温递减率约为5.9 ℃·km-1。图 1b显示平均相对湿度廓线约在1 500 m以下随高度而增大,1 500 m以上随高度而减小。图 1c和图 1 d显示此次探空过程中,约2 000 m以下主要盛行东北风,2 000 m以上转为西南风。

|
图 1 2016年11月气温(a;单位:℃)、相对湿度(b;单位:%)、纬向风速(c;单位:m·s-1)和经向风速(d;单位:m·s-1)的探空廓线 Fig.1 Sounding profiles of (a) air temperature (units:℃), (b) relative humidity (units:%), (c) zonal wind speed (units: m·s-1), and (d) meridian wind speed (units: m·s-1) in November 2016 |
再分析数据由于受观测资料变更、数值预报模式及同化方案的影响,对于研究的问题其可信度常常需要进一步检验,支星和徐海明[18]对比了ERA-Interim再分析数据和探空数据,发现在对流层中下层ERA-Interim再分析数据能够较好地接近探空数据。本文选取与探空数据观测时间、观测位置接近的ERA-Interim再分析数据,并提取与ERA-Interim再分析数据相同气压层的数据进行对比分析。由图 2分析可知探空数据与ERA-Interim再分析数据的气温平均绝对误差在0~3 ℃范围内,相对湿度的平均绝对误差在1 000 m以下基本位于5%左右,在1 000 m以上绝对误差平均值随着高度而增大,在1 700 m左右高度处达到最大值约为20%,然后随高度减小。纬向风速与经向风速的平均绝对误差均在2~4.5 m·s-1的范围内。
|
图 2 探空数据与ERA-Interim的气温(a;单位:℃)、相对湿度(b;单位:%)、纬向风速(c;单位:m·s-1)和经向风速(d;单位:m·s-1)的平均绝对误差廓线 Fig.2 Profiles of mean absolute errors of sounding data with ERA-Interim (a) air temperature (units:℃), (b) relative humidity (units:%), (c) zonal wind speed (units: m·s-1), and (d) meridian wind speed (units: m·s-1) |
通过以上分析可知,探空数据与ERA-Interim再分析数据之间存在一定的差异,气温平均差异在0~3 ℃,相对湿度在5%~20%,纬向风与经向风在2~4.5 m·s-1。整体上ERA-Interim再分析数据与探空数据各要素的误差稳定在一定的范围内,因此可以用ERA-Interim再分析数据来分析该冷空气过程。
1.2 计算方法 1.2.1 MABL类型判断方法Liu and Liang[19]对探空数据的垂直分辨率进行了10~100 m的敏感性分析,结果表明50 m的垂直间隔最为有效,因此本文将频率为1 Hz的探空数据线性插值到50 m垂直间隔的标准层数据进行分析。通常边界层被分为3类主要的形式:对流性边界层(convective boundary layer,CBL),稳定边界层(stable boundary layer,SBL)和中性边界层(neutral residual layer,NRL)[20],根据位温来判定边界层的类型[19]:
| $ {{\theta }_{5}}-{{\theta }_{2}}\left\{ \begin{array}{*{35}{l}} <-{{\delta }_{\text{s}}},\text{for}\ \text{CBL} \\ >+{{\delta }_{\text{s}}},\text{for}\ \text{SBL} \\ \text{else,for}\ \text{NRL} \\ \end{array} \right. $ | (1) |
其中,θ5为下垫面向上第5层位温,相应的θ2为下垫面向上第2层位温,δs为位于对流边界层顶上方或稳定边界层顶下方稳定层最弱时对应的位温参数,在海面上空通常取0.2 K[19]。另外,由于观测资料中没有位温要素,需要通过位温的定义计算得到[21]:
| $ \theta=T \times(1000 / p)^{0.286} $ | (2) |
其中,T为气温,单位:K;p为气压,单位:hPa。
1.2.2 MABL高度计算方法在混合层中,由于位温近于常量,而出混合层后,位温梯度迅速增大,因此本文定义位温梯度变化最大时的高度为MABL的高度(marine atmospheric boundary layer height,MABLH),一般出现在逆温层的中间高度[22]。
位温梯度则采用中央差分的方法计算:
| $ \frac{\partial \theta_{i}}{\partial Z_{i}}=\frac{\Delta \theta_{i}}{\Delta Z_{i}}=\frac{\theta_{i+1}-\theta_{i-1}}{Z_{i+1}-Z_{i-1}} $ | (3) |
其中,θ为位温,单位:K;Z为高度,单位:m。
1.2.3 混合比及比湿的计算通过气温、气压、相对湿度计算了混合比及比湿,计算公式如下[21]:
| $ e=6.112 \times \exp \left(\frac{17.67 t}{t+243.5}\right) \times R H $ | (4) |
| $ s=\frac{0.622 e}{p-e} $ | (5) |
| $ q=\frac{0.622 e}{p-0.378 e} $ | (6) |
其中,t为气温,单位:℃;RH为相对湿度,单位:%;e为水汽压,单位:hPa;s为混合比,单位:g·kg-1;q为比湿,单位:g·kg-1。
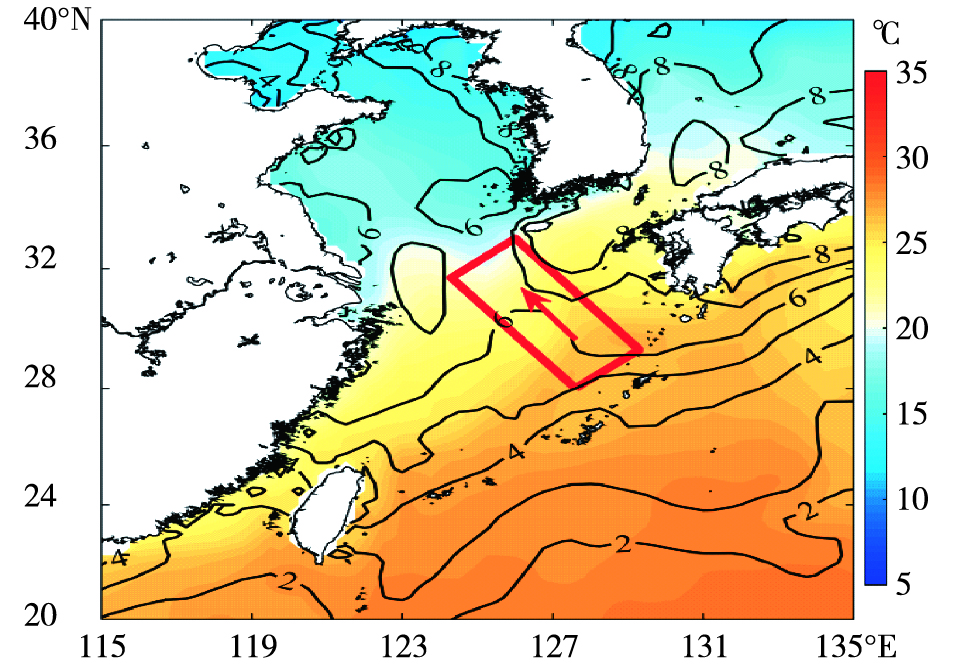
1.3 观测概况2016年11月3—11日期间,研究人员在东海和黄海采用GPS探空系统进行了高空气象探测,观测要素主要包括高空气温、气压、相对湿度、风速和风向。观测的大致区域如图 3所示,其中红色箭头表示船航行的基本方向。11月7日06:00 UTC—11月10日00:00 UTC有冷空气进入黄海及东海北部,针对该冷空气过程,研究人员进行了加密探空观测(施放探空气球的平均时间间隔为2~3 h),共获取了14组探空数据。
|
图 3 2016年11月7日06时—10日00时(UTC)探空观测区域(红框为观测区域,框内红箭头为航行基本方向)、平均海温场(阴影;单位:℃)和海气温差场(等值线;单位:℃) Fig.3 Sounding observation area (Red frame is the observation area and red arrow in the red frame is basic direction of navigation), mean sea surface temperature field (shaded areas; units:℃) and sea-air temperature difference field (contours; units:℃) from 0600 UTC 7 to 0000 UTC 10 November 2016 |
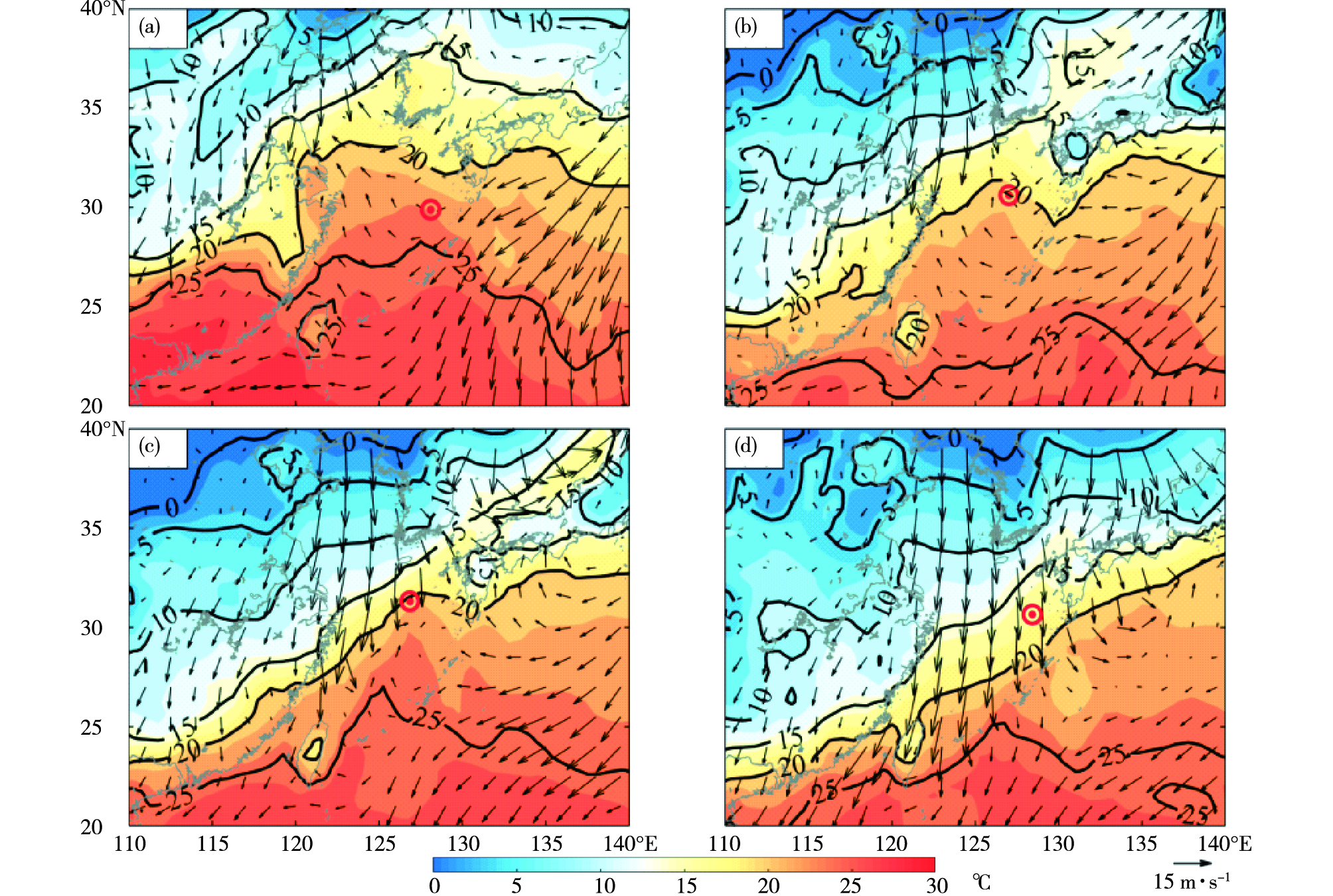
2016年11月7日—10日冷空气影响黄东海区域,带来大风降温天气,分析500 hPa位势高度场、850 hPa风场和850 hPa温度平流场(图 4)可知,这是一次典型的冷空气锋面系统。系统过境期间,观测站位上空500 hPa受低压槽的控制,槽线随时间向东移动,850 hPa盛行偏北大风,风场切变线于500 hPa低压槽前向东移动,属于缓行冷锋。图 4a显示7日06:00 UTC,观测站位处于500 hPa高空槽前,850 hPa风场表现为弱东风,风场切变线位于观测站位的西北侧。图 4b显示7日18:00 UTC,观测站位处于500 hPa低压槽线前方附近,850 hPa风场转为西北风,风力较小,风场切变线位于观测站位的西北侧不远处,随后观测站位被冷锋控制。由图 4c可知8日00:00 UTC,观测站位处于500 hPa低压槽附近,850 hPa风场为西北风向西南风逆时针切变,风速较小,此时为冷锋锋面过境的时段。图 4d显示8日12:00 UTC,500 hPa低压槽处于观测站位的东侧,850 hPa风为很强的偏北风,此时观测站位被锋后冷空气控制。

|
图 4 2016年11月7日0600 UTC (a)、7日1800 UTC (b)、8日0000 UTC (c)、8日1200 UTC (d) 500 hPa位势高度(等值线;单位:dagpm)、850 hPa风速(箭矢;单位:m·s-1)和850 hPa温度平流(阴影;单位:K·s-1)(红色圆圈为观测位置) Fig.4 Geopotential height at 500 hPa (contours; units:dagpm), wind speed at 850 hPa (arrows; units:m·s-1) and temperature advection at 850 hPa (shaded areas; units:K·s-1) at (a) 0600 UTC 7, (b) 1800 UTC 7, (c) 0000 UTC 8, and (d) 1200 UTC 8 November 2016 (Red circle is the observation position) |
气温的局地变化可用热流量方程来表示[23]:
| $ \begin{align} \frac{\partial T}{\partial t}=-\mathit{\boldsymbol{V}}\nabla T-\omega \left( {{\gamma }_{\text{d}}}-\gamma \right)+ \\ \frac{{{\gamma }_{\text{d}}}}{\rho g}\left( \frac{\partial p}{\partial t}+\mathit{\boldsymbol{V}}\nabla p \right)+\frac{1}{{{c}_{p}}}\frac{\text{d}Q}{\text{d}t} \\ \end{align} $ | (7) |
影响气温变化的因素有温度平流、垂直运动、变压和气压平流以及非绝热因子,在近地层,由垂直运动、变压和气压平流以及非绝热运动引起的温度局地变化很小,主要以温度平流为主,强的冷平流通常给局部地区带来剧烈的降温。850 hPa温度平流分析可知(图 4),11月7日06:00 UTC,观测站位位于暖平流后、冷平流前的位置,受到暖气团的影响,海表面气温较高(图 5),处于22~25 ℃之间,海面为弱东风,与850 hPa风场吻合。7日18:00 UTC,观测站位处于850 hPa冷平流区,冷平流强度约为-30×10-5 K·s-1,海表面气温下降至21 ℃,海面10 m风场切变线位于观测站位西北,之后受冷平流影响,海面气温持续下降,并带来偏北大风,10日00:00 UTC,观测站位海面气温下降至17 ℃,北风减弱,冷空气过程结束。
|
图 5 2016年11月7日0600 UTC (a)、7日1800 UTC (b)、8日0000 UTC (c)、8日1200 UTC (d) 2 m温度(阴影;单位:℃)和海面10 m风速(箭矢;单位:m·s-1)(红色圆圈为观测位置) Fig.5 Temperature at 2 m (shaded areas; units:℃) and sea surface wind speed at 10 m (arrows; units: m·s-1) at (a) 0600 UTC 7, (b) 1800 UTC 7, (c) 0000 UTC 8, and (d) 1200 UTC 8 November 2016 (Red circle is the observation position) |
冷锋过境前后,SST、气温、比湿、风速和海面气压的变化是显著的(图 6)。图 6a和图 6b显示SST和气温具有相同的变化趋势,随着观测时间气温和SST均下降,但气温最大降温幅度达到6 ℃,而SST的最大降温幅度只有4 ℃,气温比SST下降得更为剧烈。图 6c为海气界面比湿的时间序列,由图分析可知比湿先呈上升趋势并达到11.7 g·kg-1,之后比湿迅速减小至7.6 g·kg-1,与之变化相反的是海面气压,由图 6e可知,忽略日周期变化,海面气压开始呈下降趋势,之后海面气压一直升高,峰值达到1 022 hPa。图 6d为海面10 m风速的时间序列,开始阶段,风速缓慢增大,平均风速为5.3 m·s-1,属于3~4级风,之后风速剧烈增大,最大风速达到15.2 m·s-1,属于7级风。

|
图 6 海表温度(a;单位:℃)、气温(b;单位:℃)、比湿(c;单位:g·kg-1)、海面10 m风速(d;单位:m·s-1)和海面气压(e;单位:hPa)的时间序列(黑竖线间区域为冷锋过境时段) Fig.6 Time series of (a) sea surface temperature (units:℃), (b) air temperature (units:℃), (c) specific humidity (units: g·kg-1), (d) sea surface wind speed at 10 m (units: m·s-1), and (e) sea surface pressure (units:hPa) (Area between black vertical lines represents cold front passing period) |
根据冷锋过境前后海面气象要素的变化特征,结合500 hPa低压槽线和850 hPa风切变线,推测7日06:00 UTC至7日19:00 UTC为冷锋过境前的阶段,7日19:00 UTC至8日12:00 UTC为冷锋过境的阶段,之后至10日00:00 UTC的时间为冷锋过境后的阶段。通过上述分析,此冷锋过程带来大风降温天气,使北方的干冷空气向南入侵。锋面过境前,低空为偏东风,风速较小,平均海气温差约为2 ℃,海面气压较低;锋面过境时,由于锋面处于低压槽中,偏东风转为偏北风,风速开始增大,大风带来北方的干冷空气,使气温剧烈下降,平均海气温差增加至5 ℃以上,海面气压开始升高,海气界面比湿开始减小;锋面后被冷高压控制,气压升高,气温继续下降,海气界面比湿减小。
3 海气边界层结构分析 3.1 MABL变化特征利用Liu and Liang[19]对边界层的分类方法,分析冷锋过境前后MABL的变化特征(图 7),结果显示,冷锋到达观测站位之前,7日06:00 UTC、11:00 UTC、17:00 UTC的MABLH变化很小,处于1 500~1 800 m的位置,边界层表现为对流和中性边界层特征。根据之前对锋面过境前后时刻的定义,8日01:00 UTC为冷锋锋面过境的时段,近海面位温减小,位温廓线表现为对流边界层的特征,MABLH明显降低至1 000 m以下;8日05:00 UTC至8日08:00 UTC,位温廓线仍表现出对流边界层的特征,MABLH迅速升高至2 500 m以上,此时边界层顶处逆温较小。9日07:00 UTC之后处于锋面过境后的时段,边界层高度处于1 700 m至2 800 m之间,边界层顶逆温特征明显,边界层以对流为主。

|
图 7 2016年11月7—9日(世界时)位温(红线;单位:℃)、温度(棕线;单位:℃)和混合比(绿线;单位:mg·kg-1)的廓线(黑色横线为边界层顶高度的位置) Fig.7 Profiles of potential temperature (red line; units:℃), air temperature (brown line; units:℃) and mixing ratio (green line; units: mg·kg-1) during 7—9 November 2016 (Black horizontal line is the boundary layer height) |
对比冷空气锋面过境前后,冷空气过境使得平均MABL高度升高,MABL底部的静力稳定性减弱,对流活动加强,锋面后MABL表现为对流边界层特征。Tokinaga et al.[24]通过观测发现,近地表大气稳定性除了受SST的影响,还受到天气干扰的影响,当有南风经过,为暖平流,会增强近地表大气的稳定度,而北风带来冷平流,使近地表的稳定度减弱,这与该文研究人员的观测结果是一致的。
探空观测区域的日出时间为北京时间05:55,日落时间为北京时间16:40,以此为界分析冷锋过境前后边界层高度的变化特征(图 8)。锋面过境前,北京时间8日03:00前受锋前暖湿空气的影响,日落前后边界层高度的变化不大,处于1 500~1 800 m的高度。锋面过境时,探空观测的时刻全部处于白天,可以看到北京时间09:00—16:30边界层高度一直升高,除了锋面抬升作用外,白天下垫面持续受热,使得边界层高度在傍晚时分达到最高。锋面过境后,探空观测基本处于晚上,分析发现受锋后冷高压的影响,边界层高度并没有降低,反而持续升高,这说明天气过程对边界层的影响非常显著。

|
图 8 边界层高度的时间序列(单位:m) Fig.8 Time series of the boundary layer height(units:m) |
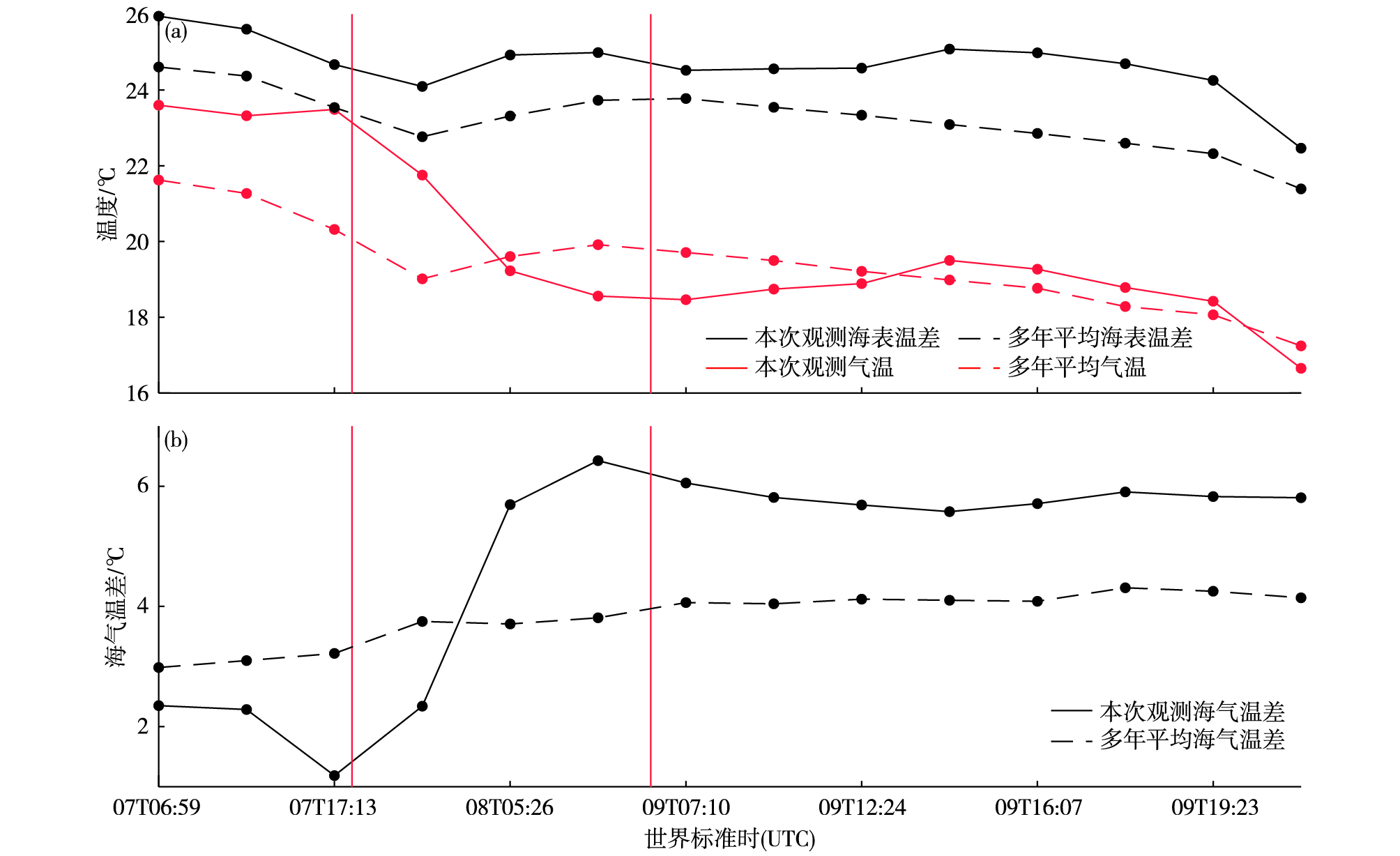
提取距离探空观测点最近格点处同时期的ERA-Interim(0.125°×0.125°)海表温度与海面2 m气温数据以及1979—2015年对应的气候平均态,分析观测过程中海气温差的变化特征(图 9)。Tokinaga et al.[24]将海气温差这一大气稳定参数S分为三类:
|
图 9 海表温度、气温(a;海表温度为黑色线,气温为红色线;虚线为1979—2015年平均值,实线为与观测同时期、同格点处的观测值)及海气温差(b;黑色虚线为1979—2015年平均海气温差,黑色实线为与观测同时期、同格点处的海气温差)的时间序列(单位:℃;红色竖线间区域为冷锋过境时段) Fig.9 Time series of (a) sea surface temperature, air temperature (Black lines are sea surface temperature, red lines are air temperature, dashed lines are annual mean values during 1979—2015, and solid lines are observations with same observation period and position), and (b) sea-air temperature difference (Black dashed line is annual mean sea-air temperature difference during 1979—2015 and black solid line is sea-air temperature difference with same observation period and position)(units:℃; Area between red vertical lines represents cold front passing period) |
| $ S=S S T-S A T $ | (8) |
其中SST为海表温度,SAT为海面气温。S<1 ℃为中性大气,1<S<5 ℃为中度静力不稳定,S>5 ℃为高度静力不稳定。分析可知,观测站位气候平均海表温度比气温高3~4 ℃,整个海气界面常年处于中度静力不稳定状态。本次观测锋面过境前,SST与SAT之间相差不大,S约为2 ℃,海气界面大气为中度静力不稳定状态。锋面过境时,SST没有明显变化,SAT剧烈降低6 ℃左右,S由1 ℃增加至6 ℃以上,海气界面大气呈现高度静力不稳定状态。锋面过境后,锋面后冷空气导致海气温差继续增大,大气为高度静力不稳定状态。冷空气过境中,海气界面大气静力不稳定增强导致边界层高度的明显变化,由图 10可知,观测过程中,有4次观测是在中度静力不稳定大气中进行的,海气温差处于1~3 ℃之间,对应的MABLH在800~1 800 m之间,边界层顶高度平均约为1 430 m;其他10次观测均是在高度静力不稳定大气中进行观测,海气温差处于5~7 ℃之间,对应的MABLH也相对较高,处于1 800~2 800 m之间,边界层顶高度平均约为2 300 m。MABLH与海气温差之间存在正的相关关系,相关系数为0.73,通过了99%的置信水平,这与Tokinaga et al.[24]观测得到的海气温差与边界层顶高度之间的相关系数为0.68是接近的。
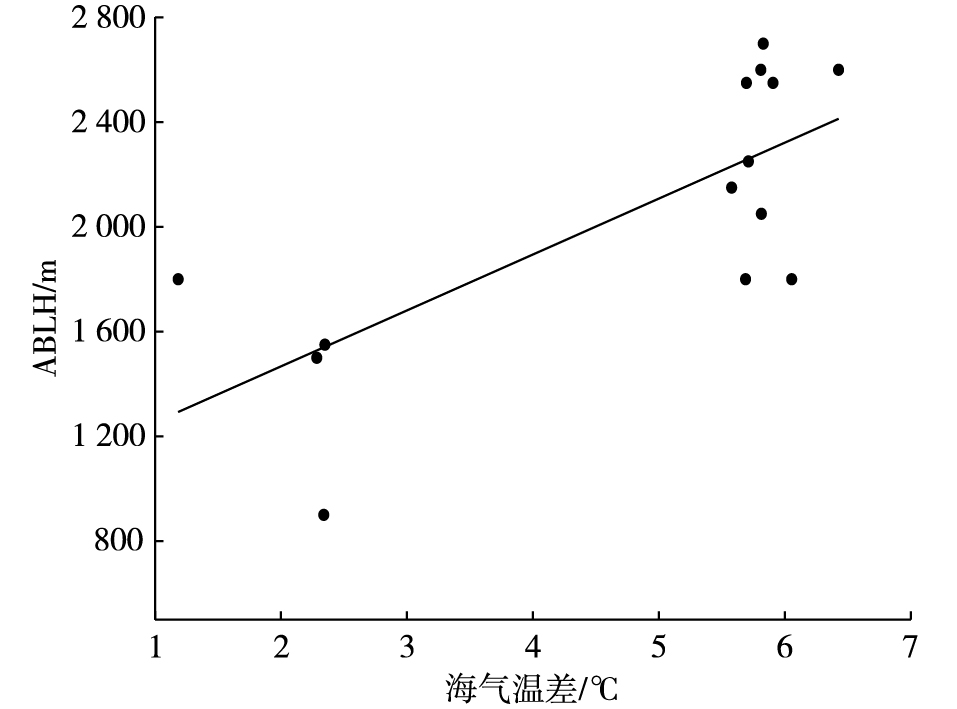
|
图 10 海气温差与ABLH的散点图及其线性拟合直线(ABLH=213.71S+1 039.9) Fig.10 Scatter plot of sea-air temperature difference and ABLH, and their linear fitting line (ABLH=213.71S+1 039.9) |
本文利用GPS探空数据,结合ERA-Interim再分析数据对冷空气影响下大气边界层结构特征进行分析,结果显示:
1) 冷锋过境对海气边界层的静力稳定度有很大的影响,冷锋过境造成气温下降幅度达到6 ℃,海气温差增大,使得边界层不稳定度增大,边界层对流活动增强。
2) 冷锋过境使海气边界层顶的平均高度增加,边界层顶处逆温梯度增大。锋面过境前,边界层顶高度处于1 500~1 800 m之间,边界层顶处逆温梯度较大,温度随高度的升高而增大的程度较小。锋面过境时,边界层顶高度先下降至900 m,之后迅速升高至2 500 m以上,此时边界层顶处逆温梯度减小。锋面过境后,边界层顶高度一直保持在较高的位置,边界层顶处呈现明显的逆温层,逆温的垂直梯度很大。
3) 边界层顶高度与海气界面稳定度之间存在相关关系,两者之间的相关系数为0.73。当海气温差处于1~3 ℃之间,边界层大气处于中度静力不稳定状态,观测的平均边界层顶高度约为1 430 m,当海气温差大于5 ℃,边界层大气处于高度静力不稳定状态,观测的平均边界层顶高度约为2 300 m,这也解释了锋面过境初期,由于海气温差还没有增大,导致观测的边界层顶高度较低。
本文利用探空资料研究了冷锋过境对边界层结构的影响,主要针对边界层的高度和静力稳定度进行了分析,除此之外,锋面过程对边界层的动力场和海气交换的影响,以及大气与海洋对暖锋过程的响应,还需要进一步的研究。
| [1] |
Stull R B. An introduction to boundary layer meteorology[M]. Dordrecht: Springer Netherlands, 1988.
|
| [2] |
刘辉志, 冯健武, 王雷, 等. 大气边界层物理研究进展[J]. 大气科学, 2013, 37(2): 467-476. |
| [3] |
Medeiros B, Hall A, Stevens B. What controls the mean depth of the PBL?[J]. J Climate, 2005, 18(16): 3157-3172. DOI:10.1175/JCLI3417.1 |
| [4] |
孟庆珍, 冯艺. 成都大气混合层厚度的计算和分析[J]. 成都气象学院学报, 1996, 11(1): 73-81. |
| [5] |
孟庆珍, 朱炳胜. 重庆市大气混合层厚度的计算和分析[J]. 成都气象学院学报, 1999, 14(2): 163-171. DOI:10.3969/j.issn.1671-1742.1999.02.007 |
| [6] |
杨勇杰, 谈建国, 郑有飞, 等. 上海市近15 a大气稳定度和混合层厚度的研究[J]. 气象科学, 2006, 26(5): 536-541. DOI:10.3969/j.issn.1009-0827.2006.05.010 |
| [7] |
周国兵. 重庆市不同天气背景下边界层高度和风场对PM10浓度影响数值模拟研究[J]. 贵州气象, 2016, 40(6): 5-12. DOI:10.3969/j.issn.1003-6598.2016.06.002 |
| [8] |
张鑫, 蔡旭晖, 柴发合. 北京市秋季大气边界层结构与特征分析[J]. 北京大学学报(自然科学版), 2006, 42(2): 220-225. DOI:10.3321/j.issn:0479-8023.2006.02.014 |
| [9] |
杜川利, 唐晓, 李星敏, 等. 城市边界层高度变化特征与颗粒物浓度影响分析[J]. 高原气象, 2014, 33(5): 1383-1392. |
| [10] |
Tanimoto Y, Xie S P, Kai K, et al. Observations of marine atmospheric boundary layer transitions across the summer Kuroshio Extension[J]. J Climate, 2009, 22(6): 1360-1374. DOI:10.1175/2008JCLI2420.1 |
| [11] |
Kim C K, Yum S S. Marine boundary layer structure for the sea fog formation off the west coast of the Korean Peninsula[J]. Pure Appl Geophys, 2012, 169(5/6): 1121-1135. |
| [12] |
Tokinaga H, Tanimoto Y, Nonaka M, et al. Atmospheric sounding over the winter Kuroshio extension: Effect of surface stability on atmospheric boundary layer structure[J]. Geophys Res Lett, 2006, 33(4): L04703. |
| [13] |
Friehe C A, Shaw W J, Rogers D P, et al. Air-sea fluxes and surface layer turbulence around a sea surface temperature front[J]. J Geophys Res: Oceans, 1991, 96(C5): 8593-8609. DOI:10.1029/90JC02062 |
| [14] |
Nonaka M, Xie S-P. Covariations of sea surface temperature and wind over the Kuroshio and its extension: Evidence for ocean-to-atmosphere feedback[J]. J Climate, 2003, 16(9): 1404-1413. DOI:10.1175/1520-0442(2003)16<1404:COSSTA>2.0.CO;2 |
| [15] |
Xu H, Xu M, Xie S-P, et al. Deep atmospheric response to the spring Kuroshio over the East China Sea[J]. J Climate, 2011, 24(18): 4959-4972. DOI:10.1175/JCLI-D-10-05034.1 |
| [16] |
Minobe S, Kuwano-Yoshida A, Komori N, et al. Influence of the Gulf stream on the troposphere[J]. Nature, 2008, 452(7184): 206-209. DOI:10.1038/nature06690 |
| [17] |
Minobe S, Miyashita M, Kuwano-Yoshida A, et al. Atmospheric response to the Gulf stream: Seasonal variations[J]. J Climate, 2010, 23(13): 3699-3719. DOI:10.1175/2010JCLI3359.1 |
| [18] |
支星, 徐海明. 3种再分析资料的高空温度与中国探空温度资料的对比:年平均特征[J]. 大气科学学报, 2013, 36(1): 77-87. DOI:10.3969/j.issn.1674-7097.2013.01.009 |
| [19] |
Liu S, Liang X-Z. Observed diurnal cycle climatology of planetary boundary layer height[J]. J Climate, 2010, 23(21): 5790-5809. DOI:10.1175/2010JCLI3552.1 |
| [20] |
Garratt J R. The atmospheric boundary layer[J]. Earth-Science Reviews, 1994, 37(1/2): 89-134. |
| [21] |
盛裴轩, 毛节泰, 李建国, 等. 大气物理学[M]. 北京: 北京大学出版社, 2003: 134-135.
|
| [22] |
Sullivan P, Moeng C-H, Stevens B, et al. Structure of the entrainment zone capping the convective atmospheric boundary layer[J]. J Atmos Sci, 1998, 55(19): 3042-3064. DOI:10.1175/1520-0469(1998)055<3042:SOTEZC>2.0.CO;2 |
| [23] |
张林梅, 庄晓翠, 胡磊. 新疆阿勒泰地区一次强寒潮天气过程分析[J]. 干旱气象, 2010, 28(1): 71-75. DOI:10.3969/j.issn.1006-7639.2010.01.012 |
| [24] |
Tokinaga H, Tanimoto Y, Nonaka M, et al. Atmospheric sounding over the winter Kuroshio extension: Effect of surface stability on atmospheric boundary layer structure[J]. Geophys Res Lett, 2006, 33(4): L04703. |
 2018, Vol. 38
2018, Vol. 38


