引言

气象预报与情报都是以大量的数据分析为基础的，等值线图是数据分析结果的重要表现形式，依据等值线分析自动填充的色斑图能够直观反映各种气象要素的空间分布特征，在气象业务与服务中得到广泛应用。国内气象业务制作等值线图主要采取封装Surfer软件的等值线分析模块和自主开发等值线分析软件两种方式，大型综合业务支撑平台多采用ArcGIS、WebGIS等地理信息软件来制作业务产品的等值线图。

等值线自动填充的本质是对等值线与网格边界构成的多边形区域进行填充。多边形区域填充比较典型的方法有种子填充法和扫描线填充法两种^[1-4]，诸多学者从不同的角度进行改进，衍生出活性(化)边表^[5-6]、边标志^[7]、种子扫描线^[8-9]等方法，这些方法同样被应用于等值线围成的多边形区域填充^{[3, 10-11]}，计算机实现时，可以利用Windows的GDI函数FillRgn()^[12-14]或者FloodFill()完成颜色填充。FloodFill()实际上就是种子填充法，只需要确定区域属性值及种子点，即可填充，缺点是确定种子点比较困难，对于高密度等值线图或者进行图形缩小操作时，部分区域会因种子点靠近等值线而导致填充失败；FillRgn()可归属于扫描线法，准确高效，便于各类地图操作，但需要确定多边形边界、区域属性值、开闭区域的包含关系及排序等，难度较高，近十多年来，国内学者对这类等值线填充方法研究较多^[12-24]。

等值线追踪完成后，等值线闭区域就已经产生，要进行颜色填充，还需要创建开区域、确定区域属性值及排序等步骤。

创建开区域比较多见的方法有两种。一是按顺序每次取一条开曲线(不闭合等值线，下同)与网格边界围成开区域，形成郑元满等^[14]所述的层状结构，相邻两开区域总是前者包含后者，称之为“分层法”^[14-16]。二是沿网格边界顺序搜索，遇到开曲线端点，自动沿开曲线到达另一端，继续顺序搜索，直至搜索起点，得到相互独立的开区域，称之为“切割法”^[17-21]。两种方法得到的开区域无需排序即可依次填充，比较而言，“分层法”得到的多边形区域之间存在重叠部分，填充效率比“切割法”低。

等值线颜色填充的难点是如何自动确定填充区域的属性值。利用等值线的线值^{[15, 17-19, 22]}，方法简单快速，但对于只有一条等值线围成的区域，直接采用等值线的线值^{[16-17, 19]}不够准确。引入参考格点^{[14, 18, 23-24]}，可以保证区域属性值的正确性，通常情况需要申请内存块建立临时区域，判断参考格点与临时区域之间的包含关系。郑元满等^[14]、张道军等^[18]在确定开区域属性值时，直接利用边界网格点和等值线的线值确定开区域属性值，避免了包含关系的判断。

区域的排序方法关系到区域能否正确填充及填充的速度，由于闭区域一定被开区域包含，所以总体填充顺序是先开区域后闭区域。将所有区域依据包含关系建立树状结构^{[15, 25-29]}，可以一次遍历节点，完成填充，但建立树状结构的过程比较复杂。孙桂茹等^[13]、郑元满等^[14]、刘冬韡等^[23]依据开曲线与边界的交接特征分类填充开区域，同时郑元满等^[14]还提出依据区域外接矩形大小排序，但求解外接矩形及分类过程依然比较复杂。对于闭区域之间的排序，依据闭区域边界点中横坐标的最小值进行排序^{[11, 13-14, 20]}，方法最为简单。

综上所述，前人研究使用的方法互有优劣，都是局部性的改善，没有体现出整体的优化，难免造成整个等值线绘图过程中的资源浪费和重复计算，尤其格点与区域、区域与区域之间的包含关系判别，需要反复遍历格点数组和创建临时区域，占用内存较多，影响运行效率。本文基于有序标记，采用简单的位置关系全面摆脱传统的包含关系判别，难度与复杂度大大降低。

对于离散的气象要素场，因梯度过大导致的两网格点之间密集的等值线在一定应用场景下并无实际意义，如果能隐藏部分过密的等值线，图形会变得清晰直观，然而，国内外文献中尚鲜见到关于等值线自动隐藏的介绍。本文根据人工绘图的习惯，制定合理的隐藏规则，通过等值点的有序标记及等值线的弯曲特征，确定需要隐藏和保留的等值线，实现每两条等值线之间至少存在一个站点，以期达到人工绘图的效果。

1 基本原理 1.1 有序化与解决思路

一条等值线追踪完成后，所经过的网格、围成的区域及区域和网格点之间的包含关系已然客观存在，如果能同时记录下这些信息，就可以用来确定区域属性值及排序，这就是解决方案的整体思想。若要计算机直接获取这些信息，而不必重复遍历网格点数组及检验包含关系，就需要建立一套规则，让相关信息有序化。

1.2 术语约定

为了便于理解，对文中采用的部分术语定义如下：

1) 站点。三角网中的网格点包括有原始数据的网格点(如气象观测站)和没有数据的网格点(如凸多边形边界上的网格点)，这些有原始数据的网格点被称为“站点”。

2) 区域属性值。根据填充区域所包含网格点数值的范围，赋给区域一个特征值，依据这个特征值可以给区域分配填充颜色，这个特征值被称为“区域属性值”。

3) 左极点。等值线最左边的等值点或者区域最左边网格点。

1.3 规则

通过观察三角网格与等值线，发现存在一些规律性特征，称之为“规则”，这些规则是文中所述“整体解决方案”的依据。

规则1：闭合等值线左极点所在的网格边一定不是竖直的，因为如果是竖直的，等值线就会继续向前游走，那么这个点也就不会是最左边的。

规则2：根据规则1，闭合等值线左极点所在的网格边的右端点一定被该闭合等值线围成的闭区域所包含。

规则3：根据相邻两条等值线不相交原理，如果两个闭区域存在包含关系，左极点横坐标小的闭区域一定包含横坐标大的闭区域。

规则4：在网格、网格边界及边界扫描均按照逆时针方向，且边界网格点的数值采用最近站点数值代替的前提下，沿网格边界扫描，最先遇到的等值线端点所在边界网格边，其前端点可视为被该等值线与网格边界围成的开区域所包含(该端点是距离最近站点的映射)。

1.4 整体解决方案

依据上述“规则”，可以在等值线追踪和网格边界扫描过程中，完成区域属性值的确定；由于开区域是相互独立的，因此不需要排序，仅对闭区域依据左极点横坐标排序，即可获得正确的填充顺序。

1) 创建逆时针的三角网格。每一个三角形的边及顶点均按照逆时针方向排列。

2) 创建逆时针的网格边界。每条边界边均为有向线段，并按逆时针方向首尾相接，使计算机能够直接访问等值线端点所在的网格边的前端点。

3) 记录闭合等值线的左极点，同时确定闭区域属性值。在等值线追踪过程中，构建一个筛选器，筛选出最左边的等值点，记录其横坐标及所在网格边序号，比较所在网格边右端点的数值及等值线的线值，可以确定闭区域的属性值。

4) 网格边界上插入开曲线端点，并记录端点所在网格边。等值线追踪到网格边界时，将等值线的端点插入到网格边界数组中，并记录等值线的索引号、端点的数值及所在的网格边序号。

5)“切割法”创建开区域，同时确定开区域属性值。采用“切割法”创建开区域时，遇到第一条等值线的端点，根据之前记录的该端点所在的网格边序号，比较该网格边前端点的数值及等值线的线值，即可确定开区域的属性值。

6) 闭区域自左向右排序。将闭区域按照左极点横坐标自小到大排序，即可实现对闭区域自左向右依次填充颜色。

2 具体方法 2.1 数据结构

为了用位置关系代替传统的包含关系判别，需要在各个环节的数据结构中增加必要的储存单元。

1) 在等值线数据结构中加入闭区域的属性值和左极点横坐标，便于确定闭区域的属性值及包含关系。

typedef struct{

int nPoint1;

//等值线的端点1

int nPoint2;

//等值线的端点2

float fLv;

//等值线的线值

float fInlineValue;

//闭区域的属性值

int nLeftX;

//闭区域最左边等值点的横坐标

…

}lineinfo;

2) 在边界点数据结构中，加入边界网格点所在网格边的索引和等值线端点所在等值线的索引及等值线的线值，便于确定开区域的属性值。

a) 边界点集的数据结构

typedef struct{

CPoint ptEdge; //边界点

int nEqlineIndex; //网格边界与等值线交点对应的等值线编号，若为网格边界点，则标记为-1

float fWalue; //边界点的数值，若为等值线端点，取等值线的线值

int nLinenum; //边界在网格边数组中的序号

…

}BorderPoint;

b) 三角网格边数据结构

typedef struct{

int nPoint1;

//网格边的前端点

int nPoint2;

//网格边的后端点

…

}TripLine;

c) 填充区域的数据结构

typedef struct{

float fRegvalue;

//区域填充时判断颜色的特征值

COLORREF Fillcolor;

//区域填充颜色

int nLeftX;

//区域的最左边的点横坐标

…

}region;

2.2 创建逆时针结构的三角网格

将包括凸多边形边界点及站点的所有网格点依据横坐标从小到大排序，若横坐标相同，则按照纵坐标从小到大排序。利用排序后的网格点数组，创建三角形网格，从最左边开始，三角形的三边按照逆时针方向存放，如图 1，三角形△P₁P₂P₃三边方向为$\overrightarrow{P_{1} P_{3}}, \overrightarrow{P_{3} P_{2}}, \overrightarrow{P_{2} P_{1}}$(三角形内侧的单箭头方向)。在构筑完成最左边的逆时针三角形后，右边的新增网格点与只用过1次的非边界边构成新的逆时针三角形。这样，除了边界边，其他的三角形边最多只能使用2次。图 1中实线三角形是已经构筑好的逆时针方向三角形，P₆为新增网格点，分别在三角形边$\overrightarrow{P_{5} P_{4}}$和$\overrightarrow{P_{4} P_{2}}$的右边，可以构筑△P₂P₄P₆和△P₄P₅P₆(虚线三角形)。图中有向线段$\overrightarrow {{P_2}{P_1}}、\overrightarrow {{P_1}{P_3}} 、\overrightarrow {{P_3}{P_5}}、\overrightarrow {{P_5}{P_6}} 、\overrightarrow {{P_6}{P_2}} $构成逆时针方向的网格边界。

2.3 边界网格点的数据映射

原始的网格边界点是没有数值的，但等值线是在有数值的网格内游走，因此，必须为网格边界点赋值。文中采用最小距离法，将最近的站点数值映射到边界网格点，即凸多边形边界网格点数值与其距离最近的站点数值相等，等值线就能沿着原来的走势与边界相交，因此，该边界网格点等同于距离最近的站点，可以视为被开曲线所围成的区域包含。

2.4 边界扫描规则

按照逆时针原则，先从边界上确定一个搜索起点，开始逐点搜索，经过的边界点均标记为已用，遇到等值线的端点，就沿着该等值线到另一端点，然后继续按照逆时针方向搜索，直至回到搜索起点，构成一个开区域。以此类推，继续按照逆时针搜索确定下一个搜索起点，已经标记用过的边界点不再作为搜索起点，这样，直到所有的边界点都标记为已用，搜索结束。以图 2a为例，P₁-P₈为边界网格点，L₁-L₆是等值线与网格边界的交点，进行逆时针扫描后，得到相互独立的开区域Q₁-Q₄。搜索轨迹如下：

$ \begin{array}{l}{Q_{1} : P_{1} \rightarrow P_{2} \rightarrow L_{1} \rightarrow L_{6} \rightarrow P_{1 \circ}} \\ {Q_{2} : P_{3} \rightarrow L_{2} \rightarrow L_{5} \rightarrow P_{8} \rightarrow L_{6} \rightarrow L_{1} \rightarrow P_{3 \circ}} \\ {Q_{3} : P_{4} \rightarrow L_{3} \rightarrow L_{4} \rightarrow P_{7} \rightarrow L_{5} \rightarrow L_{2} \rightarrow P_{4 \circ}} \\ {Q_{4} : P_{5} \rightarrow P_{6} \rightarrow L_{4} \rightarrow L_{3} \rightarrow P_{5}}\end{array} $

2.5 确定开区域属性值

以图 3为例，Q₁-Q₅是5个开区域。等值线L₁-L₄数值分别为5.0、7.0、10.0、12.0，根据规则4，A点可视为被Q₁包含，Q₂-Q₄不包含A点，但L₂-L₄均有一个端点在网格边$\overrightarrow{A B}$上，根据逆时针扫描规则，B点一定在Q₂-Q₄的外侧，比较A、B两端点的数值可以确定等值线左右两侧的数值变化趋势，从而确定开区域的属性值，实际计算时，可以比较A点和等值线的线值来代替，这样，确定Q₁-Q₄的属性值转化为比较A点数值与搜索时遇到的第一条等值线的线值的大小，由于A点数值均小于L₁-L₄的数值，取相应等值线的线值减去一数学小量(本例中取0.05)作为Q₁-Q₄的属性值，分别为4.95、6.95、9.95、11.95。Q₅是L₄与网格边界围成的开区域，根据网格边界逆时针扫描规则，Q₅是从B点开始搜索，到达C点后，遇到L₄的另一端点，然后沿着L₄逆时针返回到B点，构成开区域，$\overrightarrow{C D}$是该区域搜索过程中遇到的第一条等值线的端点所在边界网格边，根据规则4，C点可视为被Q₅所包含，C的数值为12.3，大于L₄的数值，因此，Q₅的属性值大于L₄的数值，加一数学小量0.05，即12.05。

2.6 确定闭区域属性值和包含关系

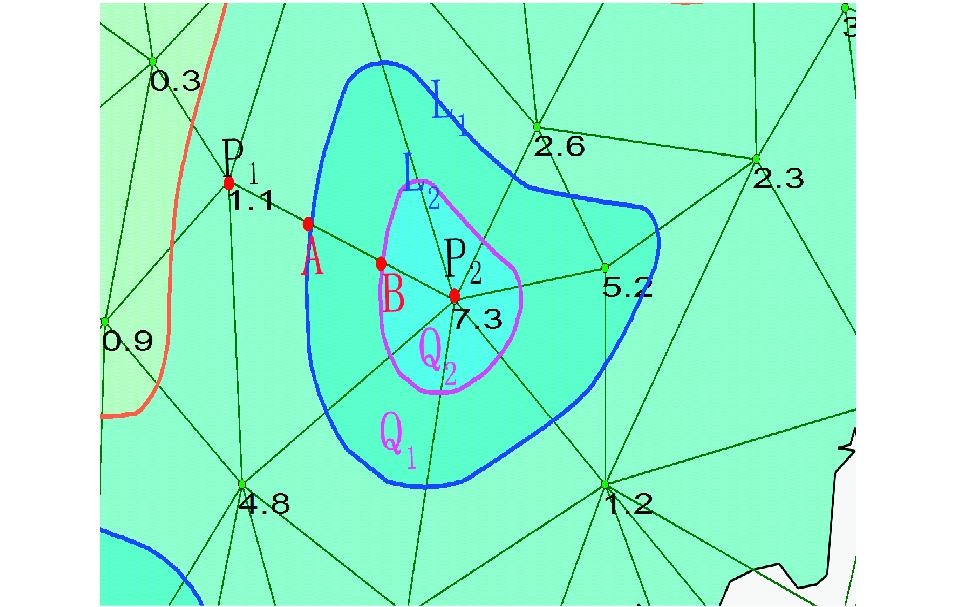
对于闭合等值线围成的闭区域，根据规则2和规则3，可以确定其属性值和包含关系。以图 4为例，A、B分别是闭区域Q₁、Q₂的左极点，P₁、P₂是左极点A、B所在的网格边的两个端点，其数值分别为1.1、7.3，L₁、L₂是数值分别为5.0、7.0的两条等值线，由于每一个三角形均为逆时针方向，同一条网格边是相邻两个三角形的公共边，在两个三角形中的方向正好相反，因此，需要判别网格边数据结构中的nPoint1和nPoint2与图 4中P₁、P₂的对应关系，实际编程时，计算机可遵循如下步骤自动判别：

1) 比较nPoint1与左极点A、B的横坐标，如果nPoint1的横坐标大于左极点A、B的横坐标，那么，图 4中的P₂对应的网格边端点是nPoint1，否则，对应的是nPoint2。

2) 因为P₂的横坐标大于左极点A、B的横坐标，所以，P₂被闭区域Q₁、Q₂包含。

3) 由于P₂的数值大于L₁、L₂的数值，因此，Q₁、Q₂的属性值均大于围成区域的等值线的线值，取数值加上一个数学小量，分别为5.05、7.05。

4) 由于A点的横坐标小于B点的，因此，Q₁包含Q₂。

3 时间复杂度分析

文中采用的整体优化方案，虽然在构筑有序化的三角网格和网格边界时，增加了一定的运算量，但是网格一旦创建完成，就不需要重复创建了，因此增加的工作量对于等值线颜色填充没有影响，却能明显降低颜色填充的时间复杂度。

3.1 开区域的创建

设有n条不闭合等值线，则将多边形边界分割成n+1个开区域，开区域创建完成后，构成区域的点集包含两部分：等值线上的等值点及边界点。“分层法”，每条等值线只调用一次，但等值线右边的边界点存在重复调用，最右边部分调用n+1次，自右向左依次递减；“切割法”，每条等值线调用两次，边界点只调用一次。当网格边界点密度与内部网格点密度相当时，“切割法”区域点集规模明显小于“分层法”。

3.2 开区域填充

图 2b中的“切割法”，每小块区域填充1次，总运算量为n，时间复杂度为O(n)。图 2c中的“分层法”自右向左，分别填充n+1，n，n-1，…，3，2，1次，总运算量为(n²+3n+2)/2，时间复杂度为O(n²)。

3.3 确定区域属性值

依据等值线的线值的双属性法，时间复杂度为O(1)；引入参考格点，判别点与区域的包含关系，需要装载区域多边形顶点，创建临时区域进行判别，直至找到被包含的格点为止，因此时间复杂度为O(n²)；张道军等^[18]创建开区域时，取不同属性值的区域轮廓点直接计算属性值，郑元满等^[14]取等值线线头所在网格边的左端点或下端点作为检测点，可以直接知道该参考点是处于等值线区域以内还是以外，避免了判断参考点与区域包含关系的复杂计算，单个开区域的时间复杂度降为O(1)，文中采用的方法类似于郑元满等的方法。

3.4 排序

对于二叉树之类的树状结构，创建的过程就是排序的过程，如果区域之间的包含关系已经确定，常规排序方法的时间复杂度为O(n²)^[30]，尽管可以优化到O(n)^[30-31]，但由于树状结构是对所有的开闭区域一起排序，不可避免的要判断开区域与闭区域之间的包含关系，通常情况下，求解一个开区域所包含的闭区域，首先需要装载多边形点集构建临时区域，时间复杂度为O(n)，然后判断闭区域上一点是否被该区域包含，需要遍历闭区域数组，时间复杂度升为O(n²)，完成所有开区域的求解，时间复杂度升为O(n³)，因此，树状结构创建的综合时间复杂度最差的情况为O(n⁵)。采用文中的方法，开区域由于相互独立，无需排序；采取开闭区域独立填充的方案，也无需判断开闭区域之间的包含关系。依据左极点横坐标对闭区域排序，时间复杂度为O(n²)，由于是只对闭区域排序，数据规模远小于开闭区域一起排序。

4 等值线自动隐藏

关于等值线的疏密程度，在气象行业得到广泛应用的Surfer、MICAPS等软件都提供相关设置，通常是通过设置等值线的分析等级来实现，归纳起来，不外乎以下三种方法，一是设定等值线的等级间隔。比如温度场，可以设定每隔2 ℃画一条等值线；二是指定要分析的等级。比如降水场，可以根据降水量级指定0 mm、10 mm、25 mm、50 mm、100 mm、250 mm的分析等级；三是运用智能算法自动分配分析等级。对于连续场，上述方法已经很完善，但对于离散场，如果相邻两格点数据梯度太大，比如一个站点无降水，而另一相邻站点出现100 mm的局地大暴雨，采用上述方法获得的所有落在0~100 mm区间的分析等级都要画，还是会出现密集的等值线。实际上，受天气系统本身特征影响，降水空间分布不均匀，特别是强对流天气影响时，降水量空间差别巨大，不属于连续场，因此两格点间密集的等值线并无实际意义，而降水等值线图的宗旨在于直观地反映降水的空间分布特征，密集的等值线无疑降低了图形的显示效果，因此，有必要隐藏部分等值线，只保留能够反映分布特征的等值线，在实际业务应用中，以气象站点为格点构成的各类气象要素场，均可如此处理。

4.1 隐藏规则

等值线是计算机根据事先设置的分析等级自动绘制而成，要实现等值线的自动隐藏，难点在于如何让计算机能自动确定哪些等值线需要隐藏，如何自动适应隐藏后的颜色填充，遵循文中的有序标记原理，同时制定一个合理的隐藏规则，是保证自动隐藏的前提。通过观察人工绘图的习惯，可以确定隐藏的规则：任意两条等值线之间至少存在一个站点，也就是说，如果两条等值线之间不存在站点，就认为其中一条可以隐藏。如果是高值中心，只保留靠近中心的那一条，以突出高值中心的分布特征，其他的全部隐藏，反之，如果是低值中心，则保留靠近低值中心的那一条。

4.2 标记等值点

对于一张绘制完成的等值线图，容易识别需要隐藏的等值线，但计算机绘图是逐条等值线在网格中追踪而成，追踪的过程中无法确定哪条等值线需要隐藏，因此需要按照一个规则进行标记。一条网格边两格点之间往往有多条等值线通过，需要保留的等值线一定是靠近某一格点的那条，这个格点可能趋向低值中心，也可能趋向高值中心，因此，等值点标记时，需要体现格点的数值趋势，文中由高向低标记，靠近网格边高值格点的第一个等值点，标记为1，依次递增，靠近低值格点的那个等值点标记为9999，如果该网格边只有一条等值线通过，则标记为0。

4.3 确定等值线的弯曲特征

不同的弯曲特征决定了等值线是否需要隐藏，如果等值线弯向高值区，那么包含标记为1的等值点的等值线，都是要显示的，其他的均需要隐藏，反之，如果等值线弯向低值区，那么包含标记为9999的等值点的等值线，都是要显示的。实际情况，等值线往往很复杂，一条较长的等值线可能凹凸交错，要判断其弯曲特征很困难。通过观察等值线与网格的关系可以发现，如果一条等值线弯向某中心区域，通常情况下，等值线两侧的格点数是不相等的，格点少的一边趋向中心区域，具体地说，等值线两侧的网格点数值是不相等的，如果高值网格点的数量小于低值网格点的数量，可以认为等值线是弯向高值区的，反之，如果低值网格点数量小于高值网格点数量，等值线是弯向低值区的，这样就可以自动识别出需要隐藏的等值线了。

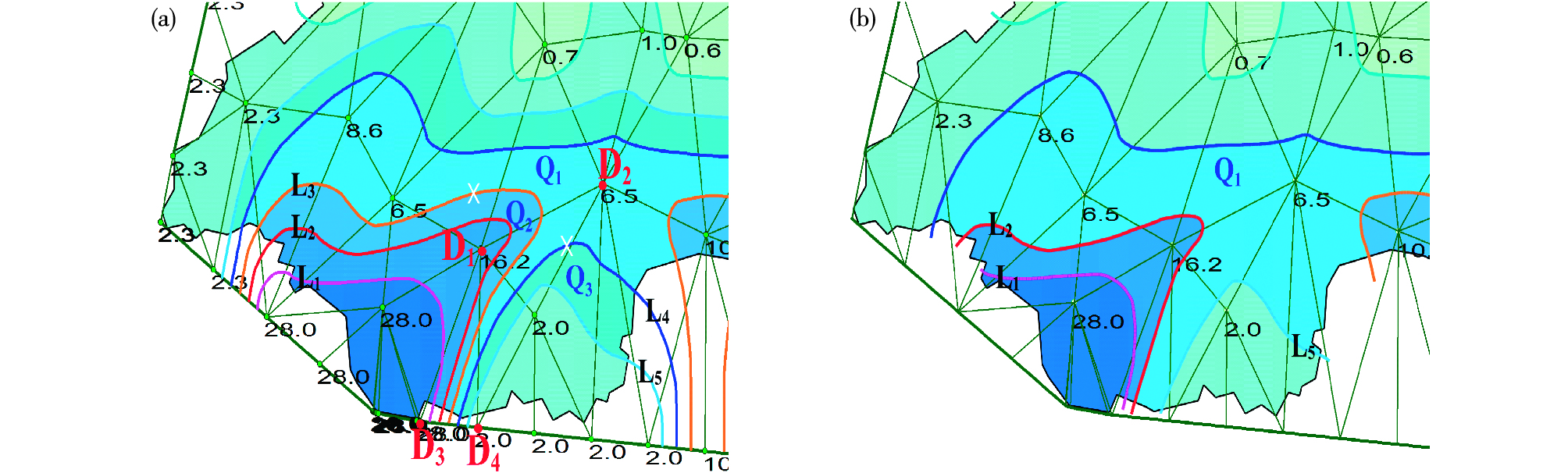
图 5a中，等值线L₁-L₅均与网格边$\overrightarrow{D_{3} D_{4}}$相交，D₃的数值大于D₄的数值，根据上述标记规则，等值点自左向右依次标记为1、2、3、4、9999。沿着逆时针方向，L₁-L₃的左侧为高值区，右侧为低值区，左侧的网格点数均小于右侧网格点数，因此弯向高值区，L₁上的等值点在所经过的网格边上均标记为1，L₂在网格边$\overrightarrow{D_{1} D_{2}}$上的等值点标记为1，均应该保留，而L₃在所有经过网格边上的等值点标记均不是1，需要隐藏；L₄-L₅沿着逆时针方向，左侧为低值区，右侧为高值区，左侧的网格点数均小于右侧网格点数，因此弯向低值区，L₅在所有经过的网格边上均标记为9999，应该保留，L₄在所有经过的网格边上的标记均不是9999，因此应该隐藏。

4.4 等值线隐藏后的填充处理

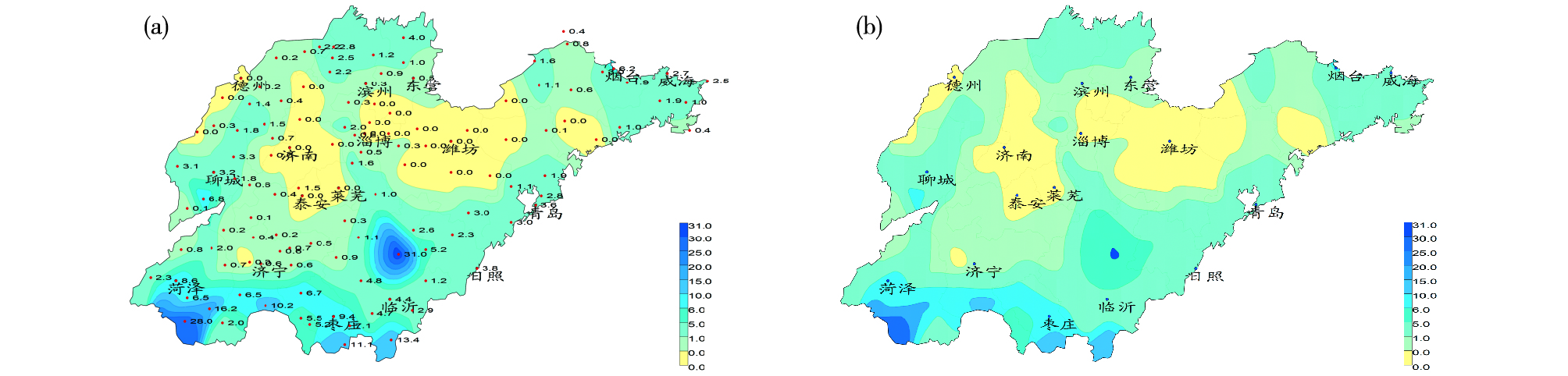
闭合区域的填充颜色是依据围成区域的等值线的线值来确定的，隐藏部分等值线后不受影响。对于开区域，按照逆时针方向，每个开区域的填充颜色由第一条与边界相交的开曲线线值确定，等值线被隐藏后，相对应开区域的填充颜色由最外层被隐藏等值线的线值来确定，这样得到的视觉效果是被保留下来的开区域延伸填充，因此，确定开区域填充颜色时，需要回溯到最外层被隐藏等值线，然后确定区域填充颜色。在图 5a中，多边形区域Q₁的填充颜色是由L₃的数值来确定的，Q₂的填充颜色由L₂的数值来确定，L₃隐藏后，按照搜索规则，由L₂的数值来确定原来Q₁、Q₂合并区域的颜色，这样的话，得到的效果就是原来Q₂区域延伸覆盖了原来Q₁区域(相当于Q₁被隐藏)，这与实际情况不符，因此需要回溯找到最外层的隐藏等值线L₃的数值来确定原来Q₁、Q₂合并区域的填充颜色，这样得到的效果是原Q₁区域延伸覆盖了原来的Q₂区域(原Q₂区域被隐藏)，同样的，原Q₃区域被隐藏，原Q₁区域延伸覆盖了原来的Q₃区域(图 5b)。图 6是采用自编软件制作的隐藏等值线前后的效果对比，图 6b中可以看出，隐藏部分密集的等值线后，只保留了高值中心部分的色斑，降水的空间分布更加清晰。

5 应用情况

基于VC++开发平台，自主开发的等值线分析业务软件，2000年开始应用于各类气象要素场的等值线绘图，早期版本采用FloodFill()函数填色，当种子点靠近边界线的时候，常有填色失败的情况，2014年全面改版，采用文中介绍的整体解决方案，自动创建逆时针方向的三角网格及网格边界，实现等值线的自动填充与隐藏。该软件与后台自动统计数据(逐日、周、旬、月、季、年)建立连接，根据预设的参数自动绘图，保证了农业气象日常业务制图的方便快捷；采用动态创建网格法，借助于粘贴板功能，把电子表格、文本文件、Microsoft Word文档甚至于QQ聊天中的数据复制到粘贴板上，程序就能读取粘贴板信息自动绘图，大大提高了临时制图的便利性。

6 结论与讨论

本文将三角网格与边界、等值线追踪、区域创建、属性值确定与排序作为一个整体来处理，依托有序标记和规律性网格特征，巧妙地利用位置关系来确定格点与区域、区域与区域之间的包含关系，全面摆脱传统方法的包含关系判别，显著减少计算量，提高运行效率。等值线的自动隐藏对于突显离散场的空间分布特征是有现实意义的，通过制定合理的隐藏规则，依托等值点的有序标记，计算机可以自动确定需要隐藏和显示的等值线；并自动适应部分等值线隐藏后的颜色填充，使计算机绘图更接近于人工绘图。

等值线图颜色填充的正确与否取决于多边形区域的填充顺序是否正确，一般是先填充的区域包含后填充的或者并列，因此需要确定区域之间的包含关系。判断区域包含关系的传统方法是将一个区域边界上所有格点装入数组，在内存中创建临时区域，然后在另一区域边界上选取参考格点，利用函数PtInRegion()进行判断，每次判别都要重复这个过程，占用内存较多而且复杂。文中方法则利用左极点的位置关系直接给出区域的包含关系，按照文中方法创建的开闭区域，左极点横坐标小的区域要么包含左极点横坐标大的区域，要么与之并列，因此，只需按照区域左极点的横坐标排序，即可自小到大(自左向右)一次完成颜色填充。

此方法依赖于每个环节的有序标记，从网格构建到等值线追踪，都会访问到具体的网格边，顺便记录下必要的信息，并不增加太多的计算量，计算机因此可以直接获取网格边信息，而不需要反复遍历网格数组和复杂的算法，效率自然得到提高。

文中介绍的方法是基于三角网格的，对于矩形网格，依据左极点横坐标对闭区域排序、比较等值线与左侧的边界点数值确定开区域属性值也同样适用，尽管等值线在一个矩形网格有三条可能的出边，但只有横向网格边上的等值点才可能是左极点，因此，左极点所在网格边的右端点也一定被该等值线围成的闭区域包含。