2. 中国海洋大学工程学院,山东 青岛 266100;
3. 国家海洋局北海分局,山东 青岛 266061
2. College of Engineering, Ocean University of China, Qingdao 266100, China;
3. State Oceanic Administration Beihai Branch, Qingdao 266061, China
很多研究表明,当流体遇到障碍物时,障碍物迎风面和背风面均会产生回流并伴随着漩涡脱落现象,且在不同流速下,现象有显著差异[1-2]。田东霞等[3]将障碍物迎风向的风速风向作为基准,与障碍物背风向不同距离处的风速风向做对比,得出障碍物对风速的衰减作用与背景风速大小有关,风速越大衰减作用越强的结论。
海气通量观测一般选择船基、塔基、浮标、石油平台等。王仁磊[4]选用“908专项”中通量数据质量相对较好的春季和秋季航次海洋气象和边界层数据资料,研究分析了如何滤除船体晃动造成的涡动相关系统观测误差。胡敦欣等[5]通过对船体运动和姿态的校正,消除船体运动对风资料的影响,基于涡动相关技术计算湍流通量,研究分析海气之间通量交换特征。王娟娟[6]基于一个海气界面通量浮标的观测数据,围绕海气界面通量的涡相关计算和参数化方法问题,展开了大气边界层湍流分析、非湍流运动对涡相关通量的影响等多方面的研究。徐静琦和魏皓[7]在离小麦岛岸边200 m的海底礁石上架设6 m高的铁塔,进行了海气通量观测实验,并利用梯度法计算通量。黄艳松[8]提出了一种去除浮标晃动对观测风速影响的晃动矫正方法,并以黄海北部连续14天的浮标观测资料为例,研究了晃动矫正对湍流能谱密度、协谱函数及海气通量的影响。
海气通量计算方法主要有梯度法、整体动力学法、遥感法和涡动相关法。梯度法计算通量,至少需要两层通量数据,适合运用到塔基的多层观测。整体输送法基于不同的经验公式和参数化方案,所以该方法有很大的不确定性。遥感法是利用卫星资料反演的算法,精度不高,不能满足边界层研究的需要。目前涡动相关法在通量的测量计算中被广泛运用,因为该方法观测和计算过程中几乎没有假设,具有坚实的理论基础[9]。其次是涡动相关系统没有任何动力响应元件,因而不存在风杯和螺旋桨风速仪所固有的非线性效应、惯性滞后等缺点[10-12]。基于涡动相关法,薛宇欢等[13]建立了新型的船载涡动系统,通过在渤海的实验观测,证实该系统可以有效去除船体运动对海气之间能量交换的影响。顾明[14]利用涡动相关法研究了北黄海、南海北部和吕宋海峡海域及西太平洋近海面部分特征量与水平平均风速的关系。王洁等[15]基于船基资料,通过对停航样本和走航样本资料的对比,引进带通滤波法去除船体影响,利用涡动相关法计算西北太平洋海域的湍流通量。闫俊岳等[16]采用涡动相关法和TOGA COARE2.5b版本的通量计算方案,计算了西南季风爆发前后南海海气通量,讨论了辐射、通量、海洋热量收支的时间变化特征及其与气象要素变化之间的关系。
Edson et al.[17]指出,利用涡动相关法计算海气通量时船体对气流的扰动会对通量观测造成影响,对动量通量大约有15%的系统误差。很多学者都选择盛行风向为仪器迎风向的季节进行实验[7],或者将仪器尽量安装在空旷、周围无大型障碍物的地方[4, 13, 15],以此来降低平台障碍物对风场的影响,并忽略此影响。海岸附近地形条件复杂,即便利用海上石油平台进行海气通量的观测,观测仪器附近环境也会对实际观测记录造成影响,但是很少有文献对平台障碍物对超声风速仪测量的迎风向数据有多大影响做出说明。夏季常出现前期为低风速条件下的强对流性天气,而海气通量对大气的垂直稳定度具有明显的影响,海气通量的更准确计算对于提高对流性天气预报的准确性可能具有潜在的意义和价值。本研究借助CFD模型,根据实际观测,定量研究了有效数据的选取范围,对比分析了迎风向数据产生的误差大小。
1 观测环境与数据处理通量系统安装在小麦岛八角亭外侧,八角亭在廊桥尽头,距离海面高11 m,其中六面墙宽1.6 m,两面墙宽1.5 m,亭盖内侧距地3 m,飞檐距地2.65 m。超声风速仪和红外气体分析仪安装在八角亭的西南侧(208°),悬臂长3 m,离亭面约1.2 m,其上有斜梁固定(图 1)。

|
图 1 通量观测环境及仪器安装环境(a.小麦岛八角亭外部环境图,b.超声风速仪和红外气体分析仪安装图) Fig.1 The site of flux observation (a. outside Octagonal Pavilion at Xiaomai Island; b. installing the ultrasonic anemometer and the infrared gas analyzer) |
利用CFD分别在2 m·s-1、4 m·s-1和6 m·s-1风速下对八角亭周围风场进行了模拟计算,选取在不同的背景风下障碍物对风场影响最小的区域。
1.1.1 GAMBIT建模与网格划分GAMBIT是面向CFD分析的高质量前处理器,其主要功能包括几何建模和网格生成。为使计算域的设置不影响计算结果,需使计算域的边界离物体足够远,使得边界对研究对象的影响忽略不计[18],本研究中将流域设置为70 m×50 m×60 m。本文对计算区域进行体网格划分,为使网格较为平滑,对亭子近壁区进行适当加密,在其他区域的网格逐渐稀疏。由于亭子实体较为复杂,所以对模型进行简化,具体模型和网格划分情况如图 2所示。

|
图 2 通量平台障碍物模型和计算域(a)及计算域体网格划分情况(b) Fig.2 The model and calculation domain (a) designed for flux platform obstacles & mesh generation (b) of the calculation domain |
FLUENT是通用CFD软件包,用来模拟从不可压缩到高度压缩范围内的复杂流动,本研究利用FLUENT进行求解计算,边界条件设置为:入口为速度入口,出口为压力出口,其他壁面为wall类型, 亭子设置为壁面,中间流体为空气。湍流模型选择RNG κ-ω模型,采用SIMPLEC算法求解压力与速度相关的控制方程组。由于模型整体为对称结构,故定义入口方向为西南方向(即通量观测仪器架设方向208°)。
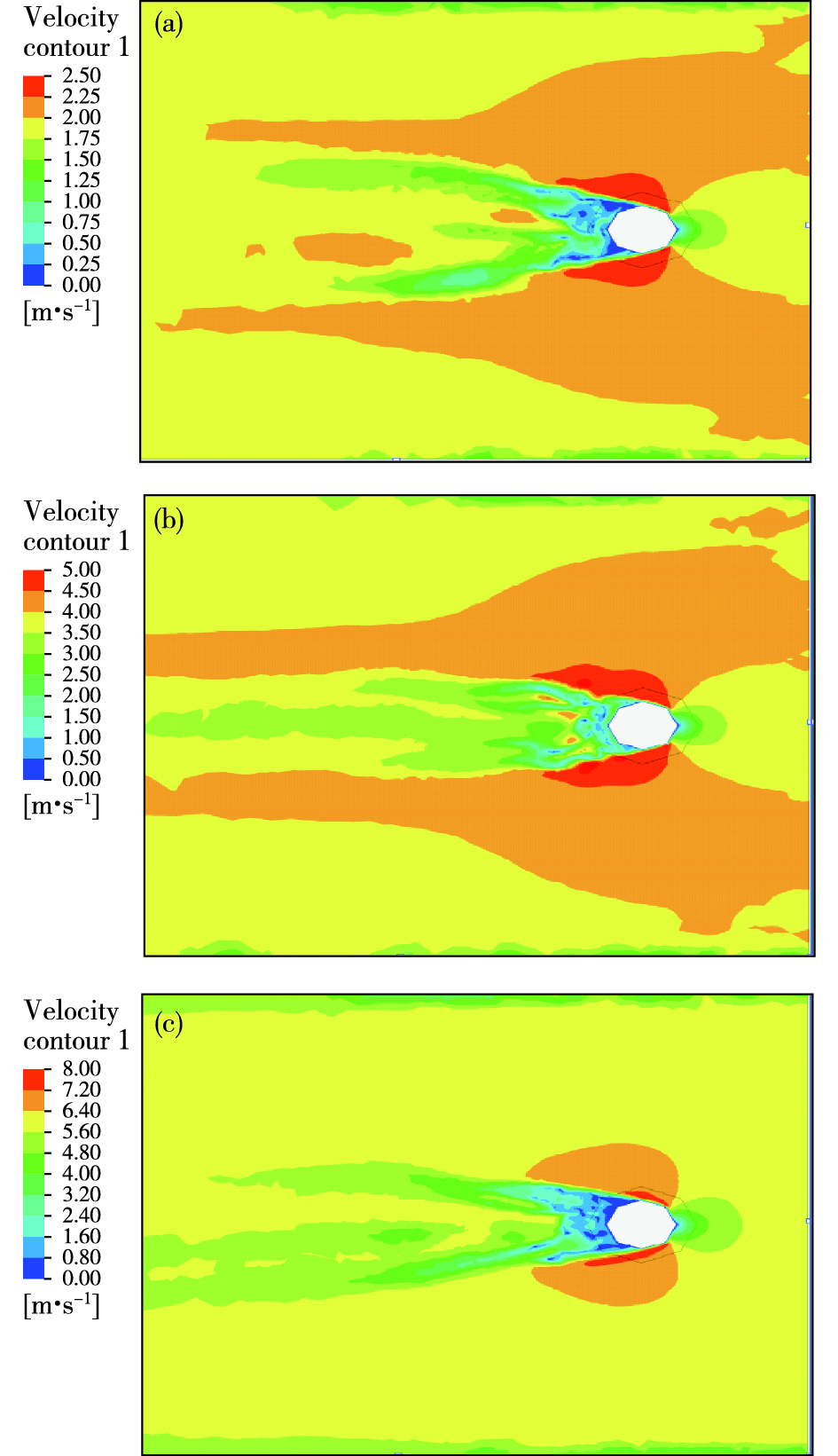
模拟发现,由于亭子的作用导致风场绕流现象(图 3),亭子两侧的速度最大,前后速度较小,前面由于壁面作用,风会撞击在亭子上导致速度降低,后面由于亭子的阻挡风速减小。在前人的研究中,往往忽略平台迎风向的壁面作用,直接利用超声风速仪的迎向数据进行通量计算。
|
图 3 不同风速下八角亭周围风场绕流情况(a. 2 m·s-1,b. 4 m·s-1,c. 6 m·s-1) Fig.3 Wind flow around Octagonal Pavilion under different wind speed conditions (a. 2 m·s-1, b. 4 m·s-1, c. 6 m·s-1) |
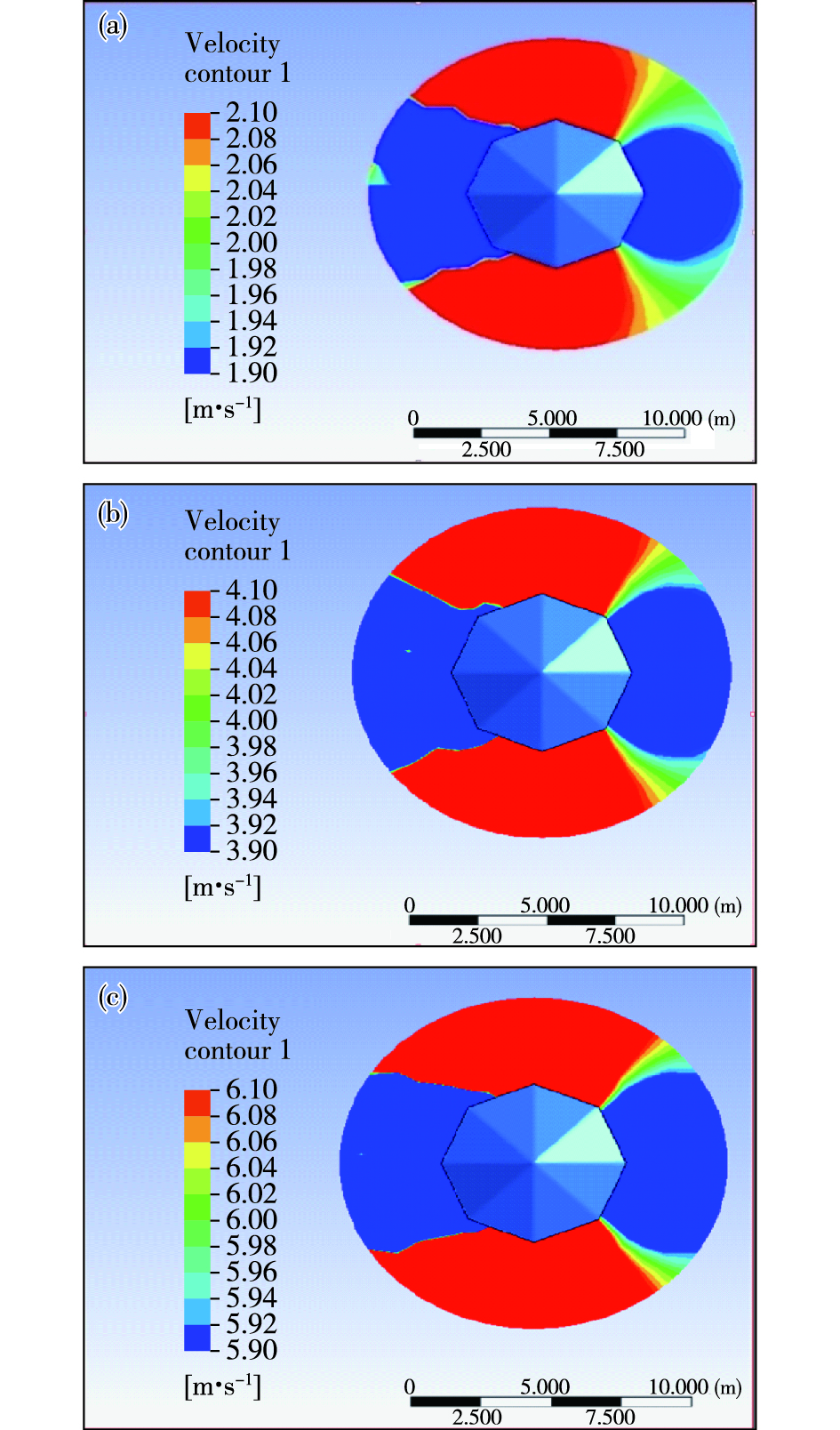
图 3分别模拟了背景风为2 m·s-1、4 m·s-1、6 m·s-1下的亭子周围流场。图 4是对不同风速下最优观测角度的测量。图 4中红色表示在受到观测平台影响后,速度增大区域。蓝色表示速度受影响减小的区域。与图 3方向一致,图 4右侧蓝色区域表示平台障碍物迎风向风场情况,左侧蓝色区域表示背风向风场情况。黄色、绿色区域风速大小接近模拟时的背景风,代表平台障碍物对风场影响最小的区域,此时风速的相对误差在3%以内。以迎风向蓝色区域中心为起点,分别向右向左测量黄色、绿色区域的范围及与起点的偏角。发现风速为2 m·s-1时,风向与仪器朝向偏16°~64°时,观测数据受平台的影响最小。在本研究中超声风速仪探头朝西南方208°架设,即影响最小角度为地理方位144°~192°或224°~272°。风速为4 m·s-1时,偏35°~50°影响最小,风速为6 m·s-1时,偏37°~47°影响最小。可以看出风速越大,不受平台影响的角度范围越小,或者说平台障碍物对仪器测量影响范围越大。
|
图 4 不同风速条件下八角亭周边最优观测角度测量(a. 2 m·s-1,b. 4 m·s-1,c. 6 m·s-1) Fig.4 Optimum observation angle around Octagonal Pavilion under different wind speed conditions (a. 2 m·s-1, b. 4 m·s-1, c. 6 m·s-1) |
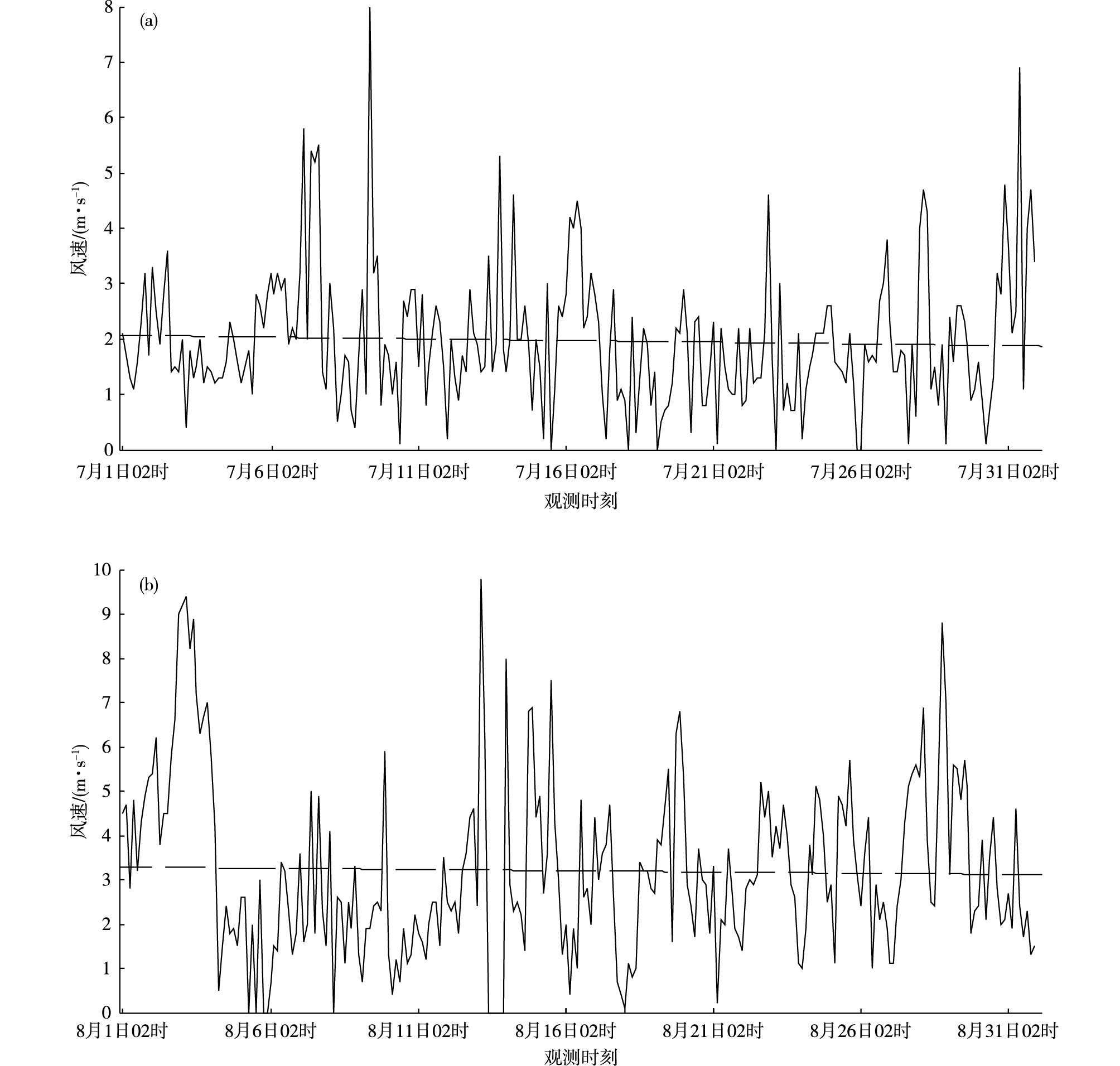
根据7、8月的风速序列图(图 5)可知,7、8月的风速较为稳定,大都在2~3 m·s-1上下波动,为使7月和8月两个月形成对比,本研究选取背景风为2 m·s-1进行计算分析,选取范围为1.5~2.5 m·s-1。
|
图 5 2017年7(a)、8(b)月风速(单位:m·s-1)时序图 Fig.5 Time series of wind speed (units: m·s-1)in July (a) and August (b) 2017 |
根据FLUENT模拟结果与图 4测量结果,定义风向在蓝色区域的为迎向风,下文简称迎向。风向在黄色、绿色区域的为侧向风,下文简称侧向。根据小麦岛观测站提供的每3 h一次的自动气象站数据,对于2 m·s-1的背景风,取风向144°~192°和224°~272°为侧向风,取风向192°~224°为迎向风。为保证在相近的背景天气下比较迎向和侧向通量,日期相邻,夜间时刻限制在20时—次日02时(北京时),白天时刻限制在11—14时(北京时)。表 1列出了观测资料选取的具体日期和时刻。7月11—12日,青岛处于副热带高压北侧的偏西气流中,地面气压稳定在1 008 hPa左右,地面10 m风以西南风为主。7月8日,青岛处于低压南侧的西南风中。随后该低压系统不断向东北移动,副热带高压北上。7月14日,青岛受副热带高压西侧的偏南风影响。所以,7月8日和14日这两天的天气系统有一定的变动,而且该组数据选取角度主要在通量观测仪的西侧,可能受陆地影响大,故对该组数据不做计算分析。8月26—27日副热带高压北线到达青岛地区,青岛完全被副热带高压控制。这段时间内,地面始终受到高压西侧影响,10 m高度风以东南风为主。
|
|
表 1 不同风向的数据选取时间 Table 1 Data selection time for different wind directions |
根据表 1选取的时刻,前后各延0.5 h选取10 Hz高频资料,计算通量时做10 min平均,1 h得出来的6组数据,称为6个研究样本。
1.3 通量计算利用7、8月的观测数据,结合CFD模拟结果选取八角亭上超声风速仪对应方向的数据,利用涡动相关法计算迎向和侧向的海气通量,对比分析海气通量的差异。
本文利用涡动相关法进行通量计算,主要参考王介民[19]涡动相关通量观测指导手册2012年版本。动量通量τ,感热通量H,潜热通量λLE分别按照以下方法计算:
| $ \tau=\left[\left(\overline{w^{\prime} u^{\prime}}\right)^{2}+\left(\overline{w^{\prime} v^{\prime}}\right)^{2}\right]^{1 / 2} $ | (1) |
| $ H=\rho C_{p} \overline{w^{\prime} \theta^{\prime}} $ | (2) |
| $ \lambda L_{E}=\lambda \rho \overline{w^{\prime} q^{\prime}} $ | (3) |
其中,ρ是空气密度,Cp是定压比热,λ是蒸发潜热,均为常数,故本文λLE表示海气之间的潜热通量,
利用涡动相关法计算通量时,要对超声风速仪测得的原始数据进行质量控制和预处理,以及对得出的通量数据进行后处理,主要包括以下几项。
1)野点去除。运用通量处理软件Edire中的“野点去除”的方法。
2) 坐标旋转(采用二次旋转)。第一次旋转为x-y平面绕z轴旋转,使x-z平面与平均风向一致,平均v=0。如测量的风速分量用下标m表示,则新坐标系的各分量为:
| $ \begin{array}{c}{u_{1}=u_{m} \cos \alpha+v_{m} \sin \alpha} \\ {v_{1}=u_{m} \sin \alpha+v_{m} \cos \alpha} \\ {w_{1}=w_{m}}\end{array} $ | (4) |
其中,旋转角
第二次旋转为新的x-z平面绕y轴旋转,使平均w=0:
| $ \begin{array}{c}{u_{2}=u_{1} \cos \beta+w_{1} \cos \beta} \\ {v_{2}=v_{1}} \\ {w_{2}=-u_{1} \sin \beta+w_{1} \cos \beta}\end{array} $ | (5) |
其中,旋转角
3) 感热通量的超声虚温修正。超声风速仪输出的温度实际上是与空气湿度有关的虚温Ts,按照Van Dijk et al.[20]提出的方案,由T=Ts/(1+0.51q),近似得:
| $ \overline{{{w}^{\prime }}{{T}^{\prime }}}=\overline{{{w}^{\prime }}T_{s}^{\prime }}-0.51\bar{q}\overline{{{w}^{\prime }}T_{s}^{\prime }}-0.51\overline{{{T}_{s}}}\overline{{{w}^{\prime }}{{q}^{\prime }}}\ $ | (6) |
进而有q=ρv/ρa,最终感热通量为:
| $ \begin{aligned} H=&\left(1-0.51 \overline{q^{\prime}}\right) \rho C_{p} \overline{w^{\prime} T_{s}^{\prime}}-\\&0.51 \rho C_{p}\left(\overline{T} / \rho_{a}\right) \overline{w^{\prime} T_{s}^{\prime}} \end{aligned} $ | (7) |
4) WPL修正。Webb et al.[21](WPL)指出,如果空气密度有脉动,应考虑由垂直平均流动引起的输送,所以修正后的潜热通量为:
| $ \lambda L_{E}=\lambda \overline{w^{\prime} \rho_{v}^{\prime}}+\lambda \overline{\mu \sigma w^{\prime} \rho_{v}^{\prime}}+\lambda(1+\mu \sigma) \frac{\overline{\rho_{v}}}{\overline{T}} w^{\prime} \overline{T^{\prime}} $ | (8) |
其中,μ为1.608,σ为干空气与水汽的密度比。
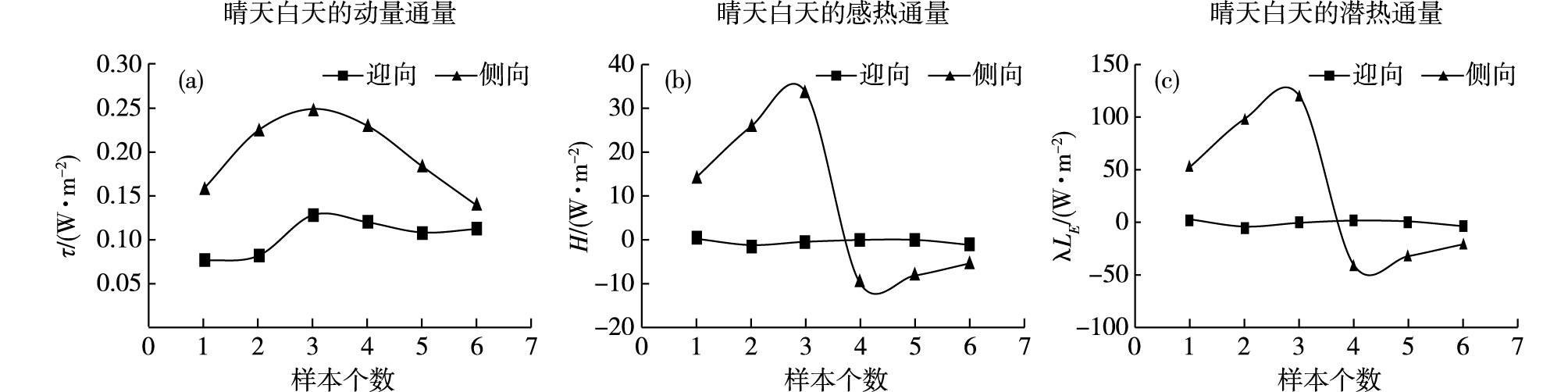
2 结果分析图 6显示了7月不同风向下的通量变化,可以看出,潜热与感热通量变化趋势基本一致,但潜热远远大于感热,说明海气之间的热量传输主要以潜热释放为主,这是海洋上海气通量的一般特性。动量通量始终在零值周围波动(图 6a),且迎向小于侧向,说明通量观测平台对迎向的动量通量有削弱作用。侧向的感热通量和潜热通量均有正有负,说明有一段时间是大气向海洋传输热量,有一段时间是海洋向大气传输热量,但是迎向的感热通量和潜热通量变化幅度不大(图 6b、c)。为了验证这种现象是否普遍存在,对8月的数据做进一步分析。
|
图 6 7月2 m·s-1时不同风向下的海气通量对比(a.动量通量,b.感热通量,c.潜热通量) Fig.6 Comparison of air-sea flux in different wind directions at the wind speed of 2 m·s-1 in July (a. momentum flux; b. sensible heat flux; c. latent heat flux) |
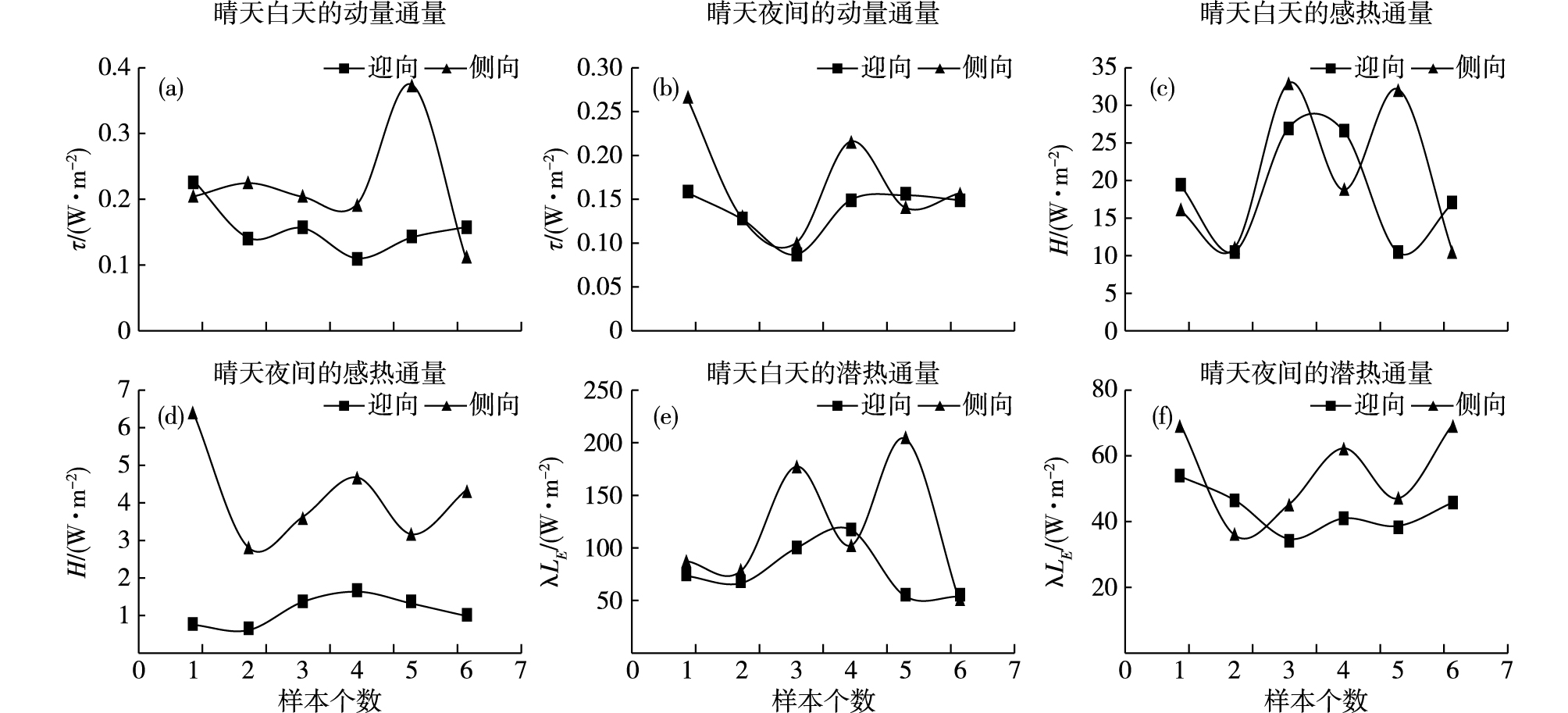
图 7显示了8月不同风向下的通量变化,图 7a和图 7b分别显示了白天和夜间不同方向的动量通量,可以看出不论白天还是夜间,动量通量始终在零值附近波动,且迎向小于侧向,这与7月的动量通量情况一致。白天和夜间的感热通量(图 7c、d)和潜热通量(图 7e、f)均为正值,且出现了迎向小于侧向的现象,这与7月的热量通量情况一致。以上分析说明,以往按照经验处理迎向的通量观测数据时,会低估海气间的动量通量和热量通量。
|
图 7 8月风速度2 m·s-1时不同风向下的海气通量对比(a、c、e.白天,b、d、f.夜间) Fig.7 Comparison of air-sea flux in different wind directions at the wind speed of 2 m·s-1 in August (a, c, e. day; b, d, f. night) |
表 2统计了通量观测仪器测得的迎向和侧向的10 min平均风速,用平均风速减去背景风2 m·s-1,假定偏差的绝对值<0.5 m·s-1,即风速大小在1.5~2.5 m·s-1之间的数据是超声风速仪测得较准确的数据。那么,迎向时较好数据只有41.5%(7、8月迎向时较好数据分别占总样本数的16.7%、66.7%),而侧向时达70.9%(7、8月侧向时较好数据分别占总样本数的50.0%、91.7%)。
|
|
表 2 7月和8月10 min平均风速统计表 Table 2 Average wind speed in 10 min in July and August |
利用CFD对通量观测平台周围的2 m·s-1、4 m·s-1、6 m·s-1风场做了模拟,发现除平台障碍物对背风面风场产生很大的影响外,障碍物迎风面同样也会有影响。利用7、8月的自动站观测资料与通量观测资料,对2 m·s-1风速下迎向、侧向的动量通量和热通量进行计算比较,得到如下结论:
1) 风向与通量观测仪器有一定的偏角时,受到平台障碍物影响最小。选取盛行风方向的数据计算通量会产生一定的偏差,风速越大,偏差越大。
2) 通过对比迎向、侧向的动量通量和热量通量,发现不论夜间还是白天,迎向的动量通量、感热通量、潜热通量均小于侧向,说明选取迎向数据计算的动量通量和热量通量可能比实际偏小。
3) 通过计算风速的变化,发现迎向风速更容易受到通量平台的干扰,风速准确率小于侧向。
4) 若已知一段时间的盛行风向,在平台上安装仪器时,与盛行风向偏转一定的角度,可使测量的数据更接近实际情况,需要通过流体力学模拟来确定该角度。
利用CFD模型细致刻画了平台障碍物对观测的影响,说明在海上进行高频通量观测时不能凭经验选取迎风向数据作为有效数据。
由于选取数据时需要受风向和风速两个条件的约束,研究采用的样本还不是很多,今后需要更多的数据对文中结论做进一步说明。
| [1] |
金思宇, 张治国, 吴琦. 流速对圆柱绕流旋涡脱落的分析[J]. 化学工程与装备, 2012(12): 48-52. |
| [2] |
吉鸿敏. 圆柱桥墩绕流的数值模拟研究[D]. 杨凌: 西北农林科技大学, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10712-1015332391.htm
|
| [3] |
田东霞, 郭建侠, 陈挺, 等. 障碍物对风速风向影响的观测试验[J]. 气象科技, 2014, 42(5): 881-887. DOI:10.3969/j.issn.1671-6345.2014.05.027 |
| [4] |
王仁磊. 北黄海春秋季海气通量的观测研究[D]. 青岛: 中国海洋大学, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10423-2009171645.htm
|
| [5] |
胡敦欣, 赵永平, 陆蔼庆, 等. 船上海气之间湍流通量的观测研究[J]. 海洋与湖沼, 1996, 27(2): 163-168. DOI:10.3321/j.issn:0029-814X.1996.02.008 |
| [6] |
王娟娟. 海气通量的涡相关计算和参数化方法研究[D]. 北京: 中国科学院大学, 2013. http://cdmd.cnki.com.cn/Article/CDMD-80068-1013299948.htm
|
| [7] |
徐静琦, 魏皓. 青岛市海雾海气通量观测及其作用初探[J]. 气象学报, 1996, 54(2): 207-215. |
| [8] |
黄艳松. 基于浮标观测资料的海气通量计算方法研究[D]. 青岛: 中国科学院研究生院(海洋研究所), 2011. http://cdmd.cnki.com.cn/Article/CDMD-80068-1011093961.htm
|
| [9] |
陈陟, 吴志明. TOGA—COARE IOP期间的海气通量观测结果[J]. 地球物理学报, 1997, 40(6): 753-762. DOI:10.3321/j.issn:0001-5733.1997.06.004 |
| [10] |
Baldocchi D, Meyers T. On using eco-physiological micrometeorological and biogeochemical theory to evaluate carbon dioxide, water vapor and trace gas fluxes over vegetation[J]. Agric For Meteor, 1998, 90(1/2): 1-25. |
| [11] |
Baldocchi D, Valentini R, Running S, et al. Strategies for measuring and modelling carbon dioxide and water vapour fluxes over terrestrial ecosystems[J]. Glob Change Biol, 1996, 2(3): 159-168. DOI:10.1111/gcb.1996.2.issue-3 |
| [12] |
Aubinet M, Grelle A, Ibrom A, et al. Estimates of the annual net carbon and water exchange of forests: the EUROFLUX methodology[J]. Adv Ecolog Res, 2000, 30(1): 113-175. |
| [13] |
薛宇欢, 高会旺, 高增祥. 船载涡动相关观测系统及其有效性研究[J]. 中国海洋大学学报(自然科学版), 2009, 39(增刊): 177-183. |
| [14] |
顾明. 海-气动量通量及海洋大气边界层湍流特征分析[D]. 青岛: 中国海洋大学, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10423-1011030044.htm
|
| [15] |
王洁, 段自强, 姚小红, 等. 西北太平洋船载海面风速脉动资料校正及湍流特征分析[J]. 热带海洋学报, 2013, 32(3): 9-15. DOI:10.3969/j.issn.1009-5470.2013.03.002 |
| [16] |
闫俊岳, 唐志毅, 姚华栋, 等. 2002年南海季风爆发前后西沙海区海-气通量交换及其变化[J]. 地球物理学报, 2005, 48(5): 1000-1010. DOI:10.3321/j.issn:0001-5733.2005.05.005 |
| [17] |
Edson J B, Hinton A A, Prada K E, et al. Direct covariance flux estimates from mobile platforms at sea[J]. J Atmos Oceanic Technol, 1998, 15(2): 547-562. DOI:10.1175/1520-0426(1998)015<0547:DCFEFM>2.0.CO;2 |
| [18] |
熊凤鸣. 基于Fluent的高耸塔体风荷载数值模拟[J]. 化工与医药工程, 2016, 37(6): 18-23. |
| [19] |
王介民. 涡动相关通量观测指导手册[R]. 2012: 9-16.
|
| [20] |
Van Dijk A, Moene A F, De Bruin H A R. The principles of surface flux physics: Theory, practice and description of the ECPACK library[R]. Meteorology and Air Quality Group, Wageningen University, 2004: 99.
|
| [21] |
Webb E K, Pearman G I, Leuning R. Correction of flux measurements for density effects due to heat and water vapour transfer[J]. Quart J Roy Meteor Soc, 1980, 106(447): 85-100. DOI:10.1002/(ISSN)1477-870X |
 2018, Vol. 38
2018, Vol. 38


