2. 青岛市气象灾害防御工程技术研究中心,山东 青岛 266003;
3. 淄博市气象局,山东 淄博 255000
2. Qingdao Engineering Technology Research Center for Meteorological Disaster Prevention, Qingdao 266003, China;
3. Zibo Meteorological Bureau, Zibo 255000, China
海雾是海面上大气水平能见度(简称能见度)降低到1 km以下的天气现象[1]。海雾形成后,大多数向下风向扩展,可影响到沿海地区,给海上和沿海地区的交通、各种海上作业带来严重影响。黄海是我国几个边缘海中海雾出现频率最高的海区[2],青岛位于黄海之滨,每年4—7月频受海雾影响[3],准确预报海雾的发生及大气低能见度的演变至关重要。
海雾的预报方法主要有天气学方法、统计预报方法以及数值预报方法[4],均在我国沿海地区海雾的业务预报中取得了一定成效[3, 5-9],尤其是随着数值预报技术的快速发展,通过在数值模式后处理模块中增加雾的诊断算法,我国初步建立了黄渤海、华东沿海海雾数值预报系统,为沿海地区海雾预报业务提供了技术支撑[8-9]。数值预报方法可以实现海雾及大气低能见度的精细化预报,弥补了天气学以及统计学方法预报海雾的不足,但由于海上观测资料的匮乏以及海雾形成物理过程的复杂性,海雾预报准确率以及能见度精细化预报水平仍有待不断提高。能见度演变属于复杂的大气光学现象,导致其变化的直接原因是大气中气溶胶的变化,而气溶胶的变化是受气象条件和气象要素所制约的[10]。因此,海雾及能见度预报的准确性一方面取决于模式对与海雾形成的相关气象要素的预报准确性,另一方面取决于基于气象要素的能见度算法。国外学者根据当地观测资料提出了多种能见度算法,最常用的算法是基于能见度和液态水含量的经验关系[11-15],经验公式系数略有差异,傅刚等[16]对黄海海雾的个例研究表明,不同经验公式计算的能见度差异较小。此外,还有算法基于相对湿度[17]或相对湿度与温度露点差[18]实现能见度计算。上述能见度算法都是利用当地观测资料确定的,Bang et al.[19]以及林艳等[20-21]的研究表明,不同环境条件下,利用数值模式做雾及能见度的预报,需要对能见度算法的适用性做进一步检验。
本文利用WRF模式对2014—2016年青岛近海海雾个例的模拟结果,根据3种算法分别计算了能见度,旨在研究当数值模式及其所用初始场已经确定的前提下每种算法的能见度预报情况,以确定一个适用于本地的能见度算法。
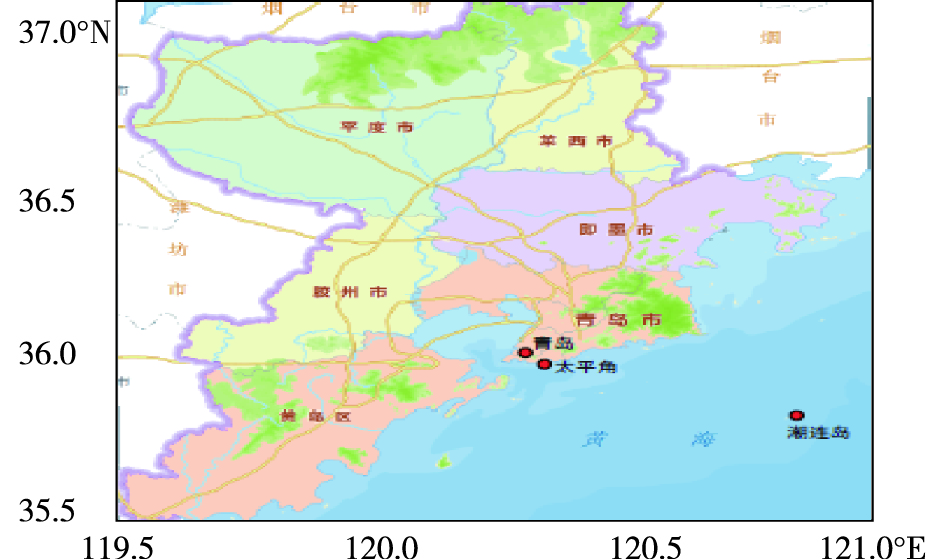
1 数据及能见度算法简介 1.1 观测资料所用数据包括2014—2016年高空、地面常规气象观测资料以及沿海站青岛站、岸基站太平角站和海岛站潮连岛站等3个自动站(图 1)逐小时气象观测资料。其中,青岛站为国家基准气候站,经纬度为36.07°N、120.33°E,海拔高度76 m,相对海洋距离在2 km以内;太平角站为岸基站,经纬度为36.05°N、120.37°E,海拔高度25 m,相对海洋距离在50 m以内;潮连岛站为海岛站,经纬度为35.89°N、120.88°E,海拔高度52 m,距离青岛站50 km左右。太平角站和潮连岛站均为区域自动站,是上海长望公司DZZ3型6要素(风、温、压、湿、能见度和降水)自动气象站;青岛站为DZZ4型7要素自动站,增加了露点温度观测。这3个站能见度情况基本可以代表青岛近海海域及沿海地区的海雾情况。
|
图 1 自动气象站分布(红实心圆为青岛站、太平角站、潮连岛站所在位置) Fig.1 Distribution of automatic meteorological stations (Red solid circles for locations of Qingdao Station, Taipingjiao Station and Chaolian Island Station) |
基于天气形势以及能见度小于1 km、风向为偏南风、有雾时无强降雨等条件初步挑选了25个海雾个例(表 1)。就这25个个例而言,太平角站海雾持续时间较其他两站要偏长,持续时间平均为15 h,青岛站持续时间最短平均为10 h;从最小能见度来看太平角站海雾最强,一般每次过程最小能见度为0.1 km左右。
|
|
表 1 25个海雾个例日期及各站雾起止时间、持续时间和最小能见度 Table 1 The date, start and end time, duration and minimum visibility of 25 selected sea fog cases |
所用模式为WRF V3.3,模式覆盖区域110~140°E,25~45°N,水平分辨率为9 km,模式背景场为GFS全球模式预报,模式结果逐时输出,其他参数设置见表 2。模式采用了ADAS(ARPS Data Assimilation System)即中尺度预报模式ARPS的数据同化系统[22],这是一个能同化常规、非常规资料的中尺度分析系统,最初由俄克拉荷马州立大学开发,2009年上海台风所引进到华东区域数值预报模式系统SMB-WARMS[9]。ADAS采用了Bratseth连续迭代方法、微物理调整系统和复杂云分析系统,对地面观测、探空资料、雷达资料等进行同化和三维云分析。本文中ADAS同化的观测数据包括模式范围内探空观测和地面气象站观测(包括常规天气观测SYNOP,船舶观测SHIP,机场地面报METAR,浮标BUOY等),为模式提供初始场,空间分辨率为9 km。
|
|
表 2 WRF模式参数设置 Table 2 Parameter settings for WRF model |
选用的3种能见度算法如下。
1) Steolinga and Warner(SW99)算法。
SW99算法[12]基于液态水含量,液态水含量包括云水(cw)、云冰(ci)、雨水(rw)、雪水(sn)混合,综合考虑了多种水凝性物质对消光系数的影响,即:
| $ \frac{\begin{matrix} \mathit{vis}(\text{km})= \\ -\ln (0.02) \\ \end{matrix}}{144.7\mathit{c}{{\mathit{w}}^{0.88}}+1.1\mathit{r}{{\mathit{w}}^{0.75}}+163.9\mathit{c}{{\mathit{i}}^{1.00}}+10.4\mathit{s}{{\mathit{n}}^{0.78}}} $ | (1) |
本研究利用模式输出的最低层液态水含量计算的能见度[29],该算法当计算的能见度数值大于20 km时,设定能见度为20 km。
2) Forecast Systems Laboratory (FSL)算法。
FSL算法由美国NOAA预报系统实验室研发,基于相对湿度RH和温度露点差[18],即:
| $ \mathit{vis}\left( \text{mile} \right)=6\ 000\times \frac{t-{{t}_{d}}}{R{{H}^{1.75}}} $ | (2) |
其中1mile=1.609 344 km。该算法当相对湿度为100%时,能见度为0 km。
3) CVIS(Combined Visibility)算法。
CVIS算法是基于SW99算法和FSL算法的混合算法,同时计算两种能见度,取能见度较小的[19],即:
| $ \mathit{vis}(\text{km})=\min (\text{SW}99, \text{FSL}) $ | (3) |
为了解模式结果的可靠性,首先对模式输出的与海雾形成有关的近地面层要素(2 m温度、10 m风速以及2 m温度露点差和相对湿度)进行了均方根误差(RMSE)检验,另外,也进行了晴雨检验。青岛站观测要素最为齐全,所以检验基于该站进行,每个个例RMSE检验时次为实际有雾时次,其公式为:
| $ X=\sqrt{\frac{\sum\limits_{i=1}^{n}{{{\left( {{X}_{\text{obs}, i}}-{{X}_{\text{model}, i}} \right)}^{2}}}}{n}} $ | (4) |
其中,Xobs, i为i时次自动站能见度观测值,Xmodel, i为i时次该站点能见度预报值,n为每个个例海雾持续时间。
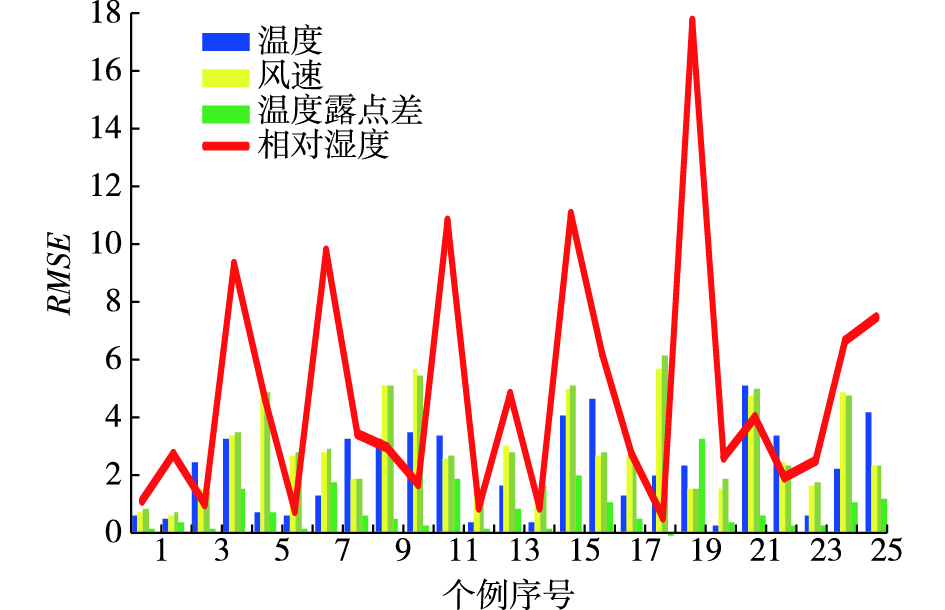
初选25个海雾个例中,2 m气温RMSE介于0.2~4.8 ℃之间,平均为2.1 ℃;温度露点差预报误差总体上要小于温度预报误差,RMSE介于0.1~3.0 ℃之间,平均为0.7 ℃;10 m风速RMSE介于0.5~5.3 m/s之间,平均为2.7 m/s;2 m相对湿度RMSE介于0.4%~16.4%之间,平均为4.4%。庄晓翠等 指出,均方根误差<4.5个单位可评价要素预报具有参考价值。如图 2所示,2 m气温1例、10 m风速5例、相对湿度8例RMSE大于4.5个单位。根据能见度计算公式,露点温度差和相对湿度两个要素预报水平对能见度至关重要,所以剔除了这两个要素预报均方根误差大于4.5个单位的个例(4、7、11、15、16、19、24、25)。降水检验结果表明,青岛站无降水15次,有降水10次,其中1.0 mm以上降水3次,雾出现于降雨接近结束阶段,1.0 mm及以下降水7次,主要为伴随雾出现的毛毛雨。模式预报有雨正确10次,预报无雨正确8次,空报7次,无漏报,可见模式对72%个例是预报准确的。雨量预报上,个例24、25与实况差异较大,按上面个例筛除标准这两个个例被删除,这样WRF模式基本可满足有雾时无强降雨的条件。
|
图 2 青岛站25个初选海雾个例2 m气温(单位:℃)、温度露点差(单位:℃)、10 m风速(单位:m/s)、2 m相对湿度(单位:%)的均方根误差 Fig.2 RMSE of surface temperature (units: ℃) at 2 m, depression of the dew point (units: ℃), wind speed (units: m/s) at 10 m and relative humidity at 2 m at Qingdao station based on 25 sea fog cases |
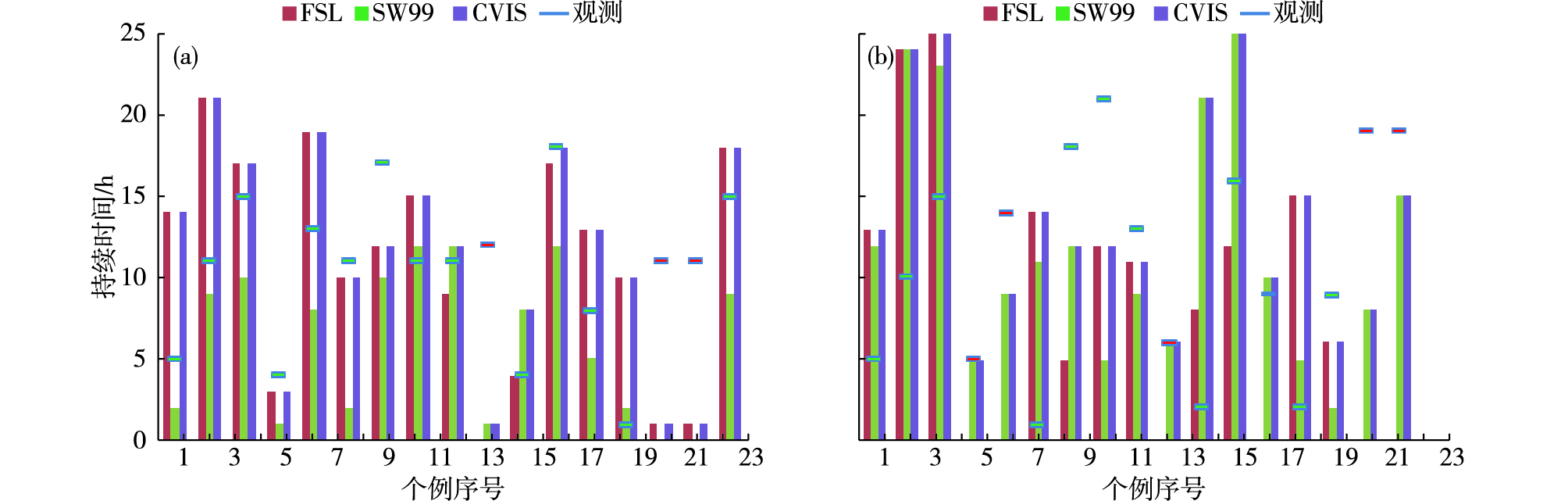
为了解基于WRF模式的各种算法对青岛近海海雾的预报准确性,对所选17个个例均进行了有雾、无雾的检验,即对某一站点的某一海雾个例各算法计算的能见度小于1 km即预报该站有雾正确,否则为漏报。图 3a、b分别为青岛站和潮连岛站17个海雾个例雾持续时间与不同算法预报的雾持续时间对比,持续时间为0表明该算法预报无雾。
|
图 3 青岛(a)、潮连岛(b)雾实际持续时间与不同算法预报的持续时间对比 Fig.3 Observed and forecast duration of sea fog cases at Qingdao Station (a) and Chaolian Island Station (b) |
所选17个海雾个例中,对于青岛站而言(图 3a),FSL算法、SW99算法、CVIS算法漏报次数分别为1次、2次、0次。CVIS算法预报准确率为100%,FSL算法为94%,SW99算法为88%。对于太平角站(图略),三种算法漏报个例与青岛站相同。对于潮连岛站(图 3b)而言,FSL算法漏报次数增加到6次,而SW99算法、CVIS算法无漏报,这样FSL算法预报准确率降为65%,SW99算法和CVIS算法预报准确率为100%。雾有无预报准确率较高,是因为没有考虑非海雾日时模式及算法的空报个例情况。
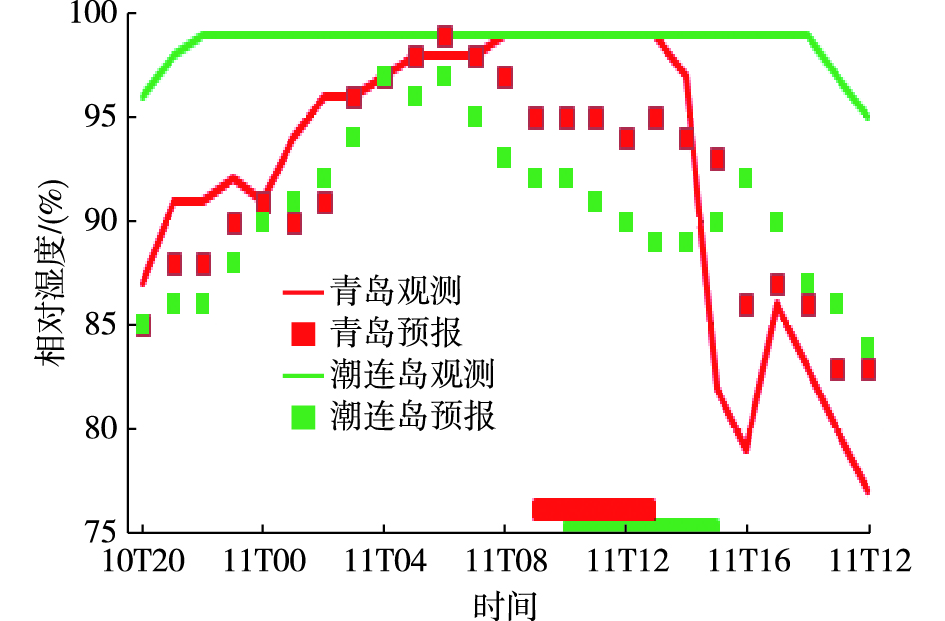
可见,基于WRF模式的不同能见度算法对不同测站预报准确率有所不同。其中,CVIS算法由于综合考虑了SW99算法和FSL算法,对3个站均无漏报,预报准确率为100%;对于沿海站青岛站、太平角站而言,FSL算法略优于SW99算法;对于海岛站潮连岛站而言,SW99算法则明显优于FSL算法。FSL算法对于沿海站与海岛站这种海雾预报准确率的差异与模式对沿海站的相对湿度预报准确率略高于海岛站有关。以个例5为例,基于FSL算法计算的能见度可预报青岛站有雾,但是潮连岛站雾漏报(图 3),由图 4不难发现,潮连岛站相对湿度预报误差明显大于青岛站,而且整个过程中相对湿度预报值始终较观测值偏低,模式对海岛站相对湿度预报的干偏差大于沿海站,导致该站能见度数值较大,从而导致雾漏报。SW99算法对于海岛站雾预报的优势,一方面可能是液态水含量的预报差异;另一方面可能是该算法没有考虑气溶胶和霾的影响[31],青岛站距海岸线2 km左右,污染较海岛站要重,对能见度降低有一定作用,导致雾的漏报,这仍有待于今后进一步研究。
|
图 4 2014年5月11日(个例5)青岛站与潮连岛站相对湿度观测和预报对比(横轴红色、绿色线条分别表示青岛站、潮连岛站有雾时次) Fig.4 Observed and forecast relative humidity at Qingdao Station and Chaolian Island Station on 11 May 2014 (Case 5) (X-axis: red line for fog time at Qingdao Station, green line for fog time at Chaolian Island Station) |
表 3为雾开始时间误差绝对值、雾结束时间误差绝对值及雾持续时间误差绝对值在不同时段所占比例统计结果。
|
|
表 3 三站雾开始时间误差绝对值、结束时间误差绝对值和持续时间误差绝对值不同时段所占比例 Table 3 Ratio of the absolute value of errors of the start time, end time and duration of sea fog cases at three stations during different periods |
以开始时间误差绝对值在6 h以内比例来看,青岛站3种算法(FSL、SW99、CVIS)分别为100%、87%和94%,太平角站为87%、60%和83%,潮连岛站为72%、82%和76%;以结束时间误差绝对值在6 h以内比例来看,青岛站3种算法分别为75%、87%和76%,太平角站为69%、80%和70%,潮连岛站为63%、59%和59%;以持续时间误差绝对值在6 h以内比例来看,青岛站3种算法分别为68%、80%和65%,太平角站为63%、47%和65%,潮连岛站为36%、49%和48%。可见,基于WRF模式的各能见度算法对青岛站雾起止时间、持续时间预报略好于太平角站和潮连岛站;各能见度算法对于雾结束时间预报误差一般大于开始时间预报误差。其中,基于FSL算法的青岛站雾开始时间误差绝对值平均最小为2.4 h;基于SW99算法的青岛站雾结束时间误差绝对值平均最小为3.6 h;基于SW99算法的青岛站雾持续时间误差绝对值平均最小为4.5 h。基于CVIS算法的雾起止时间误差、持续时间误差多介于两个单一算法之间,可见CVIS算法在雾起止时间方面较单一算法改进不大。
由雾起止时间比实况早晚次数以及持续时间比实况长短次数来看(表略),SW99算法对青岛站、太平角站雾开始时间预报较实况多偏晚,平均分别偏晚4 h、6 h;而对这两个站雾结束时间预报较实况多偏早,持续时间预报较实况多偏短。
2.4 能见度均方根误差和偏差检验为了解基于WRF模式不同算法的能见度预报误差情况,分别计算了3个站每个海雾个例有雾时段的能见度均方根误差(RMSE,km)和能见度预报偏差(km),如表 4所示。误差反映了模式及初始场导致的误差以及能见度算法本身的误差。
|
|
表 4 三个站17个个例平均的RMSE和偏差 Table 4 Mean RMSE and mean errors of 17 cases at 3 stations |
17个个例有雾时段3站平均RMSE结果表明,SW99算法RMSE最大为12.7 km,FSL算法和CVIS算法RMSE较小,分别为1.8 km、1.7 km。不同算法对不同站能见度预报的误差也存在差异,其中SW99算法差异最大,潮连岛站RMSE较青岛站和太平角站要偏小,这与SW99算法对海岛站上雾预报准确率高于沿海站是一致的。
由平均偏差来看,上述3种算法是高估能见度的,尤其是SW99算法,能见度预报偏差最大,FSL算法和CVIS算法最小。SW99算法有雾时段3站平均偏差为9.6 km,主要是由于这种算法计算的能见度突变特征较明显,另外这种算法预报的沿海站、岸基站雾持续时间较实况明显偏短。
3 结论与讨论基于WRF模式对青岛近海17个海雾个例的模拟结果,采用3种不同算法对青岛近海海雾及能见度预报进行了比较研究。通过对模式输出的近地面层气象要素的检验,表明该模式对青岛沿海地区的要素预报具备一定参考价值。
对于所选的17个海雾个例,基于WRF模式的不同能见度算法对青岛沿海海雾具有不同的预报能力。其中,FSL算法对于青岛站和岸基站太平角站海雾预报准确率达94%,较SW99算法略有优势;但对于海岛站潮连岛站而言,SW99算法预报准确率可达100%,明显优于FSL算法。CVIS算法由于综合考虑了SW99算法和FSL算法,预报准确率为100%。
基于WRF模式的各能见度算法预报的雾起止时间、持续时间与实况一致次数较少,而且起止时间误差、持续时间误差不确定性较大,表明了雾及能见度的精细化预报难度之大。相对而言,各算法对青岛站雾起止时间、持续时间预报略好于太平角站和潮连岛站。另外,基于WRF模式的各能见度算法对于雾结束时间预报误差一般大于开始时间预报误差。CVIS算法在雾起止时间方面较单一算法改进甚微。
SW99算法能见度RMSE最大,相对而言,潮连岛站RMSE较青岛站和太平角站要略偏小,从偏差来看,上述能见度算法基本上是高估能见度的,尤其SW99算法。SW99算法基于液态水含量,由于边界层、微物理过程的复杂性数值模式预报的液态水含量误差较其他常规气象要素预报误差大得多[32],进而导致能见度的误差也较大。鉴于此Zhou and Du[33]、Zhou et al.[29]、Payra and Mohan[34]以及陈东辉等[7]分别建立了基于气象要素的多规则雾诊断预报方法。Zhou and Du[33]、Zhou et al.[29]研究表明,利用模式输出的液态水含量、相对湿度、风速、云顶、云底高度建立的雾的诊断方法,比利用能见度与液态水含量关系诊断雾的预报评分提高了1倍,但这种诊断方法只能识别是否有雾。兼顾雾及能见度的预报,CVIS算法较单一算法有一定的优势,可作为青岛近海海雾及能见度预报行之有效的算法。
| [1] |
王彬华. 海雾[M]. 北京: 海洋出版社, 1983: 352.
|
| [2] |
张苏平, 鲍献文. 近十年中国海雾研究进展[J]. 中国海洋大学学报, 2008, 38(3): 359-366. |
| [3] |
江敦双, 张苏平, 陆惟松. 青岛海雾的气候特征和预测研究[J]. 海洋湖沼通报, 2008(3): 7-11. DOI:10.3969/j.issn.1003-6482.2008.03.002 |
| [4] |
章国材. 中国雾的业务预报和应用[J]. 气象科技进展, 2016, 6(2): 42-48. |
| [5] |
胡波, 杜惠良, 郝世峰, 等. 一种统计技术结合动力释用的沿海海雾预报方法[J]. 海洋预报, 2014, 31(5): 82-86. |
| [6] |
高荣珍, 李欣, 任兆鹏, 等. 青岛沿海海雾决策树预报模型研究[J]. 海洋预报, 2016, 33(4): 80-87. |
| [7] |
陈东辉, 尚子微, 宁贵财, 等. 环渤海地区雾天气分型及预报方法[J]. 气象, 2017, 43(1): 46-55. |
| [8] |
黄彬, 陈涛, 陈炯, 等. 黄渤海海雾数值预报系统及检验方法研究[J]. 气象科技, 2009, 37(3): 271-275. DOI:10.3969/j.issn.1671-6345.2009.03.003 |
| [9] |
徐同, 李佳, 杨玉华, 等. SMS-WARMS V2. 0模式预报效果检验[J]. 气象, 2016, 42(10): 1176-1183. DOI:10.7519/j.issn.1000-0526.2016.10.002 |
| [10] |
盛立芳, 申莉莉, 李秀镇, 等. 水平能见度经验公式在青岛沿海地区的应用[J]. 中国海洋大学学报, 2009, 39(5): 877-882. |
| [11] |
Gultepe I, Isaac G A, Strawbridge K. Variability of cloud microphysical and optical parameters obtained from aircraft and satellite remote sensing during RACE[J]. Int J Climatol, 2001, 21(4): 507-525. DOI:10.1002/(ISSN)1097-0088 |
| [12] |
Stoelinga M T, Warner T T. Nonhydrostatic, mesobeta-scale model simulations of cloud ceiling and visibility for an East Coast winter precipitation event[J]. J Appl Meteor, 1999, 38(4): 385-404. DOI:10.1175/1520-0450(1999)038<0385:NMSMSO>2.0.CO;2 |
| [13] |
Pinnick R G, Hoihjelle D L, Fernandez G, et al. Vertical structure in atmospheric fog and haze and its effects on visible and infrared extinction[J]. J Atmos Sci, 1978, 35(10): 2020-2032. DOI:10.1175/1520-0469(1978)035<2020:VSIAFA>2.0.CO;2 |
| [14] |
Eldridge R G. The relationship between visibility and liquid water content in fog[J]. J Atmos Sci, 1971, 28(7): 1183-1186. DOI:10.1175/1520-0469(1971)028<1183:TRBVAL>2.0.CO;2 |
| [15] |
Kunkel B A. Parameterization of droplet terminal velocity and extinction coefficient in fog models[J]. J Climate Appl Meteor, 1984, 23(1): 34-41. DOI:10.1175/1520-0450(1984)023<0034:PODTVA>2.0.CO;2 |
| [16] |
傅刚, 李晓岚, 魏娜. 大气能见度研究[J]. 中国海洋大学学报, 2009, 39(5): 855-862. |
| [17] |
Smirnova T G, Benjamin S G, Brown J M. Case study verification of RUC /MAPS fog and visibility forecasts[C]//AMS: The 9th Conference on Aviation, Range, and Aerospace Meteorology, Orlando, Florida. Boston: AMS, 2000: 31-36.
|
| [18] |
Doran J A, Roohr P J, Beberwyk D J, et al. The MM5 at the Air Force Weather Agency-New products to support military operations[C]//AMS: The 8th Conference on Aviation Range and Aerospace Meteorology, Dallas, Texas, 10-15 January, 1999. Boston: AMS, 1999.
|
| [19] |
Bang C H, Lee J W, Hong S-Y. Predictability experiments of fog and visibility in local airports over Korea using the WRF Model[J]. J Korean Soc Atmos Environ, 2008, 24(E2): 92-101. |
| [20] |
林艳, 杨军, 鲍艳松, 等. 山西省冬季雾中能见度的数值模拟研究[J]. 南京信息工程大学学报(自然科学版), 2010, 2(5): 436-444. |
| [21] |
林艳, 王茂书, 林龙官. 四川省冬季雾的数值模拟及能见度参数化[J]. 南京信息工程大学学报(自然科学版), 2013, 5(3): 222-228. |
| [22] |
Brewster K. Application of a Bratseth analysis scheme including Doppler radar[C]// AMS. The 15th Conference on Weather Analysis and Forecasting, Norfolk, Virginia, August, 1996. Boston: AMS, 1996: 92-95.
|
| [23] |
Hong S-Y, Lim J-O J. The WRF single-moment 6-class microphysics scheme (WSM6)[J]. J Korean Meteor Soc, 2006, 42(2): 129-151. |
| [24] |
Mlawer E J, Taubman S J, Brown P D, et al. Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave[J]. J Geophys Res: Atmos, 1997, 102(D14): 16663-16682. DOI:10.1029/97JD00237 |
| [25] |
Dudhia J. Numerical study of convection observed during the winter monsoon experiment using a mesoscale two-dimensional model[J]. J Atmos Sci, 1989, 46(20): 3077-3107. DOI:10.1175/1520-0469(1989)046<3077:NSOCOD>2.0.CO;2 |
| [26] |
Zhang D L, Anthes R A. A high-resolution model of the planetary boundary layer-sensitivity tests and comparisons with SESAME-79 data[J]. J Appl Meteor, 1982, 21(11): 1594-1609. DOI:10.1175/1520-0450(1982)021<1594:AHRMOT>2.0.CO;2 |
| [27] |
Chen F, Dudhia J. Coupling an advanced land surface-hydrology model with the Penn State-NCAR MM5 modeling system. Part I: Model implementation and sensitivity[J]. Mon Wea Rev, 2001, 129(4): 569-585. DOI:10.1175/1520-0493(2001)129<0569:CAALSH>2.0.CO;2 |
| [28] |
Hong S-Y, Noh Y, Dudhia J. A new vertical diffusion package with an explicit treatment of entrainment processes[J]. Mon Wea Rev, 2006, 134(9): 2318-2341. DOI:10.1175/MWR3199.1 |
| [29] |
Zhou B B, Du J, Gultepe I, et al. Forecast of low visibility and fog from NCEP: Current status and efforts[J]. Pure Appl Geophy, 2012, 169(5): 895-909. |
| [30] |
庄晓翠, 周鸿奎, 李博渊. T639模式在新疆北部暖区强降雪中的预报检验[J]. 干旱气象, 2015, 33(6): 1031-1037. |
| [31] |
周斌斌, 蒋乐, 杜钧. 航空气象要素以及基于数值模式的低能见度和雾的预报[J]. 气象科技进展, 2016, 6(2): 29-41. |
| [32] |
Gultepe I, Muller M D, Boybeyi Z. A new visibility parameterization for warm-fog applications in numerical weather prediction models[J]. J Appl Meteor climatol, 2006, 45(11): 1469-1480. DOI:10.1175/JAM2423.1 |
| [33] |
Zhou B B, Du J. Fog prediction from a multimodel mesoscale ensemble prediction system[J]. Wea Forecasting, 2010, 25(1): 303-322. DOI:10.1175/2009WAF2222289.1 |
| [34] |
Payra S, Mohan M. Multirule based diagnostic approach for the fog predictions using WRF modelling tool[J]. Adv Meteor, 2014(1): 1-11. |
 2018, Vol. 38
2018, Vol. 38

