Stull[1]将大气边界层定义为直接受下垫面影响的那部分大气,它在自由大气和下垫面的动力和热力相互作用中起着十分重要的作用。太阳辐射是大气运动的主要动力来源,下垫面吸收短波辐射后,下垫面和自由大气之间的热量交换主要通过边界层的湍流热量输送完成。边界层内的湍流动量输送能有效地耗散大气运动,从而不会使其无限制地发展。边界层内的物质和水汽输送对云和降水的形成,污染物的扩散以及大气化学变化都有着非常重要的作用。此外,边界层内的低云可有效地反射太阳短波辐射,对全球辐射收支平衡也有着重要的作用。鉴于大气边界层在天气和气候系统中的重要作用,在数值模式中对边界层内物理过程的合理描述是十分必要的,但由于模式本身的垂直和水平分辨率限制和边界层内湍流运动的复杂性,边界层内的一些物理过程不能被模式中的动力框架描述出来,因此需要将这些物理过程进行参数化,即将一些次网格尺度的变量用网格可解析的变量描述出来,使模式的模拟结果中能够体现这些过程的影响。合理的边界层参数化方案在一个成熟的数值模式中是不可或缺的。
数值模式中通过雷诺平均的形式将风速、水汽、位温等物理量分解为网格尺度的平均量和次网格尺度的扰动量,再将其代入原始的纳维-斯托克斯方程组,方程组会因为多了湍流通量项而不能闭合。在边界层中垂直方向湍流输运的重要性要远大于水平方向,边界层参数化方案主要解决的就是垂直湍流通量项的闭合问题,该问题可用公式(1)简单地描述出来:
| $ \frac{\partial \overline{\chi}}{\partial t}=-\frac{\partial \overline{w^{\prime} \chi^{\prime}}}{\partial z} $ | (1) |
其中
从闭合框架的角度来划分,常用的边界层参数化方案可分为1阶闭合,1.5阶闭合以及2阶或更高阶闭合。闭合阶数一般是通过引入的最高阶预报方程来确定的,1阶闭合直接将湍流通量项描述为已知量的函数,1.5阶闭合在描述湍流通量项时引入了部分二阶矩(例如湍流动能)的预报方程,2阶闭合引入了全部二阶矩的预报方程,更高阶的闭合可以此类推。
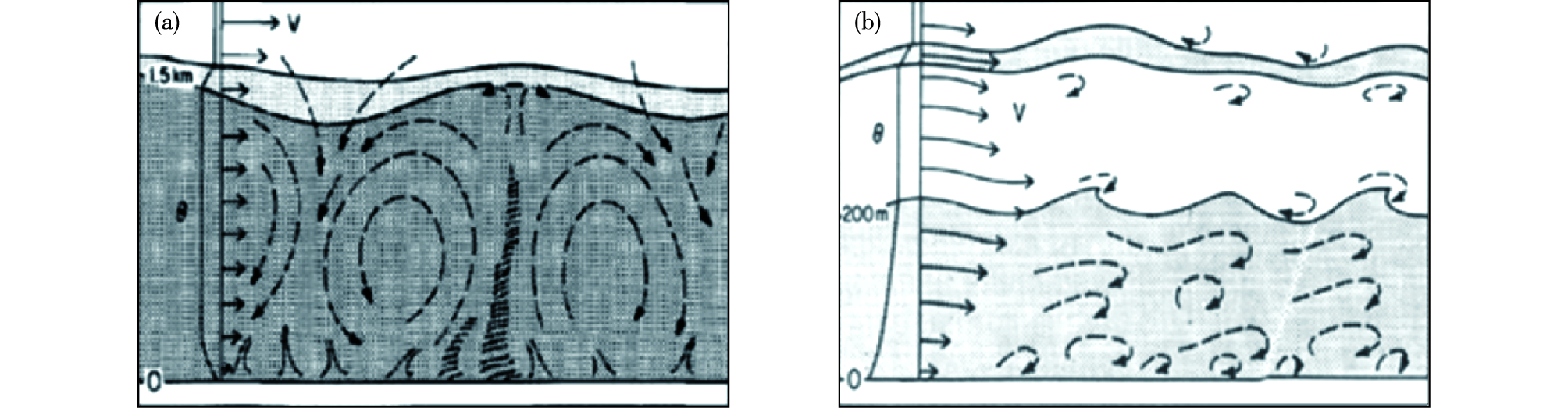
影响边界层内垂直湍流通量项的物理过程主要有下垫面的湍流输运、边界层顶的夹卷以及边界层顶层积云的长波辐射冷却等。浮力和底层风切变对下垫面的湍流输运有着至关重要的影响,依据浮力对湍流混合是增强还是抑制作用可将大气边界层划分为不稳定边界层(也称对流边界层)和稳定边界层。不稳定边界层多发生在晴朗的白天,下垫面受太阳辐射加热,浮力和风切变共同促进湍流混合;而稳定边界层多发生在夜间,下垫面自然冷却,仅有风切变促进湍流混合,浮力反而对湍流混合具有抑制作用。这两类边界层具有非常不同的内部结构,在一些参数化方案中也进行了区别对待。图 1表示不稳定边界层和稳定边界层的内部结构[2]。在稳定边界层中,湍流主要由风切变产生和维持,具有较强的局地性,不能形成较大尺度的涡旋;在不稳定边界层中,由于浮力对湍流的促进作用会出现许多上冲的热泡,这些热泡在垂直方向上具有较大的尺度,有些甚至可以跨越整个边界层,它们将近地面的空气带到边界层的中上部,使边界层内部充分混合,因此不稳定边界层内的湍流输送具有很强的非局地性,很多工作对边界层参数化方案中如何考虑这种非局地性进行了研究[3-6]。在不稳定边界层的顶部,上冲热泡由于惯性作用可突破顶部逆温的限制进入到自由大气,通过周围空气的下曳作用将自由大气中的空气卷入边界层中,使其与边界层内的空气进行混合,这个过程被称为不稳定边界层顶部的夹卷过程。夹卷过程对不稳定边界层的发展有十分重要的作用,对该过程的深入研究一方面是通过对实际观测资料的分析[7-9],另一方面通过实验室的理想实验和大涡模拟等数值模拟技术[10-14]。根据边界层顶是否有云覆盖可将边界层分为晴空边界层和有云覆盖的边界层,特别是有海洋层积云覆盖的边界层。海洋层积云主要存在于副热带大陆西岸的冷洋面之上,顶部具有较强的长波辐射冷却[15],这也是它区别于其他种类云的一个显著特征。层积云顶的长波辐射冷却过程会产生自上而下的湍流混合,从而成为除下垫面之外的另外一个驱动边界层内湍流维持和发展的重要来源[16-17]。Wood[18]对海洋层积云的物理性质及其与边界层过程之间的相互作用进行了详细的综述。
|
图 1 不稳定边界层(a)和稳定边界层(b)的内部结构[2] Fig.1 Schematics of unstable (a) and stable (b) boundary layer circulations[2] |
本文将从闭合框架以及对边界层内重要物理过程的考虑这两个层面总结回顾常用的边界层参数化方案,介绍了几个主要数值预报模式中的业务方案,并且对边界层方案的发展方向进行简要概述。
1 闭合框架 1.1 1阶闭合方案1阶闭合方案多采用K理论,假设湍流运动与分子运动具有一致性,得出湍流通量是湍流输运系数与网格尺度物理量梯度的乘积,以纬向风速u和位温θ为例:
| $ \overline{w^{\prime} u^{\prime}}=-K_{m} \frac{\partial \overline{u}}{\partial z} $ | (2) |
| $ \overline{w^{\prime} \theta^{\prime}}=-K_{h} \frac{\partial \overline{\theta}}{\partial z} $ | (3) |
其中Km和Kh分别代表动量和热量的湍流输运系数。
1.1.1 K(Ri)方案此类方案采用经典的普朗特半经验公式,又被称为混合长方案:
| $ K_{m, h}=l^{2}\left[\left(\frac{\partial \overline{u}}{\partial z}\right)^{2}+\left(\frac{\partial \overline{v}}{\partial z}\right)^{2}\right]^{1 / 2} F_{m, h}(R i) $ | (4) |
l表示湍流混合长,Fm, h(Ri)为理查森数Ri的函数,Ri是表征边界层内稳定度的一个重要的无量纲数:
| $\ R i=\frac{g}{\overline{\theta}_{v}} \frac{\partial \overline{\theta}_{v} / \partial z}{(\partial \overline{u} / \partial z)^{2}+(\partial \overline{v}/\partial z)^{2}} $ | (5) |
Louis[19]和Louis et al.[20]利用近地层的莫宁-奥布霍夫相似律[21-24]导出了函数Fm,h(Ri)并将其扩展到了整个边界层, Beljaars[25]对稳定边界层下的函数Fm, h(Ri)进行了改进。类似莫宁-奥布霍夫相似律的形式,Nieuwstadt[26]提出了局地相似律,Duynkerke[27]利用该理论导出了Fm,h(Ri)。此外,混合长l多采用Blackadar[28]的形式:
| $ \frac{1}{l}=\frac{1}{\kappa z}+\frac{1}{l_{0}} $ | (6) |
其中κ为卡曼常数,l0为渐进混合长,根据需要可取常数值或函数形式。
1.1.2 K廓线方案此类方案直接预先给定湍流输运系数K的垂直廓线形式[5, 29]:
| $ K_{m, h}=\kappa u_{*}\phi_{m, h}^{-1} z\left(1-\frac{z}{h}\right)^{2} $ | (7) |
其中u*表示摩擦速度,h表示边界层高度,ϕm和ϕh是莫宁-奥布霍夫相似律中关于z/L的函数,L表示莫宁-奥布霍夫长度。不同于K(Ri)方案,该类方案在计算湍流输运系数时引入了边界层高度,Seidel et al.[30]利用观测、模式和再分析资料对多种计算边界层高度的公式进行了检验,并指出Vogelezang and Holtslag[31]提出的通过整体理查森数诊断得到边界层高度的方法能较好地适用于各类情况。
1.2 1.5阶闭合方案1.5阶闭合方案在数值模式中应用最广泛的是K(TKE)方案[32-34], K(TKE, ε)方案虽然也有应用[35],但并不多见,因此该小节主要对K(TKE)方案进行介绍。K(TKE)方案仍采用K理论(见公式(2)和(3)),但是在计算湍流输运系数的过程中引入了湍流动能e的预报方程:
| $ \begin{align} \frac{\text{d}e}{\text{d}n}=\underbrace{-\overline{u'w'}-\frac{\partial \overline{u}}{\partial z}-\overline{u'w'}\frac{\partial \overline{v}}{\partial z}}_{S}+\underbrace{\frac{g}{{{\overline{\theta }}_{v}}}\overline{w'\theta {{'}_{v}}}}_{B}- \\ \ \ \ \ \ \ \ \ \underbrace{\frac{\partial }{\partial z}\left( \overline{w'e}+\frac{1}{\overline{\rho }}\overline{w'p'} \right)}_{T}-\varepsilon \\ \end{align} $ | (8) |
湍流动能e是表征湍流强度的重要物理量,S表示湍流的切变产生项,B表示湍流的浮力产生项,T表示湍流输运项和气压相关项,ε表示湍流耗散项。在K(TKE)方案中湍流输运系数K的公式可表示为:
| $ K_{m, h}=c l e^{1 / 2} $ | (9) |
其中c为一个常数,l表示湍流混合长。不同的方案针对混合长l以及湍流动能方程(公式(8))中的各项有不同的假设[32-34],但基本框架均大致相同。
1.3 2阶闭合方案这类方案引入了所有二阶矩的预报方程,并且为了使这些方程闭合,通过一定的假设和简化,将方程中出现的三阶矩转换成由二阶矩和平均量表示的形式,然后联立这些预报方程计算出湍流通量。Mellor and Yamada[36-37]建立了完整的2阶闭合的参数化框架,并通过进行不同的假设得到不同复杂度的参数化方案。采用他们文章中的术语[37],依据不同的假设将方案复杂度分为Level 4、Level 3、Level 2.5和Level 2等四个级别。Level 4的复杂度需求解完整的关于二阶矩的预报方程组,Level 3的复杂度仅需求解湍流动能e和位温扰动的方差
| $ K_{m, h}=l e^{1 / 2} S_{m, h} $ | (10) |
其中Sm,h为
相对于晴空边界层,有云覆盖的边界层因为要考虑边界层与云的相互作用,所以需要使用湿绝热守恒量qt和θl来替代干绝热守恒量q和θ,若模式中使用的是干静力能s=cpT+gz而不是θ,则用sl替代。这样做的好处是可以在描述湍流输运的过程中不需要显式地表达出蒸发和凝结过程[47],湿绝热守恒量可以表示为:
| $ q_{t}=q+q_{l} ; \theta_{l}=\theta\left(1-\frac{L_{v} q_{l}}{c_{p} T}\right) ; s_{l}=c_{p} T+g z-L_{v} q_{l} $ | (11) |
其中ql表示液态水混合比,Lv为水汽蒸发潜热系数,cp为大气比热。若边界层方案中需要湍流通量
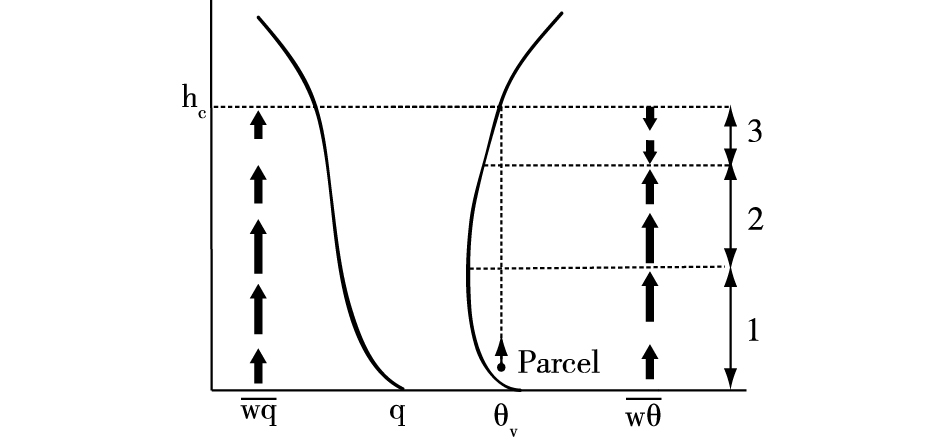
本文引言中提到不稳定边界层内的湍流输运具有很强的非局地性,但是针对参数化方案中经常采用的K理论(公式(2)和(3)),湍流输运仅与物理量的局地垂直梯度有关,并且都是沿着梯度的方向输运,这是不符合实际的。由图 2可以看出由于大尺度湍涡导致的非局地输运,在不稳定边界层的中上部可能存在逆梯度输运的情况。为了考虑这种非局地性质,K理论的公式可改写为[4-5, 32-33]:
| $ \overline{{{w}^{\prime }}{{\chi }^{\prime }}}=-{{K}_{\chi }}\left( \frac{\partial \bar{\chi }}{\partial z}-{{\gamma }_{\chi }} \right) $ | (12) |
|
图 2 不稳定边界层内的湍流输运(区域2代表热量的逆梯度输送)[5] Fig.2 Turbulent transport in unstable boundary layer (region 2 represents the countergradient transport of heat)[5] |
其中γχ为逆梯度项,与对应物理量的下垫面湍流通量有关。
除了在K理论的公式中加入逆梯度项这一方法之外,方案中还可采用直接混合的方法来描述不稳定边界层的非局地特性,Pleim[6]的方案就是这种方法的一个典型例子。如图 3所示,方案假设对流输送源于模式的最低层,从最低层向上直接输送到其他每一层,并且用逐层的向下输送表示补偿下沉运动,方案还用K理论来表示局地的湍流输送:
| $ \begin{align} \frac{\partial {{{\bar{\chi }}}_{i}}}{\partial t}=\underbrace{Mu{{{\bar{\chi }}}_{1}}}_{\text{非局地输送}}+\underbrace{M{{d}_{i+1}}{{{\bar{\chi }}}_{i+1}}\frac{\Delta {{z}_{i+1}}}{\Delta {{z}_{i}}}-M{{d}_{i}}{{{\bar{\chi }}}_{i}}}_{\text{补偿下沉}} +\\ \underbrace{\frac{1}{\Delta {{z}_{i}}}\left[ \frac{{{K}_{i+1/2}}\left( {{{\bar{\chi }}}_{i+1}}-{{{\bar{\chi }}}_{i}} \right)}{\Delta {{z}_{i+1/2}}}-\frac{{{K}_{i-1/2}}\left( {{{\bar{\chi }}}_{i}}-{{{\bar{\chi }}}_{i-1}} \right)}{\Delta {{z}_{i-1/2}}} \right]}_{\text{局地输送}} \\ \end{align} $ | (13) |
其中下标代表模式层,Mu和Md表示混合系数。
另外一种表示不稳定边界层非局地特性的方法借鉴了浅对流方案中的质量通量方案[52],在不稳定边界层的情形下将局地的K理论与非局地的质量通量结合起来[53-58]:
| $ \overline{w^{\prime} \chi^{\prime}}=-K_{\chi} \frac{\partial \overline{\chi}}{\partial z}+M\left(\chi_{u}-\overline{\chi}\right) $ | (14) |
其中M表示质量通量,下标u表示边界层内的强上升气流,如图 4所示。这类方案统称为EDMF(Eddy-Diffusivity Mass-Flux)方案。
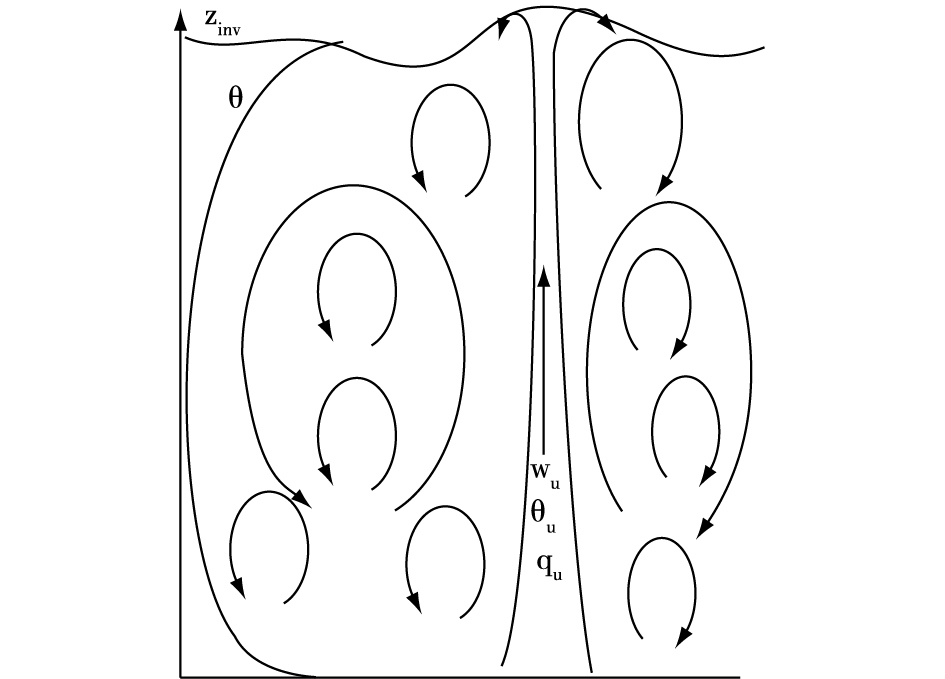
|
图 4 不稳定边界层内的湍流结构示意图[54] Fig.4 Sketch of a convective updraft embedded in a turbulent eddy structure[54] |
本文引言中提到层积云顶的长波辐射冷却和不稳定边界层顶的夹卷过程对于边界层的发展有十分重要的作用。对于有层积云覆盖的边界层,云顶辐射冷却是驱动边界层内湍流发展的一个重要来源,在边界层方案中主要有两种方式表示这个过程。在1阶闭合的框架下一般采取双K廓线的方法,即除了预先给定类似公式(7)所示的这条K廓线外,在其基础上再叠加一条K廓线,这条K廓线表示云顶辐射冷却作为湍流动力来源在边界层内产生的湍流混合[59-62],其中云顶辐射冷却的强度在模式中通常由辐射通量的散度表示。在1.5阶、2阶和高阶闭合的框架下,方案中通常将云顶辐射冷却产生的浮力项直接写入湍流动能和高阶矩的收支方程中,在方程中将该过程隐式地表达出来[42, 63]。
针对不稳定边界层顶的夹卷过程,通用的参数化框架可表示为如下形式:
| $ \overline{\left(w^{\prime} \chi^{\prime}\right)}_{h}=-w_{e} \Delta \overline{\chi} $ | (15) |
其中
在早期的数值模式中大多参照公式(2)和公式(3)所示的K理论,使用计算较为简单和稳定的1阶闭合方案,后续又有很多模式通过使用1.5阶的闭合方案,引入湍流动能这一重要物理量,更细致地对边界层进行描述。但是传统的K理论方案属于局地方案,并不能很好地模拟出不稳定边界层的非局地性。为避免此问题,二阶或更高阶的闭合方案得以在模式中开始进行应用,这类方案通过增加多个湍流预报方程能较真实地反映边界层的特征,但是这类方案计算量较大,对多数模式特别是全球模式来说,计算过于复杂,同时引入了很多的不确定参数,对模式的调试也带来了很大的挑战。在此之后,越来越多的非局地方案在模式中得到应用和发展,它在克服传统的局地方案缺点的同时,也不增加太多的计算量(见本文2.2部分)。
数值模式是一个复杂的系统性工程,在一个模式中使用哪种边界层方案要根据模式的动力框架、模式中其他各类参数化方案、模式分辨率、模式具体模拟结果等多种因素综合考虑,并没有哪一种方案可以适应于所有模式。但是综合来说,使用1阶或1.5阶闭合的非局地方案,并在方案中引入不稳定边界层顶的夹卷和层积云顶的长波辐射冷却,是目前较为主流的形式。另外随着计算能力的迅速发展,2阶或更高阶的方案也在模式中得到更为广泛的应用。
本文选取了在日常天气预报业务中预报员使用较多并且整体预报性能较好的三个业务模式,介绍它们所使用的边界层方案。
3.1 GRAPES_MesoGRAPES是中国气象局自主开发建立的多尺度通用资料同化与数值预报系统,其中GRAPES_Meso模式是GRAPES的区域中尺度预报模式,该模式的水平分辨率为0.1°,垂直方向有50层[74]。它使用的边界层方案主要有三个[75],分别是如公式(7)和公式(12)所示的使用K廓线并在不稳定边界层中加入了逆梯度项的MRF方案[5],在MRF方案的基础上考虑不稳定边界层顶部夹卷的YSU方案[64-65]以及如公式(10)所示的使用TKE进行1.5阶闭合的MYJ方案[39]。
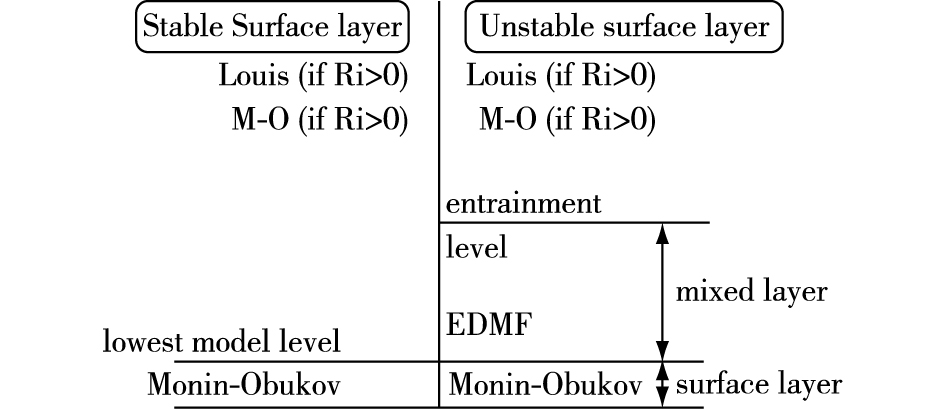
3.2 ECMWF IFS-HRESECMWF IFS是欧洲中期天气预报中心研发的一套集成预报系统,HRES是系统中的高分辨率大气模式,该模式的水平分辨率约为9 km,垂直方向有137层。如图 5所示,模式根据边界层的性质不同使用不同的方案[76]。混合层表示不稳定边界层中充分混合的部分,混合层内使用的边界层方案属于如公式(14)所示的EDMF方案。若边界层内无云或者顶部被层积云覆盖,混合层高度即为边界层高度,混合层中的大尺度非局地混合通过EDMF方案中的质量通量项描述;若边界层内存在浅积云,混合层高度为浅积云的云底高度,此时EDMF方案中的质量通量项变为零,非局地混合由浅积云中的浅对流方案描述。混合层中的局地混合通过湍流输运系数K来描述,K的计算方案属于如公式(7)所示的K廓线方案,并且方案还考虑了混合层顶部的夹卷过程以及通过双K廓线的形式考虑了层积云顶的长波辐射冷却过程。稳定边界层以及不稳定边界层中混合层之上的部分使用的方案均属于如公式(4)所示的K(Ri)方案。
3.3 NCEP GFSNCEP GFS是美国国家环境预报中心研发的全球预报系统,其中它的高分辨率版本的大气模式水平分辨率约为13 km,垂直方向有64层。模式根据边界层的稳定度不同使用不同的边界层方案[77],模式将边界层分为强不稳定边界层、弱不稳定边界层、弱稳定边界层以及强稳定边界层。强不稳定边界层使用的方案属于如公式(14)所示的EDMF方案,方案的局地混合部分由公式(7)所示的K廓线方案描述;弱不稳定边界层使用的方案属于K廓线方案,同时加入了如公式(12)所示的逆梯度项;弱稳定边界层使用的方案也属于K廓线方案;强稳定边界层使用的方案属于如公式(4)所示的K(Ri)方案。
4 发展方向尽管边界层方案历经多年发展,各方面已考虑得较为完善,但是随着模式水平的不断发展,仍有需要改进和继续深入研究的方向。首先是对边界层(特别是有云覆盖的边界层)内各物理过程的更为深入和细致地研究,深化对内在物理机制的认识。其次是考虑边界层方案和其他物理参数化方案(特别是对流参数化方案和云物理方案)之间的联系,建立一个统一的参数化框架,使得模式在边界层湍流输送,浅对流和深对流发展,以及云的形成等各主要物理过程之间能够更加自然地切换。前文所述的EDMF方案就为建立统一的参数化框架提供了很好的基础[57-58],另外也有研究在高阶闭合的框架下将各物理方案统一起来,CLUBB(Cloud Layers Unified by Binormals)方案[78-81]在3阶闭合的框架下以多元高斯分布为基础进行闭合假设,通过求解八个二阶矩和一个三阶矩的预报方程组将边界层、浅对流以及云物理方案统一到同一个计算框架内。此外,随着模式分辨率的不断提高,当模式的网格距小于1 km时,模式的动力框架便可部分分辨湍流过程,这时传统的边界层方案可能就不太适用了,如何处理这种高分辨率下边界层的参数化也是未来研究的主要方向之一[82-84]。
| [1] |
Stull R B. An introduction to boundary layer meteorology[M]. Dordrecht: Kluwer Academic Publishers, 1988: 1-3.
|
| [2] |
Wyngaard J C. Scalar fluxes in the planetary boundary layer: Theory, modeling, and measurement[J]. Bound-Lay Meteorol, 1990, 50(1-4): 49-75. DOI:10.1007/BF00120518 |
| [3] |
Stull R B. Transilient turbulence theory. Part Ⅰ: The concept of eddy-mixing across finite distances[J]. J Atmos Sci, 1984, 41(23): 3351-3367. DOI:10.1175/1520-0469(1984)041<3351:TTTPIT>2.0.CO;2 |
| [4] |
Deardorff J W. Theoretical expression for the countergradient vertical heat flux[J]. J Geophys Res, 1972, 77(30): 5900-5904. DOI:10.1029/JC077i030p05900 |
| [5] |
Holtslag A A M, Boville B A. Local versus nonlocal boundary-layer diffusion in a global climate model[J]. J Climate, 1993, 6(10): 1825-1842. DOI:10.1175/1520-0442(1993)006<1825:LVNBLD>2.0.CO;2 |
| [6] |
Pleim J E. A combined local and nonlocal closure model for the atmospheric boundary layer. Part Ⅰ: model description and testing[J]. J Appl Meteor Climatol, 2007, 46(9): 1383-1395. DOI:10.1175/JAM2539.1 |
| [7] |
Nicholls S, Turton J D. An observational study of the structure of stratiform cloud sheets: Part Ⅱ. Entrainment[J]. Quart J Roy Meteor Soc, 1986, 112(472): 461-480. DOI:10.1002/(ISSN)1477-870X |
| [8] |
Canut G, Lothon M, Saïd F, et al. Observation of entrainment at the interface between monsoon flow and the Saharan Air Layer[J]. Quart J Roy Meteor Soc, 2010, 136(S1): 34-46. DOI:10.1002/qj.v136.1s |
| [9] |
Träumner K, Kottmeier C, Corsmeier U, et al. Convective boundary-layer entrainment: short review and progress using doppler lidar[J]. Bound-Lay Meteorol, 2011, 141(3): 369-391. DOI:10.1007/s10546-011-9657-6 |
| [10] |
Sullivan PP, Moeng C-H, Stevens B, et al. Structure of the entrainment zone capping the convective atmospheric boundary layer[J]. J Atmos Sci, 1998, 55(19): 3042-3064. DOI:10.1175/1520-0469(1998)055<3042:SOTEZC>2.0.CO;2 |
| [11] |
Kim S-W, Park S-U, Moeng C-H. Entrainment processes in the convective boundary layer with varying wind shear[J]. Bound-Lay Meteorol, 2003, 108(2): 221-245. DOI:10.1023/A:1024170229293 |
| [12] |
Conzemius R J, Fedorovich E. Dynamics of sheared convective boundary layer entrainment. Part Ⅰ: Methodological background and large-eddy simulations[J]. J Atmos Sci, 2006, 63(4): 1151-1178. DOI:10.1175/JAS3691.1 |
| [13] |
Yamaguchi T. Analysis of PBL-TOP entrainment using LES[D]. Colorado: Colorado State University, 2005.
|
| [14] |
Moeng C-H, Lenschow D H, Randall D A. Numerical investigations of the roles of radiative and evaporative feedbacks in stratocumulus entrainment and breakup[J]. J Atmos Sci, 1995, 52(16): 2869-2883. DOI:10.1175/1520-0469(1995)052<2869:NIOTRO>2.0.CO;2 |
| [15] |
Schubert W H, Wakefield J S, Steiner E J, et al. Marine stratocumulus convection. Part Ⅰ: Governing equations and horizontally homogeneous solutions[J]. J Atmos Sci, 1979, 36(7): 1286-1307. DOI:10.1175/1520-0469(1979)036<1286:MSCPIG>2.0.CO;2 |
| [16] |
Moeng C-H, Stevens B. Representing the stratocumulus-topped boundary layer in GCMs[J]. Int Geophys, 2000, 70: 577-604. DOI:10.1016/S0074-6142(00)80067-4 |
| [17] |
Ciesielski P E, Schubert W H, Johnson R H. Diurnal variability of the marine boundary layer during ASTEX[J]. J Atmos Sci, 2001, 58(16): 2355-2376. DOI:10.1175/1520-0469(2001)058<2355:DVOTMB>2.0.CO;2 |
| [18] |
Wood R. Stratocumulus clouds[J]. Mon Wea Rev, 2012, 140(8): 2373-2423. DOI:10.1175/MWR-D-11-00121.1 |
| [19] |
Louis J-F. A parametric model of vertical eddy fluxes in the atmosphere[J]. Bound-Lay Meteorol, 1979, 17(2): 187-202. DOI:10.1007/BF00117978 |
| [20] |
Louis J F, Tiedtke M, Geleyn J F. A short history of the operational PBL-parameterization at ECMWF[C]. Workshop on boundary layer parameterization, ECMWF, Reading, United Kingdom, 1982: 59-79.
|
| [21] |
Monin A S, Obukhov A M. Basic laws of turbulent mixing in the surface layer of the atmosphere[J]. Tr Akad Nauk SSSR Geofiz Inst, 1954, 24(151): 163-187. |
| [22] |
Dyer A J. A review of flux-profile relationships[J]. Bound-Lay Meteorol, 1974, 7(3): 363-372. DOI:10.1007/BF00240838 |
| [23] |
Högström U L F. Non-dimensional wind and temperature profiles in the atmospheric surface layer: A re-evaluation[J]. Bound-Lay Meteorol, 1988, 42(1-2): 55-78. DOI:10.1007/BF00119875 |
| [24] |
Högström U L F. Review of some basic characteristics of the atmospheric surface layer[J]. Bound-Lay Meteorol, 1996, 78(3-4): 215-246. DOI:10.1007/BF00120937 |
| [25] |
Beljaars A C M. The impact of some aspects of the boundary layer scheme in the ECMWF model[C]. ECMWF Seminar on Parameterization of Sub-grid Scale Physical Processes, Reading, United Kingdom, 1994: 125-161.
|
| [26] |
Nieuwstadt F T M. The turbulent structure of the stable, nocturnal boundary layer[J]. J Atmos Sci, 1984, 41(14): 2202-2216. DOI:10.1175/1520-0469(1984)041<2202:TTSOTS>2.0.CO;2 |
| [27] |
Duynkerke P G. Radiation fog: a comparison of model simulations with detailed observations[J]. Mon Wea Rev, 1991, 119(2): 324-341. DOI:10.1175/1520-0493(1991)119<0324:RFACOM>2.0.CO;2 |
| [28] |
Blackadar A K. The vertical distribution of wind and turbulent exchange in a neutral atmosphere[J]. J Geophys Res, 1962, 67(8): 3095-3102. DOI:10.1029/JZ067i008p03095 |
| [29] |
Troen I B, Mahrt L. A simple model of the atmospheric boundary layer; sensitivity to surface evaporation[J]. Bound-Lay Meteorol, 1986, 37(1-2): 129-148. DOI:10.1007/BF00122760 |
| [30] |
Seidel D, Zhang Y, Beljaars A, et al. Climatology of the planetary boundary layer over the continental United States and Europe[J]. J Geophys Res: Atmospheres, 2012, 117(D17): D17106. |
| [31] |
Vogelezang D H P, Holtslag A A M. Evaluation and model impacts of alternative boundary-layer height formulations[J]. Bound-Lay Meteorol, 1996, 81(3-4): 245-269. DOI:10.1007/BF02430331 |
| [32] |
Therry G, Lacarrère P. Improving the eddy kinetic energy model for planetary boundary layer description[J]. Bound-Lay Meteorol, 1983, 25(1): 63-88. DOI:10.1007/BF00122098 |
| [33] |
Bougeault P, Lacarrère P. Parameterization of orography-induced turbulence in a mesobeta-scale model[J]. Mon Wea Rev, 1989, 117(8): 1872-1890. DOI:10.1175/1520-0493(1989)117<1872:POOITI>2.0.CO;2 |
| [34] |
Brinkop S, Roeckner E. Sensitivity of a general circulation model to parameterizations of cloud-turbulence interactions in the atmospheric boundary layer[J]. Tellus Ser A Dyn Meteor Oceanogr, 1995, 47(2): 197-220. DOI:10.3402/tellusa.v47i2.11501 |
| [35] |
Duynkerke P G. Application of the E-ε turbulence closure model to the neutral and stable atmospheric boundary layer[J]. J Atmos Sci, 1988, 45(5): 865-880. DOI:10.1175/1520-0469(1988)045<0865:AOTTCM>2.0.CO;2 |
| [36] |
Mellor G L, Yamada T. A hierarchy of turbulence closure models for planetary boundary layers[J]. J Atmos Sci, 1974, 31(7): 1791-1806. DOI:10.1175/1520-0469(1974)031<1791:AHOTCM>2.0.CO;2 |
| [37] |
Mellor G L, Yamada T. Development of a turbulence closure model for geophysical fluid problems[J]. Rev Geophys, 1982, 20(4): 851-875. DOI:10.1029/RG020i004p00851 |
| [38] |
Galperin B, Kantha L H, Hassid S, et al. A quasi-equilibrium turbulent energy model for geophysical flows[J]. J Atmos Sci, 1988, 45(1): 55-62. DOI:10.1175/1520-0469(1988)045<0055:AQETEM>2.0.CO;2 |
| [39] |
Janjić Z I. Nonsingular implementation of the Mellor-Yamada level 2. 5 scheme in the NCEP meso model[R]. USA: National Centers for Environmental Prediction, 2001: 1-61.
|
| [40] |
Nakanishi M, Niino H. Development of an improved turbulence closure model for the atmospheric boundary layer[J]. J Meteor Soc Japan, 2009, 87(5): 895-912. DOI:10.2151/jmsj.87.895 |
| [41] |
Grenier H, Bretherton C S. A moist PBL parameterization for large-scale models and its application to subtropical cloud-topped marine boundary layers[J]. Mon Wea Rev, 2001, 129(3): 357-377. DOI:10.1175/1520-0493(2001)129<0357:AMPPFL>2.0.CO;2 |
| [42] |
Bretherton C S, Park S. A new moist turbulence parameterization in the Community Atmosphere Model[J]. J Climate, 2009, 22(12): 3422-3448. DOI:10.1175/2008JCLI2556.1 |
| [43] |
Nakanishi M. Improvement of the Mellor-Yamada turbulence closure model based on large-eddy simulation data[J]. Bound-Lay Meteorol, 2001, 99(3): 349-378. DOI:10.1023/A:1018915827400 |
| [44] |
Nakanishi M, Niino H. An improved Mellor-Yamada Level-3 model with condensation physics: Its design and verification[J]. Bound-Lay Meteorol, 2004, 112(1): 1-31. DOI:10.1023/B:BOUN.0000020164.04146.98 |
| [45] |
Sommeria G, Deardorff J W. Subgrid-scale condensation in models of nonprecipitating clouds[J]. J Atmos Sci, 1977, 34(2): 344-355. DOI:10.1175/1520-0469(1977)034<0344:SSCIMO>2.0.CO;2 |
| [46] |
Nakanishi M, Niino H. An improved Mellor-Yamada level-3 model: its numerical stability and application to a regional prediction of advection fog[J]. Bound-Lay Meteorol, 2006, 119(2): 397-407. DOI:10.1007/s10546-005-9030-8 |
| [47] |
Sommeria G. Parameterization of the planetary boundary layer in large-scale atmospheric models[C]. Dordrecht: Kluwer Academic Publishers, 1988: 331-374.
|
| [48] |
Deardorff J W. On the entrainment rate of a stratocumulus-topped mixed layer[J]. Quart J Roy Meteor Soc, 1976, 102(433): 563-582. DOI:10.1002/(ISSN)1477-870X |
| [49] |
Deardorff J W. Stratocumulus-capped mixed layers derived from a three-dimensional model[J]. Bound-Lay Meteorol, 1980, 18(4): 495-527. DOI:10.1007/BF00119502 |
| [50] |
Cuijpers J W M, Duynkerke P G. Large eddy simulation of trade wind cumulus clouds[J]. J Atmos Sci, 1993, 50(23): 3894-3908. DOI:10.1175/1520-0469(1993)050<3894:LESOTW>2.0.CO;2 |
| [51] |
Smith R N B. A scheme for predicting layer clouds and their water content in a general circulation model[J]. Quart J Roy Meteor Soc, 1990, 116(492): 435-460. DOI:10.1002/(ISSN)1477-870X |
| [52] |
Siebesma A P, Cuijpers J W M. Evaluation of parametric assumptions for shallow cumulus convection[J]. J Atmos Sci, 1995, 52(6): 650-666. |
| [53] |
Koehler M. Improved prediction of boundary layer clouds[N]. ECMWF Newsletter, No. 104, ECMWF, Reading, United Kingdom, 2005: 18-22.
|
| [54] |
Siebesma A P, Soares P M M, Teixeira J. A combined eddy-diffusivity mass-flux approach for the convective boundary layer[J]. J Atmos Sci, 2007, 64(4): 1230-1248. DOI:10.1175/JAS3888.1 |
| [55] |
Soares P M M, Miranda P M A, Siebesma A P, et al. An eddy-diffusivity/mass-flux parameterization for dry and shallow cumulus convection[J]. Quart J Roy Meteor Soc, 2004, 130(604): 3365-3383. DOI:10.1256/qj.03.223 |
| [56] |
Witek M L, Teixeira J, Matheou G. An integrated TKE-based eddy diffusivity/mass flux boundary layer closure for the dry convective boundary layer[J]. J Atmos Sci, 2011, 68(7): 1526-1540. DOI:10.1175/2011JAS3548.1 |
| [57] |
Sušelj K, Teixeira J, Matheou G. Eddy diffusivity/mass flux and shallow cumulus boundary layer: An updraft PDF multiple mass flux scheme[J]. J Atmos Sci, 2012, 69(5): 1513-1533. DOI:10.1175/JAS-D-11-090.1 |
| [58] |
Sušelj K, Teixeira J, Chung D. A unified model for moist convective boundary layers based on a stochastic eddy-diffusivity/mass-flux parameterization[J]. J Atmos Sci, 2013, 70(7): 1929-1953. DOI:10.1175/JAS-D-12-0106.1 |
| [59] |
Lock A P, Brown A R, Bush M R, et al. A new boundary layer mixing scheme. Part Ⅰ: Scheme description and single-column model tests[J]. Mon Wea Rev, 2000, 128(9): 3178-3199. |
| [60] |
Shin S-H, Ha K-J. Implementation of turbulent mixing over a stratocumulus-topped boundary layer and its impact in a GCM[J]. Adv Atmos Sci, 2009, 26(5): 995-1004. DOI:10.1007/s00376-009-8145-0 |
| [61] |
Van Meijgaard E, Van Ulden A P. A first order mixing-condensation scheme for nocturnal stratocumulus[J]. Atmos Res, 1998, 45(4): 253-273. DOI:10.1016/S0169-8095(97)00080-X |
| [62] |
Sun W Q, Li L J, Wang B. Reducing the biases in shortwave cloud radiative forcing in tropical and subtropical regions from the perspective of boundary layer processes[J]. Sci China Earth Sci, 2016, 59(7): 1427-1439. DOI:10.1007/s11430-016-5290-z |
| [63] |
Konor C S, Boezio G C, Mechoso C R, et al. Parameterization of PBL processes in an atmospheric general circulation model: description and preliminary assessment[J]. Mon Wea Rev, 2009, 137(3): 1061-1082. DOI:10.1175/2008MWR2464.1 |
| [64] |
Noh Y, Cheon W G, Hong S Y, et al. Improvement of the K-profile model for the planetary boundary layer based on large eddy simulation data[J]. Bound-Lay Meteorol, 2003, 107(2): 401-427. DOI:10.1023/A:1022146015946 |
| [65] |
Hong S-Y, Noh Y, Dudhia J. A new vertical diffusion package with an explicit treatment of entrainment processes[J]. Mon Wea Rev, 2006, 134(9): 2318-2341. DOI:10.1175/MWR3199.1 |
| [66] |
Turton J D, Nicholls S. A study of the diurnal variation of stratocumulus using a multiple mixed layer model[J]. Quart J Roy Meteor Soc, 1987, 113(477): 969-1009. DOI:10.1002/qj.49711347712 |
| [67] |
Moeng C-H, Sullivan P P. A comparison of shear- and buoyancy-driven planetary boundary layer flows[J]. J Atmos Sci, 1994, 51(7): 999-1022. |
| [68] |
Lilly D K. Models of cloud-topped mixed layers under a strong inversion[J]. Quart J Roy Meteor Soc, 1968, 94(401): 292-309. DOI:10.1002/(ISSN)1477-870X |
| [69] |
Lilly D K. Entrainment into mixed layers. Part Ⅱ: A new closure[J]. J Atmos Sci, 2002, 53(23): 3353-3361. |
| [70] |
Lock A P. The parameterization of entrainment in cloudy boundary layers[J]. Quart J Roy Meteor Soc, 1998, 124(552): 2729-2753. DOI:10.1002/(ISSN)1477-870X |
| [71] |
Randall D A, Schubert W H. Dreams of a stratocumulus sleeper[M]//Fedorovich E, Rotunno R, Stevens B. Atmospheric turbulence and mesoscale meteorology: Scientific research inspired by Doug Lilly. Cambridge: Cambridge University Press, 2004: 71-94.
|
| [72] |
Moeng C-H. Entrainment rate, cloud fraction, and liquid water path of PBL stratocumulus clouds[J]. J Atmos Sci, 2000, 57(21): 3627-3643. DOI:10.1175/1520-0469(2000)057<3627:ERCFAL>2.0.CO;2 |
| [73] |
Stevens B. Entrainment in stratocumulus topped mixed layers[J]. Quart J Roy Meteor Soc, 2002, 128(586): 2663-2690. DOI:10.1256/qj.01.202 |
| [74] |
黄丽萍, 陈德辉, 邓莲堂, 等. GRAPES_Meso Ⅴ4.0主要技术改进和预报效果检验[J]. 应用气象学报, 2017, 28(1): 25-37. |
| [75] |
中国气象局数值预报中心. GRAPES_Meso中尺度数值预报系统用户指南[M]. 2013: 56-57.
|
| [76] |
ECMWF. IFS Documentation-CY43r3, Part Ⅳ:Physical processes[M]. Reading, United Kingdom: ECMWF, 2017: 33-58.
|
| [77] |
Han J, Witek M L, Teixeira J, et al. Implementation in the NCEP GFS of a hybrid Eddy-Diffusivity Mass-Flux(EDMF) boundary layer parameterization with dissipative heating and modified stable boundary layer mixing[J]. Wea Forecasting, 2016, 31(1): 341-352. DOI:10.1175/WAF-D-15-0053.1 |
| [78] |
Golaz J-C, Larson V E, Cotton W R. A PDF-based model for boundary layer clouds. Part Ⅰ: Method and model description[J]. J Atmos Sci, 2002, 59(24): 3540-3551. DOI:10.1175/1520-0469(2002)059<3540:APBMFB>2.0.CO;2 |
| [79] |
Guo H, Golaz J-C, Donner L J, et al. Multi-variate probability density functions with dynamics for cloud droplet activation in large-scale models: single column tests[J]. Geosci Model Dev, 2010, 3(2): 475-486. DOI:10.5194/gmd-3-475-2010 |
| [80] |
Bogenschutz P A, Gettelman A, Morrison H, et al. Unified parameterization of the planetary boundary layer and shallow convection with a higher-order turbulence closure in the Community Atmosphere Model: single-column experiments[J]. Geosci Model Dev, 2012, 5(6): 1407-1423. DOI:10.5194/gmd-5-1407-2012 |
| [81] |
Bogenschutz P A, Gettelman A, Morrison H, et al. Higher-order turbulence closure and its impact on climate simulations in the community atmosphere model[J]. J Climate, 2013, 26(23): 9655-9676. DOI:10.1175/JCLI-D-13-00075.1 |
| [82] |
Shin H H, Hong S-Y. Analysis of resolved and parameterized vertical transports in convective boundary layers at gray-zone resolutions[J]. J Atmos Sci, 2013, 70(10): 3248-3261. DOI:10.1175/JAS-D-12-0290.1 |
| [83] |
Shin H H, Dudhia J. Evaluation of PBL parameterizations in WRF at subkilometer grid spacings: turbulence statistics in the dry convective boundary layer[J]. Mon Wea Rev, 2016, 144(3): 1161-1177. |
| [84] |
Ma L, Bao X. Research progress on physical parameterization schemes in numerical weather prediction models[J]. Adv Earth Sci, 2017, 32(7): 679-687. |
 2018, Vol. 38
2018, Vol. 38