2. 辽宁省气象台,辽宁 沈阳 110166
2. Liaoning Meteorological Observatory, Shenyang 110166, China
由于地理位置的原因,渤海主要受中高纬度天气系统影响。尤其冬半年,较强的大陆冷高压前锋移动到海面时,海上会出现大风天气。除了冷空气以外,温带气旋、热带气旋及强对流天气也可以造成海上大风[1-3]。海上观测风资料来源于海上石油平台、海岛、浮标、灯船等站点,这些都是海面上的直接观测资料,可以对单点进行长时间序列的观测,但是由于站点选择困难,安装及维修等花费昂贵,广阔的海面上观测站点非常稀疏,对海面风场在时空分布等方面的研究与分析造成很大影响。另外,站点观测的高度差别很大,不同安置高度而引起的观测偏差非常严重[4],将站点观测风速修正到统一的高度上进行比较是很有必要的。
搭载在卫星上的微波散射计等传感器反演出的海上风场,在一定程度上弥补了海洋气象观测不足的状况。散射计反演风场是通过观测海面粗糙度来完成的,因此卫星反演风的风速和风向与海面站点观测资料在特定海域的一致性需要进行评估。关于卫星反演风在中国近海的适用性前人做了很多工作,早期针对QuikSCAT反演风与海岛和船舶观测风进行了一些对比研究[5-6]。QuikSCAT退役之后,ASCAT卫星反演风[7]获得了重视,国外的研究者[8-9]利用浮标对ASCAT风场进行检验,认为二者有着良好的一致性;近几年国内气象工作者[10-15]对ASCAT反演风在中国近海的质量也进行了分析,结果表明,ASCAT反演风在开阔海域有较好的精度,近岸海域偏差相对较大。在这些研究中站点风速大多选用了直接观测结果,没有对站点观测进行高度修正,其对比结果存在着一定的适用性限制。
本文选择渤海海域浮标、石油平台和海岛三类观测站中资料连续性较好的部分站点,利用COARE算法将站点观测风速修正到10 m高度上,分析修正后的站点风与ASCAT卫星反演风之间的平均偏差及均方根偏差,以及不同风速区间和不同风向条件下偏差的分布状况。通过分析,提高了对渤海海域不同来源观测风资料之间差别的认识。文中的ASCAT卫星反演风简称为卫星风,站点观测风简称为站点风,具体包括浮标风、平台风和海岛风。
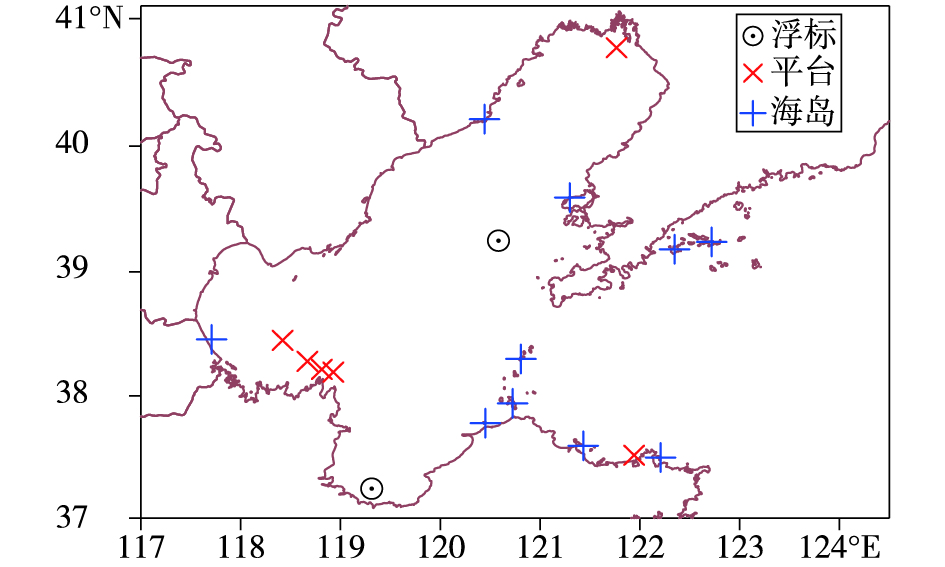
1 资料 1.1 站点观测资料环渤海海域布设了多个浮标、平台、灯塔和海岛站点,但受海上环境影响,观测仪器安装、维护都非常困难,很多站点的观测资料时间序列都有严重的缺失。这里选择的18个站中,有13个站的样本量占全部观测时次的90%以上,3个站为70%左右,2个站为50%左右。浮标选用了位于渤海中部的大连气象1号灯浮标和位于莱州湾的潍坊港浮标,其中前者为直径10 m的大浮标,后者为直径3 m的小浮标;平台站选用了包括渤海A平台在内的共计6个站点;海岛站选用了受周围环境影响较小、距离卫星风覆盖范围较近的10个站点。站点资料的时段为2015年7月—2017年12月,要素为2 min平均风速和风向,资料来源于国家气象信息中心的全国综合气象信息共享平台(CIMISS)。站点位置如图 1所示,站点的高度、站名、类型等信息见表 1。根据站点类型将站点分为三组,第一组为浮标站点,第二组为平台站点,第三组为海岛站。三组的样本量分别为浮标站1 952个,平台站10 434个,海岛站25 691个。
|
图 1 观测站点分布 Fig.1 Geographic locations of observation stations used in the study |
|
|
表 1 观测站点信息 Table 1 Information of observation stations |
ASCAT散射计搭载在欧洲卫星气象组织(EUMETSAT)发射的Metop卫星上,工作频率为C波段(5.255 GHz),散射计获得海面后向散射系数来探测海面粗糙度,再通过地球物理模型(CMOD5.n)来反演海洋表面10 m高度上的风速和风向。2006年10月发射Metop-A星,2012年9月发射Metop-B星。两颗星的ASCAT反演风都有25 km和12.5 km两种分辨率的洋面风产品,本文中所用的洋面风数据包括A星和B星的12.5 km分辨率产品,资料来源于皇家荷兰气象研究协会(KNMI)。
1.3 再分析资料利用COARE3.5算法进行风速高度修正的过程中,海面要素例如海浪和海面温度资料使用的是ERA-Interim再分析资料,空间分辨率为0.125°×0.125°,时间分辨率为6 h,在进行时间空间匹配时,空间上用的是距离站点位置最近的一个再分析格点,时间上用的是观测资料向前和向后3 h内最近时间的再分析资料。
2 方法 2.1 样本统计对比分析采用样本平均偏差和均方根偏差等参数来完成,公式如下。
| $ 平均偏差: B=\frac{1}{N} \sum\limits_{i=1}^{N}\left(A_{i}-S_{i}\right) $ | (1) |
| $ 均方根偏差: R M S D=\sqrt{\frac{1}{N} \sum\limits_{i=1}^{N}\left(A_{i}-S_{i}\right)^{2}} $ | (2) |
其中,A表示卫星散射计(ASCAT)反演风,S表示站点(Station)观测风,N表示分析样本量。在本文中风速和风向的偏差统计采用A-S的方式,即卫星风减去站点风。风速差正值表示卫星风速大于站点观测风速,负值表示卫星风速小于站点观测风速;风向偏差的正值表示卫星风相对于观测风顺时针旋转一定的角度数,负值表示卫星风相对于观测风逆时针旋转一定的角度数。
2.2 空间插值采用反距离权重插值方法计算卫星风在观测站点上的风向和风速,具体的方法是先将卫星风分解为u、v分量,利用反距离权重插值方法得到站点位置上的U、V,然后再合成为风向和风速值。
反距离权重插值公式:
| $ Z_{P}=\sum\limits_{i=1}^{N} \frac{Z_{i}}{d_{i}^{k}} / \sum\limits_{i=1}^{N} \frac{1}{d_{i}^{k}} $ | (3) |
式中,Z为站点P的U、V风速值,Zi为第i个卫星风的u、v风速值,di为站点P与其邻域内第i个卫星风之间的距离,k为次幂,这里取k=2,也就是反距离平方插值方法,邻域半径为ASCAT卫星风分辨率的一半。
2.3 风速的高度修正ASCAT卫星风为海面10 m高度上的反演风,而站点的高度各有不同,为了能对比风速的一致性,需要将不同高度的风修正到10 m高度上。高度修正的方法有很多,最常用的有指数风廓线公式和对数风廓线公式,这两种方法都没有考虑海面温度以及海浪等对风速的影响,本文中使用的COARE3.5的块体算法[16-17]将海面要素作为输入项进行计算将风速修正到10 m的高度上。COARE算法是由热带海洋与全球大气计划“耦合海气响应试验”(TOGA-COARE)发展起来的,以Monion-Obukhov(MO)相似理论为基础,主要利用风速、温度、湿度等计算海气界面之间的热通量和动量通量等,该算法最初只适用于热带海域,发展到3.0版本可适用于中纬度地区,风速限制扩展至20 m·s-1,3.5版本的时候风速的限制扩展到25 m·s-1,并可以计算输出10 m高度的风速。
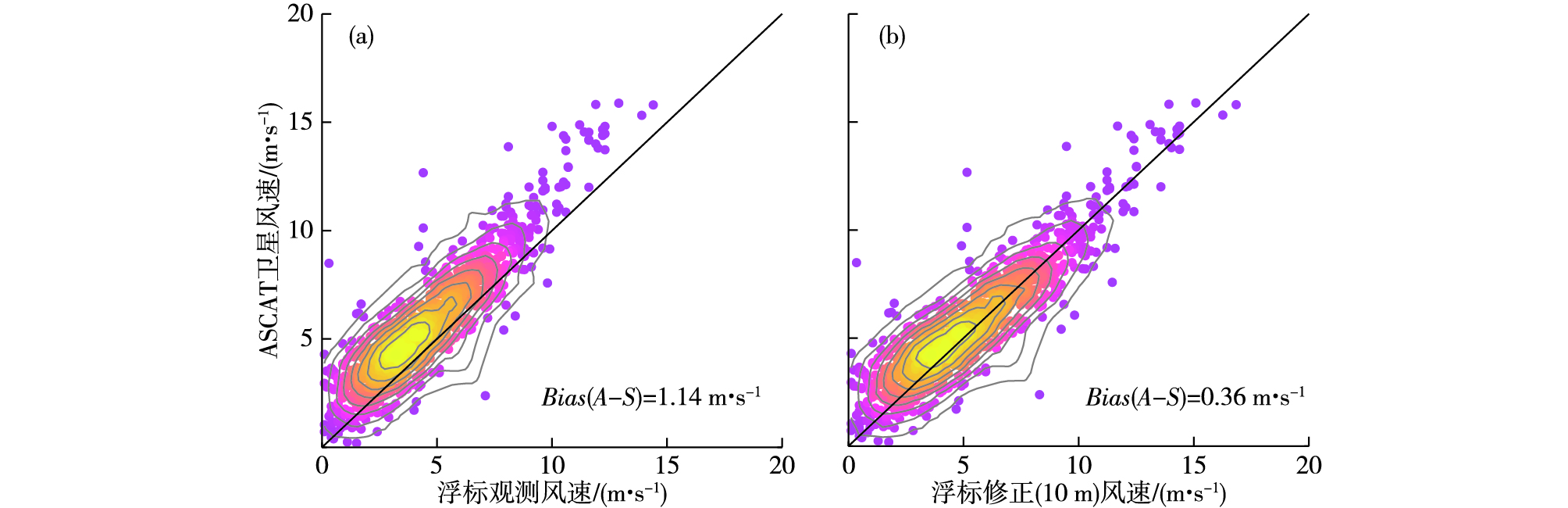
3 分析与讨论 3.1 站点风与卫星风的整体对比潍坊港浮标的高度为3.2 m左右,利用COARE算法对该浮标的观测风进行高度修正,并与卫星风进行对比(图 2)。由散点图可以看出,修正前浮标风速整体上偏小于卫星风,大量样本位于对角线的左侧,进行风速的高度修正之后,对比样本向对角线靠近。定量计算卫星风减去浮标风的风速差,均值由原来的1.14 m·s-1减小为0.36 m·s-1,平均风速增加了0.78 m·s-1。作为对比,用指数公式进行高度修正,平均风速增加的量值为0.74 m·s-1,二者相近。
|
图 2 潍坊港浮标风速高度修正前后与卫星风的对比分析(a.观测风速,b.修正到10 m高度的风速) Fig.2 Comparison of wind speed between buoy (54748) in the Weifang Harbor before/after adjustment and ASCAT satellite (a. the observed wind speed, b. the wind speed when the anemometer height is adjusted to 10 m) |
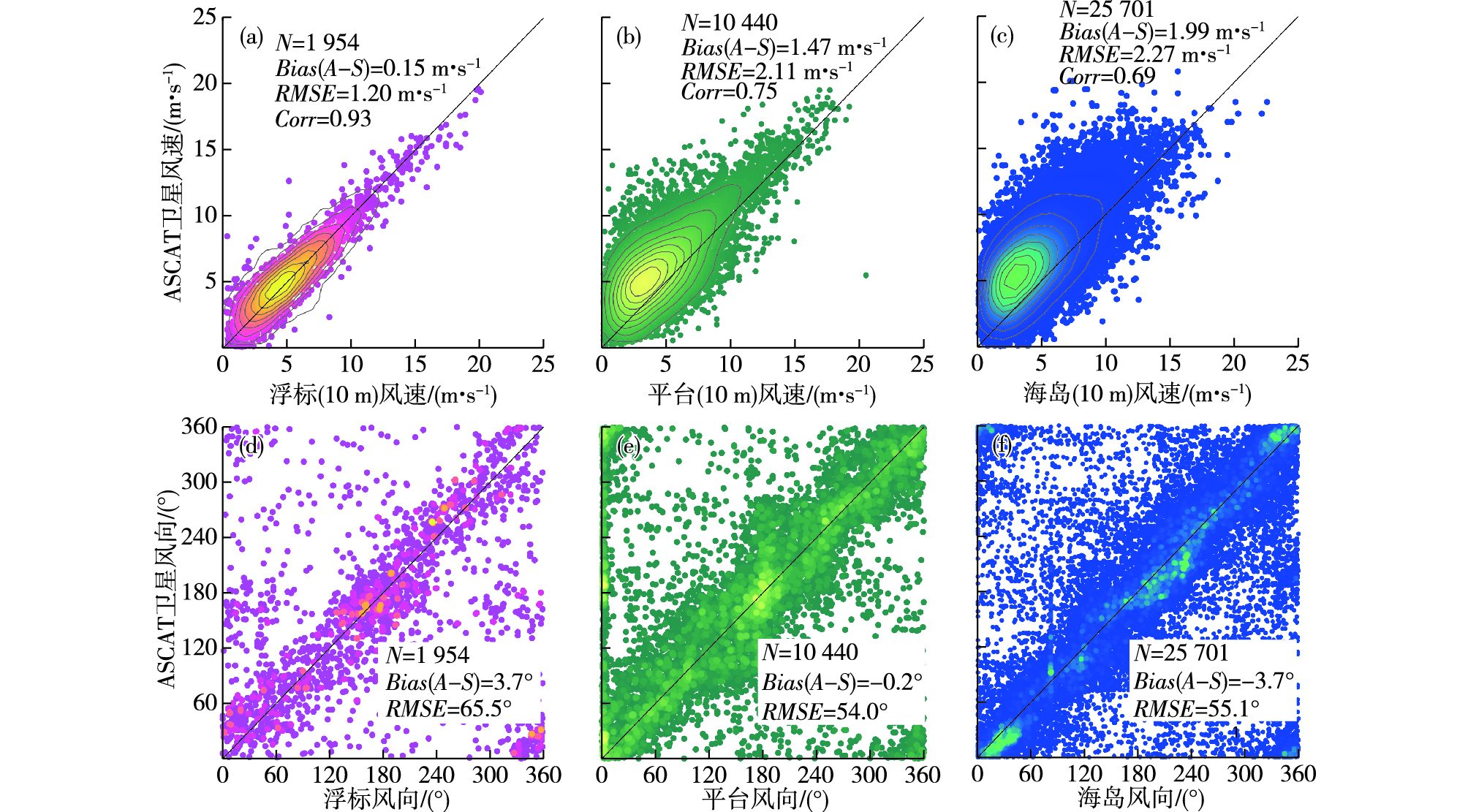
分别对三个分组所有站点的风速样本(图 3a、b、c)进行对比分析,风速修正后,卫星风减去浮标风的平均偏差为0.15 m·s-1,卫星风比浮标风偏大,而未修正之前二者的风速偏差为0.58 m·s-1。浮标风速修正后均值是变大的,主要是因为潍坊港浮标站观测仪器的高度大约低于10 m,修正到10 m高度上后,风速变大,而大连1号灯浮标站的高度为10 m,风速不需要修正。浮标风整体样本的风速均值增加了0.43 m·s-1左右,与卫星风速的相关系数由0.92增至0.93,相关性略有提高。0.15 m·s-1的偏差与自动站仪器0.1 m·s-1的观测精度[18]非常接近,并且在实际的业务预报中已经完全满足需求,在一定程度上证明,针对站点观测资料的高度修正是可信的。用同样的方法将平台站和海岛站的观测风速修正到10 m的高度上,修正后的风速与卫星风的对比才更具有针对性。由于平台站和海岛站的站点高度大部分都在10 m以上,从整体上看,风速的高度修正结果是风速值降低了,风速偏差比修正之前变得更大,修正后,平台风速偏差为1.47 m·s-1,海岛风速偏差为1.99 m·s-1。卫星风与三类站点风的均方根偏差分别为1.2 m·s-1、2.11 m·s-1和2.27 m·s-1。下文分析中所用站点的风速皆为进行高度修正之后的风速值。
|
图 3 站点观测风和ASCAT卫星风的对比统计(a、b、c.浮标、平台、海岛测风与卫星风速的对比,d、e、f.风向的对比) Fig.3 Statistical comparison between the observed wind and ASCAT satellite wind (a-c. comparison of wind speed between the observed speed from the buoy/platform/island and the satellite, d-f. comparison of wind direction between the observed direction from the buoy/platform/island and the satellite) |
由风向的对比散点图(图 3d、e、f)可以看出,站点风与卫星风的风向样本密集区都集中在对角线附近,部分样本点集中在左上角和右下角的区域。统计结果显示,卫星风与三类站点风向的平均偏差分别为3.7°、0.2°和-3.7°,卫星风向相对浮标观测风逆时针旋转3.7°,相对平台站和海岛站分别为顺时针旋转0.2°和3.7°。风向偏差的平均值显示站点风向和卫星风向一致性较好,但是由图上还可以看出样本点并非全在对角线上,也分布在对角线两侧,风向偏差在具体的观测样本上还是有很大的差异,三类站点风与卫星风的风向均方根偏差都比较大,分别为66°、54°和55°。
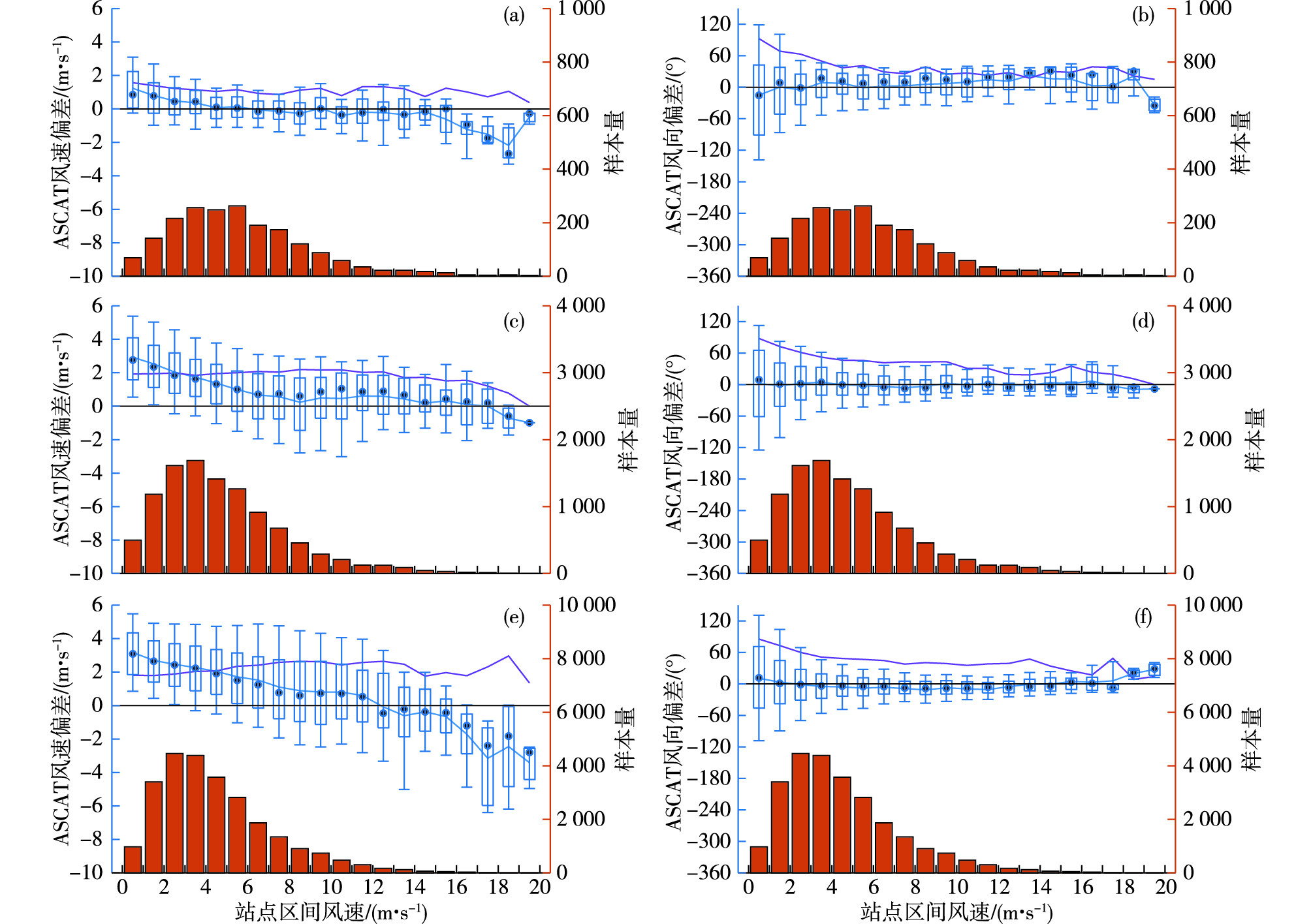
3.2 偏差和均方根偏差随风速的分布图 4给出了风速偏差和风向偏差随着风速增加的变化曲线,并且给出了在不同范围内风速偏差的统计分位数箱线图,上下短线的范围分别为10%、90%分位数,中间矩形为25%和75%的分位数,黑色圆点为中位数,蓝色曲线为平均偏差,紫色曲线为均方根偏差,柱状图为样本量。图 5和图 6中采用与此一致的分位数划分方式。
|
图 4 卫星风与站点风平均偏差和均方根偏差随站点风风速的变化(a.与浮标站的风速偏差,b.与浮标站的风向偏差,c.与平台站的风速偏差,d.与平台站的风向偏差,e.与海岛站的风速偏差,f.与海岛站的风向偏差) Fig.4 Variation of mean deviation and RMSD between the satellite wind and the observed wind with the change of wind speed at stations (a/c/e. wind speed deviation between the satellite and buoys/platforms/island stations, b/d/f. wind direction deviation between the satellite and buoys/platforms/island stations) |
|
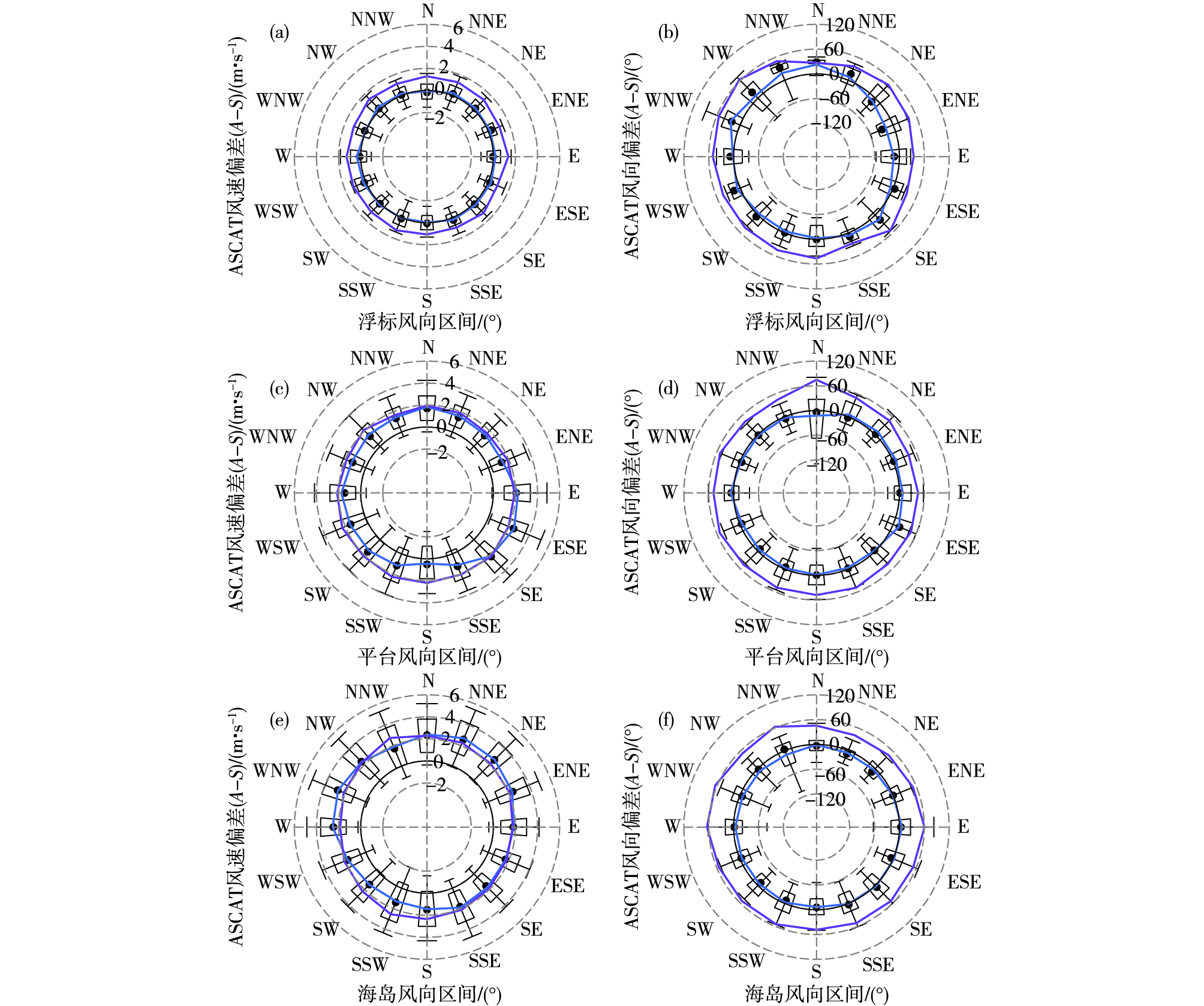
图 5 卫星风与站点风平均偏差和均方根偏差随站点风风向的变化(a.与浮标站的风速偏差,b.与浮标站的风向偏差,c.与平台站的风速偏差,d.与平台站的风向偏差,e.与海岛站的风速偏差,f.与海岛站的风向偏差) Fig.5 Variation of mean deviation and RMSD between the satellite wind and the observed wind with the change of wind directions at stations (a/c/e. wind speed deviation between the satellite and buoys/platforms/island stations, b/d/f. wind direction deviation between the satellite and buoys/platforms/island stations) |

|
图 6 卫星风与站点风平均偏差和均方根偏差的季节分布(a.与浮标站的风速偏差,b.与浮标站的风向偏差,c.与平台站的风速偏差,d.与平台站的风向偏差,e.与海岛站的风速偏差,f.与海岛站的风向偏差) Fig.6 Monthly variation of mean deviation and RMSD between the satellite wind and the observed wind (a/c/e. wind speed deviation between the satellite and buoys/platforms/island stations, b/d/f. wind direction deviation between the satellite and buoys/platforms/island stations) |
由图 4a、c、e可以看出,随着风速的增大,风速的平均偏差由大到小变化,弱风的时候卫星风比站点风大,强风的时候卫星风比站点风小。卫星风速与浮标风速的偏差在0~4 m·s-1的区间是正值,卫星风速大于浮标风速0~1 m·s-1;在5~15 m·s-1的区间内,风速偏差的均值在零值附近,在此区间中,卫星风与浮标风速具有良好的一致性,基本上能够满足WMO[4]对观测仪器精度的要求;15 m·s-1以上大风情况下的风速差以负值为主,卫星风速比浮标风速小1~2 m·s-1。风速差的平均值在大风(例如19 m·s-1)的时候出现大的风速差可能与此时样本量偏少有关,不过也在一定程度上说明,ASCAT很难能反演出大的风速。平台风在0~7 m·s-1之间时,风速差从3 m·s-1变化减小到1 m·s-1,7~17 m·s-1以上的风速区间里面,卫星风速比平台风略大0~1 m·s-1,在18 m·s-1以上风速的时候出现卫星风小于平台风的情况。海岛风因为受岛屿及站点选址等的影响,在测风小于12 m·s-1(6级)时都是卫星风比海岛风大,且风速越小时风速差越大;而12 m·s-1以上的强风或大风出现时,海岛站又能观测到比卫星风大的量值。
图中还给出了风速均方根偏差随风速的分布。浮标风速差的均方根偏差大小在0.5~1.5 m·s-1之间,随风速的增加变化不大;平台风速差的均方根偏差在1.5~2.0 m·s-1之间,随风速的增加略有减小;海岛风速差的均方根偏差在2.0~3.0 m·s-1之间,随风速的增加均方根偏差增大。
卫星风与站点风的风向偏差随着风速的变化曲线如图 4b、d、f所示。浮标风向差的平均偏差随风速增加主要以正值为主,特别是大于10 m·s-1的风速情况下,卫星风向相对于浮标风顺时针偏转10°~40°,而0~1 m·s-1的风速存在较大风负值偏差。平台风向偏差和海岛风向偏差的均值都比较小,特别是在2~15 m·s-1的区间中,风向偏差最大也在10°以内。
风向的均方根偏差随着风速的增加都呈现下降的趋势。对于平台站和海岛站来说,0~5 m·s-1的弱风区均方根偏差在50°~80°,5~12 m·s-1风速区间的风向均方根偏差下降到30°~50°,12 m·s-1以上的风向均方根偏差下降到30°以内,浮标风向偏差的量值相对偏小,6 m·s-1以上的风向偏差在20°~40°之间。但从全部样本上来看,风速5 m·s-1的样本占整个样本量的70%左右,表明弱风的风向偏差是影响风向整体精度的一个主要因素,这与谢小萍等[13]的结论相同,但是在6 m·s-1以上的情况下,卫星风与站点风的风向偏差基本能满足业务需求。
3.3 偏差与均方根偏差随风向的分布图 5中给出了卫星风与站点风风速和风向偏差及均方根偏差随风向的分布情况,风向按照16个方位进行划分,在图上以N和NNE等表示。在风向的各个方位上,浮标的风速偏差均值和中位数都几乎为零,风速的均方根偏差在1.4 m·s-1左右,此结果与张增海等[10]分析中国近海浮标与卫星风的结果一致,浮标风和卫星风的风向保持了良好的一致性,但是平台站和海岛站的表现则略有不同。平台站的风速平均偏差在偏北风和东南风方向上量级最大,卫星风比平台风大2 m·s-1以上,而其他风向上在2 m·s-1以下,尤其是偏南风方向上最小为1 m·s-1以下,这样的结果应该与平台站点布设的位置有关。海岛站的风速平均偏差在东北风和西北风方向上较大,量级与平台站在东南风方向上相当,而在西南风方向上风速平均偏差最小,在1.5 m·s-1左右。三类站点风与卫星风的风速均方根偏差在各个风向上的差别并不是很大。在量级上,平台站和海岛站的均方根偏差在2 m·s-1左右,浮标站略小,在1.5 m·s-1上下。
由风向平均偏差和均方根偏差随风向的分布来看,三类站点分布类似,风向平均偏差在零值附近。浮标站的风向偏差在北到西北方向上为正值,在东北到偏东风方向以负值为主,在不同的风向存在一定的波动性。平台站的风向偏差和海岛站的风向偏差都比较小。风向偏差的表现与三类站点布设方式有直接关系,浮标站在海上测风时并不是固定的,而是在海面随波浪起伏转动,观测风向时应该引入了传感器自身的影响。平台站点通常是在石油钻井平台的适当位置安装气象观测仪,一般难以达到风传感器的安装要求[18],是否由于风传感器的相对位置造成偏北风情况下有较大的风向均方根偏差,还需要对不同的站点做详细分析。
3.4 偏差的季节变化图 6给出了卫星风与站点风之间风速及风向偏差的季节分布。浮标的风速偏差逐月均值分布均匀,没有明显的季节分布,平均值差别不大,在-0.5~0.5 m·s-1之间。但是平台站及海岛站的风速偏差平均值存在着明显的季节变化,秋冬季大而春夏季小,3—5月,平均值分别为0.5 m·s-1和1.0 m·s-1左右,11月—次年1月的平均值较大,分别为2.0 m·s-1和3.0 m·s-1左右。由风速差的均方根偏差分布来看,三类站点的偏差随季节变化不大,但是在量值上有所不同,浮标风的均方根偏差较小为1.2 m·s-1,而平台风和海岛风的稍大,为2.0 m·s-1左右。
三类站点的风向平均偏差在零线附近,没有明显的季节变化。从量值上看,浮标站的风向平均偏差在7月为负值,在3—5月及10—12月为正值,而平台站及海岛站的风向平均偏差在4—7月为负值,其他月份基本为零。浮标风向的均方根偏差在4—8月偏大,为50°左右,其他月份的偏小一些,其均值为40°。平台站和海岛两类站点的风向均方根偏差都是在3—9月偏高,分别为58°和60°左右,10月—次年2月最小,相应的量值都为48°左右。
4 小结通过利用环渤海海域的浮标、平台、海岛的观测风资料与ASCAT卫星风场进行对比分析得到如下结论:
1) 对站点风速进行高度修正后,卫星风速与三类站点风速的平均偏差分别为0.15 m·s-1、1.47 m·s-1和1.99 m·s-1,均方根偏差分别为1.20 m·s-1、2.11 m·s-1和2.27 m·s-1,相关系数分别为0.93、0.75和0.69。浮标风速与卫星风速的平均偏差最小,相关性也最高。卫星风与站点风向的平均偏差都很小,分别为3.7°、0.2°和-3.7°,但是均方根偏差较大,分别为65.5°、54.0°和55.1°。
2) 在弱风区,卫星风比站点风的风速偏大;在强风区,卫星风的量值低于站点风;卫星风与站点风差别相对小的区间对不同的站点类型来说则有所不同。因观测样本较多,弱风区的风向偏差是影响整体偏差的重要原因。
3) 在不同的风向上,各个站点风与卫星风之间风速偏差和风向偏差等统计量的区别都不是太大。
4) 随季节的变化中,平台站和海岛站的风速与卫星风速的平均偏差秋冬季大而春夏季小,而浮标风的平均偏差并没有明显的季节变化。三类站点风速的均方根偏差、风向的平均偏差及均方根偏差等统计量的季节变化也不明显。
| [1] |
辛宝恒. 黄海渤海大风概论[M]. 北京: 气象出版社, 1991: 40-62.
|
| [2] |
阎俊岳, 陈乾金, 张秀芝, 等. 中国近海气候[M]. 北京: 科学出版社, 1993: 281-284.
|
| [3] |
李延江, 陈小雷, 卢宪梅. 渤海气象灾害与海洋灾害预报技术[M]. 北京: 气象出版社, 2014: 16-20.
|
| [4] |
WMO. Guide to meteorological instruments and methods of observation (WMO-No.8)[M]. Geneva, Switzerland: Secretariat of the World Meteorological Organization, 2008.
|
| [5] |
刘春霞, 何溪澄. QuikSCAT散射计矢量风统计特征及南海大风遥感分析[J]. 热带气象学报, 2003, 19(增刊): 107-117. |
| [6] |
方翔, 咸迪, 李小龙, 等. QuikSCAT洋面风资料及其在热带气旋分析中的应用[J]. 气象, 2007, 33(3): 33-39. |
| [7] |
Ocean and Sea Ice SAF. ASCAT wind product user manual (Version1. 14)[R]. 2016.
|
| [8] |
Bentamy A, Croize-Fillon D, Perigaud C. Characterization of ASCAT measurements based on buoy and QuikSCAT wind vector observations[J]. Ocean Sci, 2008, 4(4): 265-274. |
| [9] |
Verspeek J, Stoffelen A, Portabella M, et al. Validation and calibration of ASCAT using CMOD5.n[J]. IEEE Trans Geosci Remote Sens, 2010, 48(1): 386-395. DOI:10.1109/TGRS.2009.2027896 |
| [10] |
张增海, 曹越男, 刘涛, 等. ASCAT散射计风场在我国近海的初步检验与应用[J]. 气象, 2013, 40(4): 478-481. |
| [11] |
沈春, 项杰, 蒋国荣, 等. 中国近海ASCAT风场反演结果验证分析[J]. 海洋预报, 2013, 30(4): 27-33. |
| [12] |
高留喜, 朱蓉, 常蕊. QuikSCAT和ASCAT卫星反演风场在中国南海北部的适用性研究[J]. 气象, 2014, 40(10): 1240-1247. DOI:10.7519/j.issn.1000-0526.2014.10.008 |
| [13] |
谢小萍, 魏建苏, 黄亮. ASCAT近岸风场产品与近岸浮标观测风场对比[J]. 应用气象学报, 2014, 25(4): 445-453. DOI:10.3969/j.issn.1001-7313.2014.04.007 |
| [14] |
杨晓君, 张增海. ASCAT洋面风资料在中国北方海域的真实性检验[J]. 海洋预报, 2014, 31(5): 8-12. |
| [15] |
姚日升, 涂小萍, 丁烨毅, 等. 华东沿海ASCAT反演风速的检验和订正[J]. 应用气象学报, 2015, 26(6): 735-742. |
| [16] |
Yu L S, Weller R A. Objectively analyzed air-sea heat fluxes for the global ice-free oceans (1981-2005)[J]. Bull Amer Meteor Soc, 2007, 88(4): 527-539. DOI:10.1175/BAMS-88-4-527 |
| [17] |
Edson J B, Jampana V, Weller R A, et al. On the exchange of momentum over the open ocean[J]. J Phys Oceanogr, 2013, 43(8): 1589-1610. DOI:10.1175/JPO-D-12-0173.1 |
| [18] |
胡玉峰. 自动气象站原理与测量方法[M]. 北京: 气象出版社, 2004: 9-10.
|
 2018, Vol. 38
2018, Vol. 38

