引言

1978年Hoskins et al.^[1]提出的“ Q矢量分析方法”用于诊断准地转垂直运动，具有物理意义明确、计算简单，且能适用于整个对流层的特点。20世纪90年代以后，准地转Q矢量在国内得到广泛的发展和应用^[2-4]。张兴旺^[5]通过对一次华南暴雨过程诊断分析认为湿Q矢量与次级环流有良好的对应关系，还与降水落区有良好的配置关系。姚秀萍和于玉斌^[6]对一次台风暴雨研究发现，非地转湿Q矢量场流线的辐合中心或辐合线对应于气流的上升区，是降水之所在，非地转湿Q矢量与降水落区存在最佳的对应关系，是一种十分有效的暴雨天气系统诊断和预报工具。之后，很多学者^[7-12]利用湿Q矢量对暴雨开展了一些诊断分析工作，得出一些有意义的结果。2012年7月30日—8月1日鲁西北地区连续3天出现暴雨或大暴雨，并出现严重洪涝灾害，直接经济损失4.37亿元, 旱涝急转。魏国盼等^[13]对德州降雨进行长时间序列分析，得出德州降水资源呈减少趋势，但短时强降水等极端灾害性天气事件有增加趋势。朱义青等^[14]用中尺度模式WRF对山东中北部地区一次低槽冷锋暴雨天气过程进行数值模拟，较好地模拟再现了暴雨过程降水带走向、落区、范围和降水中心特征与演变。高帆等^[15]对2015年山东西北部一次暴雨过程进行中尺度特征分析，得出一些有价值的结论。近几年对鲁西北降水虽有过一些研究，但鲜见用湿Q矢量工具对鲁西北暴雨进行研究。本文利用每6 h一次的1°×1°的FNL全球再分析资料及常规观测的高空、地面资料和山东逐时地面降水数据，用湿Q矢量分析方法对这次暴雨过程进行了诊断，以期为今后此类天气预报提供有益的参考信息。

1 诊断方法

根据文献[6]，定义湿Q矢量(记为$\overrightarrow{{{\mathit{\pmb{Q}}}^{*}}}$)在p坐标系中的表达式为：

$ \begin{matrix} \overrightarrow{{{\pmb{\mathit{Q}}}^{*}}}=\left( Q_{x}^{*},Q_{y}^{*} \right) \\ Q_{x}^{*}=\frac{1}{2}\left[ f\left( \frac{\partial v}{\partial p}\frac{\partial u}{\partial x}-\frac{\partial u}{\partial p}\frac{\partial v}{\partial x} \right)-h\frac{\partial \overrightarrow{\mathit{\pmb{V}}}}{\partial x}\cdot \nabla \theta +\frac{\partial (h\mathit{\pmb{H}})}{\partial x} \right] \\ Q_{y}^{*}=\frac{1}{2}\left[ f\left( \frac{\partial v}{\partial p}\frac{\partial u}{\partial y}-\frac{\partial u}{\partial p}\frac{\partial v}{\partial y} \right)-h\frac{\partial \overrightarrow{\mathit{\pmb{V}}}}{\partial y}\cdot \nabla \theta +\frac{\partial (h\mathit{\pmb{H}})}{\partial y} \right] \\ h=\frac{R}{p}{{\left( \frac{p}{1000} \right)}^{\frac{R}{{{c}_{p}}}}},H=-\frac{1}{{{C}_{p}}}{{\left( \frac{1000}{p} \right)}^{\frac{R}{{{C}_{p}}}}}\omega \frac{\partial {{q}_{s}}}{\partial p} \\ \end{matrix} $

(1)

其中Q_x^*、Q_y^*为x、y方向的湿Q矢量分量，q_s为饱和比湿，$ \overrightarrow{\boldsymbol{V}}(u, v)$代表水平风场，其他符号为气象通用符号。由式(1)可知，湿Q矢量取决于风水平和垂直切变的差异效应，风的水平梯度和温度梯度的乘积及非绝热效应。

以湿Q矢量散度为唯一强迫项的非地转ω方程为：

$ f \frac{\partial^{2} \omega}{\partial p^{2}}+\nabla^{2}(\sigma \omega)=-2 \nabla \cdot \overrightarrow{\pmb{\mathit{Q}}^{*}} $

(2)

如果大气垂直运动是一种波动形式，根据任何波动形式物理量的拉普拉斯与该物理量本身负值成正比的关系，有ω正比于$\nabla \cdot \overrightarrow{\boldsymbol{Q}^{*}}$。当湿Q矢量场辐合时，ω＜0为上升运动；反之，ω＞0，即为下沉运动。

根据文献[7]，定义湿Q矢量的涡度δ_Q*、湿Q矢量的锋生函数F_Q*:

$ {{\delta }_{{{Q}^{*}}}}=\frac{\partial Q_{y}^{*}}{\partial x}-\frac{\partial Q_{x}^{*}}{\partial y}=\frac{1}{2}{{f}^{2}}\frac{\partial }{\partial p}\left( \frac{\partial {{v}_{a}}}{\partial x}-\frac{\partial {{u}_{a}}}{\partial y} \right) $

(3)

$ F_{Q^{*}}=Q^{*} \cdot \nabla \theta_{s e}=Q_{x}^{*} \cdot \frac{\partial \theta_{s e}}{\partial x}+Q_{y}^{*} \cdot \frac{\partial \theta_{s e}}{\partial y} $

(4)

式(3)表示非地转风涡度的垂直梯度与湿Q矢量的涡度成正比，θ_se为假相当位温。

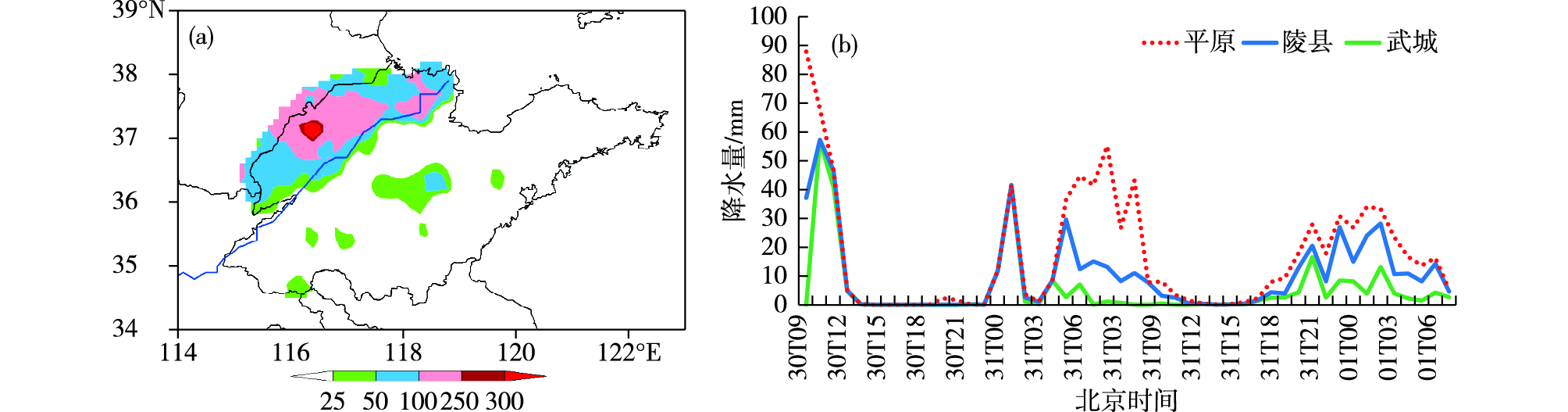
2 暴雨过程实况和环流背景

2012年7月30日08时—8月1日08时，在副热带高压(以下简称“副高”)稳定的环流形势下，受切变线和冷锋影响，山东出现了一次大暴雨天气过程，其中大暴雨21站，特大暴雨3站，强降雨主要出现在鲁西北地区，降水区域非常集中，降雨中心在平原县的前曹乡，降水量为417.0 mm，48 h累计降雨量达当地年降水总量的80%。鲁西北≥100 mm的降水区呈东北—西南向，100 mm的雨量外廓线是一大致为100 km×350 km的区域；黄河以南降水明显少，多数台站降水量＜25 mm(图 1a)。由图 1b发现，鲁西北持续暴雨分三个阶段，分别为30日上午、31日凌晨至中午、31日夜间。山东多站逐小时雨量超过20 mm，具有明显的中尺度特征。30日上午武城、平原、陵县附近大致有35 km×70 km的区域出现≥50 mm暴雨，最大降水超过100 mm；31日凌晨至中午，从茌平、济阳到滨州、东营出现多个强对流风暴和多个暴雨中心，茌平—滨州有70 km×150 km的区域出现≥50 mm暴雨，多站超过100 mm，其中商河降水量达192.1 mm，31日夜间茌平—利津100 km×300 km的区域出现≥50 mm暴雨，空间上具有中小尺度特征。

暴雨期间，500 hPa贝加尔湖区附近有一宽广低槽, 鄂霍次克海至我国东北北部为低涡(槽)控制, 中高纬40°N以北为两槽一脊形势。40°N以南形成海上高压和大陆高压对峙的形势，高压呈东西带状分布，呈现明显纬向环流。副高基本位于日本及其以东的西北太平洋上空，中心强度(590~592 dagpm)没有明显变化，脊线北抬至35°N附近稳定维持。副高南侧的两个台风(1209“苏拉”，1210“达维”)北抬，黄淮地区受副高北侧的偏西气流控制，鲁西北地区位于584 dagpm边缘的西南气流中(图 2)。台风不仅对副高的稳定有很大贡献，其北侧的东南气流与副高南侧偏东气流叠加沿高压边缘向鲁西北地区输送水汽，为鲁西北地区出现暴雨提供水汽和能量条件，还为鲁西北提供正涡度扰动^[16], 为增强低压提供动力条件, 有利于切变线增强和维持，对产生持续强降水有积极作用。河套地区低槽东移和中高纬贝加尔湖冷空气的下滑渗透受到阻挡，两高压对峙时间长, 使鲁西北地区长时间处在槽前的西南气流中, 高空不断有正涡度向鲁西北地区输送，低层减压，气旋型环流加强，切变线在鲁西北地区长时间维持，在这样的环流背景下，鲁西北出现持续性暴雨。

30日08时925 hPa鲁西北附近有一纬向切变线，存在明显的风向、风速辐合，随后6 h，切变线附近的武城、平原、陵县出现暴雨、大暴雨天气。31日02时925 hPa鲁西北有清楚的纬向切变线，之后出现与切变线走向基本一致的大范围暴雨、大暴雨天气。31日20时鲁西北的纬向切变线被新生的东北—西南向的经向切变线代替，暴雨区的走向发生明显变化，呈东北—西南向，8月1日20时切变线减弱消失，降水结束。切变线与暴雨关系密切。鲁西北长时间存在切变线，有很好的动力辐合条件和触发机制，是此次持续暴雨的一个重要原因。

3 湿Q矢量诊断分析 3.1 湿Q矢量散度场和降水落区的关系

分析不同高度湿Q矢量散度时间演变图发现，925~850 hPa湿Q矢量散度场对降水指示意义明显，辐合、辐散区多呈块状或条状正、负相间的分布，反映了中尺度特性。降水与湿Q矢量散度负值辐合区有很好的对应，大降水发生在湿Q矢量散度梯度比较大的负值区一侧。

7月30日08时925 hPa (38°N，116°E)处有一湿Q矢量散度为-50×10^-17 hPa^-1·s^-3的负值中心，随后6 h，处于其南侧的武城(37.22°N，116.07°E)出现102.5 mm降水，降水区与湿Q矢量散度负值区形状对应较好(图 3a)。14时，湿Q矢量散度负值区向东移动并明显减弱，中心值为-20×10^-17hPa^-1·s^-3，随后6 h降水明显减弱，中心降水仅出现大雨，降水落区与湿Q矢量散度负值区形状相似。

7月31日02时925 hPa鲁西北有明显的湿Q矢量散度负值区(图 3b)，其值在-100×10^-17~-50×10^-17 hPa^-1·s^-3，随后6 h出现明显降水，02—08时，≥50 mm降水区大致为一东西向100 km×200 km的区域，≥100 mm降水区分为相近的两块，也大致呈东西向，其整体外廓线大致为50 km×100 km的区域，最大降水出现在商河(151.9 mm)。31日08时湿Q矢量散度负值中心值为-70×10^-17 hPa^-1·s^-3，比02时明显弱，08—14时≥25 mm降水区与02—08时≥50 mm降水区大致相仿，08—14时≥50 mm降水区域明显变小，降水中心禹城的降水量为51 mm，降水减弱明显。14时，鲁西北地区主要为湿Q矢量散度正值区，随后6 h降水范围变小、强度更弱。

31日，随着天气系统的东移，北方的冷空气主要从925 hPa以下入侵，鲁西北地区925 hPa比上层较早转为东北气流，湿Q矢量的散度由负转为正值区，925 hPa湿Q矢量散度对8月1日02—08时的强降水没能很好地反应。而31日20时850 hPa一新的湿Q矢量散度负值中心移到鲁西北地区，负值中心＜-150×10^-17 hPa^-1·s^-3，随后6 h鲁西北的德州地区出现≥50 mm降水，呈南北向，范围大致为40 km×100 km。由图 3c可见，8月1日02时850 hPa湿Q矢量散度负值中心＜-200×10^-17 hPa^-1·s^-3，随后6 h鲁西北出现≥100 mm降水，从聊城的阳谷到滨州的无棣出现≥50 mm降水，降水区呈东北—西南向，范围大致为40 km×300 km，暴雨范围变大、强度增强。8月1日08时鲁西北大部地区为湿Q矢量散度正值区，随后6 h降水基本＜10 mm，减弱明显。这个阶段850 hPa比925 hPa湿Q矢量散度对强降水有更好的反应。

暴雨期间, 925~850 hPa ω负值区(图略)比$ \nabla \cdot \overrightarrow{\boldsymbol{Q}^{*}}$辐合区明显宽阔，难以较准确地预计暴雨落区，而低层湿Q矢量散度对强降水落区有更确切的预报指示意义。

综上分析可知，强降水并不总是出现在低层湿Q矢量散度负值中心，有时发生在湿Q矢量散度梯度比较大的负值区一侧，与过去研究结论“强降水出现在低层湿Q矢量散度负值中心”^[6]显然是有差异的。最强降水中心并不与辐合中心一一对应，可能有几个原因: 1)只有在假定ω是一个具有波状特征的函数时, 才能得到ω与$ \nabla \cdot \overrightarrow{\pmb{\mathit{Q}}^{*}}$成正比的关系，实际大气中最大的垂直运动并不一定与最强$ \overrightarrow{\boldsymbol{Q}^{*}}$辐合区对应；2)$ \overrightarrow{\boldsymbol{Q}^{*}}$矢量的诊断场时间与暴雨的发生时间不同期。另外，梯度比较大的地方意味着锋生比较强，更容易触发对流，从而利于出现强降水。

3.2 湿Q矢量散度垂直剖面分析

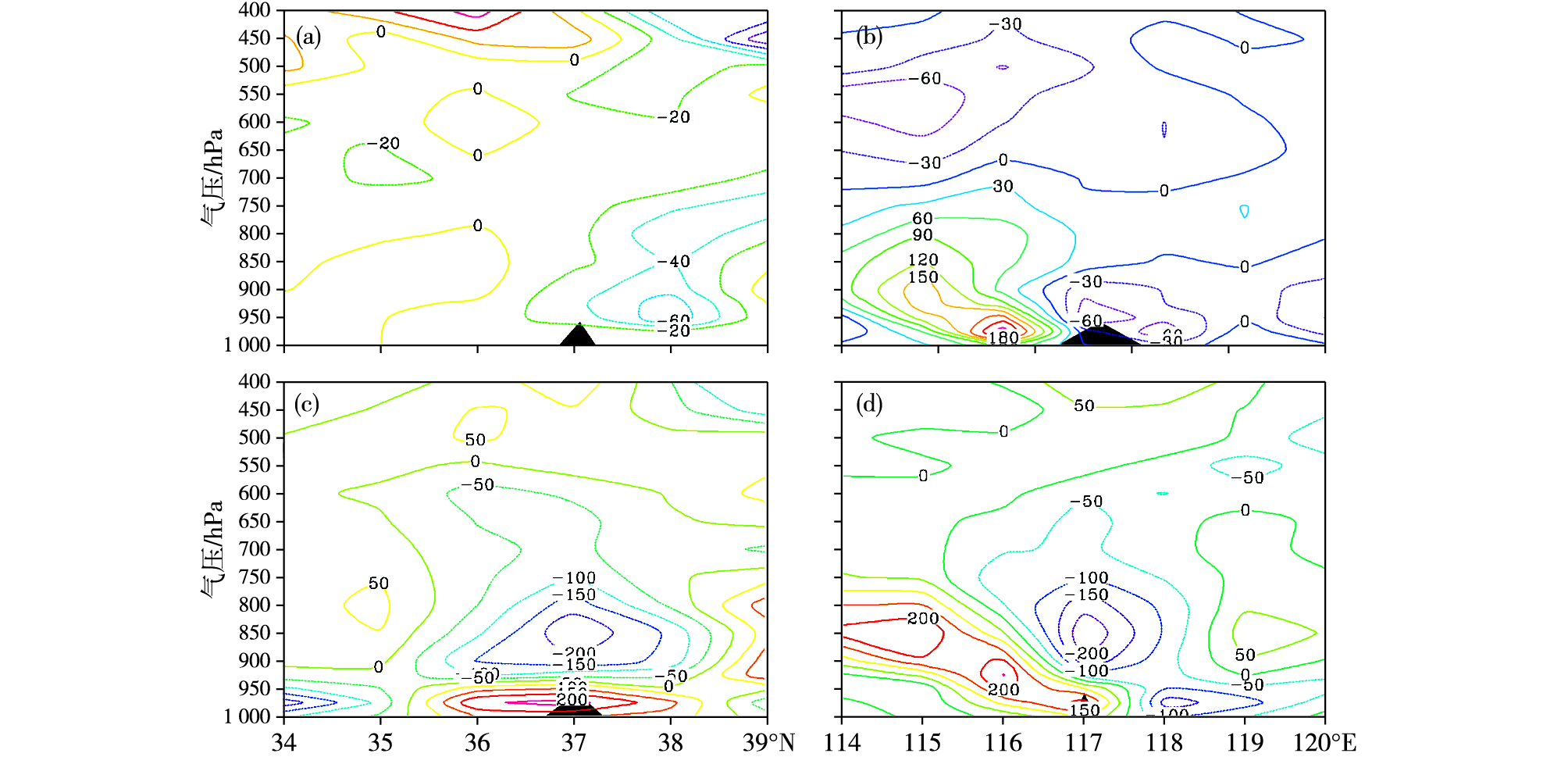
选择7月30日08时、31日02时、8月1日02时湿Q矢量散度过暴雨中心剖面图(图 4)对暴雨3个阶段进行分析。

第一阶段，暴雨区大致范围为36.9~37.2°N，116.1~116.8°E。由图 4a看出，36°N以北500 hPa以下基本为$ \nabla \cdot \overrightarrow{\pmb{\mathit{Q}}^{*}}＜0$，700 hPa以下负值区随高度明显向北倾斜，表明暴雨区上空有明显的系统性倾斜上升运动，暴雨区南侧约1纬度内有较弱的$\nabla \cdot \overrightarrow{\pmb{\mathit{Q}}^{*}} \geqslant 0$，即存在下沉补偿运动，有利于形成次级环流，暴雨出现在下沉气流北侧上升气流中心南侧辐合上升运动较明显的区域。暴雨区上空最大辐合中心位于950~900 hPa之间，500~400 hPa之间存在明显的辐散，暴雨强盛时期低层有明显的湿Q矢量散度的辐合强迫作用。37.5~38.5°N辐合都较好，但该区域斜压性不明显，实况降水较弱。暴雨区上空倾斜上升运动导致强降水的发生。

第二阶段，暴雨区大致范围为36.7~37.4°N，116.5~118.0°E。由图 4b看出，暴雨区上空850 hPa以下存在$\nabla \cdot \overrightarrow{\pmb{\mathit{Q}}^{*}}$负值区，呈倾斜结构，最大辐合中心位于950~900 hPa之间，中心值＜-60×10^-17hPa^-1·s^-3，$\nabla \cdot \overrightarrow{\pmb{\mathit{Q}}^{*}}$辐合区将强迫出非地转上升运动，即次级环流的上升支，同时暴雨区西侧有明显正值辐散区，对应非地转下沉运动，700 hPa以下为强下沉运动，中心位于950 hPa以下，中心值＞200×10^-17 hPa^-1·s^-3。此时暴雨区925 hPa以下有明显西北侧来的冷空气入侵，对流系统的发展有可能与底层冷空气入侵触发有关，西侧的补偿下沉气流促进对流系统的强烈发展，随后6 h出现超过100 mm的降水。强降水区附近的辐散比辐合强得多, 这可能与持续暴雨造成的下沉气流有关。

第三阶段，由图 4c看出，36~38°N，400 hPa以下$\nabla \cdot \overrightarrow{\pmb{\mathit{Q}}^{*}}$基本呈现正负相间的结构，950~550 hPa之间为辐合上升区，最大辐合中心位于900~800 hPa之间，中心值＜-200×10^-17hPa^-1·s^-3，950 hPa以下为强下沉运动，存在明显的辐散，中心值＞200×10^-17hPa^-1·s^-3，暴雨区南北两侧存在大范围$\nabla \cdot \overrightarrow{\pmb{\mathit{Q}}^{*}}$≥0，北侧尤为明显，暴雨区周围大气中有明显补偿下沉气流，促进对流系统发展。暴雨区边界层湿Q矢量散度的强烈辐散下沉运动有可能是强降水下沉和暴雨区两侧补偿下沉气流共同造成的。由图 4d同样可看出，有明显的次级环流，暴雨区上空存在清楚的倾斜上升运动，暴雨出现在辐合中心西侧倾斜上升运动明显的区域。

综上分析可知，暴雨区上空存在明显的倾斜上升运动，最强出现在950~800 hPa之间，强烈的上升运动将低层的水汽、能量、热量抬升到高空，形成发展旺盛的对流云，造成暴雨的出现。暴雨区上空湿Q矢量散度倾斜分布实际上反应了一种锋面结构，倾斜分布的Q矢量辐合区的加强反映锋生作用和倾斜上升运动的加强。斜升气流使得降水物降落时可以很快脱离上升气流，上升气流不至于遭到削弱，从而使得强对流得以维持，出现强降水。湿Q矢量散度场剖面说明倾斜上升运动是这次持续暴雨发生的重要原因之一。

3.3 湿Q矢量涡度场分析

当δ_Q^*＞0时，由式(3)可知非地转风气旋涡度随高度的升高而减小，若存在上升运动($\nabla \cdot \overrightarrow{{\pmb{\mathit{Q}}^{*}}}$为负值)，就有向上输送的正涡度平流存在，有利于低值系统的垂直发展。在一些研究中，低值系统的移动和发展与Q矢量正涡度中心^[17]或Q矢量正涡度带^[18]的移动和加强相联系。在暴雨和其他强天气预报中，一般认为500 hPa强的正涡度是有利的大尺度条件^[19]，因而低层低值系统的垂直发展对强对流天气的形成起着非常重要的作用。下面分析700 hPa湿Q矢量涡度在此次暴雨天气过程中的反应。

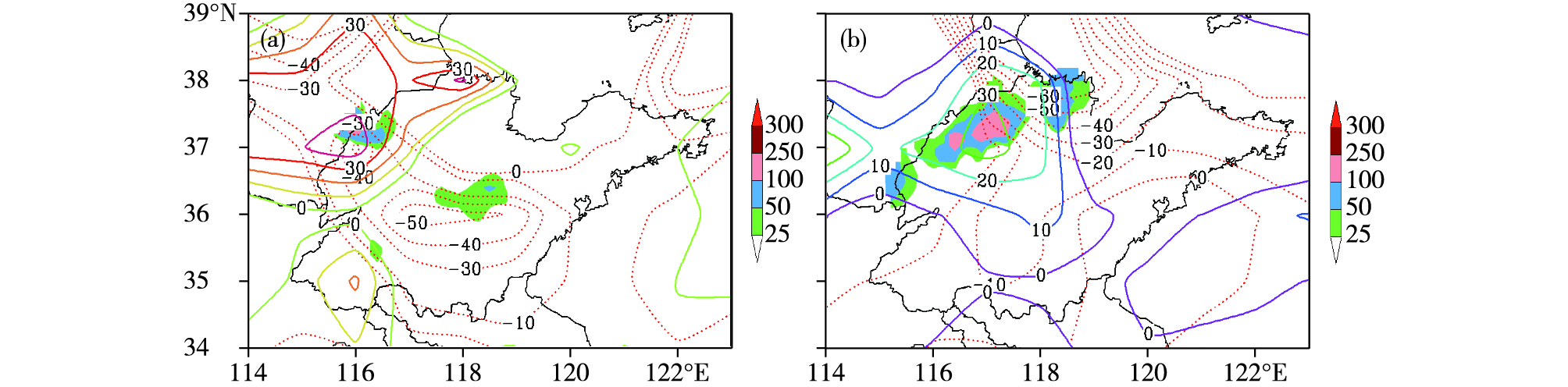
7月30日02时，700 hPa湿Q矢量涡度在(37°N，116°E)是一个中心值为40×10^-17hPa^-1·s^-3的正涡度中心，此时的垂直速度ω为负值，因此有向上输送的正涡度平流存在，有利于低值系统的垂直发展。08时仍有向上输送的正涡度平流存在，但比较弱，低值系统继续发展，700 hPa湿Q矢量涡度正值中心与散度负值重叠的区域在08—14时出现大暴雨天气(图 5a)。随着降水的减弱结束，14时暴雨区转为下沉运动或弱的上升运动，弱的上升运动向上输送负涡度平流，低值系统消失。30日20时鲁西北地区又出现明显的700 hPa湿Q矢量涡度正值中心与散度负值重叠的区域，与31日02—08时出现的主要暴雨区有很好的对应(图 5b)。

分析表明，700 hPa湿Q矢量涡度正值中心与散度负值重叠的区域是中尺度低值系统发展有利的区域，说明非地转风正涡度垂直向上输送对低值系统的发展有重要作用，对随后6~12 h的暴雨落区有很好的指示意义。

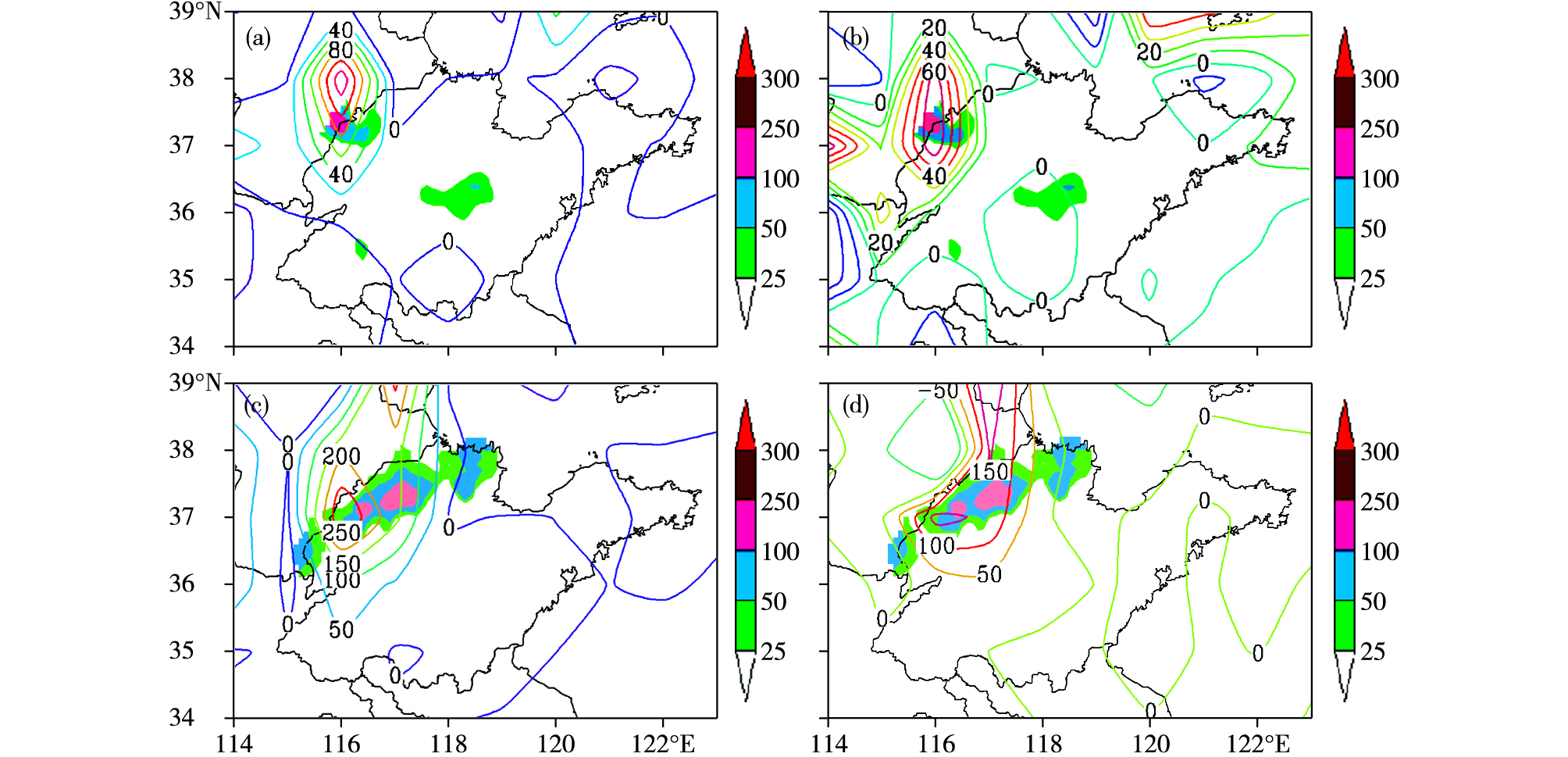
3.4 湿Q矢量锋生函数分析

湿Q矢量锋生函数是反映锋区加强或减弱的物理量，当F_Q*＞0时锋生, 反之锋消。通过分析发现，鲁西北暴雨锋生主要出现在大气低层(850 hPa以下)。图 6为7月30日08时—8月1日02时部分时次6 h降水分布、925 hPa湿Q矢量锋生函数分布和925 hPa湿Q矢量锋生函数差值分布(与前一时次的差值)，30日08时鲁西北西部出现明显锋生，锋生中心位于比邻的河北，最大锋生强度＞120×10^-17 K·hPa^-1·s^-3，随后6 h鲁西北西部出现暴雨(图 6a)，14时鲁西北地区锋生函数值在0附近，降水基本趋于结束。20时鲁西北开始出现新的锋生现象，31日02、08时鲁西北地区锋生明显，锋生强度＞50×10^-17 K·hPa^-1·s^-3，最大锋生强度＞250×10^-17K·hPa^-1·s^-3，31日凌晨至中午鲁西北出现大范围暴雨(图 6c)。鲁西北强降水区与锋生区形状极为相似。邢台探空站7月30日08时—8月1日08时T-lnp图(图略)上，850 hPa以下由偏南风逐渐转为偏北风，低层有冷空气侵入。由锋生区时间演变结合邢台探空资料发现鲁西北暴雨阶段底层大气存在明显的冷锋锋生作用。准地转理论认为锋生强迫将通过热成风平衡来激发非地转垂直环流，即暖湿空气上升、冷空气下沉的热力直接环流^[20-21]，促使不稳定能量释放，造成暴雨天气，与杨学斌等^[22]对这次天气过程的分析结果是一致的。

7月30日08时锋生函数差值中心更靠近强降水中心(图 6b)，31日02时锋生函数差值鲁西北为一正的大值带，大值带北侧的河北有明显的负值中心(图 6d)，正的大值带与鲁西北随后6 h的实际强降水落区比较吻合，而锋生函数虽然也能反映出鲁西北强降水的落区，但锋生范围非常大，预报暴雨落区能力显然不如锋生函数差值。河北南部有明显的锋生，很多情况下比鲁西北锋生更明显，但降水比鲁西北明显偏弱。中尺度气象学认为锋生是大尺度现象，强降水常常是中小尺度系统作用的结果，锋生函数变化具有中尺度特点，因此，锋生函数差值对诊断强降水落区有更好的应用价值，且对强降水落区预报准确度明显优于锋生函数。

4 结论

1) 此次持续性暴雨出现在有利的环流背景下，低层切变线在鲁西北地区长时间维持，为暴雨提供了很好的动力辐合条件。斜升运动是这次持续暴雨发生的重要原因之一。斜升气流使得降水物降落时可以很快脱离上升气流，上升气流不至于遭到削弱，从而使得强对流得以维持，出现强降水。

2) 湿Q矢量散度辐合区激发和维持上升运动，辐散区激发和维持下沉运动，出现次级环流。低层湿Q矢量散度是强降水落区定性诊断分析的有力工具，能提前0~6 h对强降水进行反应。强降水与低层湿Q矢量散度负值辐合区有很好的对应，但并不总是出现在湿Q矢量散度负值区中心，有时出现在湿Q矢量散度梯度大值区的负值区一侧。湿Q矢量散度辐合区的强弱变化与强降水强度变化有密切关系, 辐合强，随后6 h易出现强降水, 辐合减弱, 随后6 h降水强度减弱。

3) 700 hPa湿Q矢量涡度正值中心与散度负值重叠的区域与暴雨区有很好的对应，是中尺度低值系统发展有利的区域，与随后6~12 h暴雨落区有很好的对应。

4) 湿Q矢量锋生函数差值与强降水落区的对应关系明显优于锋生函数。