2. 中国海洋大学物理海洋教育部重点实验室,山东 青岛 266100
2. Key Laboratory of Physical Oceanography (Ocean University of China), Ministry of Education, Qingdao 266100, China
海雾是受海洋影响发生在海上或沿岸大气边界层内的水汽凝结现象,悬浮的大量水滴或冰晶使海面大气水平能见度(以下简称“能见度”)显著降低[1]。海雾导致的低能见度对海上航运、港口作业及沿岸交通等都可造成严重影响[2],使得社会对海雾发生时能见度的准确预报需求迫切。虽然数值模式已成为预报海雾的一种有效手段,但它并不能直接预报能见度,能见度的预报是借助能见度诊断算法实现的。
理论上而言,能见度直接由空气中水凝物与气溶胶污染物(粒子成分、半径、数浓度等)的消光系数来决定。已有能见度算法大致分为3类:一是根据水凝物信息计算能见度[3-5],二是根据气溶胶浓度和相对湿度等要素来构建能见度的统计回归方程[6-9],三是仅基于湿度信息诊断能见度[10-11]。由STOELINGA and WARNER[3]提出的算法(记为SW算法)作为第一类算法的代表,在能见度的数值研究中已被广泛使用[12-14]。这一算法以云水、雨水、云冰和雪的消光系数之和作为总的消光系数计算能见度[3]。然而,由于模式微物理方案的缺陷与其他不确定性,数值模式很难准确预报水凝物信息,导致此算法给出的能见度存在一定误差。另外,SW算法使用了KUNKEL[15]提出的云水消光系数公式,但没有考虑至关重要的雾滴谱信息(即雾滴粒径与数浓度)[4]。进一步地,GULTEPE et al.[4]提出了包含雾滴数浓度和液态水含量的能见度计算公式,该公式大大降低了仅按液态水含量计算能见度的不确定性。但目前的业务预报模式往往没有雾滴数浓度的输出,因此这种方法不能投入业务应用。第二类算法综合考虑了气溶胶对消光的贡献以及气象条件,主要用于城市能见度的计算,它需要气溶胶污染物的组成信息。但对海雾而言,海上气溶胶观测数据的匮乏以及模式对气溶胶有限的预报能力导致该算法难以应用于海雾天气。第三类算法只基于湿度信息(如相对湿度与水汽混合比),代表性算法有美国空军气象局(Air Force Weather Agency,AFWA)提出的算法[10](记为AFWA算法)与美国国家海洋和大气管理局(National Oceanic and Atmospheric Administration,NOAA)预报系统实验室(Forecast Systems Laboratory,FSL)提出的算法[11](记为FSL算法)。相比于第二类算法,这类算法包含了更多的湿度变量,能更加确切地描述能见度与湿度的关系。由于湿度信息可从观测数据与模式预报中得到,因此它比较适合海雾能见度诊断算法的统计构建以及应用于模式能见度的诊断预报。
高荣珍等[13]基于数值模式预报输出,比较分析了FSL算法与SW算法对青岛近海海雾能见度的计算效果,发现FSL算法比SW算法更适合海雾天气低能见度(< 1 km)的诊断。尽管FSL算法不适合轻雾(能见度1~10 km),但AFWA算法可能适合。大多数黄渤海海雾过程中,有些时段是雾或轻雾,有些时段雾和轻雾会相互转化,或者某一时段雾与轻雾同时分布在不同区域。因此,研究目的是基于AFWA算法与FSL算法构建一种适合黄渤海海雾天气的能见度诊断算法。
1 方法与数据 1.1 AFWA算法与FSL算法AFWA算法所使用的公式为:
| $ {X_{{\rm{vis}}}} = 1.5 \times (105-RH) \times (5/Mix) $ | (1) |
其中Xvis为能见度(km),RH与Mix分别为相对湿度(%)与水汽混合比(g·kg-1)[10]。
FSL算法除了使用相对湿度RH(%),还使用温度T(K)与露点温度Td(K)[11]:
| $ {X_{{\rm{vis}}}} = a \times \frac{{T-{T_{\rm{d}}}}}{{R{H^{1.75}}}} $ | (2) |
其中a=6 000,对应Xvis单位为mile,当换算为km时,a=9 656.1。由式(2)可知,当T=Td(即RH=100%)时,Xvis=0 km。
1.2 观测数据及其处理选取了黄渤海23个沿岸与岛屿测站(图 1a)的地面观测数据(3 h/次;2013—2017年)来进行能见度算法的统计拟合,要素包括风向、气压、温度、露点温度、能见度和天气现象。

|
图 1 黄渤海23个沿岸与岛屿观测站分布(a)与WRF区域设计(b) Fig.1 Distribution of the 23 coastal and island stations of the Yellow and Bohai Seas (a) and the WRF domain (b) |
首先根据天气现象筛选出雾天的数据。由于海上观测匮乏,为了尽可能地利用沿岸观测代表海上情况,且最大限度地排除陆上气溶胶和污染物的干扰,所以只保留风向为向岸风的观测数据。向岸风是从海上吹向陆地的风,相比于离岸风,吹向岸风时测站气象条件与海上的情况更接近。根据公式(1)的需要,将观测要素进行转换,得到AFWA算法所需的变量。
值得指出的是,观测数据中相同的相对湿度与水汽混合比,有可能对应不同的能见度。产生这一结果的原因可能包括气溶胶、边界层高度、风速等[6-9, 16]因素。为使能见度观测值能代表同一空气湿度状态下最主要的情况,首先剔除湿度相近但对应能见度迥异的观测数据,接着将相对湿度和水汽混合比数据网格化(格距分别为0.5%和0.25 g·kg-1),对剩余的能见度进行Cressman插值(即平滑掉偏离平均值较远的数据)。为得到FSL算法中需要的温度露点差,假定为标准大气压①。最终得到了约5 000组数据(记为观测数据集),每组包含相对湿度、水汽混合比、温度露点差和能见度。
① 地面温度露点差的计算对观测气压不敏感,采用最高(1 040.9 hPa)和最低(987.2 hPa)的观测气压值分别计算温度露点差,两者的差值大多不超过0.04 K。由这一差值导致的FSL算法能见度计算结果的差值大多在0.2 km以下。
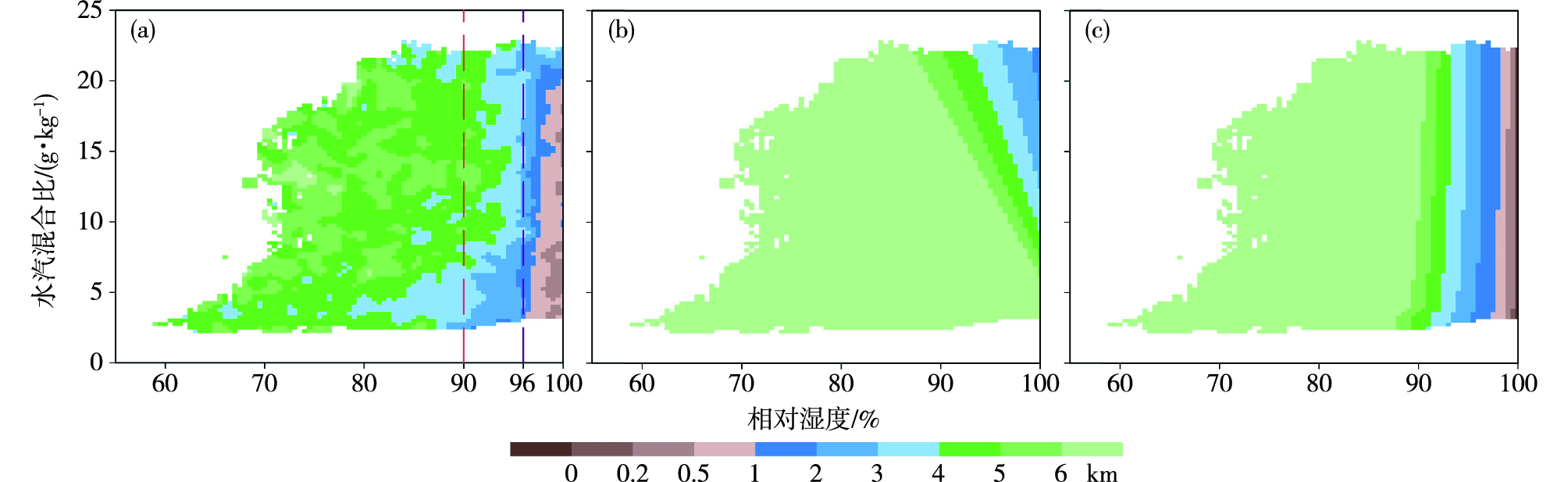
图 2a给出了观测数据集中能见度随相对湿度和水汽混合比的分布。可见,能见度范围为0.20~7.00 km,水汽混合比在2~23 g·kg-1之间;相对湿度较低时,能见度由它与水汽混合比共同决定;随着相对湿度逐渐增大,能见度与水汽混合比的关系越来越弱。
|
图 2 能见度随相对湿度和水汽混合比的分布(a.能见度观测数据,b.AFWA算法能见度计算值,c.FSL算法能见度计算值) Fig.2 Distribution of visibility according to relative humidity and water vapor mixing ratio (a. observed visibility, b. calculated visibility by the AFWA algorithm, c. calculated visibility by the FSL algorithm) |
利用观测数据集,依据式(1)与(2)分别对AFWA算法与FSL算法进行检验,考察它们是否直接适合于黄渤海。图 2b和图 2c分别是它们的表现,发现对于较高的能见度,两者表现都很差,而对于低能见度,FSL算法明显优于AFWA算法。
尽管由AFWA算法得到的能见度计算值的均方根误差(RMSE)高达25.96 km,能见度计算值与观测相差甚远(对比图 2b与图 2a),但它可以描述能见度与相对湿度、水汽混合比的关系,三者的关系可参照观测事实(图 2a)。因此,针对黄渤海区域,首先改进AFWA算法让它适合较高能见度的诊断,然后融合进适合低能见度诊断的FSL算法,从而构建一个新的能见度公式(记为A-F算法)。
2 A-F算法的构建 2.1 AFWA算法的改进将AFWA算法能见度公式(1)中的常数分别设为待定参数r与m,得到:
| $ {X_{{\rm{vis}}}} = (r-RH) \times m/Mix $ | (3) |
利用观测数据集中的全部数据进行拟合,确定r与m之值,得到公式:
| $ {X_{{\rm{vis}}}} = (304.2-RH) \times 0.098/Mix $ | (4) |
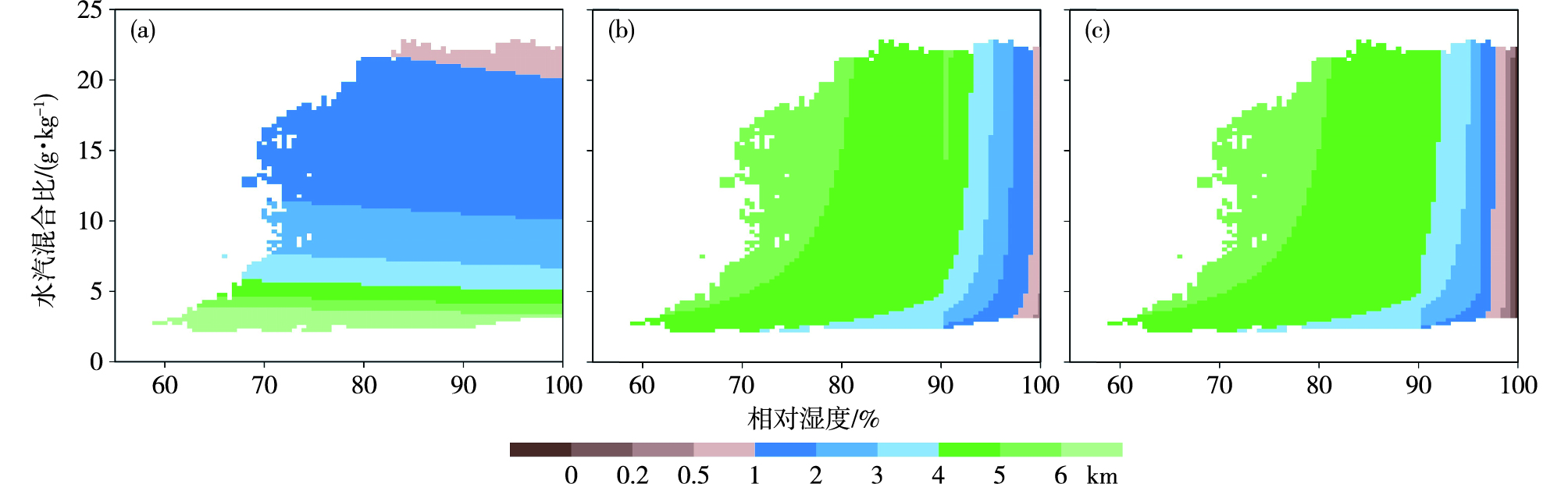
此时,式(4)能见度计算值的RMSE为2.76 km,降低为式(1)的1/10左右。它所给出的能见度与相对湿度、水汽混合比之间的关系如图 3a所示,这与观测事实(图 2a)不符。仔细观察图 2a,对于某一给定水汽混合比而言,能见度随相对湿度的增大而降低,降低的幅度随相对湿度增大而变大,90%的相对湿度(图 2a中红色虚线)前后能见度降幅差异很大。式(3)显示在水汽混合比一定时,能见度随相对湿度的增大而降低的速度取决于参数m。因此,参数m可能是水汽混合比的函数,而且在相对湿度90%以上和以下的变化规律不同。
|
图 3 能见度计算值随相对湿度和水汽混合比的分布(a.式(4),b. AFWA改进算法,c. A-F算法) Fig.3 Distribution of calculated visibility according to relative humidity and water vapor mixing ratio (a. by Equation (4), b. by the modified AFWA algorithm, c. by the A-F algorithm) |
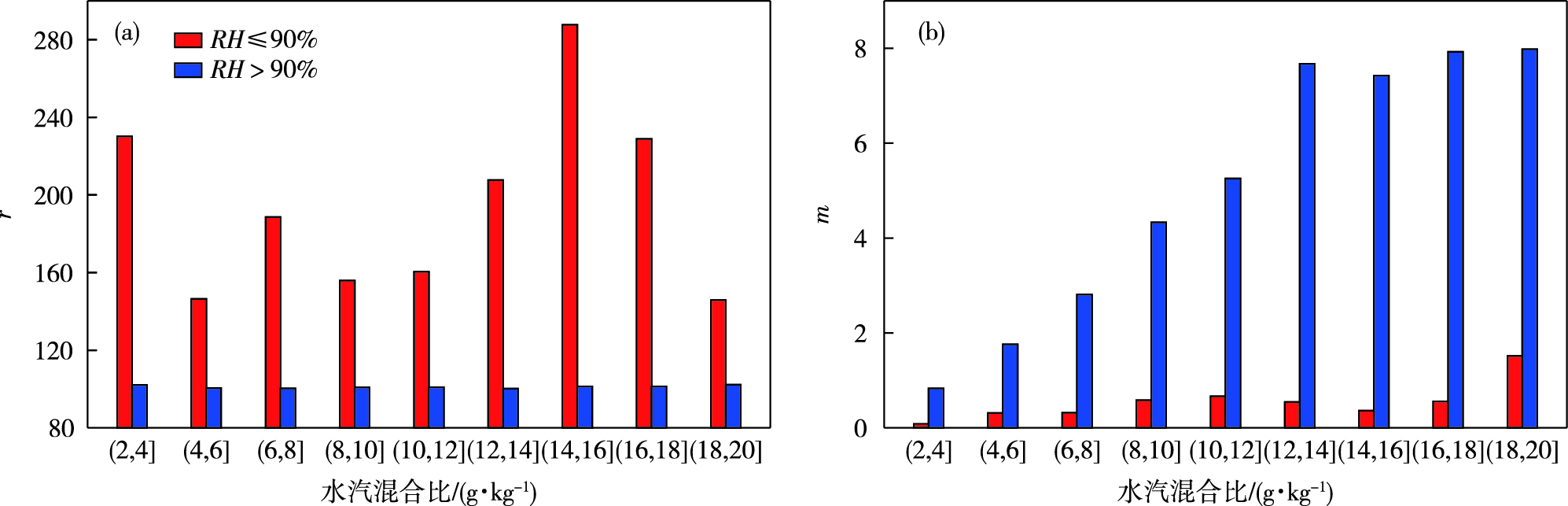
以2%(或2 g·kg-1)为间隔将观测数据集中的相对湿度(或水汽混合比)进行等级划分,基于式(3)对不同等级的相对湿度(或水汽混合比)分别拟合,得到参数r、m随不同等级相对湿度(或水汽混合比)的变化情况。结果显示,参数r、m随相对湿度的变化没有明显规律(图略),但随水汽混合比的变化规律显著:图 4a中,参数r可以看做定值(相对湿度≤90%,参数r的取值范围为145.8~287.6,平均约为170;相对湿度>90%,参数r为100左右);图 4b中,参数m随水汽混合比变大而增大。因此,将参数r近似为常数,将参数m近似为水汽混合比的线性函数,公式(3)可变为:
|
图 4 参数r(a)和m(b)随水汽混合比的变化(横坐标中的“(”与“]”分别表示“>”与“≤”之意) Fig.4 Variation of parameter r (a) and parameter m (b) with water vapor mixing ratio ("(" and "]" in the X-axis denote ">" and "≤", respectively) |
| $ \begin{array}{l} {X_{{\rm{vis}}}} = (r-RH)\left( {{m_1}Mix + {m_2}} \right)/Mix = \\ \;\;\;\;\;\;\;\;(r-RH)\left( {{m_1} + {m_2}/Mix} \right) \end{array} $ | (5) |
分别针对观测数据集中相对湿度>90%和≤90%的两部分,拟合确定式(5)中的待定参数后,得到如下公式:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{X_{{\rm{vis}}}} = \\ \left\{ {\begin{array}{*{20}{l}} {(170.2-RH)(0.058-0.039/Mix), RH \le 90\% }\\ {(101.5-RH)(0.518-0.908/Mix), RH > 90\% } \end{array}} \right. \end{array} $ | (6) |
进一步将观测数据集中的相对湿度与水汽混合比代入式(6)(记为AFWA改进算法),得到能见度分布(图 3b),发现它与观测事实(图 2a)的分布特征基本一致。
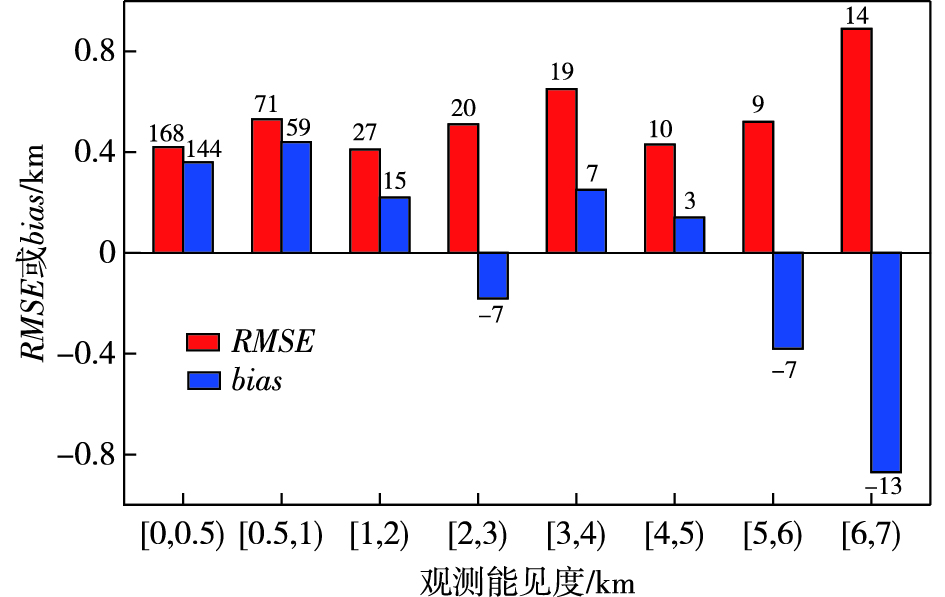
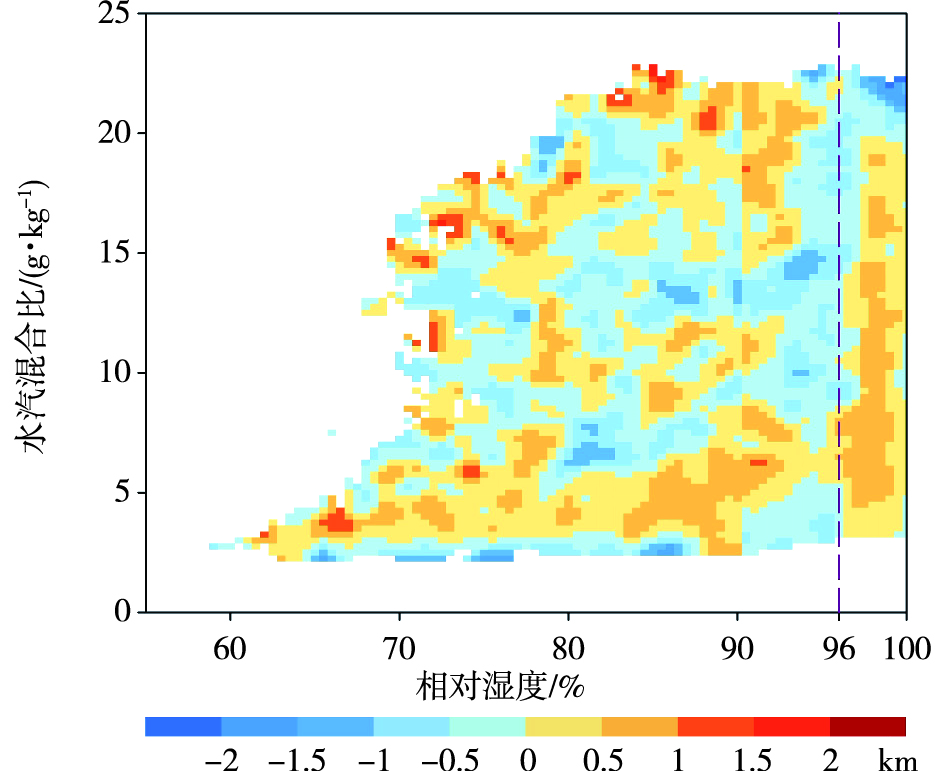
2.2 AFWA改进算法的评估AFWA改进算法的能见度计算值RMSE为0.52 km,与式(4)的2.76 km相比,降低的幅度超过80%。图 5给出了不同能见度区间的RMSE与偏差(bias)分布,可见:能见度 < 2 km时,RMSE约为0.4 km,能见度>6 km时,RMSE也不超过1 km。值得注意的是,0~500 m和500~1 000 m区间内的bias分别为0.36 km和0.44 km,相对区间中值的相对误差分别为144%和59%,表明低能见度区间存在过高估计的倾向。图 6给出了详细的能见度bias分布,很清楚地看到相对湿度>96%所对应的能见度明显被高估,图 2a显示这部分能见度属于低能见度区间,而其中很大一部分bias>0.5 km,意味着几乎超过了观测值的50%。
|
图 5 不同能见度区间AFWA改进算法的能见度RMSE与bias分布(直方图上的数值为相对区间中值的相对误差,单位:%;横坐标中的“[”与“)”分别表示“≥”与“<”之意,下同) Fig.5 RMSE and bias of the calculated visibility by the modified AFWA algorithm within different visibility ranges (the values above or below bars are the relative errors relative to the middle values of the intervals, units: %; "[" and ")" in the X-axis denote "≥" and " < ", respectively, hereinafter the same) |
|
图 6 AFWA改进算法能见度bias分布(紫色虚线代表 96%的相对湿度) Fig.6 Distribution of bias of calculated visibility by the modified AFWA algorithm (the purple dashed line for the relative humidity of 96%) |
除了RMSE与bias,进一步定义了能见度保证率来定量评估能见度算法的效果。若能见度计算值误差在观测值±20%范围内,则认为计算正确。经统计,总体而言AFWA改进算法的能见度保证率为82%,它基本适用于黄渤海海雾天气能见度的计算,但在0~500 m和500~1 000 m观测能见度区间的保证率分别仅为11%和13%(表 1)。这再次说明,AFWA改进算法对低能见度(< 1 km)的计算存在问题。由此看来,AFWA改进算法对低能见度的计算需要修正。
|
|
表 1 AFWA改进算法的能见度保证率 Table 1 Guarantee rate of visibility by the modified AFWA algorith |
利用FSL算法来修正AFWA改进算法对低能见度的计算。表 2列出了FSL算法与AFWA改进算法对0~1 km能见度的计算效果,可知FSL算法对0~500 m和500~1 000 m能见度的计算效果均优于AFWA改进算法,RMSE平均降低了0.12 km,保证率的平均提高率为76%左右。
|
|
表 2 FSL算法较AFWA改进算法对0~1 km能见度计算的优势 Table 2 Advantage of the FSL algorithm in the calculation of visibility between 0 and 1 km compared to the modified AFWA algorith |
为了进一步改进FSL算法对0~1 km能见度的计算效果并兼顾其他能见度范围,通过比较将参数a调整为7 650。接着,将AFWA改进算法与调整后的FSL算法结合起来,公式(6)中相对湿度>96%的部分用调整后的FSL算法能见度公式取代。为了保证不同相对湿度区间的能见度计算结果的平滑过渡,对结合后的公式稍作调整,得到了A-F算法能见度计算公式:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{X_{{\rm{vis}}}} = \\ \left\{ {\begin{array}{*{20}{l}} {(170.2-RH)(0.058-0.039/Mix), }&{RH \le 90}\\ {(103.7-RH)(0.379-0.578/Mix), }&{90 < RH \le 96}\\ {7\;650\left( {T-{T_{\rm{d}}}} \right)/R{H^{1.75}}, }&{RH > 96} \end{array}} \right. \end{array} $ | (7) |
基于观测数据集,A-F算法计算的能见度随相对湿度和水汽混合比的分布见图 3c。与图 3b中AFWA改进算法的分布图相比,图 3c更接近观测事实(图 2a)。此算法在0~500 m和500~1 000 m能见度区间的RMSE分别为0.30 km和0.37 km,相比AFWA改进算法分别减小了0.12 km和0.16 km。
3 A-F算法的检验与应用 3.1 基于观测数据的检验选取2018年3—5月黄渤海沿岸和岛屿测站的观测数据来检验A-F算法。只使用天气现象为雾天且为向岸风的观测数据,剔除了2次观测能见度>10 km的数据,此外没有进行额外的质量控制。表 3给出了不同观测能见度区间的检验结果。由于统计样本数量远远小于观测数据集,表 3中的结果总体上明显不如2.3节中的结果。然而,即使样本较少,表 3还是一定程度上反映出了A-F算法对雾天能见度计算的能力。譬如3~4 km区间bias仅为0.04 km,4~5 km区间保证率达到63%。
|
|
表 3 利用2018年3—5月观测数据对A-F算法的检验结果 Table 3 Verification result of the A-F algorithm using observations from March to May in 2018 |
能见度不是数值模式的直接预报变量,已有关于雾的数值研究中,它多是根据云水含量的预报值来诊断得到[4, 12-13, 17-21]。与云水含量相比,模式对相对湿度与水汽混合比的预报误差较小。因此,利用A-F算法诊断的能见度极有可能优于依据云水含量诊断的能见度。接下来将A-F算法应用于黄海海雾能见度的数值预报①。
① A-F算法已经应用于“区域大气与海洋短期实时预报系统”(http://222.195.136.24)。
借助WRF模式(V3.8.1版本)对发生在黄海海域的2次典型海雾个例进行数值预报试验。海雾个例分别发生在2008年4月28—30日(记为C-2008个例)和2009年4月9—11日(记为C-2009个例)。WRF模式区域设计与模式参数设置分别见图 1b与表 4。2次个例的预报起始时刻分别为2008年4月28日20时(北京时,BST;UTC+08,下同)和2009年4月9日20时,预报时长均为24 h。
|
|
表 4 WRF模式设置 Table 4 Setting of the WRF mode |
② η=1.000 0,0.997 5,0.992 5,0.985 0,0.977 5,0.970 0,0.954 0,0.934 0,0.909 0,0.880 0,0.850 6,0.821 2,0.791 8,0.762 5,0.708 4,0.657 3,0.609 0,0.563 4,0.520 4,0.479 8,0.441 5,0.405 5,0.371 6,0.339 7,0.309 7,0.281 5,0.255 1,0.230 3,0.207 1,0.185 4,0.165 1,0.146 1,0.128 4,0.111 8,0.096 5,0.082 2,0.068 9,0.056 6,0.045 2,0.034 6,0.024 9,0.015 9,0.007 6,0.000 0。1 000 m以下各中间层对应的海拔高度分别大约为10、40、91、153、214、313、465、660、899 m。
初始时刻的背景场与时变侧边界由NCEP(National Centers for Environmental Prediction)的FNL(Final Analysis Data of Global Forecast System)再分析数据(1°×1°,6 h/次)提供,底边界采用NEAR-GOOS(North-East Asian Regional Global Ocean Observing System)日平均海温数据(0.25°×0.25°)。使用循环3DVAR(3-Dimensional Variational)方法[19-20]以同化尽可能多的观测数据来改善初始场质量,同化时段为模拟起始时刻前12 h,同化的数据包括GTS常规地面、船舶与岛屿观测数据(3 h/次)、常规探空数据(12 h/次),以及NCEP提供的BUFR格式的多种观测数据。利用NMC(National Meteorological Center)方法为2次海雾个例分别统计出背景误差协方差CV5。
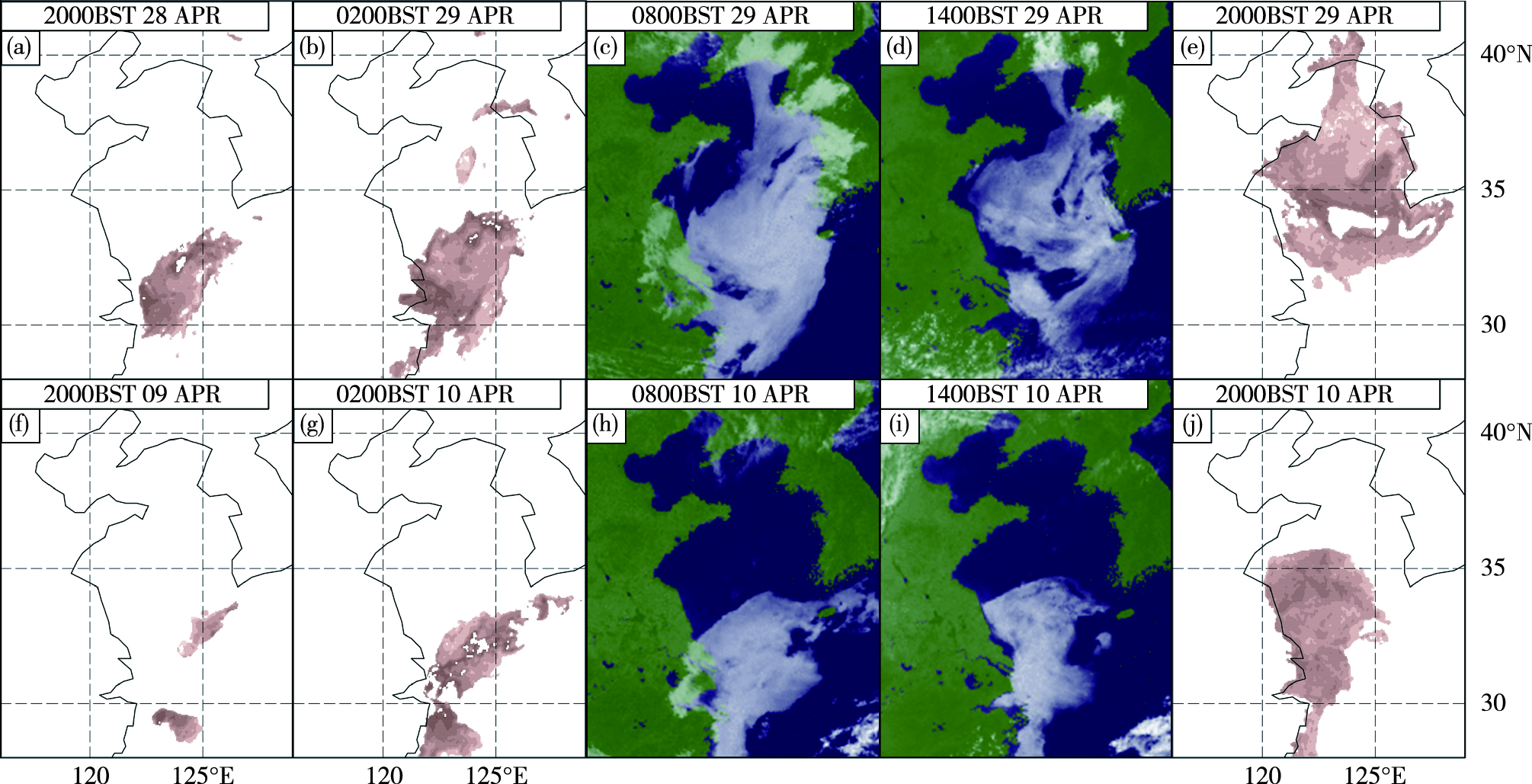
白天借助MTSAT(Multi-functional Transport Satellite)可见光云图,夜间利用WANG et al.[21]发展的海雾反演方法,获取了这2次海雾的观测事实(图 7),作为海雾预报结果的对比依据。分别使用SW算法(详见文献[3])与A-F算法,诊断出2次海雾个例的海面能见度预报结果(图 8)。SW算法使用了模式最底层(高度约10 m)的云水含量信息,而A-F算法则使用了模式最底层的相对湿度、水汽混合比、温度与露点温度信息。对比图 8中的能见度分布与图 7中的海雾观测事实,总体而言SW算法与A-F算法给出的结果很相似。然而,它们之间存在较多细节上的差异。
|
图 7 C-2008个例(a-e,上排)与C-2009个例(f-j,下排)的海雾观测事实(图 7a、b、e、f、g、j棕色区域与图 7c、d、h、i白色区域为雾区) Fig.7 Observed sea fog of C-2008 case (a-e, the upper row) and C-2009 case (f-j, the lower row) (the brown area in Fig. 7a, b、e、f、g, and j and the white area in Fig. 7c, d, h, and i for sea fog area) |

|
图 8 C-2008个例(a-j,上面2排)与C-2009个例(k-t,下面2排)的能见度预报结果(第1、3排为SW算法诊断,第2、4排为A-F算法诊断) Fig.8 Predicted visibility of C-2008 case (a-j, the first two rows) and C-2009 case (k-t, the last two rows) (the first and the third rows are the diagnosed results by the SW algorithm, and the second and the fourth rows are the diagnosed results by the A-F algorithm) |
对于图 7云图中颜色乳白的雾区(浓雾区;图 7c、h、i),A-F算法与SW算法的结果比较一致,两者诊断的能见度基本在1 km以下,分布形态也相似(图 8c与8h,图 8m与8r,图 8n与8s)。
与图 7中的海雾观测事实相比,SW算法存在明显的漏报雾区,而A-F算法在这些漏报雾区内给出了1~3 km的能见度分布。如C-2008个例中的4月29日02时长江口以东的近海海雾(图 7b),C-2008个例中4月29日08时山东半岛南岸小范围的近岸海雾(图 7c),以及C-2009个例中的4月9日20时济州岛西南海域观测到的一小片雾区(图 7f)等,这些被SW算法所漏报的雾区,均在A-F算法中被体现出来,而且与观测事实较为接近(譬如将图 8b、图 8g分别与图 7b对比)。
针对薄雾的诊断,如C-2008个例中4月29日14时,SW算法给出的雾区(图 8d)与云图(图 7d)相比,其北部与南部均漏报了较大的薄雾区(颜色灰白的区域)。A-F算法给出的结果显示其漏报的雾区要小很多(对比图 8i与图 7d)。
总的来说,A-F算法的表现明显优于强烈依赖模式预报云水含量的SW算法,这归功于它可以刻画出轻雾(1~3 km的能见度区域)的分布。由于模式预报的云水含量在空间分布上一般是突变的,即云区向晴空区的过渡往往是云水含量急剧变为0,从而导致SW算法无法给出可能的轻雾区。需要注意的是,对于实际无雾的高湿度模拟区域,A-F算法诊断的低能见度区域不一定由海雾造成。
4 小结利用2013—2017年黄渤海23个沿岸和岛屿测站的地面观测,针对黄渤海海雾天气过程中海面大气水平能见度的诊断问题,对常用能见度诊断公式进行了对比与分析,提出了一个新能见度公式——A-F算法,并对它进行了初步检验与模式预报应用。主要发现与结论如下:
1) AFWA算法必须改进后才能用于黄渤海海雾能见度的诊断,FSL算法适合高相对湿度(96%以上)条件下低能见度区间的诊断。
2) A-F算法结合了AFWA算法与FSL算法的优点,可以兼顾不同区间能见度的诊断。与SW算法不同的是,由于A-F算法利用的是湿度信息,不依赖于模式预报的空间分布不连续的云水含量,所以它可以诊断出被SW算法漏报的能见度为1~3 km的轻雾,但它诊断的低能见度区域不一定都是由海雾造成的。
在提出A-F算法的过程中,AFWA算法的改进与FSL算法的调整,都是基于沿岸站与岛屿站的观测数据。倘若能够加入带有能见度观测的气象浮标观测数据和质量较高的船舶观测数据,A-F算法能见度公式的具体形式会有所变化,诊断效果可能会更佳。所以,本文给出的A-F算法公式是可以进一步改进的,而且可以依据此算法的构建思路,去发展适合其他海域的海雾天气能见度诊断公式。
| [1] |
王彬华. 海雾[M]. 北京: 海洋出版社, 1983: 352.
|
| [2] |
张苏平, 鲍献文. 近十年中国海雾研究进展[J]. 中国海洋大学学报(自然科学版), 2008, 38(3): 359-366. |
| [3] |
STOELINGA M T, WARNER T T. Nonhydrostatic, mesobeta-scale model simulations of cloud ceiling and visibility for an east coast winter precipitation event[J]. J Appl Meteor, 1999, 38(4): 385-404. DOI:10.1175/1520-0450(1999)038<0385:NMSMSO>2.0.CO;2 |
| [4] |
GULTEPE I, MVLLER M D, BOYBEYI Z. A new visibility parameterization for warm-fog applications in numerical weather prediction models[J]. J Appl Meteor Climatol, 2006, 45(11): 1469-1480. DOI:10.1175/JAM2423.1 |
| [5] |
徐静琦, 张正, 魏皓. 青岛海雾雾滴谱与含水量观测与分析[J]. 海洋湖沼通报, 1994(2): 174-178. |
| [6] |
王淑英, 张小玲, 徐晓峰. 北京地区大气能见度变化规律及影响因子统计分析[J]. 气象科技, 2003, 31(2): 109-114. DOI:10.3969/j.issn.1671-6345.2003.02.009 |
| [7] |
宋明, 韩素琴, 张敏, 等. 天津大气能见度与相对湿度和PM10及PM2.5的关系[J]. 气象与环境学报, 2013, 29(2): 34-41. DOI:10.3969/j.issn.1673-503X.2013.02.006 |
| [8] |
侯灵, 安俊琳, 朱彬. 南京大气能见度变化规律及影响因子分析[J]. 大气科学学报, 2014, 37(1): 91-98. DOI:10.3969/j.issn.1674-7097.2014.01.011 |
| [9] |
樊高峰, 马浩, 张小伟, 等. 相对湿度和PM2.5浓度对大气能见度的影响研究:基于小时资料的多站对比分析[J]. 气象学报, 2016, 74(6): 959-973. |
| [10] |
CREIGHTON G, KUCHERA E, ADAMS-SELIN R, et al.AFWA diagnostics in WRF[EB/OL].(2014-09-10)[2019-03-28].http://www2.mmm.ucar.edu/wrf/users/docs/AFWA_Diagnostics_in_WRF.pdf.
|
| [11] |
DORAN J A, ROOHR P J, BEBERWYK D J, et al.The MM5 at the Air Force Weather Agency—New products to support military operations[C]//AMS: The 8th Conference on Aviation, Range, and Aerospace Meteorology, Dallas, Texas, 10-15 January, 1999. Boston: AMS, 1999.
|
| [12] |
傅刚, 李晓岚, 魏娜. 大气能见度研究[J]. 中国海洋大学学报(自然科学版), 2009, 39(5): 855-862. |
| [13] |
高荣珍, 李欣, 时晓曚, 等. 基于WRF模式的青岛近海能见度算法比较研究[J]. 海洋气象学报, 2018, 38(2): 28-35. |
| [14] |
BANG C H, LEE J W, HONG S Y. Predictability experiments of fog and visibility in local airports over Korea using the WRF model[J]. J Korean Soc Atmos Environ, 2008, 24(E2): 92-101. |
| [15] |
KUNKEL B A. Parameterization of droplet terminal velocity and extinction coefficient in fog models[J]. J Climate Appl Meteor, 1984, 23(1): 34-41. DOI:10.1175/1520-0450(1984)023<0034:PODTVA>2.0.CO;2 |
| [16] |
王晓丽, 张苏平, 张晓梅, 等. 青岛市水平能见度变化特征及气象影响因子分析[J]. 气象科学, 2008, 28(增刊): 31-36. |
| [17] |
GAO S H, LIN H, SHEN B, et al. A heavy sea fog event over the Yellow Sea in March 2005: Analysis and numerical modeling[J]. Adv Atmos Sci, 2007, 24(1): 65-81. |
| [18] |
FU G, GUO J T, ANGELINE P, et al. An analysis and modeling study of a sea fog event over the Yellow and Bohai Seas[J]. J Ocean Univ Chin, 2008, 7(1): 27-34. DOI:10.1007/s11802-008-0027-z |
| [19] |
高山红, 齐伊玲, 张守宝, 等. 利用循环3DVAR改进黄海海雾数值模拟初始场Ⅰ:WRF数值试验[J]. 中国海洋大学学报(自然科学版), 2010, 40(10): 1-9. |
| [20] |
高山红, 张守宝, 齐伊玲, 等. 利用循环3DVAR改进黄海海雾数值模拟初始场Ⅱ:RAMS数值试验[J]. 中国海洋大学学报(自然科学版), 2010, 40(11): 1-10. |
| [21] |
WANG Y M, GAO S H, FU G, et al. Assimilating MTSAT-derived humidity in nowcasting sea fog over the Yellow Sea[J]. Wea Forecasting, 2014, 29(2): 205-225. DOI:10.1175/WAF-D-12-00123.1 |
| [22] |
HONG S Y, NOH Y, DUDHIA J. A new vertical diffusion package with an explicit treatment of entrainment processes[J]. Mon Wea Rev, 2006, 134(9): 2318-2341. DOI:10.1175/MWR3199.1 |
| [23] |
KAIN J S, FRITSCH J M. An one-dimensional entraining/detraining plume model and its application in convective parameterization[J]. J Atmos Sci, 1990, 47(23): 2784-2802. DOI:10.1175/1520-0469(1990)047<2784:AODEPM>2.0.CO;2 |
| [24] |
LIN Y L, FARLEY R D, ORIVILLE H D. Bulk parameterization of the snow field in a cloud model[J]. J Climate Appl Meteor, 1983, 22(6): 1065-1092. DOI:10.1175/1520-0450(1983)022<1065:BPOTSF>2.0.CO;2 |
| [25] |
IACONO M J, DELAMERE J S, MLAWER E J, et al. Radiative forcing by long-lived greenhouse gases: Calculations with the AER radiative transfer models[J]. J Geophys Res:Atmos, 2008, 113(D13): D13103. DOI:10.1029/2008JD009944 |
| [26] |
DUDHIA J. A nonhydrostatic version of the Penn State—NCAR mesoscale model: Validation tests and simulation of an Atlantic cyclone and cold front[J]. Mon Wea Rev, 1989, 121(5): 1493-1513. |
| [27] |
CHEN F, DUDHIA J. Coupling an advanced land surface-hydrology model with the Penn Stat—NCAR MM5 modeling system. Part Ⅰ: Model implementation and sensitivity[J]. Mon Wea Rev, 2001, 129(4): 569-585. DOI:10.1175/1520-0493(2001)129<0569:CAALSH>2.0.CO;2 |
 2019, Vol. 39
2019, Vol. 39


