2. 福建省气象台,福建 福州 350000
2. Fujian Meteorological Observatory, Fuzhou 350000, China
能见度反映大气浑浊的程度,是气象观测的常规项目。大气低能见度是重要危险天气,严重影响着航空航海和道路交通[1]。低能见度事件如雾的产生是物理、化学、辐射过程在不同空间和时间尺度上活动的结果。这些过程受到局部地形条件如不规则地形、海陆边界、海面条件,和大气状态如污染物、云凝结核、冷却率、湿度、热通量的影响[2-3]。虽然大气观测手段不断提高,相关研究成果不断涌现,但气溶胶浓度改变、湍流混合、辐射等复杂过程及其在短时间、小尺度上的变化仍使低能见度预测困难[4]。
目前,能见度预报的主要方法有天气图诊断分析,数值模式和统计模型[1]。天气图诊断分析难以实现定时定量的精细化预报;在数值模式中,根据GULTEPE提出的一种基于可见光消光理论的微物理参数化方法以及KOSCHMIEDER公式,能见度可以使用参数化方案进行计算[3]:
| ${V_{{\rm{is}}}} = 5.126\left( {{\rho _{\rm{w}}}{r_{{\rm{eff}}}}} \right)/\left( {{Q_{{\rm{ex}}}}{C_{{\rm{LW}}}}} \right) $ | (1) |
其中Vis表示能见度,ρw为液态水密度,reff为有效半径,Qext为常数,CLW为液态水含量。但由于数值模式对液态水含量、雾滴数浓度、粒径等重要微物理参数的预报能力有限,雾等低能见度事件的定量预测仍然是一个难题[5-7];统计模型中,传统的回归模型如线性回归、逐步回归,可以直观展示预报量和预报因子的关系,但在解决复杂非线性变化上有局限性。
作为统计模型的一种,人工神经网络(artificial neural network, ANN)由以一定方式互相连接的神经元构成能够描述和模拟许多复杂的行为。神经网络系统具有集体运算能力和自适应的学习能力,可实现函数逼近、数据聚类、优化计算、自适应模式识别和非线性预测等功能[8]。在理论上,可以无限逼近任意连续函数。人工神经网络的这种特性,为能见度的精细化预报提供了可能。刘德等[9]利用数值预报产品、站点观测资料及重庆雾的实况资料建立重庆雾的BP神经网络(back-propagation neural network,BPNN)预测模型,对重庆雾进行短期预报并取得了一定的效果;李法然等[8]应用BP神经网络建立湖州市大雾预报模型;李沛等[1]利用BP神经网络建立北京地区能见度预报模型,平均绝对值误差为4.42 km,好于统计回归预报方法。徐志鹏等[10]使用BP神经网络建立了青岛近岸逐小时的能见度分级预报模型。
可以看到,作为人工神经网络的一种,BP神经网络曾在能见度预报中得到应用,并取得了一定效果。而近些年来,数学和计算机技术迅速发展,一些新的神经网络逐渐涌现出来,并被归类为深度学习方法,深度学习强调使用复杂结构和多重非线性变换对数据进行高层次抽象,能够处理各种复杂非线性问题。其中,循环神经网络由于其独特的结构,能够接受并理解长时间序列[11],识别气象要素的变化趋势,从数据中抽象出更多有效信息。本文应用循环神经网络对福州气象观测站的历史观测数据建立单站能见度短临预报模型,进行能见度定量预报,用多种指标评判该种方法的预报效果,并与BP神经网络的预报效果进行对比,探究循环神经网络在能见度短临预报上的可行性和预报能力,为能见度的精细化预报提供新的途径。
1 数据与方法 1.1 数据集福州气象观测站位于福建省东部沿海(119.3°E, 36.1°N),海拔84 m。本文采用其2016年1月1日至2018年8月21日逐5 min地面观测资料。其中,无连续缺省的要素为风向(0~360°)、风速(m·s-1)、海平面气压(hPa)、6 h降水(mm)、露点(℃)、温度(℃)、能见度(最大量程35 km)。前人研究指出地面气压、风、相对湿度是能见度变化的重要影响因子[12],同时,福州地区时常有雨雾发生。因此,选取全部无连续缺省的要素作为预报因子,并去除能见度缺测的时刻,总计200 000个样本。除风向以外的预报因子按照下式进行标准化处理:
| ${x^*} = \left( {x - {X_{\min }}} \right)/\left( {{X_{\max }} - {X_{\min }}} \right) $ | (2) |
上式为min-max标准化转换公式,其中x是某时刻某要素的值,Xmin是数据集中该要素的最小值,Xmax是数据集中该要素的最大值,x*是标准化之后的值。该标准化公式可将数据映射到[0, 1]区间,解决各要素量纲及数量级不一致的问题,同时也可提高模型建立的效率。
使用风向的正弦值和余弦值表示风向:
| ${\theta ^*} = (\sin (\theta ), \cos (\theta )) $ | (3) |
其中θ是某时刻的风向(0~360°),θ*为该时刻风向标准化之后的值。即风向被表示为两个值:风向的正弦值和风向的余弦值[13],同样将风向信息映射到[0, 1]区间。
1.2 循环神经网络简介如图 1所示,循环神经网络(Recurrent Neural Network, RNN)中每一个节点A包含一系列时间步t。某一个节点A的输入不仅包括输入X还包括该节点上一个时间步的输出, 从而生成一个输出h。这个过程可以表示为该节点自己对自己存在一个反馈环路(等号左侧)。如果把这个环路展开,就会展现为等号右侧的形式:在每一个时间步中,该节点获取对它的输入Xt和上一个节点的输出ht-1,执行运算获取一个输出ht,这个输出也会被提供给下一个时间步t+1作为它的输入。基于这种结构,RNN可以接受时间序列作为输入,理解并记忆序列的变化信息[14]。当使用气象要素时间序列作为输入时,RNN可以识别该序列中蕴含的变化趋势,而并非仅仅将其看作一个个离散的要素。RNN的这种特性,使其相比于BP神经网络等,能够在同样的数据中提取更多的特征。

|
图 1 循环神经网络基本结构示意图 Fig.1 Basic structure of RNN (Recurrent Neural Network) |
本文使用的是由HOCHREITER and SCHMIDHUBER[15]提出的Long Short-Term Memory Recurrent Neural Network(LSTM-RNN),是RNN的一种改良形态,解决了原始RNN中随时间步长增大而出现的梯度消失问题,可以处理长达1 000步的时间步长。
1.3 模型建立采用输入层和隐藏层均为LSTM-RNN、输出层为全连接层的3层神经网络。对所有样本进行min-max标准化之后,随机选取其中的80%作为训练样本,20%作为测试样本。为了保证测试样本中各样本具有较好的独立性,将测试样本进行了随机排序,评价误差和计算相关系数。训练样本用于建立预报模型,测试样本用于测试模型的预报效果。输入以上全部预报因子及能见度的12 h逐5 min时序变化序列(三阶张量(160 000, 144, 8),160 000个训练样本、144个时间步长、8个因子),输出为1 h、3 h、6 h之后的能见度值。
为对比RNN和BP的预报效果,使用同一套数据利用BP神经网络建立了能见度预报模型。
1.4 评价方法假设有一组预报值{f1, f2, …, fn},其实测值为{y1, y2, …, yn},预报值平均值f,实测值平均值为y。
平均绝对值误差公式为:
| $MAE = \frac{1}{n}\sum\limits_{i = 1}^n {\left| {\left( {{f_i} - {y_i}} \right)} \right|} $ | (4) |
与平均误差相比,平均绝对值误差由于误差值被绝对值化,不会出现正负相抵消的情况,因而后者能更好地反映预测值误差的实际情况。
均方根误差公式为:
| $RMSE = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{\left( {{f_i} - {y_i}} \right)}^2}} } $ | (5) |
均方根误差反映了误差的离散程度,均方根误差越小,说明误差值变化越小,模型对所有样本点的预报能力是近似一致的。
相关系数计算公式为:
| $r = \frac{{\sum\limits_{i = 1}^n {\left( {{f_i} - \bar f} \right)} \left( {{y_i} - \bar y} \right)}}{{\sqrt {\sum\limits_{i = 1}^n {{{\left( {{f_i} - \bar f} \right)}^2}} } \sqrt {\sum\limits_{i = 1}^n {{{\left( {{y_i} - \bar y} \right)}^2}} } }} $ | (6) |
相关系数反映了预报值与实测值变化趋势的符合程度。
时滞相关性指两组数据错开m个(m为整数)时间单位后它们之间的相关性,如果两组数据之间的时滞相关系数比同期相关系数大,则说明两组数据之间有时滞相关性。
对于一组预报值{f1, f2, …, fn}, 预报值平均值为f,对应实测值为{y1, y2, …, yn}, 实测值平均值为y,当滞后m(m<n)个时间单位后,二者之间的时滞相关系数为:
| ${r_m} = \frac{{\sum\limits_{i = 1}^n {\left( {{f_i} - \bar f} \right)} \left( {{y_{i - m}} - \bar y} \right)}}{{\sqrt {\sum\limits_{i = 1}^n {{{\left( {{f_i} - \bar f} \right)}^2}} } \sqrt {\sum\limits_{i = 1}^n {{{\left( {{y_{i - m}} - \bar y} \right)}^2}} } }} $ | (7) |
低能见度预报评估指标定义如下。
1) 命中:实测值< 1 000 m,预报值< 1 000 m。
2) 漏报:实测值< 1 000 m,预报值>1 000 m。
3) 空报:实测值>1 000 m,预报值< 1 000 m。
4) 正确否定:实测值>1 000 m,预报值>1 000 m。
2 结果分析 2.1 模型预报效果随机检验表 1为模型在测试样本中的各种误差指标。可以看到,RNN在1 h、3 h、6 h测试样本中,模型平均绝对值误差分别为2 215.77 m、3 027.53 m、3 039.86 m,均方根误差分别为3 558.39 m、4 328.24 m、4 775.64 m。预报值与实测值的相关系数分别为0.928 5、0.893 0、0.889 8,说明预报值与实测值的变化趋势良好吻合。随着预报时效的延长,预报准确度有所降低。与基于实况的预报(直接使用预报时效前的能见度实况作为预报值,即分别使用1 h、3 h、6 h前的能见度实况值作为目标时刻能见度的预报值)相比,均方根误差减小15.75%、31.66%、41.26%,并且,不论在何种评价方式上,RNN的预报效果均好于基于实况的预报。随着预报时效的延长,RNN的优势愈加明显,说明RNN在给出预报值的过程中,充分应用了各预报因子及其时序信息,而并非只考虑到了能见度实况,确实具有预报能力。
|
|
表 1 RNN与基于实况的预报在不同预报时效下的误差对比 Table 1 Comparison of 1-h, 3-h, and 6-h forecast error between RNN and forecast based on actual situations |
表 2为BP神经网络预报效果,由表 1和表 2对比可以看出:在1 h、3 h、6 h预报中,RNN平均绝对值误差比BP神经网络分别减小12.90%、24.45%、38.99%。随着预报时效的延长,RNN相对于BP的优势更明显。其他各指标也表现出了类似的趋势。
|
|
表 2 BP神经网络在不同预报时效下的误差 Table 2 One-h, 3-h, and 6-h forecast error of BPNN (Back Propagation Neural Network) |
综上所述,RNN、BP在整体上均有一定的预报效果,但RNN在各项指标上均好于BP。以上是随机检验的结果,测试样本中的能见度变化范围为61 m到35 000 m。为了检验模型对低能见度事件的预报能力,下面,针对一次低能见度事件检验RNN的预报效果。
2.2 一次低能见度事件的预报试验2016年3月12日23时(北京时间,下同),在福建沿海出现了一次由海雾导致的低能见度事件。地面天气图表明一个高压中心位于日本岛附近,高压脊向西南延伸到我国东部沿海地区[16]。受此高压影响,福州沿岸为东北风,该向岸的东北风为福州地区带来丰富水汽,有利于发生大雾(图 2)。在雾发生发展时段能见度明显下降;雾持续过程中能见度较低但有明显波动;雾消散时段能见度迅速升高(图 3)。这种能见度的变化特征与前人的观测研究[3]类似。

|
图 2 2016年3月12日23时地面天气图(红点标注为福州气象观测站的位置) Fig.2 Surface synoptic chart at 23:00 BST on 12 March 2016 (the red dot for the location of Fuzhou Meteorological Observation Station) |
|
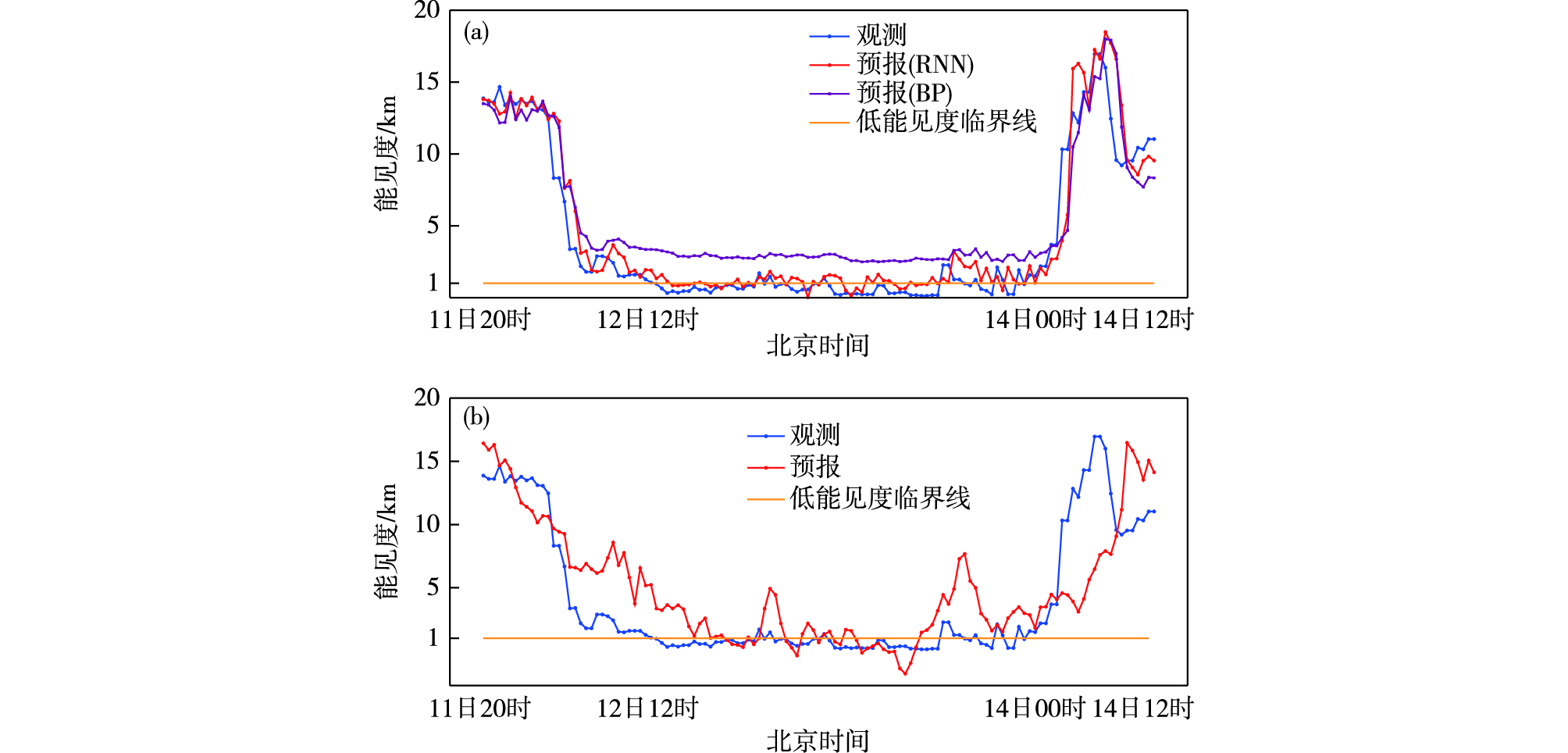
图 3 一次低能见度事件中预报与观测结果对比(a.1 h预报,b.6 h预报) Fig.3 Comparison of forecast results and observations in a low-visibility event (a. 1-h forecast, b. 6-h forecast) |
利用上述预报模型对该低能见度事件进行1 h、6 h预报,结果表明:RNN能够基本预报出此次低能见度事件并反映出雾的发生发展、维持、消散过程。对于1 h预报,在雾发生发展和消散时段,能见度下降和上升的幅度与观测相当,但能见度突变点上预报稍有滞后。总体上RNN对于低能见度的预报能力明显强于BP(图 3a)。对于6 h预报,能见度下降和上升的幅度均明显比观测平缓(图 3b)。
表 3为此次个例中RNN与BP在不同预报时效下的误差。1 h、6 h预报中RNN平均绝对值误差分别为1 010.34 m、2 566.35 m,而随机检验中分别为2 215.77 m、3 039.86 m。个例中各误差值小于随机检验,可能是由于个例中的样本以低能见度为主。相比于BP神经网络,1 h、6 h预报中RNN平均绝对值误差分别减小49.67%、27.46%,均方根误差分别减小29.76%、22.18%。从个例验证中可以更明显地看到随预报时效的延长预报准确度降低。
|
|
表 3 RNN与BP在不同预报时效下的误差 Table 3 One-h and 6-h forecast errors of RNN and BPNN |
低能见度(能见度≤1 000 m)对人类活动影响最大,是气象部门进行能见度预报的重点。以下,在此次低能见度事件中对能见度观测值≤1 000 m的时段进行模型预报能力评估。
表 4为预报时效1 h、6 h的各误差指标。预报时效为1 h、6 h时,平均绝对值误差分别为653.17 m、1 814.93 m,均方根误差分别为791.30 m、2 468.51 m。6 h相比于1 h误差明显变大。1 h、6 h预报中空报均较少,漏报均较多。说明,该种方法对能见度的预报整体偏高。
|
|
表 4 低能见度部分误差评测(RNN) Table 4 Evaluation of 1-h and 6-h forecast errors in the low-visibility case (RNN) |
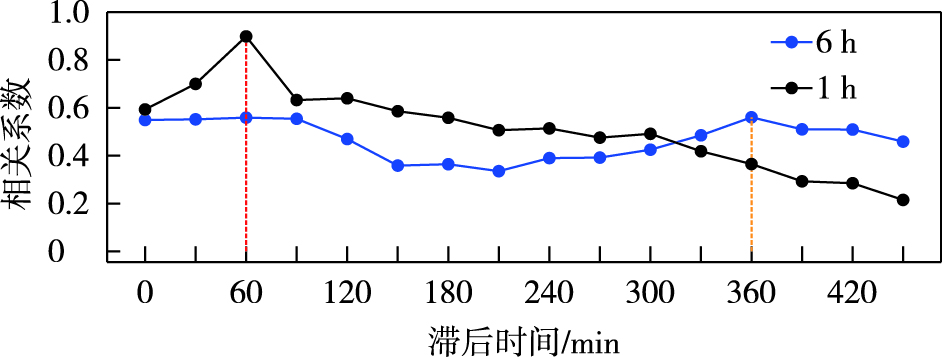
在1 h、6 h时效上分别计算了预报值和观测值的时滞相关系数。如图 4所示,预报时效为1 h时相关系数在时滞为1 h时达到最大,预报时效为6 h时相关系数在时滞为6 h时达到最大,说明模型预报效果对实况存在依赖,若能结合模式预报结果,这种滞后性有可能得到改善。
|
图 4 时滞相关系数 Fig.4 Lag correlation coefficient |
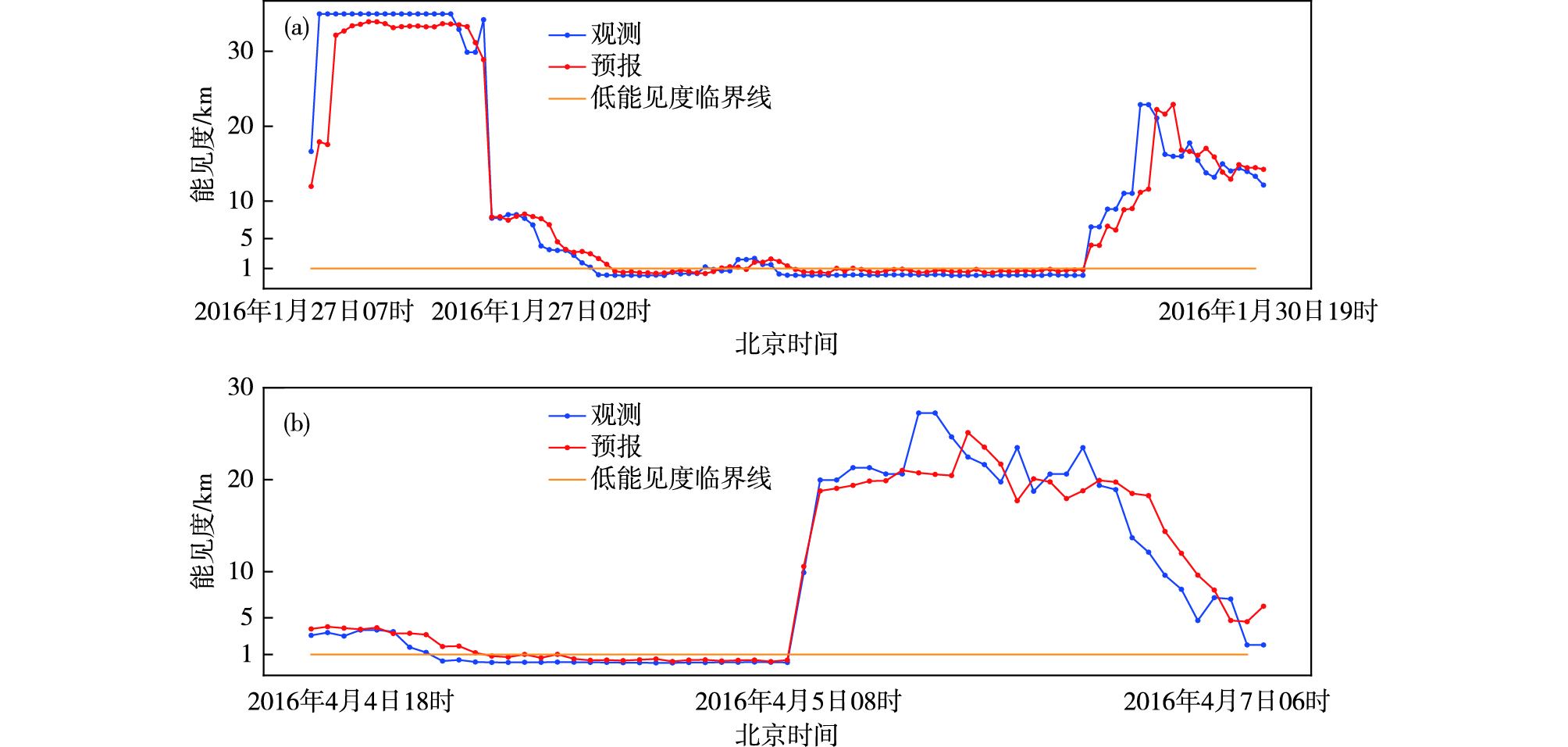
使用观测资料进行预报时该种滞后性并非总是存在。图 5为利用厦门气象观测站的2段时间序列进行预报效果检验的结果,可以看到在2016年1月27日02时和4月5日08时的能见度突变点均被较好地预报了出来。
|
图 5 厦门气象观测站一段时间序列中1 h预报与观测结果对比(a.序列1,b.序列2) Fig.5 Comparison of forecast and observation results in time series at Xiamen Meteorological Observation Station (a. Series 1, b. Series 2) |
为了探究模型输入因子对预报结果的影响,使用风速、风向的正弦值、风向的余弦值、温度、露点、能见度等6个气象要素建立预报模型,并与风速、风向的正弦值、风向的余弦值、海平面气压、6 h降水、露点、温度、能见度等8个气象要素建立的模型进行对比。结果表明,当输入因子减少为6个时,预报效果较使用8因子模型整体偏差(表 5)。说明使用较多的预报因子有利于RNN从更多的数据中提取有效信息,提高预报能力。
|
|
表 5 不同因子个数预报模型效果对比 Table 5 Comparison of forecasting skills by models using different number of factors |
本文利用循环神经网络,采用福州地面观测资料建立了福州单站能见度短临预报模型,并进行了随机样本测试和个例预报检验,同时与BP神经网络的效果进行了对比,得到如下结论。
1) 随机检验表明:循环神经网络在1 h、3 h、6 h预报的测试样本中(40 000个独立样本)预报与观测的相关系数分别为0.928 5、0.893 0、0.889 8,预报与观测的变化趋势一致性较好。平均绝对值误差和均方根误差均有随预报时效延长而增大的趋势。
2) 不论在何种评价方式上,循环神经网络的预报效果均好于基于实况的预报,表明其具备较好的预报能力。在1 h、3 h、6 h预报中平均绝对值误差比BP神经网络分别减小12.90%、24.45%、38.99%,同时在各种误差指标上均好于BP神经网络。
3) 在一次海雾导致的低能见度事件中,循环神经网络能够基本预报出此次低能见度事件并反映出雾的发生发展、维持、消散过程。1 h、6 h的预报的平均绝对值误差分别为1 010.34 m、3 537.71 m,随着预报时效延长,误差有增大的趋势。相比BP神经网络,循环神经网络平均绝对值误差分别减小49.67%、27.46%,均方根误差分别减小29.76%、22.18%。总体上RNN对于低能见度的预报能力明显强于BP神经网络。
4 讨论统计结果表明,空报很少,漏报较多,说明模型预报的能见度整体偏高。可能与建模时所采用的数据集中高能见度样本占大多数有关。如果数据集中低能见度样本增多,并且使用更大的数据集进行建模,可能改善预报值偏高的问题。
在部分能见度突变时段的预报存在滞后于观测的情况,说明模型的预报效果对实况的依赖性,若能结合模式预报结果,这种滞后性有可能得到改善。
随机检验显示,随着预报时效的延长,预报准确度有所降低。但3 h较1 h的下降比6 h较3 h的下降明显,说明随时效的延长,对实况的依赖有所减少。
前人使用BP神经网络对能见度的预报表明:使用少数关键因子可以提高预报效果[10]。而循环神经网络中,使用少数关键预报因子预报时结果变差,说明循环神经网络可以从更多的数据中提取有效信息,并将其应用到预报中,从而提高预报能力。在建立模型时可选取尽可能多的相关因子。
本文仅使用了一个低能见度过程进行了预报试验,对试验结果的统计具有一定的局限性。今后将使用更多个例对试验结果进行检验。
| [1] |
李沛, 王式功, 尚可政, 等. 基于神经网络逐级分类建模的北京地区能见度预报[J]. 兰州大学学报(自然科学版), 2012, 48(3): 52-57. DOI:10.3969/j.issn.0455-2059.2012.03.009 |
| [2] |
BAGUSKAS S A, PETERSON S H, BOOKHAGEN B, et al. Evaluating spatial patterns of drought-induced tree mortality in a coastal California pine forest[J]. Forest Ecol Manag, 2014(315): 43-53. |
| [3] |
KORAČIN D, DORMAN C E. Marine fog: Challenges and advancements in observations, modeling, and forecasting[M]. Switzerland: Springer International Publishing, 2017.
|
| [4] |
GULTEPE I, TARDIF R, MICHAELIDES S C, et al. Fog research: A review of past achievements and future perspectives[J]. Pure Appl Geophy, 2007, 164(6/7): 1121-1159. |
| [5] |
BOTT A, SIEVERS U, ZDUNKOWSKI W. A radiation fog model with a detailed treatment of the interaction between radiative transfer and fog microphysics[J]. J Atmos Sci, 1990, 47(18): 2153-2166. DOI:10.1175/1520-0469(1990)047<2153:ARFMWA>2.0.CO;2 |
| [6] |
ZHANG X J, MUSSON-GENON L, DUPONT E, et al. On the influence of a simple microphysics parametrization on radiation fog modelling: A case study during Parisfog[J]. Bound-Layer Meteor, 2014, 151(2): 293-315. DOI:10.1007/s10546-013-9894-y |
| [7] |
ZHANG S P, XIE S P, LIU Q Y, et al. Seasonal variations of Yellow Sea fog: Observations and mechanisms[J]. J Climate, 2009, 22(24): 6758-6772. DOI:10.1175/2009JCLI2806.1 |
| [8] |
李法然, 周之栩, 陈卫锋, 等. 湖州市大雾天气的成因分析及预报研究[J]. 应用气象学报, 2005, 16(6): 794-803. DOI:10.3969/j.issn.1001-7313.2005.06.011 |
| [9] |
刘德, 李永华, 喻桥, 等. 基于客观分析的重庆雾的BP神经元网络预报模型研究[J]. 气象科学, 2005, 25(3): 293-298. DOI:10.3969/j.issn.1009-0827.2005.03.011 |
| [10] |
徐志鹏, 张苏平, 衣立, 等. 青岛近岸能见度逐小时分级预报模型初探[J]. 海洋湖沼通报, 2018(1): 9-17. |
| [11] |
FERNÁNDEZ S, GRAVES A, SCHMIDHUBER J.An application of recurrent neural networks to discriminative keyword spotting[C]//DE SÁ J M, ALEXANDRE L A, DUCH W, et al. Artificial Neural Networks-ICANN 2007.Berlin: Springer Berlin Heidelberg, 2007: 220-229.
|
| [12] |
王晓丽, 张苏平, 张晓梅, 等. 青岛市水平能见度变化特征及气象影响因子分析[J]. 气象科学, 2008, 28(增刊): 31-36. |
| [13] |
范高锋, 刘纯, 王伟胜, 等.风电功率预测的多扇区BP神经网络模型[C]//中国电机工程学会. 2009年中国电机工程学会年会论文集.天津: 中国电机工程学会, 2009.
|
| [14] |
OLAH C.Understanding LSTM networks[EB/OL]. (2015-08-27)[2019-03-02]http://colah.github.io/posts/2015-08-Understanding-LSTMs/.
|
| [15] |
HOCHREITER S, SCHMIDHUBER J. Long short-term memory[J]. Neural Comput, 1997, 9(8): 1735-1780. DOI:10.1162/neco.1997.9.8.1735 |
| [16] |
高山红.保存的CMA天气分析图[EB/OL].(2018-12-27)[2019-03-02]http://222.195.136.24/.
|
 2019, Vol. 39
2019, Vol. 39


