2. 中国气象科学研究院,北京 100086;
3. 枣庄市气象局,山东 枣庄 277800;
4. 山东省气象科学研究所,山东 济南 250031
2. Chinese Academy of Meteorological Sciences, Beijing 100086, China;
3. Zaozhuang Meteorological Bureau, Zaozhuang 277800, China;
4. Shandong Institute of Meteorological Sciences, Jinan 250031
精细化预报是天气预报业务的发展方向。20世纪80年代以来,各地开展了大量的空间分辨率到县的精细预报技术研究;进入2000年后,随着大城市和乡镇精细化预报业务的推进,乡(镇)、重点功能区、重要交通枢纽等精细化站点要素预报逐渐在全国展开;目前智能网格预报又成为中国气象局主推的天气预报业务,时空无缝隙的网格预报必将极大地推动气象要素预报的流程再造和预报精细程度的快速提高[1-11]。
在精细化要素预报的县级—乡镇—格点业务形态逐级推进中,预报站点、预报要素以及预报时效不断精细,预报员的工作量呈几何级数增长。在这样的形势下,精细化客观气象预报的支持是必不可少的,基于数值预报产品释用技术的精细化客观预报在气象预报业务中越来越重要[4]。美国是开展数值预报释用技术研究较早的国家,20世纪50年代末进行试验,60年代末模式输出统计(model output statistical,MOS)预报方法进入业务运行;国家气象中心基于T639模式重点发展县级以上城镇客观要素预报业务[4];乡镇级客观预报主要由省级业务承担,辽宁、宁夏、广东、陕西、山西、湖北等省分别建立各自的乡镇预报系统,但预报技术方案不尽统一,有的基于DMO输出,有的基于县级客观预报结果插值,有的基于县级预报方程替代[7-11];在网格预报方面,国家气象中心开展了基于格点编辑平台的降水定量预报业务,广东省气象局建立了基于格点交互系统的数字化预报业务[2]。
在现行的县级—乡镇—格点级要素精细化预报体系中,网格预报成为各级气象部门的发展重点,而乡镇级站点预报的关注度则被逐渐弱化。然而,大量工作[4, 12]表明乡镇级站点预报对网格预报有着重要的支撑作用。GLAHN et al.[12]基于BERGTHORSSEN、CRESSMAN和DOOS提出了逐步订正插值分析方法(BCD法),同时考虑不同下垫面和地形高度影响,在站点MOS系统基础上插值分析生成2.5 km分辨率的网格预报产品,为美国网格预报业务提供支撑[13]。赵声蓉等[4]指出网格化的MOS预报本质上是在站点预报的基础上通过一定的分析方法得到格点上的MOS预报结果,网格化的MOS预报核心问题是分析方案和比较准确的具有一定空间密度的站点MOS预报。因此对做好乡镇级站点客观化预报工作仍有需求。
以山东省乡镇级精细化预报为例,较先前的县级预报,站点数目由123个增至1 561个。在相应的客观预报方法开发中,不同站点间各气象要素有何差异?是否1 561个站点都需要建立预报方程?相关工作目前国内尚未开展。本文的主要目标是针对精细化要素客观预报所面临的海量预报站(格)点问题,利用山东省稠密的区域自动站观测资料,分析各类气象要素不同级别站点的代表性和差异性,为精细化要素客观预报业务中的站(格)点处理提供理论和技术支撑。
1 资料处理乡镇精细化气象要素客观预报以全省区域自动观测站点为预报站点,预报要素包括日最高、最低气温,日最大风速、风向,日降水量,整点温度和风等。上述要素均源于各区域自动站逐时观测数据推算获取。考虑各区域站建站时间不一,选取截至2014年3月1日所建测站共1 561个作为研究对象,收集2010年3月1日—2014年2月28日共4 a的逐时观测资料。为保证所用测站观测资料日期统一,2014年3月1日之后新建测站不再选取。
区域气象观测站观测质量问题较多。本文基于“箱线图”异常值判别法进行数据质量控制。箱线图通过不同分位数描述数据的整体分布情况。定义大(小)于75%(15%)分位数1.5倍四分位间距的数值为异常值。剔除异常率超过10%的测站,经过质控后的区域站总数为1 420个。
2 不同站点空间分辨率的观测要素统计学特征差异山东地形复杂,东部为半岛,西部及北部属黄泛平原,中南部多山地丘陵,丰富的下垫面属性造就了天气、气候的多样性。通过对123个国家级自动气象站(因布设在县级及以上市区,以下简称县级站)和1 420个区域自动气象观测站(多布设在乡镇和城市街区,以下简称区域站或乡镇站)等两种不同站点分辨率下的夏季总降水、日极端气温和风速等要素气候平均分布的差异对比,分析提高预报站点空间分辨率的必要性。
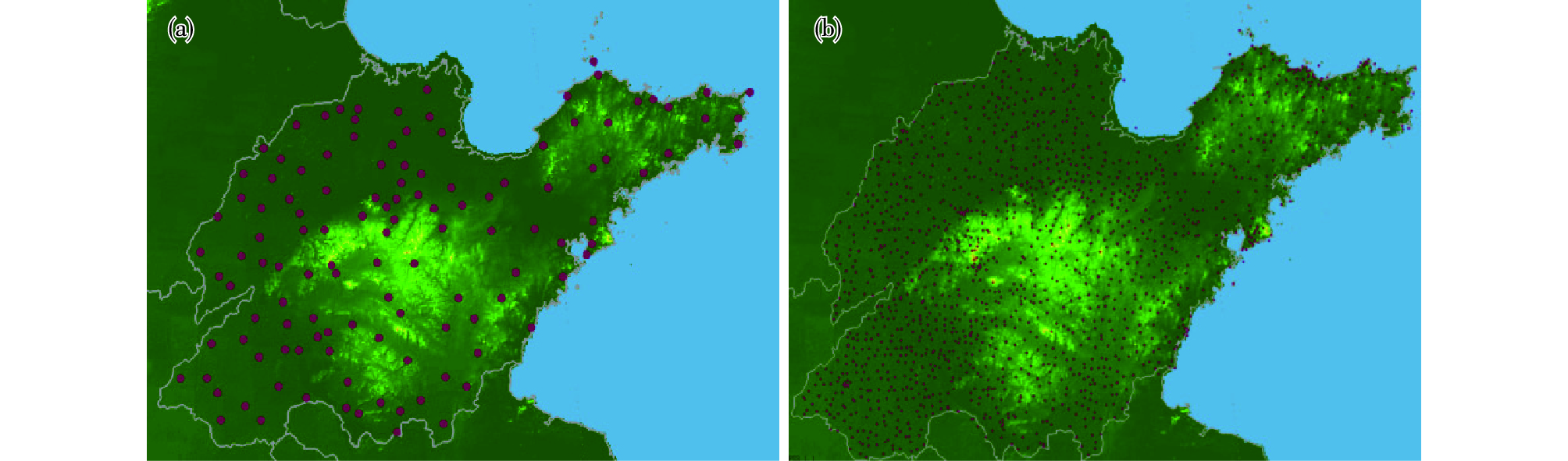
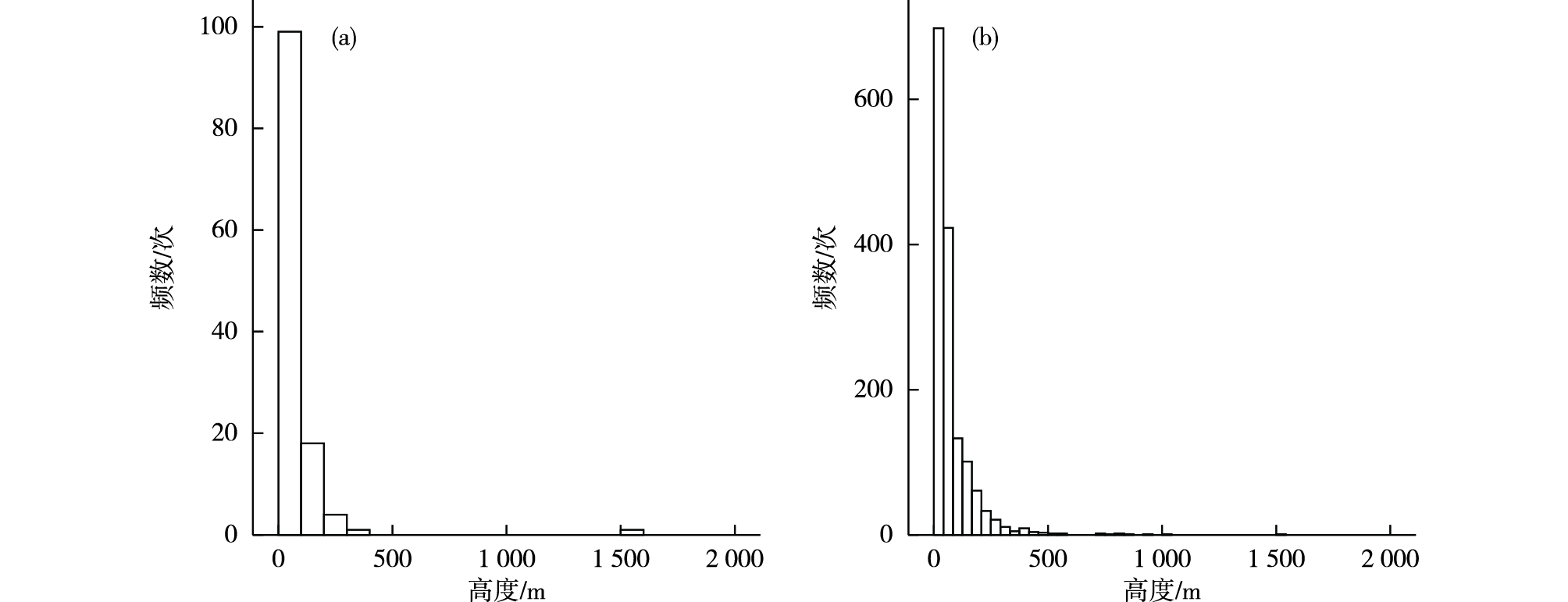
2.1 站点地理属性差异图 1给出两种空间分辨率的测站分布情况,可以看出1 420个区域站空间覆盖密度远高于123个县级站,特别在海岸和山区附近,区域自动站有效填补了县级站点的探测空白。由图 2所示的不同分辨率站点海拔高度频数直方图看,县级站点海拔高度位于0~300 m区间内,而区域站可覆盖0~1 000 m区间内的大部分高程,这说明乡镇级站点较县级站点具有更为完整的地形属性代表性。
|
图 1 山东省县级站点(a)和乡镇级站点(b)空间分布图(实心圆圈为观测站点) Fig.1 Spatial distribution of county-level stations (a) and township-level stations (b) in Shandong Province (solid circles for locations of stations) |
|
图 2 山东省县级站点(a)和乡镇级站点(b)的海拔高度频数直方图 Fig.2 Frequency histogram of altitudes at county-level stations (a) and township-level stations (b) in Shandong Province |
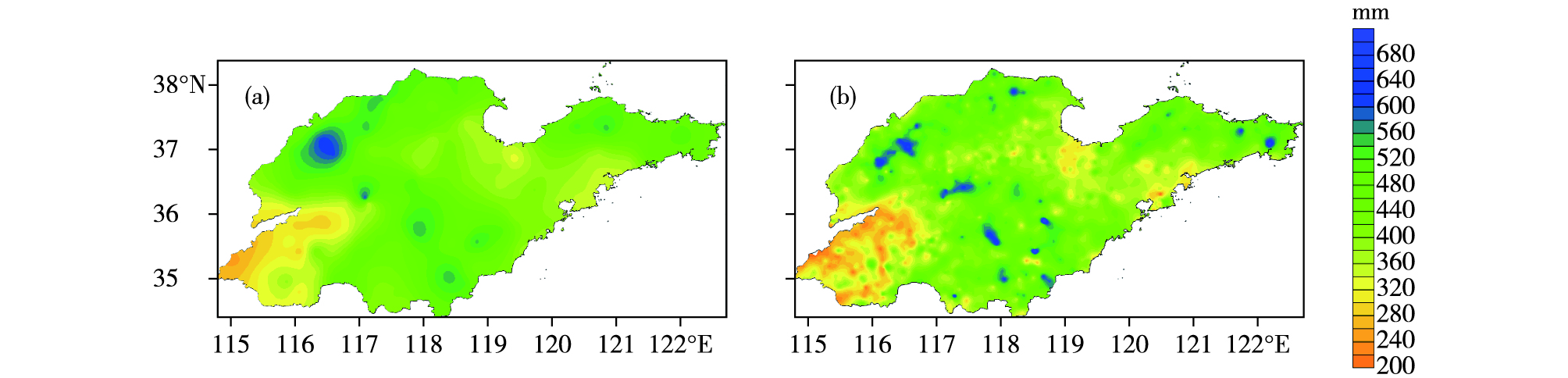
山东位于季风区,降水多出现在夏季。对比分析不同分辨率下单站平均夏季总降水量的空间分布差异(图 3), 可以得出以下几点结论:两类分辨率下夏季总降水量整体气候区形态基本一致,降水大值区在鲁西北、鲁中山区以及鲁东南、半岛沿海地区;两类分辨率降水雨区形态的差异主要体现在大气候区内较小尺度的次气候区分布细节上,高分辨率站网可以捕捉尺度更小的局地小气候区,分布形态呈尺度较小的多中心分布,结构更精细。
|
图 3 山东省不同站点分辨率的年平均夏季总降水量的空间分布(a.县级站点,b.乡镇站点;单位:mm) Fig.3 Spatial distribution of annual mean summer total precipitation at stations with different resolutions in Shandong Province (a. county-level stations, b. township-level stations; units: mm) |
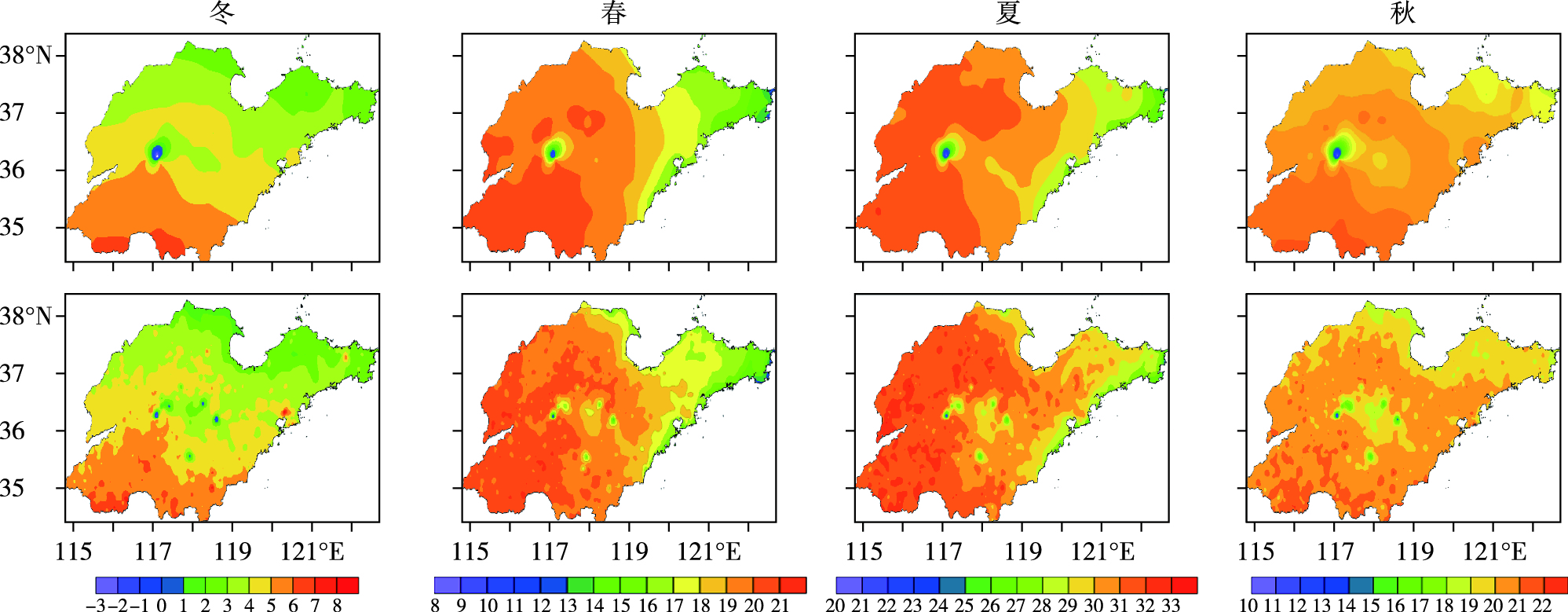
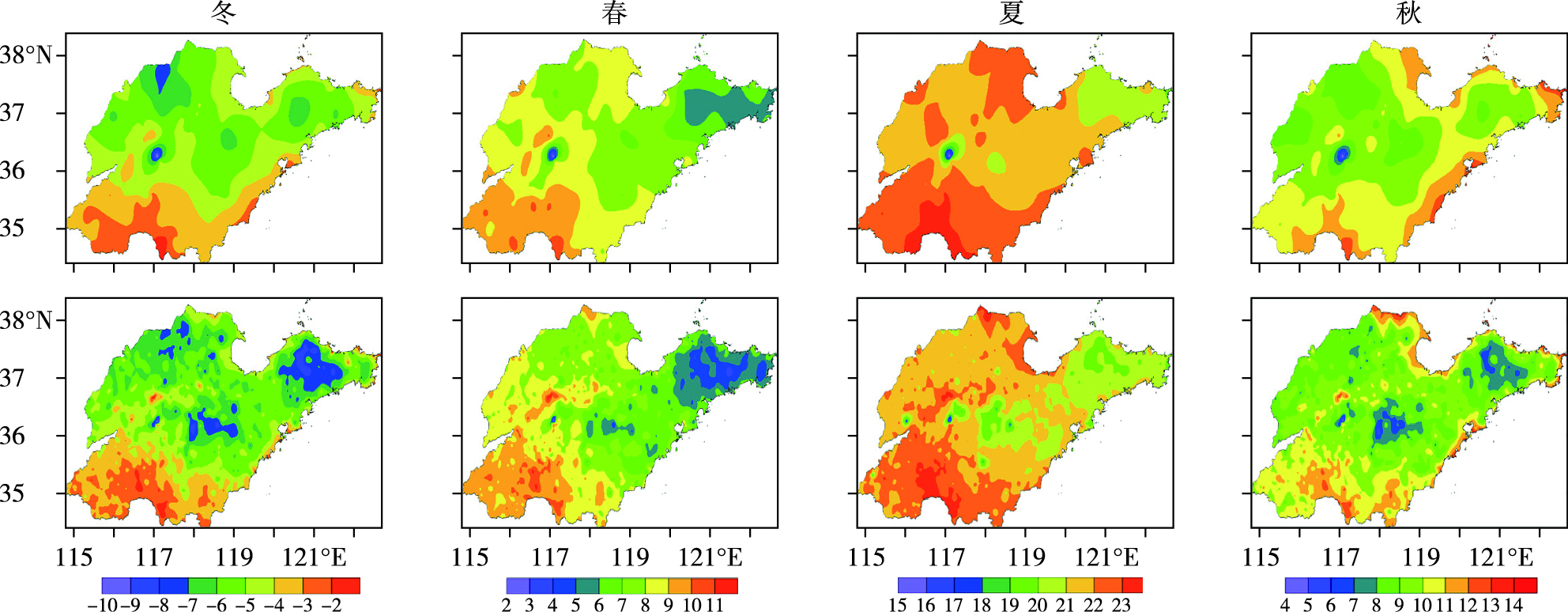
图 4分季给出不同站点分辨率的单站平均最高气温的空间分布,对比可见:春、夏、秋、冬四季,两类分辨率的最高气温整体空间分布形态基本一致,即冬、秋季南低北高,春、夏季转为东低西高。但由高分辨率分布图可以看到更小尺度的局地小气候区,这在低分辨率图上是无法识别的。此外,两类空间分辨率的平均最低气温的空间分布形态差异特征与最高气温基本一致,且最低气温高分辨率分布图上局地小气候区的分布特征较最高气温更明显(图 5)。
|
图 4 山东省不同站点分辨率的季节平均最高气温区域分布(第一行为县级站点,第二行为乡镇级站点;单位:℃) Fig.4 Regional distribution of seasonal mean maximum air temperature at stations with different resolutions in Shandong Province (the first row for county-level stations, the second row for township-level stations; units: ℃) |
|
图 5 山东省不同站点分辨率的季节平均最低气温区域分布图(第一行为县级站点,第二行为乡镇级站点;单位:℃) Fig.5 The same as Fig. 4, but for seasonal mean minimum air temperature |
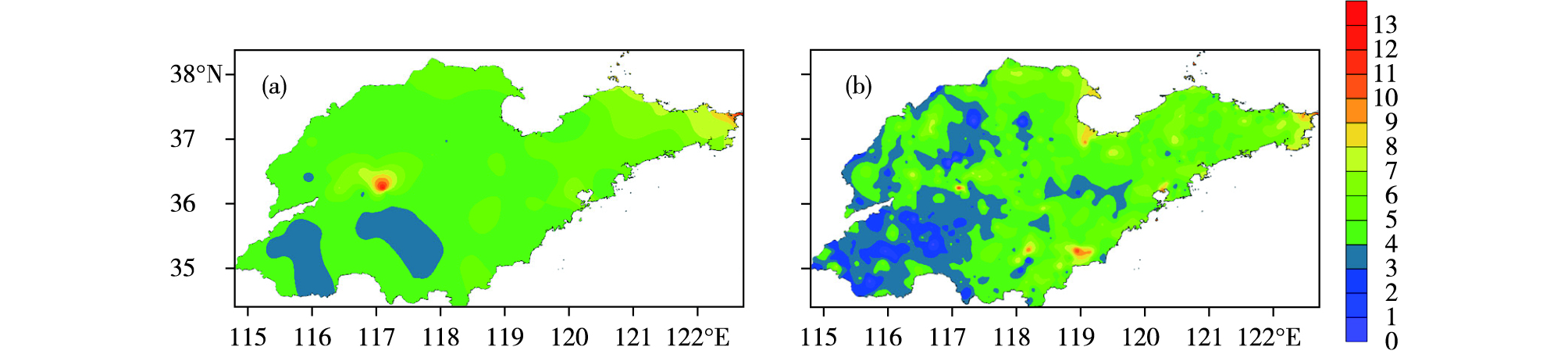
冬半年是山东区域性大风天气的主发期。图 6给出冬季不同站点分辨率的单站平均日极大风速的空间分布,对比可见,同温度和降水等要素相似,高站点分辨率的空间分布图(图 6b)上,冬季平均日极大风速表现出更为精细的较小空间尺度的局地气候区分布特征,如位于半岛海岸附近和鲁中山区的多个局地风速大值区,以及位于鲁西北平原和鲁西南平原的多个局地风速低值区,在低站点分辨率的空间分布图(图 6a)上均无法识别。
|
图 6 山东省不同站点分辨率的冬季平均日极大风速的空间分布图(a.县级站点,b.乡镇站点;单位:m·s-1) Fig.6 Spatial distribution of hibernal mean daily maximum wind speed at stations with different resolutions in Shandong Province(a. county-level stations, b. township-level stations; units: m·s-1) |
综上分析可见,降水、气温和风速均具有局地小气候分布特征,需要更高分辨率的站点布局尚能捕捉,这也说明要素精细化客观预报的站点或格点空间分辨率越精细越好。
3 不同地形属性的观测要素统计学特征差异要素的局地小气候分布特征可能与地形有关。本节以济南区域为例研究不同地形属性站点间气象要素的差异性。充分考虑山区地形以及城市热岛等因素,分别选取济南、长清、市政府、地震局、西营北和跑马岭等6个代表站,其中长清、市政府和地震局三站分别位于西部城郊、市中心和东部城郊,海拔高度均在100 m左右;西营北和跑马岭两站位于东部山区,站点地形高度自北向南依次升高,分别在200 m和300 m左右。
主要从气候统计值,相关性和正态性等不同方面分析气象要素站点间差异性,其中采用分位数作为气候统计值参量;相关性分析采用Pearson相关系数及Euclidean距离;正态性分析则采用频率直方图。分析要素以气温和风速等连续性变量为主,对于小概率事件特征明显降水要素暂不考虑。
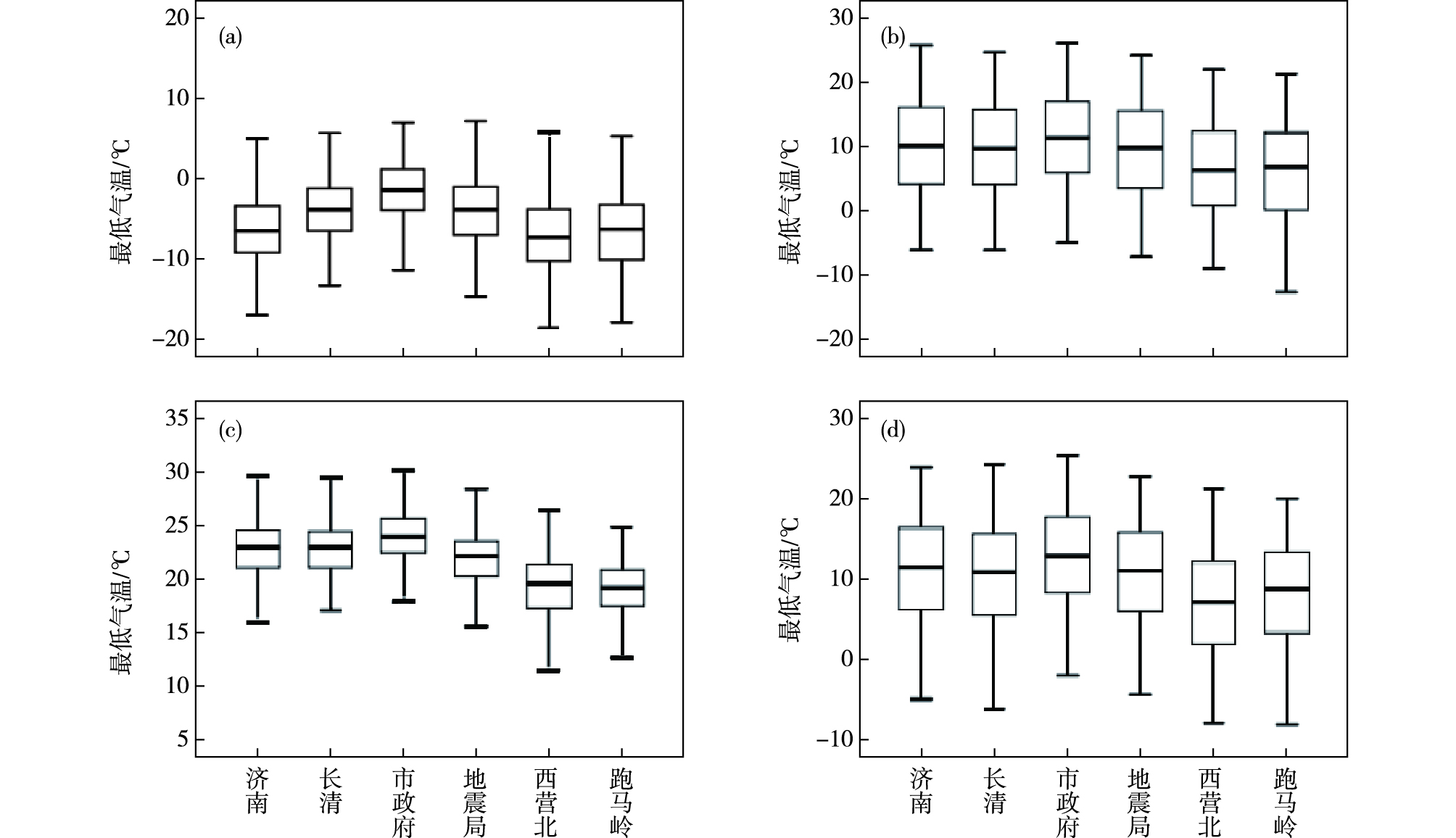
3.1 日最低气温以最低气温为例分析不同地形属性站点间日极端气温的统计学差异性。图 7给出6个测站最低气温箱线图的各项统计值,对比分析可见:四个季节各站间最低气温的箱线图统计量差异均较大,一般位于市中心的市政府站各项统计值最高,分别位于东、西城郊的地震局和长清两站略偏低,位于东部山区,海拔较高的西营北和跑马岭两站各项数值显著偏低;最低气温自城区向城郊和山区,由低海拔向高海拔逐次降低,这可能与城市热岛效应有关。冉桂平等[14]也指出济南城市热岛以市政府为中心呈环状放射发展。
|
图 7 6个代表站的最低气温箱线图(a.冬季,b.春季,c.夏季,d.秋季) Fig.7 Box plot of minimum air temperature at 6 representative stations (a. winter, b. spring, c. summer, d. autumn) |
分季计算6个测站间最低气温的相关系数,结果(表 1-4)表明,各站间相关系数均很高,多数站超过90%,其中城区间各站相关系数超过95%,而山区测站相对较小,表现出一定的区域差异。此外,各站间最低气温的相关系数还存在较为明显的季节差异,通常春、秋两季略高于冬季和夏季。统计分析6个站点的最低气温Euclidean距离(表 1-4)同样显示,因距离和地形属性的不同,各站间Euclidean距离呈现规律性变化,地形属性相同且距离相近的站点间Euclidean距离偏小,地形属性不同且距离较远的测站间Euclidean距离偏大。如冬季济南站,与地形高度相似且距离相近的长清、地震局和市政府等测站间的Euclidean距离数值较小,分别为24、31和45,与位于山区海拔较高且空间距离较远的跑马岭和西营北等测站间的Euclidean距离则明显增大至77和82。
|
|
表 1 冬季6个代表站的最低气温相关系数(Euclidean距离) Table 1 Correlation coefficient (Euclidean distance) of minimum air temperature at 6 representative stations in winter |
|
|
表 2 春季6个代表站的最低气温相关系数(Euclidean距离) Table 2 The same as Table 1, but for spring |
|
|
表 3 夏季6个代表站的最低气温相关系数(Euclidean距离) Table 3 The same as Table 1, but for summer |
|
|
表 4 秋季6个代表站的最低气温相关系数(Euclidean距离) Table 4 The same as Table 1, but for autumn |
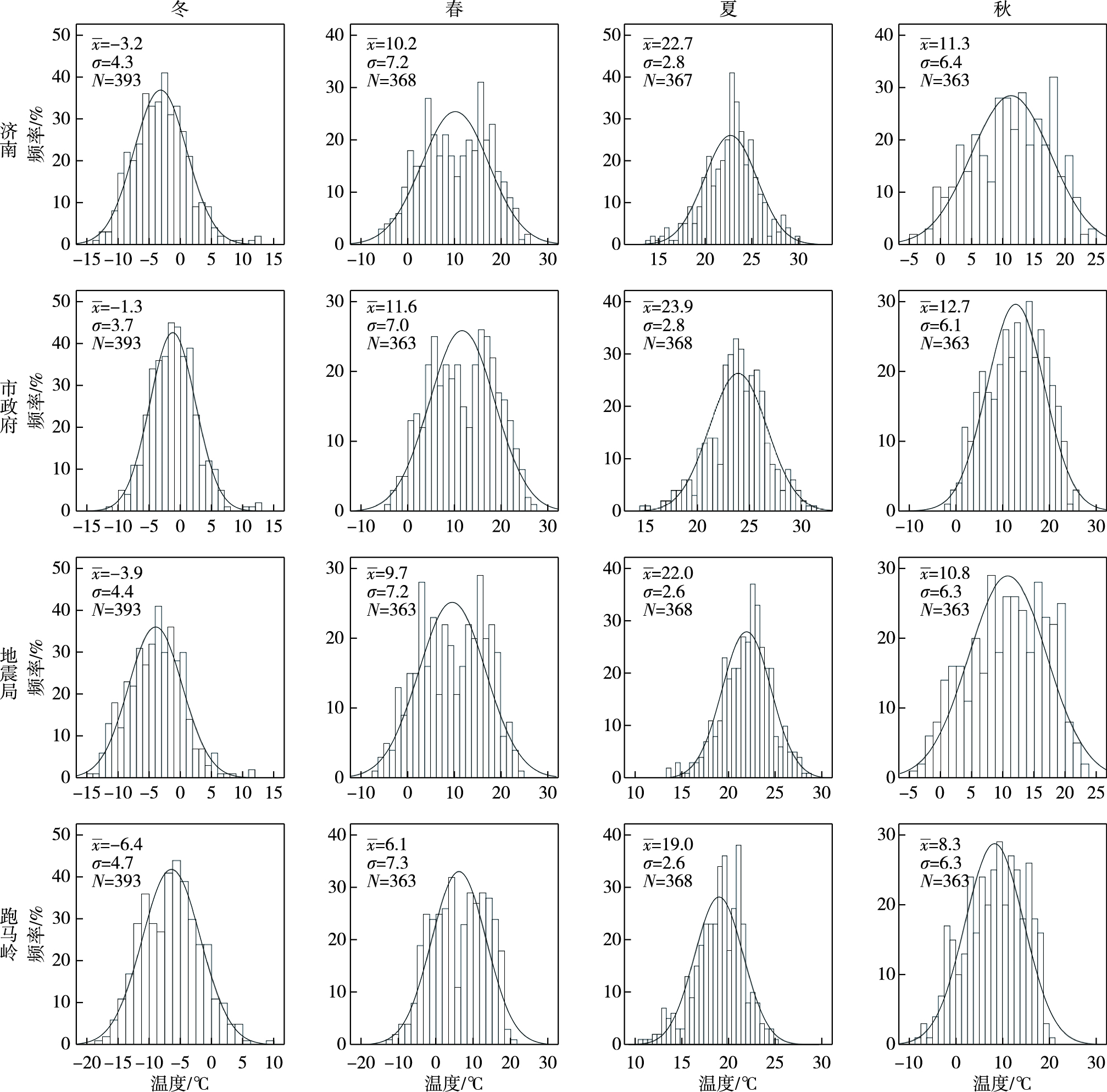
对比各站不同季节最低气温的频率分布情况(图 8)可见,同一季节不同测站的频率分布形态基本相同,而同一站点不同季节的分布形态差异较大。通常冬季最低气温频率分布形态与标准正态曲线拟合较好,夏季次之,而春、秋两季偏差较大。最低气温的站点差异性结果与最高气温基本一致[15]。业务中常用的温度MOS预报均以正态分布假设为前提,分季节建立预报方程。上述分析结果表明,春、秋两季气温较正态分布偏离较大,以季为段建方程的常规做法不能满足正态分布假设要求,必然会影响预报方程的质量。
|
图 8 不同代表站的最低气温频率直方图(第一列:冬季,第二列:春季,第三列:夏季,第四列:秋季) Fig.8 Frequency histogram of minimum air temperature at different stations (the first/second/third/fourth column for winter/spring/summer/autumn) |
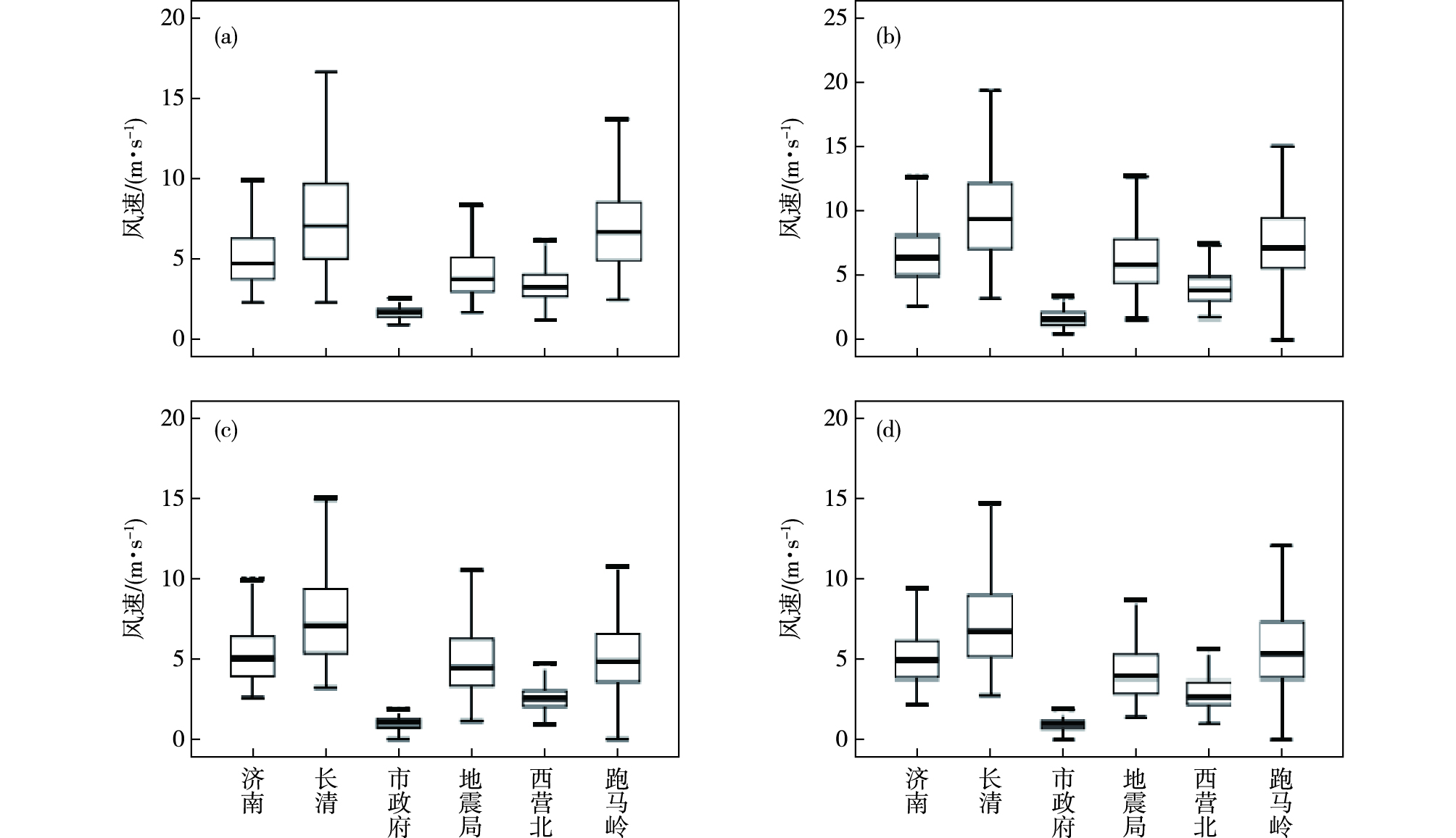
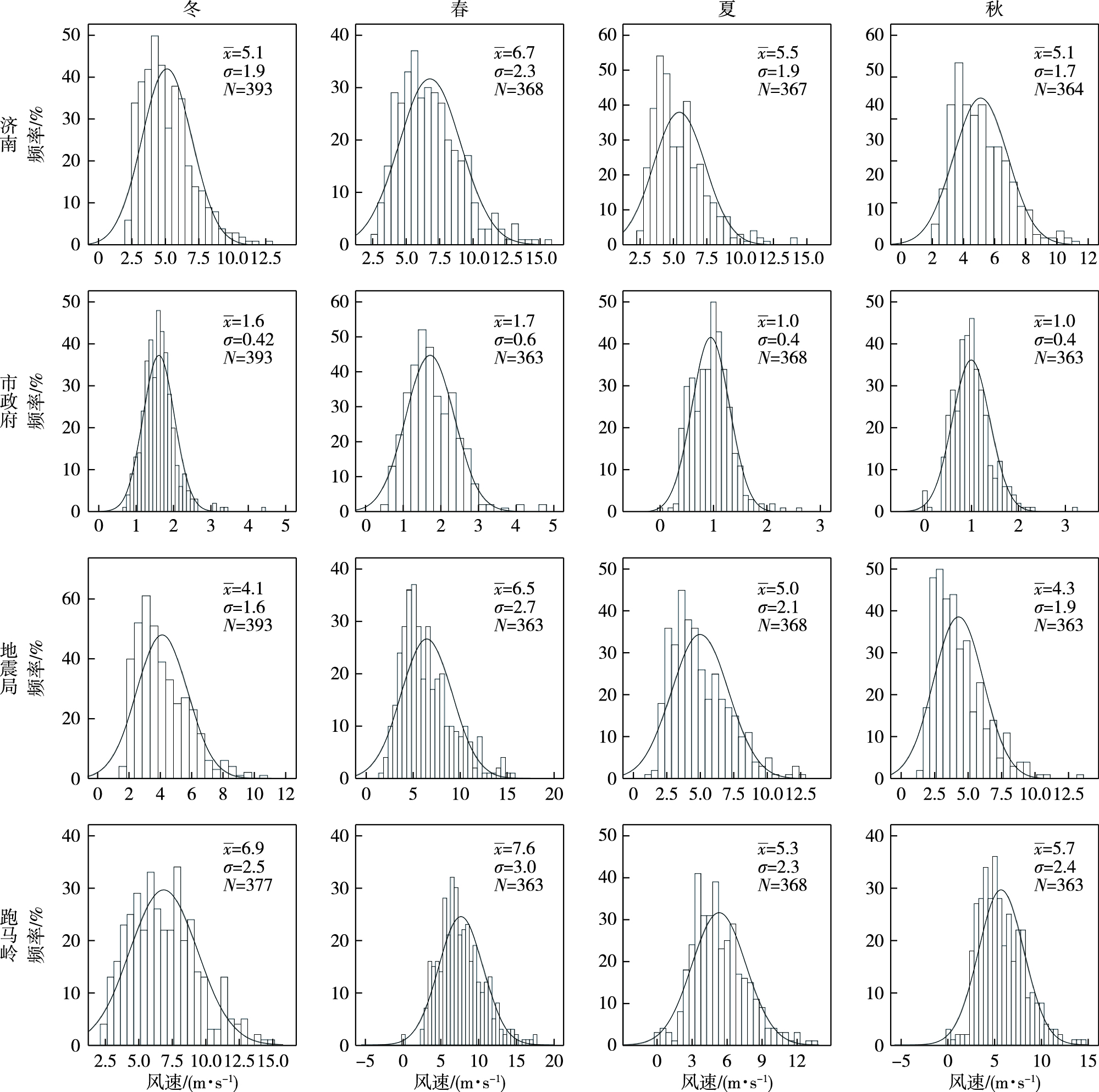
风速反映大气的动力特性。图 9分季给出6个站点的地面风速箱线图。与不同站点间最低气温随地形有规律变化(图 7)不同,各站风速箱线图的各项统计值(高值、低值、中位数和四分位数)差异更大,且无规律可循。此外,各站间地面风速相关系数较低(表 5—8),且不因距离远近,地表属性不同出现规律性变化,如冬季济南站,与市政府、地震局和跑马岭等三个不同地形属性测站的相关系数基本相当(大约65%)。与之相应,各站间Euclidean距离(表 5—8)较大,随地形远近和地形属性规律性变化特征同样不明显。另外,不同测站间风速频率分布差异特征(图 10)也与最低气温(图 8)不同,具体表现为:同一季节不同测站间差异较大,但同一测站不同季节间差异较小。除市政府站外,其他测站均与标准正态分布明显不同。无论风速均值,还是频率分布形态都表现出很强的地区差异性,这说明风速对于地形更为敏感,如测站周边建筑物布局,地形坡度走向等因素都可以对风速产生影响。
|
图 9 不同代表站的地面风速箱线图(a.冬季,b.春季,c.夏季,d.秋季) Fig.9 The same as Fig. 7, but for surface wind speed |
|
图 10 不同代表站的地面风速频率直方图(第一列:冬季,第二列:春季,第三列:夏季,第四列:秋季) Fig.10 The same as Fig. 8, but for surface wind speed |
|
|
表 5 冬季6个代表站的地面风速相关系数(Euclidean距离) Table 5 Correlation coefficient (Euclidean distance) of surface wind speed at 6 representative stations in winter |
|
|
表 6 春季6个代表站的地面风速相关系数(Euclidean距离) Table 6 The same as Table 5, but for spring |
|
|
表 7 夏季6个代表站的地面风速相关系数(Euclidean距离) Table 7 The same as Table 5, but for summer |
|
|
表 8 秋季6个代表站的地面风速相关系数(Euclidean距离) Table 8 The same as Table 5, but for autumn |
对于精细化要素客观预报开发中面临的海量预报站(格)点问题,本文利用山东省稠密的自动气象站观测资料,通过分析不同空间分辨率和地形属性的观测要素的统计学差异,研究各种气象要素的站点差异性,得出以下几点结论:
1) 温度、降水和风等要素具有明显的局地小气候特征,需要更高空间分辨率的预报站点方能捕捉。
2) 市区、市郊以及不同高度山区等不同站点间最低气温的分位数、相关系数等统计参量因距离和地形属性的不同呈规律性变化,但不同测站间最低气温的频率分布形态则基本相似。
3) 风对地形更敏感,不同测站间相关系数较低,分位数统计值和频率分布形态差异均较大。
上述结果表明,精细化要素客观预报中预报站点的空间分辨率越精细越好。对于气温而言,不同站点间的均值、中位数等“定量”参量差异较大,而频率分布等“定性”参量差异较小。因此,在温度的客观预报方法开发中,适合采用统计学预报方法,在站点处理上可以根据计算资源需求通过选取代表站点的方式减少建方程的站点数目。但在时间处理上需要考虑季节差异,尤其对于春、秋两季,传统的以季节为段建立统计方程的做法需要改进[16]。风对地形更敏感,无论“定量”还是“定性”统计参量不同站点间的差异均较大,对于风的预报客观方法处理更为复杂,需要综合考虑统计与动力相结合的释用方法。对于小概率事件特征明显的降水要素的不同站点间统计学差异特征尚未分析,有待未来选取适用于非连续性以及小概率事件等特征变量的统计学方法开展更为详细的研究。
| [1] |
连志鸾, 李国翠, 卞韬, 等. 基于多级相似-差额方法制作乡镇气温预报[J]. 气象, 2008, 34(5): 113-117. |
| [2] |
王海宾, 杨引明, 范旭亮, 等. 上海精细化格点预报业务进展与思考[J]. 气象科技进展, 2016, 6(4): 18-23. |
| [3] |
潘留杰, 薛春芳, 王建鹏, 等. 一个简单的格点温度预报订正方法[J]. 气象, 2017, 43(12): 1584-1593. |
| [4] |
赵声蓉, 赵翠光, 赵瑞霞, 等. 我国精细化客观气象要素预报进展[J]. 气象科技进展, 2012, 2(5): 12-21. |
| [5] |
吴乃庚, 曾沁, 刘段灵, 等. 日极端气温的主客观预报能力评估及多模式集成网格释用[J]. 气象, 2017, 43(5): 581-590. |
| [6] |
吴启树, 韩美, 郭弘, 等. MOS温度预报中最优训练期方案[J]. 应用气象学报, 2016, 27(4): 426-434. |
| [7] |
黄治勇, 张文, 陈璇, 等. 湖北省乡镇温度预报方法初探[J]. 气象, 2011, 37(12): 1578-1583. DOI:10.7519/j.issn.1000-0526.2011.12.015 |
| [8] |
秦爱民, 张洪涛, 魏建军, 等. 山西省乡镇最高最低气温预报方法[J]. 山西气象, 2009(1): 18-21. |
| [9] |
吴建秋, 郭品文. 基于统计降尺度技术的精细化温度预报[J]. 中国科技信息, 2009(12): 44-45,48. DOI:10.3969/j.issn.1001-8972.2009.12.020 |
| [10] |
邱学兴, 王东勇, 朱红芳. 乡镇精细化最高最低气温预报方法研究[J]. 气象与环境学报, 2013, 29(3): 92-96. DOI:10.3969/j.issn.1673-503X.2013.03.015 |
| [11] |
赵玉洁, 张民凯, 张文琴. 基于相关分析的日照市乡镇温度精细预报方法[J]. 山东气象, 2011, 31(3): 18-21. DOI:10.3969/j.issn.1005-0582.2011.03.005 |
| [12] |
GLAHN B, GILBERT K, COSGROVE R, et al. The gridding of MOS[J]. Wea Forecasting, 2009, 24(2): 520-529. DOI:10.1175/2008WAF2007080.1 |
| [13] |
RUTH D P, GLAHN B, DAGOSTARO V J, et al. The Performance of MOS in the digital age[J]. Wea Forecasting, 2009, 24(2): 504-519. DOI:10.1175/2008WAF2222158.1 |
| [14] |
冉桂平, 胡鹏, 张宁, 等. 济南市城市热岛效应分析[J]. 气象科技, 2010, 38(增刊): 97-101. |
| [15] |
张立文, 车军辉, 黄燕玲, 等. 济南市不同地形背景下最高气温的差异性分析[J]. 海洋气象学报, 2017, 37(4): 113-119. |
| [16] |
车钦, 赵声蓉, 范广洲. 华北地区极端温度MOS预报的季节划分[J]. 应用气象学报, 2011, 22(4): 429-436. DOI:10.3969/j.issn.1001-7313.2011.04.005 |
 2019, Vol. 39
2019, Vol. 39

