在大气科学领域,随着大数据时代的到来,气象资料的种类、数据量、发布频率等与日俱增。这一变化对气象软件的交互效率提出了更高的要求。同时,科研工作者和预报业务人员希望软件工具能够输出高质量图像文件,以便让同行对自己的工作成果留下深刻的印象。
当今的大气科学领域中有许多功能强大的数据分析、显示软件系统。例如,我国气象台站业务中广泛使用的MICAPS[1-2];国内气象工作者作图时经常使用的GrADS[3];北京大学陶祖钰教授主持开发的虚拟现实可视化系统LiveView[4];中国气象局郑永光等研究开发的客观分析诊断图形系统[5],国家气候中心开发的CIPAS系统[6]。国际上流行的气象业务系统包括美国NOAA的AWIPS[7]、欧洲中期天气预报中心的MetView[8]、德国的Ninjo[9]等,以及定位于科研的软件例如NCL[10]、Vis5D[11]、IDV[12]等。对以上软件的长处和不足进行比较(表 1)可见,我国的气象软件没有考虑矢量图形输出问题。针对此问题,实现了一个方便国内气象工作者使用、满足业务工作需要、具有高质量图形输出功能的气象软件系统MeteoExplorer[13]。此系统中的一个特色是设计并实现了一种新型的集多种图形渲染技术于一体的图形渲染引擎,它既能够提供硬件图形加速技术所享有的速度和效率,又能够提供软件图形渲染技术所特有的矢量图形输出功能。使用该图形渲染引擎的软件程序,能够在运行当中切换图形渲染技术,并保持图形图像的显示属性不变,而无须重新启动程序。此外,通过对引擎模型中实体对象相互关系的低耦合设计,该引擎能够更为方便地移植到不同构架的操作系统和硬件设备上。
|
|
表 1 常用气象软件绘图功能的优势与不足 Table 1 Strengths and weaknesses of rendering function by commonly-used meteorological applications |
此文的组织如下:第1节对所提出的图形渲染引擎的抽象模型和实现方法进行剖析;第2节介绍常见的图形坐标系统;第3节对图形渲染引擎实现中的一个关键技术,即不同坐标系统之间的坐标转换进行分析;第4节对使用图形渲染引擎的气象软件系统在业务和科研中的应用做简要的介绍;第5节总结全文。
1 多功能图形渲染引擎要实现图形渲染功能,软件开发者一般有两种选择。第一种选择是使用集成开发环境(例如Java SDK、.NET Framework、Qt、Python等)中提供的图形渲染接口。第二种选择偏于底层,即使用图形渲染函数库(以下简称“图形函数库”)。当前流行的选择有DirectX[14]、OpenGL[15]、GDI/GDI+[16]、Magics等。上一节中介绍的软件系统一般使用单一的图形函数库来实现图形渲染功能,例如MICAPS、CIPAS、Vis5D使用OpenGL,MeteoView使用Magics,GrADS使用GDI+,IDV使用JAVA 3D。
这两种选择各有其优缺点。使用集成开发环境优势在于易于上手,缺点是功能实现与平台支持依赖于集成开发环境。使用图形函数库的优点包括:1)灵活性强,便于将系统移植到集成开发环境尚不支持的操作系统或计算平台上;2)独立性强,项目开发进度不会受到集成开发环境开发进度和代码错误的影响。使用图形函数库带来的问题有3个方面。
1) 由于各个图形函数库各具特点,图形函数库的选择是项目负责人面临的难题。例如Direct3D在Windows下兼容性最好,但它仅支持Windows平台。OpenGL在跨平台上具有优势,但是各个平台之间实现的功能差异较大。在手机等移动设备上只实现了OpenGL的一个子集:OpenGL ES。与之相反,Linux图形工作站能够支持OpenGL 4,甚至厂商提供了各种OpenGL的扩展,以增强OpenGL的功能。GDI/GDI+虽然是矢量格式,但是渲染效率不高。
2) 图形渲染功能的实现依赖于图形函数库。例如GDI/GDI+没有三维显示功能,这样基于GDI/GDI+的渲染引擎同样无法实现三维渲染。
3) 当把已有的软件系统移植到图形函数库不支持的操作系统上时,需要重新实现图形渲染引擎。例如把使用GDI/GDI+的应用程序移植到Linux操作系统下时,需要使用诸如OpenGL这样的图形函数库重写图形显示模块。
1.1 图形渲染抽象层概念与设计实现由上述讨论可知,任何一种技术路线都不是完美的。图形渲染引擎实现的出发点是取各家之长,舍各家之短。针对当前信息技术产业领域多个生态系统和软件技术并存的现实,作者在设计阶段提出下列目标:
1) 依赖性低。图形渲染引擎的实现不依赖于具体的生态环境。它既可以部署在PC、图形工作站这样的桌面系统上,又可以在新兴的智能手机、平板电脑等移动计算设备上流畅运行。
2) 移植性强。可以在图形渲染引擎中无缝接入新的图形函数库,或者比较方便地将图形渲染引擎移植到新的生态环境上。
3) 组件可替换性强。应用程序可以根据配置信息,或者各个图形函数库的功能特点,实时切换到由某一图形函数库实现的组件,并且保证图形显示属性在切换过程中保持不变。例如,用户希望把显示内容输出为矢量图形文件时,程序应该自动切换到软件渲染模式下,输出完毕后再切换到硬件加速渲染模式下。另外一个常见的例子是当用户通过远程连接登录到另一台主机时,因为远程连接程序无法提供硬件加速渲染驱动,因此渲染引擎需要切换到对显示功能要求较低的图形函数库(例如GDI及低版本的OpenGL或Direct3D)下。
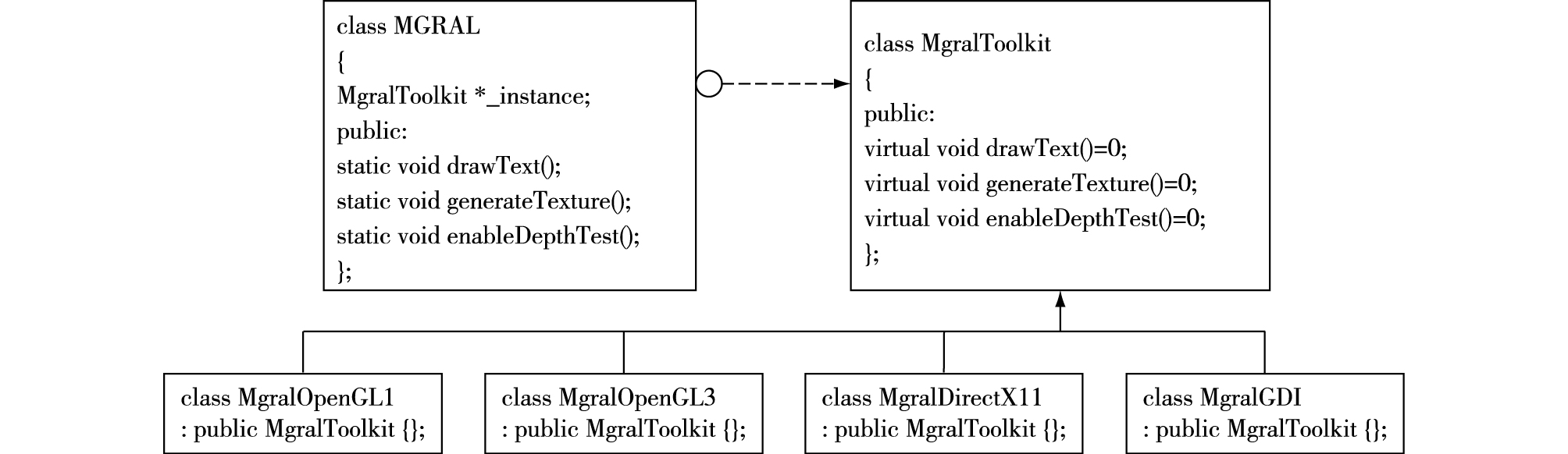
为实现上述设计目标,作者使用抽象工厂(abstract factory)设计模式[17]设计了气象图形渲染抽象层(meteorological graphics rendering abstract layer,MGRAL)模型。该模型的早期实现在文献[13]中进行了详细的讨论。近年来不断优化该模型的逻辑关系并完善功能实现。模型的逻辑结构如图 1所示。
|
图 1 气象图形渲染抽象层模型中主要C++类之间的逻辑关系 Fig.1 Logical relation among major C++ classes in MGRAL model |
在模型的设计初期,需要将图形渲染引擎应该提供的所有功能列举出来。接下来设计一个抽象基类,对每一个功能加以抽象描述,作为抽象基类的一个纯虚拟函数。然后针对具体的图形函数库设计一个实体类,作为抽象基类的子类。在实体子类中需要定义并覆盖抽象基类中的纯虚拟函数。最后还需要定义一个面向客户(即上层调用代码)的静态接口类以调用抽象基类中的虚拟函数,以实现客户请求的功能。引入静态接口类的目的是让客户不用跟实体类发生联系,减少了代码之间的耦合性。
下面结合图 1详细分析模型的工作原理。首先定义面向客户的静态类MGRAL作为模型的对外接口。类MGRAL中的函数对应渲染引擎所提供的所有功能。例如显示字符的函数drawText;生成纹理的函数generateTexture等。其次定义抽象基类MgralToolkit以纯虚函数的形式描述所有渲染功能。类MgralToolkit的子类使用相应的图形函数库实现并覆盖父类中的所有虚函数。例如,实体子类MgralGDI中所有的虚函数使用GDI API实现。
在类MGRAL中定义了一个类型为MgralToolkit的指针型成员变量_instance,利用C++的多态性,它实际上是MgralToolkit某个子类的实例。通过这个成员调用类MgralToolkit子类的函数,以完成相应的功能。下面的代码示例了两者之间的关系:
MgralToolkit *_instance;
void MGRAL::drawText(const char *text, float x, float y, float dx, float dy, float rotation, float scale)
{
if (_instance)
_instance->drawText(text, x, y, dx, dy, rotation, scale);
else
fprintf(stderr, "toolkit is not instantiated\\n");
}
在此例中,当客户需要绘制文本时,就调用类MGRAL的函数drawText。在此函数的定义中,根据成员_instance是否已被实例化,或调用MgralToolkit子类中的同名函数,或输出错误提示信息。
气象图形渲染抽象层模型不仅避免了本节开头提出的采用图形函数库带来的问题,而且具有以下优点:
1) 使上层调用程序代码与底层渲染引擎的功能实现代码相分离,降低了两者之间的耦合性。实现了第一个目标。
2) 使加入新的实体对象变得容易。当需要加入新的实体对象时,只需定义类MgralToolkit的实体子类即可。原有的实体子类和客户程序代码都不受影响。这样就实现了第二个目标。
3) 让实时切换实体对象成为可能,实现了第三个目标。当需要在各个图形函数库之间切换时,只需首先删除变量_instance,然后生成对应于新的图形函数库实体子类的实例,最后将变量_instance指向这个实例。
抽象工厂模式的一个优势是非常自然地约束了各个实体对象之间的依赖关系。例如,当使用OpenGL函数库进行渲染时,只能使用OpenGL函数;而使用Direct3D函数库进行渲染时,只能使用Direct3D函数。
1.2 多功能图形渲染引擎——图形渲染抽象层的实现目前,多功能图形渲染引擎实现了对四种图形函数库的封装:OpenGL1、OpenGL3、DirectX 11、GDI,其中OpenGL1对应OpenGL早期的固定函数管线(fixed-function pipeline)编程模型,OpenGL3对应现代OpenGL的可编程管线(programmable pipeline)模型。它们分别用抽象基类MgralToolkit的四个实体子类MgralOpenGL1、MgralOpenGL3、MgralDirectX11和MgralGDI表示。多功能图形渲染引擎实现了如下功能:
1) 摄像机、投影、裁剪、窗口视图的设置;
2) 颜色、深度测试、模板测试、表面剔除的设置;
3) 几何图形和字体属性设置,包括颜色、大小、旋转、线宽、线型等;
4) 多个坐标系之间的顶点坐标变换(本文第2节将讨论这些坐标系);
5) 纹理生成与显示;
6) 灯光与材料;
7) 字体、几何图形、常见气象符号的渲染;
8) 显示列表、帧缓冲区和顶点数组;
9) 多边形三角化(tesselation);
10) 粒子系统;
11) 体绘制和等值面绘制。
抽象基类MgralToolkit的四个实体子类根据各自对应的图形函数库提供的API实现上述接口的定义。
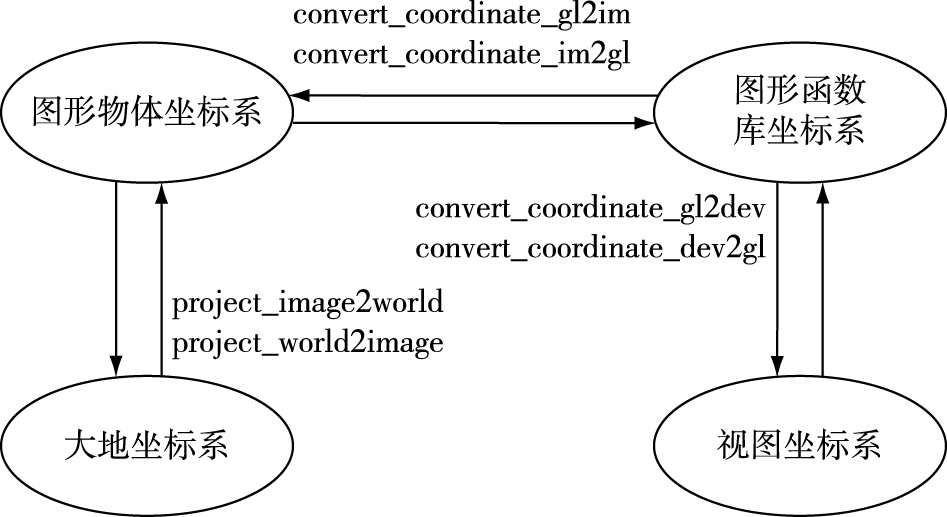
2 图形坐标系统由上一节的讨论可知,在多功能图形渲染引擎中可以根据用户需要灵活地变换图形显示技术。在这一变换中,需要保持程序窗口中所有图形、图像物体的显示属性不变。这里的显示属性包括缩放比例、位置、颜色、纹理等。然而,不同的图形函数库对坐标系的定义各不相同,这给引擎在变换图形显示技术时进行坐标变换带来了困难。因此有必要对图形显示系统中的坐标系有一个清晰的理解。
在一个图形显示系统中存在四个性质、用途不同的坐标系。本节详细讨论这些坐标系。
2.1 设备视图坐标系每个操作系统中的窗口管理器(例如Windows中的GDI,Unix中的X Window等)都使用视图坐标系来表示图形物体的坐标值。在视图坐标系中,原点总是在显示器屏幕的左上角。x轴沿水平方向,向右增长;y轴沿垂直方向,向下增长。视图坐标系的单位是像素,在Windows图形系统中视图坐标系也被称为设备坐标系(device coordinate system)。
2.2 图形函数库内部定义的坐标系在目前主流的图形函数库例如OpenGL、GDI和Direct3D中都定义了自己的坐标系统。这里分别介绍这三个图形函数库使用的坐标系。
2.2.1 OpenGL坐标系在默认配置下,OpenGL坐标系中坐标轴的方向与数学中的笛卡儿坐标系中坐标轴的方向一致,即x轴沿水平方向,向右增长;y轴沿垂直方向,向上增长。z轴与x、y轴成右手坐标系关系。与视图坐标系相比,OpenGL坐标系的单位同样是像素,但具有浮点精度,而视图坐标系只具有整数型精度。
将一个三维场景显示在二维显示器平面上,这一过程实际上包括了如下坐标变换过程:
1) 模视变换。模视变换包括模型变换(modeling transformation)和视角变换(viewing transformation)。模型变换包括旋转、平移和缩放变换三种。视角变换指定了摄像机的位置和视线方向。由于摄像机与物体方位,距离之间的对偶性,因此通常把模型变换和视角变换放到一起,统称为模视变换(model view transformation)。模视变换把物体点的坐标从局部坐标系转换到摄像机坐标系中。
2) 投影和裁剪变换。在计算几何学中,投影变换(projection transformation)是指将三维空间点映射到二维投影平面上的过程[18]。然而,OpenGL中的投影变换不等于几何学中的投影变换,前者包含了投影和裁剪两个过程,并定义了可视空间(称为裁剪金字塔)。位于可视空间外部的点将被丢弃,位于可视空间内部的点将被保留。投影过程将三维空间点的坐标从摄像机坐标系变换到裁剪坐标系。裁剪过程再将裁剪坐标转换为归一化设备坐标(normalized device coordinates,NDC)。
3) 视图变换。视图变换将投影平面上的归一化设备坐标变换到视图窗口坐标。
2.2.2 Windows GDI坐标系GDI是Graphics Device Interface的缩写,是Windows操作系统内核中的图形显示模块。GDI中的坐标系称为逻辑(logical)坐标系或视窗(window)坐标系。逻辑坐标系的单位可以是像素、米、英尺、点(point)或者用户自定义的单位。Windows SDK中提供了相应的函数设置逻辑坐标系的单位、原点和范围。
2.2.3 Direct3D坐标系除了少数细微差别外,Direct3D坐标系与OpenGL坐标系基本上相同。在将场景中的三维点显示在程序窗口的二维平面这一过程中,Direct3D定义了与OpenGL相同的坐标变换过程。
2.3 图形物体坐标系在图形编辑程序中,图形物体显示在程序窗口的客户区中。为了描述图形物体中的某些特征点的位置,一般有两种选择:1)使用图形函数库中的坐标系;2)引入图形物体坐标系。在实际应用中,用户需要对图形进行缩放、平移、旋转等操作,使用图形函数库坐标系时无法刻画图形物体坐标值的固有特性,因此有必要引入图形物体坐标系。在此坐标系中,图形物体上的某一点相对图形物体坐标系原点的位置是不变的;图形物体上任意两点之间的距离也是不变的。这一不变性在图形处理中是必不可少的。
2.4 大地坐标系在大气科学或者地理信息系统(GIS)软件中,需要把图形显示在地图上。这样就引入大地坐标系。在此坐标系中物体的空间位置通常使用经度、纬度和海拔高度来表示。
3 不同坐标系之间的坐标变换图形、图像物体在不同坐标系之间坐标变换功能的正确实现是保证渲染引擎在变换图形函数库时显示属性不变的前提。
3.1 设备视图坐标系与图形函数库坐标系之间的转换 3.1.1 OpenGL/Direct3D坐标系与视图坐标系之间的转换设(xvp, yvp)为物体上一点在视图坐标系下的坐标值,(xGL, yGL)是该点在OpenGL坐标系下的坐标。在正交投影下,OpenGL坐标系与视图坐标系之间的坐标转换由公式(1)确定:
| $ \begin{array}{l} {x_{{\rm{vp}}}} = {\rm{sgn}}\left( {{E_{{\rm{right}}}} - {E_{{\rm{lef}}t}}} \right)\left( {{x_{{\rm{GL}}}} - {E_{{\rm{left}}}}} \right)\\ {y_{{\rm{vp}}}} = {\rm{sgn}}\left( {{E_{{\rm{top}}}} - {E_{{\rm{bottom}}}}} \right)\left( {{y_{{\rm{GL}}}} - {E_{{\rm{bottom}}}}} \right) \end{array} $ | (1) |
其中sgn为阶跃函数,且Eleft,Eright,Etop,Ebottom分别是裁剪平面左、右、上、下边界的范围。
在透视投影下,坐标转换由公式(2)确定:
| $ \begin{array}{l} {x_{{\rm{vp}}}} = {\rm{sgn}}\left( {{E_{{\rm{right}}}} - {E_{{\rm{left}}}}} \right)\left( {\frac{{{D_{{\rm{near}}}} \times {x_{{\rm{GL}}}}}}{{ - {z_{{\rm{GL}}}}}} - {E_{{\rm{left}}}}} \right)\\ {y_{{\rm{vp}}}} = {\rm{sgn}}\left( {{E_{{\rm{top}}}} - {E_{{\rm{bottom}}}}} \right)\left( {{E_{{\rm{top}}}} - \frac{{{D_{{\rm{near}}}} \times {y_{{\rm{GL}}}}}}{{ - {z_{{\rm{GL}}}}}}} \right) \end{array} $ | (2) |
式中Dnear表示裁剪金字塔近平面到摄像机的距离。注意到透视投影下视图坐标系中一点对应向量(xGL, yGL, zGL)上的所有点。
3.1.2 GDI坐标系与视图坐标系之间的转换GDI坐标系在Windows中称为逻辑坐标系,只支持二维坐标。令(xo, vp, yo, vp),wVP, hVP为视图坐标系的原点和范围;(xo, log, yo, log), wlog, hlog为逻辑坐标系的原点和范围,则有下式成立:
| $ \begin{array}{l} {x_{{\rm{log}}}} = \left( {{x_{{\rm{vp}}}} - {x_{{\rm{o, vp}}}}} \right)\frac{{{w_{log}}}}{{{w_{{\rm{vp}}}}}} + {x_{{\rm{o, log}}}}\\ {y_{{\rm{log}}}} = \left( {{y_{{\rm{vp}}}} - {y_{{\rm{o, vp}}}}} \right)\frac{{{h_{{\rm{log}}}}}}{{{h_{{\rm{vp}}}}}} + {y_{{\rm{o, log}}}} \end{array} $ | (3) |
通过公式(3)即能实现GDI坐标系(xlog, ylog)与视图坐标系(xvp, yvp)之间的坐标转换。这也是Windows应用程序接口(API)函数LPtoDP和DPtoLP的实现方法。
3.2 图形函数库坐标系与图形物体坐标系之间的转换 3.2.1 OpenGL坐标系与图形物体坐标系之间的转换尽管图形物体坐标系提供了物体上一点位置和两点之间距离的不变性,开发人员还是要把它转换到图形函数库中坐标系下,以调用图形函数库提供的函数完成绘图操作。在这一转换过程①中,需要引入三个变量:前两个变量(xC, yC),描述了整个图形物体(常用该物体的质心点描述)在OpenGL坐标系中的位置。当图形物体被移动时,这两个变量也要随之更新。第三个变量z,描述了OpenGL坐标系与图形物体坐标系单位长度之间的比例因子②,当缩放图形物体时,变量z需要随之更新:
| $ z'= z \times f $ | (4) |
①这里仅讨论二维坐标变换,同样的思路可以推广到三维坐标变换。
②这里只考虑各向同性的缩放情况。在各向异性的缩放情况下,应该引入两个变量(z_x, z_y)来分别表示水平和垂直两个方向上的比例因子。
其中f为缩放因子。
设(xCL, yGL)和(xI, yI)分别表示图形物体上一点A在OpenGL坐标系和在图形物体坐标系中的坐标值。两者之间的关系是:
| $ \begin{array}{l} {x_{\rm{I}}} = \frac{{{x_{{\rm{GL}}}} - {x_{\rm{C}}}}}{z}\\ {y_{\rm{I}}} = \frac{{{y_{{\rm{GL}}}} - {y_{\rm{C}}}}}{z} \end{array} $ | (5) |
当移动图形物体时,图形物体质心在OpenGL坐标系中的坐标值变化为:
| $ \begin{array}{l} {x_{\rm{C}}}' = {x_{\rm{C}}} + \Delta {x_{{\rm{GL}}}}\\ {y_{\rm{C}}}' = {y_{\rm{C}}} + \Delta {y_{{\rm{GL}}}} \end{array} $ | (6) |
其中(ΔxGL, ΔyGL)代表鼠标光标在OpenGL坐标系中的偏移量。
在对图形物体进行缩放时,用户一般希望图形物体上对应鼠标光标点的位置在缩放后仍然对应着鼠标光标点。从功能实现的角度上看,这意味着图形物体上对应鼠标光标的点在OpenGL坐标系下的坐标值(xCL, yGL)不变。此外,该点图形物体坐标系中的坐标值(xI, yI)因存在不变性也不会发生改变。因此,由公式(5)平移变量(xC, yC)应该移动到(xC', yC'):
| $ \begin{array}{l} {x_{\rm{C}}}' = {x_{{\rm{GL}}}} - {x_{\rm{I}}}z' \\ {y_{\rm{C}}}' = {y_{{\rm{GL}}}} - {y_{\rm{I}}}z' \end{array} $ | (7) |
其中z′为缩放后的比例因子。
联立公式(5)和(7),平移变量(xC, yC)的位移为:
| $ \begin{array}{l} \Delta {x_{\rm{C}}} = {x_{\rm{C}}}' - {x_{\rm{C}}} = \left( {1 - \frac{{z' }}{z}} \right)\left( {{x_{{\rm{GL}}}} - {x_{\rm{C}}}} \right)\\ \Delta {y_{\rm{C}}} = {y_{\rm{C}}}' - {y_{\rm{C}}} = \left( {1 - \frac{{z' }}{z}} \right)\left( {{\rm{ }}{y_{{\rm{GL}}}} - {y_{\rm{C}}}} \right) \end{array} $ | (8) |
因为GDI逻辑坐标系与图形物体坐标系都是用来描述物体的特征位置,因此可以将两者合并,即用GDI逻辑坐标系作为图形物体坐标系。这样就不存在GDI逻辑坐标系与图形物体坐标系之间的转换问题。
剩下的唯一问题是处理进行图形物体缩放时平移变量(xC, yC)和缩放变量z的计算。此问题开始看起来较困难,因为Windows应用程序接口中没有提供类似OpenGL中glScale*和glTranslate*这样的函数。经过分析,有两种方法可供选择,一种是改变图形物体的位置坐标属性。这样做的弊端是当更换图形函数库时,还要把图形物体的位置坐标属性改回来,这一操作难度较大,甚至在OpenGL和Direct3D中是不能做到的。同时破坏了图形物体坐标系中坐标值恒定这一优点。另一种方法是改变逻辑坐标系中窗口的范围。这样,在保持视图范围不变的情况下,增大或者缩小窗口范围等价于缩小或者放大图形物体。因此本文在渲染模型的实现中使用了后一种方法。
3.2.3 Direct3D坐标系与图形物体坐标系之间的转换由于Direct3D提供了与OpenGL相同的坐标转换功能,因此第3.2.1节中的讨论结果(公式(5)—公式(8))仍然适用于本节所讨论的主题,这里不再重复。
3.3 图形物体坐标系与大地坐标系之间的转换物体的空间位置通常使用经度、纬度和海拔高度来表示。将三维坐标转换到程序窗口中的二维坐标涉及到地图投影和裁剪技术,幸运的是,目前已经有许多成熟的地理信息软件库实现了这一功能。注意到只有大地坐标系与图形物体坐标系之间的转换才有意义,因为图形物体上的一点与某一个地理位置一一对应。在缩放或者平移操作中,该点的图形函数库坐标和视图坐标发生变化,但其对应的大地坐标不变。
综合上面的讨论,图 2给出了四个坐标系之间坐标转换关系及实现坐标变换的函数。
|
图 2 四个坐标系之间的坐标转换关系 Fig.2 Coordinate transformation relation among 4 coordinate systems |
本文所提出的图形渲染抽象层模型及其实现——多功能图形渲染引擎,作为图形渲染模块集成在气象信息分析处理软件系统MeteoExplorer[13]中。该系统构架采用层次化,模块化设计,使用C++语言开发,支持包括Windows,Linux,SGI Irix,Mac OS X和iOS在内的多种操作系统。系统的用户界面简洁友好,针对移动计算设备还提供触控操作功能。本节针对科研与预报业务中的实际用户需求从数据可视化、矢量图形输出和多平台支持三个方面进行讨论。
4.1 实时数据可视化图形渲染速度是用户最为关心的指标。对于高分辨率数值模式数据,图形渲染引擎在普通PC机上能够提供较好的性能,满足实时可视化的需要。图 3给出了MeteoExplorer对欧洲中期天气预报中心高分辨率数值模式2016年7月7日00时的三个预报要素的实时可视化结果。图中灰度色斑图为海平面气压、黑色等值线为850 hPa等风速线,体渲染为整层大气液态水含量。程序运行在一台配置了2.5 GHz Intel Xeon E5-2609 CPU和NVIDIA Quadro K600显卡的PC机上,能够提供每秒31帧的显示速度(图 3窗口右上角)。因此,图形渲染引擎在普通PC机上能够提供较好的性能,满足实时可视化的需要。

|
图 3 满足实时可视化需求的图形渲染性能 Fig.3 Competent rendering performance that meets the requirement of real-time visualization |
MeteoExplorer系统可以将当前程序窗口中显示的内容保存为多种格式的图像文件,包括位图BMP、JPG、PNG、EMF等。其中EMF称为增强型Windows图元文件,是一种在图像被缩放时不失真的矢量图像格式。如图 4所示,用户可以轻易地把程序窗口中显示的内容忠实原样地保存为EMF格式的图像文件(或者复制到系统剪贴板上),然后插入(或者粘贴)到常用的图像编辑和办公软件,例如Illustrator、Word、PowerPoint中。这样,用户以所见即所得的操作方式,得到可视化显示结果的矢量图像。

|
图 4 方便的矢量图形格式内容导出 Fig.4 Convenient export of rendition content as vector graphics |
随着移动计算设备的流行和Linux系统应用的不断扩大,用户希望在自己选择的平台上完成工作。此文所提出的混合图形渲染引擎,由于其具备与图形函数库和开发框架的独立性,因此能够方便地在多种操作系统或计算平台上实现,从而满足用户的个性化需求。图 5a和图 5b分别显示了在Windows RT和iOS操作系统上的渲染结果,其中分别使用了Direct3D 11和OpenGL ES 2函数库。图 5中等值线为NCEP-GFS数值预报模式2016年11月8日14时的海平面气压场。

|
图 5 将多功能图形渲染引擎移植到Windows RT(a)和iOS(b)操作系统上的渲染结果 Fig.5 Rendition of the proposed versatile rendering engine that is ported to Windows RT (a) and iOS (b) platform |
大气科学技术的迅速发展,天气预报业务改革创新的不断深入,对相关软件系统的图形显示功能提出了更高的要求,即在高效稳定地渲染海量数据的同时,又能生成高质量的图像文件。针对这一需求,本文提出了一种新型的集多种图形渲染技术于一体的多功能图形渲染引擎,该渲染引擎的特点有:1)既具有硬件图形加速技术所带来的速度和效率,又能够提供软件图形渲染技术所特有的矢量图形输出功能;2)图形渲染引擎能够动态切换图形函数库,这样使用该图形渲染引擎的软件程序,能够在运行当中切换图形渲染技术,并保持图形图像的显示属性不变,而无须重新启动程序;3)能够方便地移植到不同构架的操作系统平台和计算设备上;4)支持多种编码格式的图像文件输出。
此文还重点讨论了在实现多功能图形渲染引擎时遇到的技术难题——不同坐标系之间的坐标转换问题,并对一些关键技术给出了详细的数学分析和具体的示例程序代码。
此文讨论的多功能图形渲染引擎已经通过程序实现并集成在气象信息分析处理系统中,该系统在日常天气预报业务和气象科学研究中能够提供以下帮助。首先,实现天气图的交互制作;其次,提供海量气象数据的实时显示功能;第三,具有高质量图形输出功能,满足用户制作气象预报图形产品和科研论文插图的需求。
| [1] |
李月安, 曹莉, 高嵩, 等. MICAPS预报业务平台现状与发展[J]. 气象, 2010, 36(7): 50-55. |
| [2] |
于连庆, 胡争光. MICAPS中天气图交互制作子系统[J]. 应用气象学报, 2011, 22(3): 375-384. DOI:10.3969/j.issn.1001-7313.2011.03.015 |
| [3] |
DOTY B E, KINTER J L Ⅲ.Geophysical data analysis and visualization using GrADS[M]// SZUSZCZEWICZ E P, BREDEKAMP J H.Visualization techniques in space and atmospheric sciences.NASA: Washington D C, 1995: 209-219.
|
| [4] |
王洪庆, 张焱, 陶祖钰, 等. 五维大型复杂数据集计算机可视化[J]. 自然科学进展, 1998, 8(6): 742-747. DOI:10.3321/j.issn:1002-008X.1998.06.015 |
| [5] |
郑永光, 王洪庆, 陶祖钰. Windows下二维气象绘图软件:客观分析诊断图形系统[J]. 气象, 2002, 28(3): 42-45. |
| [6] |
吴焕萍, 张永强, 孙家民, 等. 气候信息交互显示与分析平台(CIPAS)设计与实现[J]. 应用气象学报, 2013, 24(5): 631-640. DOI:10.3969/j.issn.1001-7313.2013.05.013 |
| [7] |
GRIFFITH F.AWIPS-Ⅱ into the future[C]//Proceedings of 27th ⅡPS for Meteorology, Oceanography, and Hydrology, 2011.
|
| [8] |
DAABECK J.Overview of meteorological workstation development in Europe[C]//Proceedings of 21st International Conference on Interactive Information Processing Systems (ⅡPS) for Meteorology, Oceanography, and Hydrology, 2005.
|
| [9] |
JOE P, KOPPERT H-J, HEIZENREDER D, et al.Severe weather forecasting tools in NinJo workstation[C]//Proceedings of World Weather Research Program Symposium on Nowcasting and very short range forecasting, 5-9 September 2005, Toulouse, France.Geneva: World Meteorological Organization, 2005.
|
| [10] |
NCAR. CISL's NCAR Command Language (NCL)[EB/OL]. [2019-06-22].http://www.ncl.ucar.edu.
|
| [11] |
HIBBARD W L, PAUL B E, SANTEK D A, et al. Interactive visualization of earth and space science computations[J]. Computer, 1994, 27(7): 65-72. DOI:10.1109/2.299413 |
| [12] |
MURRAY D, McWHIRTER J, HO Y.The IDV at 5: New features and future plans[C]//Proceedings of 25th Conference on International Interactive Information and Processing Systems (ⅡPS) for Meteorology, Oceanography, and Hydrology, 2009.
|
| [13] |
于连庆. 基于触控操作方式的大气科学数据可视化系统技术研究与实现[J]. 南京信息工程大学学报(自然科学版), 2014, 6(6): 530-538. |
| [14] |
LUMA F D. Introduction to 3D game programming with DirectX 10[M]. Plano, Texas: Wordware Publishing, Inc, 2008.
|
| [15] |
WOO M, NEIDER J, DAVIS T, et al. OpenGL programming guide:The office guide to learning OpenGL, Version 1.2[M]. 3rd ed. New Jersey: Addison-Wesley Professional, 1999.
|
| [16] |
PETZOLD C. Programming windows[M]. 5th ed. Seattle: Microsoft Press, 1998.
|
| [17] |
GAMMA E, HELM R, JOHNSON R, et al. Design patterns:Elements of reusable object-oriented software[M]. New Jersey: Addison Wesley Professional, 1995.
|
| [18] |
HARTLY R, ZISSERMAN A. Multiple view geometry in computer vision[M]. 2nd ed. Cambridge: Cambridge University Press, 2004.
|
 2019, Vol. 39
2019, Vol. 39

