2. 中国海洋大学, 山东 青岛 266100;
3. 俄亥俄州立大学地理系, 俄亥俄 哥伦布 43210
2. Ocean University of China, Qingdao 266100, China;
3. Department of Geography, Ohio State University, Columbus 43210, USA
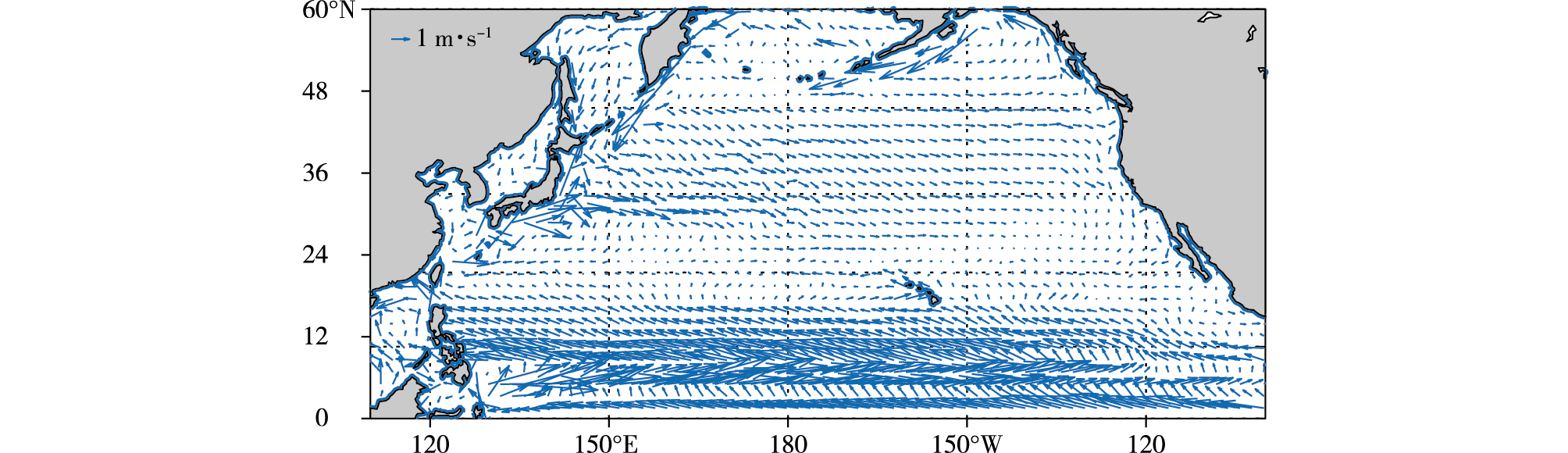
根据SODA(Simple Ocean Data Assimilation)数据集中的水平流速u和垂直速度v绘制了北太平洋冬季气候态的表层流场图, 流场分布如图 1所示, 流速最大的区域出现在赤道附近, 流速为1~2m·s-1, 并且自东向西逐渐增大。表层流场基本符合风生环流理论, 南北赤道流是由赤道上的信风驱动的, 所以也称作信风流。在北半球副热带海区有对应副热带高压的反气旋(顺时针)大环流, 该大环流的南侧即为北赤道流。值得注意的是, 由于赤道无风带在3°~10°N范围内, 所以赤道流系并不关于赤道对称, SODA冬季流场图显示, 赤道附近0°~3°N范围内存在向西的南赤道流, 3°~10°N范围内存在向东的赤道逆流,10°~18°N为向西的北赤道流。
|
图 1 北太平洋表层冬季气候态流场 Fig.1 Surface current of winter climatology in the North Pacific |
根据STOMMEL的西向强化理论, 由于科氏参量随纬度升高而增大, 北太平洋西部有较强的北向西边界流, 即黑潮, 大洋西部的流线比较密集, 流速较大, 为1~2m·s-1, 而大洋东部的流线比较稀疏, 流速基本小于1m·s-1。黑潮是北赤道流的延续, 具有北赤道流高温的特征, 不断向高纬度地区输送热量, 影响着海况和气候。黑潮进入黄海的分支即为黄海暖流, 进入日本海的分支称为对马暖流。黑潮在35°N分出黑潮延伸体, 另一支向北流动直至与南向的寒流亲潮交汇。
0.2 太平洋年代际振荡太平洋年代际振荡(Pacific decadal oscillation, PDO)模态由MANTUA et al.[1]于1997年首次提出, 人们注意到PDO这一现象的契机是1976-1977年的年代际尺度突变对海洋生态系统造成了明显的影响:在之前的二十年, 阿拉斯加海域的大马哈鱼产量多于西北太平洋海域的大马哈鱼产量, 但是在20世纪六七十年代阿拉斯加海域的大马哈鱼产量突然开始减少, 而西北太平洋海域的大马哈鱼产量开始增加。科学家意识到这可能与太平洋的气候变化紧密相关。
北太平洋地区海气系统于1976-1977年、20世纪20年代和40年代均发生了年代际尺度的突变, 北太平洋海洋与大气低频的波动对北美和欧亚大陆的天气和气候均有显著影响[2-4]。PDO的暖位相是指北太平洋中西部海面温度(sea surface temperature, SST)异常偏冷, 而北美西部沿岸和热带中东太平洋异常偏暖的位相; PDO的冷位相则与之相反, 通过对20世纪的观测, PDO暖位相与全球变暖加速同期出现, 而PDO冷位相时全球变暖减缓甚至"停滞"[5]。PDO模态与ENSO类似, 但与ENSO的区别主要在于:1)PDO的周期更长, 通常为20~30a, 而ENSO的周期为2~7a; 2)ENSO的主信号在热带, 而PDO的主信号位于北太平洋[6]。
PDO不只是一个现象, 更是一系列的物理过程[7], PDO也可以通过海表面高度异常[8]或者北太平洋不同的生物要素的主要模态表现[9-11]。尽管PDO解释了北太平洋低频变化的最主要部分, 但北太平洋的年代际动力过程的体现还包括NPGO(North Pacific Gyre oscillation)气候模态。NPGO定义为180°~110°W, 25°~62°N范围内海表面高度异常EOF的第二模态, 它驱动着跨太平洋的物理和生物要素的变化, 如温度、盐度、海平面高度、营养盐、叶绿素等[12-13]。PDO和NPGO都有其对应的大气模态来源, 分别为AL(Aleutian Low)和NPO(North Pacific oscillation)[8, 12, 14]。AL定义为北太平洋海面气压的第一模态[15-16], NPO定义为北太平洋海面气压异常的第二模态[17-18], NPO影响着欧亚大陆和北美的气候, 尤其改变着台风路径、温度和降水[19-20]。
海气相互作用和温盐环流都可能导致海洋的年代际变率, 由于太平洋的温盐环流相比于大西洋很弱, 所以海气相互作用更可能是PDO的形成机制。目前对于PDO产生来源的讨论主要有以下3种观点:热带海气耦合系统、中纬度海气耦合系统、热带与中纬度的相互作用。但这3类观点均存在争议, 如认为PDO起源于热带海气耦合系统的理论无法解释PDO在中纬度更强这一现象, 中纬度海气耦合系统理论中用到的Latif-Barnett假说与观测事实不符等问题。此外, 副极地海洋涡旋对北太平洋的贡献、中纬度地区海气之间的正反馈机制、中纬度和热带之间的相互作用等问题仍需进一步研究[6]。气候模式为PDO的研究提供了一些补充方法, 近期GFDL气候模式揭示, PDO的多年代际时间尺度更可能来源于北太平洋热带外的海气耦合作用, 然后被热带的气候变化增强[21]。也就是说, 虽然热带在统计和观测意义上与PDO关系更密切, 但它并不是PDO的来源。利用"区域锁定"的方法, 模式的结果表明, 在北太平洋副极地地区, PDO的多年代际变化是由西向的海洋Rossby(罗斯贝)波导致的[21-22]。与现实海洋情况相比, 模式有一些不符之处, 比如模式中热带对北太平洋的影响比现实更弱[23-24]。未来应对模式进一步优化, 并发展高级的诊断分析方法来研究PDO。
气候系统中的非线性和随机因素使得PDO的预测非常困难, 不同区域对于不同的气候变化, PDO的可预测性尚不明确。基于模式的可预测性研究表明, 预测年际到年代际类似PDO变化的平均温度是有可能的, 但是预测降水等具有社会意义的变量长于年际尺度的变化则是几乎不可能的[25]。目前的研究[26]主要有以下几种结论:第一, 最先进的耦合气候模式中PDO的可预测性可以通过海洋中初始几年更精确的初始场而得到提高, 但是在更长的时间尺度上由温室气体和气溶胶等辐射强迫所主导; 第二, PDO在北太平洋的可预测性低于它的类似模态在北大西洋的可预测性, 这种预测性差异产生的原因尚不明确。最近的研究提出, SST等气候变量的年代际预测可以放在线性统计模型和最先进的动力气候模型中进行比较[15, 23]。
包括PDO在内的年代际气候变率的研究对于预测近期的气候变化非常重要, 并且对人类活动造成的全球变暖也有重要的调节作用, 能够吸收温室气体增加产生的热量, 将其带进深海[27]。年代际气候变率的研究已经有了重要进展, 但是仍有一些尚未解决的问题。其中一个重要的问题是, 年代际的气候变率是如何对全球变暖进行响应的, 陈幸荣等[28]研究表明, 海洋次表层也存在显著的年代际变率, 即PDO具有三维结构, 对PDO三维结构的研究有利于进一步认识北太平洋的年代际变率及其对全球变暖的响应, 对气候的年代际变化的预测也具有重要作用。为了更准确地反映海洋的年代际变化, 剔除由于海气相互作用对海表面温度带来的影响[29], 采用SODA资料垂直积分的上层海洋热含量来表征上层海洋的变化。内容具体安排如下:第1节对研究所使用的SODA数据和EOF分解、功率谱分析等方法进行介绍; 第2、3、4节是对空间模态和时间序列的分析; 第5节是研究的总结与讨论。
1 数据及方法 1.1 SODA数据简介及分析方法SODA数据的水平分辨率为0.5°×0.5°, 垂直分层有40层, SODA数据是由美国马里兰大学在20世纪90年代研发的海洋再分析资料, 与大气再分析资料相匹配, 同化了观测数据, 使结果更加准确[30]。本研究选取了时间序列为1815-2013年共199a不同深度的温度、流速及盐度资料, 主要使用了EOF分解和功率谱分析的方法。
1.2 Rossby波相速度的计算以科氏力随纬度的变化率, 即
1) 海水无辐散;
2) 水平流动, 并且三个方向的速度满足u>>v>>w;
3) 初始流动满足地转平衡且不随x轴变化, 并且
Rossby波相速度计算公式为:
| $ C = - \beta {\left( {\frac{1}{{m\pi \left| f \right|}}\int_{ - H}^0 {N\left( z \right){\rm{d}}z} } \right)^2} $ | (1) |
式中, H为深度,
首先进行热含量的计算, 由于热含量的值与深度和温度成比例, 用如下公式进行计算:
| $ Q\left( {x, y, z} \right) \sim \frac{{\int_{ - h}^0 {T\left( {x, y, z} \right){\rm{d}}z} }}{h} $ | (2) |
式中Q为热含量, h为深度, T为温度。由于PDO在冬季最为显著, 所以选用了每年1-3月的热含量进行平均, 得到时间序列长度为199 a的北太平洋热含量数据。为了剔除全球变暖的影响, 对数据进行了去趋势处理, 并针对不同的场点进行了纬度加权, 即每个场点乘以其对应纬度的余弦值, 以此来消除地球形状带来的影响。
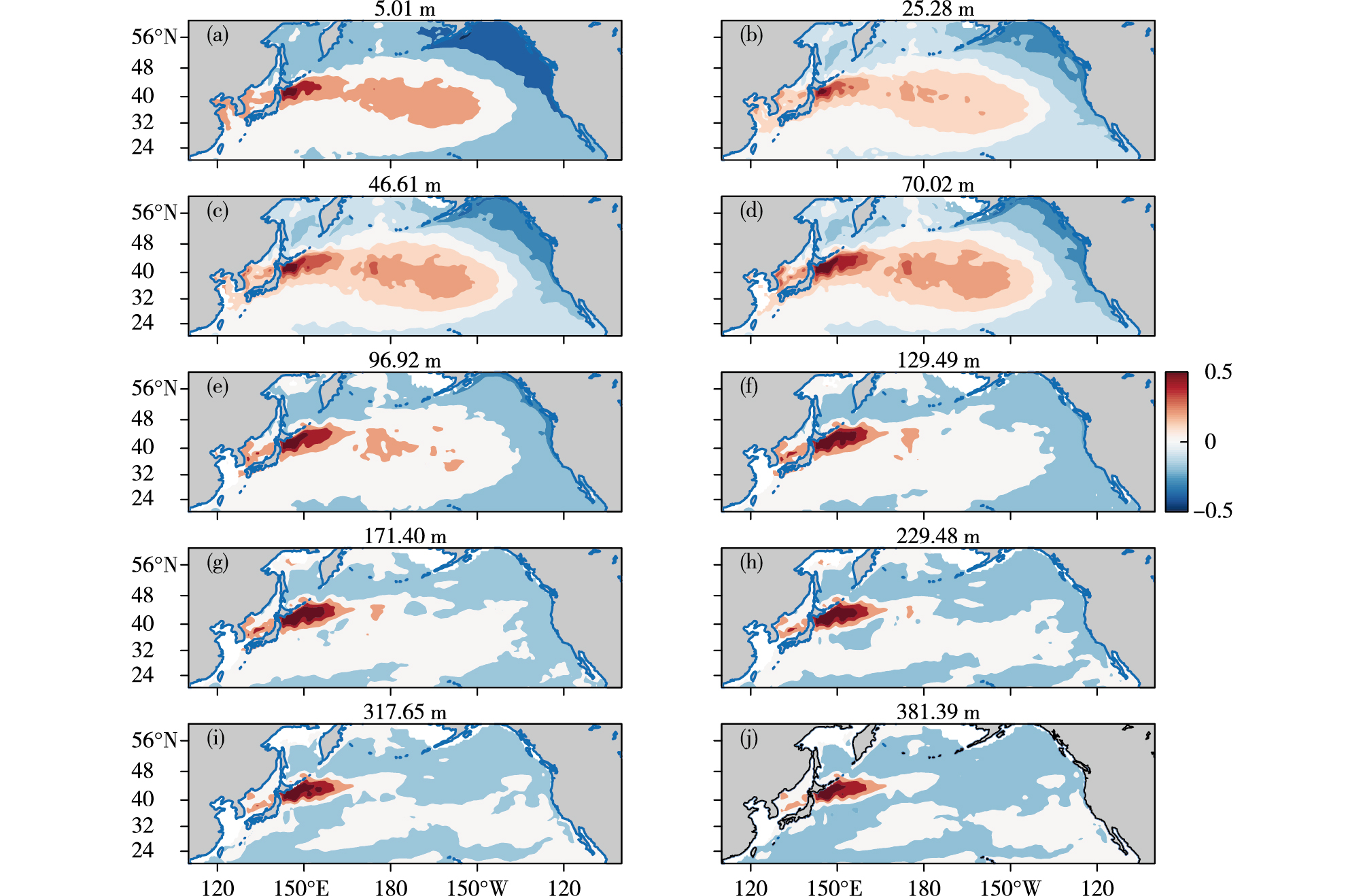
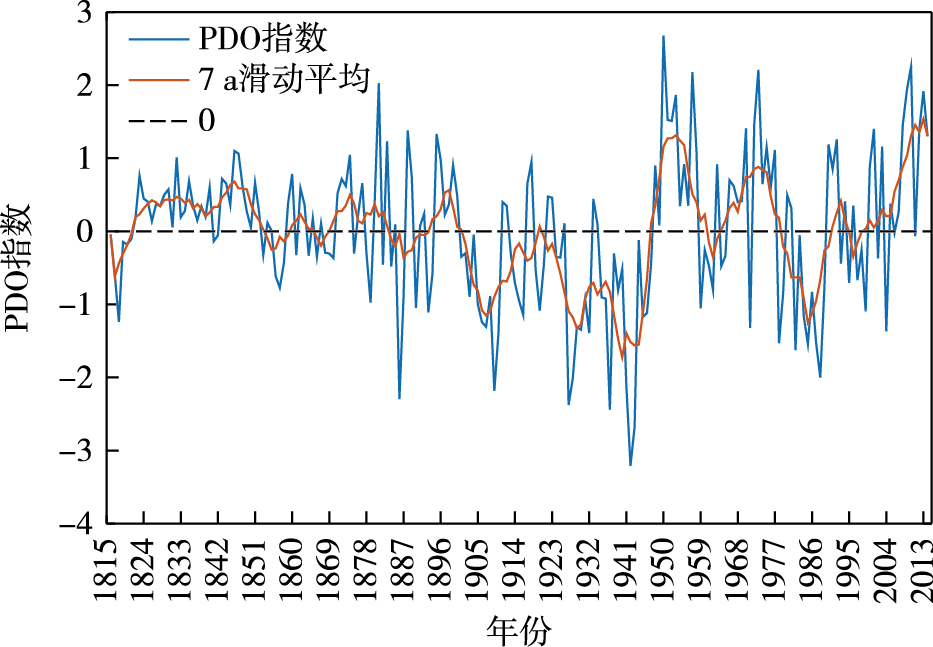
2 PDO的基本特征对20°~60°N范围内不同深度的热含量异常场进行EOF分解, 各层第一模态的空间分布如图 2所示。从图 2中可以看出, PDO呈现"马蹄形"的空间特征, 即北太平洋中西部的海温异常与周边海域的海温异常相反, 当北太平洋中西部为正的温度异常, 北美沿岸和副热带东部海域为负温度异常时, 称为PDO的冷位相, 反之称为PDO的暖位相。PDO不仅仅存在于表层, 而是具有三维结构, 在70m深度左右最显著, "马蹄形"的范围也更大。PDO最深可达300m。这种表层与次表层不一致的情况也导致了PDO预测的困难[31], 同时导致了和北太平洋不同大气变率之间相互作用有关的间断性过程[32]。尽管有了以上研究, 但究竟是什么机制导致了北太平洋的这种低预测性尚不明确, 甚至PDO在自然界中是否真是低预测性的也无定论[25]。PDO指数定义为表层EOF分解第一模态的时间序列, 如图 3所示, 为了滤掉高频的年际信号, 对其进行了7a滑动平均。图 3显示, PDO具有明显的年代际变化特征, 1947-1976年为PDO冷位相, 1925-1946年、1977年-20世纪90年代中期为PDO的暖位相, 其中1976、1977年北美洲西部海区从负温度异常到正温度异常的转相即为北太平洋大马哈鱼产量分布发生转变的原因。
|
图 2 各层海温EOF分解的第一模态(a. 5.01 m, b. 25.28 m, c. 46.61 m, d. 70.02 m, e. 96.92 m, f.129.49 m, g. 171.40 m, h. 229.48 m, i. 317.65 m, j. 381.39 m) Fig.2 The first EOF modes of oceanic temperature at different depths (a. 5.01 m, b. 25.28 m, c. 46.61 m, d. 70.02 m, e. 96.92 m, f.129.49 m, g. 171.40 m, h. 229.48 m, i. 317.65 m, j. 381.39 m) |
|
图 3 PDO指数(蓝线)及其7 a滑动平均(黄线)图 Fig.3 PDO index (blue line)and its 7-a moving average (yellow line) |
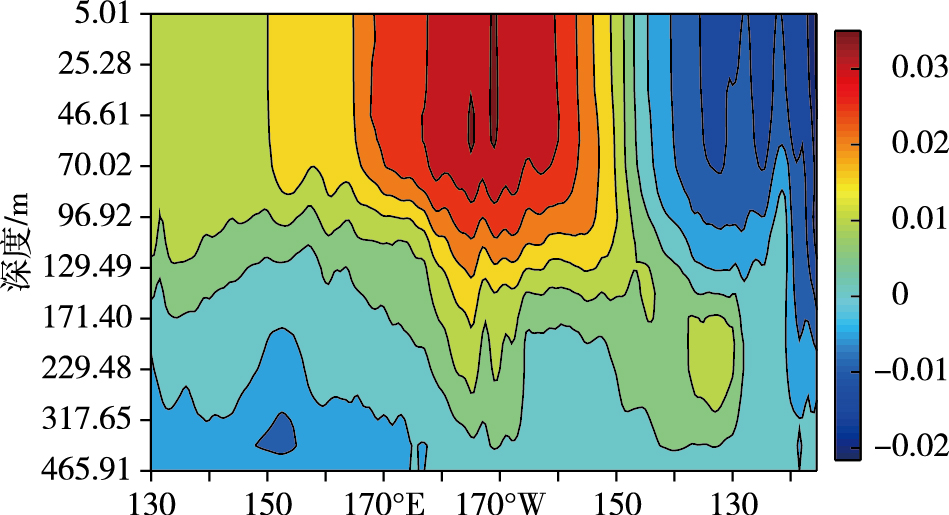
在32°N处取一个断面, 并对其进行EOF分解, 第一模态图(图 4)中可以看出, 北太平洋中部和东部具有反相变化的特征, 并且这种反相特征存在于300m以浅的海洋中。
|
图 4 EOF分解第一模态沿32°N深度剖面图 Fig.4 Cross section of the first mode of EOF decomposition along 32°N |
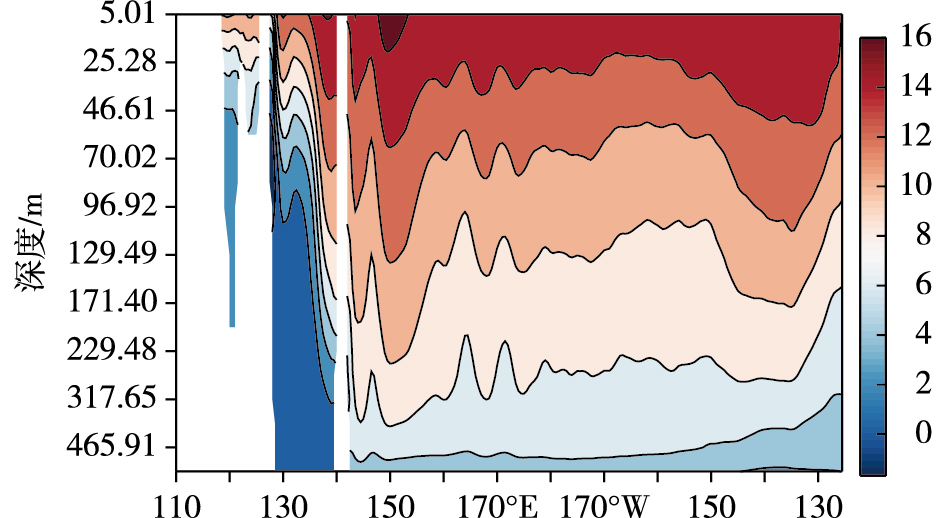
值得注意的是, 北太平洋西部的PDO信号比东部的PDO信号传递的深度更深, 尤其是在日本东部黑潮与亲潮交汇的地方。在40°N取一个东西向的温度断面(图 5)可以看出, 温度等值线自西向东倾斜, 北太平洋西部的温跃层相比于东部较深, 这意味着北太平洋西部的混合层更厚, 有利于信号传递到更深的深度。北太平洋东部温跃层的抬升是因为赤道上方常年盛行东风, 使得海洋上层的海水向西输送, 于是东部形成上升流补偿这部分水体, 温跃层也相应上升, 研究表明, 在东太平洋秘鲁沿岸海域温跃层最浅, 大约为40m[33]。
|
图 5 温度等值线(单位:℃)沿40°N深度剖面图 Fig.5 Cross section of isotherm (units:℃)along 40°N |
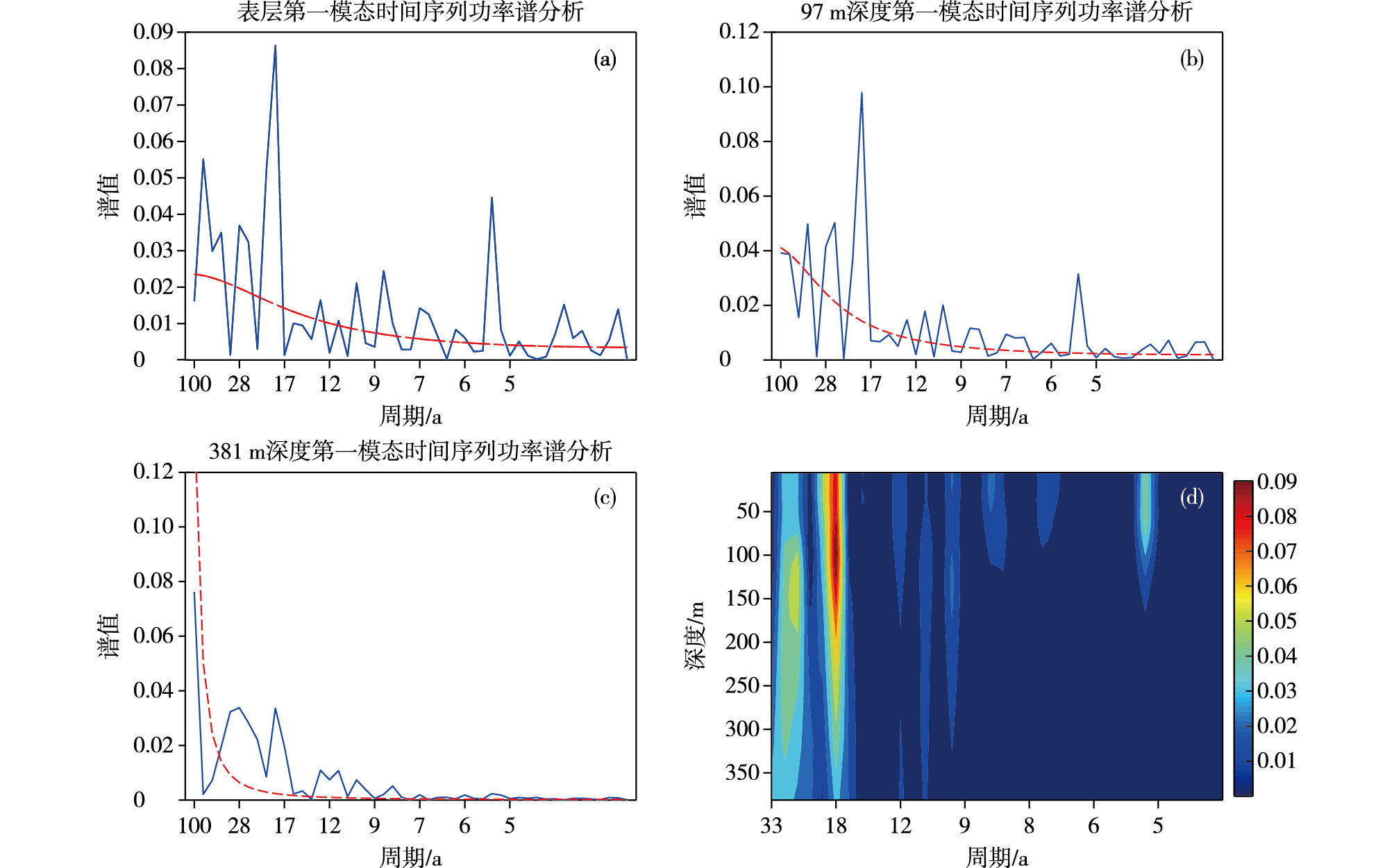
使用功率谱分析方法来分析PDO的周期性特征, 并进行了红噪声显著性检验(图 6), 从图 6中可以看出, PDO通过显著性检验的年际周期为5~6a, 通过显著性检验的年代际周期大约为18a, 相比于年代际周期, 年际周期可达到的深度较浅, 只在100m深度以浅存在年际信号, 而代际信号可以传至350m的深度。28a左右的周期在表层没有通过检验, 但是在表层以下至350m的深度内通过了显著性检验。值得注意的是, 年际信号的强度随深度的增加而减小, 而年代际信号则是在97m左右的次表层最强, 这与陈幸荣等[28]研究中PDO在次表层最强的结论一致。
|
图 6 表层(a)、97m(b)、381m(c)的功率谱分析(蓝实线为谱值, 红虚线为红噪声)和各周期的谱值随深度的变化(d) Fig.6 Power spectrum analysis (blue solid line for spectral value, red dashed line for red noise)at surface (a), 97 m (b), and 381 m(c)and change of spectrum value of different periods with depth (d) |
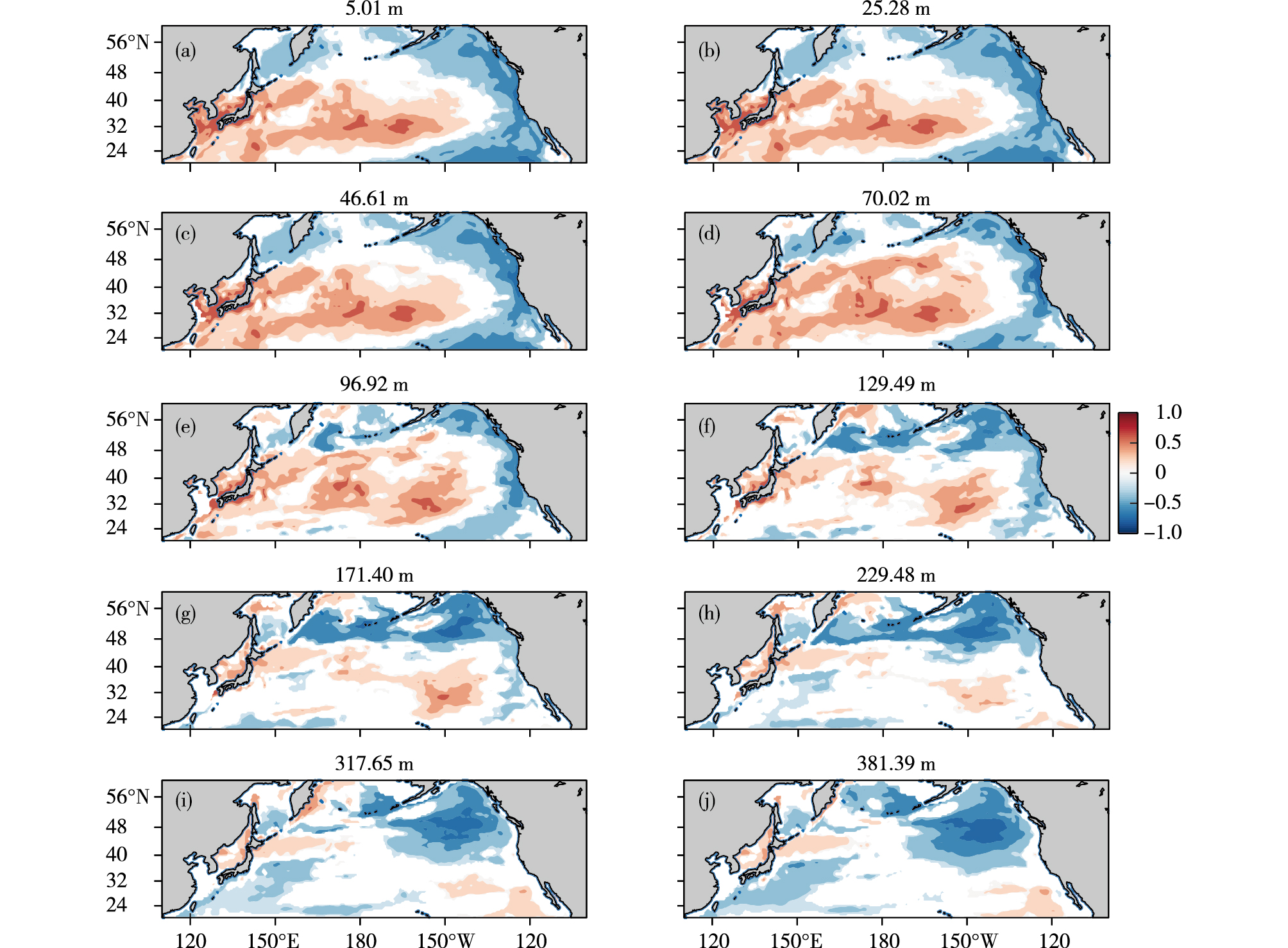
为了探究不同深度与PDO指数的关系, 对各层的热含量时间序列和PDO指数均进行了7a滑动平均的处理, 过滤掉年际信号, 然后进行相关性分析, 结果如图 7所示。北太平洋中西部的热含量时间序列和PDO指数的相关性与其周边海域热含量时间序列和PDO指数的相关性相反, 北太平洋中西部的热含量与PDO指数呈正相关关系, 北美沿岸海区热含量与PDO指数呈负相关关系。从图 7中可以看出, PDO的"马蹄形"结构在次表层范围最大, 该形态可以保持到300m左右的深度。
|
图 7 各层热含量时间序列与PDO指数的相关系数分布(a. 5.01 m, b. 25.28 m, c. 46.61 m, d. 70.02 m, e. 96.92 m, f.129.49 m, g.171.40 m, h. 229.48 m, i. 317.65 m, j. 381.39 m) Fig.7 Correlation coefficients between heat content time series and PDO index at different depths (a. 5.01 m, b. 25.28 m, c. 46.61 m, d.70.02 m, e. 96.92 m, f. 129.49 m, g.171.40 m, h. 229. 48 m, i.317.65 m, j.381.39 m) |
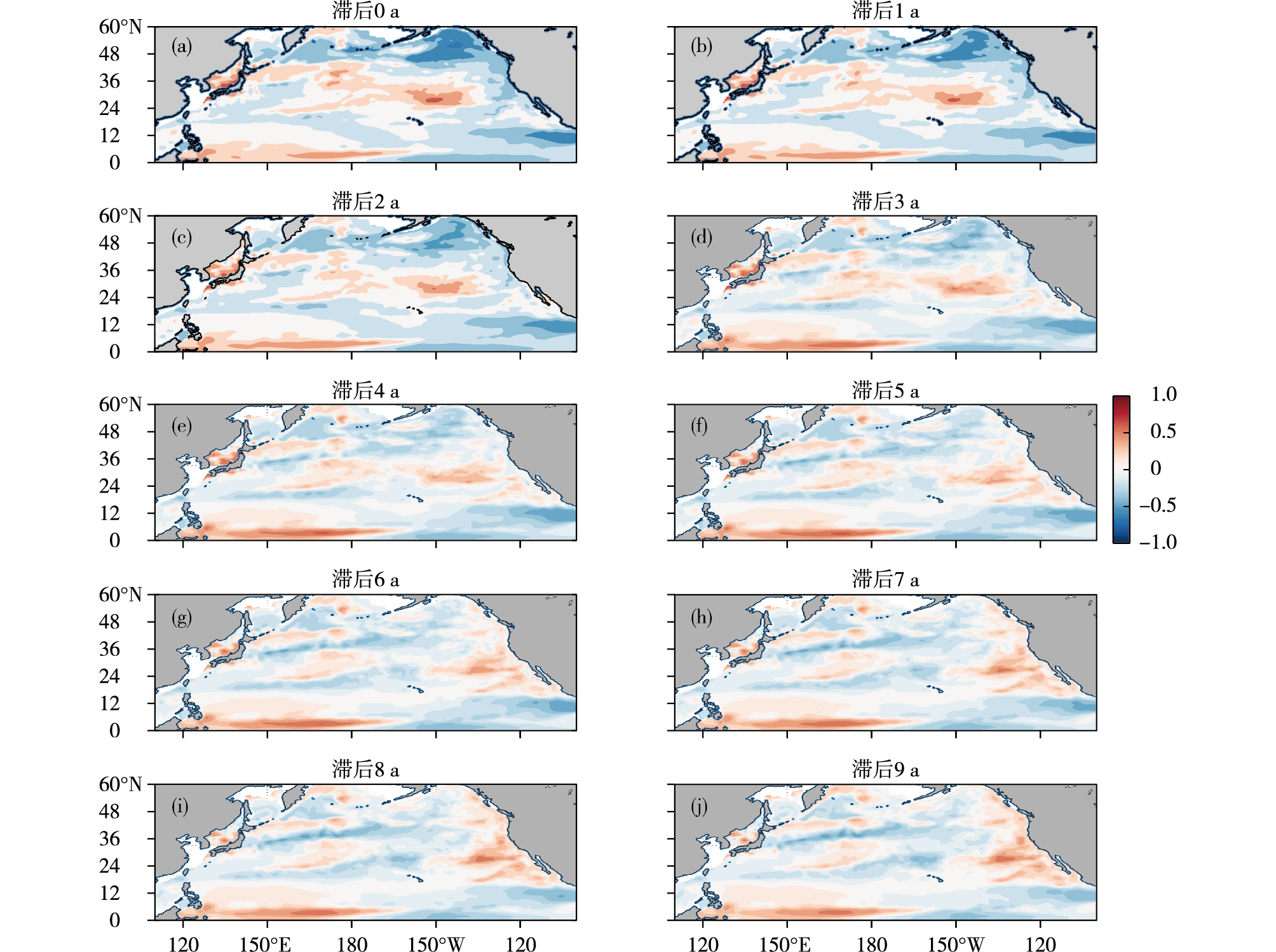
对300 m以浅水体的热含量时间序列与PDO指数进行了7a滑动平均, 然后将处理好的两组数据进行超前滞后相关性分析, 结果如图 8a-j所示。从同期相关图中可以看出, 赤道西部附近海域的热含量与PDO指数呈正相关关系, 赤道东部附近海域热含量与PDO指数呈负相关关系; 北太平洋中西部热含量与PDO指数呈正相关关系, 北美沿岸热含量与PDO指数呈负相关关系, 相关系数在50°~60°N、140°W附近较大。由于谱分析结果显示PDO的主要年代际周期为18a, 所以当300m以浅水体的热含量时间序列滞后PDO指数9a左右时, 相关系数的分布与同期相关系数的分布呈现反相的状态, 即北太平洋中西部海域相关系数为负, 北美沿岸海域相关系数为负。
|
图 8 300 m以浅水体的热含量与PDO指数的超前滞后相关系数分布(a.同期相关, b.热含量序列滞后1 a, c.热含量序列滞后2 a, d.热含量序列滞后3 a, e.热含量序列滞后4 a, f.热含量序列滞后5 a, g.热含量序列滞后6 a, h.热含量序列滞后7 a, i.热含量序列滞后8 a, j.热含量序列滞后9 a) Fig.8 Lead-lag correlation coefficients between heat content and PDO index in the ocean shallower than 300 m(a. contemporaneous correlation; b, c, d, e, f, g, h, i, and j for heat content lags PDO index by 1 a, 2 a, 3 a, 4 a, 5 a, 6 a, 7 a, 8 a, and 9 a, respectively) |
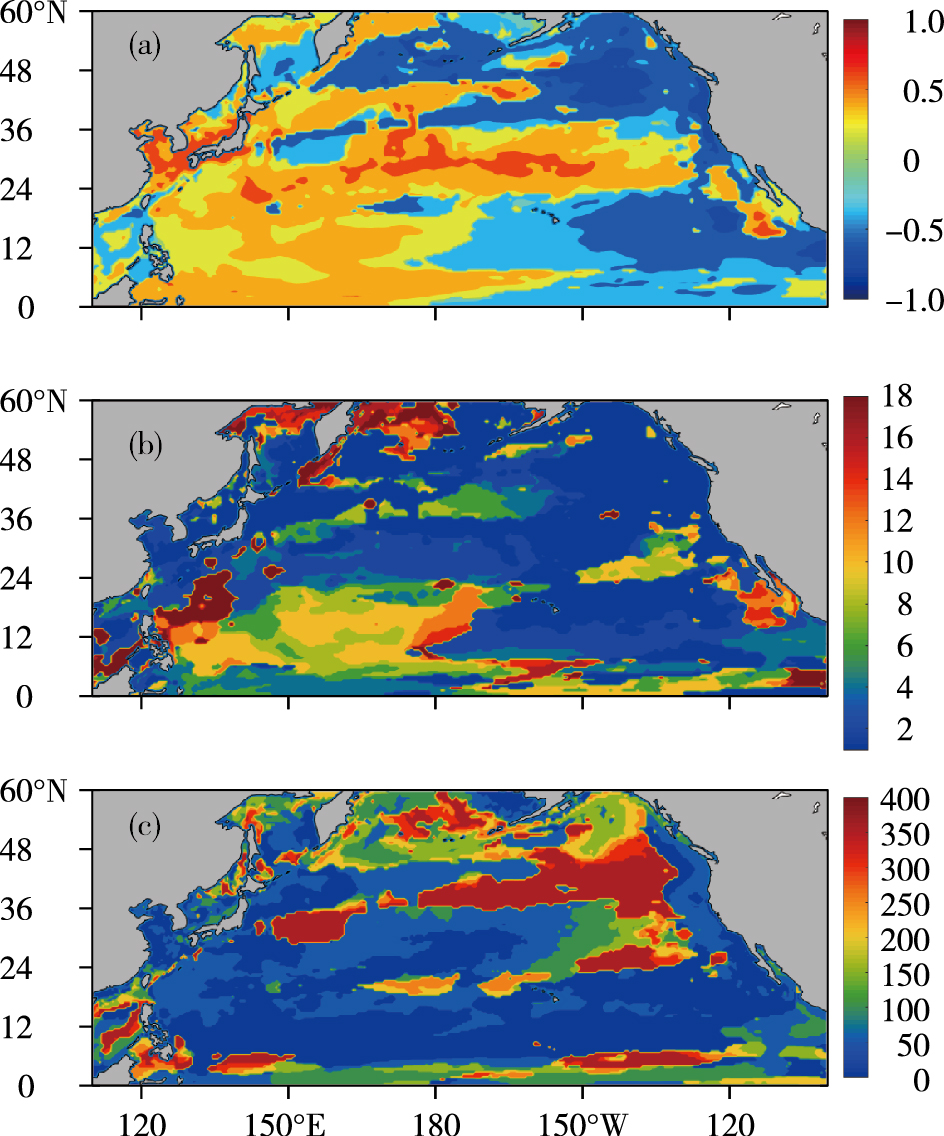
为了探究PDO的演变过程, 将每一层经过7 a滑动平均处理后的热含量时间序列与PDO指数进行超前滞后相关, 然后找出每一个场点对应的不同深度不同滞后时间的绝对值最大的相关系数, 绘制了图 9a, 该相关系数对应的滞后年数如图 9b所示, 该相关系数对应的深度如图 9c所示。图 9a显示, 最大的正相关系数分布在北太平洋中西部, 以及低纬度中西部海域, 负相关系数绝对值最大的区域分布在北太平洋北部、北美沿岸以及低纬度东部。图 9b显示最大相关系数基本出现在同期相关中, 在低纬度西部最大相关系数对应的滞后年数较大, 约为10a。图 9c显示北太平洋东北部的最大相关系数对应的深度较深。
|
图 9 某空间位置对应的所有深度不同滞后时间相关系数中绝对值最大的相关系数(a)及最大相关系数对应的滞后年数(b; 单位:a)和深度(c; 单位:m)分布 Fig.9 Correlation coefficient with the maximum absolute value among all the lag time correlation coefficients of different depths corresponding to a spatial position (a)and distribution of the number of lag year (b; units:a)and depth (c; units:m)corresponding to the maximum correlation coefficien |
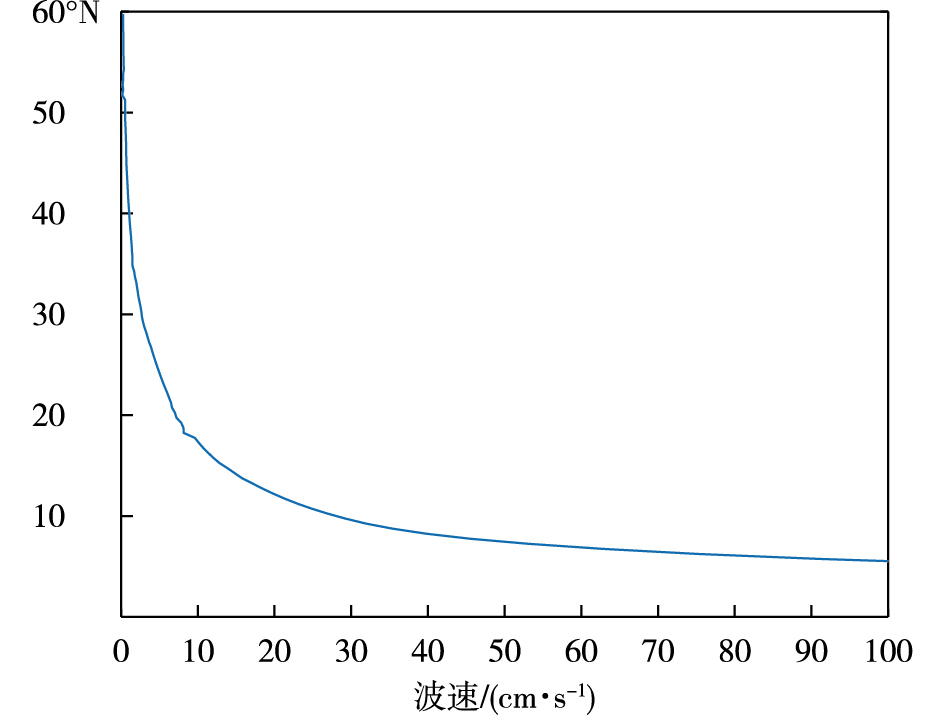
由于PDO信号的传播与Rossby波有关, 根据SODA数据集中的温度、盐度数据计算了Rossby波的相速度, 结果如图 10所示。计算结果显示, Rossby波向西传播, 速度随着纬度的升高而减小, 在10°N, Rossby波的速度大约为30cm·s-1, 在此纬度上Rossby波自东向西跨越海盆大概需要两年时间, 在40°N以北, Rossby波的速度几乎为零。基于Rossby波的速度分布特征, 推测低纬度的PDO信号的传播主要通过Rossby波向西传播, 而由于40°N以北海域Rossby波的波速很小, PDO信号可能是通过平流作用向东传播。在传播的过程中, PDO信号的深度也不断加深。对于PDO信号在中纬度的传播通道, ZHANG and DELWORTH[21]的模式结果表明, SST异常会导致风应力异常, 进而激发Rossby波, 在这个过程中会加大SST的异常, 是一个正反馈的过程。
|
图 10 沿180°E经向Rossby波相速度 Fig.10 Rossby wave phase speed along 180°E |
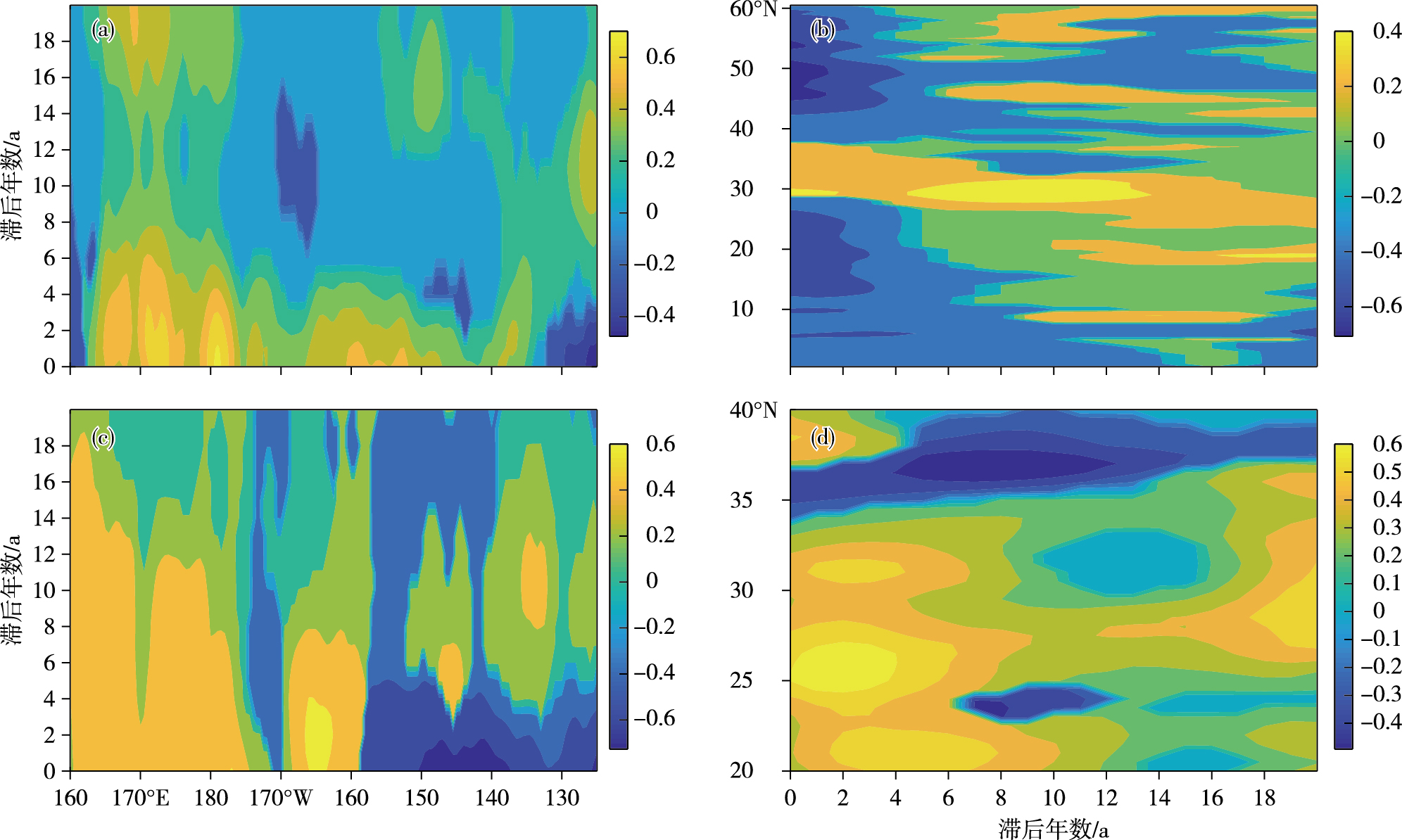
在北太平洋取四个断面, 分别位于36°N、46°N、140°W和145°E, 首先找出该经线或纬线上的每一个场点在不同深度上最大的相关系数, 然后绘制最大相关系数随滞后年数的变化, 结果如图 11所示。从图中可以看出, 36°N纬度上的PDO信号是向西传播的(图 11a), 这符合Rossby波在低纬度速度较大并且向西传播的特点; 在46°N纬度上PDO信号是向东传播的(图 11c), 这可能是平流作用的结果; 在145°E经向PDO信号向北传播(图 11d), 这是由于北赤道流在向西遇到大陆后有一部分向北传播; 在140°W经线上PDO信号向南传播(图 11b)。综上, 这反映了PDO信号在北太平洋副热带顺时针传播的特征, 与副热带环流的传播方向一致。该结论与前人的研究一致, ZHANG and LEVITUS[34]于1997年基于观测数据对北太平洋上层海洋年代际温度变化的演变过程和三维结构进行了描述, 其中一个主要的模态即次表层温度异常在副热带地区的顺时针旋转, 与副热带环流一致, 这个信号与中纬度海区温度异常的潜沉有关。
|
图 11 四个断面上对应的最大相关系数随滞后年数的变化(a. 36°N, b. 140°W, c. 46°N, d. 145°E) Fig.11 Change of maximum correlation coefficient as lag year increases at 4 sections (a. 36°N, b. 140°W, c. 46°N, d. 145°E) |
为了避免海面海气相互作用的强烈调制, 更准确地得到PDO的特征, 利用SODA数据资料基于热含量对PDO的结构以及传播特征进行了研究, 研究结论主要有以下几点:
1) PDO不仅仅存在于海洋表层, 而是具有三维结构, 在海洋表层以下也存在"马蹄形"模态的年代际变化, 深度可达300m, 在70m左右的次表层PDO的信号最强、"马蹄形"范围最大, 此结论与前人的研究基本一致。
2) 各层热含量与PDO指数的相关系数反映了PDO在70m左右次表层存在最强的三维结构特征, 并且热含量与PDO指数的相关性可持续至350 m深度。
3) PDO中包含的年际周期为5~6a, 年代际周期大约为18a, 年代际周期在100m左右次表层最强, 深度可达350m。相比于年代际周期, 年际周期的谱值随深度的增加递减, 存在的深度也比年代际周期浅, 大约为100m深度。
4) 300 m以浅水体的热含量与PDO指数的超前滞后相关结果表明, 在热含量时间序列滞后9a时, 相关系数分布与同期相关系数分布基本反相, 即同期相关系数在北太平洋中西部为正, 在北美沿岸海域为负, 滞后9a的相关系数在北太平洋中西部为负, 北美沿岸海域为正, 这符合谱分析结果中年代际周期为18a的周期特征。
5) Rossby波是向西传播的, 其波速随着纬度的升高而减小, 不同纬度上Rossby波的波速差距较大, 在10°N波速约为30cm·s-1, 在40°N以北波速几乎为0。
6) PDO信号在低纬度向西传播, 在高纬度向东传播, 并且在传播过程中信号深度不断加深。Rossby波均为向西传播, 只是在较高纬度传播速度过小, 对于PDO的信号传播起到的作用不大, 所以在40°N附近, PDO信号的向东传播可能是平流的作用。陈幸荣等[28]基于CCSM3模式的研究结果与本研究结果有所差异, 其研究显示最大相关系数对应的滞后年数较大的区域位于中纬度海域。
7)36°N、46°N、140°W和145°E四个断面上最大相关系数随滞后年数的变化表明, PDO信号在副热带顺时针传播。
本研究工作的不足之处在于不够深入, 仅局限于北太平洋的年代际变化, 没有对PDO的形成和影响机制进行更具体的探讨, 也没有与模式的结果进行对比。下一步工作应结合模式数据对比分析, 并针对不同海域进行类似的研究。
| [1] |
MANTUA N J, HARE S R, ZHANG Y, et al. A pacific interdecadal climate oscillation with impacts on salmon production[J]. Bull Amer Meteor Soc, 1997, 78(6): 1069-1079. DOI:10.1175/1520-0477(1997)078<1069:APICOW>2.0.CO;2 |
| [2] |
ALEXANDER M A, BLADEI, NEWMAN M, et al. Theatmospheric bridge: The influence of ENSO teleconnections on air-sea interaction over the global oceans[J]. J Climate, 2002, 15(16): 2205-2231. DOI:10.1175/1520-0442(2002)015<2205:TABTIO>2.0.CO;2 |
| [3] |
DESER C, PHILLIPS A S, HURREL J W. Pacific interdecadal climate variability:Linkages between the tropics and the North Pacific during boreal winter since 1900[J]. J Climate, 2004, 17(16): 3109-3124. DOI:10.1175/1520-0442(2004)017<3109:PICVLB>2.0.CO;2 |
| [4] |
LIU Z Y, FAN L, SHIN S I, et al. Assessing atmospheric response to surface forcing in the observations Part II:Cross validation of seasonal response using GEFA and LIM[J]. J Climate, 2012, 25(19): 6817-6834. DOI:10.1175/JCLI-D-11-00630.1 |
| [5] |
ENGLAND M H, MCGREGOR S, SPENCE P, et al. Recent intensification of wind-driven circulation in the Pacific and the ongoing warming hiatus[J]. Nat Clim Change, 2014, 4(3): 222-227. |
| [6] |
杨修群, 朱益民, 谢倩, 等. 太平洋年代际振荡的研究进展[J]. 大气科学, 2004, 28(6): 979-992. DOI:10.3878/j.issn.1006-9895.2004.06.15 |
| [7] |
NEWMAN M, ALEXANDER M A, AULT T R, et al. The Pacific decadal oscillation, revisited[J]. J Climate, 2016, 29(12): 4399-4427. DOI:10.1175/JCLI-D-15-0508.1 |
| [8] |
CHHAK K C. Forcing of low-frequency ocean variabilityin the Northeast Pacific[J]. J Climate, 2009, 22(5): 1255-1276. DOI:10.1175/2008JCLI2639.1 |
| [9] |
HARE S R, MANTUA N J, FRANCISR C. Inverse production regimes: Alaska and West Coast Pacific salmon[J]. Fisheries, 1999, 24(1): 6-14. DOI:10.1577/1548-8446(1999)024<0006:IPR>2.0.CO;2 |
| [10] |
MARTINEZ E, ANTOINE D, D'ORTENZIO F, et al. Climate-driven basin-scale decadal oscillations of oceanic phytoplankton[J]. Science, 2009, 326(5957): 1253-1256. DOI:10.1126/science.1177012 |
| [11] |
HARE S R, MANTUA N J. Empirical evidence for North Pacific regime shifts in 1977 and 1989[J]. Prog Oceanogr, 2000, 47((2 / 3 / 4)): 103-145. |
| [12] |
LORENZO E D, SCHNEIDER N, COBB K M, et al. North Pacific Gyre oscillation links ocean climate and ecosystem change[J]. Geophys Res Lett, 2008, 35(8): 1-6. |
| [13] |
LORENZO E D, FIECHTER J, SCHNEIDER N, et al. Nutrient and salinity decadal variations in the central and eastern North Pacific[J]. Geophys Res Lett, 2009, 36(14): 61-65. |
| [14] |
LORENZO E D, COBB K M, FURTADO J C, et al. Central Pacific El Ni o and decadal climate change in the North Pacific Ocean[J]. Nat Geosci, 2010, 3(11): 762-765. DOI:10.1038/ngeo984 |
| [15] |
NEWMAN M, COMPO G P, ALEXANDER M A. ENSO- forced variability of the Pacific decadal oscillation[J]. J Climate, 2003, 16(23): 3853-3857. DOI:10.1175/1520-0442(2003)016<3853:EVOTPD>2.0.CO;2 |
| [16] |
SCHNEIDER N, CORNUELLE B D. The forcing of the Pacific decadal oscillation[J]. J Climate, 2005, 18(18): 4355-4373. |
| [17] |
WALKER G T. World weather[J]. Quart J Roy Meteor Soc, 1928, 54(226): 79-87. |
| [18] |
ROGERS J C. The North Pacific Oscillation[J]. J Climate, 1981, 1(1): 39-57. |
| [19] |
SEAGER R, HARNIK N, ROBINSON W A, et al. Mechanisms of ENSO: Forcing of hemispherically symmetric precipitation variability[J]. Quart J Roy Meteor Soc, 2010, 131(608): 1501-1527. |
| [20] |
LINKIN M E, NIGAM S. The North Pacific Oscillation- west Pacific teleconnection pattern: Mature-phase structure and winter impacts[J]. J Climate, 2008, 21(9): 1979-1997. |
| [21] |
ZHANG L P, DELWORTH T L. Analysis of the characteristics and mechanisms of the Pacific decadal oscillation in a suite of coupled models from the Geophysical Fluid Dynamics Laboratory[J]. J Climate, 2015, 28(19): 7678-7701. DOI:10.1175/JCLI-D-14-00647.1 |
| [22] |
ZHONG Y F, LIU Z. On the mechanism of Pacific multidecadal climate variability in CCSM3:The role of subpolar North Pacific Ocean[J]. J Phys Oceanogr, 2009, 39(9): 2052-2076. DOI:10.1175/2009JPO4097.1 |
| [23] |
NEWMAN M. Interannual to decadal predictability of tropical and North Pacific sea surface temperatures[J]. J Climate, 2007, 20(11): 2333-2356. DOI:10.1175/JCLI4165.1 |
| [24] |
NEWMAN M. An empirical benchmark for decadal forecasts of global surface temperature anomalies[J]. J Climate, 2013, 26(14): 5260-5269. DOI:10.1175/JCLI-D-12-00590.1 |
| [25] |
LIU Z, LORENZO E D. Mechanisms and predictability of pacific decadal variability[J]. Current Climate Change Reports, 2018, 4(2): 1-17. |
| [26] |
DOBLAS-REYES F J, ANDREU-BURILLO I, CHIKAMOTO Y, et al. Initialized near-term regional climate change prediction[J]. Nat Commun, 2013, 4(7): 1715-1724. |
| [27] |
LIU Z, YUN L, WU L, et al. Seasonal and long-term atmospheric responses to reemerging North Pacific Ocean variability: A combined dynamical and statistical assessment[J]. J Climate, 2007, 20(6): 955-980. DOI:10.1175/JCLI4041.1 |
| [28] |
陈幸荣, 王彰贵, 巢纪平, 等. PDO的三维空间结构和时间演变征[J]. 海洋学报, 2011, 33(6): 19-28. |
| [29] |
王东晓, 刘征宇. 太平洋年代际海洋变率的信号通道[J]. 科学报, 2000, 45(8): 808-815. |
| [30] |
CARTON J A, GIESE B S. A reanalysis of ocean climate using simple ocean data assimilation (SODA)[J]. Mon Wea Rev, 2008, 136(8): 2999-3017. DOI:10.1175/2007MWR1978.1 |
| [31] |
MOCHIZUKI T, ISHII M, KIMOTO M, et al. Pacific decadal oscillation hindcasts relevant to near-term climate prediction[J]. Proc Nati Acad Sci USA, 2010, 107(5): 1833-1837. DOI:10.1073/pnas.0906531107 |
| [32] |
SUGIURA N, AWAJI T, MASUDA S, et al. Potential for decadal predictability in the North Pacific region[J]. Geophys Res Lett, 2009, 36(20): 20701. DOI:10.1029/2009GL039787 |
| [33] |
高晓倩. 热带太平洋温跃层深度的年代际变化特征及原因[J]. 青岛:国家海洋局第一海洋研究所, 2015. |
| [34] |
ZHANG R H, LEVITUS S. Structure and cycle of decadal variability of upper ocean temperature in the North Pacific[J]. J Climate, 1997, 10(4): 710-727. DOI:10.1175/1520-0442(1997)010<0710:SACODV>2.0.CO;2 |
 2020, Vol. 40
2020, Vol. 40


