2. 高唐县气象局,山东 高唐 252800
2. Gaotang Meteorological Bureau, Gaotang 252800, China
雾是一种灾害性天气,雾的出现会使能见度下降,导致交通系统瘫痪,严重影响人们出行和运输业。我国对雾的研究起步较晚,目前准确地预报雾还有一定难度,预报员多凭借经验对雾进行短时效的主观预报。近些年随着对雾的各项研究工作[1-2]深入开展,不少学者尝试用天气学[3-4]与统计学[5-7]原理对雾进行预报。陈东辉等[3]总结了雾天气出现时高空与地面天气形势并与T639输出的模式诊断量相结合,以此预报未来1~3 d环渤海雾天气。周须文等[7]利用相关分析法找出与低能见度雾相关的气象因子,建立了低能见度雾的分级预报方程。
这些方法可以提供雾的有、无二分类预报或者是分级预报,无法给出雾出现时能见度的定量预报,这已经不能满足公众日益增长的气象服务需求。例如,高速公路交通管理制度标准给出明确要求:当能见度低于200 m时应实行限速管制,当能见度低于50 m时应当关闭。针对出现雾天气时低能见度的预报,国外学者根据大量观测数据和试验设计了不少能见度诊断方案,如Kunkel方案[8]、Stoelinga and Warner(SW)方案[9]、Gultepe方案[10-11]、NCEP的Rapid Update Cycle(RUC)方案[12]以及Forecast Systems Laboratory(FSL)方案[13]等,这些能见度方案利用模式输出的液态含水量、相对湿度与温度露点差等要素值计算能见度,从而为雾出现时能见度的定量预报提供了参考依据。国内学者利用这些方案对低能见度雾进行初步预报试验,夏凡和李昌义[14]比较了SW方案、RUC方案与FSL方案对雾和能见度的预报效果。高荣珍等[15]利用Combined Visibility(CVIS)方案将SW方案与FSL方案进行融合,结果显示融合方案对雾的预报效果优于任何一种单一方案。
上面提到的能见度方案均是由国外学者根据大量观测试验得到,然而不同区域气候特征存在差异,因此这些方案对本地的能见度与雾是否有可预报性还要进一步验证。林艳等[16]利用太原机场2009年冬季能见度与相对湿度数据改进了RUC方案的计算公式,改进后的方案预报能见度与观测值更为接近。管琴等[17]在RUC方案加入了空气污染对能见度的影响。夏凡和李昌义[14]在研究中还发现,除了计算公式,方案所包含的气象要素的准确性也会影响到雾与能见度的预报效果。本文针对这些问题,对业务上常用的SW与FSL两种能见度方案进行改进,以期提高各方案对雾与能见度的预报效果,为预报员提供更加客观准确的预报产品。
1 资料与方法简介 1.1 资料简介山东省气象科学研究所于2015年实时业务运行逐小时更新循环(hourly update cycle,HUC)模式,使用国家气象信息中心下发的0.5°×0.5°的T639模式数据作为初始条件和边界条件;模拟区域的中心经纬度为116.5°E,36.5°N;垂直分层为51层;双层嵌套,外、内层网格的分辨率分别为27 km与9 km,本文选取第二层模式资料作为预报数据。观测资料为山东123个国家级气象观测站(以下简称“山东123站”)数据。选取2015—2016年山东10次低能见度雾天气个例(表 1),对应选取雾天气出现前一天20:00(北京时,下同)作为HUC模式起报时刻,将0~24 h时效,即20:00—次日20:00的模式数据作为预报场。
|
|
表 1 2015—2016年10次雾天气个例的出现日期 Table 1 Dates of 10 fog cases that occurred from 2015 to 2016 |
STOELINGA and WARNER[9]基于大气中各液态含水量的密度与消光系数的经验关系,给出了SW方案的计算公式,如下:
| $ V i s=\frac{-\ln (0.02)}{\beta} $ | (1) |
式中,-ln(0.02)是经验系数,β=βcw+βrw+βci+βsn,βcw、βrw、βci与βsn分别代表模式预报的云水(cw)、雨水(rw)、云冰(ci)与雪(sn)含量的消光系数,均是三维预报量,能见度值的计算只用到模式最底层的液态含水量,是二维预报量,各液态含水量密度与消光系数的经验关系由表 2给出,其中Ccw、Crw、Cci与Csn分别表示云水、雨水、云冰与雪的密度。
|
|
表 2 SW方案中各种液态水的密度(单位:g·m-3)与消光系数(单位:km-1)的关系 Table 2 Relationship between concentration (units: g·m-3) of liquid water and extinction coefficient (units: km-1) in SW scheme |
GULTEPE et al.[10]试验发现,在固定的空气体积中不改变水凝物的含量,能见度与水凝物粒子数存在较强的负相关,在SW方案的基础上,GULTEPE et al.[10]给出了综合考虑空气中水凝物含量和水凝物粒子数浓度的能见度计算公式,如下:
| $ V i s=\frac{1.002}{\left(C \times N_{d}\right)^{0.6473}} $ | (2) |
式中,C=Ccw+Crw+Cci+Csn,Nd表示液态水粒子浓度。在大量外场观测试验分析的基础上,GULTEPE et al.[11]又对公式(2)进行改进,改进后的公式如下:
| $ V i s=\frac{0.87706}{\left(C \times N_{d}\right)^{0.49034}} $ | (3) |
GULTEPE and ISAAC[18]研究发现Nd与温度T存在如下拟合关系:
| $ N_{d}=-0.071 T^{2}+2.213 T+141.56 $ | (4) |
本文将公式(3)定义为SW-V1方案。将式(4)代入式(3),与SW方案计算公式相比,当温度在-10~30 ℃之间时,雨水与雪这两项的系数变大,SW-V1方案增强了雨水与雪对能见度的削弱作用。
1.2.2 FSL方案改进方法FSL方案由美国国家海洋和大气管理局(National Oceanic & Atmospheric Administration,NOAA)的预报系统实验室研发,该方案基于大量观测试验,利用能见度和温度露点差与相对湿度的关系进行拟合,公式如下:
| $ F S L=6000 \times \frac{t-t_{\mathrm{d}}}{V_{\mathrm{rh}}^{1.1} 5} $ | (5) |
式中,t(单位:℃)、td(单位:℃)与Vrh(单位:%)分别表示温度、露点温度与相对湿度。夏凡和李昌义[14]研究指出,FSL方案对相对湿度误差较敏感,相对湿度误差较大的试验,FSL方案对雾与能见度的预报效果均较差。
相对湿度是由温度与露点温度共同计算,本文利用递减平均法分别对温度与露点温度进行订正,该方法可以不断对模式误差进行更新来降低模式系统误差,邱学兴等[19]利用该方法对国家气象中心T639预报系统的500 hPa高度、850 hPa温度与2 m温度成功进行订正,递减平均法计算流程如下:
第一步为误差估计。
| $ e_{i}(t)=f_{i}(t)-o_{i}(t) $ | (6) |
式中,oi(t)表示t时刻第i站的观测值,fi(t)表示对应t时刻第i站的预报值,ei(t)表示t时刻第i站的误差值。
第二步为误差累加。
选择适当的权重系数,将前24 h各预报时效的误差值累加到前48 h相同预报时效的误差值,得到更新后各个预报时效的误差值。
| $ E_{i}(t)=(1-w) E_{i}(t-2)+w e_{i}(t-1) $ | (7) |
式中,Ei(t)为对应t时刻第i站更新后的误差值,w为权重系数。当t=1,对式(7)进行冷启动,即w=1,Ei(t-2)=0,经过一段时间的迭代累加,Ei(t)变化较小,本文误差计算需要的迭代累加时间为两个月。
第三步为误差改进。
将t时刻对应的预报值减去更新误差值得到最终的预报值。
| $ F_{i}(t)=f_{i}(t)-E_{i}(t) $ | (8) |
式中,Fi(t)为t时刻第i站订正后的预报值。
图 1给出了权重系数0.01~0.20对应的HUC模式2 m预报温度的山东123站0~24 h预报时效平均绝对误差(mean absolute error,MAE)[14],随着系数的增大,MAE有减小的趋势,在0.12后MAE变化较小,最小值对应的系数为0.11,因此,选用0.11作为HUC模式递减平均法的订正权重系数。

|
图 1 权重系数0.01~0.20对应的山东123个站点0~24 h时效2 m预报温度平均绝对误差(MAE)的时效平均(单位:℃) Fig.1 Mean MAE of 0-24 h forecast temperature at 2 m in the 123 stations of Shandong (units: ℃) corresponding to the weight coefficient between 0.01 and 0.20 |
利用订正后的温度与露点温度分别计算饱和水汽压与水汽压(公式(9)),然后计算相对湿度(公式(10)),其中t与td分别表示温度与露点温度,es与e分别表示饱和水汽压与水汽压,Vrh为相对湿度。利用订正后的温度、露点温度和相对湿度并基于FSL方案重新计算能见度(公式(5)),本文将其定义为FSL-V1方案。
| $ \begin{array}{l} e_{s}=6.11 \times 10^{7.5 t /(t-35.85+273.15)} \\ e=6.11 \times 10^{7.5 t_{\mathrm{d}} /\left(t_{\mathrm{d}}-35.85+273.15\right)} \end{array} $ | (9) |
| $ V_{\mathrm{rh}}=\frac{e}{e_{s}} \times 100 \% $ | (10) |
CVIS原理是基于SW与FSL方案计算能见度,取两者最小值[20]。公式如下:
| $ \mathrm{CVIS}=\min (\mathrm{SW}, \mathrm{FSL}) $ | (11) |
本文利用MAE[14]来评估各方案改进前后对能见度的预报效果,使用这种评估方法可以避免正负误差相互抵消。
以能见度低于1 km的站点判定为有雾(包括大雾、浓雾与强浓雾)出现,使用二分类事件评估方法对雾的预报进行检验,方法主要包括TS(threating score)评分与空报率(false alarm rate,FAR)(公式(12)—(13))。由表 3可见,式(12)与式(13)中,a表示预报正确的站点数;b表示空报的站点数;c表示漏报的站点数;d表示观测与预报均没有出现雾的站点数。
| $ T S=\frac{a}{a+b+c} \times 100 \% $ | (12) |
| $ F A R=\frac{b}{b+d} \times 100 \% $ | (13) |
|
|
表 3 雾预报检验分类表 Table 3 Verification of fog forecast |
为避免赘述,本文只对2015年11月13—14日雾天气的模式预报(13日20时起报,进行24 h预报)结果进行详细分析。由地面填图(图略)来看,13日20时,地面形势较稳定,山东处于均压场中,以北风为主,风速1~2 m·s-1,温度露点差较小,全省大部地区在1 ℃左右,除了鲁西北西部与鲁西南地区,其他地区有0~5 mm降水,这些条件均有利于雾的出现。14日08时,山东全省大部地区温度露点差依旧保持在1 ℃左右,降水落区主要在鲁西北东部、鲁中东部与鲁东南地区,雨量在0~1 mm。
2.1 SW方案改进效果评估由2015年11月13日23时实况(图 2a)可以看出,雾出现的站点主要集中在鲁西北、鲁中北部和半岛西部,SW方案(图 2b)预报出的雾站点零星分布在鲁西北、鲁南与半岛地区。SW-V1(图 2c)方案预报出雾站点明显多于SW方案,预报出鲁西北大部分出雾站点,但是在鲁南出现空报。在实况中,这一区域多为能见度1~3 km的轻雾区。
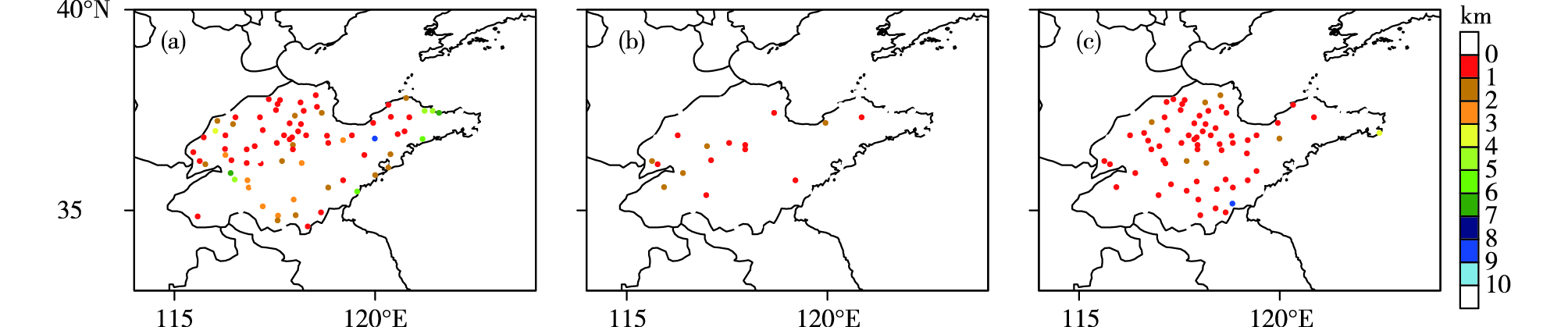
|
图 2 2015年11月13日23时观测站点雾分布(a)、SW(b)与SW-V1(c)方案预报站点雾分布(能见度小于1 km) Fig.2 Distribution of stations with observed fog (a) and distribution of stations with forecast fog by SW scheme (b) and SW-V1 scheme (c) at 23:00 BST 13 November 2015 (visibility less than 1 km) |
由SW与SW-V1预报的0~24 h能见度的MAE(图 3)可以看出,改进方案预报的能见度在0~12 h预报时效MAE值较SW方案降低,在13~24 h预报时效,SW-V1方案预报能见度的MAE较SW方案改进效果不明显。
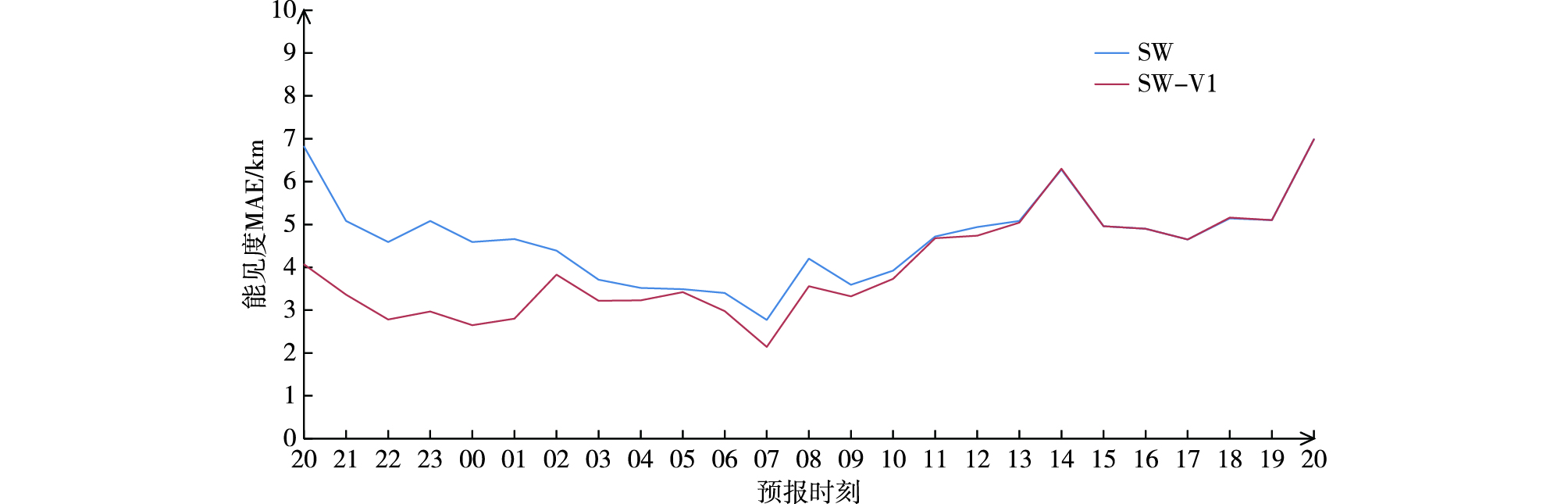
|
图 3 2015年11月13日20时起报0~24 h预报时效SW与SW-V1方案预报能见度的平均绝对误差(MAE;单位:km) Fig.3 MAE of 0-24 h visibility forecast(units: km) by SW scheme and SW-V1 scheme initiated at 20:00 BST 13 November 2015 |
SW方案改进前后预报雾的TS评分(图 4a)显示,SW-V1方案在0~9 h预报时效有正效果,尤其在0~5 h预报时效,TS评分由10%~20%提高到50%~60%,改进前后方案在16~24 h预报时效TS评分为0。空报率分布图(图 4b)显示,SW-V1方案在大部分预报时效略高于或等于SW方案。
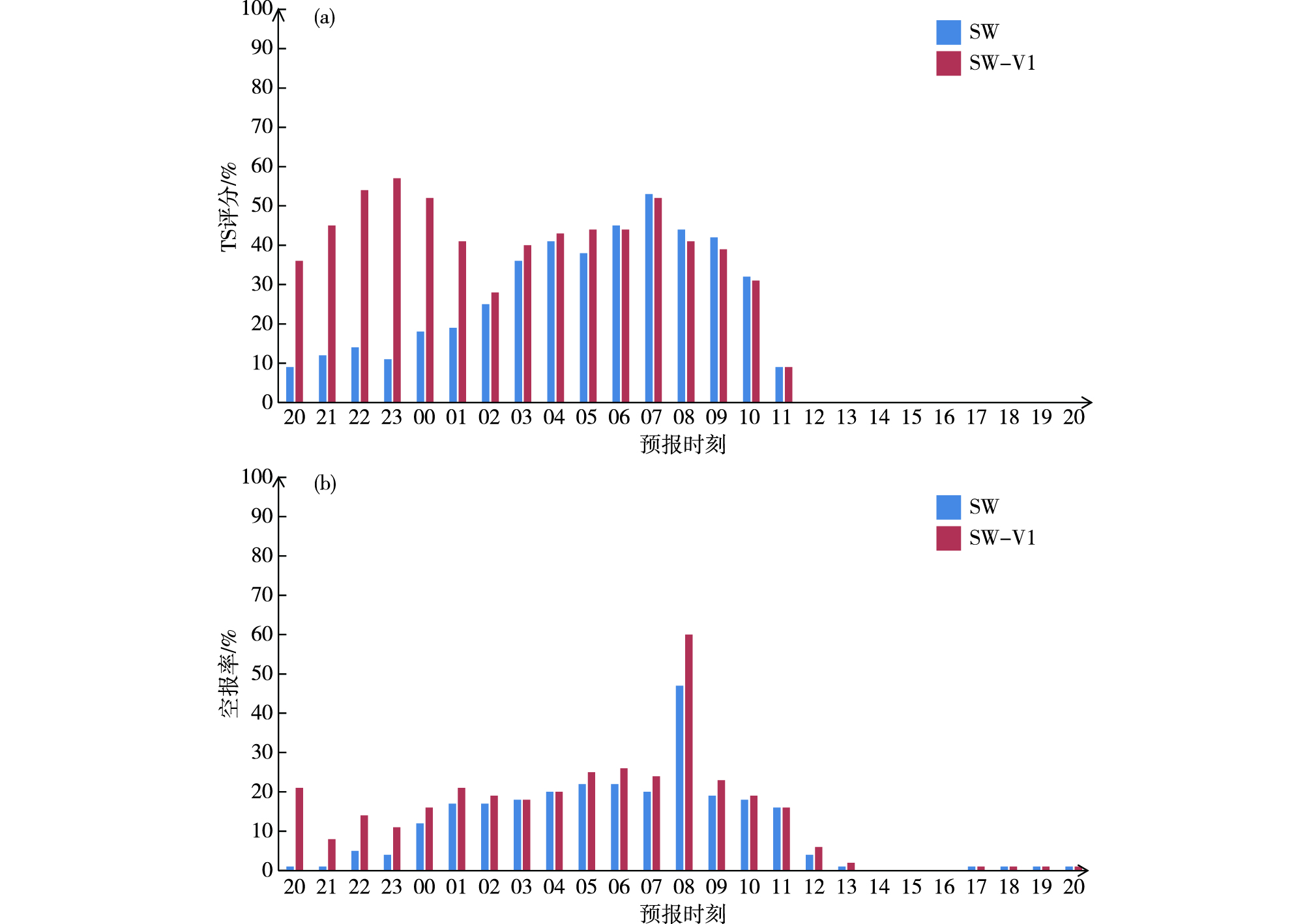
|
图 4 2015年11月13日20时起报0~24 h预报时效SW与SW-V1方案预报雾的TS评分(a)与空报率(b) Fig.4 TS (a) and FAR (b) of 0-24 h fog forecast by SW scheme and SW-V1 scheme initiated at 20:00 BST 13 November 2015 |
模式预报的总液态含水量,除了云水含量还有雨水含量,由图 5可以看出,当雨水含量占总液态含水量比例较高的预报时效,SW-V1方案预报雾的TS评分提升明显,比例较低时,TS评分提高不明显。这是由于改进方案均增强了雨水含量对能见度的削弱作用。而在16~24 h这个预报时段,HUC模式预报的总液态含水量近乎为0,因此改进前后方案预报雾的TS评分为0,同时两者预报的能见度差异不明显。
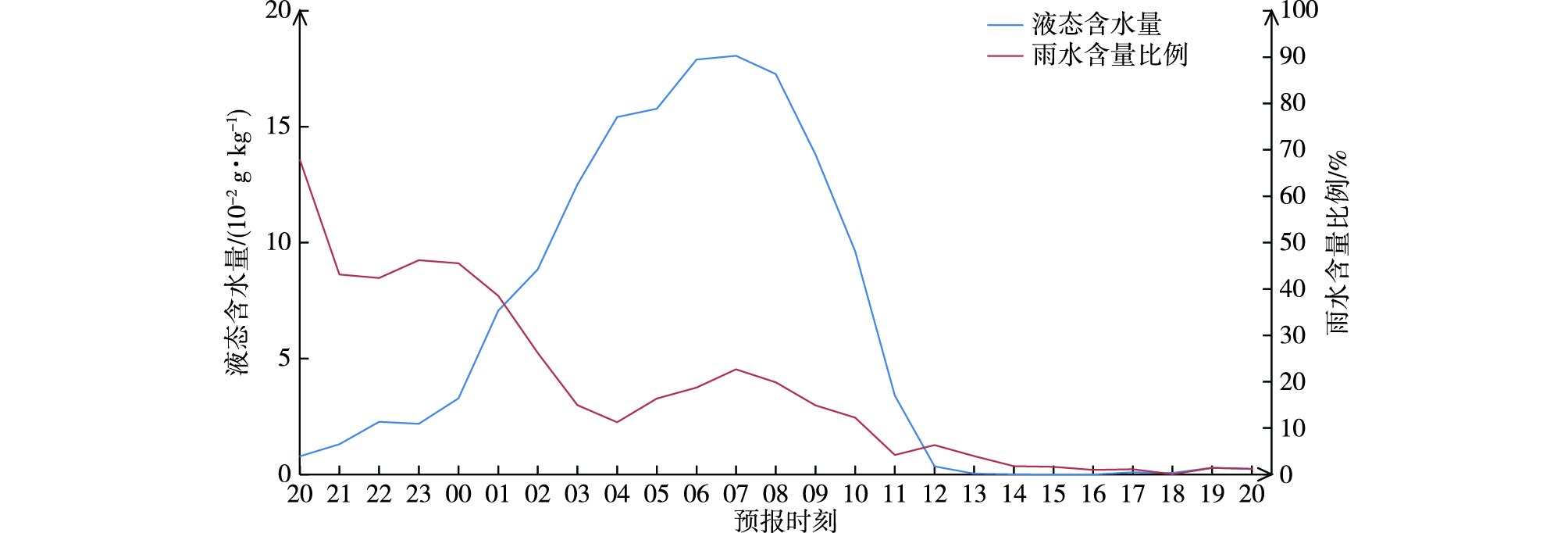
|
图 5 2015年11月13日20时起报0~24 h预报时效HUC模式预报的总液态含水量(单位:10-2 g·kg-1)与雨水含量占总液态含水量比例(单位:%) Fig.5 Total liquid water content (units: 10-2 g·kg-1) and proportion of rain water content (units: %) in total liquid water content by 0-24 h forecast of HUC model initiated at 20:00 BST 13 November 2015 |
2015年11月14日09时实况(图 6a)显示,雾主要出现在鲁西北、鲁西南和山东半岛地区。FSL方案(图 6b)预报出雾站点较少,零星分布在山东半岛地区,在鲁西北地区漏报站点较多,FSL-V1方案(图 6c)较好地模拟出了鲁西北与山东半岛出雾的站点。
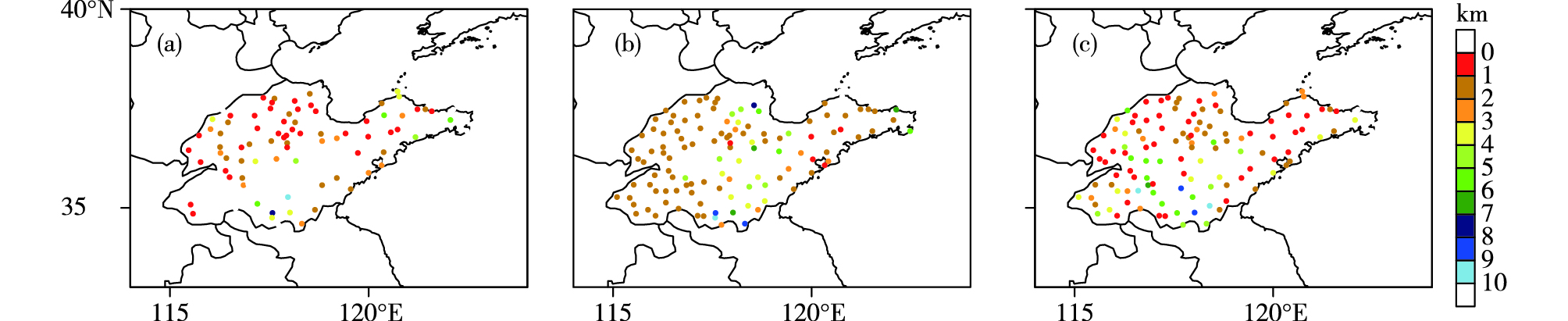
|
图 6 2015年11月14日09时观测站点雾分布(a)、FSL(b)与FSL-V1(c)方案预报站点雾分布(填色为能见度,单位:km) Fig.6 Distribution of stations with observed fog (a) and distribution of stations with forecast fog by FSL scheme (b) and FSL-V1 scheme (c) at 09:00 BST 14 November 2015 (colored area for visibility, units: km) |
由图 7可以看出,在0~12 h预报时效,FSL-V1方案预报能见度的MAE较FSL方案降低并不明显,在13~24 h预报时效,FSL-V1方案预报能见度的MAE降低更为明显。
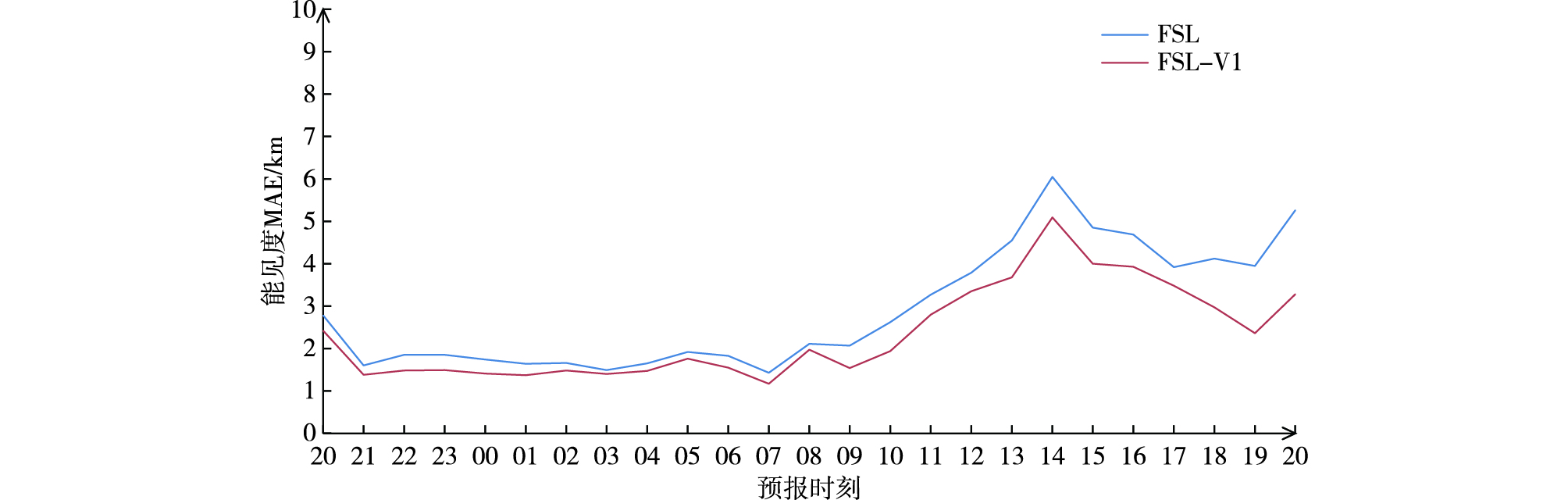
|
图 7 2015年11月13日20时起报0~24 h预报时效FSL与FSL-V1方案预报能见度的平均绝对误差(MAE;单位:km) Fig.7 MAE of 0-24 h visibility forecast(units: km) by FSL scheme and FSL-V1 scheme initiated at 20:00 BST 13 November 2015 |
由各预报时效的TS评分(图 8a)来看,在0~12 h预报时效FSL-V1的改进效果不明显,有的预报时效TS评分低于FSL方案,在之后的预报时效FSL-V1方案明显高于FSL方案;由两种方案预报雾的空报率(图 8b)来看,在整个预报时段,两者差异并不明显。
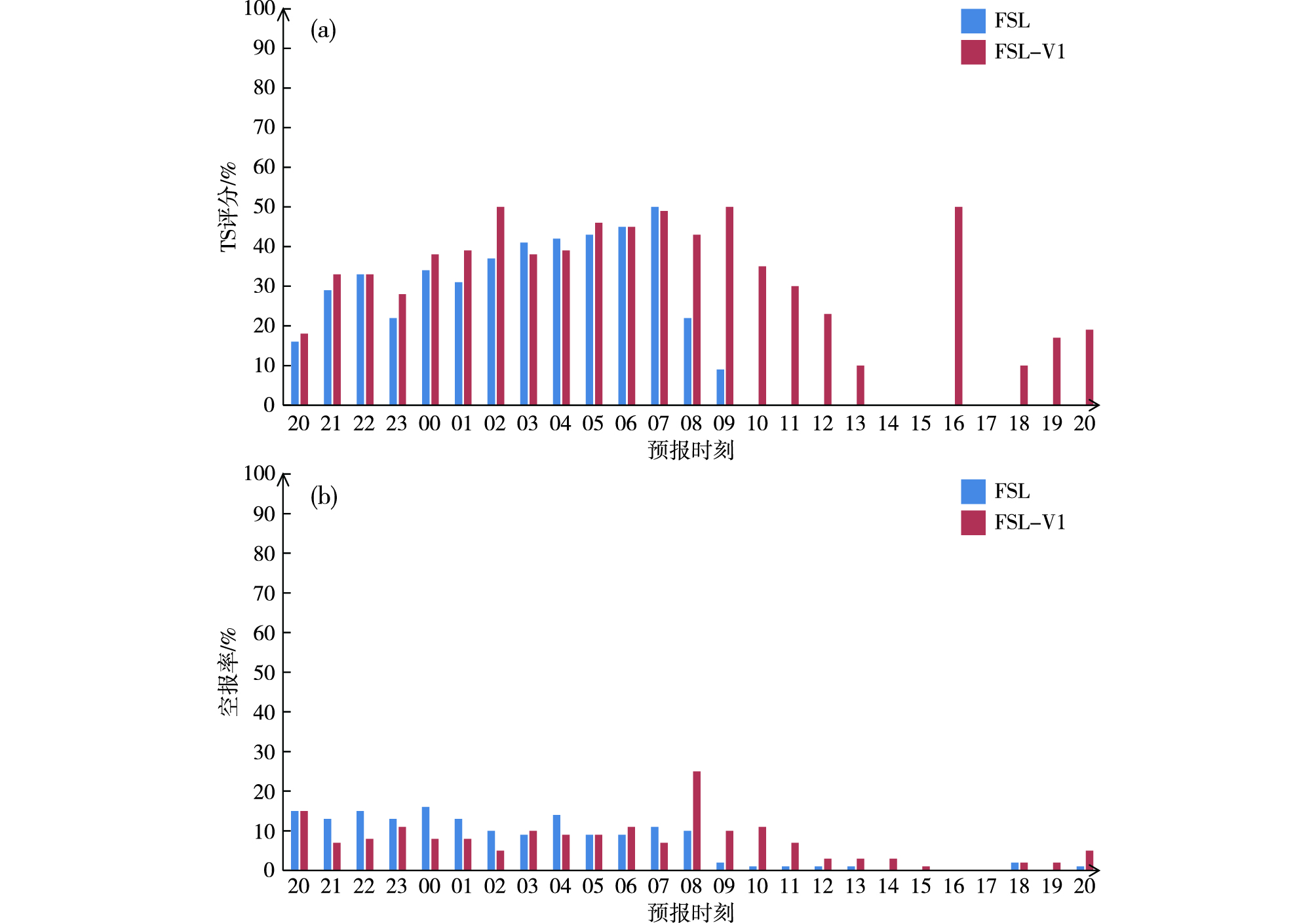
|
图 8 2015年11月13日20时起报0~24 h预报时效FSL与FSL-V1方案预报雾的TS评分(a)与空报率(b) Fig.8 TS (a) and FAR (b) of 0-24 h fog forecast by FSL scheme and FSL-V1 scheme initiated at 20:00 BST 13 November 2015 |
由订正前后相对湿度在各预报时效的MAE(图 9)可以看出,在0~12 h订正效果不显著,MAE大致相同,在13~24 h订正后的相对湿度MAE明显小于订正前,这使得FSL-V1方案在0~12 h时效对能见度与雾的预报效果的改进不明显,而在13~24 h则有明显的改进效果。
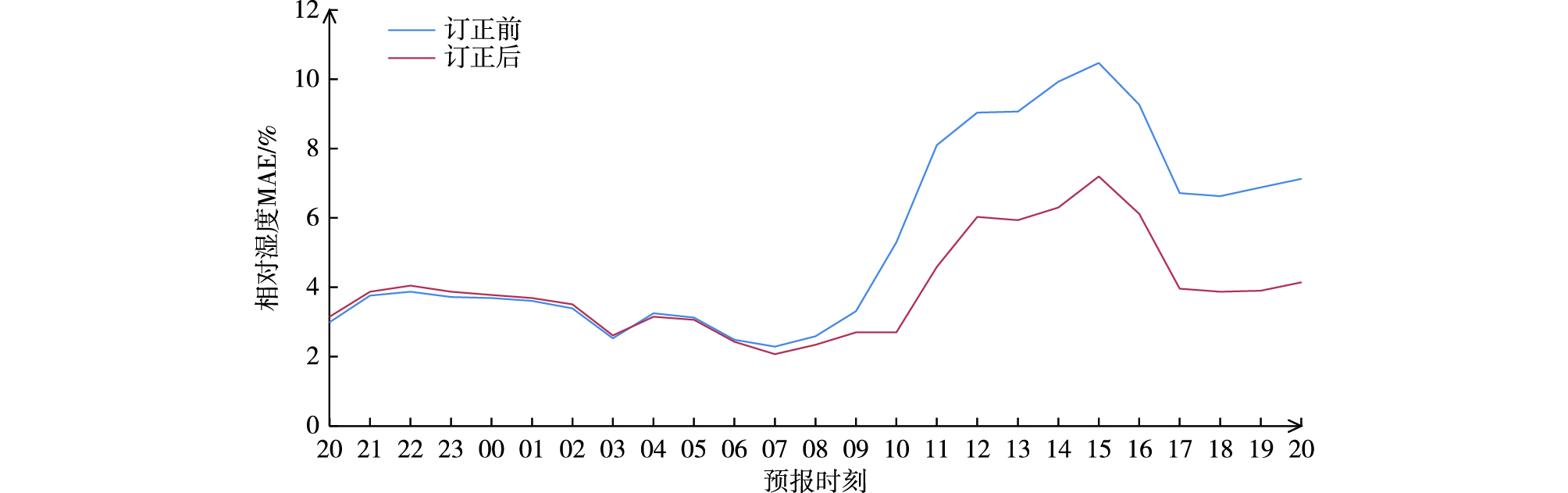
|
图 9 2015年11月13日20时起报0~24 h预报时订正前后相对湿度的平均绝对误差(MAE;单位:%) Fig.9 MAE of 0-24 h relative humidity (units: %) forecast before and after correction initiated at 20:00 BST 13 November 2015 |
通过以上的对比试验发现,SW-V1方案与FSL-V1方案分别对SW方案与FSL方案改进效果较好,下面将SW-V1与FSL-V1方案进行融合,计算CVIS,并且比较这三种方案对能见度与雾的预报效果。
由三种改进方案预报能见度的MAE(图 10)可以看出,SW-V1方案最差,CVIS与FSL-V1方案效果相当;由TS评分在各预报时效分布(图 11a)来看,模式预报的雨水含量占比较高的预报时段,SW-V1方案高于FSL-V1方案,在相对湿度订正效果较明显的预报时段,FSL-V1方案高于SW-V1方案,由空报率在各预报时效分布(图 11b)来看,大部分预报时段,SW-V1方案高于FSL-V1方案,模式没有模拟出液态含水量的预报时段,SW-V1方案的空报率为0,相应的FSL-V1方案空报率也较低。CVIS方案取了两种方案能见度最小值,所以TS评分在大部分预报时效高于其他两种方案,部分预报时效略低于某一方案,空报率也略高于其他两种方案,这是由于CVIS方案预报雾空报站数增加的原因。
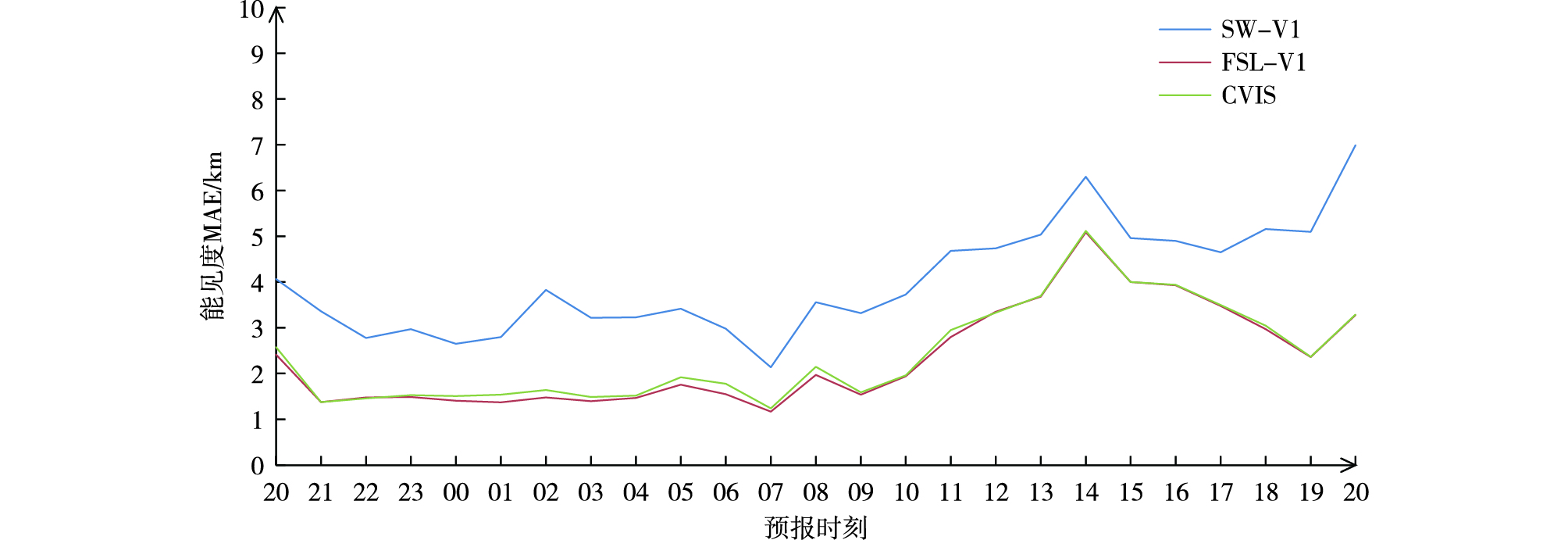
|
图 10 2015年11月13日20时起报0~24 h预报时效SW-V1、FSL-V1与CVIS方案预报能见度的平均绝对误差(MAE;单位:km) Fig.10 MAE of 0-24 h visibility forecast (units: km) by SW-V1 scheme, FSL-V1 scheme, and CVIS scheme initiated at 20:00 BST 13 November 2015 |

|
图 11 2015年11月13日20时起报0~24 h预报时效SW-V1、FSL-V1与CVIS方案预报雾的TS评分(a)与空报率(b) Fig.11 TS (a) and FAR (b) of 0-24 h fog forecast by SW-V1 scheme, FSL-V1 scheme, and CVIS scheme initiated at 20:00 BST 13 November 2015 |
为了对上述检验结果进一步验证,图 12—14分别给出其他9次雾天气SW-V1、FSL-V1与CVIS方案计算能见度的MAE,对雾预报的TS评分与空报率,由图可见,各次天气的检验结果与2015年11月13日这次过程大致相似,大部分预报时效,CVIS计算能见度的MAE低于或等于其他两种方案,CVIS方案对雾预报的TS评分与空报率在大部分预报时效高于或等于其他两种方案,当两种方案对雾预报的空报站数较多时,CVIS的TS评分会低于其中一种方案。总体来看,CVIS方案对能见度与雾的预报效果优于其他两种改进方案。
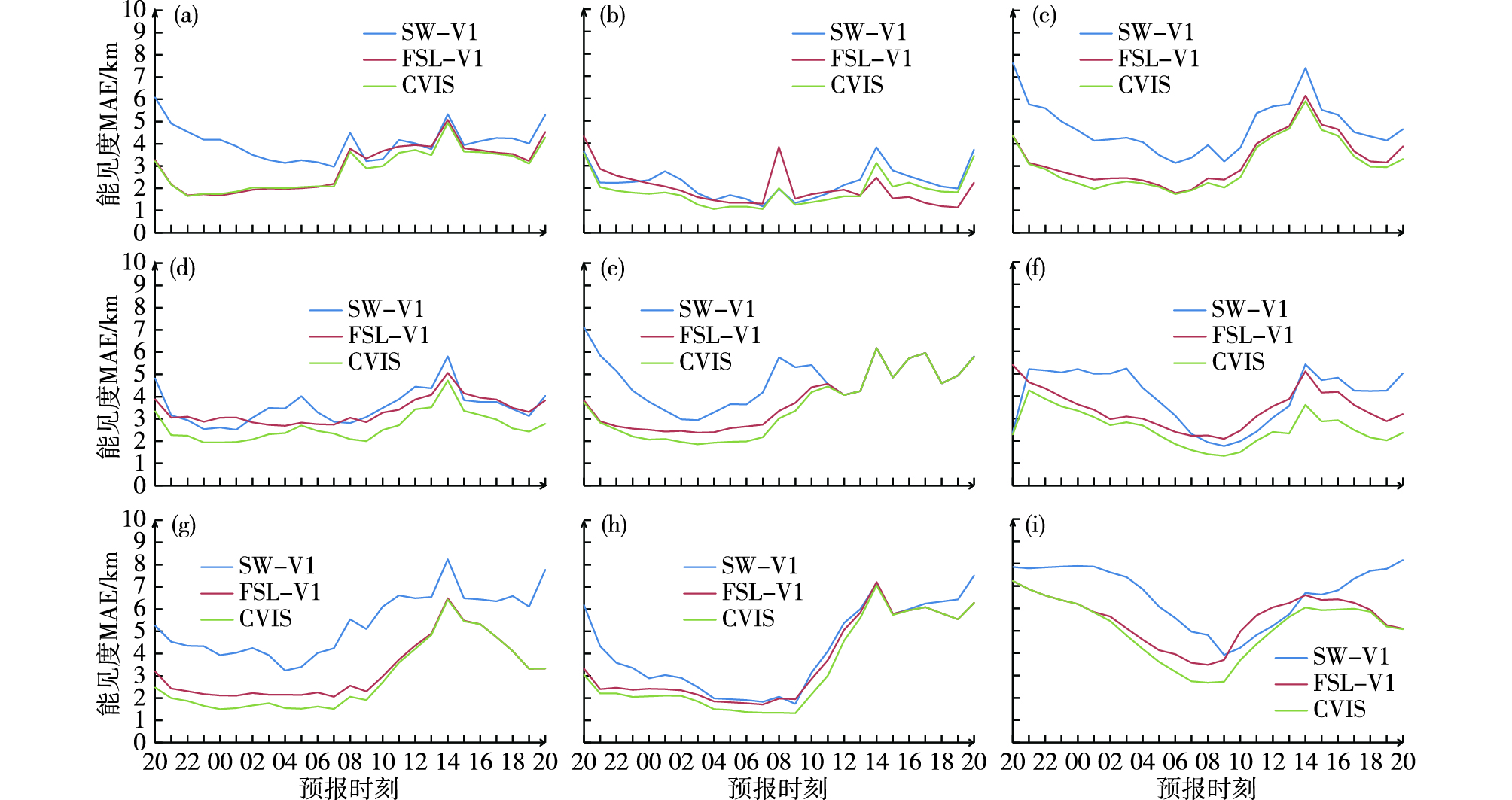
|
图 12 20时起报0~24 h预报时效SW-V1、FSL-V1与CVIS方案预报能见度的平均绝对误差(MAE;单位:km; a. 2015年11月14日,b. 2015年11月20日,c. 2015年11月29日,d. 2015年11月30日,e. 2015年12月1日,f. 2015年12月22日,g. 2015年12月23日,h. 2015年12月24日,i. 2016年1月2日) Fig.12 MAE of 0-24 h visibility forecast (units: km) by SW-V1 scheme, FSL-V1 scheme, and CVIS scheme initiated at 20:00 BST (a. 14 November 2015, b. 20 November 2015, c. 29 November 2015, d. 30 November 2015, e. 1 December 2015, f. 22 December 2015, g. 23 December 2015, h. 24 December 2015, i. 2 January 2016) |

|
图 13 20时起报0~24 h预报时效SW-V1,FSL-V1与CVIS方案预报雾的TS评分(单位:%;a. 2015年11月14日,b. 2015年11月20日,c. 2015年11月29日,d. 2015年11月30日,e. 2015年12月1日,f. 2015年12月22日,g. 2015年12月23日,h. 2015年12月24日,i. 2016年1月2日) Fig.13 The same as Fig. 12, but for TS (units: %) |
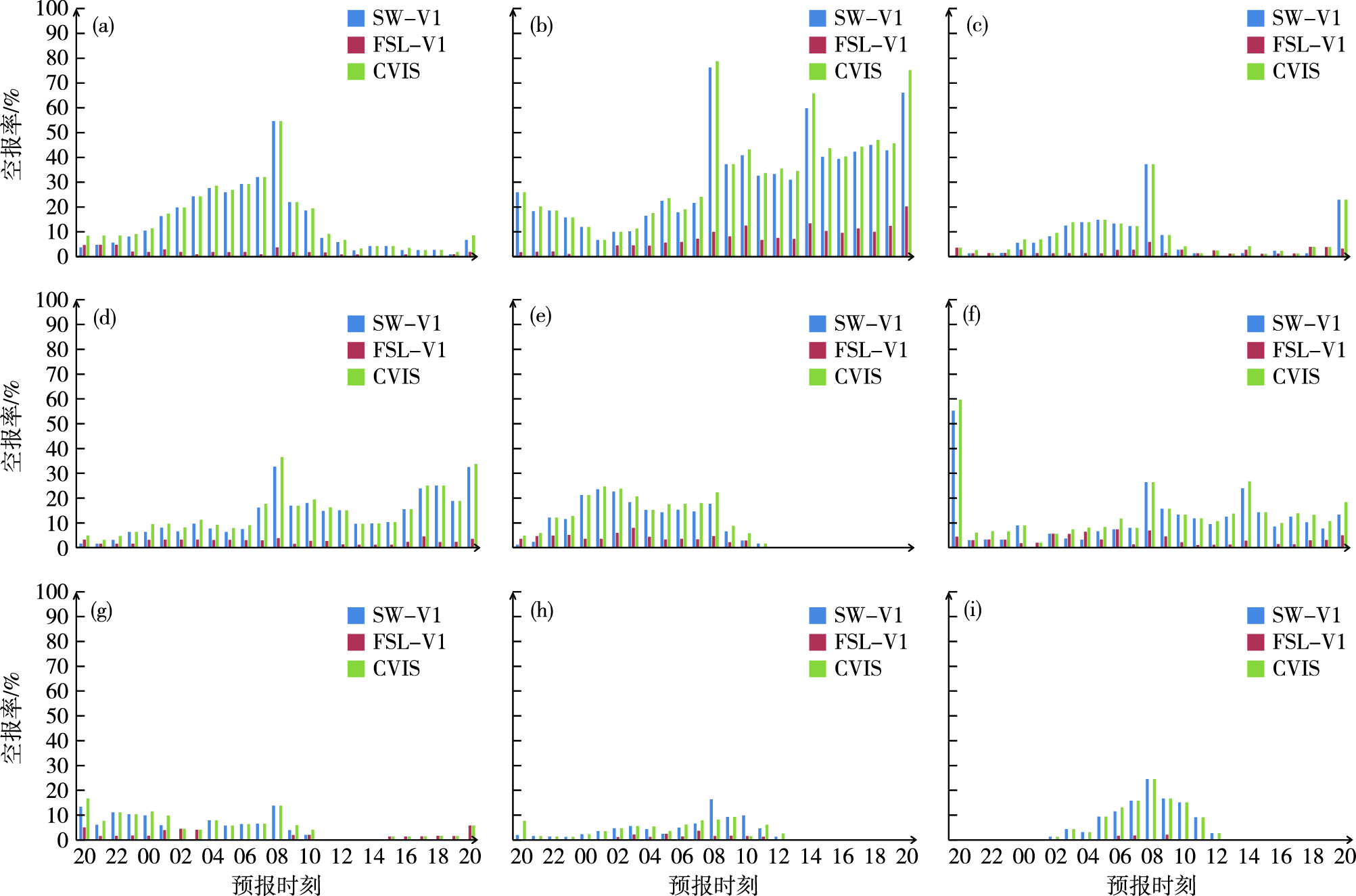
|
图 14 20时起报0~24 h预报时效SW-V1,FSL-V1与CVIS方案预报雾的空报率(单位:%;a. 2015年11月14日,b. 2015年11月20日,c. 2015年11月29日,d. 2015年11月30日,e. 2015年12月1日,f. 2015年12月22日,g. 2015年12月23日,h. 2015年12月24日,i. 2016年1月2日) Fig.14 The same as Fig. 12, but for FAR (units: %) |
本文基于Gultepe方案与递减平均法分别对SW与FSL诊断方案进行改进,对2015—2016年山东10次出雾天气进行预报试验,并详细分析了2015年11月13—14日雾天气预报结果,对比了各方案改进前后对能见度与雾的预报效果,最后将改进效果较好的方案融合并进行了对比,得到以下结论:
1) 13—14日雾天气的模式结果显示,在模式雨水含量占总液态含水量比例较大的预报时段,SW-V1方案预报能见度的MAE小于SW方案,对雾预报的TS评分高于SW方案;当模式预报液态含水量接近0的预报时段,改进前后SW方案对雾与能见度的预报效果基本相同。
2) 13—14日雾天气的模式结果显示,在相对湿度订正效果较小的预报时段,FSL-V1方案对FSL方案改进效果不明显,在相对湿度订正效果较大的预报时段,FSL-V1方案预报能见度的MAE明显小于FSL方案,对雾预报的TS评分也远高于FSL方案。
3) 比较SW-V1、FSL-V1与CVIS三种改进方案在雾天气时对能见度与雾的预报效果,大部分预报时效SW方案预报能见度的MAE最大,CVIS方案最低,CVIS方案预报雾的TS评分要高于其他两种改进方案,CVIS方案的空报率要高于其他两种方案,当两种方案空报站数较多的预报时效,CVIS方案的TS评分会低于其中一种改进方案。其他9次预报结果显示,CVIS方案在雾天气下对能见度与雾的预报效果最优。
| [1] |
孙颖, 马艳, 高荣珍, 等. 山东一次持续性平流辐射雾过程特征及成因分析[J]. 海洋气象学报, 2018, 38(4): 128-135. |
| [2] |
侯淑梅, 杨成芳, 王建林, 等. 上合组织青岛峰会期间海雾维持和消散阶段的环境场特征[J]. 海洋气象学报, 2019, 39(1): 86-94. |
| [3] |
陈东辉, 尚子微, 宁贵财, 等. 环渤海地区雾天气分型及预报方法[J]. 气象, 2017, 43(1): 46-55. |
| [4] |
田小毅, 朱承瑛, 张振东, 等. 长江江苏段江面雾的特征和预报着眼点[J]. 气象, 2018, 44(3): 408-418. |
| [5] |
吴兑, 邓雪娇, 游积平, 等. 南岭山地高速公路雾区能见度预报系统[J]. 热带气象学报, 2006, 22(5): 417-422. |
| [6] |
黄健, 黄辉军, 黄敏辉, 等. 广东沿岸海雾决策树预报模型[J]. 应用气象学报, 2011, 22(1): 107-114. |
| [7] |
周须文, 时青格, 贾俊妹, 等. 低能见度雾的分级预报方法研究[J]. 热带气象学报, 2014, 30(1): 161-166. |
| [8] |
KUNKEL B A. Parameterization of droplet terminal velocity and extinction coefficient in fog models[J]. J Climate Appl Meteor, 1984, 23(1): 34-41. DOI:10.1175/1520-0450(1984)023<0034:PODTVA>2.0.CO;2 |
| [9] |
STOELINGA M T, WARNER T T. Nonhydrostatie, mesobeta-scale model simulations of cloud ceiling and visibility for an East Coast winter precipitation event[J]. J Appl Meteor, 1999, 38(4): 385-404. DOI:10.1175/1520-0450(1999)038<0385:NMSMSO>2.0.CO;2 |
| [10] |
GULTEPE I, MVLLER M D, BOYBEYI Z. A new visibility parameterization for warm-fog applications in numerical weather prediction models[J]. J Appl Meteor Climatol, 2006, 45(11): 1469-1480. DOI:10.1175/JAM2423.1 |
| [11] |
GULTEPE I, PEARSON G, MILBRANDT J A, et al. The fog remote sensing and modeling field project[J]. Bull Amer Meteor Soc, 2009, 90(3): 341-359. DOI:10.1175/2008BAMS2354.1 |
| [12] |
SMIRNOVA T G, BENJAMIN S G, BROWN J M. Case study verification of RUC/MAPS fog and visibility forecasts[C]//American Meteorological Society. The 9th Conference on Aviation, Range, and Aerospace Meteorology. Orlando, Florida: AMS, 2000: 31-36.
|
| [13] |
DORAN J A, ROOHR P J, BEBERWYK D J, et al. The MM5 at the air force weather Agency-New products to support military operations[C]//American Meteorological Society. The 8th Conference on Aviation, Range, and Aerospace Meteorology. Dallas, Texas: AMS, 1999: 10-15.
|
| [14] |
夏凡, 李昌义. 基于3种能见度方案山东地区雾天气预报试验研究[J]. 气象与环境学报, 2018, 34(3): 48-57. |
| [15] |
高荣珍, 李欣, 时晓曚, 等. 基于WRF模式的青岛近海能见度算法比较研究[J]. 海洋气象学报, 2018, 38(2): 28-35. |
| [16] |
林艳, 王茂书, 林龙官. 四川省冬季雾的数值模拟及能见度参数化[J]. 南京信息工程大学学报(自然科学版), 2013, 5(3): 222-228. |
| [17] |
管琴, 李青平, 黄铃光, 等. 太原雾天能见度预报[J]. 气象与环境学报, 2013, 29(4): 47-53. |
| [18] |
GULTEPE I, ISAAC G A. Aircraft observations of cloud droplet number concentration: Implications for climate studies[J]. Quart J Roy Meteor Soc, 2004, 130(602): 2377-2390. DOI:10.1256/qj.03.120 |
| [19] |
邱学兴, 王东勇, 陈宝峰. T639模式预报系统误差统计和订正方案研究[J]. 气象, 2012, 38(5): 526-532. |
| [20] |
BANG C H, LEE J W, HONG S Y. Predictability experiments of fog and visibility in local airports over Korea using the WRF model[J]. J Korean Soc Atmos Environ, 2008, 24(E2): 92-101. |
 2020, Vol. 40
2020, Vol. 40


