多普勒天气雷达是大气风场中尺度结构的重要探测工具。在多普勒天气雷达的径向风场信息中,大部分中尺度天气系统都有其独特的二维特征结构[1],可通过研究这些二维特征结构识别和追踪中尺度天气系统[2-3]。我国内陆目前使用较多的多普勒天气雷达是CINRAD-CD,该款雷达有切变线识别产品,但它采用的算法并未把缺测区纳入到分析范畴中,仅对探测数据进行了简单的预处理,且识别产品仅限于平面位置显示(plane position indicator,PPI),没有涉及到垂直切变。
自20世纪开始,国内外的一些实验室、高校均已开展多普勒天气雷达风切变线识别领域的研究。CAMPBELL and OLSON[4]成功研发了可利用人工智能方法自动识别风切变的WX1系统。QIN et al.[5]基于多普勒天气雷达回波数据,利用集合平方根滤波法对风场变化进行了预测,该方法得到的飑线传播方向与观测值一致,其传播速度略高于观测值,其有效预报时间约为5 h。ZHENG et al.[6]研究了阵风锋发生过程中回波的反射率、速度和谱宽等统计特征,提出了一种基于滑动窗口型的阵风锋自动识别算法。胡明宝等[7]利用单部多普勒天气雷达探测低空风切变,可计算出一维径向风切变值、一维方位风切变值及二维复合风切变值。魏耀和张兴敢[8]基于多普勒天气雷达速度场合成切变,首先取不同“拟合窗口”,然后使用最小二乘拟合法进行运算,该算法在定位精度、识别能力、边缘切变识别等方面优势明显。冷亮等[9]、吴举秀等[10]提出了一种用于阵风锋自动识别的数学形态学算法,通过计算阵风锋的反射率因子差、速度切变、速度梯度等三个参量场,得到一个二维特征量,采取数字形态学算法对该二维特征量进行处理,从而获取阵风锋框架结构特性曲线。国内外相关研究均集中在识别风切变阈值及识别算法方面,并未关注探测资料的预处理,且未实际应用这些研究成果。
目前,有些厂家的天气雷达已可提供风切变产品,这些风切变产品包括径向、仰角、方位角等多个方向的风切变场[11-12]。他们采用的主流算法是:预处理天气雷达的探测数据,并对缺测区域使用线性内插技术填充,再分别计算风场的切变信息[13],但此前的风场结构可能会由于线性内插而发生变化,从而影响风切变的计算。
本文提出的处理方法可通过多普勒天气雷达的径向速度有效辨识风切变线,显示垂直切变图,可为临近预报提供更科学的参考信息。
1 计算方法CINRAD-CD多普勒天气雷达切变线识别产品的运算方法[13]为:先顺着径向选取反射率达到阈值的像素点,并滑动平均原始径向数据,随后运算这部分数据的径向切变和方位切变,最后在笛卡尔坐标系上对其进行梯度插值且对其滤波[14]。这种算法的局限之处在于:未将缺测区域和回波边缘的数据有效处理,且仅有平面位置显示(PPI)的产品,没有垂直切变的产品。
本文使用多普勒天气雷达径向速度的体积扫描数据,在极坐标上进行运算。
1.1 探测数据预处理为降低径向速度噪声,且有效保留径向速度的中尺度结构,对探测资料实施预处理。预处理步骤是:
1) 中值滤波
分别沿着方位角和径向选取n1×n2个点,对其排序,但不需选取所有目标点的数值,仅使用中间值代替即可。
2) 滑动平均
对探测数据实施中值滤波后,选取沿着方位角方向和径向的n3和n4个连续像素点,分别计算其均值作为中间点数值。针对缺少探测数据的区域及附近区域,对其采用的处理原则是:唯有满足一定数量的有效数据才进行处理,但是对其不采取外插值处理;如若有效数据不能达到一定数量,则把无数据区周边的点以无探测数据处理。如此则可有效规避边缘区域探测资料不足而导致的误差,切变线通常是连续的,但缺测区是孤立的,因此去除这部分区域对于最终计算效果影响有限。
参与计算的探测数据点数n1、n2、n3、n4不同(即计算“窗口”大小),会极大影响预处理效果。为降低差别,沿方位角方向的n1、n3通常取值为3。本文重点分析沿着径向的n2、n4变化时对预处理结果造成的影响。
1.2 计算探测数据径向速度的径向切变和方位切变对任意一组随机数据(y1, x1),y2, x2,…,(yn, xn),通过最小二乘拟合法,可得到利用这些点的最佳直线,且可得出这条直线的斜率。
将径向速度从原点出发沿任一径向随距离的变化定义为该径向速度的径向切变,即
| $ \frac{{\partial v}}{{\partial r}} = \frac{{\sum\nolimits_{i = 1}^n {{v_i}} \sum\nolimits_{i = 1}^n {{r_i} - n} \sum\nolimits_{i = 1}^n {\left( {{v_i}{r_i}} \right)} }}{{\sum\nolimits_{i = 1}^n {{r_i}} \sum\nolimits_{i = 1}^n {{r_i} - n} \sum\nolimits_{i = 1}^n {r_i^2} }} $ | (1) |
式(1)中vi示第i个点的径向速度,ri表示该点距天气雷达的距离,n表示参与运算的探测数据点数,θ表示方位角,此处为常数。
与雷达等间距的像素点,其径向速度由0°方位角开始顺时针方向的变化定义为该径向速度的方位切变,即
| $ \frac{{\partial v}}{{r\partial \theta }} = \frac{{\sum\nolimits_{j = 1}^n {{v_j}} \sum\nolimits_{j = 1}^n {{\theta _j} - n} \sum\nolimits_{j = 1}^n {\left( {{v_j}{\theta _j}} \right)} }}{{r\left( {\sum\nolimits_{j = 1}^n {{\theta _j}} \sum\nolimits_{j = 1}^n {{\theta _j} - n} \sum\nolimits_{j = 1}^n {\theta _j^2} } \right)}} $ | (2) |
式(2)中vj表示第j个点的径向速度,r在此处为常数,表示该点距天气雷达的距离,n表示参与运算的探测数据点数,θj表示相应的方位角。
1.3 计算垂直切变当方位角θ、间距r都是常数时,上下两层PPI上径向速度数值随垂直高度的变化定义为垂直切变,即
| $ \frac{{\partial v}}{{\partial h}} = \frac{{\frac{{\sum\nolimits_{k = 1}^l {{v_{1k}}} }}{l} - \frac{{\sum\nolimits_{k = 1}^l {{v_{2k}}} }}{l}}}{{{r_1}\sin {\alpha _1} - {r_2}\sin {\alpha _2}}} $ | (3) |
式(3)中v1、v2为上下两层的径向速度,并对其进行平滑拟合(对应的区间范围均为1);r1、r2为上下两层的径向间距:α1、α2为上下两层PPI的仰角。仅当上下两层数据同时有效时才进行运算,否则作为无探测数据区域处理,随后对其采取中值滤波。
1.4 计算组合切变天气雷达径向速度沿径向和方位角方向的综合变化定义为组合切变,即
本文利用的雷达探测数据来自银川新一代天气雷达(CINRAD-CD)对2019年6月26日暴雨过程、2019年8月2日带状强降水过程的探测。CINRAD-CD雷达是一种C波段全相参体制的多普勒天气雷达,工作频率为5 300~5 500 MHz,天线直径4.3 m,增益43 dB,最大可测半径为200 km,天线的方位、俯仰定位精度均为0.2°[15],银川雷达馈源海拔高度为1 070.439 m。
3 不同预处理方法试验对比对2019年6月26日多普勒天气雷达的探测数据进行预处理,探测时选择0.6°仰角,45°方位角的径向,以此次天气过程为例说明探测数据预处理的效果。
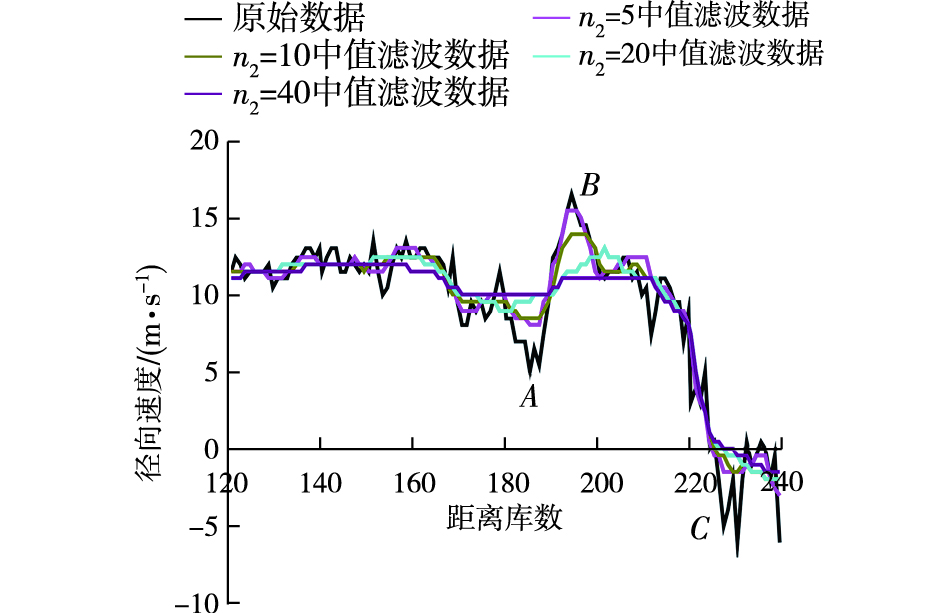
3.1 中值滤波首先分别令n2=5,n2=10,n2=20,n2=40,然后对该探测数据实施中值滤波,最后把结果和原始资料比较,将其绘成图 1。
|
图 1 中值滤波效果对比 Fig.1 Comparison between raw data and median filtering data |
图 1中的原始探测数据存在的库间脉动比较明显,经过中值滤波处理之后,库间脉动基本消失,但是曲线平滑度依然不足。图 1中A—B段、B—C段梯度较大。A—B段,当n2=5和n2=10时,滤波结果和原始资料较为相近,保持了大梯度值;当n2=20和n2=40时,梯度明显降低,甚至几乎消失。B—C段,当n2=5,n2=10,n2=20,n2=40的滤波结果和大梯度区重合度较高,与原始资料非常接近,可保持大梯度特征。由以上分析可知,对大尺度的梯度区域而言,挑选合理的滤波参数,可在消除库间脉动的情况下仍然保持探测数据的大梯度特征。
3.2 滑动平均首先分别令n4=5,n4=10,n4=20,n4=40,然后对该探测数据实施径向滑动平均,最后把结果与原始数据对比,将其绘成图 2。

|
图 2 滑动平均效果对比 Fig.2 Comparison between raw data and moving average data |
由图 2分析可得,当n4取值较小时,可以保持大的梯度区间,但不能有效去除库间脉动;当n4取值增大时,库间脉动的去除效果显著,但是大梯度区间逐渐降低。由此可见,若只对探测数据进行滑动平均,将无法满足去除库间脉动且保留大梯度区间的要求。
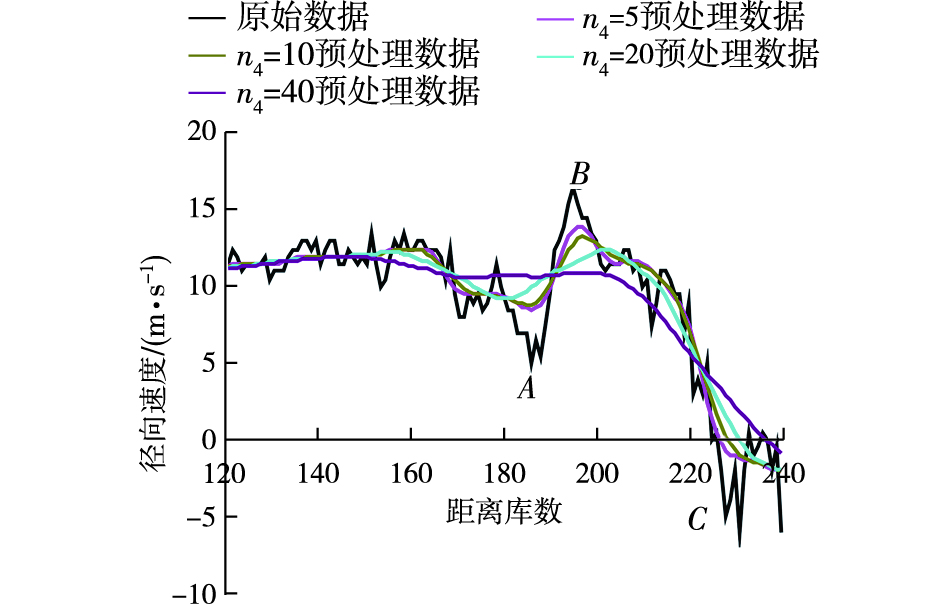
3.3 中值滤波后滑动平均首先对原始探测数据实施中值滤波(n1×n2=3×10),然后分别令n4=5,n4=10,n4=20,n4=40,对其作径向滑动平均,最后把结果与原始数据对比,将其绘成图 3。
|
图 3 先实施中值滤波再实施滑动平均的效果对比 Fig.3 Comparison between raw data and data that are successively processed with median filtering and moving average |
由图 3分析可得,当n4=5,n4=10,n4=20(即n4较小时),3个处理结果较为接近,不仅过滤了库间脉动,而且保留了原有的中尺度结构。但是当n4=40时,该处理方法会影响中尺度结构。
3.4 切变计算对探测数据实施切变计算的过程中,探测数据点数的不同表示辨识风切变的尺度不同。通过对比预处理结果发现:在预处理尺度和切变计算尺度相差不大(即都较大或较小)时,风切变的辨识效果不良;预处理尺度和切变计算尺度相差较大时可得到良好的辨识效果。
4 实例识别结果在对银川市多普勒天气雷达的探测数据处理过程中,不仅要有效过滤库间脉动,尽可能保留天气过程原有的中尺度结构,而且要尽可能多地使用探测数据,因此选用n1=3,n2=10,n3=3,n4=20。
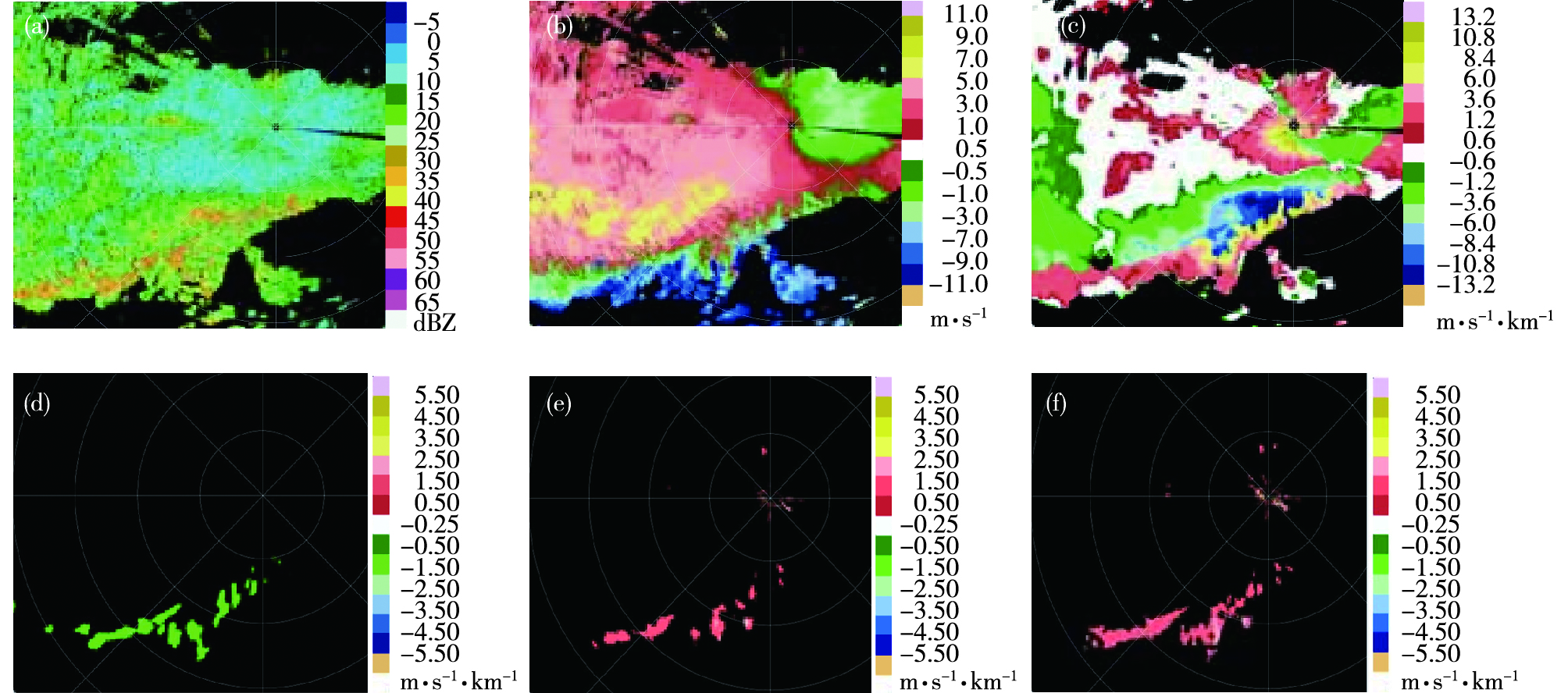
4.1 暴雨天气过程识别结果2019年6月26日银川市发生一次暴雨天气过程,与中尺度切变线有关(图 4)。分别对比同一仰角上的反射率因子和径向速度,继续对比同时次、不同仰角间的垂直切变。分析可得:此天气过程强降水区域的反射率因子为25~40 dBZ。负垂直切变和正垂直切变分别出现在切变线的北侧和南侧,该现象说明垂直切变的计算结果与实际径向风场的变化是一致的。
|
图 4 银川市2019年6月26日天气过程识别结果(a. 0.6°仰角反射率因子;b. 0.6°仰角径向速度;c. 0.6°仰角、1.4°仰角间垂直切变;d. 0.6°仰角径向切变,显示阈值:0.5 m·s-1·km-1;e. 0.6°仰角方位切变,显示阈值:0.8 m·s-1·km-1;f. 0.6°仰角组合切变,显示阈值:0.8 m·s-1·km-1) Fig.4 Identification results of Doppler weather radar during a rainstorm process in Yinchuan on 26 June 2019 (a. reflectivity factor at 0.6° elevation; b. radial velocity at 0.6° elevation; c. vertical shear between 0.6° elevation and 1.4° elevation; d. radial shear at 0.6° elevation, showing threshold value: 0.5 m·s-1·km-1; e. azimuthal shear at 0.6° elevation, showing threshold value: 0.8 m·s-1·km-1; f. combined shear at 0.6° elevation, showing threshold value: 0.8 m·s-1·km-1) |
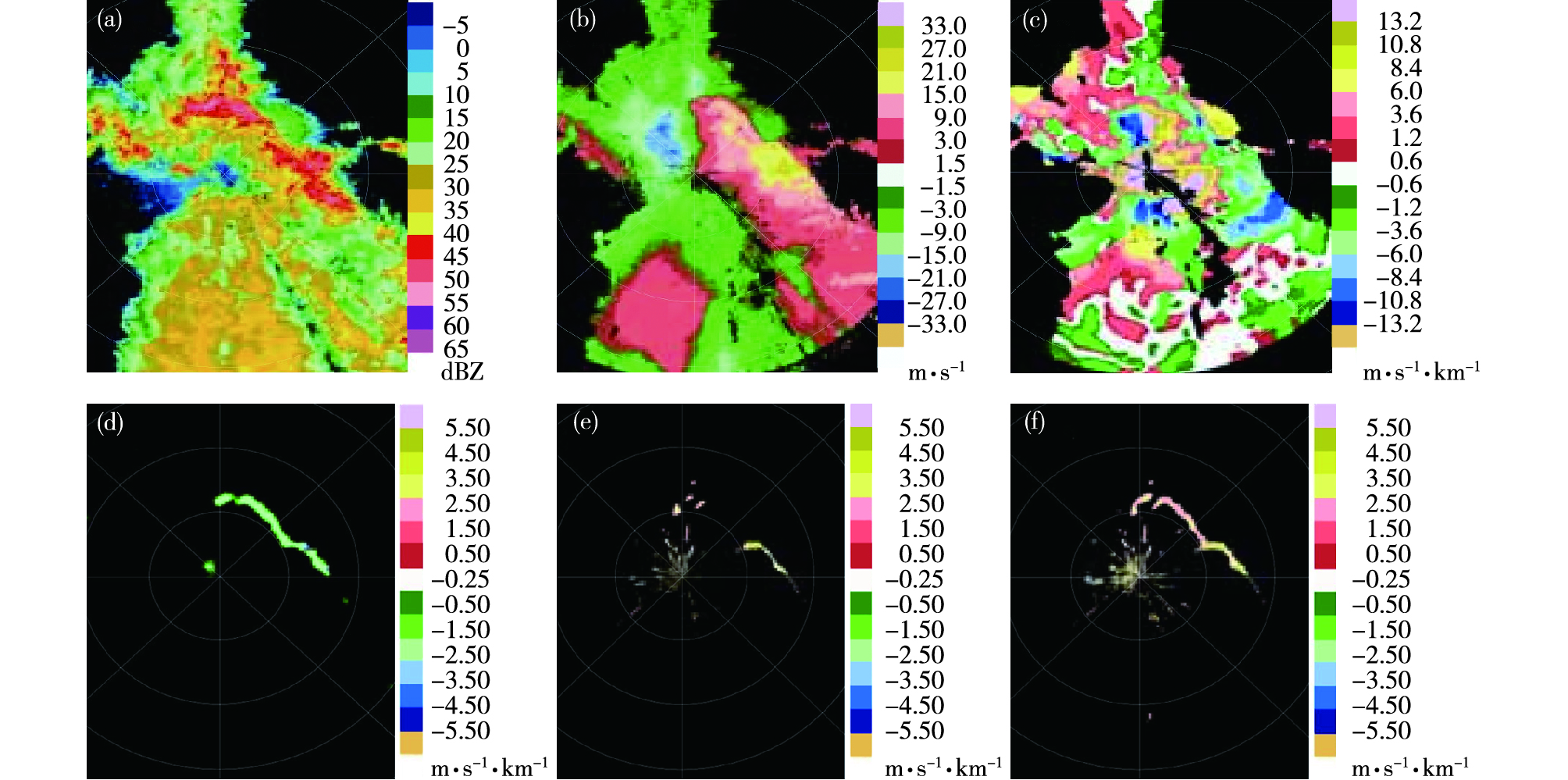
2019年8月2日银川市发生一次带状强降水天气过程(图 5)。分析可见,图 5a中强降水区的反射率因子为40~50 dBZ,正垂直切变最大值出现在降水区前部,负垂直切变出现在降水区后部。带状回波强度略有减弱,切变线识别结果强度减弱且不连续。
|
图 5 银川市2019年8月2日天气过程识别结果(a. 0.6°仰角反射率因子;b. 0.6°仰角径向速度;c. 0.6°仰角、1.4°仰角间垂直切变;d. 0.6°仰角径向切变,显示阈值:1.2 m·s-1·km-1;e. 0.6°仰角方位切变,显示阈值:1.7 m·s-1·km-1;f. 0.6°仰角组合切变,显示阈值:1.7 m·s-1·km-1) Fig.5 Identification results of Doppler weather radar during a banded heavy precipitation process in Yinchuan on 2 August 2019 (a. reflectivity factor at 0.6° elevation; b. radial velocity at 0.6° elevation; c. vertical shear between 0.6° elevation and 1.4° elevation; d. radial shear at 0.6° elevation, showing threshold value: 1.2 m·s-1·km-1; e. azimuthal shear at 0.6° elevation, showing threshold value: 1.7 m·s-1·km-1; f. combined shear at 0.6° elevation, showing threshold value: 1.7 m·s-1·km-1) |
本文通过对多普勒天气雷达径向速度的探测资料进行预处理,得出垂直切变图,探究了识别风切变线的新方法,并将该方法分别应用于暴雨和带状强降水两个案例,证明此方法可有效识别风切变。识别结果表明:
1) 首先对天气雷达的探测数据实施预处理,然后挑选合理的运算“窗口”,通过最小二乘拟合法得到径向速度沿着两个方向的切变现象,辨识结果与径向速度在图中的切变信息保持一致,证明了该方法的有效性。
2) 由于各降水过程中显示阈值存在着区别,垂直切变能够提供径向风场的高低层配置信息,径向速度水平切变的强弱和降水强度具有一定联系。
3) 通过合理运用多普勒天气雷达探测到的径向速度信息,提供垂直切变图,能够有效识别风切变,为灾害气象预报提供更科学的参考信息。
然而,需要特别指出的是,本文提供的方法可有效辨识径向速度的切变,但与真实风场的切变尚有区别。对于算法中显示阈值的设置,需根据各个地区的现实状况,对一系列天气案例采取试验、分类和归纳,方可获得最佳结果,不能将本文的阈值直接使用。
| [1] |
祁月皎, 何建新, 王旭. 多普勒天气雷达二维理想均匀风场的数值模拟[J]. 成都信息工程学院学报, 2014, 29(2): 127-132. |
| [2] |
郑永光, 周康辉, 盛杰, 等. 强对流天气监测预报预警技术进展[J]. 应用气象学报, 2015, 26(6): 641-657. |
| [3] |
牟容.利用四维变分同化技术反演低层风场的准业务应用研究[D].北京:中国气象科学研究院, 2007. http://cdmd.cnki.com.cn/Article/CDMD-85101-2007075505.htm
|
| [4] |
CAMPBELL S D, OLSON S H. Recognizing low-altitude wind shear hazards from Doppler weather radar:An artificial intelligence approach[J]. J Atmos Oceanic Technol, 1987, 4(1): 5-18. DOI:10.1175/1520-0426(1987)004<0005:RLAWSH>2.0.CO;2 |
| [5] |
QIN Y Y, GONG J D, LI Z C, et al. Assimilation of Doppler radar observations with an ensemble square root filter: A squall line case study[J]. Acta Meteor Sinica, 2014, 28(2): 230-251. |
| [6] |
ZHENG J F, ZHANG J, ZHU K Y, et al. Gust front statistical characteristics and automatic identification algorithm for CINRAD[J]. Acta Meteor Sinica, 2014, 28(4): 607-623. |
| [7] |
胡明宝, 谈曙青, 汤达章, 等. 单部多普勒天气雷达探测低空风切变方法[J]. 南京气象学院学报, 2000, 23(1): 113-118. |
| [8] |
魏耀, 张兴敢. 多普勒天气雷达合成切变算法及改进方法的研究[J]. 电子与信息学报, 2010, 32(1): 43-47. |
| [9] |
冷亮, 肖艳姣, 吴涛. 基于数学形态学的阵风锋识别算法[J]. 气象科技, 2016, 44(1): 1-6. |
| [10] |
吴举秀, 周青, 杨传凤, 等. 2015年7月14日阵风锋及锋后大风多普勒天气雷达产品特征分析[J]. 高原气象, 2017, 36(4): 1082-1090. |
| [11] |
周生辉, 魏鸣, 张培昌, 等. 多普勒雷达反演风场的风切变识别研究[J]. 热带气象学报, 2015, 31(1): 119-127. |
| [12] |
吕智. 机载风切变气象雷达地面验证系统技术研究[J]. 航空科学技术, 2015(8): 48-52. |
| [13] |
肖艳姣, 万玉发, 王志斌. 多普勒天气雷达双PRF径向速度资料质量控制[J]. 高原气象, 2016, 35(4): 1112-1122. |
| [14] |
刘彬贤, 王彦, 刘一玮. 渤海湾海风锋与阵风锋碰撞形成雷暴天气的诊断特征[J]. 大气科学学报, 2015, 38(1): 132-136. |
| [15] |
龚雪鹏, 罗红, 陈余明, 等. 毕节CINRAD/CD型天气雷达调制系统典型故障分析与处理[J]. 气象水文海洋仪器, 2019, 36(3): 106-108. |
 2020, Vol. 40
2020, Vol. 40

