2. 山东省气象台,山东 济南 250031;
3. 山东省人民政府人工影响天气办公室,山东 济南 250031;
4. 山东协和学院,山东 济南 250107
2. Shandong Meteorological Observatory, Jinan 250031, China;
3. Weather Modification Office of Shandong Province, Jinan 250031, China;
4. Shandong Xiehe University, Jinan 250107, China
双偏振雷达是监测、预警突发性灾害天气最有效的手段之一,在监测雷暴、冰雹、台风、暴雪等强天气系统中发挥着重要作用[1]。根本上讲,气象雷达探测到的数据是3D结构,但由于目前雷达产品呈现主要针对二维栅格图像的点、线、面矢量符号,缺乏立体空间的垂直连贯信息,无法展现垂直方向上气象要素的分布特征[2-3],故开展双偏振雷达的三维可视化研究具有重要意义。
国内外,针对雷达探测数据处理分析和立体可视化应用技术有很多研究。美国LAKSHMANAN et al.[4]对多部天气雷达的三维可视化组网进行了初步研究与探索,RU[5]对美国多普勒天气雷达进行了数据解析与回波立体绘制研究。国内孟昭林[6]对天气雷达数据与地理信息立体结合进行了探索,范大伟等[7]对机场多普勒天气雷达三维显示平台进行了研究开发。这些研究在立体回波透视程度上大都效果不佳,且仅对反射率产品进行了探索,未对双偏振产品展开深入研究。
本文在双偏振雷达所采集的反射率因子数据基础之上施以体绘制算法,首先对原始数据进行解析、质量控制与坐标变换等预处理,再通过立体建模形成三维数据场作为体绘制的插值初值场,最后通过插值法进行三维云体绘制,使之最终以三维透视可视化的产品形式展示,该立体回波模型可应用于基于地理信息系统(GIS)的3D雷达产品开发,也可为预报人员剖析云体内部特征提供重要依据。
1 天气雷达双偏振产品三维场建立天气雷达双偏振产品三维场的建立主要包括双偏振数据地物杂波质量控制,坐标变换,三维网格建立与插值等数据场建立过程。双偏振雷达采集到的双偏振数据在距离雷达中心较近时会受到地物遮挡影响产生杂波[8],必须排除地物杂波的干扰,并且雷达回波数据是以极坐标的方式保存,而三维场是以直角坐标的形式保存[9],这就需要对双偏振原始数据进行坐标变换与三维插值处理。
1.1 地物杂波抑制地形遮挡会严重影响回波质量,尤其近场回波干扰严重。在三维场绘制中,地物杂波干扰会影响近场数据的准确性并破坏整体数据纵向拉伸性[10-11]。由于地物杂波的平均径向速度产品特征为一个接近零速度的区域中分布着零星非零速度值,利用地物杂波径向速度趋近于零的特性,抑制掉地物杂波的干扰[12]。
1.2 坐标变换双偏振产品原始数据为同一体扫内多个离散仰角的锥面扫描数据集,是以雷达馈源为中心的仰角、方位和距离为参数的极坐标数据[13]。为了便于3D插值以及简化可视化的处理过程,需要将极坐标系下的双偏振原始数据转化为经度、纬度和高度的三维笛卡尔坐标系格点数据。在格点转换中,需要根据不同雷达型号以及不同数据类型的分辨率选择相匹配的格距[14]。对于双偏振产品,其反射率因子分辨率为250 m,单一径向双偏振反射率因子为920个库。计算双偏振数据三维格点位置时,假设雷达天线位置为极坐标原点,则双偏振原始数据的格点坐标(Xo, Yo, Zo)与每一个格点的方位角(a)、仰角(e)和径向距离(l)的计算公式如下:
| $ {X_o} = {\rm{cos}}\left( a \right)\cdot{\rm{sin}}\left( e \right)\cdot l $ | (1) |
| $ {Y_o} = {\rm{cos}}\left( a \right)\cdot{\rm{cos}}\left( e \right)\cdot l $ | (2) |
| $ {Z_o} = {\rm{cos}}\left( e \right)\cdot l $ | (3) |
本文通过插值法将极坐标系中的雷达反射率因子数据内插到笛卡尔坐标系下的三维网格点[15]。首先在笛卡尔坐标系下建立一个如图 1所示的三维网格模型,选取半径230 km数据,每个格点空间分辨率为0.5 km,故对称后确定该模型水平网格数量为920×920;为充分利用网格,减少无效填充,故只取地面以上10 km数据,垂直格点数为20,每个格点空间分辨率为0.5 km。然后根据笛卡尔坐标系中每一个格点的坐标反算出其在极坐标系中的仰角、方位和距离,方便插值中调用[16-17]。为使雷达资料插值过程中尽可能地保留雷达资料的原始回波结构特征, 故使用径向和方位上的最邻近与垂直线性插值法。假设雷达馈源位置为(Xt, Yt, Zt),则根据格点坐标(Xg, Yg, Zg)计算雷达方位角(a)、仰角(e)与距离(r)的公式如下:

|
图 1 三维网格模型 Fig.1 Three-dimensional grid model |
| $ a = {\rm{si}}{{\rm{n}}^{ - 1}}\left[ {{\rm{sin}}\left( {\frac{{\rm{\pi }}}{2} - {Y_g}} \right){\rm{sin}}\left( {{X_g} - {X_t}} \right)/{\rm{sin}}\left( {\frac{s}{R}} \right)} \right] $ | (4) |
式中R为地球半径。弧长s的计算公式如下:
| $ s = R{\rm{co}}{{\rm{s}}^{ - 1}}\left[ \begin{array}{l} {\rm{cos}}\left( {\frac{{\rm{\pi }}}{2} - {Y_t}} \right){\rm{cos}}\left( {\frac{{\rm{\pi }}}{2} - {Y_g}} \right) + \\ {\rm{sin}}\left( {\frac{{\rm{\pi }}}{2} - {Y_t}} \right){\rm{sin}}\left( {\frac{{\rm{\pi }}}{2} - {Y_g}} \right){\rm{cos}}\left( {{X_g} - {X_t}} \right) \end{array} \right] $ | (5) |
三维格点对应仰角e为:
| $ e = {\rm{ta}}{{\rm{n}}^{ - 1}}\left\{ {\frac{{{\rm{cos}}\left( {\frac{s}{n}} \right) - \frac{n}{{n + {Z_g} - {Z_t}}}}}{{{\rm{sin}}\left( {\frac{s}{n}} \right)}}} \right\} $ | (6) |
式中n为大气折射指数,一般取3/4[18]。三维格点距离雷达馈源的距离r为:
| $ r = \frac{{{\rm{sin}}\left( {\frac{s}{n}} \right)\left( {n + {Z_g} - {Z_t}} \right)}}{{{\rm{cos}}\left( e \right)}} $ | (7) |
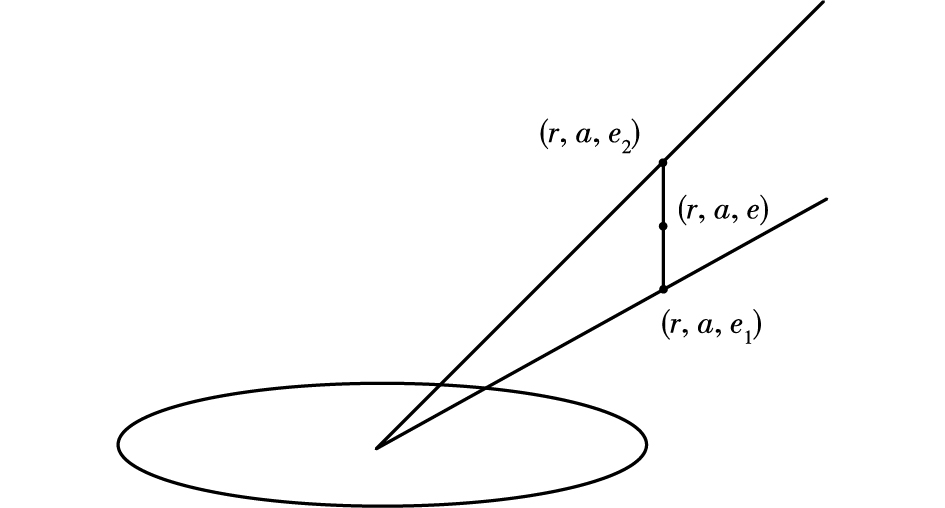
如图 2所示,(r, a, e)为格点在球坐标系中的三维坐标,r、a与e分别为距离、方位角与仰角,三维格点(r, a, e)在垂直方向上的相邻仰角分别为仰角e1与仰角e2,当相邻仰角小于15°时,三维格点(r, a, e)处的属性值可以用方位角相同处的相邻仰角格点属性值近似表示[19]。(r, a, e1)和(r, a, e2)分别为三维格点(r, a, e)垂直方向上的最邻近上点与最邻近下点,故三维格点(r, a, e)处的反射率值f(r, a, e)可通过f(r, a, e1)与f(r, a, e2)插值得到,即:
|
图 2 最邻近与垂直线性插值法 Fig.2 Nearest and vertical linear interpolation |
| $ f\left( {r, a, e} \right) = \frac{{{w_{{e_1}}}f\left( {r, a, {e_1}} \right) + {w_{{e_2}}}f\left( {r, a, {e_2}} \right)}}{{{w_{{e_1}}} + {w_{{e_2}}}}} $ | (8) |
其中we1与we2分别为插值时格点(r, a, e1)与格点(r, a, e2)的权重值:
| $ {w_{{e_1}}} = \frac{{{e_2} - e}}{{{e_2} - {e_1}}} $ | (9) |
| $ {w_{{e_2}}} = \frac{{e - {e_1}}}{{{e_2} - {e_1}}} $ | (10) |
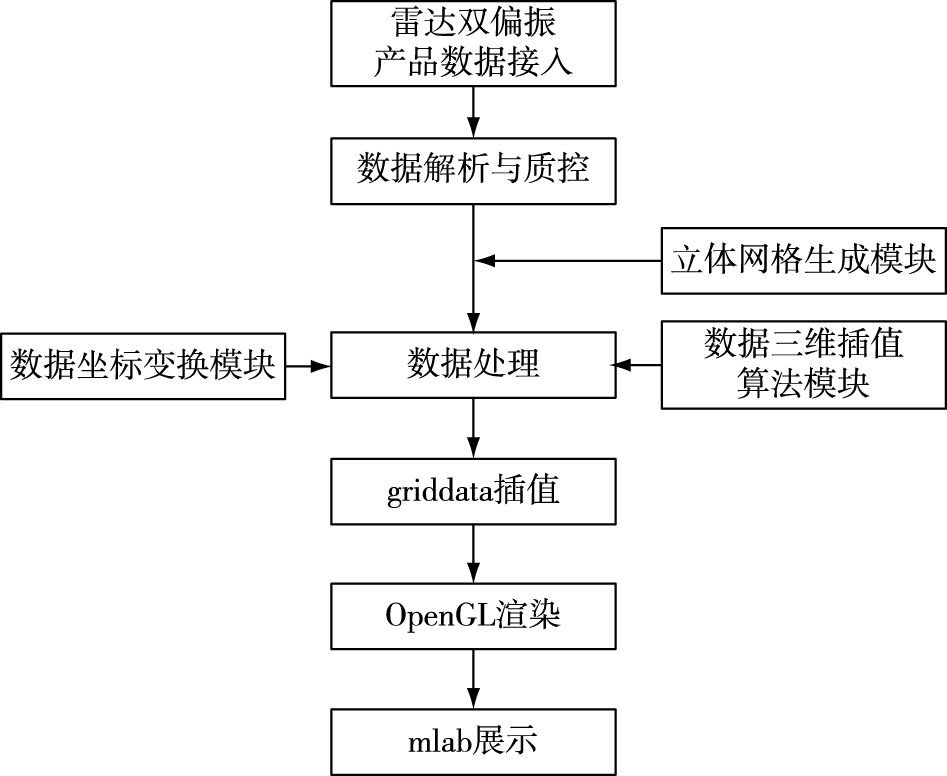
目前利用计算机图形学搭建三维网格模型并对模型填色的方法主要有等值面体绘制法与粒子系统仿真法。由于等值面体绘制法适用于数据量巨大,并且对实况显示速度要求极高的情况,故采用等值面体绘制法对每个体扫仰角的格点按数值填色,位于同一仰角的格点生成等值面体,全部等值面体依次堆叠并通过计算机渲染技术生成全彩立方体[20],计算机三维可视化流程如图 3所示。
|
图 3 计算机三维可视化流程图 Fig.3 Flow chart of computer three-dimensional visualization |
图 3中griddata插值函数调用自Python3.7的scipy库。双偏振雷达回波数据的三维体绘制主要通过Python3.7的Mayavi库实现,Mayavi高度封装的VTK工具包主要负责调用图形模块,并且VTK利用OpenGL来做底层的渲染,可实现网格平滑、锐化过渡、等值线绘制及点线面渲染等三维展示功能[21],mlab库函数调用自Python3.7的Mayavi库。绘图采用的色轴通过Mayavi pipeline中的Launch LUT editor自定义得到,三种双偏振产品的绘制透明度Alpha均设置为0.5,对近场非敏感回波透明度Alpha设置为0.8。
3 三维体绘制个例展示通过个例全面地展示济南雷达双偏振产品的3D显示效果。受西风槽影响,2020年7月5-6日鲁西北东部、鲁中、鲁东南和半岛的部分地区出现雷雨或阵雨天气,局地出现大雨或暴雨并伴随短时强降水、冰雹和大风,潍坊临朐、临沂沂水和日照莒县出现冰雹天气。选取2020年7月6日13:27潍坊临朐境内冰雹为例,济南双偏振雷达观测到东偏南180 km处出现对流风暴(图 4),1.5°仰角强度为64.5 dBZ,高度6.8 km,3.3°仰角强度为61.5 dBZ,高度12.7 km,0 ℃层高度(4.2 km)以上存在强的反射率因子悬垂,属于典型冰雹特征。根据双偏振产品ZDR、KDP与CC的展示效果与侧重点不同,分别对三种产品的二维PPI产品图与三维体绘制效果图进行展示与比较, 其中三维体绘制效果图均可以通过鼠标灵活转动与放大。

|
图 4 2020年7月6日13:27济南雷达不同仰角反射率因子产品(a. 1.5°,b. 3.3°; 单位:dBZ) Fig.4 Radar reflectivity factor at different elevations observed by Jinan Radar at 13:27 BST 6 July, 2020 (a. 1.5°, b. 3.3°; units: dBZ) |
对2020年7月6日13:27济南双偏振雷达ZDR产品进行3D建模,ZDR产品图与ZDR三维体绘制效果图分别如图 5与图 6所示。

|
图 5 2020年7月6日13:27济南雷达不同仰角ZDR产品(a. 0.5°,b. 1.5°,c. 2.4°,d. 3.3°; 单位:dB) Fig.5 ZDR at different elevations observed by Jinan Radar at 13:27 BST 6 July, 2020 (a. 0.5°, b. 1.5°, c. 2.4°, d. 3.3°; units: dB) |

|
图 6 2020年7月6日13:27济南雷达ZDR三维体绘制图(a.前斜视图,b.后斜视图,c.正俯视图,d.正侧视图; 单位:dB) Fig.6 ZDR three-dimensional drawing observed by Jinan radar at 13:27 BST 6 July, 2020 (a. front oblique view, b. rear oblique view, c. top view, d. front side view; units: dB) |
图 5a-d分别为0.5°、1.5°、2.4°与3.3°仰角的济南双偏振雷达ZDR产品,图中蓝色圆圈与冰雹单体强回波区(≥45 dBZ)相对应。可以看出,0.5°仰角强回波区(3.5 km高度)基本对应大的ZDR值,1.5°仰角(6.8 km高度)以上强回波区基本对应偏小的ZDR值,同时强回波区一侧存在明显的旁瓣回波,ZDR表现为正的大值。图 6a-d分别展示了ZDR产品3D体绘制的前后斜视图、正俯视图与正侧视图。对比图 5与图 6发现,180 km左右存在高度较高的ZDR大值区,ZDR大值区既包含ZDR柱的信息,还包括强回波旁瓣产生的ZDR大值区。ZDR柱内含有湿冰粒子或大的液态雨滴,与强上升气流区相对应。
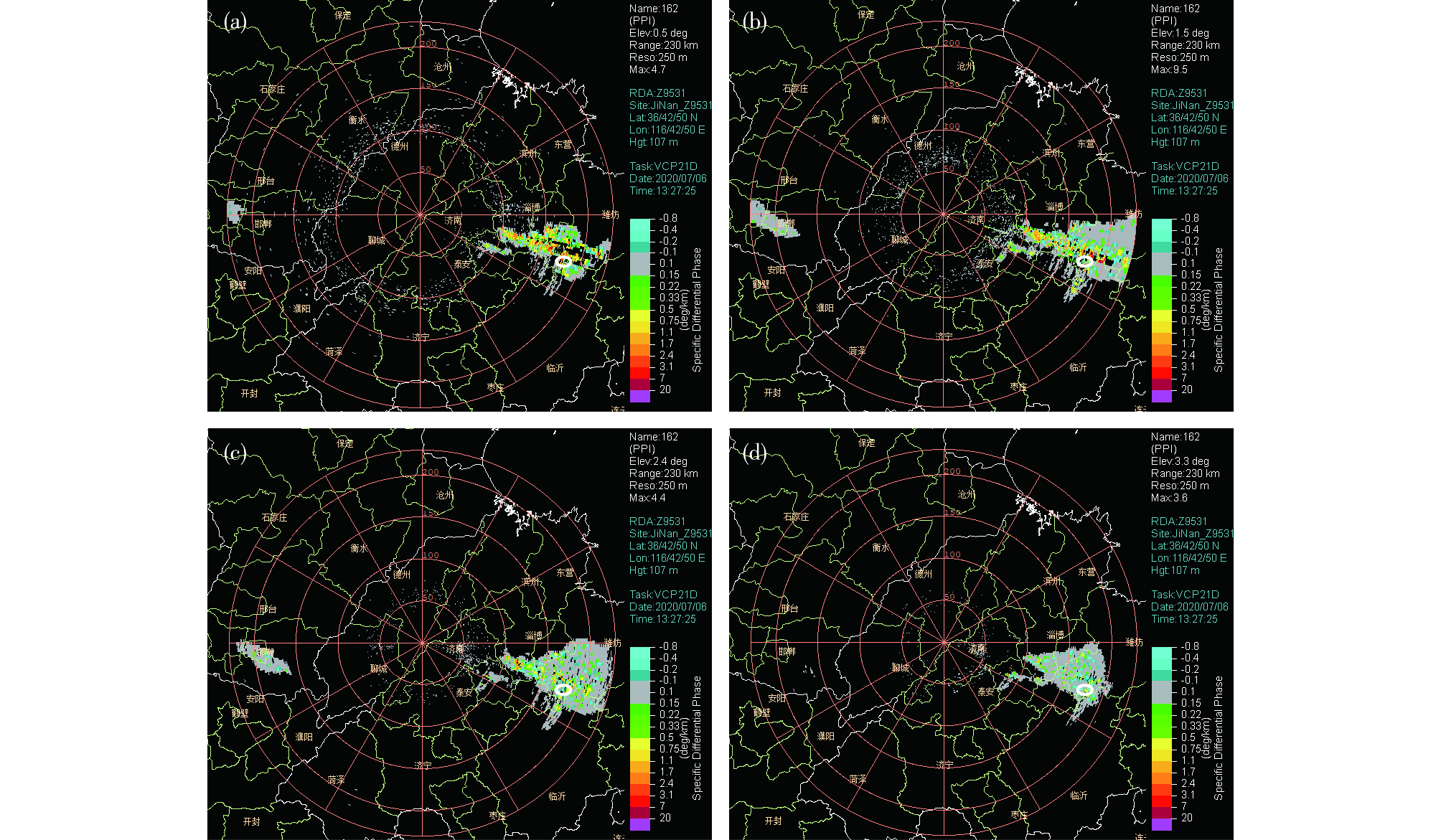
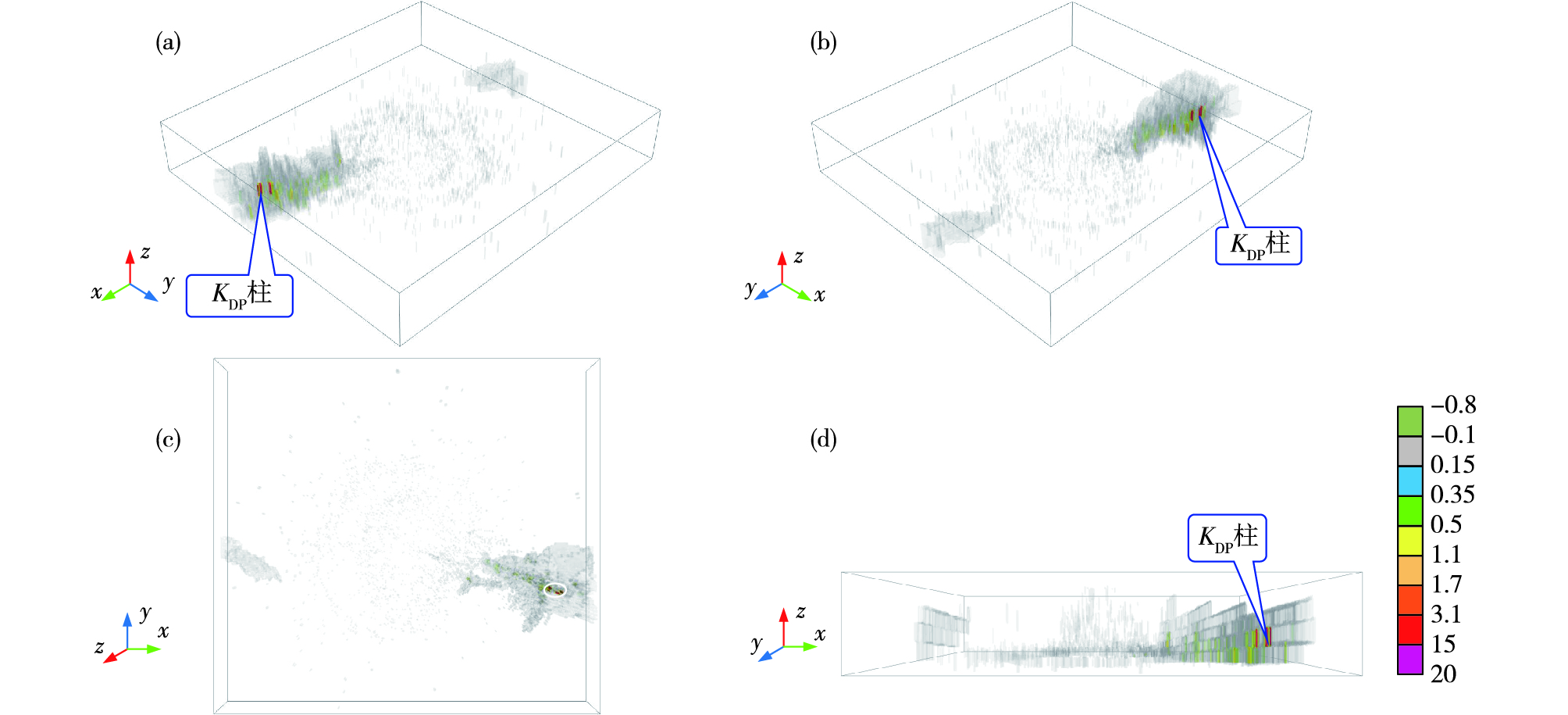
3.2 KDP产品个例展示对2020年7月6日13:27济南双偏振雷达KDP产品进行3D建模,KDP产品图与KDP三维体绘制效果图分别如图 7与图 8所示。
|
图 7 2020年7月6日13:27济南雷达不同仰角KDP产品(a. 0.5°,b. 1.5°,c. 2.4°,d. 3.3°; 单位:(°)·km-1) Fig.7 KDP at different elevations observed by Jinan Radar at 13:27 BST 6 July, 2020 (a. 0.5°, b. 1.5°, c. 2.4°, d. 3.3°; units: (°)·km-1) |
|
图 8 2020年7月6日13:27济南雷达KDP三维体绘制图(a.前斜视图,b.后斜视图,c.正俯视图,d.正侧视图; 单位:(°)·km-1) Fig.8 KDP three-dimensional drawing observed by Jinan radar at 13:27 BST 6 July, 2020 (a. front oblique view, b. rear oblique view, c. top view, d. front side view; units: (°)·km-1) |
图 7a-d分别为0.5°、1.5°、2.4°与3.3°仰角的济南双偏振雷达KDP产品,图中白色圆圈与冰雹单体各层强回波区(≥45 dBZ)相对应。可以看出,0.5°和1.5°仰角强回波区存在大的KDP,2.4°仰角以上KDP明显减小。图 8a-d分别展示了KDP产品3D体绘制前后斜视图、正俯视图与正侧视图。对比图 7与图 8发现,图 8可以透视地展现出云体中KDP大值区,环境0 ℃层高度以上有大的KDP即为KDP柱。KDP柱可作为深厚对流上升气流特征的观测度量[22-25],强上升气流可将一定浓度的液态雨滴或湿冰带至较高的高度而导致大的KDP值,三维KDP体绘制实现了全角度可视,有助于把握强对流回波内部上升气流的强度。
3.3 CC产品个例展示对2020年7月6日13:27济南双偏振雷达CC产品3D建模,CC产品图与CC三维体绘制效果图分别如图 9与图 10所示。
|
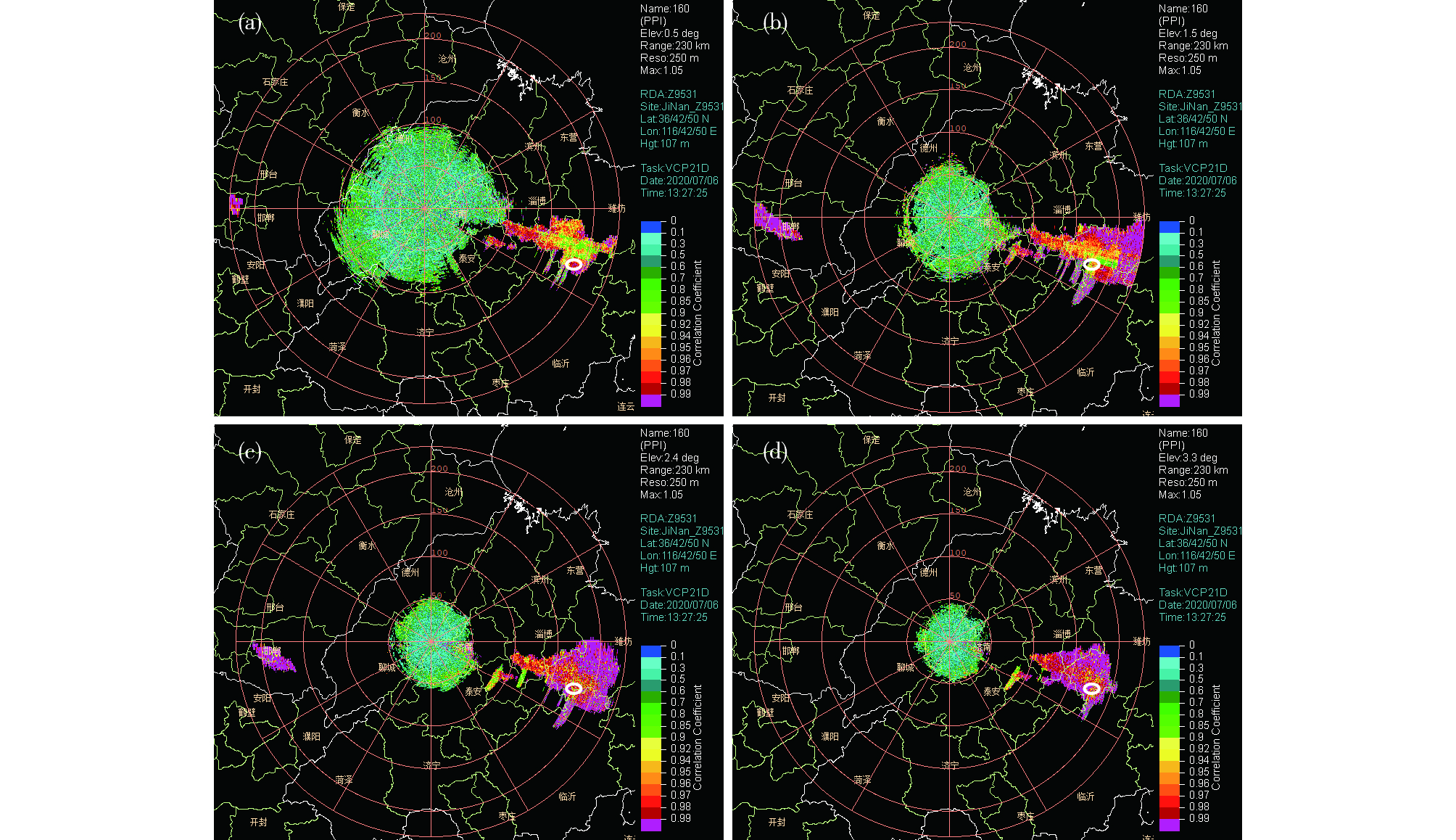
图 9 2020年7月6日13:27济南雷达不同仰角CC产品(a. 0.5°,b. 1.5°,c. 2.4°,d. 3.3°) Fig.9 CC at different elevations observed by Jinan Radar at 13:27 BST 6 July, 2020 (a. 0.5°, b. 1.5°, c. 2.4°, d. 3.3°) |
|
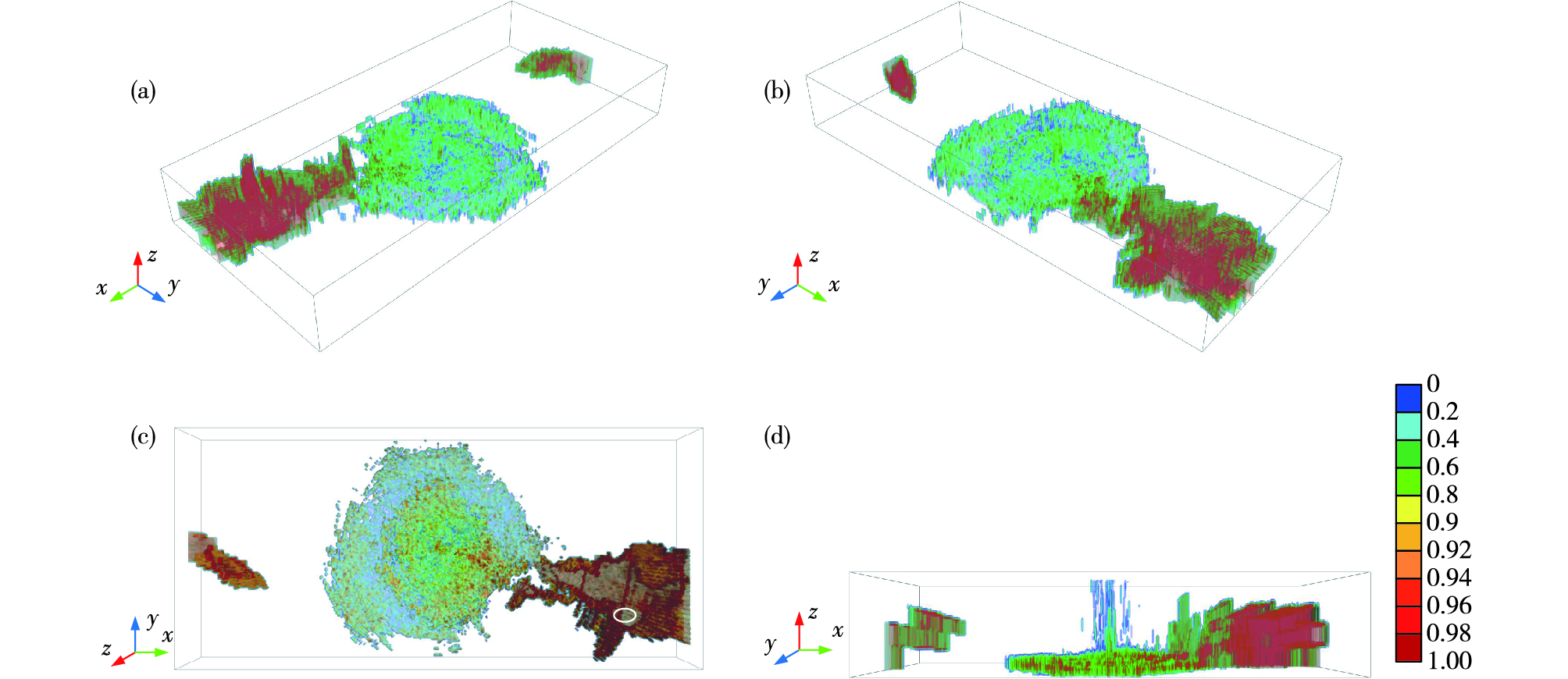
图 10 2020年7月6日13:27济南雷达CC三维体绘制图(a.前斜视图,b.后斜视图,c.正俯视图,d.正侧视图) Fig.10 CC three-dimensional drawing observed by Jinan radar at 13:27 BST 6 July, 2020 (a. front oblique view, b. rear oblique view, c. top view, d. front side view) |
图 9a-d分别为0.5°、1.5°、2.4°与3.3°仰角的济南双偏振雷达CC产品。图中白色圆圈与冰雹单体各层强回波区(≥45 dBZ)相对应。可以看出,0.5°和1.5°仰角强回波区CC较小,表现为冰粒子和液态雨滴共存。图 10a-d分别展示了CC产品3D体绘制的前后斜视图、正俯视图与正侧视图。
4 小结通过对济南雷达双偏振产品的解析与坐标变换,利用Python库函数与计算机图形学插值技术,对ZDR、KDP与CC双偏振产品数据进行了三维立体(3D)建模重绘,实现了CC、KDP与ZDR双偏振产品的三维可视化透视显示。
双偏振产品的三维可视化透视显示对认识风暴强度及强对流风暴双偏振结构特征提供了直观全面的新视角。全角度地展示了强对流风暴发展旺盛阶段在强上升气流作用下常会出现的典型双偏振参量特征如KDP柱和ZDR柱。双偏振产品的三维显示可以清晰识别出ZDR柱和KDP柱,间接表明风暴内部上升气流强度较强,将一定浓度的液态雨滴或湿冰带至环境0 ℃层高度以上,进而可判别风暴的强度,有助于强对流天气的预警。
双偏振产品的三维可视化透视显示有助于气象工作者对风暴结构的直观理解,有效地将回波信息的垂直分布特征与水平分布特征相结合,快速识别风暴发展强度,提高预警技术水平。
| [1] |
苏添记, 葛俊祥, 章火宝. 中国双偏振天气雷达系统发展综述[J]. 海洋气象学报, 2018, 38(1): 62-68. |
| [2] |
赵振东. 泰山CD与济南SA天气雷达探测强冰雹风暴参数对比分析[J]. 海洋气象学报, 2017, 37(2): 102-108. |
| [3] |
王丽荣, 杨荣珍, 李朝华, 等. 多普勒雷达三维拼图资料在强对流天气监测中的应用[J]. 气象与环境学报, 2009, 25(5): 18-23. DOI:10.3969/j.issn.1673-503X.2009.05.004 |
| [4] |
LAKSHMANAN V, SMITH T, HONDL K, et al. A real-time, three-dimensional, rapidly updating, heterogeneous radar merger technique for reflectivity, velocity, and derived products[J]. Wea Forecasting, 2006, 21(5): 802-823. DOI:10.1175/WAF942.1 |
| [5] |
RU Y. Volumetric visualization of NEXRAD Level Ⅱ doppler weather data from multiple sites[D]. West Lafayette: Purdue University, 2007.
|
| [6] |
孟昭林. 基于天气雷达探测数据构建地理空间三维云体技术[J]. 气象科技, 2013, 41(3): 425-429. DOI:10.3969/j.issn.1671-6345.2013.03.001 |
| [7] |
范大伟, 张利平, 张茜, 等. 机场多普勒天气雷达三维显示系统[J]. 气象水文海洋仪器, 2018, 35(3): 55-60. DOI:10.3969/j.issn.1006-009X.2018.03.013 |
| [8] |
文浩, 张乐坚, 梁海河, 等. 基于模糊逻辑的新一代天气雷达径向干扰回波识别算法[J]. 气象学报, 2020, 78(1): 116-127. |
| [9] |
鲍婷婷, 焦圣明, 殷笑茹. 多普勒天气雷达三维可视化分析平台设计与实现[J]. 气象科技, 2020, 48(4): 490-495. |
| [10] |
文浩, 刘黎平, 张扬. 多普勒天气雷达地物回波识别算法改进[J]. 高原气象, 2017, 36(3): 736-749. |
| [11] |
周雪松, 孟金, 姚蔚. 一种基于快速傅里叶变换的多普勒天气雷达弱杂波识别方法[J]. 海洋气象学报, 2019, 39(4): 43-51. |
| [12] |
刘娟. CINRAD/SC新一代天气雷达回波地物检测与校正方法探讨[J]. 气象, 2015, 41(10): 1286-1291. DOI:10.7519/j.issn.1000-0526.2015.10.012 |
| [13] |
杨传凤, 张骞, 陈庆亮, 等. 济南CINRAD/SA雷达双偏振升级关键技术分析[J]. 海洋气象学报, 2019, 39(4): 116-123. |
| [14] |
楚志刚, 银燕, 顾松山. 新一代天气雷达基数据文件格式自动识别方法研究[J]. 计算机与现代化, 2013(7): 180-184. |
| [15] |
周海光. 新一代多普勒天气雷达三维数字化拼图系统研究[J]. 计算机应用研究, 2007, 24(12): 226-227. |
| [16] |
付则鑫, 刘仲能, 蒋慕蓉, 等. 基于立方体网格插值算法的气象雷达数据的三维重建[J]. 计算机科学与应用, 2019, 9(8): 1536-1545. |
| [17] |
刘彩云, 杜宇人. 一种自适应极坐标变换的旋转图像配准方法[J]. 扬州大学学报(自然科学版), 2011, 14(1): 65-69. |
| [18] |
叶飞, 梁海河, 文浩, 等. 基于单站CAPPI格点数据的相邻天气雷达均一性评估系统研究[J]. 气象, 2020, 46(1): 50-62. |
| [19] |
骆兴江. 多普勒天气雷达产品终端及其回波三维显示方法的设计[D]. 南京: 南京信息工程大学, 2008.
|
| [20] |
刘仲能. 基于面绘制的气象雷达数据三维可视化方法研究[D]. 云南: 云南大学, 2017.
|
| [21] |
周权, 徐海萍, 邵立. 基于VPython的三维场景构建在光学教学中的应用[J]. 物理通报, 2015(9): 84-86. |
| [22] |
BRINGI V N, LIU L, KENNEDY P C, et al. Dual multiparameter radar observations of intense convective storms: The 24 June 1992 case study[J]. Meteor Atmos Phys, 1996, 59(1): 3-31. DOI:10.1007/BF01031999 |
| [23] |
HUBBERT J, BRINGI V N, CAREY L D. CSU-CHILL polarimetric radar measurements from a severe hail storm in eastern Colorado[J]. J Appl Meteor Climatol, 1998, 37(8): 749-775. |
| [24] |
ZRNIC D S, LONEY M L, STRAKA J M, et al. Enhanced polarimetric radar signatures above the melting level in a supercell storm[C]. // IEEE. IEEE International Geoscience and Remote Sensing Symposium. Toronto, ON, Canada: IEEE, 2002: 296-298.
|
| [25] |
SNYDER J C, BLUESTEIN H B, DAWSON Ⅱ D T, et al. Simulations of Polarimetric, X-Band Radar Signatures in Supercells. Part Ⅱ: ZDR Columns and Rings and KDP Columns[J]. J Appl Meteor Climatol, 2017, 56(7): 2001-2026. |
 2021, Vol. 41
2021, Vol. 41


