2. 南京市高淳区气象局,江苏 南京 211300;
3. 江苏省气象学会,江苏 南京 210019
2. Gaochun Meteorological Bureau of Nanjing, Nanjing 211300, China;
3. Jiangsu Meteorological Society, Nanjing 210019, China
随着经济的发展,人们已不满足于物质的追求,对精神生活有了更多的需求。近几年来,油菜花节已成为许多地方政府新开发的一项特色农业旅游项目,油菜花期持续时间长,油菜花盛开所呈现的独特风景,吸引大量游客慕名前去采风、观光、踏青。油菜花海旅游成为乡村旅游产业重要的代表品牌,也是当地重要的特色农业旅游项目,具有特点鲜明的美学及经济价值,高淳的“中国·高淳国际慢城金花旅游节”、兴化的“中国·兴化千垛菜花旅游节”等已有十年的历史。因此提前预测油菜开花期,即最佳观赏期,可以为公众最适期踏青赏花和政府招商引资提供科学的指导信息。
油菜盛花期一般持续半个月左右,影响油菜开花期的因素除了品种、种植方式、培育管理差异等外,气候条件对开花期早晚和长短的影响至关重要。有研究表明:就江苏而言,光照和降水对油菜开花早晚影响较小,热量条件是油菜开花早晚的主要限制因子[1];张佩等[2]研究分析了3个表征温度的指标(平均气温低于5 ℃的日数、积温和强冷空气日数)与油菜花期的关系,结果表明平均气温t<5 ℃积温是影响油菜花期主要因子。花期预报的方法多种多样,前人已经做过很多尝试,如花芽形态测量法[3]、周期分析方法[4]、数学公式法和物候法[5]等。本文以高淳为例,利用最优化相关分析法,筛选出影响油菜开花期早晚的最佳地面气象因子以及大尺度气候因子--海面温度、500 hPa高度场环流特征量,从而创建油菜开花期中长期预测模型,提前预报油菜花的最佳观赏期,为油菜花节的旅游气象服务提供理论依据。
1 数据筛选 1.1 气象数据选取来自江苏省气候中心60个气象台站1961-2019年的历年旬平均气温、旬降水量、旬降水日数以及旬日照时数等气象数据; 高淳观测站自1986年有记录以来的农业气象数据,按照《农业气象观测规范》[6],主要包括油菜播种、出苗、现蕾、开花期、结荚期等发育期观测。
1.2 环流特征量数据与海面温度数据由于500 hPa大气环流系统是由超长波、长波和短波大气系统组成,故它们对一般天气条件的影响也存在一定的滞后效应[7];海面温度为西太平洋网格海平面月平均温度,根据长期天气预报原理,海面温度对一般天气条件的影响亦存在一定的滞后效应[8-13],可作为长期天气预报因子。因此,选择来自国家气候中心的影响我国天气过程的88项500 hPa大气环流特征量以及西太平洋(10°S~50°N,120°E~80°W)海面温度(sea surface temperature,SST)资料,水平分辨率为5°×5°,共286个格点。
2 研究方法 2.1 开花期观测数据处理为了方便计算,将开花期进行数字化处理--序日,即:开花期时间序列以1月1日为1,依序向后推算,如2014年3月20日的序日则为79,以此类推。
2.2 膨化处理为了扩大预报因子的信息量,首先对因子进行膨化处理[14-18]。
对气象要素采用因子滑动膨化处理方法,用于确定主要影响时段,即:对m旬n年的气候资料X={xij}; (i=1,2,…,m; j=1,2,…,n)进行膨化,有
| $ x_{q k j}=\sum\limits_{i=k}^{k+q-1} x_{i j} $ | (1) |
式中:q(q=1,2, …, L)为滑动步长; L为最大滑动步长,应取L < m; k(k=1, 2, …, m-q+1)为滑动起始旬。这样处理后,由原来m个旬的资料序列可得到(2m-(L-1))*L/2个资料序列,显著扩大了因子的信息量。
对500 hPa高度场的特征量而言,在同样采用因子滑动膨化处理的基础上,累加后再求其平均值,作为预报因子,则同样增加了因子的信息量。
2.3 最优化因子相关分析技术为了提高预报准确率,针对因变量与自变量之间存在多种关系,采用最优化因子相关分析技术[19-24],对影响因子进行线性和非线性优化处理,使因子合理性判别能力增强。
将气象因子X的线性和非线性(含单调的和非单调的单峰型)化处理归纳为一种通用变换形式:
| $ Q=\left(\frac{|X-b|}{B}+0.5\right)^{a} $ | (2) |
式中:a、b为待定参数,且Xmin≤b≤Xmax,B=max(Xmax-b,b-Xmin)。经上式变换后,Q与Y(Y为因变量)必为单调关系,且(│X-b│/B+0.5)的值在区间[0.5,1.5]内变化。待定参量a、b可用最优化技术求出。令目标函数为
| $f(a, b)=1-R^{2}=\min $ | (3) |
其中,R为a、b取一定值时,Q与Y的相关系数,应用二维寻优的变量转换思路将其分解为一元问题逐步处理。
2.4 稳定性检验与独立性检验为解决所选的相关预报因子的平稳性,本文用滑动相关检验法对因子进行稳定性检验[19-20],淘汰掉某些相关程度前好后差或波动变化较大的因子,以保证预报因子与预报量之间具有稳定、显著的关系。同样针对预报因子之间的多元共线性问题,选用主成分识别法对经过稳定性检验所获得的因子进行独立性检验[21-24],剔除共线性因子,以提高模型的可预报性。
3 结果与分析 3.1 油菜生育期的基本特征以江苏省南京市高淳区为例,为分析生育期的年代际变化规律,选取1990-2019年的观测资料,可以分为整三个年代,分别为20世纪90年代、21世纪00年代和21世纪10年代。对各年代的生育期进行平均,得到各年代各生育期的平均日期(表 1),分析其年代际变化:各年代油菜播种时间较为接近,基本上在9月21日前后; 移栽-成熟期随着年代的递增在逐步提前,提前幅度在1~7 d,其中开花期提前幅度最大,21世纪10年代开花期比21世纪00年代提前2 d、比20世纪90年代提前7 d; 由整个生育期时长来看,21世纪10年代最短,播种期迟于其他两个年代,而收获期又明显提前。
|
|
表 1 高淳油菜生育期(月/日)年代际变化 Table 1 Interdecadal variation of growth period (month/date) of oilseed rape in Gaochun |
张志薇等[1]、张佩等[2]利用通径分析方法,分析了不同气象要素对油菜开花期的影响特征,结果表明热量是江苏地区油菜开花早晚的主要限制因子。因此,本文着重分析了高淳地区30多年油菜开花期与热量条件的关系。当气温t≥3 ℃时油菜开始萌发; 当油菜完成春化作用后,进入温光反应阶段,此时若气温t≥5 ℃,油菜则进入正常生长期,最适宜温度是10 ℃,此时油菜发育最快; 在抽薹到开花期,下限温度是5 ℃,最适宜温度是18 ℃; 在开花到成熟期,下限温度是10 ℃,最适宜温度是20 ℃。由此可见t≥3 ℃、t≥5 ℃、t≥10 ℃三个临界温度,对油菜的生长发育期非常重要,而有效积温能较好表征温度条件的累积效应,所以分别计算大于等于这三个临界温度的有效积温,以此探讨其与油菜开花期的相关性。
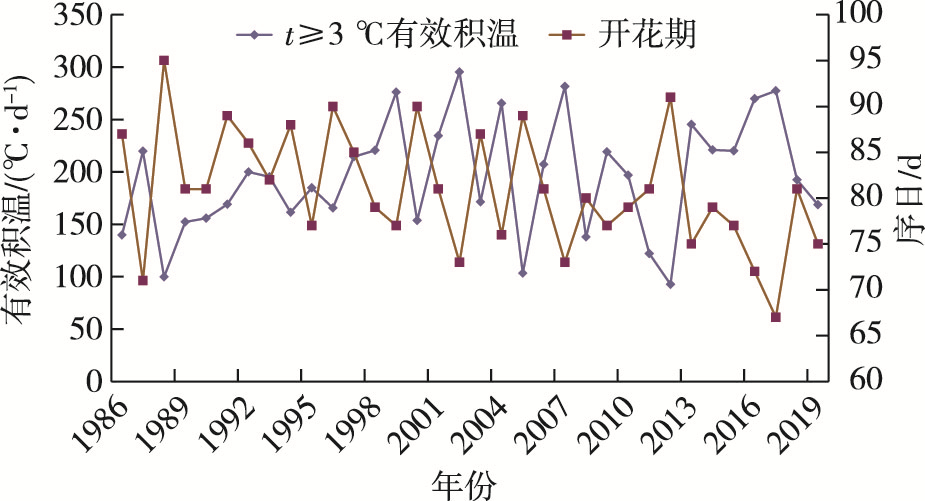
首先,分时段统计1986年以来各类积温,即:10月上旬-次年3月上旬与1月上旬-3月上旬两个时段的总积温、正积温、t≥3 ℃的有效积温、t≥5 ℃的有效积温、t≥10 ℃的有效积温,越冬期(1月上旬-2月下旬)负积温。其次,计算各时段各类积温与油菜开花期的相关系数,由表 2可见,除t≥10 ℃的有效积温和负积温外,油菜开花期与其他各类积温的相关系数均达到了极显著水平,尤其是与1月上旬至3月上旬t≥3 ℃有效积温的相关系数高达-0.772,呈明显的负相关(图 1),亦符合油菜生长的生物学特性。
|
|
表 2 各时段各类积温与油菜花期的相关系数 Table 2 Correlation coefficients between varied accumulated temperature and oilseed rape florescence in different periods |
|
图 1 1986-2019年1月上旬至3月上旬t≥3 ℃的有效积温与油菜开花期的时间序列 Fig.1 Time series of effective accumulated temperature of t equal to or higher than 3 ℃ and oilseed rape florescence from early January to early March from 1986 to 2019 |
为解决仅用温度作为建模因子过于单一的问题,根据油菜种植特点和生理特征:油菜一般是上一年的9月中下旬播种,经过冬季春化作用,至当年的5月中旬收获,通常情况下在当年的3月中下旬达到开花普遍期。因此选择地面多个气象要素作为建模因子,时间从上一年的9月上旬至当年2月下旬作为花期的建模因子,可提前一个旬做出预报。
500 hPa大气环流系统由超长波、长波和短波系统组成,它表征了大气经向和纬向环流、副热带高压(以下简称“副高”)、东西槽、印缅槽、西藏高原、南方涛动指数及极涡等大形势天气过程的活动情况,故它们对一般天气条件的影响也存在一定的滞后效应[7-8]。因此,选择影响我国天气过程的88项500 hPa大气环流特征量作为自变量,分析其与油菜开花期之间的关系。高淳油菜开花期为3月中下旬,考虑数据来源和预报时效,选取上一年1月-当年1月的环流特征量进行相关分析,建立预测模型,可提前一个月做出预报。
众所周知,海面温度可作为长期天气预报因子,天气条件又影响油菜花期的迟早。由长期天气预报的观点看,海面温度对一般天气条件的影响同样存在一定的滞后效应[7]。因此,选择西太平洋(10°S~50°N,120°E~80°W)海区5°×5°(共286个)的海面温度(sea surface temperature, SST)资料作为自变量,分析其与油菜开花期之间的关系。高淳油菜开花期为3月中下旬,考虑数据来源和预报时效,选取上一年1月-当年1月的SST进行相关分析,建立预测模型,可提前一个月做出预报。
3.3.2 油菜开花期中长期预测模型的建立已考虑建模因子相关的最优化、显著性、稳定性和独立性,因此,由自变量组合的联立方程可以达到非奇异。利用逐步回归方法,筛选出贡献最大的因子,建立稳定可靠的预报模式。因此,基于地面气象要素、500 hPa环流特征量以及北太平洋海面温度,创建了油菜开花期气象中期预报模型、环流和SST长期预测模型,见表 3-5。
|
|
表 3 基于地面气象要素创建的油菜开花期气象中期预报模型 Table 3 Mid-term meteorological predicting model for oilseed rape florescence based on surface meteorological elements |
|
|
表 4 基于500 hPa环流特征量创建的油菜开花期环流长期预报模型 Table 4 Long-term predicting model for oilseed rape florescence based on circulation data at 500 hPa |
|
|
表 5 基于北太平洋海面温度创建的油菜开花期SST长期预报模型 Table 5 Long-term predicting model for oilseed rape florescence based on SST in North Pacific |
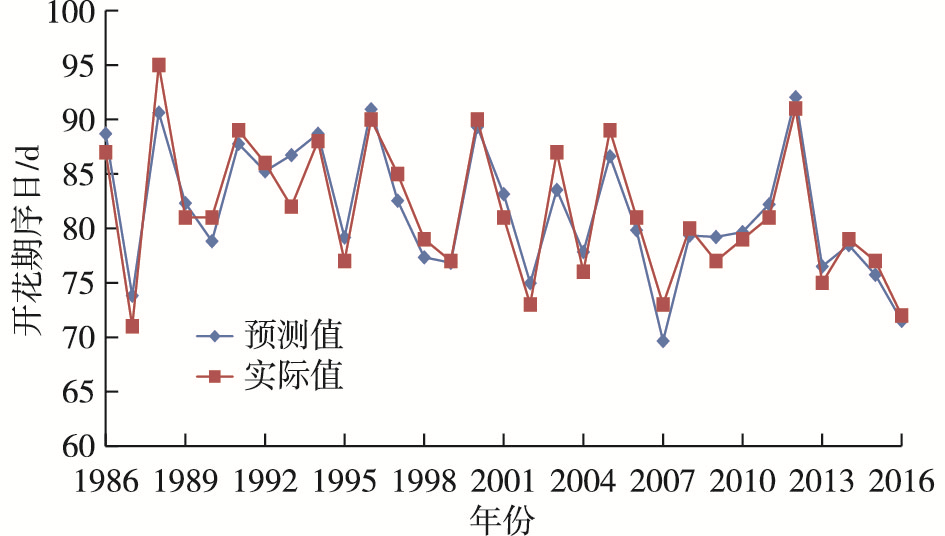
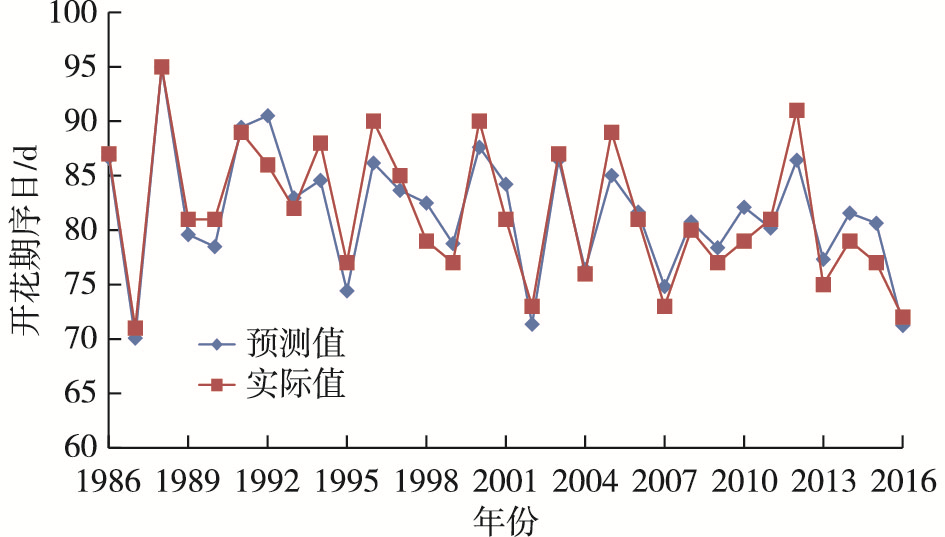
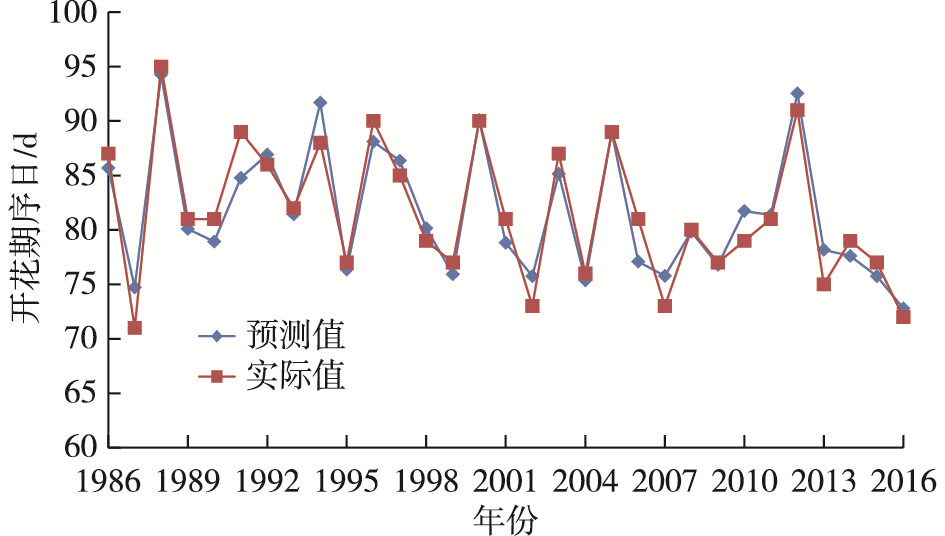
对开花期中长期预测模型进行回代检验,计算出油菜开花期的历史拟合值,与实际观测值进行比较(图 2-4)发现:三种预报模型的历史拟合效果均较好,所有模型都通过了α=0.001的显著性检验。由气象中期预测模型模拟结果(图 2)来看,大部分年份误差均在0~2 d之间; 由环流长期预测模型模拟结果(图 3)来看,有4/5年份误差在0~2 d之间,最大误差为4 d; 由SST长期预测模型模拟结果(图 4)来看,有2/3年份误差在0~2 d之间,最大误差为5 d(仅2012年); 说明油菜开花期的模拟值与实际值不仅波动趋势一致,而且数值也非常接近,模拟效果理想。
|
图 2 1986-2016年油菜开花期气象中期预报模型历史模拟值与实际观测值 Fig.2 Observed and simulated oilseed rape florescence days by mid-term meteorological predicting model from 1986 to 2016 |
|
图 3 1986-2016年油菜开花期环流长期预报模型历史模拟值与实际观测值 Fig.3 Observed and simulated oilseed rape florescence days by long-term predicting model based on circulation from 1986 to 2016 |
|
图 4 1986-2016年油菜开花期SST长期预报模型历史模拟值与实际观测值 Fig.4 Observed and simulated oilseed rape florescence days by long-term predicting model based on SST from 1986 to 2016 |
另外利用开花期的气象中期模型、环流和海温长期模型的复相关系数作为加权系数,对三种模型的预报结果进行加权平均,集成拟合效果更好(表 6),最大误差仅2 d。
|
|
表 6 油菜开花期集成预报历史回代模拟结果与实际观测值 Table 6 Observed and simulated oilseed rape florescence days by ensemble prediction from 1986 to 2016 |
利用2017-2019年资料作为独立样本,进行油菜开花期气象、环流和SST中长期预测模型试报检验,试报检验结果见表 7,可以看出,开花期预测最大误差为3 d,集成预报准确率相对更高,可见开花期的预测模型可提前10~30 d做出预报,效果理想。
|
|
表 7 油菜开花期中长期预测模型预报检验结果 Table 7 Performance of mid-term and long-term predicting models for oilseed rape florescence |
1) 通过分析高淳油菜农业气象观测数据,结果发现:就年代变化特征而言,21世纪10年代以来播种期偏晚,收获明显提前,整个生育期在缩短; 油菜开花期确实与热量关系密切,尤其是与t≥3 ℃有效积温的相关系数为-0.772,达到信度α=0.001极显著水平。
2) 油菜开花期与温度气象要素关系密切,温度的高低同样会受到其他气象要素的影响,随着其他气象要素的变化而变化,单从温度一个因子来建立预测模型,效果欠佳,因此本文除了温度外还利用降水量、降水日数、日照以及光温积和降水强度等气象要素建立模型,使得预报时效提前了10 d,模型的历史拟合率高,三年试报效果好。
3) 根据天气学原理,500 hPa环流特征量以及西太平洋海面温度可以左右地面气象条件的变化,因此也可作为油菜开花期的长期预报因子,创建油菜开花期长期预测模型并通过了α=0.001显著水平,预报时效提前了30 d左右,试报效果良好,说明预测模型切实可用。
4) 利用气象、环流和SST模型的复相关系数作为加权系数,对三种模型的预报结果进行加权平均,综合集成后,不论是历史拟合结果,还是三年试报效果,均比单一模型的效果更好,同时集成预报的时效也可提前10 d做出开花期预报。
| [1] |
张志薇, 高苹, 王宏斌, 等. 油菜花最佳观赏期变化及其对温度因子的响应[J]. 气象, 2019, 45(5): 667-675. |
| [2] |
张佩, 高苹, 钱忠海, 等. 油菜花期物候主要限制因子分析及预报模型的构建[J]. 气象, 2020, 46(2): 234-244. |
| [3] |
张明庆, 杨国栋, 许晓波. 树木花期预报的花芽形态测量法研究: 以大山樱花期预报为例[J]. 植物生态学报, 2005, 29(4): 610-614. DOI:10.3321/j.issn:1005-264X.2005.04.012 |
| [4] |
李军. 桃始花期的长期预报模型[J]. 西北植物学报, 2005, 25(9): 1876-1878. DOI:10.3321/j.issn:1000-4025.2005.09.030 |
| [5] |
吕清华, 张红霞, 潘爱芳. 阳信鸭梨花期预测方法初报[J]. 山西果树, 2008(1): 14-15. DOI:10.3969/j.issn.1005-345X.2008.01.006 |
| [6] |
黄健, 成秀虎. 农业气象观测规范[M]. 北京: 气象出版社, 1993.
|
| [7] |
章基嘉, 葛玲. 中长期天气预报基础[M]. 北京: 气象出版社, 1983: 108-174.
|
| [8] |
梁必骥. 天气学[M]. 北京: 气象出版社, 1980: 281-323.
|
| [9] |
刘梅, 高苹, 王静再, 等. 江苏夏季逐月高温日数与西太平洋海温场相关分析及预测模型建立[J]. 气象, 2011, 37(12): 1553-1559. DOI:10.7519/j.issn.1000-0526.2011.12.011 |
| [10] |
汪靖, 吕江津. 天津地区雨季降水异常年大气环流特征分析[J]. 气象, 2011, 37(8): 950-955. |
| [11] |
邓伟涛, 孙照渤, 曾刚, 等. 中国东部夏季降水型的年代际变化及其与北太平洋海温的关系[J]. 大气科学, 2009, 33(4): 835-846. DOI:10.3878/j.issn.1006-9895.2009.04.16 |
| [12] |
钱维宏, 朱江, 王永光, 等. 江淮梅雨和赤道太平洋区域海温变化的关系[J]. 科学通报, 2009, 54(l): 79-84. |
| [13] |
贾小龙, 陈丽娟, 龚振淞, 等. 2010年海洋和大气环流异常及对中国气候的影响[J]. 气象, 2011, 37(4): 446-453. DOI:10.3969/j.issn.1006-7639.2011.04.009 |
| [14] |
汤志成, 高苹. 作物产量预报系统[J]. 中国农业气象, 1996, 17(2): 49-52. |
| [15] |
魏凤英. 现代气候统计诊断与预测技术[M]. 北京: 气象出版社, 2007.
|
| [16] |
徐敏, 徐经纬, 高苹, 等. 基于大尺度因子的江苏稻区稻瘟病气象等级长期预测[J]. 植物保护, 2017, 43(4): 36-41. DOI:10.3969/j.issn.0529-1542.2017.04.006 |
| [17] |
徐敏, 高苹, 刘文菁, 等. 水稻稻曲病气象等级预报模型及集成方法[J]. 江苏农业科学, 2017, 45(17): 95-98. |
| [18] |
徐敏, 吴洪颜, 张佩, 等. 基于气候适宜度的江苏水稻气候年景预测方法[J]. 气象, 2018, 44(9): 1200-1207. |
| [19] |
朱盛明, 曲学实. 数值预报产品统计解释技术的进展[M]. 北京: 气象出版社, 1988: l12-116.
|
| [20] |
汤志成, 孙涵. 最优化因子处理及加权多重回归模型[J]. 气象学报, 1996, 50(4): 514-517. |
| [21] |
张启锐. 实用回归分析[M]. 北京: 地质出版社, 1988: 196-203.
|
| [22] |
高苹, 武金岗, 杨荣明, 等. 江苏省稻纵卷叶螟迁入期虫情指标与西太平洋海温的遥相关及其长期预报模型的研究[J]. 应用生态学报, 2008, 19(8): 2056-2066. |
| [23] |
高苹, 张佩, 谢小萍, 等. 基于海温和环流特征量的江苏省小麦适播期预测[J]. 气象, 2012, 38(12): 1572-1578. |
| [24] |
高苹, 徐敏, 徐经纬, 等. 基于大尺度海温因子的江苏省水稻适宜移栽期预报模型研究[J]. 气象, 2015, 41(11): 1439-1445. |
 2021, Vol. 41
2021, Vol. 41


