2. 山东省气候中心,山东 济南 250031
2. Shandong Climate Center, Jinan 250031, China
在气候变暖、常规能源日益紧张、环境恶化和压力增大背景下,高效利用太阳能等清洁能源已经得到世界各国的广泛关注[1]。随着技术逐步成熟,成本不断下降,太阳能发电将成为大城市的主要替代能源。大规模的太阳能资源利用以光电为主,而太阳辐射是影响光伏发电效率的最重要因素,但太阳辐射单位面积的能量密度低,日内、年内变化幅度大,且受气象条件、地理因素的影响显著,导致光伏发电效率具有较大的不连续性和不稳定性[2]。为了提高光电转换效率,保证电网安全,精准的光伏发电预测和评估显得尤为重要[3]。
近年来,国内外学者在太阳辐射预报和评估技术方面做了大量的研究,太阳辐射预报方法主要有基于实时和历史数据的统计方法或人工智能方法,基于卫星云图外推技术的0~5 h预测,还有基于数值模式结果的统计订正方法,预报时效可达数天[4-5]。WRF等数值模式系统是开展太阳能资源评估和预测的有效手段之一,可以使用模式输出的太阳辐射量[2, 6-7]、其他变量[8-10]、模式预报和观测数据建立预测模型[11-12]等方法进行太阳能评估和预测。天文因子、地理因子、气候和环境因子等要素是影响地面太阳辐射的主要因素,各因子间相互作用和影响会造成WRF模拟太阳辐射结果误差较大、可靠性低,需对结果进行订正后使用。研究发现,云[13-15]、气溶胶[15-18]等的间接效应是影响太阳辐射的主要因素之一,但在WRF模式中没有充分考虑气溶胶对辐射的影响,导致模式模拟的总辐射、直接辐射值偏高,散射辐射值偏低[17]。WRF-Solar模式[19]是美国国家大气研究中心(National Center for Atmospheric Research, NCAR)专门为太阳能资源评估和预报发展的天气预报模型,WRF-Solar模式考虑了气溶胶对辐射的直接影响,增加了云与辐射的反馈机制,显著提升了太阳辐射的评估和预报效果。WRF-Solar模式已经在美国[20-25]、科威特[26]、阿拉伯半岛[27]、西班牙[28]、新加坡[29]以及中国宁夏[3]、内蒙古[30]等地区进行了总辐射预测应用研究,相对于WRF模式,大多数研究结果表明WRF-Solar模式在不同的天气条件下,总辐射预测效果得到明显改善。
山东的太阳能资源较丰富,开发利用前景较高[31]。山东地处我国中东部沿海,区域内下垫面特征复杂,属暖温带季风气候区,夏季高温多雨,冬季寒冷干燥,年平均日照时数在2 442 h左右[32]。山东太阳能资源评估结果多是基于太阳辐射观测数据的气候学方法计算得到的[31, 33-35],而基于数值模式或其他方法的太阳能资源评估和预报成果极少见。采用专门为太阳能资源评估和预报设计的WRF-Solar模式,通过设置不同总辐射模拟方案,研究WRF-Solar模式在山东区域不同天气条件下总辐射的模拟效果,将对进一步提高区域辐射评估和预报的准确率,为区域太阳能光伏发电预报具有重要的指导意义。
1 资料和方法 1.1 研究资料 1.1.1 再分析资料采用ERA-Interim水平分辨率0.75°×0.75°的再分析资料作为WRF-Solar数值模式大尺度气象背景场和边界条件,时间间隔为6 h(00时、06时、12时、18时,世界时)。ERA-Interim是欧洲中期天气预报中心(European Centre for Medium-Range Weather Forecasts, ECMWF)第三代再分析资料,能够提供1979年以来的全球再分析资料,并不断更新,采用四维变分同化技术,结合改进的卫星数据误差校正等技术,相对于前两代(ERA-15、ERA-40)再分析资料来说,实现了再分析资料质量的提升[36]。
1.1.2 MODIS资料MODIS传感器是搭载于TERRA和AQUA卫星上的重要传感器,其提供的全球观测资料可广泛用于气溶胶等的高分辨率监测,其数据可靠性已得到国内外学者的认可[37]。本研究所用AOD550 nm数据为MOD08_M3产品暗算法与深蓝算法结合的气溶胶光学厚度数据[38],此数据包括逐日和月平均值,空间分辨率是1°×1°。使用前先将逐月气溶胶数据转为静态资料,即可在模式积分过程中调用[3]。
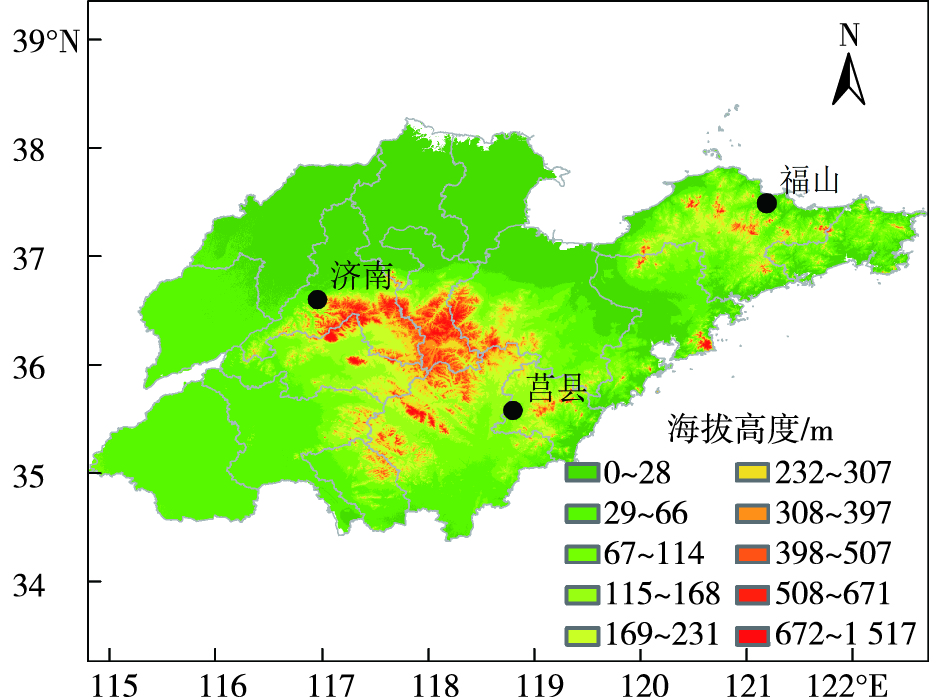
1.1.3 气象站观测资料选取山东区域济南、福山、莒县3个太阳辐射观测站2018年9月1日至2019年8月31日逐时总辐射数据检验WRF-Solar数值模式的总辐射模拟结果。3个太阳辐射观测站地理位置空间分布见图 1。逐时总辐射资料来源于山东省气象信息中心,在进行总辐射模拟结果检验前,首先对各站总辐射逐时观测结果进行气候极值检验、时间一致性和空间一致性检验,保证各站逐时总辐射数据的质量可靠性。
|
图 1 山东区域海拔高度和辐射观测站空间分布 Fig.1 Topography and distribution of solar radiation observation stations in Shandong province |
文中晴天、阴天、雨天的划分使用的是日总降水量和定时平均总云量数据,当某日降水量为0 mm且总云量少于3成时,定义该日为晴天;当某日降水量为0 mm且总云量多于3成时,定义该日为阴天;当某日降水量≥0.1 mm且总云量多于3成时,定义该日为雨天。以此标准分别统计各太阳辐射观测站模拟时段四季代表月晴天、阴天和雨天。由于莒县站没有总云量观测数据,该站总云量以日照站总云量数据代替。按照能见度低于1 km为低能见度的标准[39-40],统计得到福山、济南、莒县四季代表月低能见度日分别有11 d、12 d、15 d,其中福山站冬季、春季、夏季、秋季分别有1 d、3 d、3 d、4 d,济南站分别有1 d、4 d、4 d、3 d,莒县站分别有2 d、2 d、5 d、6 d。
1.2 研究方法 1.2.1 WRF-Solar模式简介WRF-Solar数值模式是专门为太阳能资源评估和预报需求设计的数值天气预报模型,是NCAR太阳能发电预测系统的重要组成部分,是基于WRF模式3.6版本开发的扩展模型[18]。WRF-Solar模式通过考虑云、气溶胶和太阳辐射之间的反馈过程,可以计算模式每个时间步长的总辐射、直接辐射和间接辐射,这对太阳能资源评估和预测极为重要。WRF-Solar模式每5 min更新一次[36],可以根据需要单独输出总辐射、直接辐射和间接辐射。
WRF-Solar模式的主要改进包括:1)改进了太阳位置算法,解决了由于地球轨道偏心率和倾斜导致的总辐射模拟的超前和滞后问题。2)使用辐射参数化方案可以计算输出每个时间步长的总辐射、直接辐射和间接辐射[41]。3)使用了一种避免计算三维加热率,但能提供地面总辐射的快速辐射传输方案[42]。4)采用了一种气溶胶对辐射吸收和散射的参数化方案[43]。5)增强了气溶胶和云的相互作用,这种相互作用改变了云的演变和气溶胶特性[44]。6)通过浅积云参数化方案实现次网格云物理过程对短波辐射的反馈[45]。
1.2.2 模拟方案设置通过对总辐射模拟相关文献[2, 6, 8-12, 20-29]的调研和对比,本研究利用WRF-Solar模式,通过选取不同的积云对流参数化方案、长短波辐射方案以及利用气溶胶数据对山东区域的逐时总辐射进行模拟,使用济南、福山、莒县3站逐时总辐射观测数据对相应的总辐射模拟结果进行对比检验,确定山东区域较优的总辐射模拟方案。设置的模拟检验对比方案和选取的参数化方案详见表 1和表 2。其中方案五使用的物理参数化方案是基于方案一至方案四的总辐射模拟检验结果,确定山东总辐射模拟效果较好的方案,将AOD550 nm数据设置为恒定值0进行总辐射模拟,用来对比检验加与不加气溶胶数据对总辐射模拟效果的影响。
|
|
表 1 WRF-Solar模式模拟方案设置 Table 1 Settings of different simulation schemes using for the WRF-Solar model |
|
|
表 2 WRF-Solar模式参数配置 Table 2 Configurations of the WRF-Solar model |
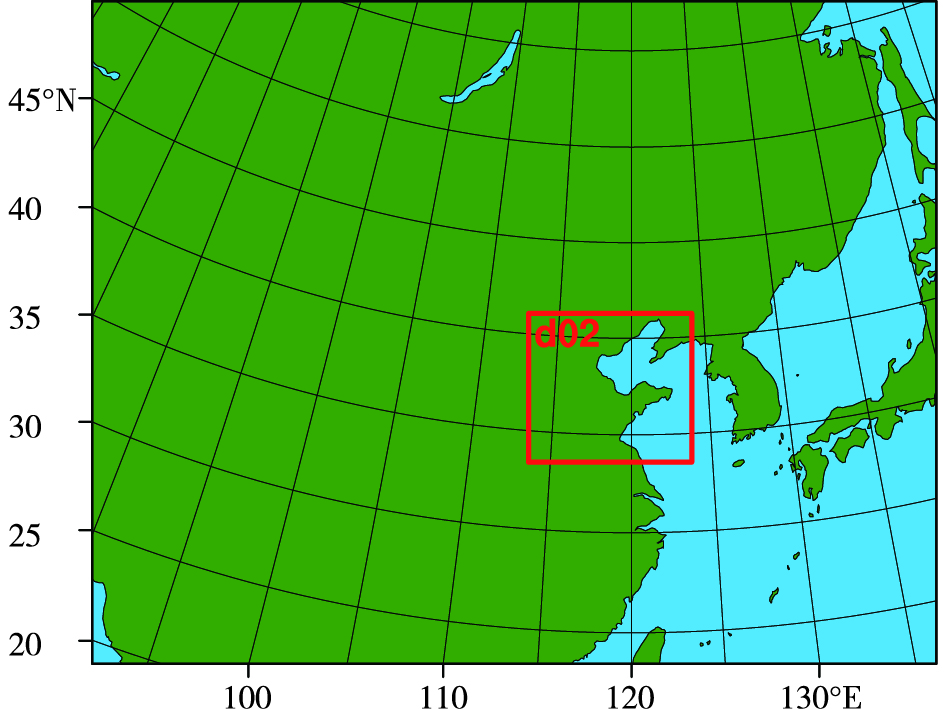
总辐射各模拟方案均设置为双重嵌套,外层模拟区域包括中国中东部大部分区域,范围为19°~49°N,92°~136°E,网格点水平分辨率为27 km,内层模拟区域为山东和环渤海区域,范围为34°~41°N,114°~124°E,网格点水平分辨率为9 km,详见图 2,选用的其他主要物理过程参数化方案见表 2。
|
图 2 WRF-Solar模式双重区域示意图 Fig.2 Two domains of WRF-Solar model in simulation area |
针对5种不同总辐射模拟方案,选取2018年9月1日至2019年8月31日的四季代表月(春季为2019年4月,夏季为2019年7月,秋季为2018年10月,冬季为2019年1月)作为各模拟方案模拟结果对比检验时段,分别对比分析典型日逐时总辐射模拟效果,确定山东区域较优的总辐射模拟技术方案。总辐射模拟起始时间为每日14时(北京时,下同),每个模拟个例模拟时长为31 h,舍弃前6 h总辐射模拟结果,选取第7~30小时(21时至次日20时)总辐射模拟结果作为研究对象,第二层模拟区域总辐射逐时整点输出,分别统计得到逐日、逐月等不同时段总辐射模拟结果。
1.2.3 模拟结果检验方法针对3个太阳辐射站逐时辐照量模拟统计结果和观测统计结果,采用相关系数、平均偏差(MB)、均方根误差(RMSE)等检验方法对辐照量模拟结果进行对比检验,分析WRF-Solar模式的不同时段总辐射模拟统计结果在山东区域的模拟能力和可靠性。
| $ r=\frac{\sum\limits_{i=1}^{n}\left(O_{i}-\bar{O}\right)\left(P_{i}-\bar{P}\right)}{\sqrt{\sum\limits_{i=1}^{n}\left(O_{i}-\bar{O}\right)^{2} \sum\limits_{i=1}^{n}\left(P_{i}-\bar{P}\right)^{2}}} $ | (1) |
| $ M B=\frac{1}{n} \sum\limits_{i=1}^{n}\left(P_{i}-O_{i}\right) $ | (2) |
| $ R M S E=\sqrt{\frac{1}{n} \sum\limits_{i=1}^{n}\left(P_{i}-O_{i}\right)^{2}} $ | (3) |
式中:r为相关系数,Pi为第i个总辐射模拟值,Oi为第i个总辐射观测值,n为时间样本总数,P 为总辐射模拟值的平均,O 为总辐射观测值的平均。在上述误差统计参数中,平均偏差、均方根误差越小表示模拟值和观测值之间的差异越小;相关系数越接近1表明模拟值和观测值之间的时空变化趋势吻合得越好,越接近0表明模拟值和观测值之间吻合得越差。
2 结果分析 2.1 模拟个例结果检验 2.1.1 晴天选取2018年10月23日作为总辐射晴天模拟个例,当日济南、福山和莒县总云量均为0,济南、福山、莒县均无降水。各模拟方案逐时总辐射模拟和观测对比结果见图 3a-c和图 4a、b。方案一至方案四总辐射模拟结果差异较小,且与观测结果接近,其中福山站各模拟方案总辐射平均偏差在26.9~39.5 W·m-2之间,均方根误差在32.8~46.0 W·m-2之间,济南站总辐射平均偏差在9.7~22.7 W·m-2之间,均方根误差在28.4~36.7 W·m-2之间,各时次总辐射模拟值与观测值相差较小。莒县站总辐射平均偏差在63.6 ~76.7 W·m-2之间,均方根误差在69.3~83.4 W·m-2之间,正午前后模拟和观测结果相差相对较大。总体上看,晴天条件下,采用RRTMG长、短波辐射方案的方案四各站总辐射模拟结果误差相对最小,方案一次之,采用new Goddard长、短波辐射方案的方案二和方案三对山东总辐射的模拟效果略差。

|
图 3 晴天(a、b、c)、阴天(d、e、f)、雨天(g、h、i)个例各模拟方案逐时总辐射模拟与实测结果对比(单位:W·m-2) Fig.3 Comparisons between hourly solar irradiance simulations and observations (units: W·m-2) on sunny day (a, b, c), cloudy day (d, e, f) and rainy day (h, g, i) cases for each simulation scheme |

|
图 4 晴天(a、b)、阴天(c、d)、雨天(e、f)个例各模拟方案总辐射平均偏差(a、c、e)、均方根误差(b、d、f)(单位:W·m-2) Fig.4 Mean bias (a, c, e; units: W·m-2) and root mean square error (b, d, f; units: W·m-2) of each simulation scheme on sunny day (a, b), cloudy day (c, d) and rainy day (e, f) cases |
选取2019年7月16日作为总辐射阴天模拟个例,当日济南、福山总云量均超过9层,莒县总云量为8成,济南、莒县无降水,福山降水量为0.1 mm。各模拟方案逐时总辐射模拟和观测对比结果见图 3d-f和图 4c、d。可见,不同模拟方案总辐射模拟结果相差较大,方案三模拟结果与观测结果最接近,方案一偏差相对最大。福山站总辐射观测值与各方案模拟值在11时以后相差较大,各模拟方案平均偏差在146.3~206.6 W·m-2之间,均方根误差在207.0~267.8 W·m-2之间。济南站总辐射平均偏差在33.5~129.7 W·m-2之间,均方根误差在202.2~261.7 W·m-2之间,10-12时总辐射观测值大于模拟值。莒县站总辐射平均偏差在136.6~242.8 W·m-2之间,均方根误差在182.8~289.0 W·m-2之间。对于阴、雨天来说,总辐射观测结果逐时波动较大,而不同模拟方案逐时模拟结果波动相对较小,且模拟和观测的总辐射差别较大,总辐射模拟结果误差相对较大。
2.1.3 雨天选取2019年4月9日作为雨天模拟个例,当日福山、济南和莒县总云量均为10成,济南、福山、莒县日降水量分别为11.6 mm、17.3 mm、15.7 mm,各模拟方案逐时总辐射模拟和观测对比结果见图 3g-i和图 4e、f。该模拟个例逐时总辐射观测结果均小于100.0 W·m-2,云和降水对总辐射观测结果影响明显,但方案一和方案四总辐射模拟结果对云和降水影响反应较弱,与观测结果偏差最大,方案二和方案三总辐射模拟结果在一定程度上能较好地反映出云和降水对总辐射的影响。福山站各模拟方案总辐射平均偏差在10.5~197.6 W·m-2之间,均方根误差在29.2~234.5 W·m-2之间,方案二模拟效果最好,方案三次之,方案四最差;济南站各模拟方案总辐射平均偏差在92.8~223.4 W·m-2之间,均方根误差在131.2~272.6 W·m-2之间,方案三模拟效果最好,方案二次之,方案一最差;莒县站各模拟方案总辐射平均偏差在14.7~127.9 W·m-2之间,均方根误差在32.6~173.2 W·m-2之间,方案三模拟效果最好,方案二次之,方案一最差。
2.2 四季代表月模拟结果检验利用福山、济南、莒县站四季代表月逐日降水量数据和福山、济南、莒县站日总云量数据,依据晴天、阴天、雨天划分方法,分别确定3站晴天、阴天和雨天,对各天气条件下福山、济南、莒县站各总辐射模拟方案四季代表月模拟结果和观测结果进行误差分析。确定的四季代表月所有晴天、阴天和雨天见表 3。
|
|
表 3 福山、济南、莒县站四季代表月晴天、阴天和雨天日数
Table 3 Sunny days, cloudy days and rainy days in months representative of four seasons in Fushan, Jinan and Juxian |
晴天条件下,各模拟方案总辐射逐时模拟结果和观测结果之间变化趋势一致性较好(表 4和图 5a、b),相关系数均在0.9以上。方案四总辐射平均偏差和均方根误差在所有方案中最小,福山、济南、莒县总辐射平均偏差分别为49.6 W·m-2、56.8 W·m-2、90.2 W·m-2,均方根误差分别为75.3 W·m-2、91.3 W·m-2、106.3 W·m-2,其次为方案一,方案二误差相对最大。各模拟方案四季代表月中以秋季总辐射平均偏差和均方根误差最小,冬季次之,春季相对最大。
|
|
表 4 四季代表月所有晴天、阴天、雨天各模拟方案总辐射检验 Table 4 Verification for each solar irradiance simulation scheme on all sunny days, cloudy days and rainy days in months representative of four seasons |
|
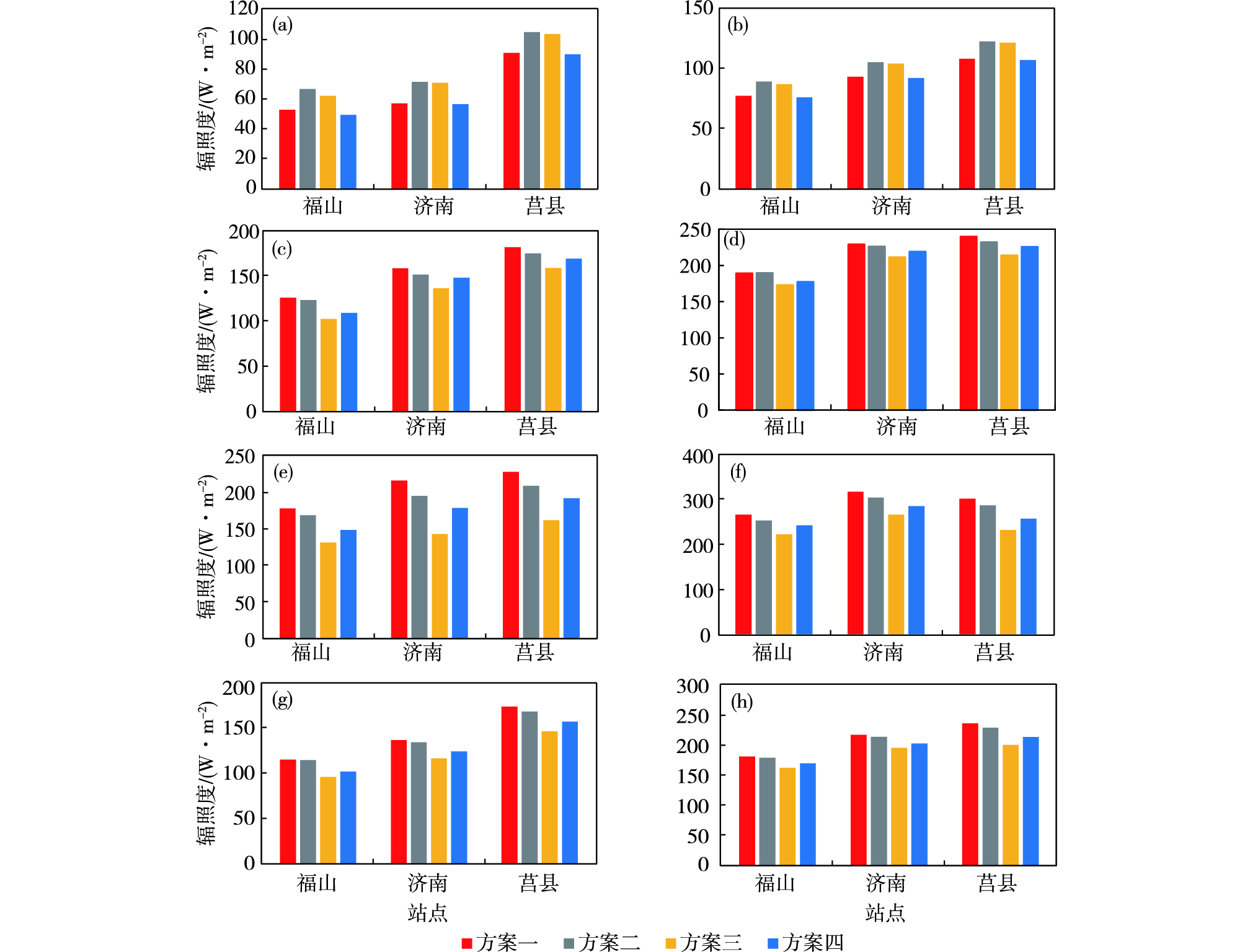
图 5 四季代表月所有晴天(a、b)、阴天(c、d)、雨天(e、f)、所有日(g、h)各模拟方案总辐射平均偏差(a、c、e、g)、均方根误差(b、d、f、h)(单位:W·m-2) Fig.5 Mean bias (a, c, e, g; units: W·m-2) and root mean square error (b, d, f, h; units: W·m-2) of each simulation scheme on all sunny days (a, b), cloudy days (c, d), rainy days (e, f) and all days (g, h) in months representative of four seasons |
阴天条件下,四季代表月各总辐射模拟方案模拟结果和观测结果相关系数在0.739~0.874之间,方案二夏季济南站相关系数相对最小,方案三冬季福山相对最大(表 4和图 5c、d)。各模拟方案总辐射模拟结果和观测结果相关系数多以方案三、方案四较大,但各站相同四季代表月各模拟方案间相关系数差异较小。四季代表月所有阴天逐时总辐射以方案三的模拟误差最小,模拟效果相对较好,平均偏差分别为102.4 W·m-2、136.7 W·m-2、159.2 W·m-2,均方根误差分别为172.8 W·m-2、211.3 W·m-2、213.9 W·m-2,其次为方案四,方案一相对较差。秋季所有日逐时总辐射以方案四的模拟误差最小,模拟效果相对较好,平均偏差分别为65.5 W·m-2、118.4 W·m-2、168.3 W·m-2,均方根误差分别为135.7 W·m-2、176.6 W·m-2、213.3 W·m-2,其次为方案三,方案二相对较差。冬季、春季和夏季所有日逐时总辐射均以方案三的模拟误差最小,模拟效果相对较好,平均偏差和均方根误差相对较小,其次为方案四,方案一相对较差。
2.2.3 雨天雨天条件下,四季代表月各总辐射模拟方案模拟结果和观测结果相关系数在0.614~0.900之间,方案三春季济南站相关系数相对最小,方案三秋季莒县相对最大(表 4和图 5e、f)。除夏季福山、夏季济南外,其他各模拟方案总辐射模拟结果和观测结果相关系数均以方案三最大,但各站相同四季代表月各模拟方案间相关系数差异较小。四季代表月所有雨天逐时总辐射以方案三的模拟误差最小,模拟效果相对较好,平均偏差分别为130.4 W·m-2、141.9 W·m-2、160.7 W·m-2,均方根误差分别为220.9 W·m-2、264.6 W·m-2、230.7 W·m-2,其次为方案四,方案一相对较差。秋季福山和莒县所有雨天逐时总辐射以方案三的模拟误差最小,其次为方案四,济南以方案四模拟误差最小,其次为方案三。冬季、春季和夏季所有雨天逐时总辐射均以方案三的模拟误差最小,模拟效果相对较好,平均偏差和均方根误差相对较小,其次为方案四,方案一相对较差。
2.2.4 所有日四季代表月所有日各总辐射模拟方案模拟结果和观测结果相关系数在0.759~0.914之间,方案三夏季济南站相关系数相对最小,方案三秋季莒县相对最大(表 5和图 5g、h)。除冬季福山、夏季济南外,其他各模拟方案总辐射模拟结果和观测结果相关系数均以方案三最大,但各站相同四季代表月各模拟方案间相关系数差异较小。四季代表月所有日逐时总辐射以方案三的模拟误差最小,模拟效果相对较好,平均偏差分别为95.9 W·m-2、116.5 W·m-2、146.7 W·m-2,均方根误差分别为163.5 W·m-2、196.6 W·m-2、201.6 W·m-2,其次为方案四,方案一相对较差。秋季所有日逐时总辐射以方案四的模拟误差最小,模拟效果相对较好,平均偏差分别为60.8 W·m-2、72.2 W·m-2、115.2 W·m-2,均方根误差分别为129.7 W·m-2、126.8 W·m-2、152.2 W·m-2,其次为方案三,方案二相对较差。冬季、春季和夏季所有日逐时总辐射均以方案三的模拟误差最小,模拟效果相对较好,平均偏差和均方根误差相对较小,其次为方案四,方案一相对较差。
|
|
表 5 四季代表月所有日各模拟方案总辐射检验 Table 5 Verification for each solar irradiance simulation scheme on all days in months representative of four seasons |
通过对山东区域WRF-Solar模式模拟方案一至方案四的四季代表月晴天、阴天、雨天总辐射模拟检验结果发现,在晴天条件下,WRF-Solar模式对山东区域总辐射模拟结果的平均偏差和均方根误差最小,模拟效果最优,其次为阴天,雨天总辐射模拟结果的平均偏差和均方根误差最大,模拟效果较差。在晴天条件下,方案四总辐射模拟效果最优,方案三次之,阴天和雨天条件下,方案三总辐射模拟效果最优,方案四次之。在不考虑天气条件下,四季代表月所有日总辐射模拟结果以方案三的平均偏差和均方根误差最小,模拟效果最优,方案四次之。因此,利用山东总辐射模拟效果较优的方案三的物理参数化方案,使用MODIS的AOD550 nm气溶胶数据对山东四季代表月逐时总辐射进行模拟,检验气溶胶数据对山东总辐射模拟结果的影响。
福山、济南、莒县站四季代表月平均气溶胶光学厚度(aerasol optical depth, AOD)分别为0.476、0.662、0.617,济南气溶胶浓度最高,福山最低。四季代表月中以秋季各站气溶胶光学厚度最小,分别为0.339、0.452、0.431,其次为冬季,再次为夏季,春季各站气溶胶光学厚度最大,分别为0.641、0.812、0.717。
2.3.1 晴天晴天条件下,在WRF-Solar数值模式中加入气溶胶对总辐射的影响后,山东各站总辐射模拟结果相对于观测结果的误差明显减小(表 4中晴天方案三和表 6晴天结果,图 6a、b),加入气溶胶数据后,四季代表月所有晴天福山、济南、莒县站总辐射模拟结果的平均偏差分别减小了14.6 W·m-2、15.6 W·m-2、16.7 W·m-2,均方根误差分别减小了12.0 W·m-2、11.3 W·m-2、15.0 W·m-2。各季节四季代表月总辐射模拟结果的平均偏差和均方根误差均明显减小,其中平均偏差减小在5.6~18.7 W·m-2之间,均方根误差减小在3.7~18.1 W·m-2之间,相对而言,夏季代表月平均偏差和均方根误差减小的最小,冬季代表月最大。总辐射模拟结果能在一定程度上反映气溶胶对实际太阳辐射的影响,在数值模式中加入气溶胶对总辐射模拟结果的影响后,可使晴天总辐射模拟结果误差明显减小。
|
|
表 6 未考虑气溶胶时山东四季代表月晴天、阴天、雨天、所有日逐时总辐射模拟结果检验 Table 6 Verification of solar irradiance simulation without aerosols on all sunny days, cloudy days, rainy days and all days in months representative of four seasons in Shandong |
|
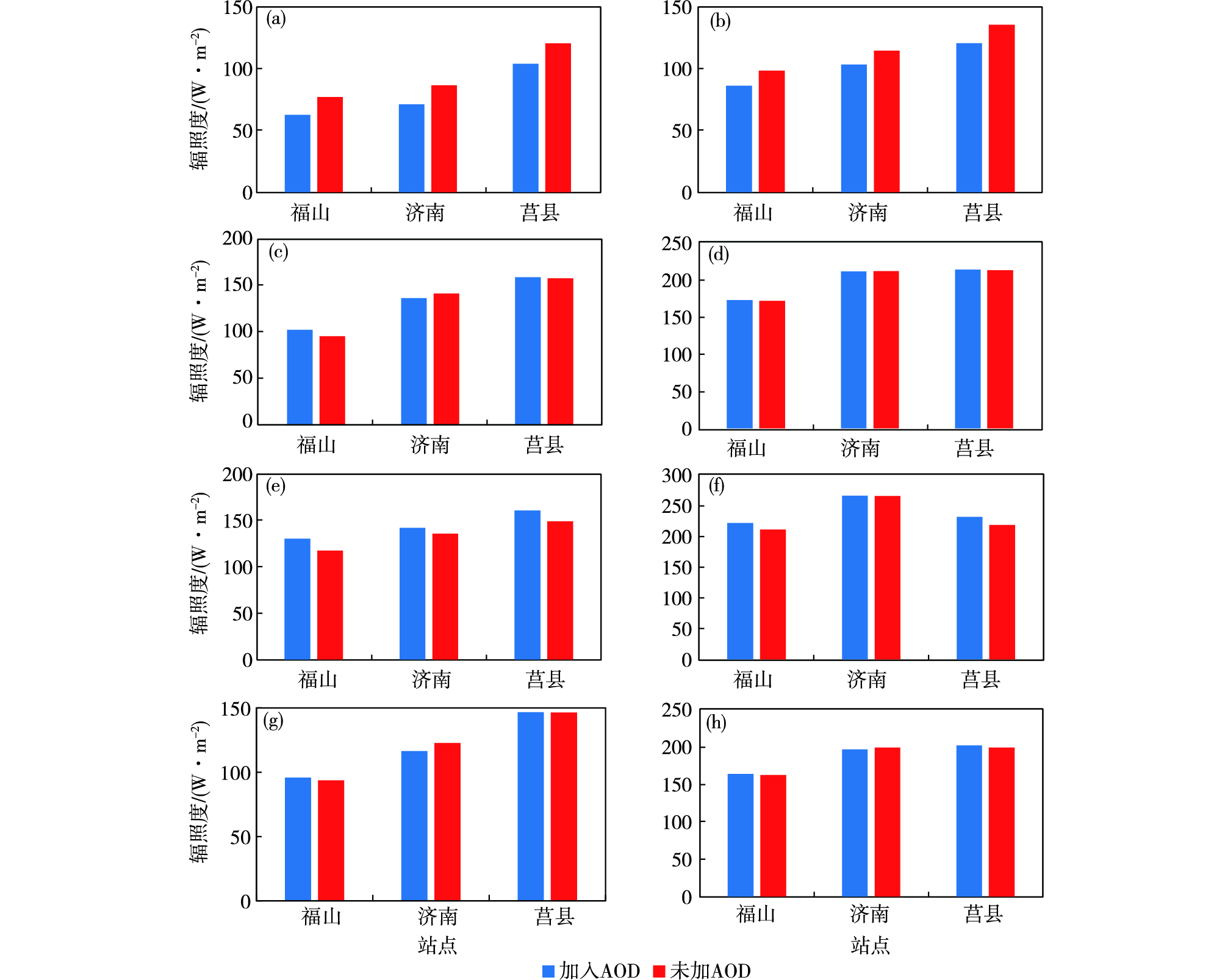
图 6 四季代表月所有晴天(a、b)、阴天(c、d)、雨天(e、f)、所有日(g、h)加与不加气溶胶数据总辐射模拟和观测平均偏差(a、c、e、g)、均方根误差(b、d、f、h)(单位:W·m-2) Fig.6 Mean bias (a, c, e, g; units: W·m-2) and root mean square error (b, d, f, h; units: W·m-2) of solar irradiance simulation with and without aerosols on all sunny days (a, b), cloudy days (c, d), rainy days (e, f) and all days (g, h) in months representative of four seasons in Shandong |
阴天条件下,山东各站加与不加气溶胶数据的总辐射模拟结果相对于观测结果的误差差异较小(表 4中阴天方案三和表 6阴天结果,图 6c、d)。加入气溶胶后,四季代表月所有阴天福山、莒县站总辐射模拟结果的平均偏差分别增大了6.7 W·m-2、1.1 W·m-2,均方根误差分别增大了1.1 W·m-2、0.9 W·m-2,济南站平均偏差则减小了4.9 W·m-2,均方根误差减小了0.4 W·m-2。秋季和冬季代表月总辐射模拟结果的平均偏差和均方根误差有所减小,其中平均偏差减小在2.5~12.9 W·m-2之间,均方根误差减小在1.5~11.4 W·m-2之间,冬季代表月平均偏差和均方根误差减小的更多。除济南春季外,其他站春季和所有站夏季代表月总辐射模拟结果的平均偏差和均方根误差有所增大,其中平均偏差增大在0.5~20.8 W·m-2之间,均方根误差增大在3.7~11.3 W·m-2之间,夏季代表月平均偏差和均方根误差增大的更多。
2.3.3 雨天雨天条件下,山东各站加入气溶胶数据的总辐射模拟结果相对于观测结果的误差有所增大(表 4中雨天方案三和表 6雨天结果,图 6e、f)。加入气溶胶后,四季代表月所有阴天福山、济南、莒县站总辐射模拟结果的平均偏差分别增大了13.0 W·m-2、6.3 W·m-2、11.7 W·m-2,均方根误差分别增大了10.9 W·m-2、0.3 W·m-2、13.2 W·m-2。秋季和冬季代表月总辐射模拟结果的平均偏差和均方根误差有所减小,其中平均偏差减小在2.8~14.2 W·m-2之间,均方根误差减小在0.3~9.9 W·m-2之间,冬季代表月平均偏差和均方根误差减小的更多。由于福山站冬季代表月仅在8日和15日分别出现了0.5 mm、0.3 mm的少量降水,且总云量较少,分别为3成和6.7成,这可能是总辐射模拟结果误差较小的原因之一。春季和夏季代表月总辐射模拟结果的平均偏差和均方根误差有所增大,其中平均偏差增大在0.4~27.8 W·m-2之间,均方根误差增大在0.5~25.8 W·m-2之间,夏季代表月平均偏差和均方根误差增大得更多。
2.3.4 所有日在WRF-Solar数值模式中加入与不加气溶胶对总辐射的影响后,四季代表月所有日平均的总辐射模拟和观测结果相差不大(表 5所有日方案三和表 6所有日结果,图 6g、h),加入气溶胶数据后,济南站平均偏差和均方根误差分别减小6.2 W·m-2、2.2 W·m-2,但福山、莒县站总辐射平均偏差和均方根误差略有增大,其中平均偏差分别增大了2.2 W·m-2、1.2 W·m-2,均方根误差分别增大了0.2 W·m-2、2.7 W·m-2。四季代表月中,秋季和冬季所有日加入气溶胶对总辐射的影响后,总辐射模拟结果误差明显减小,各站平均偏差减小在8.2~13.8 W·m-2之间,均方根误差减小在3.5~10.6 W·m-2之间。春季所有日加入气溶胶数据后,济南站平均偏差和均方根误差略减小,福山站略增大,莒县站平均偏差减小,但均方根误差略增大。夏季所有日加入气溶胶数据后,除济南站总辐射均方根误差略减小外,福山和莒县站以及济南站平均偏差有所增大。
在不区分晴天、阴天、雨天的情况下,WRF-Solar数值模式中加入气溶胶对总辐射的影响后,秋季和冬季代表月总辐射模拟结果平均偏差和均方根误差明显减小,春季差别不大,夏季误差有所增大。由于选取的秋季和冬季代表月各站晴天相对较多(表 3),同时阴雨天较少,因此在WRF-Solar数值模式中考虑气溶胶对总辐射的影响后,总辐射模拟结果误差明显减小,而选取的山东主雨季的夏季代表月各站晴天较少,阴雨天较多,即便在总辐射模拟中加入气溶胶的影响,总辐射模拟结果改进较小,甚至模拟效果变差,表明虽然气溶胶是影响总辐射模拟效果的要素之一,但云和降水也是总辐射模拟效果的关键因素。如何真实地表达云和降水对总辐射模拟的影响是解决总辐射模拟效果的关键问题之一,这仍是总辐射模拟的难点。
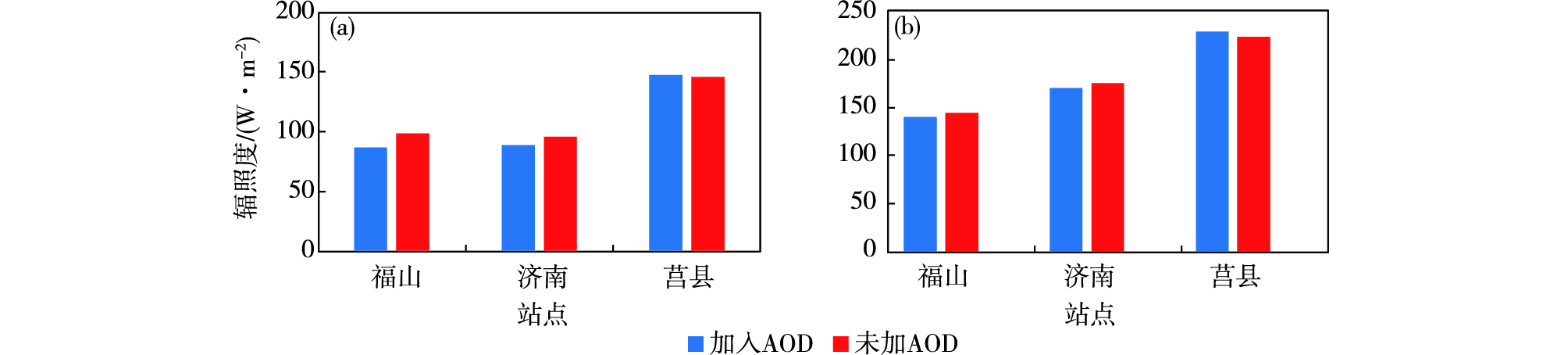
2.3.5 低能见度日在低能见度条件下,模式加入气溶胶数据后,福山、济南站总辐射模拟结果误差有所减小(表 7、图 7),平均偏差分别减小11.6 W·m-2、6.9 W·m-2,均方根误差分别减小4.4 W·m-2、5.0 W·m-2,莒县站平均偏差和均方根误差分别增加1.5 W·m-2、5.5 W·m-2。模式加入气溶胶数据后,除夏季莒县站外,其他四季代表月在低能见度日下总辐射模拟结果误差均有所减小。表明在低能见度条件下,考虑气溶胶对辐射的模拟影响后,可在一定程度上减小总辐射模拟误差。
|
|
表 7 气溶胶对山东四季代表月低能见度日逐时总辐射模拟结果检验 Table 7 Verification of solar irradiance simulation with aerosols on low visibility days in months representative of four seasons in Shandong |
|
图 7 四季代表月低能见度日加与不加气溶胶数据总辐射模拟和观测平均偏差(a)、均方根误差(b)(单位:W·m-2) Fig.7 Mean bias (a; units: W·m-2) and root mean square error (b; units: W·m-2) of solar irradiance simulation with and without aerosols on low visibility days in months representative of four seasons in Shandong |
利用专门为太阳能资源评估的WRF-Solar数值模式对山东区域四季代表月的向下短波辐射进行了回算模拟,结合福山、济南、莒县站辐射观测数据对不同模拟方案模拟结果进行了对比分析,得到以下主要结论:
1) WRF-Solar数值模式对总辐射模拟能力在晴天和少云天最好,模拟与观测总辐射相关系数均在0.9以上,阴雨天较差,模拟与观测总辐射相关系数普遍在0.8左右。秋季和冬季总辐射模拟效果较好,春季次之,夏季相对较差。
2) 晴天和少云天、阴天和雨天以及不考虑天气过程的四季代表月所有日条件下,长、短波辐射方案分别采用RRTMG方案、new Goddard方案,积云对流参数化方案均采用Grell 3D集合方案,同时使用AOD550nm的气溶胶数据的总辐射模拟能力最强。
3) 晴天和少云天条件下,考虑AOD550 nm气溶胶数据的总辐射模拟结果明显改进,加入气溶胶数据后,四季代表月所有晴天福山、济南、莒县站总辐射模拟结果的平均偏差分别减小了13.0 W·m-2、16.3 W·m-2、13.9 W·m-2,均方根误差分别减小了9.6 W·m-2、12.5 W·m-2、14.6 W·m-2。阴天和雨天以及不考虑天气过程情况下,在天气过程较少的秋季和冬季考虑气溶胶可明显提高总辐射模拟能力。低能见度日总辐射模拟结果所有改善。
通过本文的研究结论可以看到,对于晴天总辐射模拟来说,使用气溶胶数据初始化WRF-Solar数值模式是解决总辐射模拟效果的有效手段。但对于阴、雨天等复杂天气条件下,虽然考虑气溶胶数据后总辐射模拟结果有所改善,但改善效果有限。区域天气事件是产生总辐射模拟误差的主要原因之一,虽然WRF-Solar数值模式考虑了云辐射反馈和气溶胶辐射反馈等,但仍不能在模式中正确地反映云和气溶胶的结构、组成、发展时间节点等,但与WRF模式相比,总辐射的模拟效果已经有所改善[18-20, 25]。
模拟的总辐射的误差主要与云的形成和局地对流显著相关,地表和行星边界层之间的热交换驱动着大气环流和对流,从而在不同时间尺度上影响云的形成和运动[46-47]。模式中错误的云特征和对流特征会造成模拟与观测的总辐射差异较大,因此,需要在模式中使用能更加精准地描述云物理过程和对流过程的参数化方案,包括增加次网格云反馈[19]、准确的对流触发机制[48]、改进的云微物理过程[49-50]、大气边界层反演[51-52]、湍流特征[53]等。
由于本文的总辐射模拟时段有限,得到的总辐射模拟结论有待进一步验证。另外,需要设置更多的不同物理参数化方案的模拟方案对总辐射模拟结果进行效果检验,也可以考虑增加卫星遥感资料、雷达资料等的数据同化,通过优化资料质量控制方案来改进模拟初始场,提高云结构、云量、水汽等的模拟准确性,进而提升总辐射的模拟效果。
| [1] |
申彦波. 我国太阳能资源评估方法研究进展[J]. 气象科技进展, 2017, 7(1): 77-84. DOI:10.3969/j.issn.2095-1973.2017.01.008 |
| [2] |
何晓凤, 周荣卫, 申彦波, 等. 基于WRF模式的太阳辐射预报初步试验研究[J]. 高原气象, 2015, 34(2): 463-469. |
| [3] |
赵志远, 刘丹, 郭炜, 等. 气溶胶光学厚度对辐照度预报的影响[J]. 太阳能, 2018(11): 52-59. DOI:10.3969/j.issn.1003-0417.2018.11.011 |
| [4] |
何晓凤, 袁春红, 杨振斌. 3种全球预报背景场对中国太阳辐射预报的性能评估[J]. 太阳能学报, 2016, 37(4): 897-904. DOI:10.3969/j.issn.0254-0096.2016.04.014 |
| [5] |
马金玉, 罗勇, 申彦波, 等. 太阳能预报方法及其应用和问题[J]. 资源科学, 2011, 33(5): 829-837. |
| [6] |
辛渝, 王澄海, 沈元芳, 等. WRF模式对新疆中部地面总辐射预报性能的检验[J]. 高原气象, 2013, 32(5): 1368-1381. |
| [7] |
薛德强, 刘焕彬, 董旭光, 等. 光伏电站发电量的预报试验分析[J]. 可再生能源, 2013, 31(11): 13-17. DOI:10.3969/j.issn.1671-5292.2013.11.004 |
| [8] |
孙银川, 白永清, 左河疆. 宁夏本地化WRF辐射预报订正及光伏发电功率预测方法初探[J]. 中国沙漠, 2012, 32(6): 1738-1742. |
| [9] |
白永清, 陈正洪, 王明欢, 等. 关于WRF模式模拟到达地表短波辐射的统计订正[J]. 华中师范大学学报(自然科学版), 2013, 47(2): 292-296. DOI:10.3969/j.issn.1000-1190.2013.02.032 |
| [10] |
白永清, 陈正洪, 王明欢, 等. 基于WRF模式输出统计的逐时太阳总辐射预报初探[J]. 大气科学学报, 2011, 34(3): 363-369. DOI:10.3969/j.issn.1674-7097.2011.03.014 |
| [11] |
王林, 陈正洪, 唐俊. 太阳能光伏发电预报方法的应用效果检验与评价[J]. 气象, 2014, 40(8): 1006-1012. |
| [12] |
何明琼, 成驰, 陈正洪, 等. 太阳能光伏发电预报效果评价[J]. 水电能源科学, 2011, 29(12): 196-199. |
| [13] |
张星星, 吕宁, 姚凌, 等. ECMWF地表太阳辐射数据在我国的误差及成因分析[J]. 地球信息科学学报, 2018, 20(2): 254-267. |
| [14] |
陈春美, 钟珂, 陈勇航, 等. 干旱区典型城市云对太阳辐射的影响[J]. 干旱区研究, 2018, 35(2): 436-443. |
| [15] |
陆天蔚, 张晶, 乔岩, 等. 长三角地区气溶胶对辐射和降水影响的分析[J]. 北京师范大学学报(自然科学版), 2019, 55(1): 135-144. |
| [16] |
刘平平, 刘鑫, 刘琼, 等. 新疆地区气溶胶对地表太阳辐射的影响初探[J]. 环境科学学报, 2020, 40(9): 3155-3164. |
| [17] |
乔岩, 张晶, 薛文晧, 等. 基于Fu-Liou模式的气溶胶对中国、印度2011—2014年地表太阳辐射影响的研究[J]. 北京师范大学学报(自然科学版), 2019, 55(1): 114-120. |
| [18] |
齐月, 房世波, 周文佐. 近50年来中国东、西部地面太阳辐射变化及其与大气环境变化的关系[J]. 物理学报, 2015, 64(8): 089201. |
| [19] |
GUEYMARD C A, RUIZ-ARIAS J A. Validation of direct normal irradiance predictions under arid conditions: A review of radiative models and their turbidity-dependent performance[J]. Renew Sust Energ Rev, 2015, 45: 379-396. DOI:10.1016/j.rser.2015.01.065 |
| [20] |
JIMÉNEZ P A, HACKER J P, DUDHIA J, et al. WRF-Solar: Description and clear-sky assessment of an augmented NWP model for solar power prediction[J]. Bull Amer Meteor Soc, 2016, 97(7): 1249-1264. DOI:10.1175/BAMS-D-14-00279.1 |
| [21] |
JIMÉNEZ P A, ALESSANDRINI S, HAUPT S E, et al. The role of unresolved clouds on short-range global horizontal irradiance predictability[J]. Mon Wea Rev, 2016, 144(9): 3099-3107. DOI:10.1175/MWR-D-16-0104.1 |
| [22] |
LEE J A, HAUPT S E, JIMÉNEZ P A, et al. Solar irradiance nowcasting case studies near Sacramento[J]. J Appl Meteor Climatol, 2017, 56(1): 85-108. DOI:10.1175/JAMC-D-16-0183.1 |
| [23] |
REIKARD G, HAUPT S E, JENSEN T. Forecasting ground-level irradiance over short horizons: Time series, meteorological, and time-varying parameter models[J]. Renew Energ, 2017, 112: 474-485. DOI:10.1016/j.renene.2017.05.019 |
| [24] |
HAUPT S E, KOSOVIĆ B, JENSEN T, et al. Building the Sun4Cast system: Improvements in solar power forecasting[J]. Bull Amer Meteor Soc, 2018, 99(1): 121-136. DOI:10.1175/BAMS-D-16-0221.1 |
| [25] |
GAMARRO H, GONZALEZ J E, ORTIZ L E. On the assessment of a numerical weather prediction model for solar photovoltaic power forecasts in cities[J]. J Energ Resour Technol, 2019, 141(6): 061202. DOI:10.1115/1.4042405 |
| [26] |
GUEYMARD C A, JIMENEZ P A. Validation of real-time solar irradiance simulations over Kuwait using WRF-solar, September 10-13, 2018[C]. Rapperswil, Switzerland: International Solar Energy Society, 2018.
|
| [27] |
DASARI H P, DESAMSETTI S, LANGODAN S, et al. High-resolution assessment of solar energy resources over the Arabian Peninsula[J]. Appl Energ, 2019, 248: 354-371. DOI:10.1016/j.apenergy.2019.04.105 |
| [28] |
ARBIZU-BARRENA C, RUIZ-ARIAS J A, RODRIGUEZ-BENÍTEZ F J, et al. Short-term solar radiation forecasting by advecting and diffusing MSG cloud index[J]. Sol Energ, 2017, 155: 1092-1103. DOI:10.1016/j.solener.2017.07.045 |
| [29] |
VERBOIS H, HUVA R, RUSYDI A, et al. Solar irradiance forecasting in the tropics using numerical weather prediction and statistical learning[J]. Sol Energ, 2018, 162: 265-277. DOI:10.1016/j.solener.2018.01.007 |
| [30] |
吴焕波, 石岚. 基于WRF-SOLRA数值模式的太阳总辐射预报性能分析[J]. 内蒙古大学学报(自然科学版), 2019, 50(2): 154-161. |
| [31] |
董旭光. 山东省太阳能资源评估[D]. 兰州: 兰州大学, 2019.
|
| [32] |
董旭光, 邱粲, 刘焕彬, 等. 山东省日照时数的气候变化特征及其影响因素[J]. 中国农业气象, 2013, 34(2): 138-145. |
| [33] |
王建源, 冯建设, 袁爱民. 山东省太阳辐射的计算及其分析[J]. 气象科技, 2006, 34(1): 98-101. |
| [34] |
崔日鲜. 山东省太阳总辐射的时空变化特征分析[J]. 自然资源学报, 2014, 29(10): 1780-1791. |
| [35] |
XUE D Q, WANG X, WANG X T. Solar energy resource characteristics of photovoltaic power station in Shandong Province[J]. Agric Sci Technol, 2013, 14(4): 666-671. |
| [36] |
滕华超, 陈艳春, 汤子东. ERA-Interim风速再分析数据在山东省的适用性评估[J]. 山东气象, 2016, 36(1): 27-31. |
| [37] |
姚玲玲. 中国及典型地区气溶胶光学厚度的时空分布特征及影响因素研究[D]. 杭州: 浙江大学, 2017.
|
| [38] |
曾昭亮, 郭建平, 马大喜, 等. 基于CALIOP和MODIS数据的气溶胶时空分布特征对比分析[J]. 大气与环境光学学报, 2017, 12(3): 210-220. |
| [39] |
河北省邢台市气象局. GB/T 33673—2017水平能见度等级[S]. 北京: 中国标准出版社, 2017: 1.
|
| [40] |
夏凡, 李昌义, 刘诗军, 等. 雾与能见度数值预报诊断SW方案和FSL方案改进的研究及评估[J]. 海洋气象学报, 2020, 40(3): 48-59. |
| [41] |
RUIZ-ARIAS J A, ALSAMAMRA H, TOVAR-PESCADOR J, et al. Proposal of a regressive model for the hourly diffuse solar radiation under all sky conditions[J]. Energ Convers Manage, 2010, 51(5): 881-893. DOI:10.1016/j.enconman.2009.11.024 |
| [42] |
XIE Y, SENGUPTA M, DUDHIA J. A fast all-sky radiation model for solar applications (FARMS): Algorithm and performance evaluation[J]. Sol Energ, 2016, 135: 435-445. DOI:10.1016/j.solener.2016.06.003 |
| [43] |
RUIZ-ARIAS J A, DUDHIA J, GUEYMARD C A. A simple parameterization of the shortwave aerosol optical properties for surface direct and diffuse irradiances assessment in a numerical weather model[J]. Geosci Model Dev, 2014, 7(3): 1159-1174. DOI:10.5194/gmd-7-1159-2014 |
| [44] |
THOMPSON G, EIDHAMMER T. A study of aerosol impacts on clouds and precipitation development in a large winter cyclone[J]. J Atmos Sci, 2014, 71(10): 3636-3658. DOI:10.1175/JAS-D-13-0305.1 |
| [45] |
DENG A, GAUDET B, DUDHIA J, et al. Implementation and evaluation of a new shallow convection scheme in WRF, February 2-6, 2014[C]. Atlanta, GA: 26th Conference on Weather Analysis and Forecasting, 94th American Meteorological Society Annual Meeting, 2014.
|
| [46] |
ZHANG H L, PU Z X, ZHANG X B. Examination of errors in near-surface temperature and wind from WRF numerical simulations in regions of complex terrain[J]. Wea Forecasting, 2013, 28(3): 893-914. DOI:10.1175/WAF-D-12-00109.1 |
| [47] |
CHIACCHIO M, VITOLO R. Effect of cloud cover and atmospheric circulation patterns on the observed surface solar radiation in Europe[J]. J Geophys Res, 2012, 117(D18): D18207. |
| [48] |
SUHAS E, ZHANG G J. Evaluation of trigger functions for convective parameterization schemes using observations[J]. J Climate, 2014, 27(20): 7647-7666. DOI:10.1175/JCLI-D-13-00718.1 |
| [49] |
PIERI A B, VON HARDENBERG J, PARODI A, et al. Sensitivity of precipitation statistics to resolution, microphysics, and convective parameterization: A case study with the high-resolution WRF climate model over Europe[J]. J Hydrometeorol, 2015, 16(4): 1857-1872. DOI:10.1175/JHM-D-14-0221.1 |
| [50] |
辅天华, 陈海山, 曾智华, 等. 云微物理参数化对东亚近海热带气旋活动模拟的影响[J]. 海洋气象学报, 2020, 40(1): 12-21. |
| [51] |
ZHONG X H, SAHU D K, KLEISSL J. WRF inversion base height ensembles for simulating marine boundary layer stratocumulus[J]. Sol Energ, 2017, 146: 50-64. DOI:10.1016/j.solener.2017.02.021 |
| [52] |
孙文奇, 李昌义. 数值模式中的大气边界层参数化方案综述[J]. 海洋气象学报, 2018, 38(3): 11-19. |
| [53] |
KIM C K, LEUTHOLD M, HOLMGREN W F, et al. Toward improved solar irradiance forecasts: A simulation of deep planetary boundary layer with scattered clouds using the weather research and forecasting model[J]. Pure Appl Geophy, 2016, 173(2): 637-655. DOI:10.1007/s00024-015-1072-3 |
 2021, Vol. 41
2021, Vol. 41


