2. 山东省气象信息中心,山东 济南 250031;
3. 山东省气候中心,山东 济南 250031
2. Shandong Meteorological Information Center, Jinan 250031, China;
3. Shandong Climate Center, Jinan 250031, China
人们经常疑惑,气象学家能预测未来几十年后的气候变冷或是变暖,却不能预测几十天后的天气,这就是混淆了天气和气候的概念。天气和气候是两个不同时间尺度的概念,天气是指日、小时等较短时间内各种气象要素的状态,气候是指月、年或更长时间尺度的各种气象要素的平均状态。随着非线性科学理论和气候研究领域的发展,发现多尺度相互作用的气候系统具有显著的长期记忆性或持续性[1],气候系统存在的记忆性特征,描述的是气候系统各影响因子多尺度相互作用的结果。气候系统的自然变率很大程度上可以认为是气候系统记忆性的一部分[2]。研究[3]发现,火山活动等自然外强迫可以显著增强气温的记忆性,人类活动产生的温室气体,有削弱气温序列记忆性的趋势,基于记忆性的气候可预报性可能会降低,同时意味着降低碳排放和温控的重要性。由于大气运动呈现混沌规律[4],表现为气候要素随着时间尺度产生不同程度的涨落,自然界中很多物理现象是长程相关的,天气和气候要素时间序列的随机程度和时间尺度虽然不同,通过引入分数阶算子可以刻画天气和气候之间的关系[5],不同于普通的布朗运动过程,分数阶布朗运动描述了连续且长程相关的物理过程[6]。此前MANDELBROT and VAN NESS[7]利用分数阶算子在布朗运动中提取并成功模拟了分数阶布朗运动的过程。早在1976年,HASSELMANN[8]就将天气和气候与微观尺度运动和宏观尺度运动的关系进行了比较,利用Langevin方程[9]建立了气候与天气的关系,提出了气候变量对时间的一阶导数是天气变量的结果。但近些年的研究[5, 10-14]发现,简单的一阶导数已经不能很好地模拟天气和气候之间的关系,两者之间很有可能是一种分数阶导数的关系。有研究[15]已经证实了气温、相对湿度、海面温度等气候要素序列的记忆性,刘式达等[5, 10]提出并证实了多尺度的气候变化具有显著的长期记忆性或持续性。可以推断带有分数阶积分的模型不仅可以改善气候预测的精度来模拟长期记忆信号的特征,而且可以从产生长期记忆信号的原因中来理解物理过程的变化,并且将分数阶气候模型与动力模式耦合[16],对建立一种新的动力-统计气候模式预测方法具有积极意义。
济南和青岛虽然同处于中纬度地带,且同属于温带季风气候,但济南是内陆丘陵城市,属于偏大陆性温带季风气候[17],青岛是位于黄海沿岸的沿海丘陵城市,受海洋环境、东南季风、海流和海面水团的影响,使得青岛又具有显著的海洋气候特征。此前,诸多学者已经对济南和青岛的气温长期变化特征进行了大量的研究工作。胡桂芳等[18]以济南和青岛1919—2002年的气温资料为研究对象,发现济南的升温速率明显高于青岛,青岛最高气温呈上升趋势,济南则呈现下降趋势。陈志梅等[19]通过小波分析等方法分析了青岛地区1900—2002年的气温变化特征,指出青岛平均气温呈明显上升趋势,并存在准20 a的周期振荡特征。本文以1961—2020年济南和青岛气温的天气和气候时间序列为研究对象,分析济南和青岛不同时间尺度的气候记忆性特征,研究气候时间序列的记忆性对于提高当地气候预测水平有重要意义。
1 资料和方法 1.1 资料文中使用了济南和青岛1961—2020年逐日、月、年平均气温资料,资料来源于山东省气象信息中心。天气时间序列使用的是日平均气温距平,气候时间序列使用的是月、年平均气温距平。
1.2 资料预处理为得到具有相对平稳性的距平资料,去掉气温实测数据的趋势干扰,需要把原始数据转换为距平数据来分离趋势项[20]。以月平均气温资料为例,将月平均气温转换为月平均气温距平的方法如下:
设某站点的年平均气温序列为yt(i),t=1,2,…,N表示年序,i=1,2,…,12表示月序。
| $ \bar{y}(i)=\frac{1}{N} \sum\limits_{t=1}^{N} y_{t}(i), i=1, 2, \cdots, 12 $ | (1) |
式中,y(i)表示月平均气温的累年平均值,可以基本反映月平均气温距平在年尺度上的一般趋势,所以用距平法消除趋势干扰项,可以将月平均气温距平
| $ \dot{y}_{t}(i)=y_{t}(i)-\bar{y}(i), t=1, 2, \cdots, N $ | (2) |
日和年平均气温距平按照上述方法同理可得。本文中分析和计算的数据均是距平数据。
时间序列平稳性较常用的统计检验方法是ADF(Augmented Dickey-Fuller)检验,又称为单位根检验[21]。ADF检验的原理是判断时间序列是否存在单位根,如果存在单位根,则时间序列不平稳;反之,单位根不存在,则时间序列平稳。
1.3 研究方法 1.3.1 自相关函数自相关函数值表示数据相关程度,对于温度等连续变量的气象要素来说,自相关反映了变量的持续性。设时间序列变量为x,则其自相关函数Rk可表示为:
| $ {R_k} = \frac{{\sum\limits_{i = 1}^{n - k} {\left[ {\left( {{x_i} - \bar x} \right)} \right]} \left[ {\left( {{x_{i + k}} - \bar x} \right)} \right]}}{{\sum\limits_{i = 1}^n {{{\left( {{x_i} - \bar x} \right)}^2}} }} $ | (3) |
其中,xi代表变量x的第i个顺序值;x代表x的平均值;k代表时间间隔,即滞后时间。时间序列的自相关函数接近于0,可以将其近似地看作白噪声[22-23]。
1.3.2 归一化概率密度函数数据归一化是多尺度时间序列分析的一个非常重要的过程,可以消除样本取值的量纲差异干扰。归一化可以将数据转换成同一量纲,是准确分析数据之间关系的前提。采用最大值归一化的方法,将原始数据统一映射到[-1, 1]区间,其函数为:
| $ x^{*}=\frac{x}{|\max (x)|} $ | (4) |
其中,x为原始序列,x*为归一化后的序列。利用最大值归一化处理后的数据绘制归一化概率密度分布函数图像,可以直观反映极值事件发生的概率情况。
1.3.3 确定气候记忆性强度在天气和气候时间序列关系的研究[24]中,王在华[11]发现天气和气候时间序列之间存在以下分数阶导数关系:
| $ \frac{\mathrm{d}^{q} x(t)}{\mathrm{d} t^{q}}=\varepsilon(t) $ | (5) |
其中,ε(t)是天气时间序列,x(t)是气候时间序列,q为分数阶导数的阶数。
气候时间序列x(t)的功率谱S(f)是其傅里叶变换系数
| $ S(f)=|\hat{x}(f)|^{2} \propto f^{-\beta} $ | (6) |
其中
根据式(5)和式(6)以及天气ε(t)、气候x(t)之间功率谱的关系,刘式达等[5]推导出功率谱指数与分数阶导数的关系为:
| $ \beta=2 q $ | (7) |
二阶结构函数是指时间间隔τ的气温距平差值Δx(τ)平方的平均〈Δx(τ)2〉,分形系统的二阶结构函数可由布朗运动的均方位移公式推导得到,公式为:
| $ \Gamma(t)=\left\langle\Delta x(\tau)^{2}\right\rangle \propto t^{2 \alpha} $ | (8) |
利用二阶结构函数和量纲分析,得到气候时间序列赫斯特指数α和功率谱指数β之间的关系[5-6, 13]为:
| $ \beta=2 \alpha+1 $ | (9) |
通过上述关系式(7)和关系式(9)可以计算得到恰当的分数阶导数的阶数q,能够刻画气候记忆性强度。
2 结果与分析 2.1 日平均气温距平特征分析利用济南和青岛1961—2020年日平均气温距平分析其相关特征。采用气温距平序列,可以去掉实际观测数据的趋势干扰,具有相对平稳性[24]。济南和青岛日平均气温距平稳定地围绕平均值波动,通过单位根ADF方法检验日平均气温距平的平稳性[21],在原假设为时间序列存在单位根的前提下,结果表明拒绝原假设,所以日平均气温距平资料是平稳的,因此判断济南和青岛1961—2020年日平均气温距平具有平稳性的时间序列。
对于白噪声序列[20],其自相关函数的数值在0附近,表示给定时刻的状态与过去任意时刻的状态几乎无关,即连续变量几乎不存在持续性[13]。根据济南和青岛1961—2020年日平均气温资料,得到济南和青岛两地相应的日平均气温距平、自相关函数和二阶结构函数(图 1)。由济南和青岛日平均气温距平(图 1a1、b1)可以看出,日平均气温距平的变化没有明显的规律;由济南和青岛日平均气温距平的自相关函数(图 1a2、b2)可以看出,自相关函数的数值在0附近平稳波动,说明天气时间序列自相关性较差。通过济南和青岛的二阶结构函数(图 1a3、b3)计算出的济南和青岛的赫斯特指数分别为0.000 7和0.009 0,赫斯特指数均接近于0,进一步说明日平均气温距平接近于白噪声[20]。因此,由1961—2020年济南和青岛的日平均气温距平来看,在近60 a的时间尺度上,天气时间序列近似于白噪声。

|
图 1 1961—2020年济南(a1—a3)和青岛(b1—b3)的日平均气温距平(a1、b1)、自相关函数(a2、b2)和二阶结构函数(a3、b3) Fig.1 Daily mean temperature anomaly (a1/b1), autocorrelation function (a2/b2), and second-order structure function (a3/b3) in Jinan (a1-a3) and Qingdao (b1-b3) from 1961 to 2020 |
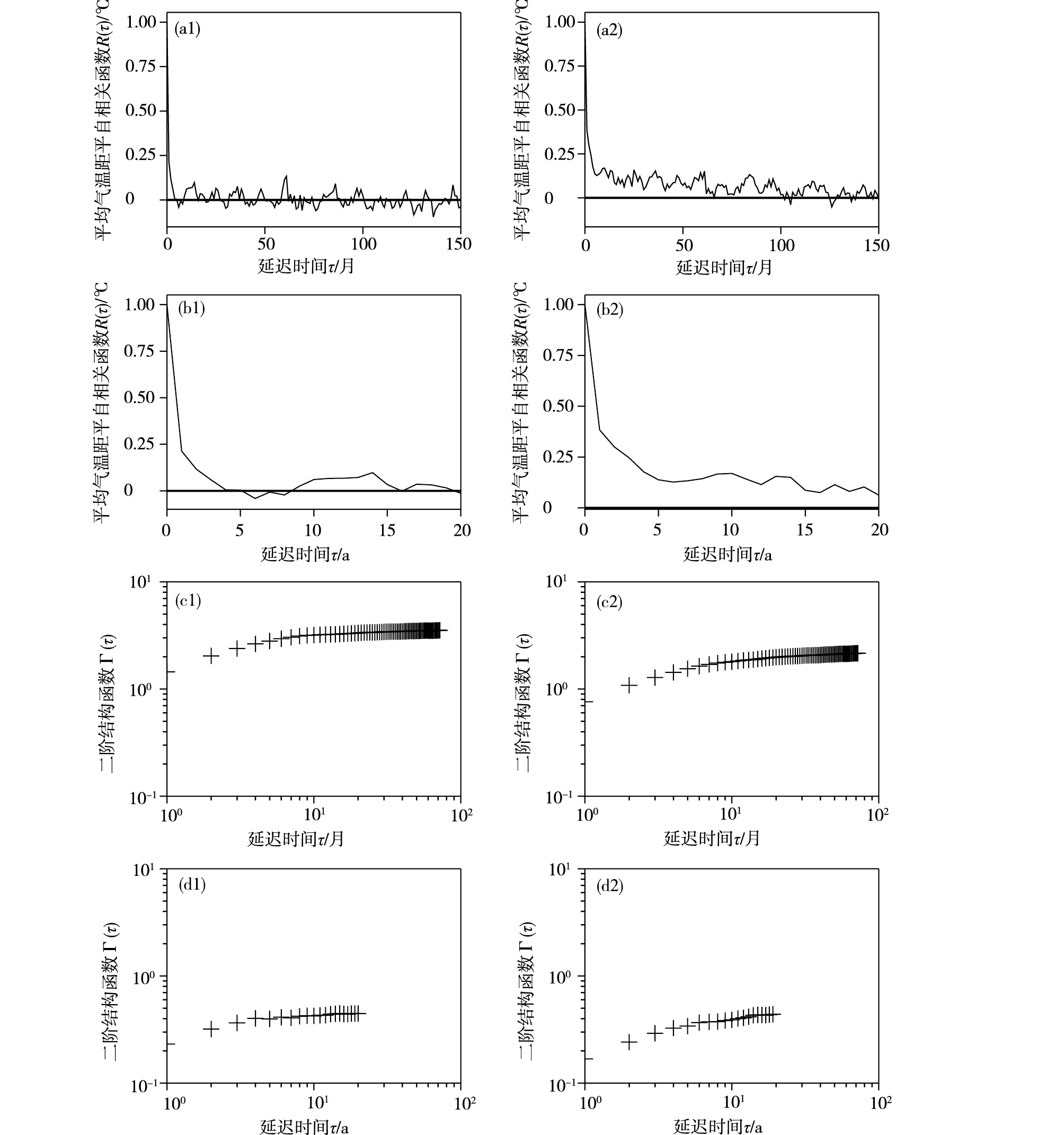
利用1961—2020年济南和青岛月、年平均气温资料,分析了济南和青岛的月、年平均气温距平的自相关函数和二阶结构函数(图 2)。由自相关函数(图 2a1、a2)可以看出,济南月平均气温距平的自相关函数在0附近上下波动,相比于济南,青岛月平均气温距平在100个月之后仍呈现出一定程度的相关性。由济南和青岛年平均气温距平的自相关函数(图 2b1、b2)可以看出,济南年平均气温距平的自相关函数值随时间迅速减小,但仍有一定的相关性,青岛的年平均气温距平在20 a之后仍保持一定的相关性。由此说明,气候时间序列都具有一定程度的自相关性,且存在幂律现象,即随着时间的变化气候时间序列虽然呈现衰减趋势,但部分特性并不会随着天气信号平滑后消失,而是依然存在于气候时间序列中,这使得月、年或更长时间尺度的时间序列结合起来,使长时间尺度的气候时间序列呈现出一定的记忆性,也就是长程相关的特征[5]。
|
图 2 1961—2020年济南(a1、b1、c1、d1)和青岛(a2、b2、c2、d2)月平均气温距平自相关函数(a1、a2)、年平均气温距平的自相关函数(b1、b2)及其月平均气温距平二阶结构函数(c1、c2)、年平均气温距平二阶结构函数(d1、d2) Fig.2 Autocorrelation function (a1/a2/b1/b2) and second-order structure function (c1/c2/d1/d2) of monthly (a1/a2 /c1/c2) and annual (b1/b2/d1/d2) mean temperature anomalies in Jinan (a1/b1/c1/d1) and Qingdao (a2/b2/c2/d2) from 1961 to 2020 |
通过对济南和青岛平均气温距平的二阶结构函数分析,计算得到济南的月和年平均气温距平的赫斯特指数分别为0.029和0.165(图 2c1、c2),青岛的月和年平均气温距平的赫斯特指数分别为0.053和0.291(图 2d1、d2)。通过计算结果可以看出,两地的赫斯特指数均不为0,且青岛的月平均气温距平的赫斯特指数比济南大0.024,年平均气温距平的赫斯特指数比济南大0.126。通过赫斯特指数和功率谱指数以及分数阶导数的阶数之间的关系,得到济南的月和年平均气温距平的功率谱指数分别为1.058和1.330,青岛的月和年的平均气温距平的功率谱指数分别为1.106和1.582,都小于HASSELMANN[8]计算出标准布朗运动功率谱的结果2,与刘式达等[5, 10]提出的气候的功率谱指数介于0~2之间的结果一致。通过此前气候时间序列与天气时间序列之间建立的分数阶导数关系[5, 10, 13, 15],进一步得到济南的月和年平均气温距平的分数阶导数的阶数q值分别为0.529和0.665,青岛的月和年平均气温距平的分数阶导数的阶数q值分别为0.553和0.791,分数阶导数的值反映了其记忆性强度的大小。由于天气时间序列作滑动平均后可以消去其中互不相关的部分结果,使得气候时间序列存在与过去状态相关的信息,从而使得记忆性变强,这与前面得到的济南和青岛月和年平均气温距平的分析结果是一致的。因此在气候时间序列中,当前的气候状态的变化在不同程度上依赖于过去的气候状态,并与过去的气候状态呈现不同程度的相关性。
通过上述分析可以得出,地处沿海的青岛相比于地处内陆的济南,其气候时间序列具有更强的记忆性。为了进一步说明气温的气候时间序列记忆性在地理位置上的规律,通过计算得到山东省10个城市的月和年平均气温距平对日平均气温距平求导的阶数(表 1)。由表 1可以看出,月尺度下山东省不同城市的q值十分接近,数值在0.5左右;年尺度下烟台和日照的求导阶数最大,数值在0.8以上;济南和聊城的求导阶数最小,数值在0.5~0.7之间,其他地区的求导阶数的数值在上述地区之间。因此可以大致认为年尺度下半岛沿海地区的求导阶数的q值大于鲁西等内陆地区。
|
|
表 1 山东省10个城市月和年平均气温距平对日平均气温距平求导的阶数q值 Table 1 The q value for the derivative order of monthly and annual mean temperature anomalies to daily mean temperature anomaly in 10 cities of Shandong Province |
为了比较天气时间序列与气候时间序列中频率分布的差异,以济南和青岛1961—2020年日、月、年平均气温距平为例进行分析。图 3是济南和青岛不同时间尺度平均气温距平的标准化频率分布,为了更直观地看出各区间频率的相对大小,对其做标准化处理。可以看出,济南和青岛日平均气温距平的频率都是大致呈正态分布,且在平均值附近的概率最大,可以将归一化后的数据落在[-1.0,-0.8]和[0.8,1.0]区间内看作本地区近60 a的高温或低温事件,济南和青岛日平均气温距平落在这两个区间的概率都接近于0(图 3a1、b1)。月平均气温距平的频率特征(图 3a2、b2)与日平均气温距平形态大致相同,但月平均气温距平直方图两端尾部厚度比日平均气温稍厚,说明其出现月平均气温极值事件的概率比日平均气温极值事件稍大。济南和青岛年平均气温距平的频率分布相对月平均气温距平更加平坦,其落在[-1.0,-0.8]和[0.8,1.0]的概率最大,接近0.1,并且青岛年平均气温极值事件发生的概率比济南稍大。比较济南和青岛两地近60 a的归一化年平均温度距平的频率分布特征,由图 3a3、b3可以看出济南和青岛受全球变暖的影响,偏暖年份数量较多。青岛年平均气温距平直方图在两端区间的概率大于济南,意味着青岛气温极值事件发生的概率较济南大,或许由于地处沿海的青岛受到海表气温强记忆性的影响有关[2]。1961—2020年济南和青岛的年平均气温距平的概率密度分布相比于日平均气温距平和月平均气温距平呈长尾特征,由于样本数受限,气候时间序列概率分布的长尾特征有待于进一步研究。

|
图 3 1961—2020年济南(a1—a3)和青岛(b1—b3)日(a1、b1)、月(a2、b2)、年(a3、b3)平均气温距平的标准化频率分布直方图 Fig.3 Normalized frequency distribution histogram of daily (a1/b1), monthly (a2/b2), and annual (a3/b3) mean temperature anomalies in Jinan (a1-a3) and Qingdao (b1-b3) from 1961 to 2020 |
通过定量分析济南和青岛气候时间序列记忆性,探究了济南和青岛1961—2020年的日、月和年平均气温距平的不同特征及关系,得出以下结论。
(1) 1961—2020年济南和青岛的年、月平均气温距平具有记忆性,且年平均气温距平与月平均气温距平相比具有更好的记忆性。日平均气温距平的自相关函数值接近于0,即日平均气温距平自相关性小,近似白噪声特征。
(2) 济南月和年平均气温距平的导数阶数为0.529和0.665,青岛相应的阶数为0.553和0.791,可以看出两地月平均气温距平的求导阶数相近,年平均气温距平的求导阶数相差较大,且青岛的大于济南的,即青岛的气候记忆性强于济南。这进一步说明了气候时间序列的一阶导数不是天气时间序列,而是q阶导数,且存在明显的地理差异。
(3) 济南和青岛日平均气温距平和月平均气温距平的标准化频率大致呈正态分布,月平均气温距平的直方图两端尾部厚度比日平均气温稍厚,即月平均气温极值事件发生的概率比日平均气温极值事件稍大。年平均气温距平的标准化频率分布相对月平均气温距平更加平坦,因此年平均气温极值事件发生的概率比日平均气温和月平均气温大,但是由于样本量较少有待进一步研究。
分析表明,地处沿海的青岛相比于地处内陆的济南,气温具有更好的气候记忆性。对于其他要素和多地域的天气和气候时间序列的记忆性特征需要进一步研究。天气气候系统是混沌动力系统,非线性大气动力学的发展为中长期预报和气候趋势预测提供了许多新方法和新技术,将时间序列的分形特征与气象预报技术结合是接下来研究的重点方向。
| [1] |
QIU M, YUAN N M, YUAN S J. Understanding long-term memory in global mean temperature: an attribution study based on model simulations[J]. Atmos Ocean Sci Lett, 2020, 13(5): 485-492. DOI:10.1080/16742834.2020.1778418 |
| [2] |
熊飞麟. 气候系统记忆性特征和外强迫对中国气候变化的影响研究[D]. 南京: 南京信息工程大学, 2019.
|
| [3] |
YUAN N, FU Z, LIU S. Extracting climate memory using Fractional Integrated Statistical Model: a new perspective on climate prediction[J]. Sci Rep, 2014, 4: 6577. |
| [4] |
LORENZ E N. The predictability of a flow which possesses many scales of motion[J]. Tellus, 1969, 21(3): 289-307. DOI:10.3402/tellusa.v21i3.10086 |
| [5] |
刘式达, 时少英, 刘式适, 等. 天气和气候之间的桥梁: 分数阶导数[J]. 气象科技, 2007, 35(1): 15-19. DOI:10.3969/j.issn.1671-6345.2007.01.003 |
| [6] |
DMOWSKA R, SALTZMAN B. Long-range persistence in geophysical time series[M]. San Diego: Elsevier Academic Press, 1999: 14-16.
|
| [7] |
MANDELBROT B B, VAN NESS J W. Fractional Brownian motions, fractional noises and applications[J]. SIAM Rev, 1968, 10(4): 422-437. DOI:10.1137/1010093 |
| [8] |
HASSELMANN K. Stochastic climate models Part Ⅰ. Theory[J]. Tellus, 1976, 28(2): 473-485. |
| [9] |
ROBERT Z. Nonlinear generalized Langevin equations[J]. J Stat Phys, 1973, 9(3): 215-220. DOI:10.1007/BF01008729 |
| [10] |
刘式达, 袁乃明, 付遵涛, 等. 气候变化的长期记忆性: 理论基础与观测证实[J]. 中国科学: 物理学力学天文学, 2013, 43(10): 1327-1331. |
| [11] |
王在华. 分数阶微积分: 描述记忆特性与中间过程的数学工具[J]. 科学中国人, 2011(3): 76-78. DOI:10.3969/j.issn.1005-3573.2011.03.017 |
| [12] |
BOEING G. Visual analysis of nonlinear dynamical systems: chaos, fractals, self-similarity and the limits of prediction[J]. Systems, 2016, 4(4): 37. DOI:10.3390/systems4040037 |
| [13] |
时少英, 刘式达, 付遵涛, 等. 天气和气候的时间序列特征分析[J]. 地球物理学报, 2005, 48(2): 259-264. DOI:10.3321/j.issn:0001-5733.2005.02.004 |
| [14] |
黄荟羽, 张琳, 王若男, 等. 基于分数阶导数的天气和气候要素时间序列关系分析[J]. 沈阳农业大学学报, 2018, 49(1): 82-87. |
| [15] |
袁乃明, 付遵涛, 刘式达. 基于气候变率长程持续性特征的可预报性研究[C]//中国气象学会. 第八次全国动力气象学术会议会议论文集. 大同: 中国气象学会, 2013: 37.
|
| [16] |
袁乃明, 杨庆, 刘健, 等. 年代际气候事件的归因及预估研究进展[J]. 中国基础科学, 2019, 21(3): 36-44, 63. DOI:10.3969/j.issn.1009-2412.2019.03.06 |
| [17] |
石振彬, 董旭光, 石兴旺, 等. 济南市近50 a高温天气的气候特征[J]. 气象与环境科学, 2007, 30(增刊): 95-97. |
| [18] |
胡桂芳, 李芸, 李德萍. 山东近百年来的最高、最低温度变化[J]. 气象, 2004, 30(11): 43-46. |
| [19] |
陈志梅, 刘秦玉, 沈小野, 等. 青岛近百年气温变化特征[J]. 中国海洋大学学报(自然科学版), 2005, 35(2): 189-194. |
| [20] |
丁裕国, 江志红. 气象数据时间序列信号处理[M]. 北京: 气象出版社, 1998.
|
| [21] |
陈昭. 时序非平稳性ADF检验法的理论与应用[J]. 广州大学学报(自然科学版), 2008, 7(5): 5-10. DOI:10.3969/j.issn.1671-4229.2008.05.002 |
| [22] |
董祺. 近似白噪声序列的一种判别方法[J]. 火控技术, 1981(1): 1-3. |
| [23] |
周雪松, 孟金, 姚蔚. 一种基于快速傅里叶变换的多普勒天气雷达弱杂波识别方法[J]. 海洋气象学报, 2019, 39(4): 43-51. |
| [24] |
ZHU X, FRAEDRICH K, LIU Z, et al. A demonstration of long-term memory and climate predictability[J]. J Climate, 2010, 23(18): 5021-5029. DOI:10.1175/2010JCLI3370.1 |
| [25] |
LAURENT H. Sur le calcul des dérivées à indices quelconques[J]. Nouv Ann de Mathémat, 1884, 3(3): 240-252. |
| [26] |
刘式达, 梁福明, 刘式适, 等. 自然科学中的混沌和分形[M]. 北京: 北京大学出版社, 2003.
|
| [27] |
江田汉, 邓莲堂. Hurst指数估计中存在的若干问题: 以在气候变化研究中的应用为例[J]. 地理科学, 2004, 24(2): 177-182. DOI:10.3969/j.issn.1000-0690.2004.02.008 |
 2022, Vol. 42
2022, Vol. 42


