2. 中国气象科学研究院灾害天气国家重点实验室, 北京 100081;
3. 西安交通大学航天航空学院, 陕西 西安 710049;
4. 西安交通大学航天航空学院机械结构强度与振动国家重点实验室, 陕西 西安 710049
2. State Key Laboratory of Severe Weather, Chinese Academy of Meteorological Sciences, Beijing 100081, China;
3. School of Aerospace Engineering, Xi'an Jiaotong University, Xi'an 710049, China;
4. State Key Laboratory for Strength and Vibration of Mechanical Structures, School of Aerospace Engineering, Xi'an Jiaotong University, Xi'an 710049, China
数值天气预报的萌芽可以追溯到1904年挪威科学家Vilhelm Bjerknes提出把天气预报看成求解描述大气运动控制方程组的科学思想,即通过实时观测的气象数据求解控制方程组来预测未来时刻的天气状态。实践证明,解析求解这些控制方程组的天气预报方法是行不通的。1922年,英国气象学家RICHARDSON[1]创造性地用数值方法求解大气运动方程组,开创了用数值方法预报天气的革命性技术,即数值天气预报。随着数值算法、高性能计算机技术、气象探测技术以及动力气象学、数值预报理论的不断发展,数值天气预报在近100年时间内取得了巨大的成功[2-3]。数值天气预报已成为现代天气预报业务的核心支撑,在气象防灾减灾、社会公众服务、国民经济建设和国防等工作中发挥着不可替代的作用。
数值天气预报系统由大气数值模式、资料同化及模式后处理等部分构成,其中数值模式是核心。大气数值模式主要由动力框架和物理参数化过程两大模块组成。大气模式中最早采用的数值方法是基于规则网格点的有限差分方法,该方法通过差分算子近似大气控制方程组中的导数项[4-6]。随后,自20世纪70年代末开始,谱模式在大气模式中占主导地位,并在业务模式中应用最为广泛[7]。谱方法(spectral method)通过一系列正交基函数对控制方程中预报量进行逼近,实现空间离散。它相比于早期格点模式的优势在于能有效避免球面的极区问题和消除相速度误差(phase-speed error)等[8]。随着模式向高分辨率方向发展,谱模式勒让德变换在高分辨率下的效率瓶颈和难以在众核超级计算机上实现高效并行化计算的缺点日益突出,基于格点模式的数值方法(如:半拉格朗日方法(semi-Lagrangain method)[9]和有限体积法(finite volume method)[10]等)在进入21世纪后再次兴起。
近年来,随着异构众核高性能并行计算机和E级计算的高速发展,大气数值模式中涌现出一系列能够高效利用超级计算机性能和保证良好计算效率的高扩展算法,高扩展算法已成为下一代大气数值模式的研究焦点[11]。世界上各主要业务中心已于2010年左右开始下一代高可扩展模式研发,如:欧洲中期天气预报中心(European Centre for Medium-Range Weather Forecasts,ECMWF)于2015年开始的用于E级计算的天气预报高能效规模算法(Energy-efficient Scalable Algorithms for Weather Prediction at Exascale,ESCAPE)计划,英国气象局于2011年开始的“工合(GungHo)”(Globally Uniform Next Generation Highly Optimized)计划,以及美国国家海洋和大气管理局(National Oceanic and Atmospheric Administration,NOAA)于2016年开始的下一代全球预报系统(Next Generation Global Prediction System,NGGPS)计划等。
一般而言,要实现未来大气状态的气象要素预报,大气数值模式需要基于球面计算网格对大气动力与热力学控制方程进行空间数值离散,继而采用时间离散格式向前推进模式积分。为此,本文将从数值算法、准均匀球面网格和时间积分方法等3个方面对国内外可扩展的下一代大气模式进行综述,希望对相关领域同行的研究起到帮助和推动作用。需要指出的是,全球模式与区域模式的差异体现在模式是否有边界处理,而在数值算法、球面网格和积分方案方面并无显著区别,因而本文所介绍内容对全球模式与区域模式均适用。
1 大气模式数值方法自20世纪20年代RICHARDSON[1]的创始性工作以来,应用在大气模式中的数值方法呈现多样性,如传统格点模式采用的有限差分方法、有限体积方法、半拉格朗日方法[12-13]和非格点模式(ECWMF)采用的谱方法等。2007年,WILLIAMSON[7]在其综述“全球大气模式动力框架演变”中详细回顾了传统数值方法在全球大气模式中的应用进展。
近年来,高性能并行计算机的迅速发展对应用于大气模拟的数值计算方法提出了新的挑战,即:数值计算方法必须能够充分利用超级计算机所提供的计算潜力[14-15]。基于这一背景,过去十多年中多种适用于大气数值模拟并能高效利用超级计算机的高精度数值方法被应用于发展新一代大气模式,代表性的方法包括:谱元(spectral element)方法[16-20]、间断伽辽金(discontinuous Galerkin)方法[21-25]、混合有限元(mixed finite element)方法[26-29]以及多矩约束有限体积(multi-moment constrained finite volume)方法[30-39]。作为有潜力的下一代大气数值模式核心基础算法,这些数值方法具有高精度、守恒、网格适应性强和可扩展等特点,国际先进业务研究中心开始或已经采用它们来发展新一代大气数值模式。与传统的有限差分和有限体积数值方法不同,这些数值方法能够在局地单元开展高阶多项式数值重构,因而获得了高精度和良好可扩展特性。然而,上述高精度格式其计算过程较为复杂、数值计算鲁棒性不高、需要与合适的时间积分方案相配合等,这些要求给大气模式开发者采用这类高精度数值方法设计下一代数值模式提出了新的挑战。
1.1 有限元方法有限元方法最早发展于20世纪40年代初[40],并在50年代后期取得重要进展并得到广泛应用。有限元方法的空间离散格式一般通过加权余量法(weighted residual method)导出。在实际应用中,通常采用伽辽金(Galerkin)方法,即:选取离散空间上的基函数(有时又称为试探函数(test function))作为权重函数,使之与误差函数具有正交性,得到空间离散公式。它的优势在于能够灵活地处理复杂几何剖分。
有限元方法在固体力学领域得到了广泛应用[41],在流体计算中主要应用于低马赫数流动的模拟[42]。多种有限元方法被应用于地球流体力学数值模拟,如:基于有限元方法的海洋模式[43-48]。有限元方法应用到大气模拟可追溯到20世纪60年代[49],这一领域至20世纪80年代涌现出更多工作。STANIFORTH[50]对有限元方法在大气模拟中的应用做过综述,强调有限元模式有望更好地探索、理解和预报潜在更复杂的天气现象。BÉLAND et al.[51]采用有限元方法研究了罗斯贝(Rossby)和重力正规模态(normal modes)模拟的准确性,并且与二阶有限差分垂直离散方案做了比较。
相比较于计算域全局展开的谱方法,有限元方法仅在局部单元进行有限元函数级数展开,没有全局并行通信,因而具有良好的计算效率。然而,与有限差分方法相比,有限元方法空间数值离散后需要求解代数方程组,因此它的复杂程度更高,计算代价相对较大[52]。此外,由于单元内未知量多于一个,有限元方法存在潜在计算模(computational mode)[53]问题,该计算模是非物理解。特别地,当表征小尺度大气波动时,非线性项的数值离散容易引起错误的数值解。为了抑制计算模,有限元方法通常需要选择性地采用耗散机制[54],这可能是该方法在大气模式水平离散中没有得到广泛应用的重要原因。相反,采用有限元方法作为垂直离散格式在大气模式中得到良好应用,因为大气数值模式的垂直数值耗散对有限元方法抑制计算模发挥了关键作用。BURRIDGE et al.[55]在欧洲中期天气预报中心(ECMWF)的预报模式中使用有限元方法完成了垂直离散;UNTCH and HORTAL[56]在ECMWF模式中引入垂直有限元平流离散方案,相对于有限差分模式极大提高了线性重力波位相速度模拟精度,减小了洛伦兹(Lorenz)交叉跳点的计算模和垂直计算噪音。
英国气象局下一代数值天气预报模式动力框架“工合(GungHo)”研究计划将混合有限元方法作为数值方法的首选。STANIFORTH et al.[28]研究表明,混合有限元离散中速度自由度与气压自由度数量比值小于2时,会出现明显的虚假惯性重力波,而两者比值大于2时,则发现类似于六边形网格上的虚假罗斯贝波[57]。COTTER and SHIPTON[26]针对线性浅水波方程进行了研究,表明混合有限元方法在三角形网格、六边形网格和正方形网格上通过选择适合的基函数对(element pair),调整气压和速度自由度数量比率,进而可以避免虚假的地转模[58],如:重力惯性模和罗斯贝模。此研究发现,在三角网格中对速度离散采用一阶Brezzi-Douglas-Fortin-Marini空间而气压采用线性不连续空间,在四边形网格中速度离散选用k阶Raviart-Thomas空间而气压则用k阶不连续空间,就可以保证速度自由度和气压自由度数量之比为2 ∶1,从而避免虚假的地转模,并最小化频散和耗散误差。同时,对非线性系统连续方程采用这样的有限元空间并运用间断伽辽金方法可以保证质量守恒。
实际上,混合有限元方法[59]是跳点网格(如C网格)上有限差分方法的拓展,对于不同变量选用不同有限元空间函数(基函数),规避了有限差分方法在A格点上的虚假气压模,同时不受数值网格正交性的约束。目前,这类应用混合有限元方法在球面浅水波模拟中已获得良好效果[28-29, 60-61],进一步推广至三维完全可压缩大气模式及针对不同变量的基函数选择还在进一步研究当中[59]。当前,MELVIN et al.[62]基于混合有限元离散格式在笛卡尔坐标下发展了三维非静力动力框架,它不仅在模式精度上与现有英国气象局业务模式ENDGame动力框架相当,而且具有潜在的众核高性能计算与不受模式数值网格约束的优势。
1.2 谱元方法谱元方法和有限元方法同属一类特殊的伽辽金(Galerkin)方法,可称为连续伽辽金方法,它们在单元边界节点定义的自由度是由相邻单元共享的。谱元方法与高阶有限元方法的区别在于谱元方法插值多项式所采用的节点(node point)是非等距分布的,如:常用的Legendre-Gauss-Lobatto(LGL)点,它是方程式(1-ξ2)L′N(ξ)=0的根,其中L′N(ξ)为N次勒让德多项式的一阶导数。插值多项式逼近同一函数时,有限元方法采用等距节点构建的多项式在逼近区间边界所产生的数值振荡比谱元方法要严重得多。特别是,随着插值多项式阶数的提高,等距有限元多项式在区间边界的振荡会更严重,相反,谱元采用非等距节点构造的数值逼近在边界引起的振荡会随之提高而减小,从而具有更好的收敛性,这是谱元方法的重要优势。
MA[63]最早将谱元方法应用于地球流体力学模拟,建立了适用于复杂几何域的谱元浅水模式,研究表明由于谱元方法的耗散和频散误差小,模式能够准确地模拟海洋锋面现象。TAYLOR et al.[64]将谱元方法应用于球面浅水模式,评估了谱元方法用于气候模式的可行性,讨论了谱元模式在气候模拟中的潜在优缺点。FOURNIER et al.[19]将谱元方法应用到静力原始方程,建立谱元大气模式(Spectral Element Atmospheric Model,SEAM)。随着当时大规模分布式高性能计算机的出现,谱元方法的高可扩展性得到了印证。GIRALDO and ROSMOND[18]在水平方向采用谱元方法发展了一套新的数值天气预报动力框架,测试了三个正压三维标准测试和四个斜压三维标准测试,如:四波罗斯贝波等;并与四个天气预报模式和气候模式相比较,模拟结果表明谱元大气模式和谱变换模式精度相当,该模式在分布式计算机上的并行度可实现线性可扩展。THOMAS and LOFT[65]建立了基于立方球网格的动力框架,该框架在水平方向使用高阶谱元方法,采用垂直混合气压坐标和半隐式时间积分方案。
当前,DENNIS et al.[15]发展的CAM-SE模式、美国海军研究院具备谱元可调的非静力通用大气模式(Nonhydrostatic Unified Model for the Atmosphere,NUMA)以及公共地球系统模式(Community Earth System Model,CESM)等均是采用谱元方法发展的新一代大气模式。韩国大气预报系统研究院(Korea Institute of Atmospheric Prediction Systems,KIAPS)在韩国气象厅下一代大气模式中采用高精度谱元方法,具体设计方案是在水平方向采用谱元方法离散,在垂直方向采用有限差分离散方法[66-67]。谱元方法具有良好的局地计算密集型特征,在分布式高性能计算机上可获得高可扩展性[15-16],同时具有谱收敛和几何灵活(geometrical flexibility)等优势,已成为下一代预报模式的优选数值计算方法之一。
1.3 间断伽辽金方法间断伽辽金方法,与前述有限元和谱元方法不同,数值解和基函数均局限于单元网格内,相邻网格内的近似函数和权重函数在单元界面上的值一般不相等。对于守恒方程,相邻单元网格界面的数值通量一般通过求解(近似)黎曼(Riemann)问题得到,因此有限体积方法中发展的(近似)黎曼问题求解器均可用于间断伽辽金方法。考虑这一特征,间断伽辽金方法也被认为是一种有限元和有限体积相混合的方法。间断伽辽金方法和谱元方法一样也采用不等间距分布的节点,但其数值解定义点不包括单元边界,如采用Legendre-Gauss(LG)点可以获得非常高的计算精度。由于间断伽辽金方法中引入了有限体积的概念,它可以保证数值守恒性。
REED and HILL[68]最早引入间断伽辽金方法用于求解静态中子线性平流问题。LESAINT and RAVIART[69]对间断伽辽金方法应用于线性平流方程的数值特性进行了分析。CHAVENT and SALZANO[70]首次将间断伽辽金方法应用到求解非线性方程,研究发现若将一阶多项式间断伽辽金方法空间离散和简单向前时间积分相结合一般计算不稳定,仅在特定情况下可保证计算稳定性。COCKBURN and SHU[71-72]采用TVB(total variation bounded)限制器、龙格-库塔(Runge-Kutta,RK)时间积分和间断伽辽金方法求解非线性方程获得了极大成功。随后涌现了大量采用间断伽辽金方法来求解实际问题的研究工作。SCHWANENBERG and KÖNGETER[73]采用龙格-库塔间断伽辽金方法研究了一维浅水方程求解及其在水利上的应用,充分展现了其质量和动量守恒、几何灵活和紧致性(compactness)好等优点。COCKBURN and SHU[74]对采用龙格-库塔时间积分和间断伽辽金方法发展的数值模型做了较详细的综述。
在大气模式领域,GIRALDO et al.[75]基于正二十面体网格在笛卡尔坐标下发展了间断伽辽金浅水波模式,其中空间离散采用nodal类型展开。NAIR et al.[76-77]基于立方球网格采用modal类型展开的方式发展了间断伽辽金平流模式和浅水波模式,研究结果表明间断伽辽金方法的精度与标准谱转换模式相当。GIRALDO and RESTELLI[22]将间断伽辽金方法应用于求解通量形式的Navier-Stokes方程,研究了非静力中尺度大气现象,数值试验表明:在热泡和山脉波试验中间断伽辽金非静力模式表现更好;考虑计算效率,在最坏情况下,间断伽辽金模式的运行速度要比非守恒谱元模式慢近一半,在最好情况下,间断伽辽金模式的运行速度与守恒的谱元模式相当。尽管目前采用间断伽辽金方法建立的大气模式还未用于实际业务预报,然而基于间断伽辽金方法的研究型大气模式一直在发展中,比如美国国家大气研究中心(National Center for Atmospheric Research,NCAR)的HOMME(high-order method modeling environment)静力模式[24],美国海军研究院的间断伽辽金全球、区域一体化NUMA[78],德国的DUNE(Distributed and Unified Numerics Environment)大气模式[79]等。
1.4 多矩约束有限体积方法有限体积方法是基于物理守恒律发展的一种数值方法,它能够严格保证数值解的守恒属性。近年来人们对具有良好局地守恒属性,如紧致模板、高强度浮点计算和极少数据通信的数值方法产生新的兴趣。为此,设计能够适应众核超级计算机的一类有限体积方法在非静力大气模式[35, 80-83]中的应用重新受到科学家们的关注和研究。
作为对传统有限体积法的扩展,多矩约束有限体积法是一种数值求解流体力学方程组的新方法。多矩方法借鉴了CIP(constrained interpolation profile)方法的基本思想[84-87],在算法构造中同时采用不同类型的矩,如:积分平均值、状态变量的点值及其导数值,不同矩可以采用不同形式的控制方程进行预报,这些预报方程必须保持与原守恒律方程相容。它的构建过程基于明确的物理概念,具有良好可扩展性、可达到高精度、并能保证严格的数值守恒。与间断伽辽金和谱元方法相比较,它较好地平衡了数值模式在计算精度、鲁棒性、算法简洁性和计算效率等各方面的要求,具有较高的实用价值。不同于传统有限体积方法在单元网格内定义单个自由度,多矩约束有限体积方法与谱元和间断伽辽金方法类似,在单元网格内定义多个自由度(或者未知量),且自由度定义节点可以自由选择,包括等距节点和Legendre-Gauss-Lobatto(LGL)节点等。该方法通过施加不同类型的约束条件,如:物理量的积分平均值、点值及导数值,导出自由度的演变方程,最后再通过龙格-库塔时间积分获得未知量(或自由度)在新时刻的预报值。由于多矩方法在空间拉格朗日(Lagrange)插值重构中引入了多矩约束条件,相比有限元方法中的等距拉格朗日插值具备更好的计算稳定性,能有效抑制高阶重构函数在网格单元边界处的数值振荡[32]。XIAO et al.[34]发展了一套基于多矩约束通量重构的通用高精度数值架构,它可以解释成拉格朗日和埃尔米特(Hermite)混合插值方法,可以从更一般的途径构造高精度数值格式。同时研究[88]表明,多矩约束方法在相同自由度下计算稳定的最大库朗条件数(Courant-Friedrichs-Lewy(CFL)数)要大于间断伽辽金方法。
多矩约束方法已被成功用于发展地球流体力学数值模式。CHEN and XIAO[33]采用多矩约束有限体积方法在立方球面网格上建立了全球浅水波模式。该模式中状态变量的点值采用微分形式方程组通过求解导数黎曼问题来更新,积分平均值采用通量形式方程组用有限体积公式更新保证数值守恒性。LI et al.[89]采用球面阴阳网格发展了球面浅水波模式,不同的是状态变量点值采用半隐式半拉格朗日方法来更新。尽管对状态变量点值的更新方法有所不同,但这两个浅水模式对球面大气波动,如:罗斯贝波、过山气流波等,均获得良好的数值模拟结果,可与国际其他先进模式相媲美。采用多矩约束有限体积框架,可以构造基于局地重构的任意高阶格式。采用三阶、四阶和五阶多矩约束有限体积方法,基于不同球面准均匀网格,如:阴阳网格、立方球网格、正二十面体三角形网格和六边形网格,已发展了各类全球浅水模式[36, 38-39, 90-91]。综合考虑模式的计算精度、效率等因素,多矩方法相比其他先进数值方法有其独特优势。
LI et al.[35]首次将多矩约束有限体积方法应用于完全可压缩、非静力大气模式。一系列标准数值试验,如:密度流试验、惯性重力波试验、热泡试验、Schar复杂地形试验以及线性静力/非静力钟型山脉波试验[37]等,均表明该模式的计算精度与当前国际先进谱元模式和间断伽辽金模式相当。多矩约束有限体积方法在发展球面浅水模式和非静力大气模式中获得了良好数值结果,有望为发展我国下一代高精度、高可扩展、守恒的天气模式甚至气候模式提供可靠的动力学数值架构。
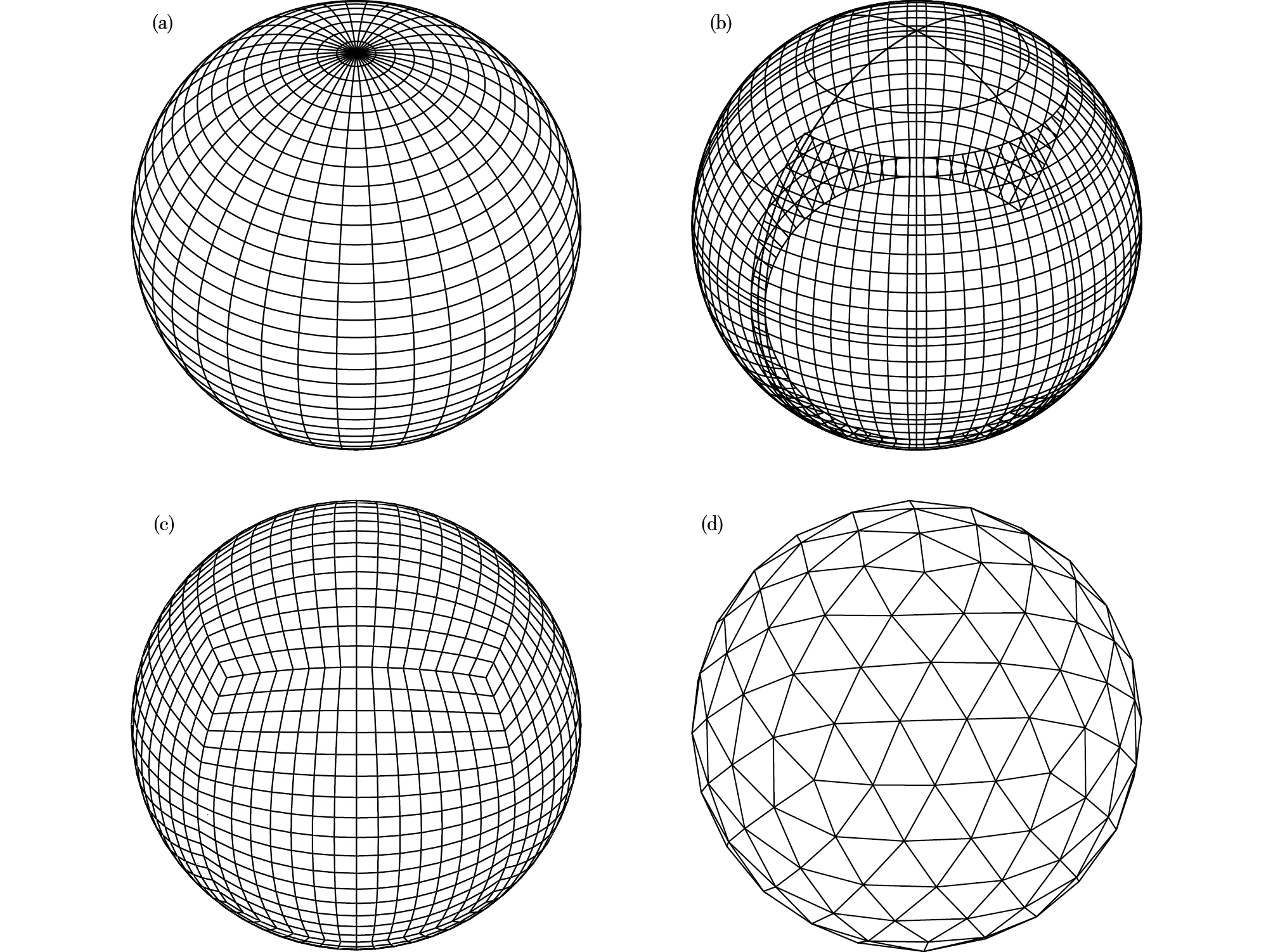
2 准均匀球面网格在大气数值模式中代表性的球面网格有:经纬度网格、阴阳网格、立方球网格和正二十面体网格(图 1)。几乎所有的业务中心均采用过经纬度网格,它具备良好的正交性,方便进行差分计算。然而在超级高性能计算环境中,经纬度网格的极区问题及其带来的数据通信瓶颈变成了制约全球模式性能的一个关键因素。
|
图 1 大气模式中代表性球面网格示意图(a.经纬度网格,b.阴阳网格,c.立方球网格,d.正二十面体网格) Fig.1 Schematic interpretation of representative spherical grid in atmospheric model (a. latitude-longitude grid, b. Yin-Yang grid, c. cubed-sphere grid, d. icosahedral grid) |
KAGEYAMA and SATO[92]提出了准均匀、无数值奇异的阴阳网格,它由两个低纬度经纬度网格相互扣接而成。阴(或阳)网格是普通经纬度网格一部分,继承了普通经纬度网格特性,且低纬度网格单元面积较均匀,并避免了普通经纬度网格数值计算奇异性问题。球面阴阳网格属于组合网格,在阴阳边界处的数据交换需要通过插值运算实现,为保证质量守恒需要特别的考虑[93]。立方球网格由SADOURNY[94]提出,该网格通过球心投影正立方体表面至球面而成,在其六个投影面上可生成网格单元面积相当均匀的结构化网格。根据投影方式不同,它可分为心射切面投影(gnomonic)立方球网格和保角(conformal)投影立方球网格[95]。前者生成的球面网格不正交,但拥有解析的坐标变换关系;后者生成的球面网格正交但不存在解析坐标变换关系。SADOURNY et al.[96]提出了正二十面体球面网格,它通过投影正二十面体至球面得到二十个球面三角,而在每个三角内又细分成多个小三角或六边形的网格单元,属于非结构网格。此外,ECWMF从2016年起在业务模式中采用立方八面体网格,它是简化的高斯网格(reduced Gaussian grid)[97]的一种,即八面体简化的高斯网格(octahedral reduced Gaussian grid),经向格点数(latitude points)保持和简化的高斯网格一样,而相对于简化的高斯网格,其纬向格点数(longitude points)越往极区格点数越少。
网格的几何属性在数值模拟中起到非常重要的作用,它和数值方法结合在一起共同影响数值模拟的准确性。STANIFORTH and THUBURN[98]对全球天气、气候模式采用的水平网格有详细综述,特别关注了球面水平网格的计算模(computational modes)和格点印记(grid imprinting)问题。他们认为网格几何属性会直接影响数值模式动力框架一些基本的理想性能,如质量守恒、准确描述大气地转平衡和调整问题、计算模消失或者被很好地控制住的问题、虚假快速传播的Rossby波问题、位势和气压梯度不应产生非物理的涡度源、最小化格点印记等。格点印记是数值模式底层网格结构潜在误差的一个典型现象。数值试验观察发现,采用准均匀球面网格的模式其底层网格结构可能会以噪音或者系统误差的形式在模拟结果中凸现出来,如浅水波试验中立方球网格内嵌立方体八个顶点对应的球面点附近的格点印记[33, 38, 76-77, 99]和阴阳网格边界处格点印记[89, 100-102]等。
在当前以及未来超级高性能计算条件下,传统数值方法,如:有限差分、有限体积方法等,配合经纬度网格在数据通信问题上遇到计算瓶颈,很可能会制约它的继续发展。毫无疑问,局地高精度、守恒、高可扩展性的数值方法,如:前述的有限元方法、谱元方法、间断伽辽金方法以及多矩约束有限体积方法,具有很好的网格灵活性,在准均匀网格上采用此类数值方法发展模式动力框架是当前的一个热点研究方向[103]。
3 动力框架时间积分方法为保证良好的计算效率,许多全球业务天气预报模式采用半隐式半拉格朗日时间积分方案,比如:平流过程采用半拉格朗日方法来计算,在上游点计算轨迹不交叉情况下时间步长不受限制,而对于声波、重力波等快波则采用半隐式方法来计算[104]。半隐式模式通过适当的线性化和空间数值离散最终得到一个大规模、稀疏和对角化的矩阵,所求解问题转换成大型代数方程,最终采用高效求解器通过迭代获得变量的数值解。
实际大气模式网格剖分时,其水平和垂直网格距之比远大于1(十倍甚至于百倍),为保证计算效率大气模式常采用水平显式-垂直隐式(horizontally explicit-vertically implicit,HEVI)的时间积分方案,即在水平方向的大气波动项采用显式积分,而隐式处理垂直传播波动项。相对于全局半隐式求解方法,它克服了垂直方向的时间步长稳定性限制,同时避免了并行计算中的全局通信。HEVI显式分裂(split-explicit)方法处理大气控制方程中不同速度的波动时,将方程中的快变项再分成多个小时间步进行积分,同时在垂直方向上用Crank-Nicolson等隐式方法求解[105],如WRF模式[106]为采用该方法的代表性大气模式。
大气模式中的显式-隐式(implicit-explicit,IMEX)多时间层方案按照波动的快慢分别采用隐式和显式方案进行处理。为了获得二阶或更高精度,一般会用到多于两个时间层的信息。DURRAN and BLOSSEY[107]用IMEX方法求解静力原始方程和可压缩Boussinesq方程。然而,通过稳定性分析可以发现,多时间层的IMEX方案会出现计算模,因此需要通过过滤计算模以得到满意的数值解[108]。相比较而言,IMEX龙格-库塔(Runge-Kutta,RK)方案可以基于单时间层内多个小时间步获得良好的稳定性和计算精度(二阶及其以上),即使处理刚性(stiff)物理问题[109-110],在数学上表现为算子特征值极大。ULLRICH and JABLONOWSKI[111]采用算子分裂(operator-split)Runge-Kutta-Rosenbrock(RKR)方法积分非静力大气模式,在垂直方向采用线性隐式Rosenbrock方法离散,而水平方向采用显式龙格-库塔方法积分,可以获得三阶精度。算子分裂RKR方法实际上是HEVI方法,因而它的积分稳定性最后受限于水平方向网格矩和波动速度。值得一提的是,ULLRICH and JABLONOWSKI[111]控制方程在垂直方向所有项均统一采用Rosenbrock方法隐式求解,没有区分波动传播特点,其代价是会减慢垂直平流。WELLER et al.[112]采用半隐式或HEVI方法,理论分析了多种龙格-库塔IMEX方法求解线性双曲问题的精度和稳定性,并提出了一种新的HEVI-split方法,指出该方案可提高重力波模拟的精度和稳定性。相对于半隐式方法,WELLER et al.[112]研究认为HEVI-split方法在保持计算精度上更有优势。BAO et al.[113]采用基于Strang类型的算子分裂HEVI方法积分间断伽辽金非静力大气模式,在水平方向采用鲁棒性强保型龙格-库塔时间积分,垂直方向的隐式积分释放了受声波约束的时间步长,获得二阶时间收敛精度。
面向未来并行超级计算机,高阶完全显式时间积分方案在计算精度方面无疑是不错选择,然而其时间步长受限于声波的快速传播,当前仍然需要在计算精度和效率上进行权衡。综合考虑各种因素,在全球模式中采用水平方向显式求解大气运动方程而垂直隐式求解快速波动的HEVI方法,并配合上述具有局地高精度特性的数值算法,在未来超级计算机平台上是一套极具吸引力的地球流体数值模式架构。
4 结语世界气象组织2015年发布的《Seamless Prediction of the Earth System: From minutes to months》(WMO-No.1156)标志着下一代业务数值预报的发展方向在世界范围内形成了共识。在地球系统科学框架下,发展天气气候一体化耦合数值预报系统以及相应的业务预报服务体系成为世界各主要数值预报业务中心的研究和应用重点。同时,众核高性能计算机和E级计算技术的发展也促使下一代业务数值预报模式在数值算法、网格结构等方面做出新的发展。美国国家环境预报中心和德国气象局近年来投入业务运行的立方球网格有限体积模式(NCEP_GFS-fv3)和基于正二十面体网格的ICON模式是这方面的代表。无疑,在准均匀网格上采用局地高精度、守恒、高可扩展性的数值方法是一个重点和热点发展方向。本着抛砖引玉的目的,本文对近年来大气模式中的数值方法进行了系统的分析总结,希望对国内同行在下一代数值预报研究中起到帮助和推动作用。
| [1] |
RICHARDSON L F. Weather prediction by numerical process[M]. Cambridge: Cambridge University Press, 1922.
|
| [2] |
BAUER P, THORPE A, BRUNET G. The quiet revolution of numerical weather prediction[J]. Nature, 2015, 525(7567): 47-55. DOI:10.1038/nature14956 |
| [3] |
SHEN X S, WANG J J, LI Z C, et al. Research and operational development of numerical weather prediction in China[J]. J Meteor Res, 2020, 34(4): 675-698. DOI:10.1007/s13351-020-9847-6 |
| [4] |
CHARNEY J G. Progress in dynamic meteorology[J]. Bull Amer Meteor Soc, 1950, 31(7): 231-236. DOI:10.1175/1520-0477-31.7.231 |
| [5] |
RICHARDSON L F. A purification method for computing the latent columns of numerical matrices and some integrals of differential equations[J]. Phil Trans R Soc Lond A, 1950, 242(852): 439-491. DOI:10.1098/rsta.1950.0007 |
| [6] |
曾庆存. 二层模式的完整流体力学热力学方程组在短期天气预报中的应用[C]//动力气象学论文集(二). 北京: 科学出版社, 1963: 133-152.
|
| [7] |
WILLIAMSON D L. The evolution of dynamical cores for global atmospheric models[J]. J Meteor Soc Japan Ser Ⅱ, 2007, 85B: 241-269. DOI:10.2151/jmsj.85B.241 |
| [8] |
ORSZAG S A. Transform method for the calculation of vector-coupled sums: application to the spectral form of the vorticity equation[J]. J Atmos Sci, 1970, 27(6): 890-895. DOI:10.1175/1520-0469(1970)027<0890:TMFTCO>2.0.CO;2 |
| [9] |
TOLSTYKH M A. Vorticity-divergence semi-Lagrangian shallow-water model of the sphere based on compact finite differences[J]. J Comput Phys, 2002, 179(1): 180-200. DOI:10.1006/jcph.2002.7050 |
| [10] |
LIN S J. A "vertically Lagrangian" finite-volume dynamical core for global models[J]. Mon Wea Rev, 2004, 132(10): 2293-2307. DOI:10.1175/1520-0493(2004)132<2293:AVLFDC>2.0.CO;2 |
| [11] |
MENGALDO G, WYSZOGRODZKI A, DIAMANTAKIS M, et al. Current and emerging time-integration strategies in global numerical weather and climate prediction[J]. Arch Comput Methods in Eng, 2018, 26(3): 663-684. |
| [12] |
ROBERT A. A stable numerical integration scheme for the primitive meteorological equations[J]. Atmos Ocean, 1981, 19(1): 35-46. DOI:10.1080/07055900.1981.9649098 |
| [13] |
ROBERT A. A semi-Lagrangian and semi-implicit numerical integration scheme for the primitive meteorological equations[J]. J Meteor Soc Japan Ser Ⅱ, 1982, 60(1): 319-325. DOI:10.2151/jmsj1965.60.1_319 |
| [14] |
DENNIS J, FOURNIER A, SPOTZ W F, et al. High-resolution mesh convergence properties and parallel efficiency of a spectral element atmospheric dynamical core[J]. Int J High Perform Comput Appl, 2005, 19(3): 225-235. DOI:10.1177/1094342005056108 |
| [15] |
DENNIS J M, EDWARDS J, EVANS K J, et al. CAM-SE: a scalable spectral element dynamical core for the Community Atmosphere Model[J]. Int J High Perform Comput Appl, 2012, 26(1): 74-89. DOI:10.1177/1094342011428142 |
| [16] |
THOMAS S J, LOFT R D. Parallel semi-implicit spectral element methods for atmospheric general circulation models[J]. J Sci Comput, 2000, 15(4): 499-518. DOI:10.1023/A:1011188832645 |
| [17] |
ISKANDARANI M, HAIDVOGEL D B, LEVIN J C, et al. Multi-scale geophysical modeling using the spectral element method[J]. Comput Sci Eng, 2002, 4(5): 42-48. DOI:10.1109/MCISE.2002.1032428 |
| [18] |
GIRALDO F X, ROSMOND T E. A scalable spectral element Eulerian atmospheric model (SEE-AM) for NWP: dynamical core tests[J]. Mon Wea Rev, 2004, 132(1): 133-153. DOI:10.1175/1520-0493(2004)132<0133:ASSEEA>2.0.CO;2 |
| [19] |
FOURNIER A, TAYLOR M A, TRIBBIA J J. The spectral element atmosphere model (SEAM): high-resolution parallel computation and localized resolution of regional dynamics[J]. Mon Wea Rev, 2004, 132(3): 726-748. DOI:10.1175/1520-0493(2004)132<0726:TSEAMS>2.0.CO;2 |
| [20] |
TAYLOR M A, FOURNIER A. A compatible and conservative spectral element method on unstructured grids[J]. J Comput Phys, 2010, 229(17): 5879-5895. DOI:10.1016/j.jcp.2010.04.008 |
| [21] |
LEVY M N, NAIR R D, TUFO H M. High-order Galerkin methods for scalable global atmospheric models[J]. Comput Geosci, 2007, 33(8): 1022-1035. DOI:10.1016/j.cageo.2006.12.004 |
| [22] |
GIRALDO F X, RESTELLI M. A study of spectral element and discontinuous Galerkin methods for the Navier-Stokes equations in nonhydrostatic mesoscale atmospheric modeling: equation sets and test cases[J]. J Comput Phys, 2008, 227(8): 3849-3877. DOI:10.1016/j.jcp.2007.12.009 |
| [23] |
RESTELLI M, GIRALDO F X. A conservative discontinuous Galerkin semi-implicit formulation for the Navier-Stokes equations in nonhydrostatic mesoscale atmospheric modeling[J]. SIAM J Sci Comput, 2009, 31(3): 2231-2257. DOI:10.1137/070708470 |
| [24] |
NAIR R D, CHOI H W, TUFO H M. Computational aspects of a scalable high-order discontinuous Galerkin atmospheric dynamical core[J]. Comput Fluids, 2009, 38(2): 309-319. DOI:10.1016/j.compfluid.2008.04.006 |
| [25] |
BLAISE S, ST-CYR A. A dynamic hp-adaptive discontinuous Galerkin method for shallow-water flows on the sphere with application to a global tsunami simulation[J]. Mon Wea Rev, 2012, 140(3): 978-996. DOI:10.1175/MWR-D-11-00038.1 |
| [26] |
COTTER C J, SHIPTON J. Mixed finite elements for numerical weather prediction[J]. J Comput Phys, 2012, 231(21): 7076-7091. DOI:10.1016/j.jcp.2012.05.020 |
| [27] |
THUBURN J, COTTER C J. A framework for mimetic discretization of the rotating shallow-water equations on arbitrary polygonal grids[J]. SIAM J Sci Comput, 2012, 34(3): B203-B225. DOI:10.1137/110850293 |
| [28] |
STANIFORTH A, MELVIN T, COTTER C. Analysis of a mixed finite-element pair proposed for an atmospheric dynamical core[J]. Quart J Roy Meteor Soc, 2013, 139(674): 1239-1254. DOI:10.1002/qj.2028 |
| [29] |
COTTER C J, THUBURN J. A finite element exterior calculus framework for the rotating shallow-water equations[J]. J Comput Phys, 2014, 257: 1506-1526. DOI:10.1016/j.jcp.2013.10.008 |
| [30] |
XIAO F, Ⅱ S. CIP/multi-moment finite volume method with arbitrary order of accuracy[C/OL]//Proceedings of the 12th Computational Engineering Conference of Japan Society for Computational Engineering and Science, Tokyo, May 22-24, 2007. [2022-01-30]. https://arxiv.org/abs/1207.6822.
|
| [31] |
Ⅱ S, XIAO F. CIP/multi-moment finite volume method for Euler equations: a semi-Lagrangian characteristic formulation[J]. J Comput Phys, 2007, 222(2): 849-871. DOI:10.1016/j.jcp.2006.08.015 |
| [32] |
Ⅱ S, XIAO F. High order multi-moment constrained finite volume method. Part I: basic formulation[J]. J Comput Phys, 2009, 228(10): 3669-3707. DOI:10.1016/j.jcp.2009.02.009 |
| [33] |
CHEN C G, XIAO F. Shallow water model on cubed-sphere by multi-moment finite volume method[J]. J Comput Phys, 2008, 227(10): 5019-5044. DOI:10.1016/j.jcp.2008.01.033 |
| [34] |
XIAO F, Ⅱ S, CHEN C G, et al. A note on the general multi-moment constrained flux reconstruction formulation for high order schemes[J]. Appl Math Model, 2013, 37(7): 5092-5108. DOI:10.1016/j.apm.2012.10.050 |
| [35] |
LI X L, CHEN C G, SHEN X S, et al. A multimoment constrained finite-volume model for nonhydrostatic atmospheric dynamics[J]. Mon Wea Rev, 2013, 141(4): 1216-1240. DOI:10.1175/MWR-D-12-00144.1 |
| [36] |
LI X L, CHEN C G, XIAO F, et al. A high-order multi-moment constrained finite-volume global shallow-water model on the Yin-Yang grid[J]. Quart J Roy Meteor Soc, 2015, 141(691): 2090-2102. DOI:10.1002/qj.2504 |
| [37] |
LI X L, SHEN X S, XIAO F, et al. An MCV nonhydrostatic atmospheric model with height-based terrain following coordinate: tests of waves over steep mountains[J/OL]. Adv Meteorol, 2016, 2016: 4513823[2022-01-30]. https://doi.org/10.1155/2016/4513823.
|
| [38] |
CHEN C G, LI X L, SHEN X S, et al. Global shallow water models based on multi-moment constrained finite volume method and three quasi-uniform spherical grids[J]. J Comput Phys, 2014, 271: 191-223. DOI:10.1016/j.jcp.2013.10.026 |
| [39] |
CHEN C G, LI X L, SHEN X S, et al. A high-order conservative collocation scheme and its application to global shallow water equations[J]. Geosci Model Dev, 2015, 8(2): 221-233. DOI:10.5194/gmd-8-221-2015 |
| [40] |
COURANT R. Variational methods for the solution of problems of equilibrium and vibrations[J]. Bull Amer Math Soc, 1943, 49(1): 1-23. DOI:10.1090/S0002-9904-1943-07818-4 |
| [41] |
ZIENKIEWICZ O C, TAYLOR R L. The finite element method for solid and structural mechanics[M]. 6th ed. Oxford: Elsevier Butterworth-Heinemann.
|
| [42] |
DONEA J, HUERTA A. Finite element methods for flow problems[M]. Chichester: John Wiley & Sons, Ltd., 2003.
|
| [43] |
WALTERS R A, CASULLI V. A robust, finite element model for hydrostatic surface water flows[J]. Commun Numer Meth Eng, 1998, 14(10): 931-940. DOI:10.1002/(SICI)1099-0887(1998100)14:10<931::AID-CNM199>3.0.CO;2-X |
| [44] |
LE ROUX D Y, STANIFORTH A, LIN C A. Finite elements for shallow-water equation ocean models[J]. Mon Wea Rev, 1998, 126(7): 1931-1951. DOI:10.1175/1520-0493(1998)126<1931:FEFSWE>2.0.CO;2 |
| [45] |
LE ROUX D Y, SÈNE A, ROSTAND V, et al. On some spurious mode issues in shallow-water models using a linear algebra approach[J]. Ocean Model, 2005, 10(1/2): 83-94. |
| [46] |
COTTER C J, HAM D A, PAIN C C. A mixed discontinuous/continuous finite element pair for shallow-water ocean modelling[J]. Ocean Model, 2009, 26(1/2): 86-90. |
| [47] |
COMBLEN R, LAMBRECHTS J, REMACLE J F, et al. Practical evaluation of five partly discontinuous finite element pairs for the non-conservative shallow water equations[J]. Int J Numer Meth Fluids, 2010, 63(6): 701-724. |
| [48] |
LE ROUX D Y, ROSTAND V, POULIOT B. Analysis of numerically induced oscillations in 2D finite-element shallow-water models part I: inertia-gravity waves[J]. SIAM J Sci Comput, 2007, 29(1): 331-360. DOI:10.1137/060650106 |
| [49] |
HOLMSTRÖM I. On a method for parametric representation of the state of the atmosphere[J]. Tellus, 1963, 15(2): 127-149. DOI:10.3402/tellusa.v15i2.8834 |
| [50] |
STANIFORTH A N. The application of the finite-element method to meteorological simulations: a review[J]. Int J Numer Meth Fluids, 1984, 4(1): 1-12. DOI:10.1002/fld.1650040102 |
| [51] |
BÉLAND M, CÔTÉ J, STANIFORTH A. The accuracy of a finite-element vertical discretization scheme for primitive equation models: comparison with a finite-difference scheme[J]. Mon Wea Rev, 1983, 111(12): 2298-2318. DOI:10.1175/1520-0493(1983)111<2298:TAOAFE>2.0.CO;2 |
| [52] |
DURRAN D R. Numerical methods for fluid dynamics: with applications to geophysics[M]. 2nd ed. New York: Springer, 2010.
|
| [53] |
STANIFORTH A N, DALEY R W. A finite-element formulation for the vertical discretization of sigma-coordinate primitive equation models[J]. Mon Wea Rev, 1977, 105(9): 1108-1118. DOI:10.1175/1520-0493(1977)105<1108:AFEFFT>2.0.CO;2 |
| [54] |
STEPPELER J. The application of the second and third degree methods[J]. J Comput Phys, 1976, 22(3): 295-318. DOI:10.1016/0021-9991(76)90051-6 |
| [55] |
BURRIDGE D M, STEPPELER J, STRVFING R. Finite element schemes for the vertical discretization of the ECMWF forecast model using linear elements[R]. Shinfield Park, Reading: ECMWF, 1986. https://www.ecmwf.int/node/8496.
|
| [56] |
UNTCH A, HORTAL M. A finite-element scheme for the vertical discretization of the semi-Lagrangian version of the ECMWF forecast model[J]. Quart J Roy Meteor Soc, 2004, 130(599): 1505-1530. DOI:10.1256/qj.03.173 |
| [57] |
THUBURN J. Numerical wave propagation on the hexagonal C-grid[J]. J Comput Phys, 2008, 227(11): 5836-5858. DOI:10.1016/j.jcp.2008.02.010 |
| [58] |
LE ROUX D Y. Spurious inertial oscillations in shallow-water models[J]. J Comput Phys, 2012, 231(24): 7959-7987. DOI:10.1016/j.jcp.2012.04.052 |
| [59] |
COTTER C J, McRAE A T T. Compatible finite element methods for numerical weather prediction[C/OL]//ECMWF Seminar Proceedings 2014. [2022-01-30]. https://arxiv.org/abs/1401.0616.
|
| [60] |
MELVIN T, STANIFORTH A, COTTER C. A two-dimensional mixed finite-element pair on rectangles[J]. Quart J Roy Meteor Soc, 2014, 140(680): 930-942. DOI:10.1002/qj.2189 |
| [61] |
McRAE A T T, COTTER C J. Energy-and enstrophy-conserving schemes for the shallow-water equations, based on mimetic finite elements[J]. Quart J Roy Meteor Soc, 2014, 140(684): 2223-2234. DOI:10.1002/qj.2291 |
| [62] |
MELVIN T, BENACCHIO T, SHIPWAY B, et al. A mixed finite-element, finite-volume, semi-implicit discretization for atmospheric dynamics: Cartesian geometry[J]. Quart J Roy Meteor Soc, 2019, 145(724): 2835-2853. DOI:10.1002/qj.3501 |
| [63] |
MA H. A spectral element basin model for the shallow water equations[J]. J Comput Phys, 1993, 109(1): 133-149. DOI:10.1006/jcph.1993.1205 |
| [64] |
TAYLOR M, TRIBBIA J, ISKANDARANI M. The spectral element method for the shallow water equations on the sphere[J]. J Comput Phys, 1997, 130(1): 92-108. DOI:10.1006/jcph.1996.5554 |
| [65] |
THOMAS S J, LOFT R D. The NCAR spectral element climate dynamical core: semi-implicit Eulerian formulation[J]. J Sci Comput, 2005, 25(1): 307-322. DOI:10.1007/s10915-004-4646-2 |
| [66] |
CHOI S J, GIRALDO F X. Development and evaluation of a hydrostatic dynamical core using the spectral element/discontinuous Galerkin methods[J]. Geosci Model Dev Discuss, 2014, 7(3): 4119-4151. |
| [67] |
CHOI S J, GIRALDO F X, KIM J, et al. Verification of a non-hydrostatic dynamical core using horizontally spectral element vertically finite difference method: 2-D aspects[J]. Geosci Model Dev Discuss, 2014, 7(6): 3717-3750. |
| [68] |
REED W H, HILL T R. Triangular mesh methods for the neutron transport equation[R]. New Mexico: Los Alamo Scientific Laboratory, 1973.
|
| [69] |
LESAINT P, RAVIART P A. On a finite element method for solving the neutron transport equation[M]//DE BOOR C. Mathematical aspects of finite elements in partial differential equations. San Diego: Academic Press, 1974: 89-123.
|
| [70] |
CHAVENT G, SALZANO G. A finite-element method for the 1-D water flooding problem with gravity[J]. J Comput Phys, 1982, 45(3): 307-344. DOI:10.1016/0021-9991(82)90107-3 |
| [71] |
COCKBURN B, SHU C W. TVB Runge-Kutta local projection discontinuous Galerkin finite element method for conservation laws Ⅱ: general framework[J]. Math Comput, 1989, 52(186): 411-435. |
| [72] |
COCKBURN B, SHU C W. The Runge-Kutta discontinuous Galerkin method for conservation laws V: multidimensional systems[J]. J Comput Phys, 1998, 141(2): 199-224. DOI:10.1006/jcph.1998.5892 |
| [73] |
SCHWANENBERG D, KÖNGETER J. A discontinuous Galerkin method for the shallow water equations with source terms[M]//COCKBURN B, KARNIADAKIS G E, SHU C W. Discontinuous Galerkin methods. Heidelberg: Springer, 2000: 419-424.
|
| [74] |
COCKBURN B, SHU C W. Runge-Kutta discontinuous Galerkin methods for convection-dominated problems[J]. J Sci Comput, 2001, 16(3): 173-261. DOI:10.1023/A:1012873910884 |
| [75] |
GIRALDO F X, HESTHAVEN J S, WARBURTON T. Nodal high-order discontinuous Galerkin methods for the spherical shallow water equations[J]. J Comput Phys, 2002, 181(2): 499-525. DOI:10.1006/jcph.2002.7139 |
| [76] |
NAIR R D, THOMAS S J, LOFT R D. A discontinuous Galerkin transport scheme on the cubed sphere[J]. Mon Wea Rev, 2005, 133(4): 814-828. DOI:10.1175/MWR2890.1 |
| [77] |
NAIR R D, THOMAS S J, LOFT R D. A discontinuous Galerkin global shallow water model[J]. Mon Wea Rev, 2005, 133(4): 876-888. DOI:10.1175/MWR2903.1 |
| [78] |
KELLY J F, GIRALDO F X. Continuous and discontinuous Galerkin methods for a scalable three-dimensional nonhydrostatic atmospheric model: limited-area mode[J]. J Comput Phys, 2012, 231(24): 7988-8008. DOI:10.1016/j.jcp.2012.04.042 |
| [79] |
BRDAR S, BALDAUF M, DEDNER A, et al. Comparison of dynamical cores for NWP models: comparison of COSMO and Dune[J]. Theor Comput Fluid Dyn, 2013, 27(3): 453-472. |
| [80] |
AHMAD N, LINDEMAN J. Euler solutions using flux-based wave decomposition[J]. Int J Numer Meth Fluids, 2007, 54(1): 47-72. DOI:10.1002/fld.1392 |
| [81] |
NORMAN M R, NAIR R D, SEMAZZI F H M. A low communication and large time step explicit finite-volume solver for non-hydrostatic atmospheric dynamics[J]. J Comput Phys, 2011, 230(4): 1567-1584. DOI:10.1016/j.jcp.2010.11.022 |
| [82] |
SKAMAROCK W C, KLEMP J B, DUDA M G, et al. A multiscale nonhydrostatic atmospheric model using centroidal Voronoi tesselations and C-grid staggering[J]. Mon Wea Rev, 2012, 140(9): 3090-3105. DOI:10.1175/MWR-D-11-00215.1 |
| [83] |
ULLRICH P A, JABLONOWSKI C. MCore: a non-hydrostatic atmospheric dynamical core utilizing high-order finite-volume methods[J]. J Comput Phys, 2012, 231(15): 5078-5108. DOI:10.1016/j.jcp.2012.04.024 |
| [84] |
YABE T, AOKI T. A universal solver for hyperbolic equations by cubic-polynomial interpolation I. One-dimensional solver[J]. Comput Phys Commun, 1991, 66(2/3): 219-232. |
| [85] |
YABE T, TANAKA R, NAKAMURA T, et al. An exactly conservative semi-Lagrangian scheme (CIP-CSL) in one dimension[J]. Mon Wea Rev, 2001, 129(2): 332-344. DOI:10.1175/1520-0493(2001)129<0332:AECSLS>2.0.CO;2 |
| [86] |
XIAO F. Unified formulation for compressible and incompressible flows by using multi-integrated moments I: one-dimensional inviscid compressible flow[J]. J Comput Phys, 2004, 195(2): 629-654. DOI:10.1016/j.jcp.2003.10.014 |
| [87] |
XIAO F, AKOH R, Ⅱ S. Unified formulation for compressible and incompressible flows by using multi-integrated moments Ⅱ: multi-dimensional version for compressible and incompressible flows[J]. J Comput Phys, 2006, 213(1): 31-56. DOI:10.1016/j.jcp.2005.08.002 |
| [88] |
ZHANG M P, SHU C W. An analysis of and a comparison between the discontinuous Galerkin and the spectral finite volume methods[J]. Comput Fluids, 2005, 34(4/5): 581-592. |
| [89] |
LI X L, CHEN D H, PENG X D, et al. A multimoment finite-volume shallow-water model on the Yin-Yang overset spherical grid[J]. Mon Wea Rev, 2008, 136(8): 3066-3086. DOI:10.1175/2007MWR2206.1 |
| [90] |
Ⅱ S, XIAO F. A global shallow water model using high order multi-moment constrained finite volume method and icosahedral grid[J]. J Comput Phys, 2010, 229(5): 1774-1796. DOI:10.1016/j.jcp.2009.11.008 |
| [91] |
CHEN C G, BIN J Z, XIAO F. A global multimoment constrained finite-volume scheme for advection transport on the hexagonal geodesic grid[J]. Mon Wea Rev, 2011, 140(3): 941-955. DOI:10.1175/MWR-D-11-00095.1 |
| [92] |
KAGEYAMA A, SATO T. "Yin-Yang grid": an overset grid in spherical geometry[J]. Geochem, Geophys, Geosyst, 2004, 5(9): Q09005. DOI:10.1029/2004GC000734 |
| [93] |
PENG X D, XIAO F, TAKAHASHI K. Conservative constraint for a quasi-uniform overset grid on the sphere[J]. Quart J Roy Meteor Soc, 2006, 132(616): 979-996. DOI:10.1256/qj.05.18 |
| [94] |
SADOURNY R. Conservative finite-difference approximations of the primitive equations on quasi-uniform spherical grids[J]. Mon Wea Rev, 1972, 100(2): 136-144. DOI:10.1175/1520-0493(1972)100<0136:CFAOTP>2.3.CO;2 |
| [95] |
RANČIĆ M, PURSER R J, MESINGER F. A global shallow-water model using an expanded spherical cube: gnomonic versus conformal coordinates[J]. Quart J Roy Meteor Soc, 1996, 122(532): 959-982. DOI:10.1002/qj.49712253209 |
| [96] |
SADOURNY R, ARAKAWA A, MINTZ Y. Integration of the nondivergent barotropic vorticity equation with an icosahedral-hexagonal grid for the sphere[J]. Mon Wea Rev, 1968, 96(6): 351-356. DOI:10.1175/1520-0493(1968)096<0351:IOTNBV>2.0.CO;2 |
| [97] |
HORTAL M, SIMMONS A. Use of reduced Gaussian grids in spectral models[J]. Mon Wea Rev, 1991, 119(4): 1057-1074. DOI:10.1175/1520-0493(1991)119<1057:UORGGI>2.0.CO;2 |
| [98] |
STANIFORTH A, THUBURN J. Horizontal grids for global weather and climate prediction models: a review[J]. Quart J Roy Meteor Soc, 2012, 138(662): 1-26. DOI:10.1002/qj.958 |
| [99] |
ULLRICH P A, JABLONOWSKI C, VAN LEER B. High-order finite-volume methods for the shallow-water equations on the sphere[J]. J Comput Phys, 2010, 229(17): 6104-6134. DOI:10.1016/j.jcp.2010.04.044 |
| [100] |
QADDOURI A. Nonlinear shallow-water equations on the Yin-Yang grid[J]. Quart J Roy Meteor Soc, 2011, 137(656): 810-818. DOI:10.1002/qj.792 |
| [101] |
ZERROUKAT M, ALLEN T. On the solution of elliptic problems on overset/Yin-Yang grids[J]. Mon Wea Rev, 2012, 140(8): 2756-2767. DOI:10.1175/MWR-D-11-00272.1 |
| [102] |
HALL D M, NAIR R D. Discontinuous Galerkin transport on the spherical Yin-Yang overset mesh[J]. Mon Wea Rev, 2013, 141(1): 264-282. DOI:10.1175/MWR-D-12-00108.1 |
| [103] |
SMOLARKIEWICZ P K, SZMELTER J, XIAO F. Simulation of all-scale atmospheric dynamics on unstructured meshes[J]. J Comput Phys, 2016, 322: 267-287. DOI:10.1016/j.jcp.2016.06.048 |
| [104] |
DAVIES T, CULLEN M J P, MALCOLM A J, et al. A new dynamical core for the Met Office's global and regional modelling of the atmosphere[J]. Quart J Roy Meteor Soc, 2005, 131(608): 1759-1782. DOI:10.1256/qj.04.101 |
| [105] |
SKAMAROCK W C, KLEMP J B. The stability of time-split numerical methods for the hydrostatic and the nonhydrostatic elastic equations[J]. Mon Wea Rev, 1992, 120(9): 2109-2127. DOI:10.1175/1520-0493(1992)120<2109:TSOTSN>2.0.CO;2 |
| [106] |
SKAMAROCK W C, KLEMP J B. A time-split nonhydrostatic atmospheric model for weather research and forecasting applications[J]. J Comput Phys, 2008, 227(7): 3465-3485. DOI:10.1016/j.jcp.2007.01.037 |
| [107] |
DURRAN D R, BLOSSEY P N. Implicit-explicit multistep methods for fast-wave-slow-wave problems[J]. Mon Wea Rev, 2012, 140(4): 1307-1325. DOI:10.1175/MWR-D-11-00088.1 |
| [108] |
GIRALDO F X. Semi-implicit time-integrators for a scalable spectral element atmospheric model[J]. Quart J Roy Meteor Soc, 2005, 131(610): 2431-2454. DOI:10.1256/qj.03.218 |
| [109] |
ASCHER U M, RUUTH S J, SPITERI R J. Implicit-explicit Runge-Kutta methods for time-dependent partial differential equations[J]. Appl Numer Math, 1997, 25(2/3): 151-167. |
| [110] |
PARESCHI L, RUSSO G. Implicit-explicit Runge-Kutta schemes and applications to hyperbolic systems with relaxation[J]. J Sci Comput, 2005, 25(1): 129-155. DOI:10.1007/s10915-004-4636-4 |
| [111] |
ULLRICH P, JABLONOWSKI C. Operator-split Runge-Kutta-Rosenbrock methods for nonhydrostatic atmospheric models[J]. Mon Wea Rev, 2012, 140(4): 1257-1284. DOI:10.1175/MWR-D-10-05073.1 |
| [112] |
WELLER H, LOCK S J, WOOD N. Runge-Kutta IMEX schemes for the horizontally explicit/vertically implicit (HEVI) solution of wave equations[J]. J Comput Phys, 2013, 252: 365-381. DOI:10.1016/j.jcp.2013.06.025 |
| [113] |
BAO L, KLÖFKORN R, NAIR R D. Horizontally explicit and vertically implicit (HEVI) time discretization scheme for a discontinuous Galerkin nonhydrostatic model[J]. Mon Wea Rev, 2015, 143(3): 972-990. DOI:10.1175/MWR-D-14-00083.1 |
 2022, Vol. 42
2022, Vol. 42


