2. 自然资源部空间海洋遥感与应用重点实验室,北京 100081
2. Key Laboratory of Space Ocean Remote Sensing and Application, Ministry of Natural Resources, Beijing 100081, China
星载微波辐射计(以下简称“微波辐射计”)属于被动微波遥感器,在海洋探测方面,主要通过接收海水分子热运动在微波频段产生的自然辐射强度,以及极化特性随波长、海面粗糙度、海水介电特性的变化,来反演海面温度、海面风速、表层海水盐度等海洋动力和热力参数[1-2],并可反演大气中的水汽含量、云液态水含量等大气参数[3]。这些反演得到的参数在全球气候变化、海洋环境预报、海洋灾害监测、海况监测以及海洋渔场监测等方面具有广泛应用。
微波辐射计数据地理定位是数据预处理的重要组成部分,直接影响后续多通道数据匹配和卫星数据应用。遥感数据地理位置的计算方法主要分为参数法和非参数法,参数法是根据遥感仪器的观测几何及空间位置,建立观测像元与地面观测位置之间的模型[4]。非参数法利用已知地理位置地物特征明显的地面点,建立遥感数据和地基坐标系之间的空间位置关系模型。目前卫星遥感数据地理定位业务中主要采用的是参数法,非参数法则可以用于成像载荷数据,对参数法的结果进行精校正,进一步提高定位精度。
目前国际上的SSM/I(Special Sensor Microwave/Imager)、AMSR-E(Advanced Microwave Scanning Radiometer for Earth Observing System)和WindSat等比较典型的微波辐射计都采用相似的地理定位算法[5-7],核心原理都是利用辐射计的波束指向和载荷的空间位置构建几何定位模型,利用矢量三角形原理解算地面观测点的坐标。POE and CONWAY[5]利用该方法对SSM/I的H极化85 GHz通道数据进行地理定位,并通过提高卫星星历精度和修正姿态角,将定位误差控制到7 km以内。由于海陆交界处的亮温梯度较大,WIEBE et al.[6]通过修正载荷的指向角和扫描角来降低海岸线附近的升降轨数据亮温差,优化了AMSR-E定位结果。PURDY et al.[7]对全极化辐射计WindSat进行了地理定位和指向精度分析,通过修正时间和波束指向误差,定位精度优于5 km,满足精确极化测量的要求。我国的微波辐射计研究起步较晚,2002年12月神舟四号飞船成功发射[8],其搭载多模态微波遥感器(包括散射计、辐射计和高度计)获取大量的在轨数据,为载荷上星积累了丰富的算法实践经验。此后的风云三号卫星和海洋二号等卫星均搭载微波辐射计,其地面系统的定位算法也采用几何定位模型,并取得了不错的精度[4, 9]。
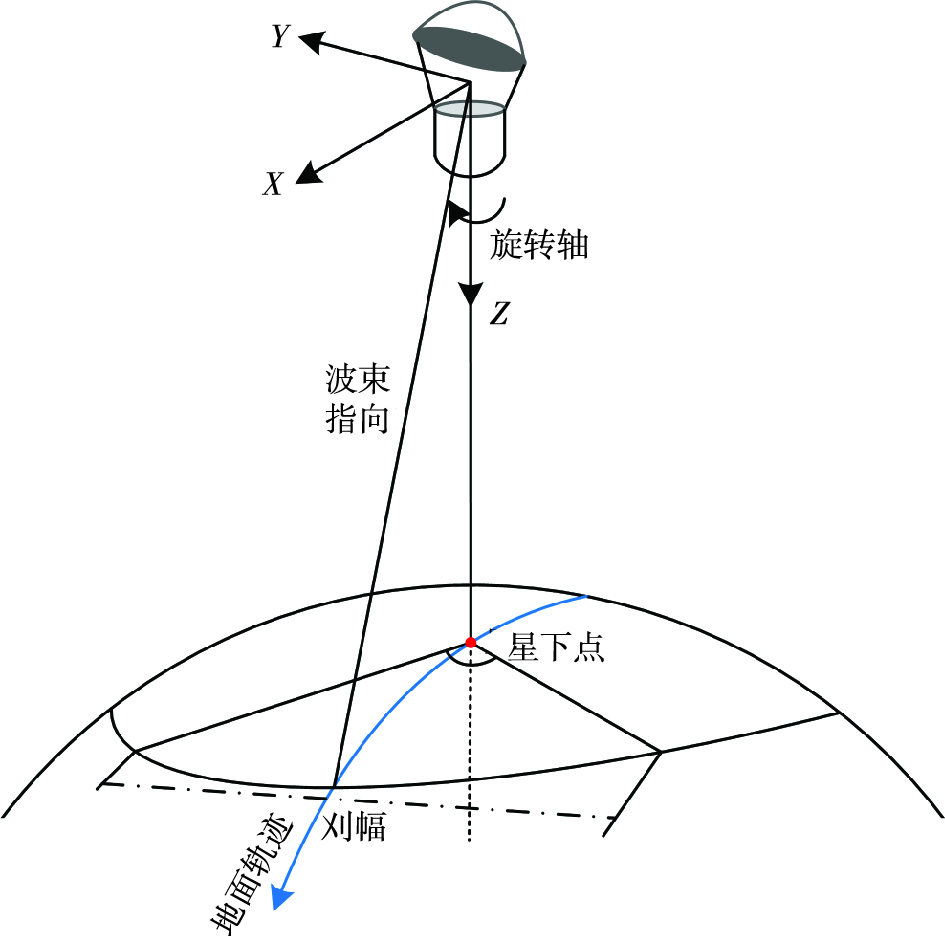
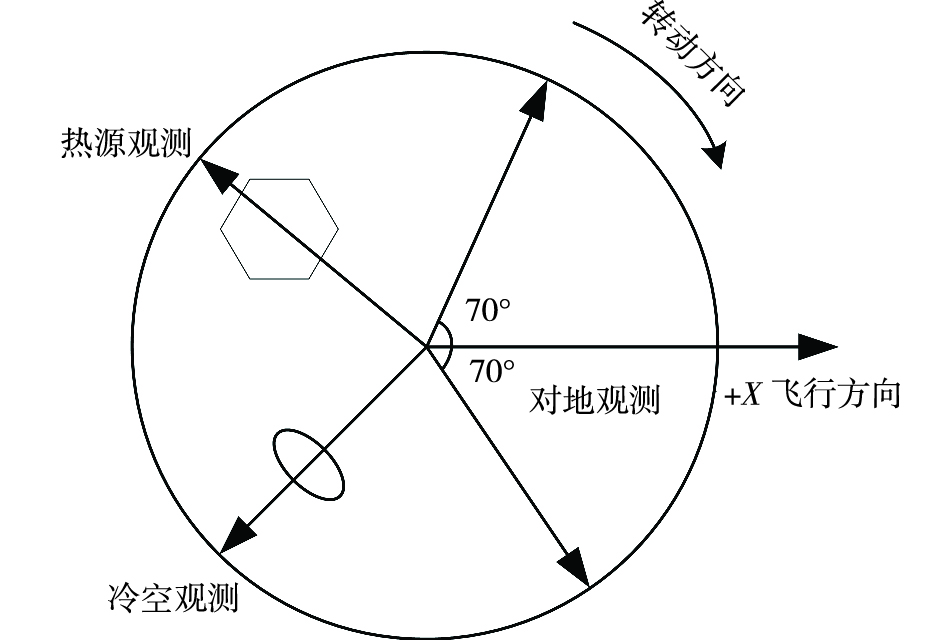
1 微波辐射计工作原理海洋二号B卫星(简记为“HY-2B”)于2018年10月25日从太原卫星发射中心发射升空,是我国第二颗极轨海洋动力环境卫星。星上搭载的微波辐射计(Scanning Microwave Radiometer,SMR)是由一个偏置抛物面反射器和馈源喇叭组成的全功率辐射计,天线波束指向与星下点方向夹角为44°,通过旋转机构的360°转动,在飞行方向一定角度范围内实现对地扫描,获取地球表面和大气的辐射数据,同时在方位向进行冷空观测和热源观测,收集到数量充足的定标数据[10]。载荷的性能指标见表 1,其观测几何如图 1和图 2所示。
|
|
表 1 HY-2B卫星微波辐射计主要技术指标 Table 1 Main technical indexes of HY-2B satellite microwave radiometer |
|
图 1 微波辐射计扫描几何示意图 Fig.1 Scanning geometry of microwave radiometer |
|
图 2 扫描系统工作模式示意图 Fig.2 Schematic diagram of scanning system's operating mode |
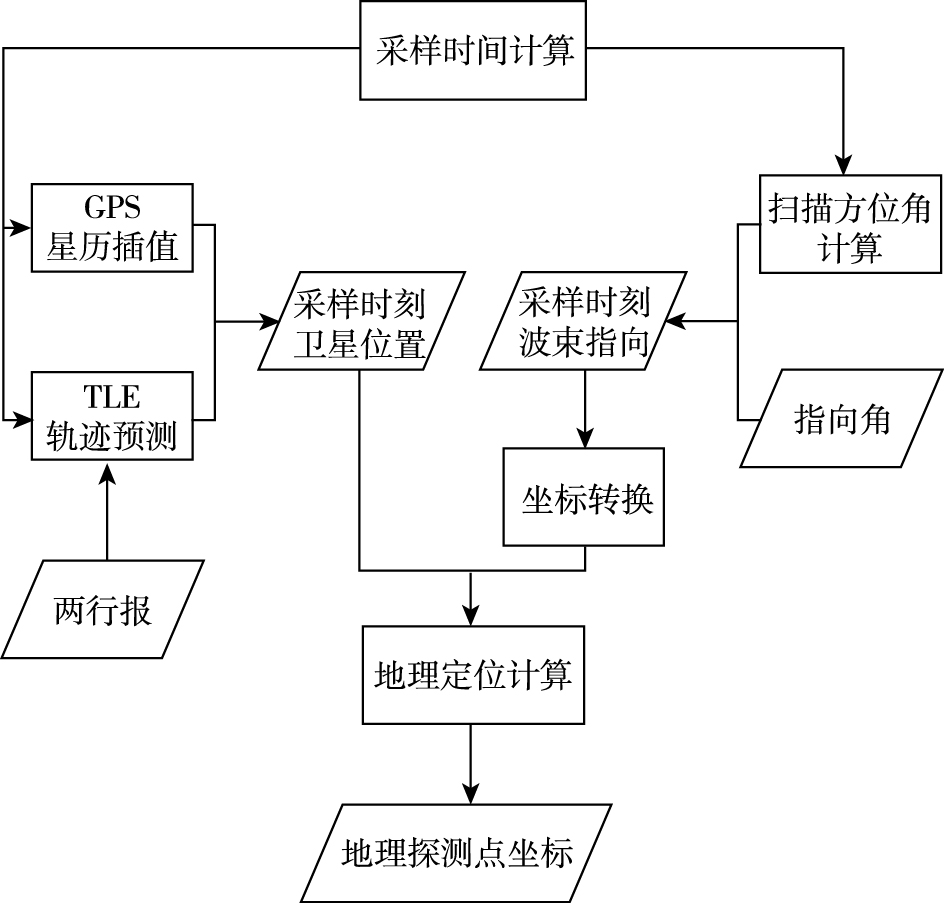
SMR地理定位算法是利用采样时刻的卫星星历和天线波束的指向,构建几何定位模型来计算地面点的位置。该方法的优势是原理简单,计算快速。影响定位精度的因素有卫星星历、卫星姿态、波束指向和时间等。地理定位流程如图 3所示。
|
图 3 地理定位流程图 Fig.3 Flow chart of geolocation |
采样时间是计算卫星星历和波束指向的基准。SMR时间采样策略是当天线旋转到某一特定角度时,记录一个星上时间,存储在载荷原始数据包。因此,计算某扫描行某采样点的时间采用如下公式:
| $ t_i=t_{\text {base }}+t_{\text {sat }}+t_{\text {local }}-t_0+(i-1) \Delta t。$ | (1) |
其中:ti为某扫描行第i个采样点的时间;tsat为星上时间码,tlocal为本地计时时间,两者均从载荷原始数据包中读取,是以基准时间为起点的累计秒;t0为从起始采样点角度旋转到载荷时间获取角度的时间间隔;Δt是采样时间间隔,为固定值10 ms;tbase为基准时间,即2016年1月1日00:00:00(UTC)。
2.2 卫星星历获取HY-2B卫星星历获取的方法一般有两种:一种是通过星载全球定位系统(Global Positioning System, GPS)接收机获取地固坐标系(Earth-Centered,Earth-Fixed,简称“ECEF”)下的卫星位置和速度,然后利用3次样条插值方法得到仪器采样时刻的卫星位置,简称“GPS法”;另一种是利用两行元素轨道报(Two-Line Element Set,简称“TLE”),结合SGP4(Simplified General Perturbations 4)轨道预测模型直接计算得到真赤道平春分点坐标系(True Equator Mean Equinox,TEME)下的仪器采样时刻卫星位置和速度,然后再转换成地固坐标,简称“TLE法”。TLE法获取的卫星位置比从星上GPS获取的位置精度低,在历元时刻的轨道计算精度为1 km左右,并以每天1~3 km的误差不断累积[11]。在HY-2B微波辐射计处理业务中,会每天更新TLE文件,因此TLE法的累积误差可以忽略。TEME坐标系到ECEF坐标系的转换公式如下:
| $ \boldsymbol{r}_{\mathrm{ECEF}}=\boldsymbol{T}_{\mathrm{ECEF} / \mathrm{TEME}} \boldsymbol{r}_{\mathrm{TEME}}, $ | (2) |
其中,rTEME为TEME坐标系下的卫星位置矢量,rECEF为ECEF坐标系下的卫星位置,TECEF/TEME是TEME至ECEF的转换矩阵。
转换矩阵可用如下公式计算[12]:
| $ \boldsymbol{T}_{\text {ECEF/TEAE }}=\boldsymbol{R}\left(y, -x_p\right) \boldsymbol{R}\left(x, -y_p\right) \boldsymbol{R}\left(z, \theta_G\right) \text { 。} $ | (3) |
其中,R表示绕某个坐标轴逆时针转动某个角度的坐标变换矩阵[12-13];xp和yp是极移两分量,可在IERS(International Earth Rotation and Reference Systems Service)网站获取;θG是格林尼治恒星时角,具体计算方法可参考文献[11]。
2.3 天线波束指向计算SMR天线波束指向的计算涉及到天线坐标系、仪器坐标系、卫星本体坐标系、轨道坐标系、J2000惯性坐标系和地心地固坐标系的相互转换。坐标系定义见表 2。
|
|
表 2 各坐标系定义 Table 2 Definition of different coordinate systems |
天线坐标系到仪器坐标系可以通过天线的安装矩阵Tinst/ante来进行转换。该矩阵一般在卫星发射前进行测量,可以视为一个常量。
2.3.2 仪器坐标系到卫星本体坐标系的转换仪器坐标系到卫星本体坐标系可以用仪器的安装矩阵Tsat/inst进行转换。该矩阵在卫星发射前进行测量,卫星在轨后可以对该矩阵进行更新。
2.3.3 卫星本体坐标系到轨道坐标系的转换卫星本体坐标系到轨道坐标系的转换矩阵Torb/sat可以通过卫星姿态角旋转的方式实现,姿态数据随时间变化。3个姿态角的旋转顺序为2-1-3(即俯仰-滚动-偏航),计算公式[14]如下:
| $ \begin{aligned} & \boldsymbol{T}_{\text {orb/ssat }}=\left[\begin{array}{ccc} \cos Y & -\sin Y & 0 \\ \sin Y & \cos Y & 0 \\ 0 & 0 & 1 \end{array}\right] \\ & {\left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & \cos R & -\sin R \\ 0 & \sin R & \cos R \end{array}\right]\left[\begin{array}{ccc} \cos P & 0 & \sin P \\ 0 & 1 & 0 \\ -\sin P & 0 & \cos P \end{array}\right], } \end{aligned} $ | (4) |
其中,P为俯仰角,R为滚动角,Y为偏航角。如果卫星的飞行姿态为0时,两个坐标系是重合的。
2.3.4 轨道坐标系到J2000惯性坐标系的转换要实现轨道坐标系与J2000惯性坐标系的坐标转换,首先要计算得到轨道坐标系的3个坐标轴在惯性坐标系中的单位矢量[15]。
| $ \begin{gathered} \boldsymbol{z}_{\text {orb }}=-\boldsymbol{r} / r \\ \boldsymbol{y}_{\text {orb }}=\boldsymbol{z}_{\mathrm{orb}} \times \boldsymbol{v} / v, \\ \boldsymbol{x}_{\mathrm{orb}}=\boldsymbol{y}_{\mathrm{orb}} \times \boldsymbol{z}_{\mathrm{orb}} \end{gathered} $ | (5) |
其中,r是卫星在惯性坐标系下的位置矢量,r是卫星位置矢量的模,v是卫星在惯性坐标系下的速度矢量,v是卫星速度矢量的模。
因此,轨道坐标系到J2000惯性坐标系的转换矩阵为:
| $ \boldsymbol{T}_{\mathrm{J} 2000 / \text {orb }}=\left[\begin{array}{lll} x_{\mathrm{orb}}(1) & y_{\mathrm{orb}}(1) & z_{\mathrm{orb}}(1) \\ x_{\mathrm{orb}}(2) & y_{\mathrm{orb}}(2) & z_{\mathrm{orb}}(2) \\ x_{\mathrm{orb}}(3) & y_{\mathrm{orb}}(3) & z_{\mathrm{orb}}(3) \end{array}\right]。$ | (6) |
J2000惯性坐标系到地心地固系的坐标转换可以采用经典的岁差章动理论方法,也可以采用无旋原点的方法。转换矩阵用TECEF/J2000表示。具体转换方法可以查阅相关文献,这里不再赘述。
2.3.6 波束指向计算波束指向在天线坐标系中,可以用单位向量表示为:
| $ \boldsymbol{u}_{\text {ante }}=[\sin \alpha \cos \varphi, \sin \alpha \sin \varphi, \cos \alpha]^\boldsymbol{T}。$ | (7) |
式中:α为波束指向角,为44°;φ为波束的扫描方位角,可通过起始扫描方位角、天线转速和采样时间间隔计算得到。
需将其天线坐标系下的波束指向单位向量转换到地心地固坐标系,使其与卫星位置处于同一坐标框架下。转换公式如下:
| $ \boldsymbol{u}_{\mathrm{ECEF}}=T_{\mathrm{ECFF} / 2000} T_{\mathrm{J} 2000 / \mathrm{ord}} T_{\text {orb/sat }} T_{\text {sav/inst }} T_{\text {ins } / \text { ante }} \boldsymbol{u}_{\text {ante }}, $ | (8) |
其中,uante为波束指向在天线坐标系下的单位矢量,uECEF为波束指向在地心地固坐标系下的单位矢量。
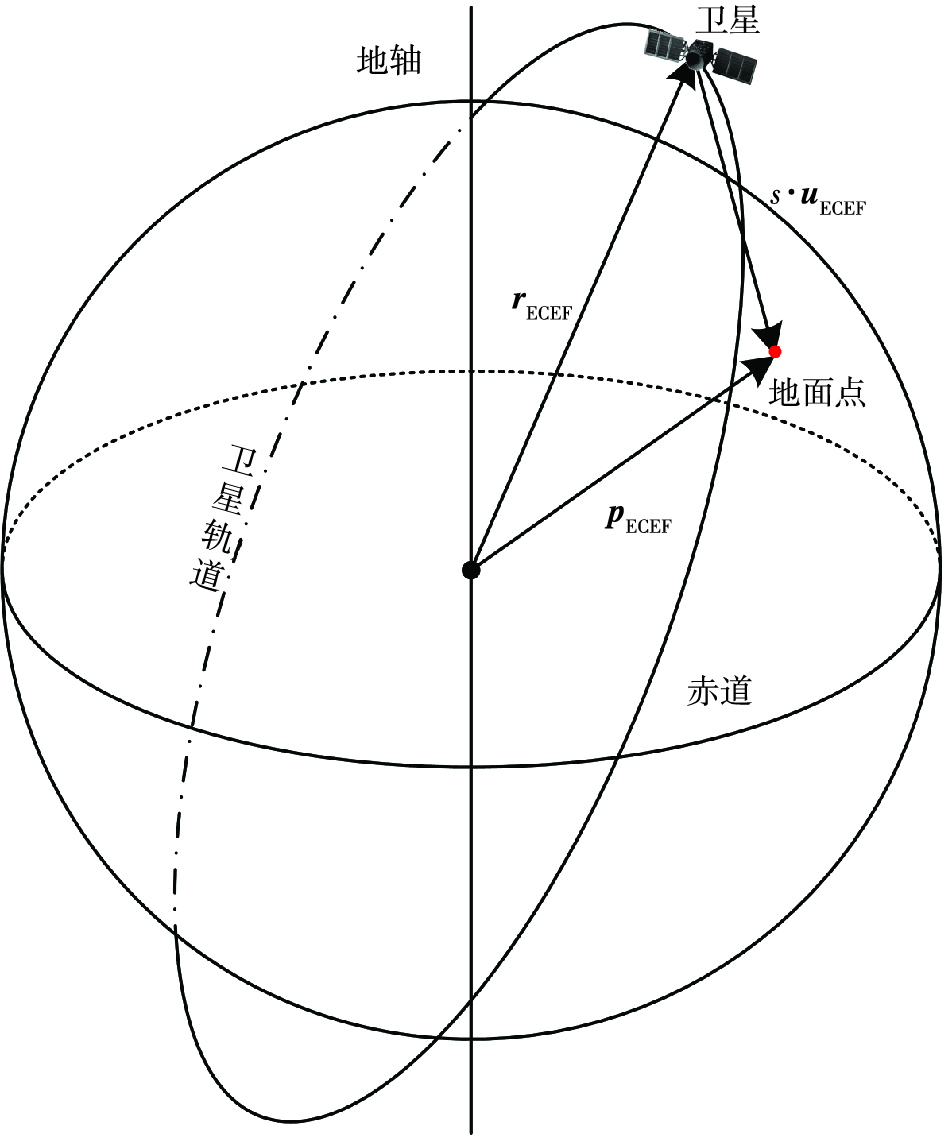
2.4 采样点位置计算已知在地心地固坐标系下的卫星位置矢量rECEF和天线波束指向矢量uECEF,构建几何定位模型,可以得到地面采样点的位置pECEF。原理图如图 4所示。
|
图 4 微波辐射计几何定位模型原理图 Fig.4 Schematic diagram of geometric positioning model of microwave radiometer |
几何模型可以用如下公式表示:
| $ \boldsymbol{r}_{\mathrm{ECEF}}+s \cdot \boldsymbol{u}_{\mathrm{ECEF}}=\boldsymbol{p}_{\mathrm{ECEF}}, $ | (9) |
其中,s为卫星到地面采样点的斜距。
由式(9)可以看出,要想得到pECEF,必须先要求解斜距s,因此建立椭球方程,将待求点pECEF带入该方程:
| $ p^2 x+p^2 y+\frac{p_z^2}{\left(1-e^2\right)}=a^2, $ | (10) |
其中,a为地球的半长轴,e为地球偏心率。
将式(9)带入式(10)得到一个简单的一元二次方程,可以很容易地求出两个解,取斜距s的两个根中较小的那一个,因为这个根是天线波束与地球近端的交点。将s带入式(9)就可以得到地心地固系中地面采样点的坐标。
| $ A \cdot s^2+B \cdot s+C=0 \text { 。} $ | (11) |
最后要将地心地固坐标转换为经纬度坐标,常用的方法是通过多次迭代、快速收敛,得到纬度值和高度值。本文采用FUKUSHIMA[16]根据Halley的三阶公式提供的一种求解纬度值的新方法,该方法无需迭代,快速高效。
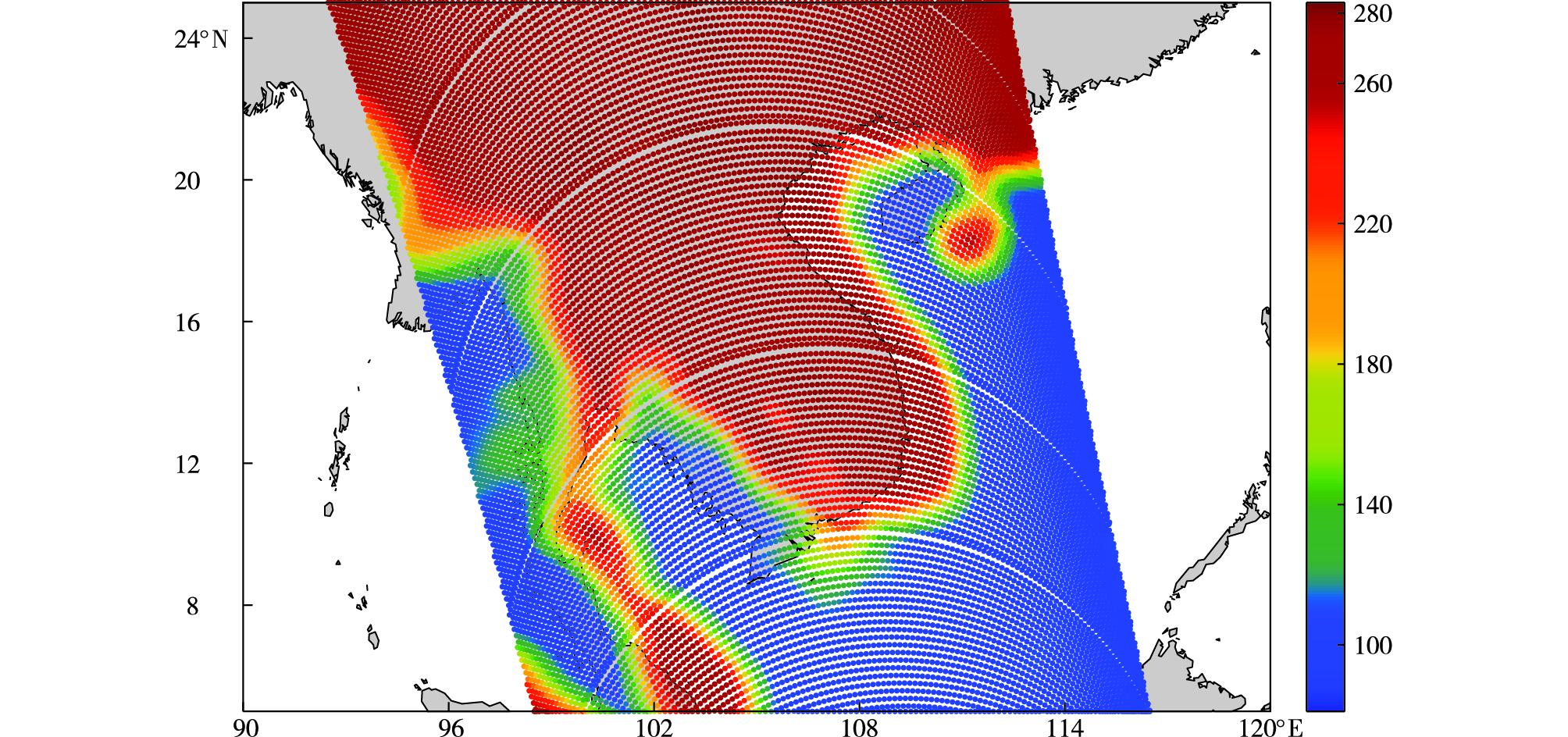
3 定位结果由于SMR的9个通道的馈源指向都略有差异,每个通道都需单独定位。这里将星载GPS数据作为卫星星历,采用上述地理定位方法,对2019年6月26日cycle号为018,pass号为0045的数据进行计算,其10.7 GHz H极化通道的定位结果如图 5所示。由于在海岸线附近的探测会同时受到陆地和海洋影响,因此亮温值介于陆地和海洋之间,呈现明显的过渡趋势。将定位结果与精确地理底图叠加显示可以看出,定位偏移比较大且相邻扫描线之间疏密不均匀。其他8个通道的定位结果也出现类似情况,将在下一节分析原因并进行改进。
|
图 5 10.7 GHz H极化通道数据定位结果(色标为亮温,单位:K) Fig.5 Geolocation results of 10.7 GHz H polarization channel data (color scale for brightness temperature, units: K) |
针对上述SMR定位结果出现的偏移问题,根据载荷的工作原理和定位模型综合分析可知,定位点偏移的原因可能是卫星星历误差或扫描方位角误差。相邻扫描线的不均匀性可能有两个原因:一是卫星姿态异常,二是扫描线的起始点的采样时间不准确。下面分别进行具体分析。
4.1 星历精度分析在SMR业务生产中,同时支持GPS插值、TLE轨道预测两种星历计算方法。星上GPS的标称精度为10 m,因此优先采用GPS法,当GPS数据异常时自动切换到TLE法。下面定量比较一下两者的精度差异。提取载荷原始数据包中2019年6月26日的GPS数据,将TLE法预测的卫星位置与其进行对比。由图 6可见,TLE法与GPS法的位置偏差小于1.4 km,与算法标称精度一致。图中的误差曲线有3处不平滑的位置(图中画圈的位置)。通过分析GPS数据可以推断不平滑的位置可能是因GPS天线锁定GPS卫星的数量过少,影响了对卫星位置的解算精度,因此有必要利用位置精度为10 cm的精密定轨实时产品(real-time orbit ephemeris,ROE)来分析一下载荷包中GPS数据的精度。由图 7可见,99.8%的GPS数据点的误差在10 m以内,少量数据点的误差大于10 m,个别点的误差超过100 m,这说明载荷包中的GPS数据精度基本达到了设计指标。对比图 6和图 7,可以发现图 6出现不平滑位置的时间与图 7精度较差的时间相吻合,从而证明了前面的推断。

|
图 6 TLE法与GPS法的位置偏差(红色圆圈代表误差曲线中不平滑的位置) Fig.6 Position errors of TLE method and GPS method (red circle for unsmoothed place in the error curve) |

|
图 7 GPS与ROE的位置偏差 Fig.7 Position errors of GPS and ROE |
上述分析表明,对于分辨率较低的微波辐射计来说,卫星星历的精度可以满足定位需求,因此可以确定扫描方位角误差是造成较大定位偏移的主要原因。
4.2 时间精度分析针对图 5中相邻扫描线疏密不均匀的现象,根据定位原理初步分析,可能是卫星姿态异常或某些扫描线起始观测点的采样时间异常导致的。经过分析,卫星姿态数据没有异常。因SMR的扫描周期是3.78 s,所以相邻扫描线起始观测点的时间差理论值应该是3.78 s。然而通过分析发现,大部分时间差值分布在标称扫描周期3.78 s附近,少量值有规律的波动。图 8a中的横坐标是扫描线的行号,纵坐标是相邻扫描行起始观测点的时间差值。图 8a中显示某些相邻扫描线的时间间隔大于4 s或小于3 s,因此推断星上时间获取有误差。通过剔除异常采样时间值,进行线性插值解决了星上时间获取误差的问题(图 8b)。修正后的时间差值分布在3.792 s周围,与设计值(3.78 s)接近。

|
图 8 相邻扫描线起始采样时间差曲线 Fig.8 Difference of start times between adjacent scanning lines |
通过修正起始观测点的采样时间和扫描方位角,对9个通道分别进行重新定位,选择了全球高中低纬度不同地区的定位结果进行展示(图 9)。地理底图选用GSHHG(Global Self-consisitent, Hierarachical, High-resolution Geography Database),该底图的位置精度为几十米的量级[17]。由图 9可以看出,海洋和陆地的亮温与地理底图的匹配性比较好,海陆边界的亮温过渡也比较自然。因此,该定位修正方法适用于对SMR全球数据的地理定位。

|
图 9 修正后的定位结果图(色阶为亮温,单位:K) Fig.9 Revised geolocation results (color scale for brightness temperature, units: K) |
本文描述了HY-2B卫星微波辐射计的工作原理,针对其圆锥扫描的工作方式,给出了一种适用的地理定位方法并对SMR的9个通道分别进行了定位。针对定位结果较差的问题,分析了GPS和TLE两种方式获取的卫星星历精度。结果表明,GPS法大部分点的精度优于10 m,基本满足指标要求,TLE法的精度优于1.4 km,相对于SMR粗糙的分辨率来说,GPS和TLE提供的星历精度都是足够的。针对起始观测点采样时间异常,利用剔除异常值进行线性插值的方法,解决了相邻扫描线之间疏密不均匀的问题。通过修正扫描方位角较好地解决了定位结果偏移比较大的问题。将定位结果与高精度的地理底图叠加发现,定位结果与海陆边界匹配较好,可以应用到业务化生产工作中。
| [1] |
蒋兴伟, 林明森, 宋清涛. 海洋二号卫星主被动微波遥感探测技术研究[J]. 中国工程科学, 2013, 15(7): 4-11. DOI:10.3969/j.issn.1009-1742.2013.07.001 |
| [2] |
ULABY F T, MOORE R K, FUNG A K. Microwave remote sensing: active and passive. Volume I: microwave remote sensing fundamentals and radiometry[M]. Reading: Addison-Wesley Publishing Co., 1981.
|
| [3] |
王兆徽, 廖菲, 宋清涛, 等. 星载微波辐射计分辨率匹配的平滑参数选择[J]. 航天器工程, 2016, 25(2): 145-152. DOI:10.3969/j.issn.1673-8748.2016.02.020 |
| [4] |
关敏, 杨忠东. FY-3微波成像仪遥感图像地理定位方法研究[J]. 遥感学报, 2009, 13(3): 463-474. |
| [5] |
POE G A, CONWAY R W. A study of the geolocation errors of the Special Sensor Microwave/Imager (SSM/I)[J]. IEEE Trans Geosci Remote Sens, 1990, 28(5): 791-799. DOI:10.1109/36.58965 |
| [6] |
WIEBE H, HEYGSTER G, MEYER-LERBS L. Geolocation of AMSR-E data[J]. IEEE Trans Geosci Remote Sens, 2008, 46(10): 3098-3103. DOI:10.1109/TGRS.2008.919272 |
| [7] |
PURDY W E, GAISER P W, POE G A, et al. Geolocation and pointing accuracy analysis for the WindSat sensor[J]. IEEE Trans Geosci Remote Sens, 2006, 44(3): 496-505. DOI:10.1109/TGRS.2005.858415 |
| [8] |
张德海, 姜景山, 郑震藩, 等. 神舟4号主载荷: 多模态微波遥感器[J]. 遥感技术与应用, 2005, 20(1): 74-80. |
| [9] |
吴奎桥, 林明森, 郭振宇. HY-2卫星微波辐射计地理定位方法[J]. 中国工程科学, 2014, 16(6): 21-26. |
| [10] |
李延明, 姜敏, 余锐, 等. 海洋二号卫星微波辐射计系统设计[J]. 中国工程科学, 2013, 15(7): 39-43. |
| [11] |
VALLADO D A, CRAWFORD P, HUJSAK R, et al. Revisiting Spacetrack Report #3: Rev 3[C]. AIAA/AAS Astrodynamics Specialist Conference, Keystone, Colorado, 2006.
|
| [12] |
李济生. 航天器轨道确定[M]. 北京: 国防工业出版社, 2003.
|
| [13] |
张玉祥. 人造卫星测轨方法[M]. 北京: 国防工业出版社, 2007.
|
| [14] |
TANG F, ZOU X L, YANG H, et al. Estimation and correction of geolocation errors in FengYun-3C Microwave Radiation Imager data[J]. IEEE Trans Geosci Remote Sens, 2015, 54(1): 407-420. |
| [15] |
DUNBAR R S, HSIAO S V, KIM Y J, et al. Science algorithm specification for SeaWinds on QuikSCAT and SeaWinds on ADEOS-Ⅱ[M]. Pasadena: Jet Propulsion Laboratory, 2001: 4-61.
|
| [16] |
FUKUSHIMA T. Transformation from Cartesian to Geodetic coordinates accelerated by Halley's method[J]. J Geodesy, 2006, 79(12): 689-693. |
| [17] |
WESSEL P, SMITH W H F. A global, self-consistent, hierarchical, high-resolution shoreline database[J]. J Geophys Res: Solid Earth, 1996, 101(B4): 8741-8743. |
 2022, Vol. 42
2022, Vol. 42

