有一些复杂的问题,不仅包含可以量化的因素,还可能包含难以量化的因素(如社会性、心理学等方面的因素),并且其中涉及的评判标准也不尽相同,这使得难以找到这类问题的最佳解决方案。针对这类问题,美国著名运筹学家SAATY[1-3]提出了一种具有很强实用性的解决方法——层次分析法(analytic hierarchy process,AHP)。对于复杂的问题,常规的思维逻辑是将复杂问题分解为相对简单的问题,这需要构建一个层次结构或网络结构来表示该问题。AHP就是基于这一逻辑思想,首先将一个复杂问题分解成若干子问题,并确定解决这些子问题的标准或准则;其次依此层层分解,最终将其分解为最容易控制、最具可操作性的因素,从而构建一个解决问题的层级结构模型;然后利用模糊数学的思想,将所有因素的相对重要性进行量化;最后将量化的各级因素汇总成一个结论,得出问题的最优解决方案。
AHP的优点:一是将定性决策与定量决策完美融为一体,尤其是能够将定性因素的重要性进行量化,便于计算和对比;二是将复杂问题简单化,将复杂问题逐级分解,最终分解为可计算的因素或可执行的方案,使复杂问题变得易于解决;三是提出层次模型,该模型结构严谨,思路清晰,科学性和实用性并重。该方法对多标准决策、规划和资源分配以及冲突解决等复杂问题具有较好的可操作性,因此该模型推出后,迅速在经济管理、安全管理和绩效评价等领域得到广泛应用[4-6]。同样,该方法也在雷电灾害风险区划和区域雷电灾害风险评估中得到应用[7-10]。
在雷电灾害风险区划和区域雷电灾害风险评估的相关标准中对AHP的叙述不够详细,在实际应用中有些地方不易操作,因此本文对此方法进行较为详尽的分析,并结合实际工作经验进行举例说明,以期能够为雷电灾害风险区划和区域雷电灾害风险评估工作提供一些借鉴和参考。
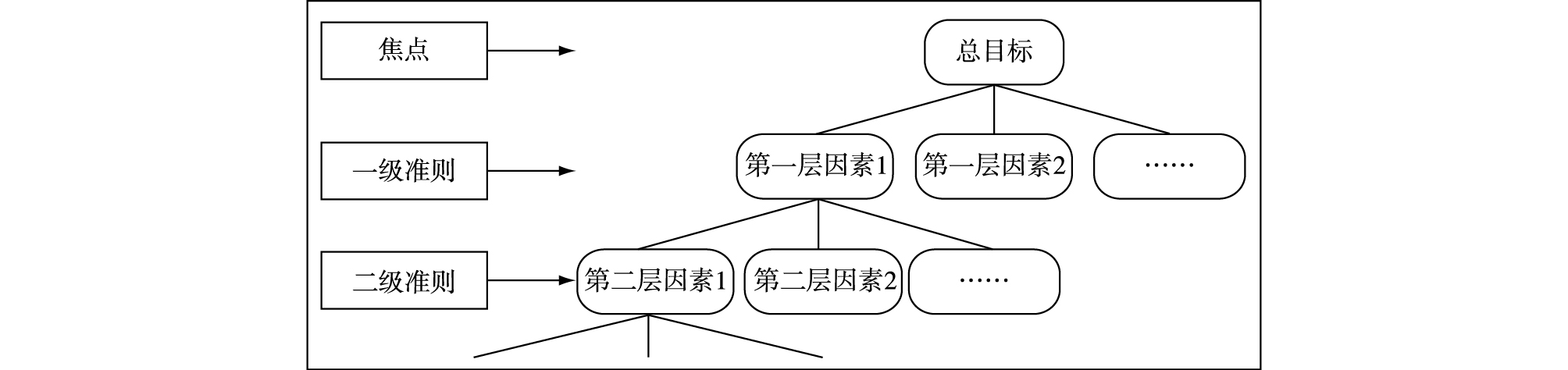
1 AHP方法介绍 1.1 AHP的原理AHP先将一个复杂的多目标多标准决策问题提炼出一个总目标作为焦点,再将总目标分解为多个次级目标和相应的决策标准或准则,然后将这些次级目标和标准进一步分解,以此类推,构建一个多层级的结构体系。利用模糊数学的思想,将各层级中的指标进行模糊量化,根据这些量化值计算出各个指标在该层级中的相对权重,或进行层次单排序,然后计算上一级的相对权重,依此递归,求得各个分目标的权重,最终得出总目标的最优解决方案(图 1)。
|
图 1 层次分析法概念模型 Fig.1 Conceptual model of AHP |
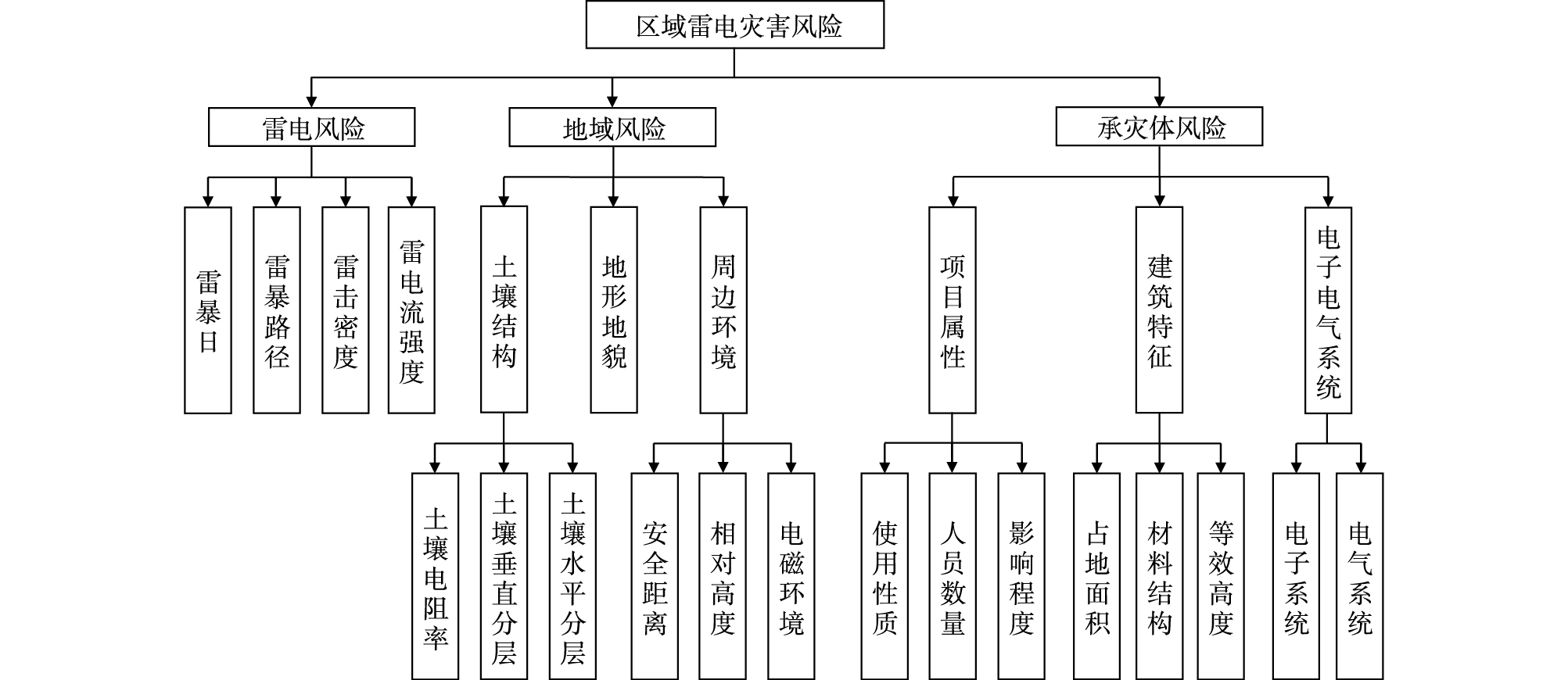
雷电风险不仅与雷电活动密切相关,还与被评估项目所处的地理环境和项目性质相关[11],因此对于区域雷电灾害风险评估,风险可划分为雷电风险、地域风险和承灾体风险3个一级指标。根据条理化、层次化的原则,又将这些风险划分为若干二级指标和三级指标,从而构成一个四级的层次结构模型(图 2)[12]。
|
图 2 区域雷电灾害风险评估的层次结构模型[12] Fig.2 Hierarchical structure model for regional lightning disaster risk assessment[12] |
对于两个因素Ai和Aj的重要性比较,首先要对因素的相对重要性进行量化,量化赋值采用1~9标度法(表 1),即将这些重要性量化值限定在1~9[1]。对同一层级中全部因素进行两两比较,得出因素间相对重要性的量化值,所有重要性量化值构成一个判断矩阵A。
如因素A2对于因素A3的重要性赋值为a23=5,则说明因素A2比因素A3明显重要,即对于它们的上层因素来说,A2的重要程度相对于A3而言是5,而A3的重要程度相对于A2而言是a32=1/5。
判断矩阵A为:
| $ \boldsymbol{A}=\left(a_{i j}\right)_{n \times n}=\left[\begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1 n} \\ a_{21} & a_{22} & \cdots & a_{2 n} \\ \cdots & \cdots & \cdots & \cdots \\ a_{n 1} & a_{n 2} & \cdots & a_{n n} \end{array}\right]。$ | (1) |
其中:aii=1, aji=1/aij;i, j=1, 2, …, n。
1.2.3 计算因素相对权重因素相对权重一般采用计算判断矩阵的最大特征值对应的特征向量来求得,但某些高阶矩阵特征向量的求解难度较大,可以采用和积法求其近似解。
1.2.4 一致性检验AHP的一个重要方面就是一致性思想。因为赋值具有主观性,所以不同赋值者得出的结果可能不同。由于对象可能涉及多个比较,并且没有统一的衡量标准,因此很可能会出现不一致的情况[13-14]。一致性检验是为了检验因素间重要性赋值的一致性,避免出现如因素A1的值大于因素A2,A2大于因素A3,而A3的赋值又大于A1的矛盾情况。
由上述两步可以看出,权重计算也是把一个n阶判断矩阵根据因素重要性赋值的大小进行n次排序的过程,如果n次排序结果都相同,则认为赋值具有判断一致性。对于AHP,文献[12]利用计算一致性率(consistency ratio,CR)Rc的大小来判断因素重要性赋值是否符合一致性原则。根据一致性原理,当判断矩阵小于三阶时,不会出现不一致的现象。
CR的具体计算方法如下:
① 根据判断矩阵计算一致性指数(consistency index,CI)Ic,公式如下:
| $ I_{\mathrm{c}}=\frac{\lambda_{\max }-n}{n-1}, $ | (2) |
其中,λmax为判断矩阵A的最大特征值,n为矩阵A的阶数。
② 根据判断矩阵的阶数,找出对应的平均随机一致性指数(average random consistency index,简记为RI)IR,其具体值可以由表 2查出。
③ 根据CI和RI的值即可求出CR。CR的计算公式如下:
| $ R_{\mathrm{c}}=I_{\mathrm{c}} / I_{\mathrm{R}}。$ | (3) |
当Rc≤0.1时,则认为判断矩阵A的一致性是可以接受的,反之,需要对判断矩阵A中要素的赋值进行调整,直到计算出Rc符合一致性要求。
至于取检验标准小于等于10%的原因,SAATY[13]认为一致性优先级应该与不一致性优先级相差一个数量级以上。
1.2.5 计算合成权重在最底层因素的相对权重值通过一致性检验后,则进行合成计算其上一级因素的权重值,从而得到其上一级因素对于上上一级因素的权重值,如此利用构建的层次结构模型,自下而上逐级计算,最终得到第二层次级目标(因素)相对于第一层总目标的权重。具体计算见3.3节。
2 群判断根据模糊数学的思想,一些因素的量化具有人为主观性。可见,在构造判断矩阵时,因素之间重要性的量化(或称“打分”)具有一定的随意性。由于在量化过程中需要考虑项目的属性、地理环境、承灾体的情况等诸多因素,加上打分者本身对项目的了解程度、专业知识等因素限制,不同打分者的量化结果不可避免地会存在一定差异,甚至不同的打分者得出的判断矩阵有可能差异较大。由于判断矩阵中的值直接决定最终的评估结果,因此这些差异就会影响评估结果。鉴于此,有学者提出,AHP应该是一种群判断, 必须依群判断才能使AHP更为科学更有针对性[15]。群判断的关键问题:一是正确选择专家,参与打分的专家应该具有相关的专业学识;二是选择适当数量的专家,一般不少于3位;三是让专家们在充分了解项目情况的基础上作出判断(打分)。
传统的群判断是采用专家一次性打分,根据经验来看,一次性打分可能会出现不符合一致性原则的问题。为解决这个问题,在群判断的过程中可以采用背对背的德尔菲法,也可以采用背对背与集体讨论相结合的方式。
背对背德尔菲法能够使各位参与打分者独立地不受影响地充分表达自己的意见,较好地解决了部分打分者可能会受参与打分的“权威人物”意见影响的问题。利用德尔菲法的思想,将第一轮专家打分结果反馈给每位专家,让每位专家进行第二轮打分。由于可以参照别人的打分结果来修正自己的打分,因此第二轮打分的结果往往更加合理,这样可以有效解决个体决策的偏差和局限性。
背对背与集体讨论相结合的方式,是每位专家打分后,将各自的打分结果拿出来进行集体讨论,对其中分歧较大的部分经过讨论得出共识。这种方法既可以有效避免单个专家对项目了解的缺乏和自身知识面的缺憾,又可以博采众长,取得共识。
群判断应该制订一个判断规则,这个判断规则应该是各位专家在对所打分的项目进行充分了解的基础上,经过专家们集体讨论,共同协商而形成,每位专家都应在这个判断规则的框架下进行打分。尤其在专家打分出现截然相反的结果的情况下,制订这样一个规则就显得非常必要。
对专家打分结果的处理,可以将各位专家的分值取平均。这种取平均数的方法,不要求优先级,不要求加权,被证明是正确的[16]。如果群体判断出现较大差异,可以通过一致性检验来解决。当几个人在矩阵的某些元素提出完全不同的判断时,可以分别将每个有争议的判断衡量其一致性,再与其他广泛一致的判断一起测试这些判断。
3 隶属度的确定在对某一事物进行评价过程中,会涉及到多种因素,这些因素的内涵和性质可能有很大的不同,甚至有的是可以定量的因素,有的是定性因素,则无法衡量各个因素对总目标的重要程度,因此也就难以做出统一的量化的评价结果。区域雷电灾害风险评估亦是如此。为了解决这一问题,在区域雷电灾害风险评估中,引入了模糊数学中隶属度这一概念。
隶属度是将事物具有的模糊性进行量化表示,这种模糊性可能随条件的变化而变化。这种变化规律可以用函数来表现,即隶属函数。
对于给定的映射μω: X→[0, 1],x→μω(x),则称μω为模糊集ω的隶属函数,μω(x)称为x对ω的隶属度[17]。
在区域雷电灾害风险评估中,隶属度是评估对象的雷电灾害风险与不同风险等级的相关性[12]。在评估过程中需要对各个影响因素进行隶属度量化计算,从而将所有因素的重要性影响值均转换为0~1之间的无量纲值,这样每个影响因素就具有了可计算性。
3.1 定量指标的隶属度在区域雷电灾害风险评估中涉及的指标中既有定量指标也有定性指标,其中定量指标可以划分为极小型指标和极大型指标。极小型指标的特点是值越小,危险性越低,如雷暴日、雷击密度、雷电流强度等;极大型指标则相反,指标值越小,其危险性越大,如土壤电阻率、安全距离等。
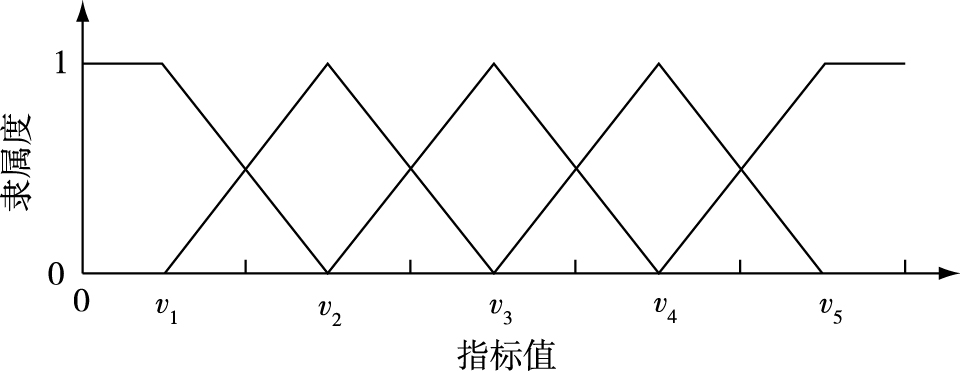
无论是定量指标还是定性指标,无论是极小型指标还是极大型指标,根据文献[12],均将这些指标划分为5个等级。设这5个等级V1、V2、V3、V4、V5的取值区间的中值分别为v1、v2、v3、v4、v5。极小型指标的隶属函数图像如图 3所示。
|
图 3 极小型隶属函数图 Fig.3 Diagram of minimal membership function |
极小型指标隶属度的计算公式如下。
(1) 对于最低级V1 (i=1):
| $ \mu_i\left(r_i\right)=\left\{\begin{array}{c} 1, r_i <v_1 \\ \frac{v_2-r_i}{v_2-v_1}, v_1<r_i<v_2 \\ 0, r_i \geqslant v_2 \end{array}\right.。$ | (4) |
(2) 对于中间等级V2、V3、V4 (i =2, 3, 4):
| $ \mu_i\left(r_i\right)=\left\{\begin{array}{c} 0, r_i \leqslant v_1, r_i \geqslant v_5 \\ \frac{r_i-v_{i-1}}{v_i-v_{i-1}}, v_{i-1}<r_i<v_i \\ 1, r_i=v_i \\ \frac{v_{i+1}-r_i}{v_{i+1}-v_i}, v_i<r_i<v_{i+1} \end{array}\right.。$ | (5) |
(3) 对于最高级V5 (i =5):
| $ \mu_i\left(r_i\right)=\left\{\begin{array}{c} 1, r_i \geqslant v_5 \\ \frac{r_i-v_4}{v_5-v_4}, v_4 <r_i<v_5 \\ 0, r_i \leqslant v_4 \end{array}\right.。$ | (6) |
其中:ri为第i个指标的值,μi(ri)为第i个指标的隶属度。
极大型指标的隶属度计算与极小型类似,不再赘述。
举例说明,以雷暴日为例。在文献[12]中将雷暴日划分为5个等级,具体划分见表 3。
|
|
表 3 雷暴日分级 Table 3 Grading of thunderstorm day |
以青岛市的年平均雷暴日r=21.2 d为例,根据表 3,则有v1=10 d/a、v2=30 d/a、v3=50 d/a、v4=75 d/a、v5=228 d/a。显然,21.2处于Ⅰ级和Ⅱ级的重叠区,根据公式(4)和公式(5),有
|
|
表 4 青岛雷暴日的隶属度 Table 4 Membership of thunderstorm day in Qingdao |
还有一些具有连续分布特征的指标,可以将其每个等级的百分率作为隶属度。如雷电流强度(雷电流强度分级见表 5),可以将雷电流在2~10 kA的闪电次数占总闪电次数的百分率作为Ⅰ级的隶属度,其他等级也是如此。因为各级百分率的和也是1,符合隶属度的定义要求。
|
|
表 5 雷电流强度分级 Table 5 Grading of lightning current intensity |
定性指标隶属度的确定则相对比较简单,根据给定的等级条件,将符合条件的等级设为1,即认为该指标的危险完全隶属于该等级,不涉及其他等级,则其余等级的取值为0。如建(构)筑物材料结构指标,其等级划分为:Ⅰ级为木结构,Ⅱ级为砖木结构,Ⅲ级为砖混结构,Ⅳ级为屋顶和主体结构为钢筋混凝土结构,Ⅴ级为屋顶和主体结构为钢结构[12]。
如果评估区域大多为住宅区,则可认定建(构)筑物材料结构为Ⅳ级,该项指标的隶属度见表 6。
|
|
表 6 材料结构的隶属度 Table 6 Membership of material structure |
在计算隶属度的时候,要先计算最底层指标的隶属度,根据上述方法,可以计算出底层指标的隶属度,再计算它们上一级指标的隶属度,具体计算方法如下:
设第n层指标为Zn1,Zn2,…,Znm的隶属度分别为μn1,μn2,…,μnm,对应的相对权重分别为wn1,wn2,…,wnm,见表 7。
|
|
表 7 第n层指标的隶属度和相对权重 Table 7 Membership and relative weight of the n-th layer indicators |
其上一级n-1层指标的隶属度等于n层每个指标的隶属度乘以其相对权重的和,即
| $ \mu_{(n-1) i}=\mu_{n 1 i} \times w_{n 1}+\mu_{n 2 i} \times w_{n 2}+\cdots+\mu_{n m i} \times w_{n m}, $ | (7) |
其中i=1, 2, …,5,为危险等级。以此类推,即可求出第二层指标的各危险等级的隶属度。
以雷电风险为例,计算该因素的隶属度。假设雷暴日为21.2 d/a,雷击密度为1.8次/(km2 ·a),雷暴路径主方向的百分比大于35%。雷电流强度的隶属度采用雷电流的概率分布。则雷电风险因素的隶属度计算如下:首先,根据专家打分得到的雷电风险各个次级因素的重要性值,计算其权重,计算结果见表 8;其次,计算每一个次级因素的隶属度,计算结果见表 9;最后,根据次级各因素的隶属度和权重,计算得到雷电风险的隶属度,隶属度各等级的值见表 10。
|
|
表 8 雷电风险各个次级因素的重要性量化值和权重值 Table 8 The importance quantification value and weight value of lightning risk's secondary factors |
|
|
表 9 雷电风险各个次级因素的隶属度 Table 9 Membership of lightning risk's secondary factors |
|
|
表 10 雷电风险的隶属度 Table 10 Membership of lightning risk |
按照上面的方法,分别计算出雷电风险、地域风险和承灾体风险的隶属度,再合并计算出总的隶属度各等级的值r1、r2、r3、r4、r5。根据文献[12]给出的区域雷电灾害风险值公式:
| $ g=r_1+3 r_2+5 r_3+7 r_4+9 r_{5}。$ | (8) |
求出总风险值g后,对照表 11[12],即可得出评估项目的雷电风险等级。
|
|
表 11 评估指标的危险等级 Table 11 Grading of assessment indicators |
本文详细介绍了层次分析法的原理,并举例说明该方法在区域雷电灾害评估中的应用。该方法的核心问题是因素间相对权重的确定方法,由于相对权重的确定要采用专家打分法,受到专家对项目的了解程度以及专家自身知识面等方面的限制,不同专家的打分结果可能差异较大,从而影响最终的评估结果。本文改进了群判断方法,建议采用背对背德尔菲法两轮打分和背对背与集体讨论相结合的两种方法,能够减少专家对项目了解的偏差,有效提高评估的客观性,使最终评估结果更趋于合理。建议建立群判断规则,避免出现分歧较大的打分结果。
| [1] |
SAATY T L. A scaling method for priorities in hierarchical structures[J]. J Math Psychol, 1977, 15(3): 234-281. DOI:10.1016/0022-2496(77)90033-5 |
| [2] |
SAATY T L. How to make a decision: the analytic hierarchy process[J]. Eur J Oper Res, 1990, 48(1): 9-26. |
| [3] |
SAATY T L. Decision making for leaders: the analytic hierarchy process for decisions in a complex world[M]. Pittsburgh: RWS Publications, 2001.
|
| [4] |
刘豹, 许树柏, 赵焕臣, 等. 层次分析法: 规划决策的工具[J]. 系统工程, 1984(2): 23-30. |
| [5] |
刘莹昕, 刘飒, 王威尧. 层次分析法的权重计算及其应用[J]. 沈阳大学学报(自然科学版), 2014, 26(5): 372-375. DOI:10.3969/j.issn.2095-5456.2014.05.007 |
| [6] |
姜启源. 层次分析法应用过程中的若干问题[J]. 数学的实践与认识, 2013, 43(23): 156-168. |
| [7] |
张科杰, 成勤. 基于层次分析法的城市轨道交通雷击风险评估研究[J]. 现代城市轨道交通, 2021(10): 79-83. |
| [8] |
赵伟, 周象贤, 张祎. 浙江电网雷害风险预警方法研究[J]. 浙江电力, 2021, 40(4): 89-93. |
| [9] |
程丽丹. 层次分析法和GIS技术在河南省雷电灾害风险区划中的应用[J]. 南京信息工程大学学报(自然科学版), 2019, 11(2): 234-240. |
| [10] |
郭媛, 吴量, 何宽, 等. 基于层次分析法的广西雷灾风险区划[J]. 气象研究与应用, 2018, 39(2): 108-113, 145. |
| [11] |
刘向科, 康宁, 邱粲, 等. 泰山景区地闪分布特征及与海拔高度关系研究[J]. 海洋气象学报, 2021, 41(4): 102-108. |
| [12] |
李良福, 覃彬全, 余蜀豫, 等. 雷电灾害风险评估技术规范: QX/T 85—2018[S]. 北京: 气象出版社, 2019.
|
| [13] |
SAATY R W. The analytic hierarchy process: what it is and how it is used[J]. Math Model, 1987, 9(3/4/5): 161-176. |
| [14] |
吴祈宗, 李有文. 层次分析法中矩阵的判断一致性研究[J]. 北京理工大学学报, 1999, 19(4): 502-505. |
| [15] |
ACZÉL J, SAATY T L. Procedures for synthesizing ratio judgements[J]. J Math Psychol, 1983, 27(1): 93-102. |
| [16] |
ACZÉL J, ALSINA C. Synthesizing judgements: a functional equations approach[J]. Math Model, 1987, 9(3/4/5): 311-320. |
| [17] |
张博侃. 模糊数学[M]. 北京: 北京大学出版社, 2021.
|
 2022, Vol. 42
2022, Vol. 42


