2. 中国气象科学研究院灾害天气国家重点实验室,北京 100081
2. State Key Laboratory of Severe Weather, Chinese Academy of Meteorological Sciences, Beijing 100081, China
热带气旋(tropical cyclone,TC)会对生命和财产造成巨大危害,为了减少这类损失,相关机构和个人都需要获得TC位置和强度的准确预报。众所周知,边界层是热带气旋的重要组成部分,边界层过程是大气的主要热量和水汽的源,是动量的汇,调节着与TC发展及增强密切相关的动量和焓的径向和垂直分布,在TC的能量传输过程中起着重要作用。然而TC边界层与大部分大气边界层不同,TC的旋转对其动力学有强烈的影响[1-5],这也进一步增加了TC数值模拟中边界层参数化的复杂性[6]。
在数值模式中,边界层高度h和动量粗糙度z0都是需要进行参数化且具有重要意义的变量。例如,在被业务数值模式广泛使用的一阶K闭合方案(如Medium Range Forecast Model(MRF)方案和Yonsei University(YSU)方案)中,混合层的湍流扩散系数需要使用混合层特征速度和边界层高度h进行参数化,而混合层特征速度的参数化也依赖于边界层高度h。YSU方案的一个特点是包含了边界层顶夹卷的参数化计算,而该夹卷项的参数化也依赖于边界层高度h。因此,在数值模式中边界层高度h影响着边界层内湍流热量通量的垂直输送,进而影响TC的发展。另外,在大多数参数化方案中,描述地(海)气交界面的动量、感热和潜热交换作用的表面通量要依赖于动量粗糙度z0,部分参数化方案会使用与z0有关的表面动量交换系数CD(也称为曳力系数)代替z0。因此,在数值模式中,边界层高度h和动量粗糙度z0(或表面动量交换系数CD)的确定在边界层参数化过程中十分关键。
但是,由于数值计算过程中参数化方法的设计及对TC缺少足够的科学认识,都会为边界层高度h和动量粗糙度z0的参数化计算带来不确定性。利用总体理查森数(VRib)确定边界层高度是边界层参数化方案中广泛使用的一种方案[7-10]。例如,MRF方案[11]和YSU方案[12]中都使用了总体理查森数法。从最低模式层向上进行寻找,取总体理查森数首次等于临界总体理查森数VRibcr(一般取VRibcr=0.5)时所在的高度作为大气边界层高度h,即认为是首次达到中性层结的高度。如果VRib=VRibcr所在的高度层出现在两个模式层之间,那么还需要通过线性插值的方法进一步确定h的值。因此,在大气边界层高度h的这一参数化过程中,参数化方法、线性插值等数值计算方法都会导致h相对于真实大气的边界层高度具有不确定性。假设地面风速为0,Hong等[12]用公式(1)定义了总体理查森数,表示浮力与切变力的比率,它们分别负责减少和产生湍流。
| $ V_{\operatorname{Rib}(z)}=\frac{g\left[\theta_{\mathrm{v}}(z)-\theta_{\mathrm{s}}\right] z}{\theta_{\mathrm{va}} U(z)^2}, $ | (1) |
其中VRib(z)为地表面层与高度z之间的总体理查森数,g为重力加速度,θv(z)为z高度处的虚位温,θs表示地表面的虚位温,且θs=θva+θT,θva为最低模式层上的虚位温,θT为地表面附近的额外虚温,U(z)为z高度处的水平风速。然而,Zhang等[13-14]的研究指出,用传统的临界总体理查森数法确定的边界层高度可能不能准确地再现飓风边界层的高度尺度。在进行TC数值模拟过程中,如何对边界层高度h进行合适的参数化表达尚没有让人十分满意的方案,仍在探索中。
在动量粗糙度z0的参数化过程中,一般先通过地形静态资料识别模式格点下方所处位置是属于陆面还是水面,并将陆面上的动量粗糙度z0设置为0.01,水面上使用比较复杂的参数化公式计算,不同的参数化方案在水面上常使用不同的参数化公式。在对水面上方的模式格点进行参数化时,通常需要使用摩擦速度、水平风速、重力加速度。其中,摩擦速度是在模式积分的每一时步通过参数化计算获得,水平风速是通过模式每一时步的积分计算获得,重力加速度取一个近似的常数。因此,在动量粗糙度z0的参数化过程中,不同参数化设计方法会导致数值模式中的z0具有不确定性。但是目前水面上的动量粗糙度z0(或曳力系数CD)的参数化尚没有让人十分满意的方案,仍然在进行探寻和摸索[15-19]。
以往的研究多集中在不同边界层参数化方案对台风模拟的影响上,然而热带气旋的模拟对边界层参数化的敏感性除对方案变化敏感以外,还可能对参数化表达的微小变化也敏感[20-23]。其影响对不同台风并不完全一致,因此针对更多台风开展数值试验来加深边界层中变量的参数化对台风模拟影响的认识至关重要。深入了解边界层参数化变量表达差异在台风过程不同阶段中的影响十分必要,可为有针对性地改进数值预报模式的边界层参数化方案提供参考依据。因此,分析台风过程中不同阶段的数值模拟对边界层参数化中变量要素的敏感性,认清这些敏感要素是如何通过影响台风结构来影响台风的路径和强度具有重要意义。
对1713号台风“天鸽”开展敏感性试验,分别对边界层高度h和动量粗糙度z0采用不同的参数化表达,考察“天鸽”生命过程中不同阶段的移动路径和强度的数值模拟结果对边界层高度h和动量粗糙度z0的敏感性,为理解边界层高度h和动量粗糙度z0参数化的差异对台风不同阶段数值模拟的影响提供参考。
1 台风“天鸽”简介1713号台风“天鸽”(Hato)于2017年8月20日14时(北京时)在西北太平洋洋面上生成,此时为热带风暴级别。8月22日08时加强为强热带风暴,22日15时加强为台风,23日07时加强为强台风,23日15时前后以强台风级别在广东省珠海市登陆,23日18时减弱为强热带风暴,23日22时开始减弱为热带风暴,24日14时减弱为热带低压。该台风最强时台风中心最小海平面气压为935 hPa,风力达15级(48 m/s),强度变化大是该台风的一个主要特点。该台风为珠海、香港、澳门等地区带来重大破坏,造成24人死亡和68.2亿美元的经济损失,于2018年的第50届台风委员会年度会议上被除名。
2 数值模式介绍本文的研究工作均是使用CMA-TYM模式系统开展的。CMA-TYM模式是国家气象中心于2010年基于中尺度数值预报系统GRAPES-Meso(Global/Regional Assimilation and Prediction System Mesoscale model)[24]开始研发的区域模式台风数值预报系统,该系统于2012年7月开始投入业务运行并得到持续改进,CMA-TYM热带气旋路径及强度预报能力不断提升。2011年实时运行结果和2012年业务运行结果表明:CMA-TYM对台风强度具有一定的预报能力,强度预报平均误差小于欧洲中期天气预报中心(European Centre for Medium-Range Weather Forecasts,ECMWF)全球模式;CMA-TYM的路径及强度预报存在明显的系统偏差,台风强度预报系统性偏强,尤其是在预报前期存在明显的快速增长(spin-up)现象,同时对南海台风的路径预报存在明显的系统性北偏[25]。
使用的CMA-TYM模式水平分辨率为0.09°×0.09°,共901×567个格点,模拟区域覆盖西北太平洋和中国南海(90°~171°E,0°~50.94°N),垂直方向采用50层地形追随高度坐标,使用的主要物理方案包括WSM6(WRF Single-Moment 6-class)微物理方案、RRTM(Rapid and Accurate Radiative Transfer Model)长波辐射方案、Dudhia短波辐射方案、Noah陆面方案、Kain-Fritsch积云参数化方案、边界层参数化使用YSU方案,并用莫宁-奥布霍夫(Monin-Obukhov)相似理论对表面层进行参数化。使用美国国家环境预报中心(National Centers for Environmental Prediction,NCEP)提供的每3 h一次0.5°×0.5°的零场和预报场进行模式驱动,并根据中央气象台的台风报文,使用涡旋重定位技术和涡旋强度调整技术对台风涡旋进行初始化调整[25-28]。
3 试验设计采用中央气象台提供的热带气旋最佳路径数据作为实况。研究使用CMA-TYM模式对台风“天鸽”(1713)进行数值模拟的过程中,选取代表“天鸽”生命过程中不同阶段的4个不同时次作为起报时间,分别进行120 h的数值模拟。
起报时间分别选取“天鸽”(1713)生命过程中不同阶段的4个时次。2017年8月20日12:00 (世界时,下同)是台风初始阶段,为热带风暴级别,中心附近最小海平面气压为1 000 hPa,风力8级(18 m/s);2017年8月22日00:00刚刚升级为强热带风暴级别,中心附近最小海平面气压为985 hPa,风力10级(25 m/s);2017年8月23日00:00刚升级为强台风不久,尚未达到最大强度,中心附近最小海平面气压为950 hPa,风力14级(42 m/s);2017年8月23日06:00即将登陆,虽然仍为强台风级别,但已经开始减弱一段时间,中心附近最小海平面气压为955 hPa,风力14级(42 m/s)。
基于CMA-TYM模式分别对混合层参数化中的边界层高度h和近地面层参数化中的动量粗糙度z0使用不同的参数化表达形式,考察h和z0的变化对台风“天鸽”不同生命阶段中路径和强度模拟的影响情况。
3.1 CMA-TYM模式的参数化方案CMA-TYM业务模式的边界层参数化方案使用YSU方案,采用如下的方法对边界层高度h和动量粗糙度z0进行参数化。
3.1.1 边界层高度h的参数化方案YSU方案是一阶非局地K闭合方案。在YSU方案中,边界层高度通过以下公式来推算:
| $ h=V_{\mathrm{Rib}_{\mathrm{cr}}} \frac{\theta_{\mathrm{va}}|U(h)|^2}{g\left(\theta_{\mathrm{v}}(h)-\theta_{\mathrm{va}}-\theta_{\mathrm{T}}\right)}, $ | (2) |
其中g为重力加速度,U为风速,h为边界层顶高度,θv(h)为边界层顶的虚位温,θva为最低模式层上的虚位温,θT为地表面附近的额外虚温,VRibcr为临界总体理查森数。该定义中的边界层为热力学边界层,边界层顶部是识别的通量最小值所在的层[12]。
3.1.2 动量粗糙度z0的参数化方案与飓风天气研究和预报(Hurricane Weather Reasearch and Forecasting, HWRF)模式一样,目前CMA-TYM业务模式中使用公式(3)-(6)对动量粗糙度z0进行参数化,该方案是对应于曳力系数CD在飓风级风力下保持恒定的观点[15]开发的,并在WRF-ARW3.4.1版本中采用[29]。
| $ \begin{gathered} z_0=\max \left\{1.27 \times 10^{-7}, \min \left[z_w z_2\right.\right. \\ \left.\left.+\left(1-z_w\right) z_1, 2.85 \times 10^{-3}\right]\right\}, \end{gathered} $ | (3) |
| $ z_w=\min \left(1, \left[\frac{u_*}{1.06}\right]^{0.3}\right), $ | (4) |
| $ z_1=0.011 \frac{u_*^2}{g}+1.59 \times 10^{-5} \text {, } $ | (5) |
| $ z_2=\frac{10}{\exp \left(9.5 u_*^{-1 / 3}\right)}+\frac{1.65 \times 10^{-6}}{\max \left(u_*, 0.01\right)}, $ | (6) |
其中u*是摩擦速度。
3.2 对边界层高度的敏感性试验方案公式(2)中的θT是一个经验项,具有一定的不确定性[30],这导致YSU方案中定义边界层高度h的不确定性。进一步,YSU方案中用于计算扩散系数的变量项kpbl(表示边界层顶在模式面中所在的位置:第k个模式层)也是会根据调制的边界层高度h进行相应的改变。因此,针对YSU方案中定义边界层高度的这种不确定性问题,本文中通过改变一个α系数,来调节边界层高度,进行针对边界层高度h的一系列敏感性试验(表 1)。
|
|
表 1 边界层高度h的敏感性试验方案 Table 1 Schemes of sensitivity experiment for boundary layer height h |
敏感性试验方案包括1组参考试验(CTRL)和5组敏感性试验(表 1)。这里,用H表示CTRL中用YSU方案(即公式(2))诊断出的边界层高度h。将H乘以一个比率系数α,通过合理地改变α的取值构造其他5组敏感性试验。因此,在CTRL中,α=1.00。根据Ma等[31]的研究,这里将H的比率系数取为α=0.50,得出的边界层高度h(即h=0.50×H)视为实际边界层高度的下限值,设计试验H0.50;取α=0.75,得出的边界层高度h(即h=0.75×H)对应边界层高度在一个合适的范围里,设计试验H0.75;取α=1.50,得出的边界层高度h(即h=1.50×H)对应于一个大约1 km的典型深度,设计试验H1.50;分别取α=2.00和α=3.00,得出的边界层高度h(即h=2.00×H和h=3.00×H)对应某些条件下边界层厚度能够比1 km深得多的情况,设计试验H2.00和试验H3.00。Ma等[31]在文中详细阐述了α取值的依据。
3.3 对动量粗糙度z0的敏感性试验方案在计算z0的时候,采用与公式(3)不同的其他几种方法,进行针对动量粗糙度z0的一系列敏感性试验(表 2)。敏感性试验方案包括1组参考试验(CTRL)和4组敏感性试验(表 2),4组敏感性试验分别记为试验z0old1.5、试验z0old、试验z0new和试验z0CRTL0.5。
|
|
表 2 动量粗糙度z0的数值试验方案 Table 2 Schemes of numerical experiment for momentum roughness z0 |
试验z0old使用公式(7)来计算粗糙度z0:
| $ z_0=0.018\ 5 \frac{u_*^2}{g}+1.59 \times 10^{-5} \text {, } $ | (7) |
公式(7)产生的曳力系数CD随风速单调增加(对应Green等[29]研究中的公式(8)),是WRF-ARW3.0版本之前就已经采用的一种方案。
试验z0new采用公式(8)的方法计算z0。该方案与Green等[29]中的第一个isftcflx选项方案一致,即粗糙度z0在低风速下使用本文公式(3)进行计算,但允许风速超过33 m/s以上时曳力系数持续增加。
| $ z_{0, z_0 \text { new }}=\left\{\begin{array}{cl} z_0, & z_0 \leqslant 2.85 \times 10^{-3} \\ \frac{z_0-2.85 \times 10^{-3}}{2}+2.85 \times 10^{-3}, & z_0>2.85 \times 10^{-3} \end{array}, \right. $ | (8) |
其中z0是由公式(3)给出的。
为了使z0在保持随风速不变的情况下变化幅度有更大的差别,另外设计了两个方案z0old1.5和z0CRTL0.5。试验z0old1.5是将试验z0old方案得到的z0乘以系数1.5,即将试验z0old得到的z0放大到原来的1.5倍。试验z0CRTL0.5是将CTRL方案得到的z0乘以系数0.5,即将试验CTRL的z0缩小到原来的0.5倍。
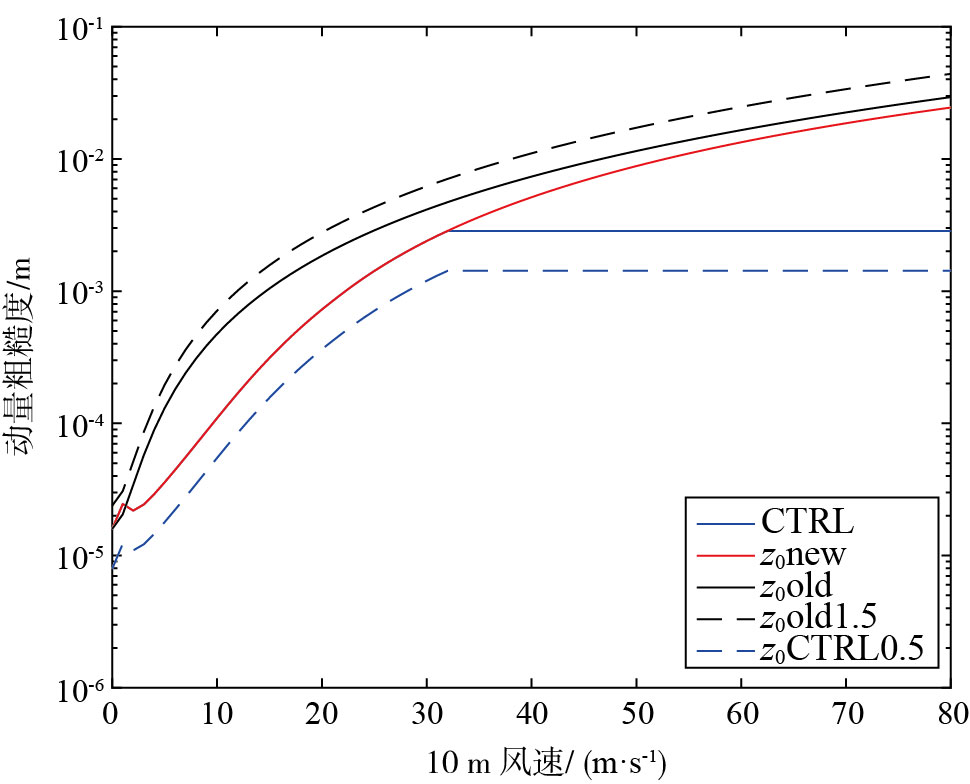
对于表 1中的5组敏感性试验方案,当使用公式(9)的摩擦速度和10 m风速的近似关系时①,可得到如图 1中所示的动量粗糙度z0随10 m风速的变化关系。
① 注意,实际的CMA-TYM模式中使用的摩擦速度与10 m风速之间的关系比公式(9)复杂得多,是使用公式
| $ u_*=\frac{\kappa u_{10}}{\ln \left(10 / z_0\right)}, $ | (9) |
|
图 1 动量粗糙度z0随10 m风速的变化 Fig.1 Variation of momentum roughness z0 with 10-m wind speed |
其中取κ=0.4,z0=0.03 m。
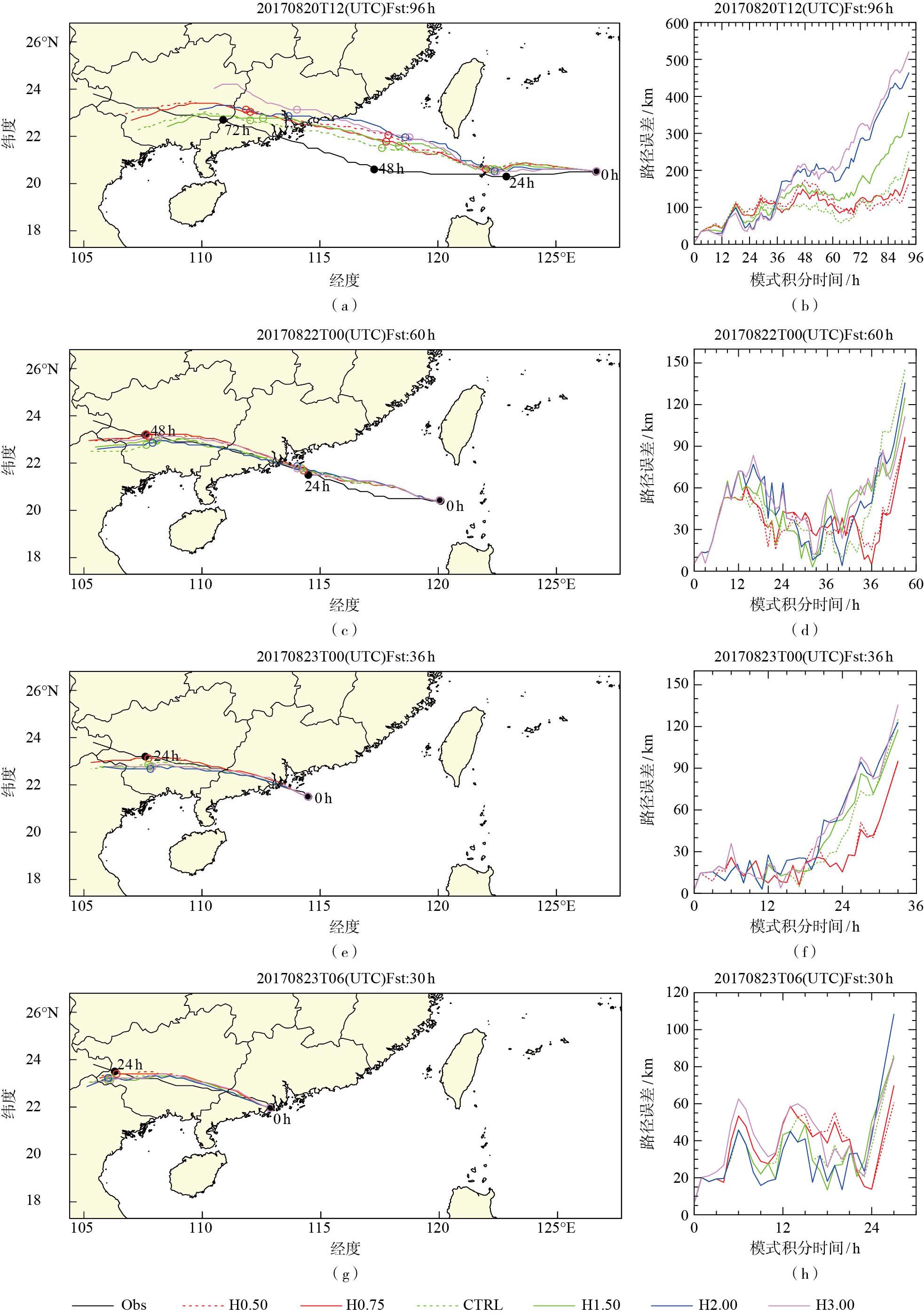
4 数值试验结果分析 4.1 边界层高度h对台风路径和强度模拟的影响 4.1.1 对台风移动路径模拟的影响分析图 2a、c、e、g给出了边界层高度h的变化对台风“天鸽”4个不同阶段起报的移动路径模拟的影响,图 2b、d、f、h给出了对应的移动路径预报误差。在初期为热带风暴的阶段(2017年8月20日12:00)起报的试验中,积分约24 h之后,各试验中的移动路径误差有明显差异,边界层高度h较薄的H0.50、H0.75和CTRL试验中移动路径误差较小,在积分84 h之前基本小于150 km,但边界层高度h较厚的H2.00和H3.00试验中的移动路径误差较大,一般超过150 km(图 2a、b)。
|
图 2 1713号台风“天鸽”在不同边界层高度h下的移动路径模拟(a、c、e、g)和其误差(b、d、f、h) Fig.2 Simulation (a/c/e/g) and errors (b/d/f/h) of moving track of Typhoon Hato (1713) from different schemes of boundary layer height h |
而在台风成熟之后(强热带风暴及后期,即2017年8月22日00:00、2017年8月23日00:00和2017年8月23日06:00)起报的试验中,边界层高度h对台风移动路径的模拟影响差异较小(图 2c-h),没有台风生命史初期(2017年8月20日12:00起报)显著。
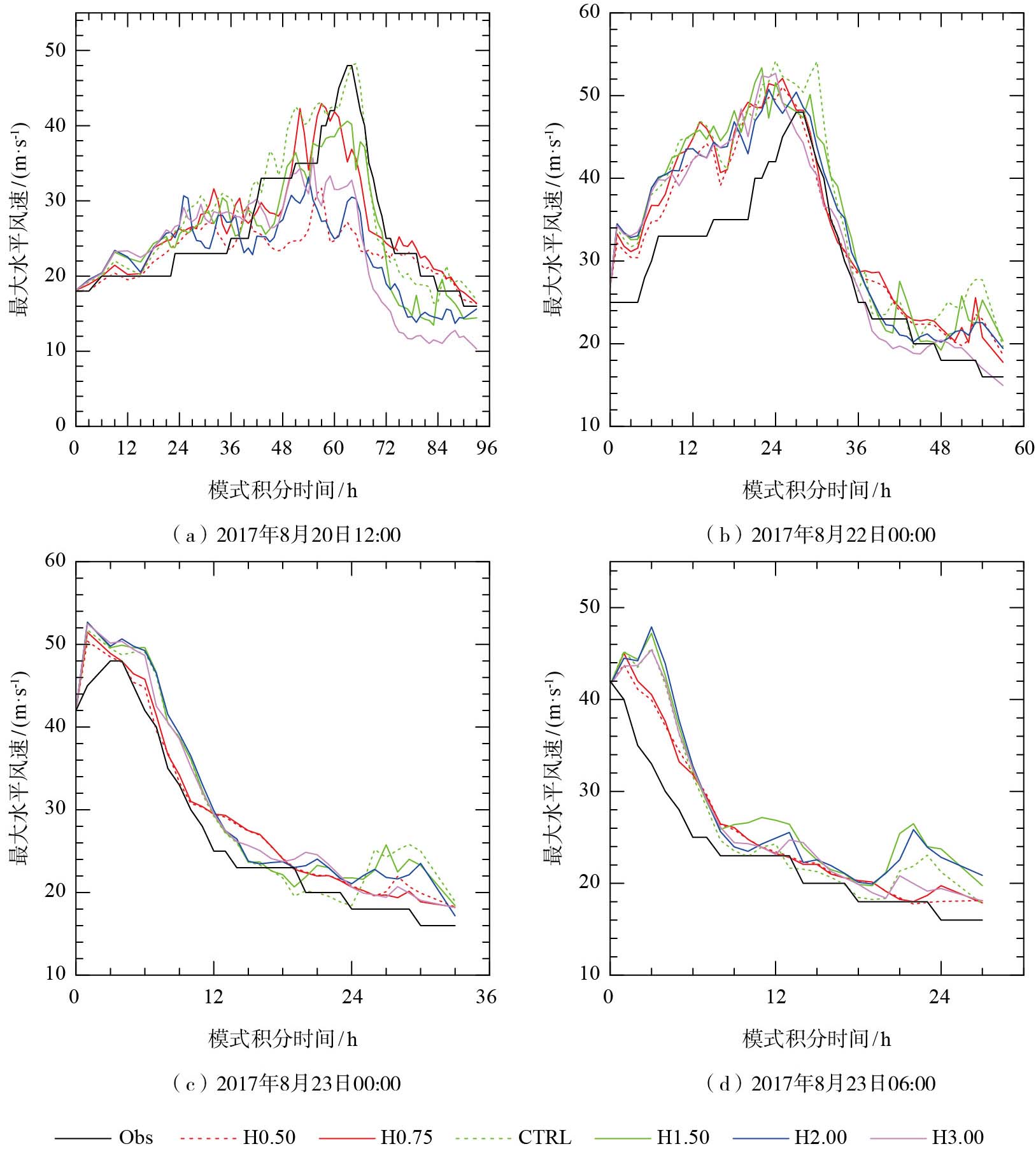
4.1.2 对台风强度模拟的影响分析图 3和图 4分别给出了边界层高度h的变化对台风“天鸽”4个不同阶段起报的台风中心附近最大10 m风速和最小海平面气压模拟的影响。由图 3a和图 4a可见,在初期为热带风暴的阶段(2017年8月20日12:00)起报的试验中,h在合适的典型深度范围(H0.75、CTRL和H1.50试验)有利于台风加强发展,h过薄(H0.50试验)或太厚(H2.00和H3.00试验)都不利于台风的发展加强。
|
图 3 1713号台风“天鸽”在4个阶段模拟的不同边界层高度h下的10 m水平风速最大值 Fig.3 Simulated maximum 10-m horizontal wind speed of Typhoon Hato (1713) from different schemes of boundary layer height h in 4 stages |

|
图 4 1713号台风“天鸽”在4个阶段模拟的不同边界层高度h下的最小海平面气压 Fig.4 Simulated minimum sea-level pressure of Typhoon Hato (1713) from different schemes of boundary layer height h in 4 stages |
在台风成熟之后(强热带风暴及以后,即2017年8月22日00:00、2017年8月23日00:00和2017年8月23日06:00)起报的试验中,台风中心附近10 m风速最大值的模拟对h的变化不敏感(图 3b-d),但台风中心附近最小海平面气压的模拟对h的变化非常敏感(图 4b-d)。图 4b表明,在台风达到最大强度之前,较浅薄的h(H0.50、H0.75和CTRL试验)导致台风加强偏快、强度发展过强。
同时发现,对于成熟的台风,台风中心附近最小海平面气压对h变化的反应约在6 h以后才显现(图 4b-d);而初期阶段的台风需要更长的响应时间(约24 h)(图 4a)。在台风达到最大强度以后的减弱阶段,台风中心附近最小海平面气压的减弱对h的变化非常敏感(图 4a-d),图 4d显示H3.00试验中台风减弱最快。
4.2 动量粗糙度z0对台风路径和强度模拟的影响 4.2.1 对台风移动路径模拟的影响分析图 5给出了粗糙度z0的变化对台风“天鸽”4个不同阶段起报的移动路径模拟的影响及其对应的预报误差。容易看出,移动路径的模拟对粗糙度z0不太敏感,仅z0old1.5方案在初期为热带风暴的阶段(2017年8月20日12:00)起报的试验有可分辨的移动路径预报误差(图 5b)。

|
图 5 1713号台风“天鸽”在不同粗糙度z0下的移动路径模拟(a、c、e、g)和其误差(b、d、f、h) Fig.5 The same as Fig. 2, but for different schemes of momentum roughness z0 |
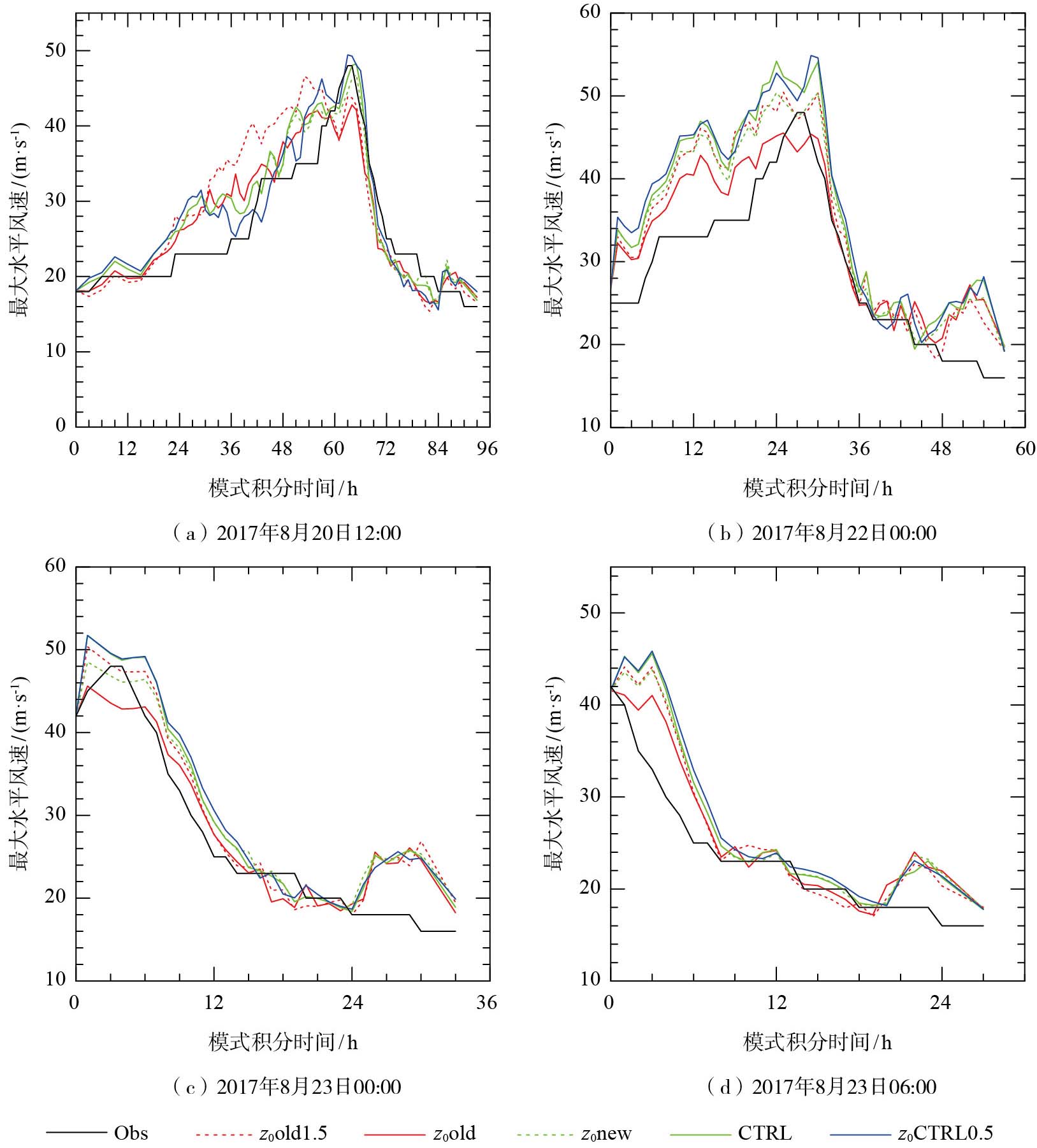
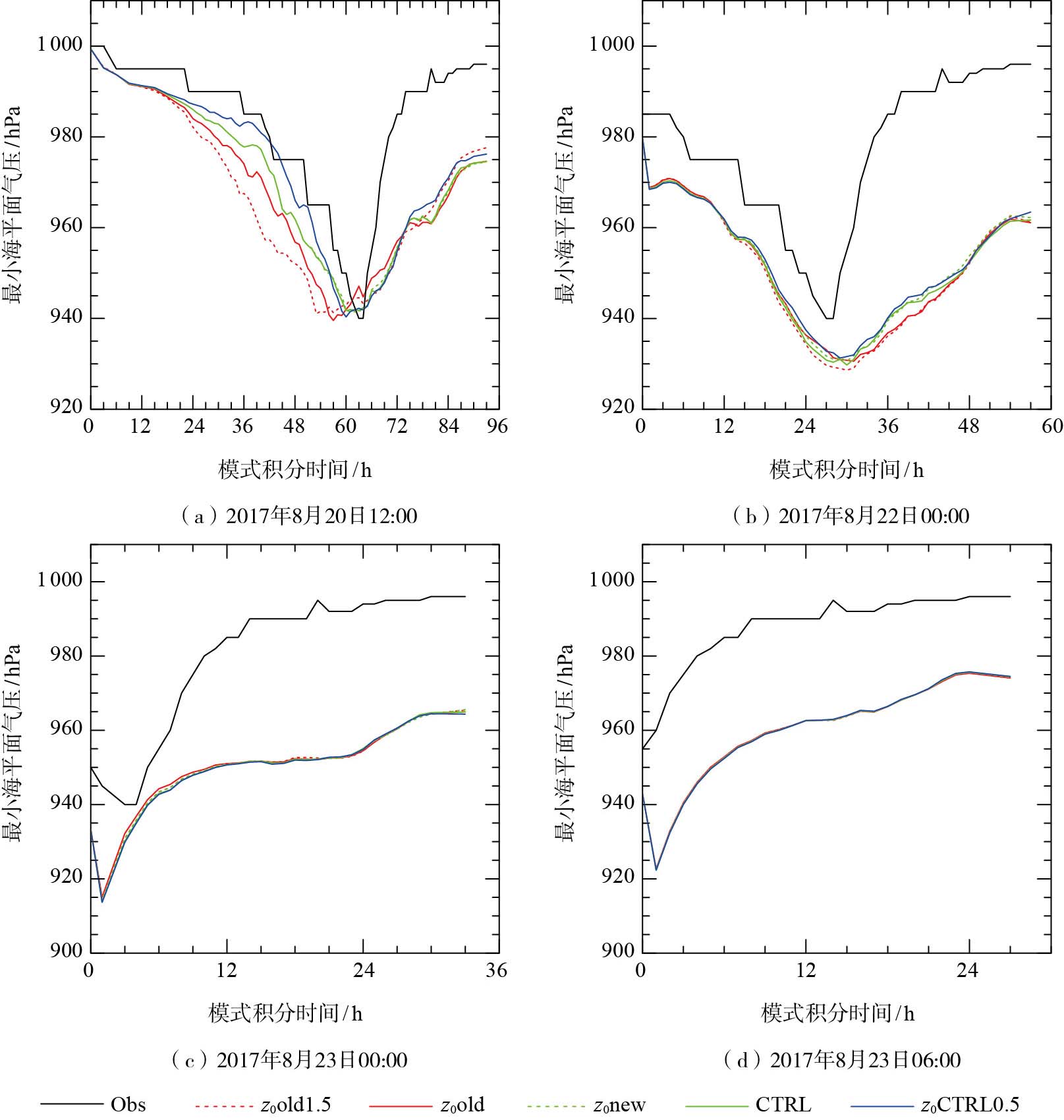
图 6和图 7分别给出了粗糙度z0的变化对台风“天鸽”4个不同阶段起报的台风中心附近最大10 m风速和最小海平面气压模拟的影响。在初期为热带风暴的阶段(2017年8月20日12:00)起报的试验中,台风在达到最大强度之前的加强过程中,台风强度(台风中心附近最大10 m风速和最小海平面气压)模拟对z0敏感,在台风减弱过程中,台风强度对z0不敏感(图 6a、7a)。由图 7a可见,z0old1.5方案在台风增强过程中产生的误差最大,使台风增强加深偏快得最多。
|
图 6 1713号台风“天鸽”在4个阶段模拟的不同粗糙度z0下的10 m水平风速最大值 Fig.6 The same as Fig. 3, but for different schemes of momentum roughness z0 |
|
图 7 1713号台风“天鸽”在4个阶段模拟的不同粗糙度z0下的最小海平面气压 Fig.7 The same as Fig. 4, but for different schemes of momentum roughness z0 |
在台风成熟之后(强热带风暴及以后,即2017年8月22日00:00、2017年8月23日00:00和2017年8月23日06:00)起报的试验中,台风中心附近最小海平面气压对z0的变化不敏感(图 7b-d);减弱阶段的台风中心附近最大10 m风速对z0的变化也不敏感(图 6b-d)。加强阶段的台风中心附近最大10 m风速对z0的变化略有差异,z0old试验的台风发展明显偏慢偏弱(图 6b)。
5 结论与讨论使用CMA-TYM模式系统,选择1713号台风“天鸽”生命过程中4个典型的不同阶段,进行一系列敏感性试验,通过分别改变边界层高度h和动量粗糙度z0,研究边界层参数化过程中的两个关键要素对该台风移动路径和强度模拟的影响。结果显示:
(1) 边界层高度h在初期的热带风暴阶段对热带气旋的移动路径有较明显影响,在台风成熟之后对热带气旋的移动路径影响不显著。反映台风强度的两个要素,即台风中心附近最大10 m风速和最小海平面气压,对边界层高度h的敏感性有很大差别。台风中心附近最大10 m风速对边界层高度h的变化不敏感,而最小海平面气压对边界层高度h的变化却非常敏感。
(2) 在台风发展初期阶段,边界层过薄或过厚(即边界层高度h过高或过低)都不利于台风强度的发展加强。这表明边界层高度h在热带气旋数值模拟中的重要性,尤其是在台风发展初期阶段。
(3) 动量粗糙度z0的变化对台风“天鸽”移动路径模拟的影响不显著,对台风减弱过程中的强度影响也不显著;动量粗糙度z0的变化对台风“天鸽”的影响主要体现在台风增强阶段。在台风增强阶段,台风强度(特别是台风中心附近最大10 m风速)的加强过程对z0很敏感,尤其是在台风发展的初期阶段。
反映台风强度的台风中心附近最大10 m风速和最小海平面气压的模拟对边界层高度h的敏感性非常不同,这是CMA-TYM模式改进的一个方向。未来还需要通过讨论和分析大量台风个例来进一步理解台风生命过程不同阶段的模拟对边界层高度h和动量粗糙度z0的敏感性问题,例如是否个例依赖、参数化方案依赖或模式依赖,希望未来能总结出普遍适用的结论来帮助数值模式中边界层参数化改进。边界层高度对模拟的台风增强的影响具有非线性特点,在台风发展初期阶段,边界层高度h过薄或过厚都不利于台风强度的发展加强,不平衡过程的作用可能是一个主要原因。基于K廓线的YSU边界层方案本质上是用热力学定义边界层的一种方案,而动力学的重要作用也是台风边界层区别于其他边界层问题的主要特点之一,台风的动力学特点如何在边界层参数化模式中合理地体现也是未来的模式边界层改进研究中需要着重考虑的一个方向。
| [1] |
ROSENTHAL S L. A theoretical analysis of the field of motion in the hurricane boundary layer: National Hurricane Research Project Report, NO. 56[R]. Weather Bureau, U. S. Department of Commerce, 1962: 12.
|
| [2] |
ELIASSEN A. On the Ekman layer in a circular vortex[J]. J Meteor Soc Japan, 1971, 49: 784-789. |
| [3] |
ELIASSEN A, LYSTAD M. The Ekman layer of a circular vortex: a numerical and theoretical study[J]. Geophys Norv, 1977, 31(7): 1-16. |
| [4] |
KEPERT J. The dynamics of boundary layer jets within the tropical cyclone core. Part Ⅰ: linear theory[J]. J Atmos Sci, 2001, 58(17): 2469-2484. DOI:10.1175/1520-0469(2001)058<2469:TDOBLJ>2.0.CO;2 |
| [5] |
KEPERT J, WANG Y. The dynamics of boundary layer jets within the tropical cyclone core. Part Ⅱ: nonlinear enhancement[J]. J Atmos Sci, 2001, 58(17): 2485-2501. DOI:10.1175/1520-0469(2001)058<2485:TDOBLJ>2.0.CO;2 |
| [6] |
KEPERT J D. Choosing a boundary layer parameterization for tropical cyclone modeling[J]. Mon Wea Rev, 2012, 140(5): 1427-1445. DOI:10.1175/MWR-D-11-00217.1 |
| [7] |
TROEN I B, MAHRT L. A simple model of the atmospheric boundary layer: sensitivity to surface evaporation[J]. Bound-Layer Meteor, 1986, 37(1): 129-148. |
| [8] |
VOGELEZANG D H P, HOLTSLAG A A M. Evaluation and model impacts of alternative boundary-layer height formulations[J]. Bound-Layer Meteor, 1996, 81(3): 245-269. |
| [9] |
NOH Y, CHEON W G, HONG S Y, et al. Improvement of the K-profile model for the planetary boundary layer based on large eddy simulation data[J]. Bound-Layer Meteor, 2003, 107(2): 401-427. DOI:10.1023/A:1022146015946 |
| [10] |
BENDER M A, GINIS I, TULEYA R, et al. The operational GFDL coupled hurricane-ocean prediction system and a summary of its performance[J]. Mon Wea Rev, 2007, 135(12): 3965-3989. DOI:10.1175/2007MWR2032.1 |
| [11] |
HONG S Y, PAN H L. Nonlocal boundary layer vertical diffusion in a medium-range forecast model[J]. Mon Wea Rev, 1996, 124(10): 2322-2339. DOI:10.1175/1520-0493(1996)124<2322:NBLVDI>2.0.CO;2 |
| [12] |
HONG S Y, NOH Y, DUDHIA J. A new vertical diffusion package with an explicit treatment of entrainment processes[J]. Mon Wea Rev, 2006, 134(9): 2318-2341. DOI:10.1175/MWR3199.1 |
| [13] |
ZHANG J A, MARKS F D, MONTGOMERY M T, et al. An estimation of turbulent characteristics in the low-level region of intense hurricanes Allen (1980) and Hugo (1989)[J]. Mon Wea Rev, 2010, 139(5): 1447-1462. |
| [14] |
ZHANG J A, ROGERS R F, NOLAN D S, et al. On the characteristic height scales of the hurricane boundary layer[J]. Mon Wea Rev, 2011, 139(8): 2523-2535. DOI:10.1175/MWR-D-10-05017.1 |
| [15] |
POWELL M D, VICKERY P J, REINHOLD T A. Reduced drag coefficient for high wind speeds in tropical cyclones[J]. Nature, 2003, 422(6929): 279-283. DOI:10.1038/nature01481 |
| [16] |
MAKIN V K. A note on the drag of the sea surface at hurricane winds[J]. Bound-Layer Meteor, 2005, 115(1): 169-176. DOI:10.1007/s10546-004-3647-x |
| [17] |
KUDRYAVTSEV V N, MAKIN V K. Aerodynamic roughness of the sea surface at high winds[J]. Bound-Layer Meteor, 2007, 125(2): 289-303. DOI:10.1007/s10546-007-9184-7 |
| [18] |
GOLBRAIKH E, SHTEMLER Y M. Foam input into the drag coefficient in hurricane conditions[J]. Dyn Atmos Oceans, 2016, 73: 1-9. DOI:10.1016/j.dynatmoce.2015.10.005 |
| [19] |
DONELAN M A. On the decrease of the oceanic drag coefficient in high winds[J]. J Geophys Res: Oceans, 2018, 123(2): 1485-1501. DOI:10.1002/2017JC013394 |
| [20] |
BRAUN S A, TAO W K. Sensitivity of high-resolution simulations of Hurricane Bob (1991) to planetary boundary layer parameterizations[J]. Mon Wea Rev, 2000, 128(12): 3941-3961. DOI:10.1175/1520-0493(2000)129<3941:SOHRSO>2.0.CO;2 |
| [21] |
NOLAN D S, ZHANG J A, STERN D P. Evaluation of planetary boundary layer parameterizations in tropical cyclones by comparison of in situ observations and high-resolution simulations of Hurricane Isabel (2003). Part Ⅰ: initialization, maximum winds, and the outer-core boundary layer[J]. Mon Wea Rev, 2009, 137(11): 3651-3674. DOI:10.1175/2009MWR2785.1 |
| [22] |
NOLAN D S, STERN D P, ZHANG J A. Evaluation of planetary boundary layer parameterizations in tropical cyclones by comparison of in situ observations and high-resolution simulations of Hurricane Isabel (2003). Part Ⅱ: inner-core boundary layer and eyewall structure[J]. Mon Wea Rev, 2009, 137(11): 3675-3698. DOI:10.1175/2009MWR2786.1 |
| [23] |
ZHANG J A, NOLAN D S, ROGERS R F, et al. Evaluating the impact of improvements in the boundary layer parameterizations on hurricane intensity and structure forecasts in HWRF[J]. Mon Wea Rev, 2015, 143(8): 3136-3155. DOI:10.1175/MWR-D-14-00339.1 |
| [24] |
陈德辉, 沈学顺. 新一代数值预报系统GRAPES研究进展[J]. 应用气象学报, 2006, 17(6): 773-777. DOI:10.3969/j.issn.1001-7313.2006.06.014 |
| [25] |
张进, 麻素红, 陈德辉, 等. GRAPES_TYM改进及其在2013年西北太平洋和南海台风预报的表现[J]. 热带气象学报, 2017, 33(1): 64-73. |
| [26] |
KURIHARA Y, BENDER M A, TULEYA R E, et al. Improvements in the GFDL hurricane prediction system[J]. Mon Wea Rev, 1995, 123(9): 2791-2801. DOI:10.1175/1520-0493(1995)123<2791:IITGHP>2.0.CO;2 |
| [27] |
KURIHARA Y, BENDER M A, ROSS R J. An initialization scheme of hurricane models by vortex specification[J]. Mon Wea Rev, 1993, 121(7): 2030-2045. DOI:10.1175/1520-0493(1993)121<2030:AISOHM>2.0.CO;2 |
| [28] |
WANG Y Q. On the bogusing of tropical cyclones in numerical models: the influence of vertical structure[J]. Meteor Atmos Phys, 1998, 65: 153-170. DOI:10.1007/BF01030785 |
| [29] |
GREEN B W, ZHANG F Q. Impacts of air-sea flux parameterizations on the intensity and structure of tropical cyclones[J]. Mon Wea Rev, 2013, 141(7): 2308-2324. DOI:10.1175/MWR-D-12-00274.1 |
| [30] |
SHIN H H, HONG S Y, DUDHIA J. Impacts of the lowest model level height on the performance of planetary boundary layer parameterizations[J]. Mon Wea Rev, 2012, 140(2): 664-682. DOI:10.1175/MWR-D-11-00027.1 |
| [31] |
MA Z, FEI J, HUANG X, et al. Sensitivity of the simulated tropical cyclone intensification to the boundary-layer height based on a K-profile boundary-layer parameterization scheme[J]. JAMES, 2018, 10(11): 2912-2932. |
 2023, Vol. 43
2023, Vol. 43


