2. 山东省气象工程技术中心,山东 济南 250031
2. Shandong Meteorological Engineering Technology Center, Jinan 250031, China
双偏振雷达与常规雷达相比能更好地观测到各种云和降水,可获取差分反射率因子(ZDR)、相关系数(ρhv)、差分传播相位(ΦDP)、差分传播相移率(KDP)等偏振参量,它们能很好地反映云、水凝物粒子相态、滴谱分布等特征,有利于提升雷达估测降水和粒子相态辨别的水平[1-5]。双偏振天气雷达的这些应用,必须依赖于其系统的稳定性能和准确的探测数据[6],然而在雷达的工作过程中,其探测资料会因为雷达自身系统及外界环境的噪声、信号衰减、周边的地物等因素而影响雷达探测数据的真实性。因此,为确保雷达数据的准确性需要对雷达资料进行质量分析与质量控制。
众多学者研究表明,双线偏振多普勒雷达数据质量的可信度与信噪比(signal-to-noise ratio,SNR)及ρhv密切相关[7-8]。杜牧云等[9]发现,SNR值较小时,噪声对ZDR的数据质量影响较为明显,可导致ZDR数据产生一定的误差。Lim等[10]指出,如果不考虑SNR对雷达数据质量的影响,雷达探测到的ρhv将有可能出现“失真”,如:对于纯降水,当SNR为10 dB时,ρhv约为0.93,而对于融化层区域,当SNR为35 dB时,ρhv约为0.95。因此,仅凭ρhv的值是无法准确判断探测区域内降水粒子相态的。Melnikov等[11]对双线偏振雷达开展了大量的外场试验,发现ZDR的标准差与SNR和ρhv都存在紧密的联系。
ZDR是识别降水粒子类型的最重要的偏振参量[12]。在雷达探测的过程中,接收机噪声以及目标粒子对水平和垂直电磁波衰减不同导致的偏振量的偏差[13]等因素都会造成ZDR的系统误差。Ryzhkov等[14]通过研究发现,ZDR误差为0.2 dB时,定量估测降水的估测误差可降到18%以下。因此,ZDR系统误差的订正是偏振参量精确应用的关键要素,对ZDR系统误差进行订正,不但能提升降水量估测的精确度,而且对水凝物类型识别的准确率也会大大提高。
本文利用济宁S波段双线偏振多普勒雷达观测的弱降水资料,分析了信噪比和相关系数对双线偏振参量产生的影响,研究了雷达近距离双线偏振参数的特征,研究结果可为双线偏振多普勒雷达产品的准确应用提供数据参考。利用自然目标物法对ZDR系统误差的订正效果进行分析,以期为业务运行的S波段双线偏振多普勒雷达在无法进行天顶垂直扫描时寻找一种较好的ZDR系统误差订正方法。
1 资料和研究方法 1.1 资料所用资料来自济宁S波段双线偏振多普勒雷达的观测资料,该雷达的观测模式为WSR-88D的21体扫模式,每6 min完成9个仰角的体扫。雷达关键性能参数见表 1。
|
|
表 1 S波段双线偏振多普勒雷达性能参数 Table 1 Performance parameters of S-band dual-linear polarization Doppler radar |
目前ZDR系统误差的订正方法主要有测试信号法、太阳辐射法、自然目标法,国内外诸多学者也采用这些方法对ZDR系统误差进行过订正[15-16]。Pratte等[17]在1989年采用太阳标定方法对ZDR系统误差进行了标定。Giangrande等[18]利用自然目标法订正过ZDR的系统误差,结果较理想。胡志群等[19]利用多种标定方法对ZDR的系统误差进行过标定,并进行了对比,对比结果证实微雨滴法是最好的方法。
1.2.1 测试信号法通过分别测量发射功率与测试信号的值来对ZDR的系统误差进行订正[20]。订正过程如下:在天线系统发射端分别测量水平通道和垂直通道的发射信号功率,计算得到发射系统的ZDR系统误差;用雷达的内置信号发生器或外接信号源使其产生信噪比超过30 dB的信号[21],然后测量出该信号到达水平通道和垂直通道的功率,用功率差计算得到接收系统的ZDR系统误差。发射和接收系统ZDR系统误差的和即为总的ZDR系统误差。
1.2.2 太阳辐射法太阳辐射各向同性,即其水平偏振方向的功率与垂直方向的一致。雷达天线的波束正对太阳并接收其最大辐射时,ZDR等于0 dB。该方法虽然能精准的标定雷达接收系统带来的ZDR系统误差,但无法获取雷达整体系统总的ZDR系统误差。不仅如此,要想将天线波束正对太阳也很难。因此,该标定方法很难应用到实际业务中去。
1.2.3 自然目标法雨滴落下的过程中,它沿垂直方向的水平剖面近似为圆形,当雷达天线90°仰角垂直探测时,其ZDR的理论值为0 dB,自然目标法是ZDR系统误差订正的较好的方法。Ryzhkov等[14]的相关研究表明,雷达在高仰角探测时,小雨和干雪粒子的ZDR接近于0 dB。因此,可选择雷达高仰角探测下呈球形的降水粒子作为自然目标物对ZDR系统误差进行标定。这种方法对于不支持垂直扫描模式的业务运行雷达来说,是对ZDR系统误差进行订正的较好替代方法,它包含了雷达接收系统和发射系统共同产生的ZDR系统误差。本文即采用自然目标物法对ZDR系统误差进行订正。
2 信噪比对双偏振参数的影响分析为研究SNR对雷达偏振参量的影响,选取济宁S波段双线偏振多普勒雷达2021年9月4日的一次弱降水过程进行分析。对于弱降水过程,ZDR的理论值接近0 dB,ρhv的理论值接近1,相邻库的ФDP增量接近0°。考虑到近距离杂波干扰以及衰减等因素的影响,选取径向距离位于15~50 km(距离库位于60~200)的数据。因底层的遮挡以及零度层亮带的影响,本研究选用1.5°仰角的数据资料。
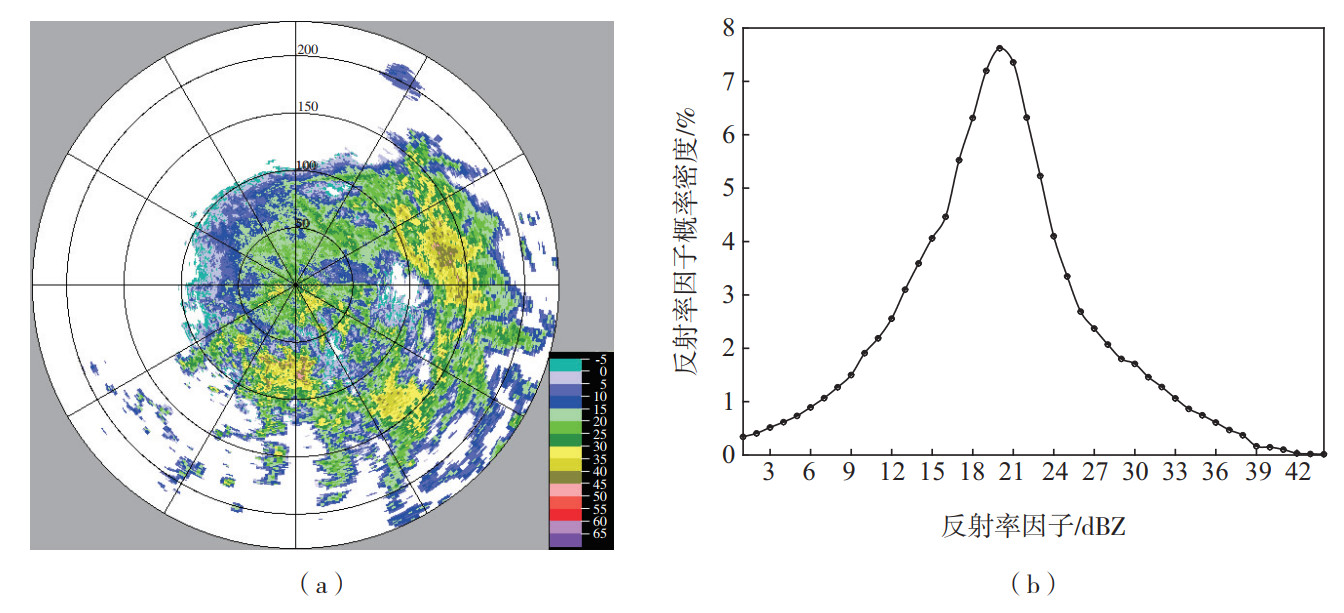
图 1a为济宁S波段双线偏振多普勒雷达2021年9月4日17:20(北京时,下同)反射率因子图;图 1b为反射率因子的概率分布曲线,由图 1b可见,反射率因子概率密度的高值位于20 dBZ附近,合乎层状云降水特征,符合本文要求的弱降水分析条件。
|
图 1 2021年9月4日17:20济宁S波段双线偏振多普勒雷达1.5°仰角反射率因子(a;色阶,单位:dBZ)和反射率因子概率密度分布(b) Fig.1 Distribution of reflectivity (a; color scale, units: dBZ) and its probability density (b) at 1.5° elevation of S-band dual-linear polarization Doppler radar in Jining at 17:20 BST 4 September 2021 |
考虑到非降水粒子的干扰,此处选取ρhv≥0.95的数据。将SNR的值按照1 dB的间隔,求取每个SNR区间间隔内ZDR的平均值和标准差(下文2.2节与2.3节中SNR的处理方法类同)。若采用新一代雷达的I/Q数据计算ZDR的标准差,分析结果会更准确。但是,由于I/Q数据容量大,目前业务规定新一代雷达数据采集机不存储I/Q数据。因此,在无法获取到I/Q数据资料的情况下,本文利用雷达基数据中的ZDR值计算得到ZDR的平均值和标准差进行分析,结果见图 2。

|
图 2 2021年9月4日17:20径向距离15~50 km的ZDR平均值和标准差随SNR的变化分布 Fig.2 Variation of mean value and standard deviation of ZDR with SNR in the range of 15-50 km at 17:20 BST 4 September 2021 |
对于弱降水过程,ZDR的理论值接近0 dB。因此,若ZDR出现不为0 dB的观测值时则可看作为ZDR的系统误差。由图 2可见,ZDR的系统误差为-0.3~0.5 dB。当SNR小于21 dB时,随着SNR的减小,ZDR标准差和平均值变化显著,其标准差快速增大,数据质量变差。当SNR大于21 dB时,随着SNR的增大,ZDR平均值呈稳中略微上升的趋势,ZDR标准差略微减小且逐渐达到稳定状态,其数据的稳定性越来越好。吴林林[22]利用雷达基数据计算了偏振参量的标准差,研究X波段双偏振雷达的不同信噪比对双偏振参量的影响发现,只有SNR大于20 dB的双偏振参量才具有可信度。姚晓娟[23]利用雷达基数据对C波段雷达ZDR标准差与SNR的关系进行研究,发现当SNR大于20 dB时,随着信噪比的增大,ZDR的标准差逐渐减小并趋于稳定。由于不同波段的雷达性能参数存在差异,影响其双偏振参量数据可信度的SNR阈值也有所差异。本文研究结果显示当SNR大于21 dB时,随着SNR的增大,ZDR的数据越来越稳定。
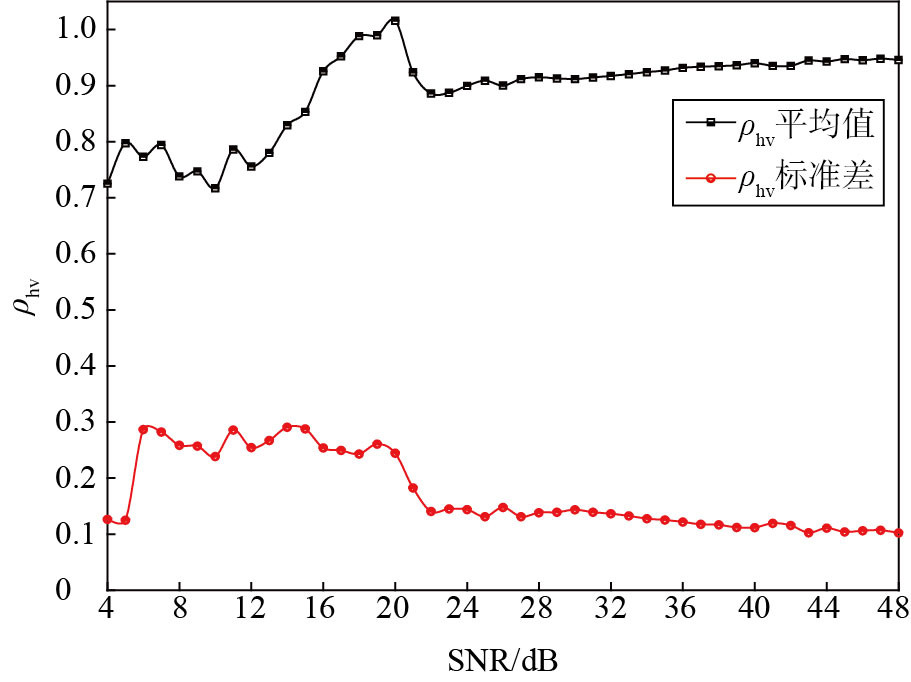
2.2 信噪比对ρhv的影响图 3为ρhv的平均值和标准差随SNR的变化曲线。对于弱降水过程,ρhv的值理论上应大于0.95并趋近1。由图 3可见,当SNR小于21 dB时,随着SNR的不断减小,ρhv的平均值迅速减小,ρhv的标准差和平均值出现明显波动,数据不稳定。当SNR大于21 dB时,ρhv的标准差随SNR的增大缓慢递减并趋于稳定状态,ρhv的平均值也缓慢增加且逐渐趋近于1,表明随着SNR的增大,ρhv的数据会越来越稳定。
|
图 3 2021年9月4日17:20径向距离15~50 km的ρhv平均值和标准差随SNR的变化分布 Fig.3 The same as Fig. 2, but for ρhv |
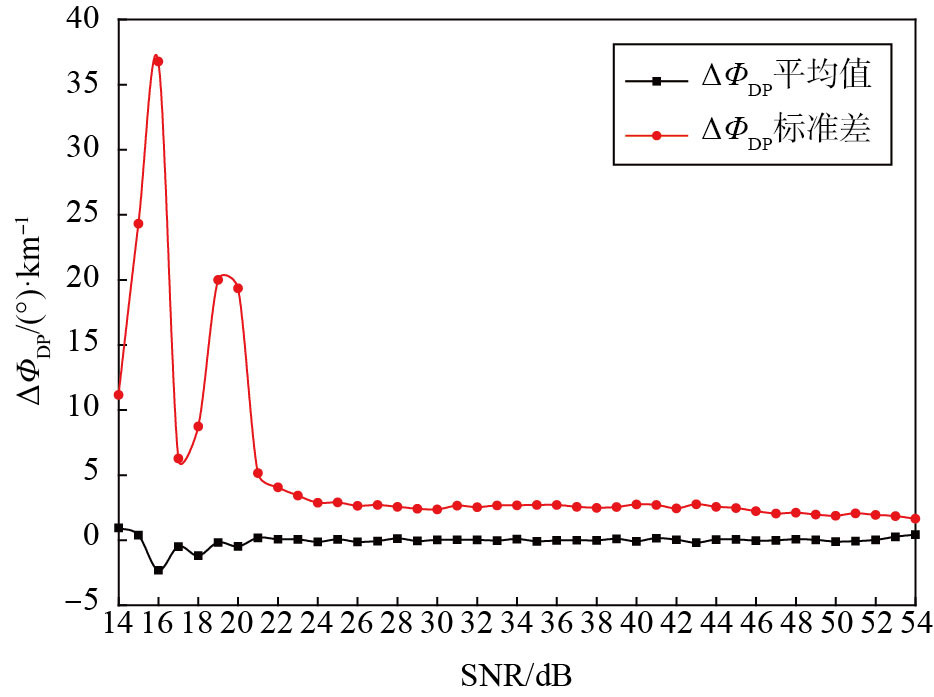
图 4为相关系数ρhv≥0.95时,ΔΦDP的平均值和标准差与SNR的变化图。由于ΦDP为一个径向的累积量,因此,采用同一个径向上某个点的ΦDP与前一个点ΦDP差值的绝对值ΔΦDP来表示ΦDP的偏差。理论上弱降水过程相邻距离库间的ΦDP变化甚微,即ΔΦDP近似为0 (°)·km-1。由图 4可见,当SNR小于21 dB时,ΔΦDP的标准差随SNR的变化波动剧烈,数据极不稳定。当SNR大于21 dB时,ΔΦDP的标准差快速变小,随着SNR的增大,ΔΦDP的标准差趋于稳定,ΔΦDP的平均值也趋于稳定且趋近于0 (°)·km-1,表明伴随着SNR的增大,ΦDP数据的稳定性越好。
|
图 4 2021年9月4日17:20径向距离15~50 km的ΔΦDP平均值和标准差随SNR的变化分布 Fig.4 The same as Fig. 2, but for ΔΦDP |
选取2021年8月20日济宁S波段双线偏振多普勒雷达观测的一次弱降水过程,选择1.5°仰角,径向距离位于15~50 km范围的数据资料研究相关系数ρhv对ΦDP的影响。由于双偏振参量受SNR的影响较大,根据前文的分析结果,此处将信噪比的阈值范围设定为SNR大于21 dB。
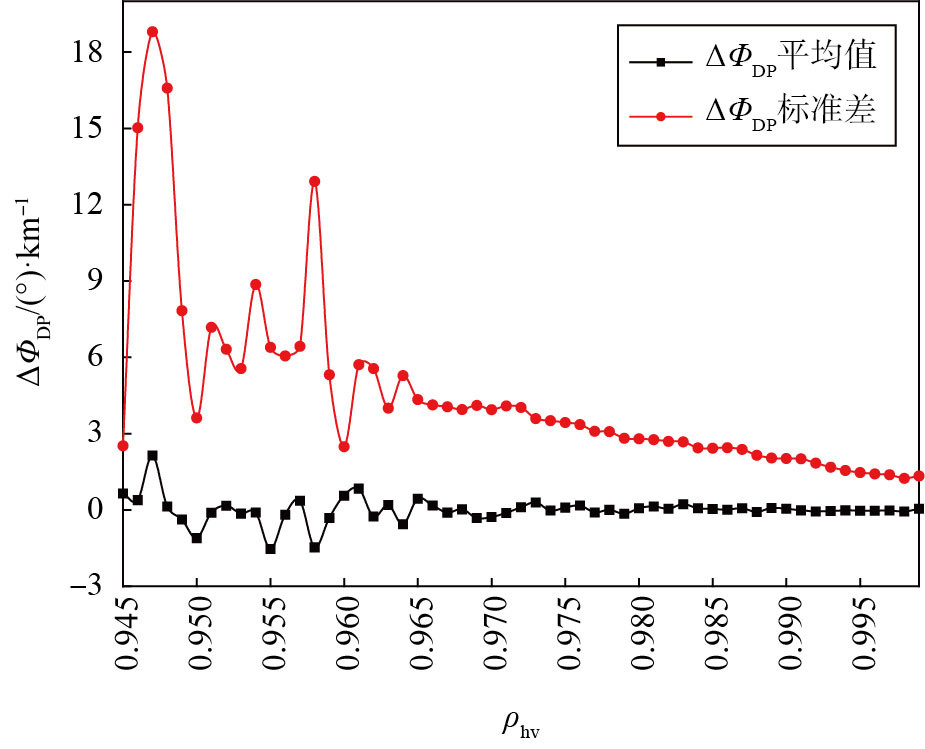
图 5为2021年8月20日08:02 ΔΦDP的平均值与标准差随ρhv的变化图。将ρhv按0.001的间隔,分析ρhv的相应区间内ΔΦDP的平均值和标准差随ρhv的变化情况。由图 5可见,当ρhv<0.965时,随着ρhv的减小,ΔΦDP的标准差和平均值变化大。当ρhv>0.965,随ρhv的增大,ΔΦDP的标准差波动平缓且呈现逐步下降的趋势,ΔΦDP的平均值略微增加并趋近于0 (°)·km-1,表明ρhv越大,ΦDP的值越稳定。
|
图 5 2021年8月20日08:02径向距离15~50 km的ΔΦDP平均值和标准差随ρhv的变化分布 Fig.5 Variation of mean value and standard deviation of ΔΦDP with ρhv in the range of 15-50 km at 08:02 BST 20 August 2021 |
为了分析研究双线偏振多普勒雷达近距离的双偏振参数的数据质量,选取2021年8月23日11:45径向距离0~15 km、15~50 km的雷达观测资料,分析了信噪比对差分反射率因子与差分传播相位的影响。
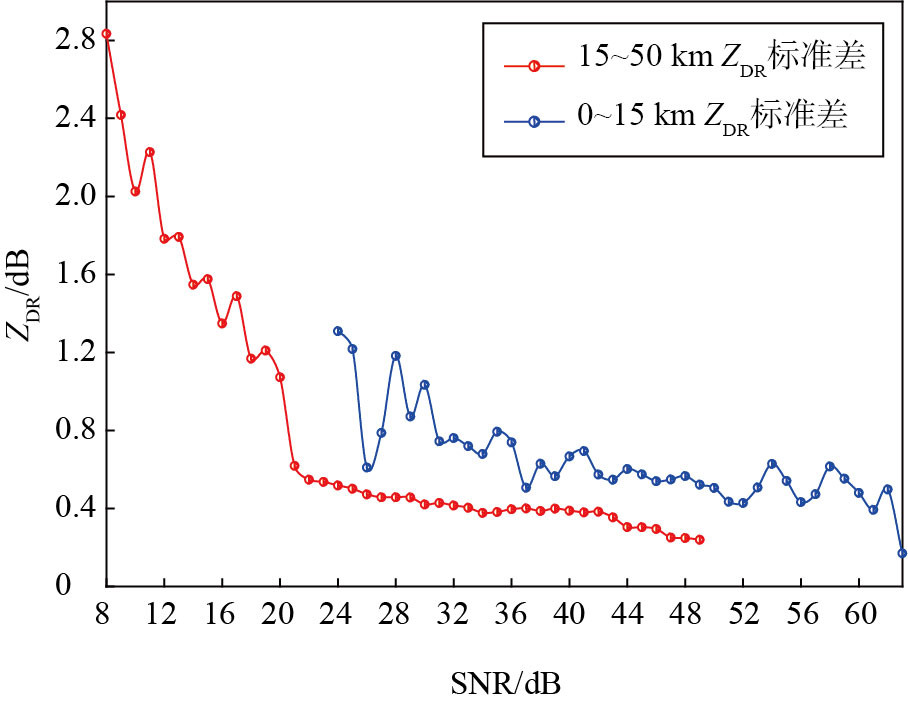
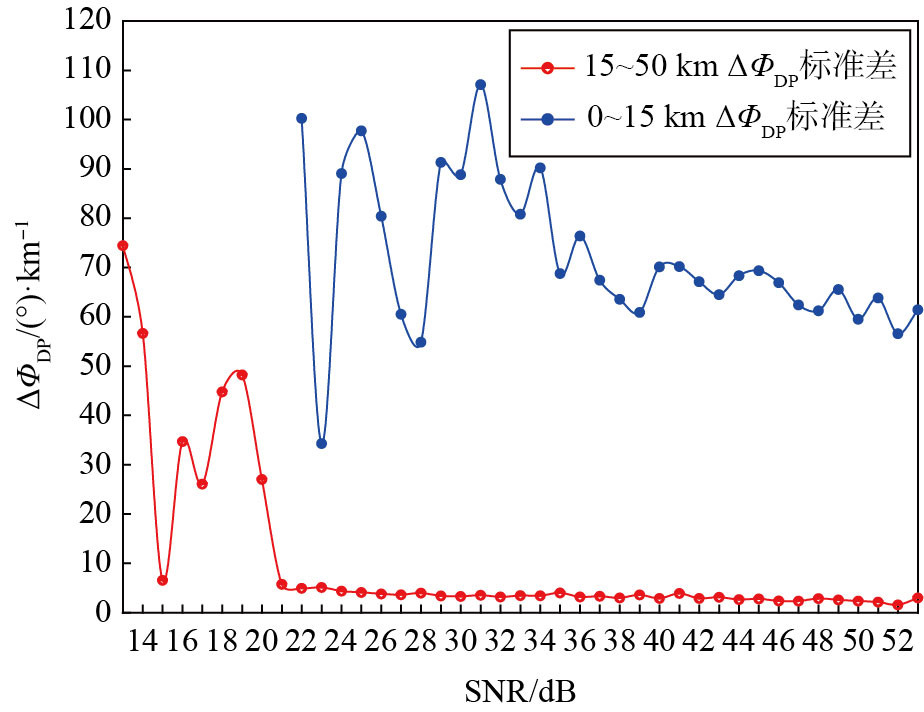
图 6和图 7分别为径向距离0~15 km和15~50 km的ZDR和ΔΦDP标准差随SNR的变化曲线。将SNR按照1 dB的间隔,求取每个SNR区间间隔内ZDR和ΔΦDP标准差。由前文2.1节和2.3节的分析可知,当SNR大于21 dB时,随着SNR的增大,ZDR和ΔΦDP的标准差略微减小且逐渐达到稳定状态,ZDR和ΦDP的数据稳定性越好。由图 6和图 7可见,15~50 km的ZDR和ΔΦDP的标准差曲线满足这个特征。而0~15 km的ZDR和ΔΦDP的标准差曲线均波动很大,数据极不稳定,且SNR越小,曲线波动越剧烈,表明雷达近距离0~15 km观测的双偏振参数不稳定,数据质量差。这与地面噪声干扰、近距离地物以及天线旁瓣的影响有关。因此,在实际的业务应用过程中,要特别注意雷达近距离低仰角的观测数据,选择合理的数据应用范围。
|
图 6 2021年8月23日11:45径向距离0~15 km和15~50 km的ZDR标准差随SNR的变化分布 Fig.6 Variation of standard deviation of ZDR with SNR in the ranges of 0-15 km and 15-50 km at 11:45 BST 23 August 2021 |
|
图 7 2021年8月23日11:45径向距离0~15 km和15~50 km的ΔΦDP标准差随SNR的变化分布 Fig.7 The same as Fig. 6, but for ΔΦDP |
基于自然目标法,利用济宁S波段双线偏振多普勒雷达最高仰角扫描下的小雨和干雪粒子对ZDR的系统误差进行了订正,并且对比分析了小雨粒子和干雪粒子的订正效果。ZDR系统误差订正方法的介绍已在1.2节中给出。
有关研究表明,小雨和干雪的差分反射率因子ZDR与扫描仰角存在公式(1)所示的关系[8, 14],即ZDR随着雷达扫描仰角的升高而逐渐减小,并趋近于0 dB。因而,在当前业务运行的双线偏振雷达不允许开展垂直扫描模式时,利用雷达最高仰角探测的小雨或干雪粒子的数据对ZDR系统误差开展订正是一种较好的方法。
| $ Z_{\mathrm{DR}}(\theta) \approx \frac{Z_{\mathrm{DR}}(0)}{\left[Z_{\mathrm{DR}}(0)^{\frac{1}{2}} \sin ^2 \theta+\cos ^2 \theta\right]^2}, $ | (1) |
式中:ZDR(0)和ZDR(θ)分别表示仰角为0°和θ°时的差分反射率因子。
信噪比、地物杂波以及融化层等是选择小雨和干雪数据时需要考虑的因素。选取2021年9月4日济宁S波段双线偏振多普勒雷达观测的一次伴有零度层亮带的层状云降水过程。此处选用雷达19.5°的最高扫描仰角探测到的小雨和干雪数据对ZDR的系统误差进行订正。根据前文的分析,将SNR的阈值设为21 dB,且小雨资料需满足雷达反射率因子Z < 28 dBZ,ρhv>0.97;干雪资料需满足Z < 35 dBZ,ρhv>0.99。研究表明,小雨和干雪数据的高度宜选取融化层以下1 km左右和融化层以上1~2 km,因该区域内的ZDR值保持在0 dB左右[24]。参照距离济宁雷达最近的徐州探空雷达的零度层高度,2021年9月3日20:00和4日08:00徐州探空雷达观测到的零度层高度分别为4 937 m和4 964 m。小雨数据选取的高度为3.0~3.9 km,干雪数据选取的高度为4.9~6.9 km。
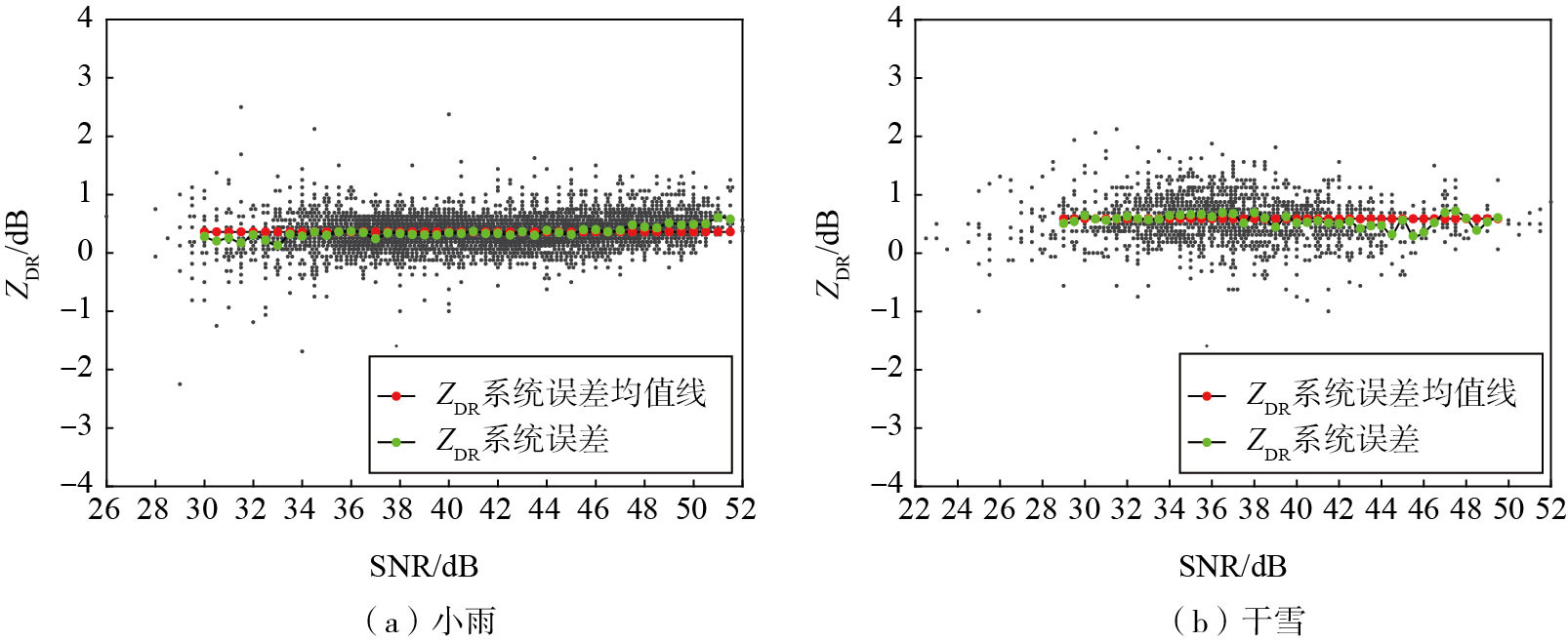
图 8为2021年9月4日01:26筛选出的19.5°仰角的小雨和干雪粒子对应的信噪比与差分反射率因子的散点图。将SNR以0.5 dB的区间进行划分,计算得到每一个SNR区间的ZDR的平均值,对应图中的绿色曲线,即为差分反射率因子系统误差的订正曲线。在计算每个SNR区间的ZDR的平均值时,考虑到数据的稳定性,对样本数小于10的SNR区间进行剔除。ZDR系统误差订正的平均值对应图中的红色虚线。由图可见,小雨与干雪两种自然目标物的ZDR系统误差的订正曲线随着SNR的增大,其波动幅度变化都不大,表明雷达观测过程中系统稳定性较好。小雨与干雪粒子相比,干雪粒子ZDR系统误差的订正曲线较小雨粒子的波动幅度大一些,也进一步说明小雨粒子的稳定性要优于干雪粒子。
|
图 8 2021年9月4日01:26济宁S波段双线偏振多普勒雷达19.5°仰角SNR-ZDR散点图 Fig.8 Scatter plot of SNR-ZDR at 19.5° elevation of S-band dual-linear polarization Doppler radar in Jining at 01:26 BST 4 September 2021 |
表 2为利用自然目标物法对2021年9月4日01:05:04—05:27:39共50个时次的雷达观测资料,计算得到的每个体扫的小雨和干雪粒子的ZDR系统误差均值、标准差以及满足筛选条件的样本个数。由表 2的统计结果可见:小雨粒子ZDR的系统误差均值普遍位于0.15~0.45 dB,标准差稳定在0.32 dB左右,波动较小;而干雪粒子的ZDR系统误差均值普遍大于小雨粒子均值,绝大部分位于0.20~0.80 dB,最大ZDR系统误差均值达到1.034 dB,标准差为0.43~0.60 dB,其标准差也大于小雨粒子的标准差。与小雨粒子相比,干雪粒子ZDR的标准差波动性大。此外,满足小雨筛选条件的样本数量有半数时次都大于干雪粒子的样本数量,主要是由于位于雷达回波边缘地带的干雪范围较小,数据稳定性略差所导致。通过ZDR系统误差结果对比分析可知,利用小雨粒子作为自然目标物可获得更为准确、稳定的ZDR系统误差标定值。根据150 540个小雨样本的统计结果,得到ZDR的系统误差的均值为0.326 2 dB,标准差均值为0.319 3 dB。
|
|
表 2 采用自然目标物法获得的2021年9月4日降水过程ZDR系统误差的均值和标准差 Table 2 Mean value and standard deviation of ZDR errors obtained by natural object method for precipitation process on 4 September 2021 |
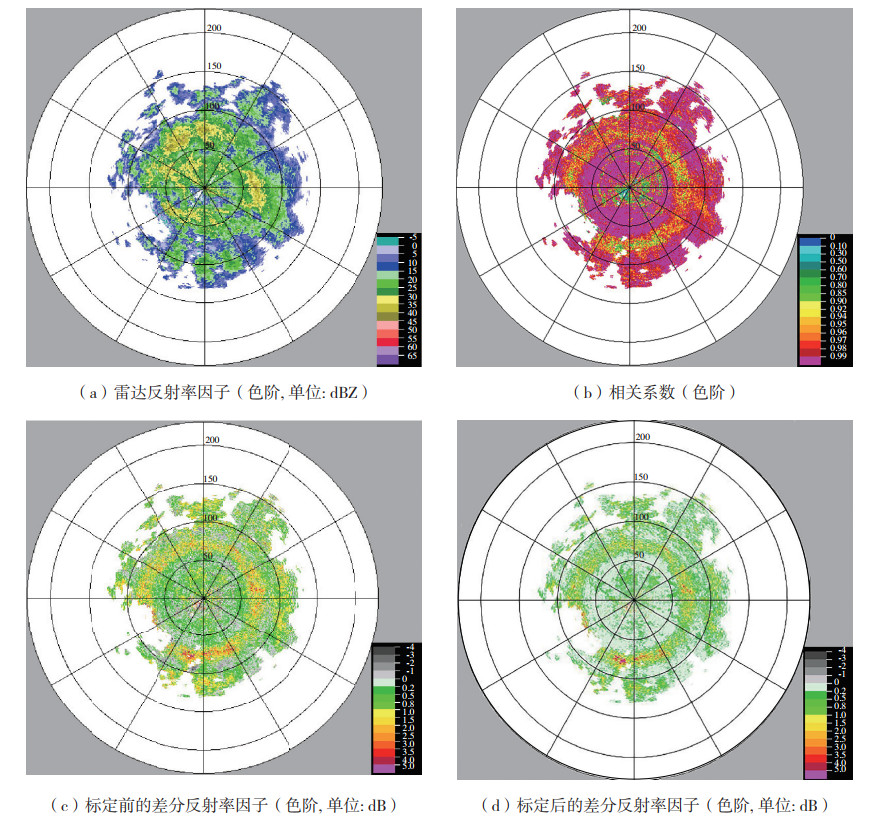
图 9所示为2021年9月4日03:35:04济宁S波段双线偏振多普勒雷达3.3°仰角的ZDR系统误差标定结果。由图 9a可见,径向距离100 km范围内,雷达反射率因子的值主要集中在10~30 dBZ,由图 9b可见,相关系数基本大于0.98。由图 9c可见,在径向距离约为75 km,方位位于0°~210°、270°~360°处可见明显的零度层亮带回波,表明在零度层以下是典型的弱降水粒子。图 9c、d为标定前与标定后的差分反射率因子ZDR的平面位置显示器(plan position indicator,PPI)图像,由图可见,ZDR标定前,径向距离75 km以内ZDR的值集中在0.5~1.0 dB,明显偏大,由计算得知ZDR系统误差为0.42 dB,经标定后,径向距离75 km以内ZDR的值大部分在0.2 dB左右,零度层亮带以上ZDR值大部分集中在0.5 dB左右,标定后的结果更加合理。姚晓娟[23]、周聪[25]曾采用此法对C波段双偏振雷达的ZDR系统误差进行过标定,结果显示标定后的效果要优于标定前。影响ZDR系统误差的因素较多,如:不同的信噪比对ZDR系统误差的影响不同。本文在订正过程中没有一一进行量化考虑这些因素,业务人员在实际应用中要综合考虑各因素的影响。
|
图 9 2021年9月4日03:35:04济宁S波段双线偏振多普勒雷达3.3°仰角PPI图 Fig.9 PPI figure at 3.3° elevation of S-band dual-linear polarization Doppler radar in Jining at 03:35:04 BST 4 September 2021 |
杜牧云等[26]利用小雨和干雪两种自然目标物对C波段双线偏振多普勒雷达的ZDR系统误差进行订正,发现对于C波段的雷达,干雪的订正效果更稳定,是ZDR系统误差订正的最优目标物。而通过本文的分析可知,在对S波段双线偏振多普勒雷达进行ZDR系统误差标定时,小雨粒子与干雪粒子相比,小雨粒子是更为合适的自然目标物。这与干雪粒子高度较高、满足筛选条件的干雪粒子数量较少有关,因而ZDR系统误差标定值的稳定性差一些。
6 结论利用济宁S波段双线偏振多普勒雷达观测的弱降水资料,分析了信噪比、相关系数对偏振参量的影响以及近距离双偏振参数的特征;同时利用雷达最高扫描仰角的层状云降水资料分析了小雨和干雪两种粒子对ZDR的订正效果。主要得到如下结论:
(1) 当SNR小于21 dB时,ZDR、ΔΦDP、ρhv的平均值和标准差随SNR的变化波动明显,ZDR、ΦDP、ρhv不稳定,数据质量差。当SNR大于21 dB时,随着SNR的增大,ZDR标准差和平均值变化缓慢并逐渐趋于稳定;ρhv的标准差缓慢递减趋于稳定,其平均值缓慢增加且趋近于1;ΔΦDP的标准差与平均值较为稳定,其平均值逐渐趋近于0 (°)·km-1。即SNR大于21 dB时,偏振参量ZDR、ρhv、ΦDP才具有可信度,且随着SNR的增大,ZDR、ρhv、ΦDP数据的稳定性越来越好。
(2) 当SNR大于21 dB、ρhv < 0.965时,随着ρhv的减小,ΔΦDP的标准差和平均值波动较大,ΦDP数据不稳定;当SNR大于21 dB、ρhv>0.965时,随着ρhv的增大,ΔΦDP的标准差波动平缓且呈逐步下降的趋势,其平均值缓慢增加并趋近于0 (°)·km-1,ΦDP的值越稳定。
(3) 受地面噪声干扰、近距离地物以及天线旁瓣的影响,在0~15 km内,无论SNR是减小还是增大,ZDR和ΔΦDP的标准差均波动大,双偏振参量不稳定,数据质量差;在15~50 km内,随着SNR的增大,ZDR与ΔΦDP的标准差略微减小且逐渐达到稳定状态,ZDR与ΦDP数据稳定性好。
(4) 利用小雨和干雪两种自然目标物对ZDR系统误差进行标定,通过对比发现,小雨粒子ZDR系统误差的平均值与标准差比干雪粒子小很多,且小雨粒子ZDR系统误差订正曲线的稳定性要优于干雪粒子,二者相比,小雨粒子的ZDR系统误差的订正效果更为稳定。经过系统误差订正后的降水粒子的ZDR值较订正前更为合理。在当前业务运行的双线偏振雷达不允许开展垂直扫描模式时,利用其最高仰角探测的小雨粒子数据对ZDR系统误差开展订正是一种较好的方法。
| [1] |
SELIGA T A, BRINGI V N. Potential use of radar differential reflectivity measurements at orthogonal polarizations for measuring precipitation[J]. J Appl Meteor, 1976, 15(1): 69-76. DOI:10.1175/1520-0450(1976)015<0069:PUORDR>2.0.CO;2 |
| [2] |
GORGUCCI E, CHANDRASEKAR V, BRINGI V N, et al. Estimation of raindrop size distribution parameters from polarimetric radar measurements[J]. J Atmos Sci, 2002, 59(15): 2373-2384. DOI:10.1175/1520-0469(2002)059<2373:EORSDP>2.0.CO;2 |
| [3] |
DOVIAK R J, BRINGI V, RYZHKOV A, et al. Considerations for polarimetric upgrades to operational WSR-88D radars[J]. J Atmos Oceanic Technol, 2000, 17(3): 257-278. DOI:10.1175/1520-0426(2000)017<0257:CFPUTO>2.0.CO;2 |
| [4] |
杨传凤, 刁秀广, 张骞, 等. 济南双偏振多普勒天气雷达在线自动标定数据质量分析评估[J]. 海洋气象学报, 2020, 40(4): 114-123. |
| [5] |
杨传凤, 张骞, 陈庆亮, 等. 济南CINRAD/SA雷达双偏振升级关键技术分析[J]. 海洋气象学报, 2019, 39(4): 116-123. |
| [6] |
苏添记, 葛俊祥, 章火宝. 中国双偏振天气雷达系统发展综述[J]. 海洋气象学报, 2018, 38(1): 62-68. |
| [7] |
吕博, 杨士恩, 王俊, 等. X波段双线偏振多普勒雷达资料质量评估[J]. 干旱气象, 2016, 34(6): 1054-1063. |
| [8] |
BRINGI V N, CHANDRASEKAR V. Polarimetric Doppler weather radar: principles and applications[M]. New York: Cambridge University Press, 2001: 636.
|
| [9] |
杜牧云, 刘黎平, 胡志群, 等. 双线偏振多普勒雷达资料质量分析[J]. 气象学报, 2013, 71(1): 146-158. |
| [10] |
LIM S, CIFELLI R, CHANDRASEKAR V, et al. Precipitation classification and quantification using X-band dual-polarization weather radar: application in the Hydrometeorology Testbed[J]. J Atmos Oceanic Technol, 2013, 30(9): 2108-2120. |
| [11] |
MELNIKOV V M, ZRNIC D S, CIRCLE H. Simultaneous transmission mode for the polarimetric WSR-88D[R]. USA: NOAA National Severe Storms Laboratory, 2004: 60-62.
|
| [12] |
曹俊武. 双线偏振多普勒雷达的资料质量控制及降水粒子相态识别方法的研究[D]. 南京: 南京信息工程大学, 2006.
|
| [13] |
魏洪峰, 薛震刚. 双偏振多普勒天气雷达差分反射率因子的测量误差[J]. 气象科技, 2008, 36(2): 223-227. |
| [14] |
RYZHKOV A V, GIANGRANDE S E, MELNIKOV V M, et al. Calibration issues of dual-polarization radar measurements[J]. J Atmos Oceanic Technol, 2005, 22(8): 1138-1155. |
| [15] |
GORGUCCI E, SCARCHILLI G, CHANDRASEKAR V. A procedure to calibrate multiparameter weather radar using properties of the rain medium[J]. IEEE Trans Geosci Remote Sens, 1999, 37(1): 269-276. |
| [16] |
GOURLEY J J, TABARY P, PARENT DU CHATELET J. Data quality of the Meteo-France C-band polarimetric radar[J]. J Atmos Oceanic Technol, 2006, 23(10): 1340-1356. |
| [17] |
PRATTE J F, FERRARO D G. Automated solar gain calibration[C]//Preprints, 24th Conference on Radar Meteorology of the American Meteorological Society. Tallahassee. Florida: Bulletin of the American Meteorological Society, 1989: 619-622.
|
| [18] |
GIANGRANDE S E, RYZHKOV A V. Calibration of dual-polarization radar in the presence of partial beam blockage[J]. J Atmos Oceanic Technol, 2005, 22(8): 1156-1166. |
| [19] |
胡志群, 刘黎平, 吴林林. C波段偏振雷达几种系统误差标定方法对比分析[J]. 高原气象, 2014, 33(1): 221-231. |
| [20] |
MELNIKOV V M, ZRNIC D S, DOVIAK R J, et al. Calibration and performance analysis of NSSL's Polarimetric WSR-88D[R]. USA: National Severe storms Laboratory, 2003: 1-72.
|
| [21] |
杜牧云. 双线偏振多普勒雷达资料分析与质量控制[D]. 成都: 成都信息工程大学, 2012.
|
| [22] |
吴林林. 利用雨滴谱对移动双偏振雷达进行质量控制及降水估测[D]. 北京: 中国气象科学研究院, 2014.
|
| [23] |
姚晓娟. NUIST-C波段双线偏振多普勒雷达资料质量控制及回波特征分析[D]. 南京: 南京信息工程大学, 2016.
|
| [24] |
IKEDA K, BRANDES E A. Freezing level determinations with polarimetric radar: retrieval model and application[C]//31st Conference on Radar Meteorolory. Boston: American Meteorological Society, 2003: 649-652.
|
| [25] |
周聪. NUIST-CDP双线偏振多普勒雷达资料质量控制[D]. 南京: 南京信息工程大学, 2019.
|
| [26] |
杜牧云, 刘黎平, 胡志群. 双线偏振雷达差分反射率因子系统误差订正[J]. 高原气象, 2013, 32(4): 1174-1185. |
 2023, Vol. 43
2023, Vol. 43


