2. 南京信息工程大学电子与信息工程学院,江苏 南京 210044;
3. 南京信息工程大学江苏省大气环境与装备技术协同创新中心,江苏 南京 210044
2. School of Electronics & Information Engineering, Nanjing University of Information Science & Technology, Nanjing 210044, China;
3. Jiangsu Collaborative Innovation Center of Atmospheric Environment and Equipment Technology, Nanjing University of Information Science & Technology, Nanjing 210044, China
量子通信是利用量子叠加态和纠缠效应进行信息传递的新型通信方式,具有无法被窃听和计算破解的绝对安全性保证,主要存在量子隐形传态和量子密钥分发两种方式。量子保密通信是未来保证网络信息安全很有发展前景的技术,以量子密钥分发为基础,已成为量子通信应用理论的研究热点[1]。
1984年,第一个量子密码通信方案提出,即著名的BB84方案,并第一次在实验上原理性地演示了量子密钥分发。2005年,潘建伟团队的研究初次证实等效于整个大气层厚薄的地面大气被纠缠光子穿透后,纠缠的特性仍然应用于高效、安全的量子通信[2]。2012年,中国科学家首次成功实现百公里量级的自由空间量子隐形传态和纠缠分发,此研究成果为中国将来“墨子号”的成功发射奠定了基础[3]。2016年,中国发射了全球首颗量子科学实验卫星“墨子号”,为进一步增大自由空间量子通信距离奠定了现实基础[4]。2020年,潘建伟团队以每秒2对光子的速度在两地之间建立起量子纠缠[5],实现了1 120 km无中继量子密钥分发。
2008年,欧洲发布《量子信息处理与通信战略报告》,提出欧洲量子通信发展包括三个阶段:第一阶段,使地面量子通信变为现实;第二阶段,使量子通信应用于卫星和地面间的传输;第三阶段,实现千公里量子通信网络,实现量子通信的空地一体化。同年,商业白皮书发布,并成立了大规模国际科技合作项目“SECOQC”工程,计划实现国际空间站与地面之间的量子通信。美国国家航空航天局(National Aeronautics and Space Administration,NASA)规划创设一个在总部与喷气推进实验室(Jet Propulsion Laboratory,JPL)之间直线距离达60 km、光纤皮长1 000 km,包含10个骨干节点的远程通信干线,并计划将其拓展到星地量子通信。
光量子信号是通过量子隐形传态的方法,基于量子纠缠态理论落实信息传达的。在量子通信的过程中,大气中存在的各种物质会对光发生散射吸收等作用。张秀再等[6]对海洋气溶胶在自由空间中的消光特性进行研究,为研究烟尘气溶胶的分布函数提供了依据。聂敏等[7]建立了不同海面风速、传输距离与量子通信系统各项性能参数之间的关系模型并进行了仿真实验,为光量子在海面上的顺利传输提供了参考。目前,国内外学者对烟尘气溶胶背景下量子通信各性能的变化鲜有研究。
烟尘气溶胶是大气气溶胶的重要组成部分之一,其中灰霾主要是生物质燃烧排放形成的颗粒物。邓丛蕊[8]研究发现引起区域严重烟尘的原因,一是硫酸根、硝酸根、铵根等相应无机盐具有高吸湿性,二是大气光学性质很可能被生物质燃烧排放物改变。黄朝军[9]借助电磁散射基本理论,使用电磁散射数值计算方法,对烟尘气溶胶凝聚粒子的光散射特性和传导特性进行分析,构建了单一粒径和多粒径烟尘凝聚粒子模型,为气溶胶凝聚粒子的光散射问题提供了研究方法。因此,分析不同浓度下烟尘粒子的消光特性及其在自由空间对量子通信各项性能的影响具有重要意义。
本文根据烟尘气溶胶粒子的尺寸分布参数,得出烟尘气溶胶的消光系数,通过仿真分析链路衰减与烟尘气溶胶粒子浓度和传输距离之间的变化关系,针对幅值阻尼信道,分别对信道容量、信道保真度和信道误码率进行仿真实验,并研究三者与烟尘气溶胶粒子和传输距离之间的关系,为在烟尘气溶胶影响下的光量子通信信号的正常传输奠定基础。
1 烟尘气溶胶对链路衰减的影响气溶胶粒子的各项性质与粒子的形状、组分、尺寸大小等参数有关。烟尘气溶胶的尺寸参数kext[10]可表示为
| $ x=2 \pi R / \lambda \text {, } $ | (1) |
式(1)中:x为尺寸参数,使粒子的概率分布参数化;R为烟尘气溶胶粒子半径,单位为μm;λ为入射光波长,单位为μm。
散射过程按照尺寸参数的大小可分为三类,分别为瑞利散射、Mie散射和几何光学散射。烟尘气溶胶的尺度参数x介于0.1~50.0,符合Mie散射的条件[11],因此采用Mie散射来计算烟尘气溶胶的消光系数。
目前,气溶胶粒子粒径分布模型普遍使用适用性较广的对数正态分布函数[12],其表达式为
| $ n(R)=\frac{\mathrm{d} n_0}{\mathrm{~d} R}=\frac{n_0}{\sqrt{2 {\rm{\pi }}} \ln 10 \cdot R \ln \sigma_{\mathrm{gm}}} \cdot \exp \left[-\frac{\left(\ln R-\ln R_{\mathrm{gm}}\right)^2}{2 \ln ^2 \sigma_{\mathrm{gm}}}\right], $ | (2) |
式(2)中:n(R)为R处单位半径间隔内的相对粒子数,n0为烟尘气溶胶粒子的数浓度,单位为m-3;Rgm为粒子平均半径,单位为μm;σgm为几何标准差。几种常见气溶胶的尺寸参数典型值[13]如表 1所示,查找可得对应粒子平均半径和几何标准差。
|
|
表 1 常见气溶胶的尺寸参数典型值 Table 1 Typical size parameters of common aerosols |
烟尘气溶胶粒子在大气传输过程中会吸收和散射部分可见光,导致光量子信号发生衰减。烟尘气溶胶的粒子消光系数kext[14]可表示为
| $ k_{\mathrm{ext}}={\rm{\pi }} \int_{R_1}^{R_2} Q_{\mathrm{ext}}(m, R, \lambda) n(R) R^2 \mathrm{~d} R \, , $ | (3) |
式(3)中:R为烟尘气溶胶粒子的半径,单位为μm;R1和R2分别为烟尘气溶胶粒子的半径下限和半径上限;λ为波长;m为烟尘气溶胶粒子的复折射率;Qext(m, R, λ)为烟尘气溶胶粒子的消光效率因子[15],可表示为
| $ Q_{\mathrm{ext}}=\frac{2}{x^2} \sum\limits_{n=1}^{\infty}(2 n+1) \operatorname{Re}\left(a_n+b_n\right) \, , $ | (4) |
式(4)中:n为烟尘气溶胶粒子数浓度,单位为m-3;Re(·)为取实部运算;an和bn为Mie系数,表示为
| $ a_n=\frac{m \Psi_n(m x) \Psi_n^{\prime}(x)-\Psi_n(x) \Psi_n^{\prime}(m x)}{m \Psi_n(m x) \xi_n^{\prime}(x)-\xi_n(x) \Psi_n^{\prime}(m x)} \, , $ | (5) |
| $ b_n=\frac{\Psi_n(m x) \Psi_n^{\prime}(x)-m \Psi_n(x) \Psi_n^{\prime}(m x)}{\Psi_n(m x) \xi_n^{\prime}(x)-m \xi_n(x) \Psi_n^{\prime}(m x)} \, , $ | (6) |
式(5)和式(6)中Ψn(x)为黎卡提-贝塞尔函数,ξn(x)为黎卡提-汉开尔函数,Ψ′n(x)和ξ′n(x)分别为Ψn(x)和ξn(x)关于x求导。
由国际气象学和大气物理学协会提出的各类型气溶胶粒子复折射率[16]如表 2所示,可得出不同气溶胶粒子在不同光波长影响下的复折射率。
|
|
表 2 不同类型气溶胶粒子的复折射率 Table 2 Complex refractive index of 4 types of aerosol particle |
实验选取λ=0.488 μm。当光信号在星地之间传输时,由烟尘气溶胶产生的能量衰减[17]可表示为
| $ E=E_0 \exp \left(-k_{\mathrm{ext}} \cdot d\right), $ | (7) |
式(7)中:E为量子信号通过烟尘气溶胶传输后的能量,单位为MeV;E0为量子信号的初始能量;d为量子信号的传输距离,单位为km。
链路衰减因子可由式(7)取对数求得,链路衰减因子Latt可表示为
| $ L_{\mathrm{att}}=10 \cdot k_{\mathrm{ext}} \cdot \operatorname{lge} \cdot d 。$ | (8) |
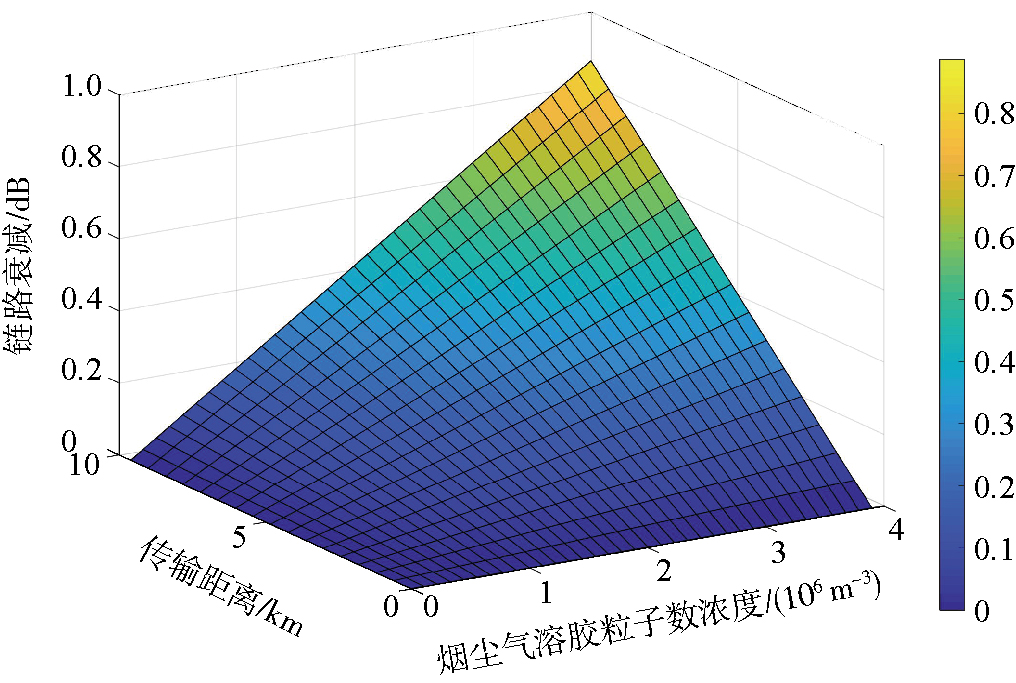
忽略大气中除烟尘气溶胶粒子外其他粒子的影响,链路衰减与传输距离、烟尘气溶胶粒子数浓度的关系如图 1所示。当传输距离不变时,随着粒子数浓度的增长,链路衰减也增长,并在n0=3.9×106 m-3和d=9.6 km时,链路衰减达到最大值0.89 dB;当粒子数浓度不变时,随着传输距离的增加,链路衰减也随之增加,当传输距离为3 km,粒子数浓度若从2.1×106 m-3增加到3.2×106 m-3时,链路衰减从0.30 dB增加到0.46 dB。因此,随着烟尘气溶胶粒子数浓度的增大,传输距离的增长,链路衰减也会随之增加,量子通信链路会受到二者的极大影响,可以通过调整发射端脉冲光子数或选择更佳的传输环境来减少链路衰减,改善通信质量。
|
图 1 烟尘气溶胶粒子数浓度、传输距离与链路衰减(色阶)之间的关系 Fig.1 Relationship between the number concentration of soot aerosol particles/transmission distance and link attenuation (color scale) |
量子信号在传输过程中,烟尘气溶胶会与光量子态发生作用,从而破坏量子态的相干性,实验选取幅值阻尼信道对烟尘气溶胶对通信信道容量的影响进行研究。由文献[18]可得幅值阻尼信道的运算算子为
| $ F_k=\sum\limits_n \sqrt{\left(\begin{array}{l} n \\ k \end{array}\right)} \sqrt{(1-p)^{n-k} p^k}|n-k\rangle\langle n| , $ | (9) |
式(9)中:〈n|表示烟尘气溶胶环境算子本征态,n表示复折射率m的实部,为烟尘气溶胶的散射入射辐射能力;|k〉表示烟尘气溶胶量子系统堙灭算子的本征态, k表示复折射率m的虚部,为烟尘气溶胶吸收入射辐射的能力;p表示量子态在传输时因烟尘气溶胶影响而丢失光量子的概率,可表示为
| $ p=\frac{E_1-E_2}{E_1}=1-\mathrm{e}^{-k_{\mathrm{ext}} \cdot d} , $ | (10) |
式(10)中,E1为量子信号的初能量,E2为量子信号在传输距离d后的能量。
量子态在处于单光子比特状态时,可定义为
| $ \boldsymbol{\rho}=\left(\begin{array}{ll} \alpha_1 & \alpha_2 \\ \alpha_2^* & \alpha_3 \end{array}\right) , $ | (11) |
式(11)中,α2*表示α2的复变换。量子态经过幅值阻尼信道后,量子系统的初始化密度矩阵演化为
| $ \boldsymbol{\varepsilon}(\boldsymbol{\rho})=\left[\begin{array}{cc} 1-(1-p)\left(1-\alpha_1\right) & \alpha_2 \sqrt{1-p} \\ \alpha_2^* \sqrt{1-p} & \alpha_3 \sqrt{1-p} \end{array}\right] , $ | (12) |
式(12)中,pi表示当信源为{pi, ρi }时,系统处于ρi的概率,其中∑pi=1,在烟尘气溶胶粒子的影响下,当输入字符为ρ1= 0〉〈0、ρ2= |1〉〈1|时,量子系统演化成为
| $ \begin{gathered} \boldsymbol{\varepsilon}(\boldsymbol{\rho})=\boldsymbol{\varepsilon}\left(\sum\limits_i p_i \boldsymbol{\rho}_i\right)=\boldsymbol{\varepsilon}\left[p_1 \boldsymbol{\rho}_i+\left(1-p_1\right) \boldsymbol{\rho}_2\right]= \\ {\left[\begin{array}{cc} p\left(1-p_1\right)+p_1 & 0 \\ 0 & (1-p)\left(1-p_1\right) \end{array}\right] \circ} \end{gathered} $ | (13) |
量子化系统对应的冯·诺依曼熵可表示为
| $ \begin{array}{r} f\left[\boldsymbol{\varepsilon}\left(\sum\limits_i p_i \boldsymbol{\rho}_i\right)\right]=-\left\{\left[p\left(1-p_1\right)+p_1\right] \log _2\left[p\left(1-p_1\right)+p_1\right]+\right. \\ \left.(1-p)\left(1-p_1\right) \log _2\left[(1-p)\left(1-p_1\right)\right]\right\} \circ \end{array} $ | (14) |
受烟尘气溶胶粒子影响,幅值阻尼信道的信道容量为
| $ C=\max \left\{f\left[\boldsymbol{\varepsilon}\left(\sum p_i \boldsymbol{\rho}_i\right)\right]-\sum p_i f\left(\boldsymbol{\varepsilon}\left(\rho_i\right)\right)\right\}_{\circ} $ | (15) |
对信道容量进行求导得
| $ p_1=\frac{y(1-p)-p}{(1+y)(1-p)}, $ | (16) |
式(16)中,y表示为
| $ y=2^{\frac{H(p)}{1-p}}, $ | (17) |
此时幅值阻尼信道的信道容量取得最大值,表示为
| $ \begin{gathered} C=\max \left\{-\left\{\left[p_1+\left(1-p_1\right) p\right] \log _2\left[p_1+\left(1-p_1\right) p\right]+\right.\right. \\ \left.(1-p)\left(1-p_1\right) \log _2\left[(1-p)\left(1-p_1\right)\right]\right\}- \\ \left.\left(1-p_1\right) H(p)\right\}, \end{gathered} $ | (18) |
式(18)中,H(p)=-plog2p-(1-p)log2(1-p)为二元熵。
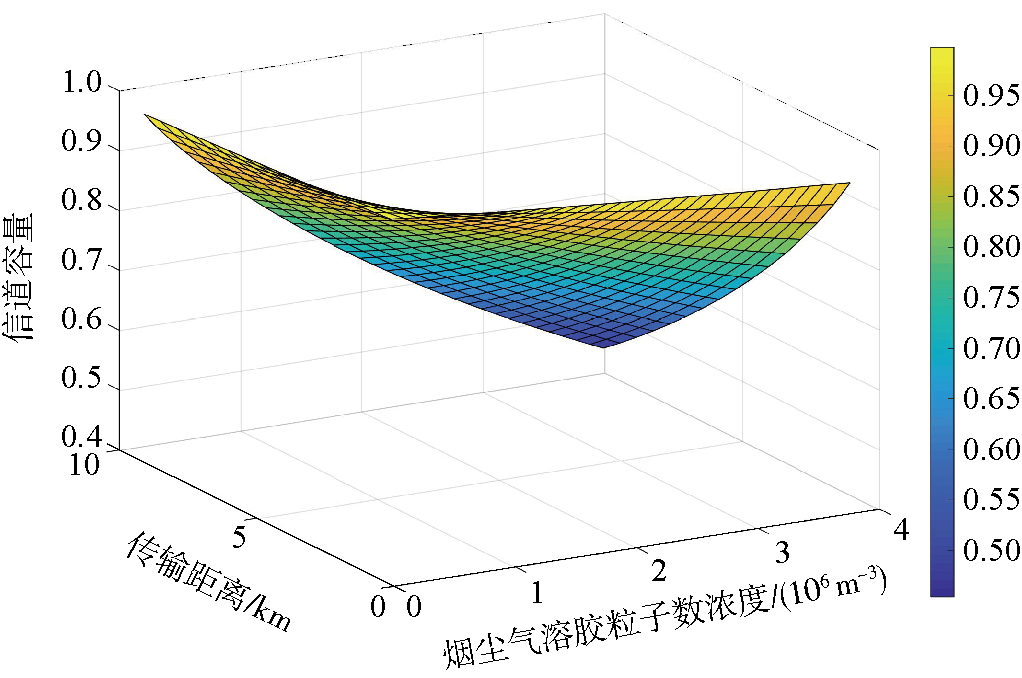
忽略大气中除烟尘气溶胶粒子外其他粒子的影响,幅值阻尼信道容量与传输距离、烟尘气溶胶粒子数浓度的关系如图 2所示。随着传输距离和烟尘气溶胶粒子数浓度的增大,幅值阻尼信道容量逐渐减小。当传输距离d=6 km,粒子数浓度为n0=0.11×106 m-3时,幅值阻尼信道传输的信道容量取得最大值0.997 2;当传输距离为d=9.6 km,粒子数浓度为n0=3.9×106 m-3时,幅值阻尼信道传输的信道容量取得最小值0.454 3。因此,量子信号在幅值阻尼信道中传输会出现能量损失,对信道容量产生较大影响。
|
图 2 烟尘气溶胶粒子数浓度、传输距离与信道容量(色阶)之间的关系 Fig.2 Relationship between the number concentration of soot aerosol particles/transmission distance and channel capacity (color scale) |
通信系统的保真度用于描述量子信号输出状态与初始状态相似度,本文将研究幅值阻尼信道平均保真度与信道生存函数之间的关系。量子信道平均保真度[19]在烟尘气溶胶粒子的影响下可表示为
| $ \begin{gathered} B\left(\boldsymbol{\rho}_1, \boldsymbol{\rho}_2\right)=B\left(\sum\limits_i p_i \boldsymbol{\rho}_i, \boldsymbol{\varepsilon}\left(\sum\limits_i p_i \boldsymbol{\rho}_i\right)\right)= \\ \operatorname{tr} \sqrt{\left(\sum\limits_i p_i \boldsymbol{\rho}_i\right)^{\frac{1}{2}} \boldsymbol{\varepsilon}\left(\sum\limits_i p_i \boldsymbol{\rho}_i\right)\left(\sum\limits_i p_i \boldsymbol{\rho}_i\right)^{\frac{1}{2}}}, \end{gathered} $ | (19) |
式(19)中,tr(·)表示对矩阵求迹,ρ1表示目的信息的密度矩阵,ρ2表示待传量子态信号的密度矩阵。
幅值阻尼信道下的量子信道平均保真度表示为
| $ \begin{gathered} B_{\mathrm{z}}=\sqrt{\frac{\left(p+2(1-p) p_1\right) p_1}{2}}+ \\ \sqrt{\frac{\left(p+2(1-p)\left(1-p_1\right)\right)\left(1-p_1\right)}{2}}, \end{gathered} $ | (20) |
式(20)中,p1表示输出字符|0〉1的概率。
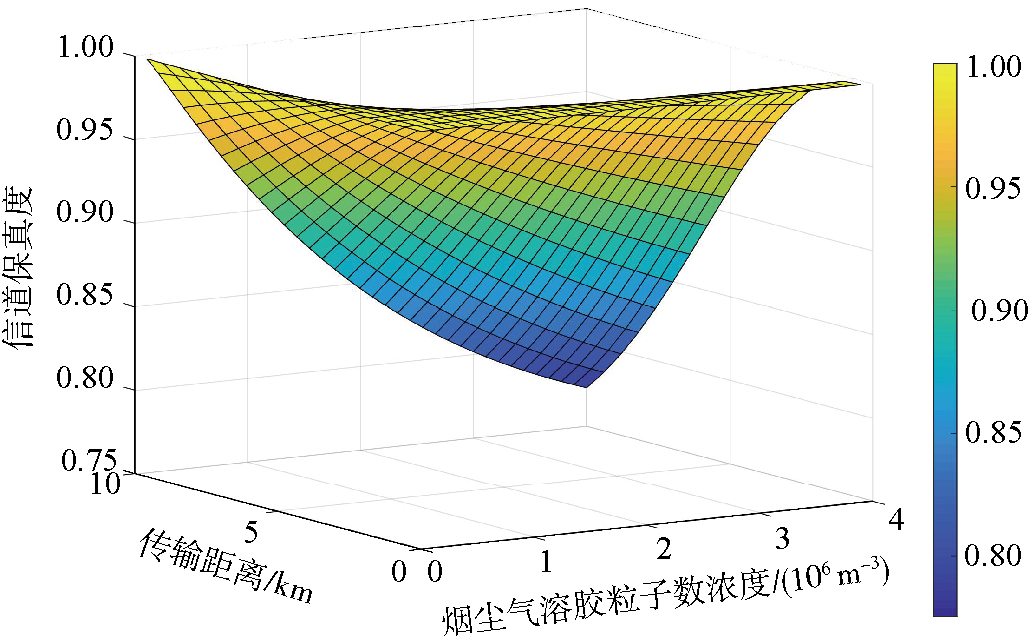
实验选取系统量子态处于ρ1时的概率p1=0.1,对幅值阻尼信道的保真度进行仿真。幅值阻尼信道保真度与传输距离、烟尘粒子气溶胶的数浓度如图 3所示。忽略大气中除烟尘气溶胶粒子外其他粒子的影响,当传输距离保持不变时,随着粒子数浓度的增大,信道保真度逐渐减小;当粒子数浓度一定时,随着传输距离的增加,信道保真度也逐渐减小。当传输距离d=9.6 km、n0=3.9×106 m-3时,保真度达到最小值0.78。当传输距离一定时,烟尘气溶胶粒子数浓度越高,保真度变化就越明显。粒子数浓度n0=2.7×106 m-3保持不变,传输距离从d=3 km增加至d=9 km时,保真度由0.98减小为0.83。传输距离和烟尘气溶胶粒子数浓度越大,对保真度的影响越明显,接收到的量子信号失真越严重。可以已知的粒子数浓度和传输距离为依据,调整信道带宽或者光量子发射功率,提高保真度,从而提高接收信号的质量。
|
图 3 烟尘气溶胶粒子数浓度、传输距离与信道保真度(色阶)之间的关系 Fig.3 Relationship between the number concentration of soot aerosol particles/transmission distance and channel fidelity (color scale) |
当光信号在星地之间传输时,会因受到烟尘气溶胶粒子的影响而发生错误,产生误码。量子系统信道误码率用来描述一定时间内量子信息传输精准性的指标,由接收到的误码率与总误码率的比值[20]表示,即
| $ W_{\mathrm{b}}=\frac{W_{\mathrm{e}}}{W_{\mathrm{s}}}, $ | (21) |
式(21)中,Wb表示烟尘气溶胶引起的误码率,We表示接收到的误码率,Ws表示总误码率。
由BB84协议可知,接收到的误码率We可表示为
| $ W_{\mathrm{e}}=\eta n_1(1-a) \mathrm{e}^{-4 \eta n_1}+a \eta n_1 \mathrm{e}^{-\eta G} , $ | (22) |
式(22)中:η表示单光子探测器探测量子的效率;a表示烟尘气溶胶所致的退极化效应因子;G=4n1+e-kextd;n1为接收方所探测到的光子计数,表示为
| $ n_1=\frac{n_2}{2}+n_3 , $ | (23) |
式(23)中,n2表示背景噪音引起的光子计数,n3表示光电探测器的暗电流指数。
总比特率Ws表示为
| $ W_{\mathrm{s}}=F_{\mathrm{s}} R_{\mathrm{r}}\left[1-\exp \left(-\beta \delta \tau T_{\mathrm{a}} \eta H_{\mathrm{c}}\right)\right], $ | (24) |
式(24)中:Fs表示筛选因子;Rr表示发射脉冲重复率;β表示每一脉冲的平均光子数;δ为退极化信道传输因子,可表示为δ=10-0.1Lattθ,其中θ表示地面到卫星的天顶角;τ表示单个光子捕获率;Ta表示系统装置的传输率;Hc表示测量因子。信道误码率部分所需各参数取值情况,以BB84协议为参考[21],如表 3所示。
|
|
表 3 信道误码率的参数 Table 3 Parameters of channel bit error rate |
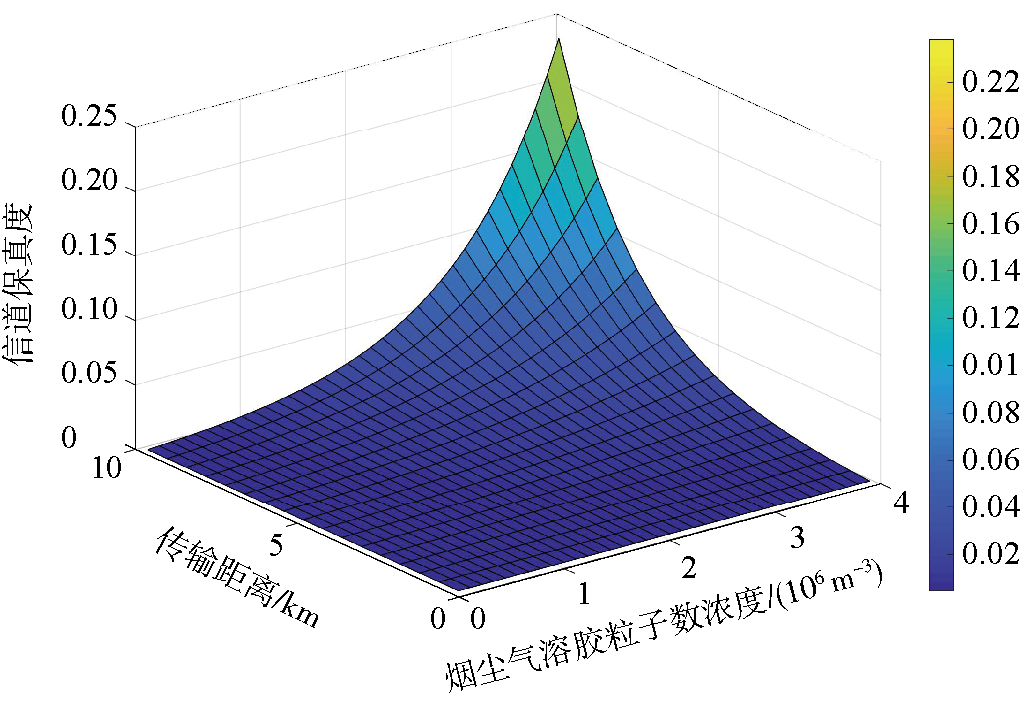
忽略大气中除烟尘气溶胶粒子外其他粒子的影响,星地量子通信链路系统误码率与传输距离、烟尘粒子气溶胶浓度的关系如图 4所示。受烟尘气溶胶粒子影响,当传输距离一定时,随着烟尘粒子数浓度的增加,烟尘粒子与更多的光量子互相影响,偏振逐渐明显,误码率逐渐变大;当烟尘粒子数浓度一定时,随着传输距离的增加,相互作用的光量子随之增加,误码率也会变大。当传输距离超过4.2 km且粒子数浓度大于2.1×106 m-3时,误码率变化较为明显,当传输距离d=9.6 km且n0=3.9×106 m-3时,误码率达到最大值0.237 9;传输距离为9 km,粒子数浓度由2.1×106 m-3增加至3.2×106 m-3时,误码率由0.032 6增加到0.096 0;传输距离为3 km,粒子数浓度由2.1×106 m-3增加至3.2×106 m-3时,误码率由0.008 7增加到0.012 2。因此,传输距离和烟尘气溶胶粒子数浓度越大,对误码率的影响越明显。
|
图 4 烟尘气溶胶粒子数浓度、传输距离与信道误码率(色阶)之间的关系 Fig.4 Relationship between the number concentration of soot aerosol particles/transmission distance and channel bit error rate (color scale) |
本文研究烟尘气溶胶对星地之间量子通信性能的影响,根据烟尘气溶胶的尺寸分布参数和复折射率计算出烟尘气溶胶粒子的消光系数,分析烟尘气溶胶粒子在不同数浓度和传输距离下对链路衰减的影响。针对幅值阻尼信道,分别对烟尘气溶胶粒子数浓度、传输距离与信道容量、信道保真度和信道误码率三者间的关系进行仿真分析。仿真实验结果表明,当传输距离一定时,随着烟尘气溶胶粒子数浓度的增加,幅值阻尼信道容量和信道保真度呈下降趋势,链路衰减和信道误码率呈现不同程度的上升趋势。当传输距离为3 km,烟尘气溶胶粒子数浓度由2.1×106 m-3增加到3.2×106 m-3时,链路衰减由0.30 dB增加到0.46 dB,误码率由0.008 7增加到0.012 2。当粒子数浓度n0=2.7×106 m-3,传输距离由d=3 km增加至d=9 km时,保真度由0.98减小为0.83。因此,本文提出的烟尘粒子对量子通信时各项性能产生的影响,可作为依据提供理论参考。可根据具体情况对各项参数进行适当调整,保证量子信号的正常传输。
| [1] |
吴冰冰, 赖俊森, 汤瑞, 等. 光网络安全现状与量子加密应用前景分析[J]. 电信网技术, 2015(10): 34-38. |
| [2] |
张军, 彭承志, 包小辉, 等. 量子密码实验新进展: 13 km自由空间纠缠光子分发: 朝向基于人造卫星的全球化量子通信[J]. 物理, 2005, 34(10): 701-702. |
| [3] |
徐兵杰, 刘文林, 毛钧庆, 等. 量子通信技术发展现状及面临的问题研究[J]. 通信技术, 2014, 47(5): 463-468. |
| [4] |
彭承志, 潘建伟. 量子科学实验卫星: "墨子号"[J]. 中国科学院院刊, 2016, 31(9): 1096-1104. |
| [5] |
YIN J, LI Y H, LIAO S K, et al. Entanglement-based secure quantum cryptography over 1, 120 kilometres[J]. Nature, 2020, 582(7813): 501-505. DOI:10.1038/s41586-020-2401-y |
| [6] |
张秀再, 刘邦宇, 徐茜. 海洋矿物质颗粒对水下量子通信信道性能的影响[J]. 光学学报, 2021, 41(19): 216-222. |
| [7] |
聂敏, 张帆, 杨光, 等. 不同海面风速对量子卫星星舰通信性能的影响[J]. 物理学报, 2021, 70(4): 97-102. |
| [8] |
邓丛蕊. 中国大气气溶胶中生物质燃烧的源追踪及灰霾的形成机制[D]. 上海: 复旦大学, 2011.
|
| [9] |
黄朝军. 烟尘和雾霾气溶胶凝聚粒子光散射及传输特性研究[D]. 西安: 西安电子科技大学, 2018.
|
| [10] |
赵文娟. 大气气溶胶对激光的衰减特性研究[D]. 西安: 西安电子科技大学, 2014.
|
| [11] |
VON SAVIGNY C, PETELINA S V, KARLSSON B, et al. Vertical variation of NLC particle sizes retrieved from Odin/OSIRIS limb scattering observations[J]. Geophys Res Lett, 2005, 32(7): L07806. |
| [12] |
孙琦云, 徐军, 高旸, 等. 可见光在不同类型气溶胶中的传输特性[J]. 激光与光电子学进展, 2018, 55(11): 80-85. |
| [13] |
JOHNSON N D. Fundamentals of atmospheric radiation[J]. Am J Phys, 2007, 75(7): 671-672. |
| [14] |
鲁先洋. 典型区域大气气溶胶参数特性分析及其测量方法研究[D]. 合肥: 中国科学技术大学, 2017.
|
| [15] |
张合勇, 赵卫疆, 任德明, 等. 球形粒子Mie散射参量的Matlab改进算法[J]. 光散射学报, 2008, 20(2): 102-110. |
| [16] |
LIOU K N. An introduction to atmospheric radiation[M]. 2nd ed. Amsterdam: Academic Press, 2002.
|
| [17] |
LEVONI C, CERVINO M, GUZZI R, et al. Atmospheric aerosol optical properties: a database of radiative characteristics for different components and classes[J]. Appl Opt, 1997, 36(30): 8031-8041. |
| [18] |
尹浩, 韩阳. 量子通信原理与技术[M]. 北京: 电子工业出版社, 2013: 76-83.
|
| [19] |
阎毅. 自由空间量子通信若干问题研究[D]. 西安: 西安电子科技大学, 2009.
|
| [20] |
张光宇, 于思源, 马晶, 等. 背景光对星地量子密钥分配量子误码率的影响[J]. 光电工程, 2007, 34(2): 126-129. |
| [21] |
刘邦宇, 张秀再, 徐茜. 煤烟凝聚粒子对量子卫星通信性能的影响[J]. 光学学报, 2020, 40(3): 175-182. |
 2023, Vol. 43
2023, Vol. 43


