2. 山东省气象服务中心,山东 济南 250031;
3. 佛罗里达州立大学,美国 佛罗里达州 32306
2. Shandong Meteorological Service Center, Jinan 250031, China;
3. Florida State University, Florida 32306, USA
2022年,山东高速公路通车里程突破7 600 km,到2025年,全省高速公路及在建里程将达到10 000 km,基本实现“县县双高速”。恶劣天气会对高速道路交通安全产生严重影响,交通安全指挥、应急处置等气象服务需求点多、线长、面广。2021年以来,公安部交管局联合交通运输部公路局、中国气象局减灾司在山东开展“一路三方”交通应急联动处置试点工作和恶劣天气高影响路段优化提升气象保障工作,其中道路结冰监测预警是交通气象应急联动处置和气象服务保障中的重点难点。青岛—兰州高速公路,即G22青兰高速,是中国国家高速公路网编号的东西方向主干线之一;青岛胶州湾大桥是国家高速公路G22青兰高速的起点段,是目前中国北方最长的跨海大桥,是山东高速公路网中的重要组成部分。因此,开展环胶州湾高速路面温度预报研究对实现山东高速公路安全和畅通运行有重要意义。
有研究表明,道路结冰的先决条件是路面温度低于0 ℃[1-3],因此路面温度是预报道路结冰的一个重要参数。美国和欧洲的一些国家在路面温度预报方法研究方面起步较早,已经具备完善的路面温度监测预报技术[4-5]。加拿大开发的路面温度预报模型METRo(Model of the Environment and Temperature of Roads)结合观测和预报数据,能够实现对路面温度的长时间预报[6]。Handler等[7]利用随机森林方法建立网格化的路面低温概率预报模型,该方法可以把物理模式不易计算的车流量、道路组成以及周边建筑和地形阴影的影响考虑在内,统计评估显示预测效果较好。近年来,我国高速公路交通气象观测站的布设也已进入高速发展阶段,北京、河北、安徽和江苏等省都相继开展路面温度监测预警与预报技术研究[8-11]。曲晓黎等[12]开展京石高速路面温度特征及预报模型研究,预报误差在2 ℃以内的站点占80%。舒斯等[13]统计分析湖北73个含有路面温度观测的交通气象观测站,得出路面温度达到0 ℃时的临界气温,进而通过概率模型计算得到结冰起始拐点,指导高速公路及时采取消冰措施。闫昕旸等[14]、田华等[15]和朱承瑛等[16]应用逐步回归、地表热量平衡方程以及机器学习等方法建立了山区和沪宁高速最低路面温度预报模型,预报结果与实况误差较小,具有实际指导应用意义。袁成松等[17]、刘梅等[18]、李蕊等[19]和史达伟等[20]采用WRF模式、支持向量机和C4.5决策树算法对沪宁高速及南京、湖北部分地区的路面温度进行预测分析,建立了路面高温及低温预报模型,对交通气象业务有重要的应用价值。李兰兰等[21]利用泰安交通气象观测站逐时观测资料建立了分季节路面温度预报模型,最高准确率出现在冬季,达到78.8%。另外,根据山东高速公安交警路上巡查记录,路面结冰的发生与路段地理地貌有很大关系,水体附近、桥梁、隧道口背阴处是路面结冰高发区。由此可见,利用交通气象观测站观测资料对路面温度的预报取得了很好的效果,但是路面低温预报模型的建立有很强的地域性特点,而关于山东沿海地区的高速路面低温研究还相当缺乏。因此本文利用山东环胶州湾高速交通气象站观测资料,通过分析路面低温发生的时空变化特征,运用支持向量机(support vector machine,SVM)和多元线性回归(multiple linear regression)方法构建环胶州湾高速路面低温预报模型,并比较两种模型的预报效果,择优应用。
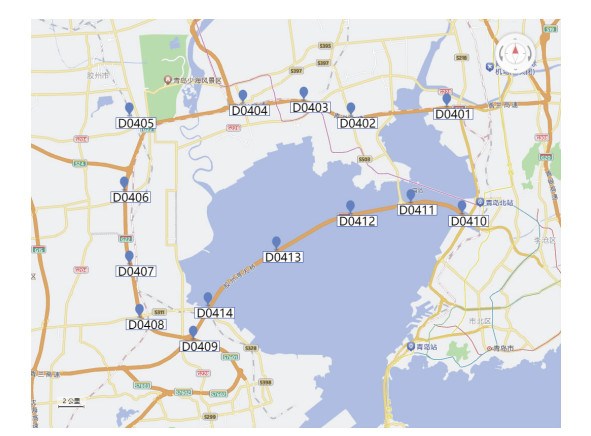
1 资料和方法研究区域(图 1)为青岛南部胶州湾附近,地处山东半岛南部,濒临黄海,受海洋和陆地气候共同影响,冬季温度较低,冬、春季出现大风的频率较高[22-23]。研究数据来自布设在G22青兰高速起始段及胶州湾大桥的14个环胶州湾交通气象观测站2015—2021年共7 a冬季(12月—次年2月)气温、路面温度、相对湿度、风向和风速等逐5 min的监测资料。本文中对监测资料偏差和缺漏数据进行必要的剔除与订正。另外,为了保证路面低温预报检验的独立性,后文中第2节和第3节统计分析和建模中采用2015—2020年6 a冬季数据;第4节模型检验中采用2021年1 a冬季数据。
|
图 1 G22青兰高速起始段和胶州湾大桥交通气象观测站点位置及微环境 Fig.1 Location and microenvironment of traffic weather monitoring stations at the beginning section of G22 Qinglan Expressway and Jiaozhou Bay Bridge |
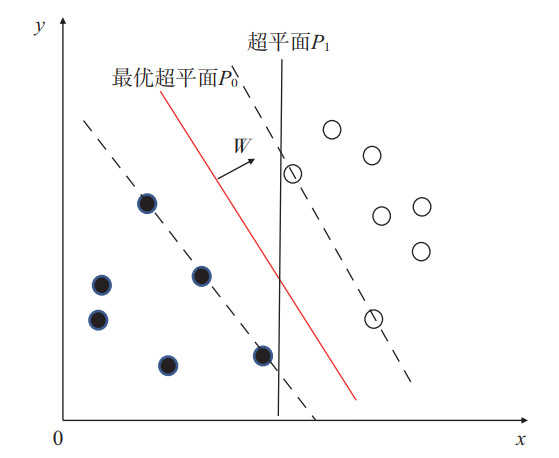
文中主要采用支持向量机(SVM)方法对路面低温进行预报,并与多元线性回归预报结果进行对比分析。SVM方法是利用核函数将自变量投射到高维空间,并利用二次规划解出可以分隔两类事件样本点的超平面,即求解支持向量,进而根据自变量在高维空间相对超平面的位置来判断分类,是一种有坚实理论基础的小样本学习方法。与传统的神经网络学习方法基于经验风险最小化(以训练误差最小化为优化目标)准则不同,SVM方法实现了结构风险最小化原理(以训练误差作为优化问题的约束条件,以置信范围最小化为优化目标)[24]。SVM方法中误差惩罚参数C是对结构风险和经验风险的折中,C越大越趋向于对训练集全分对的情况,这样会出现训练集测试时准确率很高,但泛化能力弱;C值小,容错能力增强,泛化能力较强[25]。如图 2所示,经过参数的调优,SVM学习结果是可以按照结构风险最小化原理的要求,从很多超平面P1中得到最优的超平面P0,既能将两类样本正确分开,又能使分类间隔最大,使得SVM方法的分类性能和泛化能力要好于传统的分类方法[26]。由于高斯核函数(又称径向基函数,radial basis function,RBF)具有较强的非线性映射能力,因此本文采用RBF作为核函数,其公式如下:
| $ K\left(x, x_i\right)=\exp \left(-\gamma \times\left\|x-x_i\right\|^2\right), $ |
|
图 2 支持向量机分类超平面示意图 Fig.2 Diagram of SVM classification hyperplane W—超平面的法向量;实心点和空心点—两类样本。 |
其中:x、xi为样本;K(x, xi)表示两个样本之间的关系;γ为核函数的宽度,核函数参数γ决定了样本空间至特征空间的一种映射关系。因此,需要根据实际应用对误差惩罚参数C和核函数γ进行优化,以保证模型的最佳预测效果[27]。
多元线性回归是最常用的统计分析方法,主要根据最小二乘法原理,由历史数据统计得到多个自变量与因变量之间线性的经验关系。
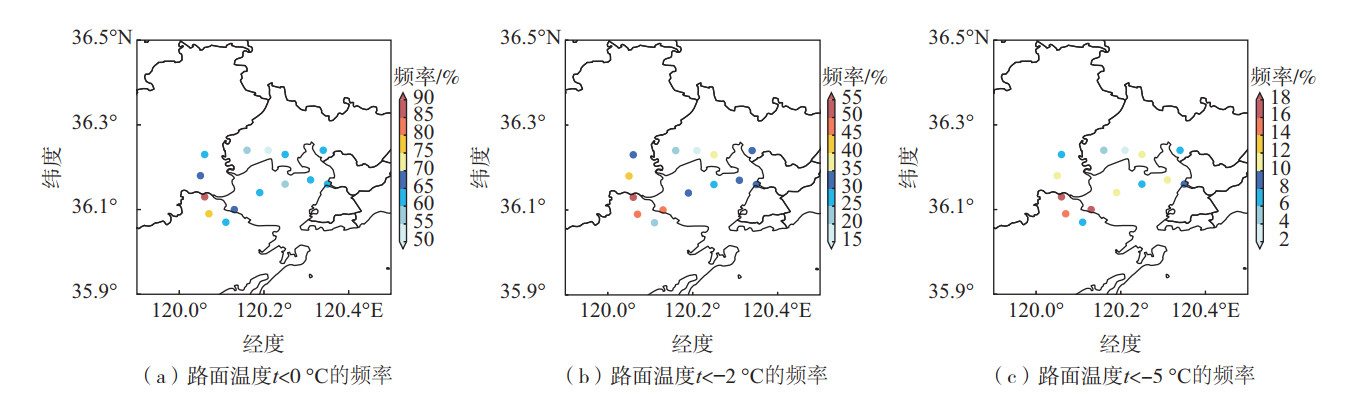
2 环胶州湾高速路面低温时间特征及影响因子分析 2.1 路面低温出现频率当统计时段内日最低路面温度低于0 ℃记为出现1次路面低温;依此计算各个站点统计时段内路面低温总次数,除以统计时段总日数,则得到各个站点路面温度低于0 ℃的平均频率。同样求出最低路面温度低于-2 ℃和低于-5 ℃的频率。
由图 3来看,研究区域内0 ℃以下的路面低温出现频率整体较高,说明环胶州湾冬季路面结冰风险普遍偏高。不同强度路面低温空间分布具有一定的相似规律,路面低温频率呈现“西南高东北低”的特点。14个站路面温度低于0 ℃的频率最小值为46.65%,该值出现在胶州湾北侧的D0403站;低于0 ℃的频率最大值达到85.50%,该值出现在胶州湾西侧的D0407站。14个站路面温度的平均值达到63.50%。14个站路面温度低于-2 ℃频率和低于-5 ℃频率最小值也都出现在D0403站,分别为17.84%和3.90%,最大值也都出现在D0407站,分别为59.67%和21.93%。
|
图 3 14个站点不同强度路面低温频率 Fig.3 Frequencies of subfreezing road temperature (t < 0 ℃, t < -2 ℃, t < -5 ℃) at 14 stations |
特征选择是机器学习过程中重要的一步,关乎最终模型性能的好坏,而且路面温度与时间变化有很大关系,所以建模之前对每个站的路面温度及低温发生的时间变化特征进行分析讨论,选择最优的自变量与因变量。首先,计算环胶州湾高速各站平均逐时最低气温和逐时最低路面温度(后文简称“最低气温”和“最低路面温度”);其次,计算各时次最低路面温度低于0 ℃的出现频率及最低路面温度为一天中最低值的频率。
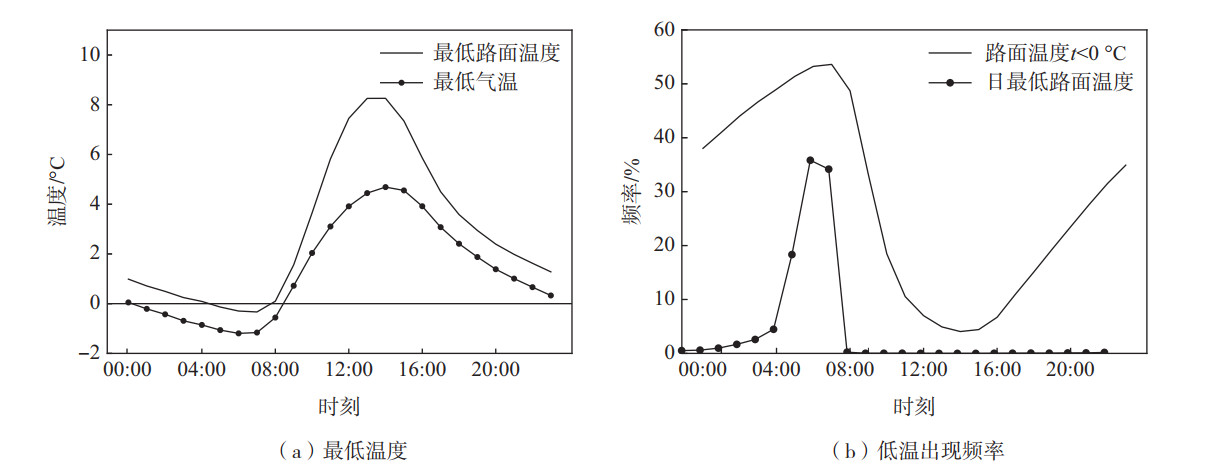
由图 4a可以看出,最低路面温度和最低气温日变化趋势基本一致,全天各时次最低路面温度均高于最低气温,最低路面温度最大值出现在13:00,早于最低气温1 h,并且二者差值在高值区(12:00—15:00)较大,最大差值达到3.81 ℃;最低路面温度和最低气温最小值都出现在07:00,都低于0 ℃,且差值不大。由图 4b来看,日最低路面温度出现的时间段相对集中,出现在06:00—08:00的频率接近90%;最低路面温度降到0 ℃以下的频率最小值4.05%出现在14:00,18:00之后开始明显变大,最大值53.60%出现在07:00,变化起伏较大,且与最低气温的日变化趋势相反。冬季日落时间在18:00之前,与降到0 ℃以下的频率增大时间一致,由此可见太阳辐射对环胶州湾高速路面温度有重要影响。为了保证预警的时效性,并且考虑夜间路面结冰对道路安全的重要影响,结合最低路面温度时间分布特征,最终,利用14:00—18:00的气象变量建立模型预报18:00—次日13:00(后文简称“夜间到次日”)最低路面温度发生情况。
|
图 4 最低温度及低温出现频率日变化 Fig.4 Diurnal variation of the minimum temperature and frequency of low temperature |
SVM是二分类模型,因此使用夜间路面温度是或否达到0 ℃以下作为因变量,多元线性回归模型可使用夜间到次日最低路面温度作为因变量。
在选择模型的自变量时,自变量与因变量的物理关系和统计学上的关联性都需要考虑,因此对最低路面温度与气象要素的相关性展开分析。表 1给出气温、路面温度等6个气象要素与夜间到次日最低路面温度的相关关系以及显著性水平检验结果。计算结果表明14:00气温、14:00路面温度和18:00相对湿度与次日最低路面温度相关性较好,相关系数都超过0.4,并且都通过了显著性检验。14:00—18:00的变温反映了温度的下降程度,温度下降速度越快越容易出现路面低温,相关系数结果表明,变温与夜间到次日最低路面温度为正相关,但是相关系数较小,相关性较弱。而18:00风速与夜间到次日最低路面温度呈现负相关,即风速越大出现路面低温的可能性越小。
|
|
表 1 6个气象要素与夜间到次日最低路面温度的相关系数 Table 1 Correlation coefficients between 6 meteorological variables and the minimum road temperature from 18:00 to 13:00 the next day |
相关系数仅反映两个变量自身均值起伏变化的一致程度,鉴于SVM方法的分类特性,还需要讨论根据夜间是否出现低温所区分的两组自变量之间是否具有显著差异,只有当两组自变量存在差异时,才有可能反过来对是否出现低温进行预报。首先将6组自变量分别按夜间是否出现低温各分为两组,选取其中4个变量的两组概率密度(图 5)进行对比举例说明。由相应结果可见,气温、路面温度等相关系数较高的要素分组概率密度存在显著差异,即通过这些变量可以对夜间是否出现低温进行一定程度的区分,而相关系数为负的风速两组差异表现为不显著。在建立模型时,应综合上述相关性分析和差异检验的结果来选择自变量。
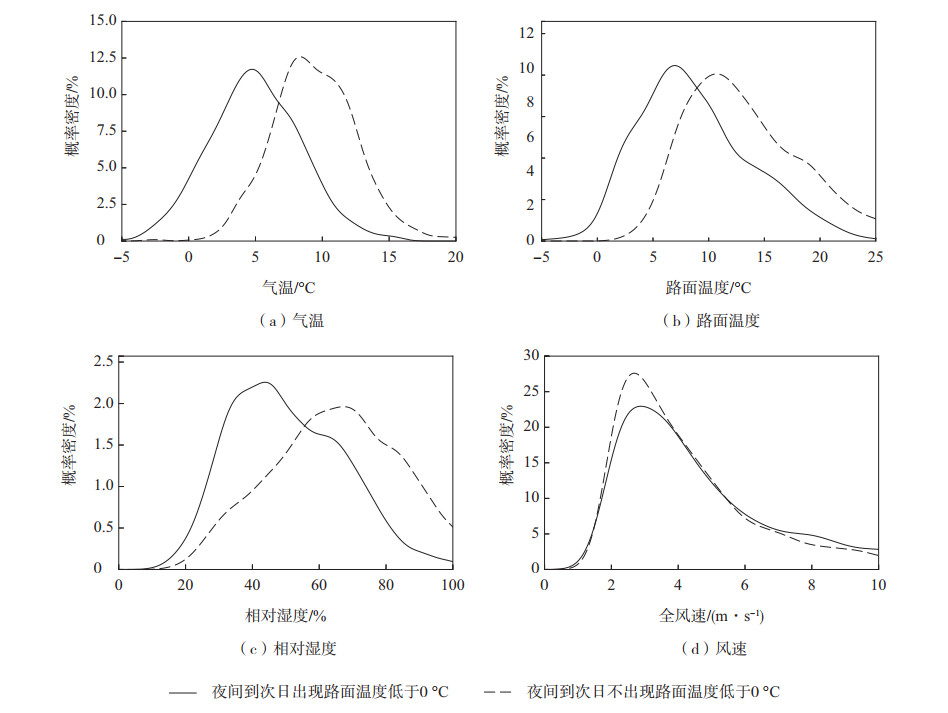
|
图 5 夜间到次日出现及不出现路面温度低于0 ℃情况下的部分变量概率密度分布 Fig.5 Probability density of meteorological variables with or without subfreezing road temperature occurring from 18:00 to 13:00 the next day |
按照相关性大小设计了4种不同的自变量组合(表 2)。组合A包含两种温度变量白天的温度数值,组合B包含两种温度变量与相关性较大的相对湿度,组合C包含所有相关性为正的变量,组合D包含全部6个变量,这样既可以对比出非温度类变量、变温等因素对预报效果的影响,也可以讨论自变量与因变量的相关性对预报效果的影响。
|
|
表 2 自变量组合方案 Table 2 Combination schemes of independent variables |
在环胶州湾14个站2015—2020年冬季数据中筛选出6 720组有效样本。为了避免各个因子之间量级差异,首先,对自变量进行归一化处理;其次,由于SVM分类性能受核函数及参数影响较大[28-29],因此选择交叉验证与网格搜索法进行参数选择优化。
交叉验证是将训练样本集均分为K组,称为K折,每次用K-1折样本为训练数据,用另一折数据测试,这样重复K次,一般折数越多,越精确,但是计算的时间会相应增加。网格搜索法是在初步设定的参数变化范围内,将惩罚因子C和核函数参数γ放在一个规定的空间内,然后设置变化步长,依据拟定的坐标系划分成等大的网格,针对每组参数进行训练,直到找到最优的(C, γ)参数值。在此次SVM参数优化过程中,采用RBF核函数,设置C和γ的取值范围为[0, 100],交叉验证折数K=5,采用交叉验证网格搜索对所有自变量组合进行参数寻优,当C=32,γ=0.6时,模型准确率最高。
3.3 预报结果对比两种统计预报模型经过参数调优后的拟合率及预报准确率如表 3所示。为与SVM模型进行平行比较,其中多元线性回归方法的拟合率与准确率是将其直接预报的夜间最低路面温度值转换为“t>0 ℃”与“t≤0 ℃”两类,再与实际观测到的类别进行对比。由结果可见,两种预报模型的最高预报准确率均出现在包含白天气温、路面温度、变温以及相关性较大的湿度的C组,并且高于包含所有变量的D组,表明白天的温度和变温对于夜间路面低温发生的预报很重要,而且自变量并非越多越好,在建模时还是应该尽量选择与因变量关联性比较好的自变量。同时结果中也分别给出了夜间路面温度“t>0 ℃”与“t≤0 ℃”时的预报准确率,这是因为我们不仅需要关注某个模型总体的预报准确率,更要关注这个模型错报的部分是漏报还是空报,从风险管理的角度来看,低温发生被漏报带来的危害更大。C组中两种模型的预报准确率都达到了84.00%以上,其中SVM模型总体预报准确率为87.30%、路面温度t≤0 ℃的预报准确率为87.78%,都略高于多元线性回归,因此在环胶州湾高速站点中,经过参数优化的支持向量机模型是更优的预报选择。
|
|
表 3 两种预报模型的拟合率及预报准确率
Table 3 Fitting performance and accuracy of two forecast models |
通过对环胶州湾高速站点路面低温出现时间特征及影响因子分析,利用支持向量机模型,建立了环胶州湾高速路面低温预报模型。为进一步检验模型的预报效果,利用2021年冬季(2021年12月—2022年2月)数据建模,自变量采用表 2中准确率最高的方案C,每个站点测试样本数为90个。因为D0401站、D0410站和D0411站2021年冬季数据缺测,因此在检验中剔除。由11个站点检验结果(表 4)来看,模型整体预报准确率高于80.00%,其中胶州湾西北侧部分站点路面温度t≤0 ℃的预报准确率超过90.00%,说明模型具有一定的实际应用价值和服务意义。
|
|
表 4 11站预报模型独立检验结果
Table 4 Test of independence of the SVM forecast model for 11 stations |
利用环胶州湾(G22青兰高速起始段及胶州湾大桥)的14个高速交通气象观测站2015—2021年共7 a冬季(12月—次年2月)气温、路面温度、相对湿度、风向和风速等逐5 min的监测资料,统计分析了环胶州湾高速路面低温出现频率、出现时间特征以及与气象要素的相关性,基于支持向量机和多元线性回归建立了环胶州湾高速路面低温(路面温度t≤0 ℃)预报模型,并对模型预报效果进行对比检验,得出以下主要结论:
(1) 冬季环胶州湾高速路面结冰风险普遍较高,路面低温的最大频率达到85.50%,空间分布上呈现“西南高东北低”的特点。
(2) 对各站点数据求平均得出,小时最低路面温度和小时最低气温日变化特征基本一致,全天中小时最低路面温度均高于小时最低气温。
(3) 在路面低温与气象要素相关性分析中发现,环胶州湾高速14:00气温、路面温度和18:00相对湿度与夜间到次日最低路面温度呈现正相关关系,且相关性较好,而18:00风速与夜间到次日最低路面温度相关系数为负值。
(4) 两种统计模型最高预报准确率均出现在包含气温、路面温度、相对湿度、空气变温和路面变温的自变量组合中,其中经过参数调优的SVM模型准确率较高,路面温度t≤0 ℃预报准确率达到87.78%,并在独立性检验中得到了验证,对实际预报服务具有指导意义。
最后,本文仅使用交通气象观测站点数据作为模型的输入参数,未考虑天气学变化、天空状况等对路面温度预报的影响,下一步将针对以上不足开展深入研究。
| [1] |
董天翔, 包云轩, 袁成松, 等. 三种统计预报模型在江苏省道路低温预警中的应用[J]. 气象科技, 2018, 46(4): 773-784. DOI:10.19517/j.1671-6345.20170411 |
| [2] |
王可心, 包云轩, 朱承瑛, 等. 随机森林回归法在冬季路面温度预报中的应用[J]. 气象, 2021, 47(1): 82-93. |
| [3] |
邹兰军, 刘姝, 陆勤静. 基于神经网络的路面温度模型与结冰潜势研究[J]. 公路, 2022, 67(10): 409-414. |
| [4] |
KARSISTO V, NURMI P, KANGAS M, et al. Improving road weather model forecasts by adjusting the radiation input[J]. Meteor Apps, 2016, 23(3): 503-513. DOI:10.1002/met.1574 |
| [5] |
MARCHETTI M, KHALIFA A, BUES M. Methodology to forecast road surface temperature with principal components analysis and partial least-square regression: application to an urban configuration[J]. Adv Meteorol, 2015, 1-10. |
| [6] |
CREVIER L P, DELAGE Y. METRo: a new model for road-condition forecasting in Canada[J]. J Appl Meteor, 2001, 40(11): 2026-2037. DOI:10.1175/1520-0450(2001)040<2026:MANMFR>2.0.CO;2 |
| [7] |
HANDLER S L, REEVES H D, MCGOVERN A. Development of a probabilistic subfreezing road temperature nowcast and forecast using machine learning[J]. Wea Forecasting, 2020, 35(5): 1845-1863. DOI:10.1175/WAF-D-19-0159.1 |
| [8] |
曾峰, 蒋勇. 路面实测温度的随机性预估模型研究[J]. 公路, 2016, 61(10): 1-8. |
| [9] |
LIU B, YAN S, YOU H L, et al. Road surface temperature prediction based on gradient extreme learning machine boosting[J]. Comput Ind, 2018, 99: 294-302. DOI:10.1016/j.compind.2018.03.026 |
| [10] |
冯蕾, 王晓峰, 何晓凤, 等. 基于INCA和METRo的江苏省路面高温精细化预报[J]. 应用气象学报, 2017, 28(1): 109-118. |
| [11] |
曲晓黎, 武辉芹, 张彦恒, 等. 京石高速路面温度特征及预报模型[J]. 干旱气象, 2010, 28(3): 352-357. |
| [12] |
曲晓黎, 齐宇超, 尤琦, 等. 基于METRo模型的冬奥高速公路示范站路面温度临近预报方法[J]. 干旱气象, 2020, 38(3): 497-503. |
| [13] |
舒斯, 熊守权, 陈英英, 等. 湖北省高速公路道路结冰预警模型[J]. 气象, 2019, 45(11): 1589-1599. |
| [14] |
闫昕旸, 王小勇, 达选芳, 等. 甘肃高速公路山区段路面温度特征及其预报模型[J]. 干旱气象, 2018, 36(5): 864-872. |
| [15] |
田华, 吴昊, 赵琳娜, 等. 沪宁高速公路路面温度变化特征及统计模型[J]. 应用气象学报, 2009, 20(6): 737-744. |
| [16] |
朱承瑛, 谢志清, 严明良, 等. 高速公路路面温度极值预报模型研究[J]. 气象科学, 2009, 29(5): 645-650. |
| [17] |
袁成松, 严明良, 王秋云, 等. 沪宁高速公路高温预警指标及预报模型的研究[J]. 气象科学, 2012, 32(2): 210-218. |
| [18] |
刘梅, 尹东屏, 王清楼, 等. 南京地区冬季路面结冰天气标准及其预测[J]. 气象科学, 2007, 27(6): 685-690. |
| [19] |
李蕊, 牛生杰, 汪玲玲, 等. 三种下垫面温度对比观测及结冰气象条件分析[J]. 气象, 2011, 37(3): 325-333. |
| [20] |
史达伟, 耿焕同, 吉辰, 等. 基于C4.5决策树算法的道路结冰预报模型构建及应用[J]. 气象科学, 2015, 35(2): 204-209. |
| [21] |
李兰兰, 宋永鹏, 韩国泳. 泰安高速公路路面温度特征及预报模型[J]. 山东气象, 2016, 36(2): 58-63. |
| [22] |
郭丽娜, 马艳, 于慧珍. 青岛沿海地区大风特征及其预警评估[J]. 海洋气象学报, 2022, 42(2): 90-98. |
| [23] |
房云龙, 郑标, 赵铁成, 等. 青岛流亭机场海风特征分析及对飞行的影响[J]. 海洋气象学报, 2018, 38(4): 115-121. |
| [24] |
李元诚, 方廷健, 于尔铿. 短期负荷预测的支持向量机方法研究[J]. 中国电机工程学报, 2003, 23(6): 55-59. |
| [25] |
史朝印, 吕震宙, 李璐祎, 等. 结构失效概率计算的ASVR-MCS方法[J]. 机械工程学报, 2019, 55(24): 260-268. |
| [26] |
祁亨年. 支持向量机及其应用研究综述[J]. 计算机工程, 2004, 30(10): 6-9. |
| [27] |
焦业峰, 王艳, 纪志成. 基于BLP-ALO-SVM的风电功率短期预测方法[J]. 系统仿真学报, 2022, 34(12): 2535-2545. |
| [28] |
奉国和. SVM分类核函数及参数选择比较[J]. 计算机工程与应用, 2011, 47(3): 123-124. |
| [29] |
孙志刚, 王国涛, 高萌萌, 等. 参数优化支持向量机的密封电子设备多余物定位方法研究[J]. 电子测量与仪器学报, 2021, 35(8): 162-174. |
 2023, Vol. 43
2023, Vol. 43


