2. 中国电子科技集团第二十八研究所,江苏 南京 210046
2. The 28th Research Institute of China Electronics Technology Group Corporation, Nanjing 210046, China
台风是发生在热带洋面上的一种强烈的暖性气旋性风暴, 是威胁船舶安全航行的最严重的灾害性天气系统之一[1-2]。台风中的强风通常伴随着巨大的海浪,对船舶的稳定性、航行性能以及船员生命安全构成直接威胁。强风可以引发船舶的倾覆、翻沉或漂流,而巨浪可能导致船体受损或货物滑移。此外,强风和巨浪还会影响船舶的操纵,增加碰撞、搁浅和港口操作事故的风险[3-6]。随着计算机和全球海洋气象预报能力的不断发展,船舶气象导航服务得到越来越多的关注。气象导航服务利用综合海洋气象预报、航运信息和船舶相关信息,能够为船舶设计一条经济、绿色和安全的气象航线[7-8]。其中,在船舶计划航线和台风预报路径发生会遇风险时,为船舶提供最佳的避台策略是船舶气象导航服务中的重要内容之一。
近年来,国内外相关学者围绕船舶避台算法开展了诸多研究。刘大刚等[9]构建了基于多源预报数据的热带气旋危险区域。杨多才等[10]通过统计分析中国沿海台风路径的规律,针对无动力或锚地抛锚的船舶提出了对应的避台方法。于丰武[11]区分了避台锚地和普通避风锚地,提出了避台中船舶锚泊地点的选择方法。张进峰等[12]同样针对中国近海航线,考虑台风引起的恶劣海况下的船舶速度损失,利用动态规划算法规划航时最短的避台航线。Wu等[13]改进了传统的扇形避台方法,基于数值预报模式和时变海况下的船舶速度变化和风险识别,提出了一种最短航时的避台算法。王军等[14]改进A星算法与人工势场法,分别应用于全局规划与局部规划中,该方法在船舶即将遭受台风影响且台风预报存在不确定性情况下,可以设计一条合理的避台路径。Liu等[15]对船舶避台航线的成本进行定量评估和控制,提出了船舶避台航线路线损失和损失矩阵的方法,为最佳避台航线决策过程中的成本分析和控制提供了定量依据。
本文在保障船舶航行安全的基础上,考虑了船舶在不同海况影响下的船舶失速,通过台风路径强度预报数据识别船舶航行风险区域,改进Dijkstra算法中的构图方法和节点探索策略,利用变向与变速相结合的方案求解船舶最短航时避台航线。
1 船舶避台问题建模在进行避台航线求解之前,需要定义船舶避台问题中3个基础的模型:(1)构建船舶避台航线的数学模型,(2)建立船舶在不同海况影响下的船舶航行性能模型,(3)辨识船舶在台风影响下的动态风险域。
1.1 避台模型数学定义船舶避台问题就是在船舶航行安全的条件下,设计一条能够躲避台风,并且在最短航时内到达目的港的航线。一条完整的避台航线由每个转向点的位置和每个航段组成,其中部分转向点是航次信息中的必经点(出发港、中间港和到达港),在避台航线设计中不允许修改。
一条完整的航线如图 1所示,计划航线由K个固定转向点P=(p1, p2, …, pK),pK=(V(lat)K,V(lon)K)和K-1个航段L=((v(w)1,d1),(v(w)2,d2),…,(v(w)K-1,dK-1))组成,其中V(lat)和V(lon)分别表示纬度值和经度值,v(w)表示船舶对水航速,d表示航段距离。在每个台风预报路径更新的t时刻,基于船舶当前位置、计划航线和台风预报路径,计算出船舶未来逐小时的船位,基于台风影响下的船舶航行风险模型,判断是否需要进行船舶避台航线设计,其数学表达式为:
| $ S_t=\sum\limits_{i=t}^T R_i\left(I(\operatorname{ship})_i, I(\mathrm{TC})_i\right) 。$ | (1) |

|
图 1 船舶航线示意图 Fig.1 Ship's route illustration 阴影部分—由深到浅分别表示台风的12级、10级和7级风圈。 |
式(1)中:T表示船舶航行至目的港的预计到达时间;I(ship)i表示在第i时船舶的位置信息;I(TC)i表示台风在第i时的位置、强度以及风圈预报信息;Ri(I(ship)i,I(TC)i)表示第i时船台会遇状态是否有航行风险;St表示在t时刻未来航线上所有逐小时点是否存在航行风险点,其计算方法在1.3节中详细说明。
假设在第K个转向点处需要进行避台航线设计,避台航线最短时间可表示为:
| $ T_{\min }=\min \left(\sum\limits_{i=K}^{K-1} \frac{d_i}{v(\mathrm{~g})_i}\right)_{\circ} $ | (2) |
其中:v(g)i表示船舶的对地航速,其计算方法在1.2节中详细说明。
1.2 船舶失速模型估计船舶对地航速是解决船舶避台问题的基础之一,船舶避台问题中船舶失速主要分为两种。第一种情况是,一旦船舶航经区域未来即将遭遇台风影响,船舶无法安全航行通过该区域时,需要采用自愿改变航速和更改航线结合的方案保障船舶航行安全。考虑到船舶航行的实际情况,船长通常以停车、经济航速或全速的用车习惯进行航行,本文在船舶主动降速的航速组合中,考虑了船舶在停车、经济航速和全速航行时的静水航速作为变速的限制:
| $ V(\mathrm{w})_i=\left[v_{\text {stop }}, v_{\text {eco }}, v_{\text {max }}\right] 。$ | (3) |
式(3)中:V(w)i为避台方案中船舶的第i个航段采用的对水航速;vstop为船舶停车时的航速;veco为船舶的经济航速,经济航速代表船舶每海里燃油消耗量最少;vmax为船舶的全速。不同船舶的经济航速和全速均不同。
第二种情况是,由于风浪流等气象水文要素带来的额外阻力导致的船舶非自愿减速,通过船舶水动力实验可以准确估算船舶在不同海况条件下的速度损失,但是其计算成本高,在远洋气象导航服务中不便应用。Mannarini等[16]通过大量船舶试验数据,利用统计方法,分析了由于波浪效应导致的船舶速度损失模型:
| $ v(\mathrm{~g})_i=v(\mathrm{w})_i-f(\theta) \cdot H_s^2 \text { 。} $ | (4) |
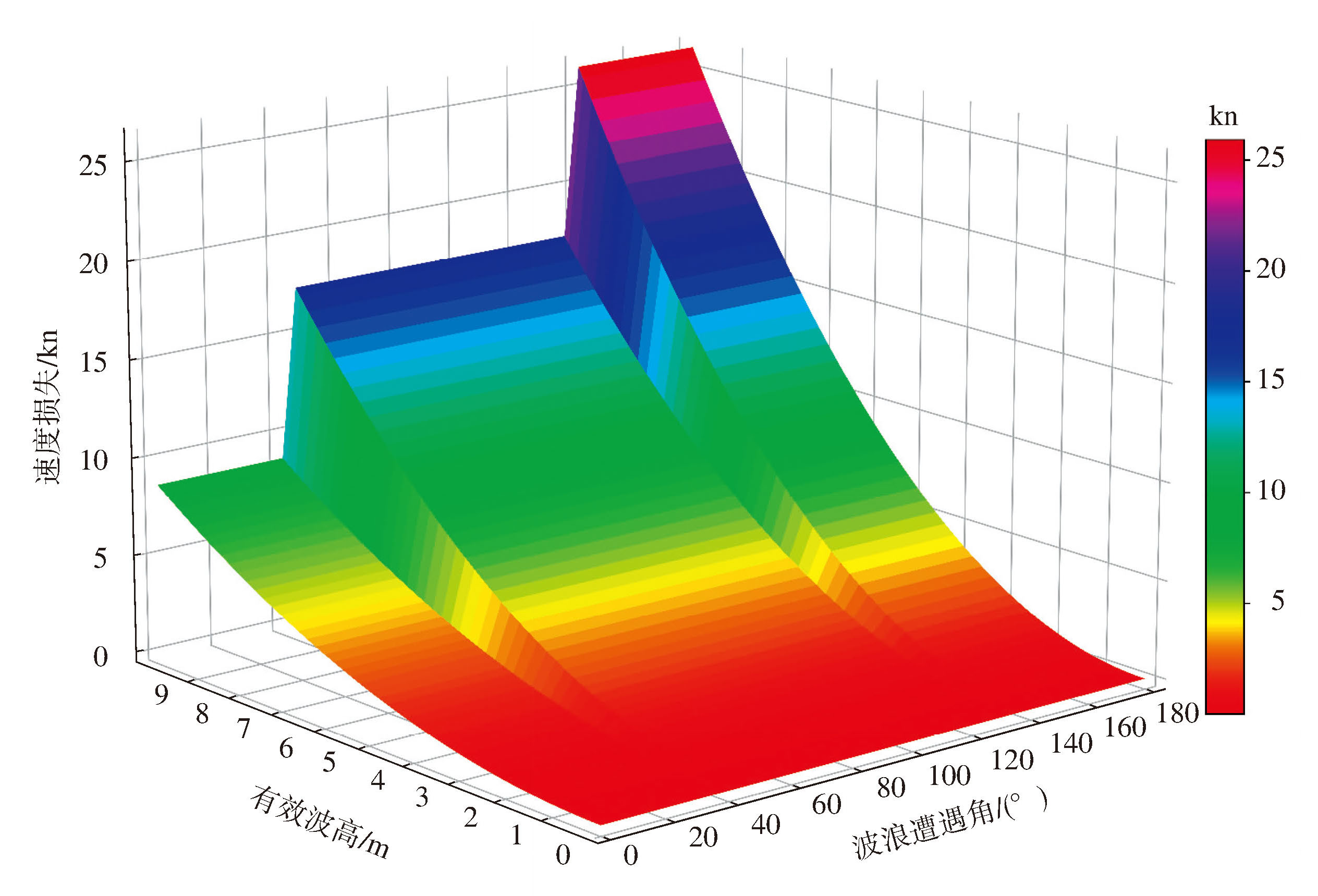
其中:θ是船艏向与波浪的遭遇角度,f(θ)为波浪阻力的惩罚系数,Hs为有效波高。具体系数的取值见表 1,该模型是目前广泛应用的经验模式之一,适用于远洋船舶的失速预测,本文选择该模型作为失速模型,该模型的船舶速度损失如图 2所示。
|
|
表 1 船舶失速模型系数 Table 1 Ship speed loss model's coefficients |
|
图 2 船舶失速模型 Fig.2 Ship speed loss model 色阶—船舶失速。 |
在船舶避台问题中,由于台风周围气压分布的疏密程度不均匀,其强风区的分布也是不均匀的。在北半球,由于台风前进方向的右侧与西太平洋副热带高压相邻,通常在台风的右半圆内风力较强,而在左半圆内风力较弱,南半球则相反[17]。本文利用台风路径的7级风圈半径作为船舶航行的危险半径:
| $ A(\text { risk })_t=f\left(\begin{array}{l} r(\mathrm{NE})_t, r(\mathrm{SE})_t, r(\mathrm{SW})_t, \\ r(\mathrm{NW})_t, d\left(\operatorname{ship}_t, \mathrm{TC}_t\right) \end{array}\right) 。$ | (5) |
其中:A(risk)t表示t时刻推算船位是否驶入危险区域,r(NE)t、r(SE)t、r(SW)t、r(NW)t表示t时刻台风在4个象限的7级风圈半径,d(shipt,TCt)表示t时刻船舶与台风中心的距离。
2 船舶避台航线求解 2.1 Dijkstra算法Dijkstra算法使用类似广度优先搜索的方法解决赋权图的单源最短路径问题, 其优点是在给定一个带权重的图G=(V,E)(V表示图中所有航路点,E表示所有带权重的航段),能计算出一个确定最优的避台航线[18]。Dijkstra算法选择未访问的具有最低距离的节点,并计算从该节点到每个未访问邻居的距离,如果该距离较小,它会更新邻居的距离。通过使用队列(或堆)这种树形数据结构来减少探索的候选节点数量,该算法提高了寻找最优路径的效率[19-20]。
Dijkstra算法可以被看作是贪婪算法之一,算法每一步选择被认为是最优的节点,从而依次从整个图中选择最优路径。该算法在存在负边权重时不适用,在船舶避台问题中,船舶航行时间不包括负值,因此在本研究中可以使用Dijkstra算法求解避台航线。Dijkstra算法的伪代码如表 2所示。其中,G=(V,E)表示一个完整航路图,Queen表示已访问航路点的优先队列,S表示已生成最佳航线的航路点,s和e分别表示起始节点和到达节点。
|
|
表 2 Dijkstra算法伪代码 Table 2 Pseudocode of Dijkstra's algorithm |
利用传统图搜索算法Dijkstra进行避台航线规划时,建立的航路图中每个节点代表地理坐标信息(V(lat)n,V(lon)n),外,以45°为间隔的8方向图搜索策略存在大量无效搜索。在实际避台时需要考虑到船舶变速,本文在计划航线的基础上,面向船舶避台航线规划提出了一种改进的Dijkstra算法。
大圆线航线是地球上两点之间的最短航线,船舶通常沿着球形地球上的大圆线航行,以最小化距离,节省航时和燃油消耗。将计划航线上的固定转向点以大圆航线相连,在该段大圆航线的基础上构建航路图,转向点A与B间的最短弧长为:
| $ \begin{gathered} \cos \mathit{Θ}_{A B}=\sin V(\text { lat })_A \sin V(\text { lat })_B+\cos V(\text { lat })_A \cos V(\text { lat })_B \\ \cos \left(V(\text { lon })_B-V(\text { lon })_A\right) 。\end{gathered} $ | (6) |
大圆航线的初始航向角αs和到达点航向角αf:
| $ \cos \alpha_s=\frac{\sin V(\text { lat })_B-\sin V(\text { lat })_A \cos \mathit{Θ}_{A B}}{\cos V(\text { lat })_A \sin \mathit{Θ}_{A B}}, $ | (7) |
| $ \cos \alpha_f=\frac{\sin V(\text { lat })_B \cos \mathit{Θ}_{A B}-\sin V(\text { lat })_A}{\cos V(\text { lat })_B \sin \mathit{Θ}_{A B}} 。$ | (8) |
大圆航线上任意一点X,其坐标和航向角为:
| $ \begin{gathered} \sin V(\text { lat })_X=\sin V(\text { lat })_A+\cos \left(\mathit{Θ}_{A B} x\right) \\ +\cos \varphi_A \sin \left(\mathit{Θ}_{A B} x\right) \cos \alpha_s, \end{gathered} $ | (9) |
| $ \begin{gathered} \cos \left(V(\text { lon })_X-V(\text { lon })_A\right)=\frac{\cos \left(\mathit{Θ}_{A B} x\right)}{\cos V(\text { lat })_A \cos V(\text { lat })_X} \\ -\tan V(\text { lat })_A \tan V(\text { lat })_X, \end{gathered} $ | (10) |
| $ \cos \alpha_X=\frac{\sin V(\text { lat })_X \cos \left(\mathit{Θ}_{A B} x\right)-\sin V(\text { lat })_A}{\cos \varphi_X \sin \left(\mathit{Θ}_{A B} x\right)} 。$ | (11) |
其中
点Y距离X点δ且XY垂直于大圆航线,Y的经纬度为:
| $ V{({\rm{ lat }})_Y} = V{({\rm{ lat }})_X} - \delta \sin {\alpha _X}{\rm{, }} $ | (12) |
| $ V(\text { lon })_Y=V(\text { lon })_X+\sigma \delta \cos \alpha_X \text { 。} $ | (13) |
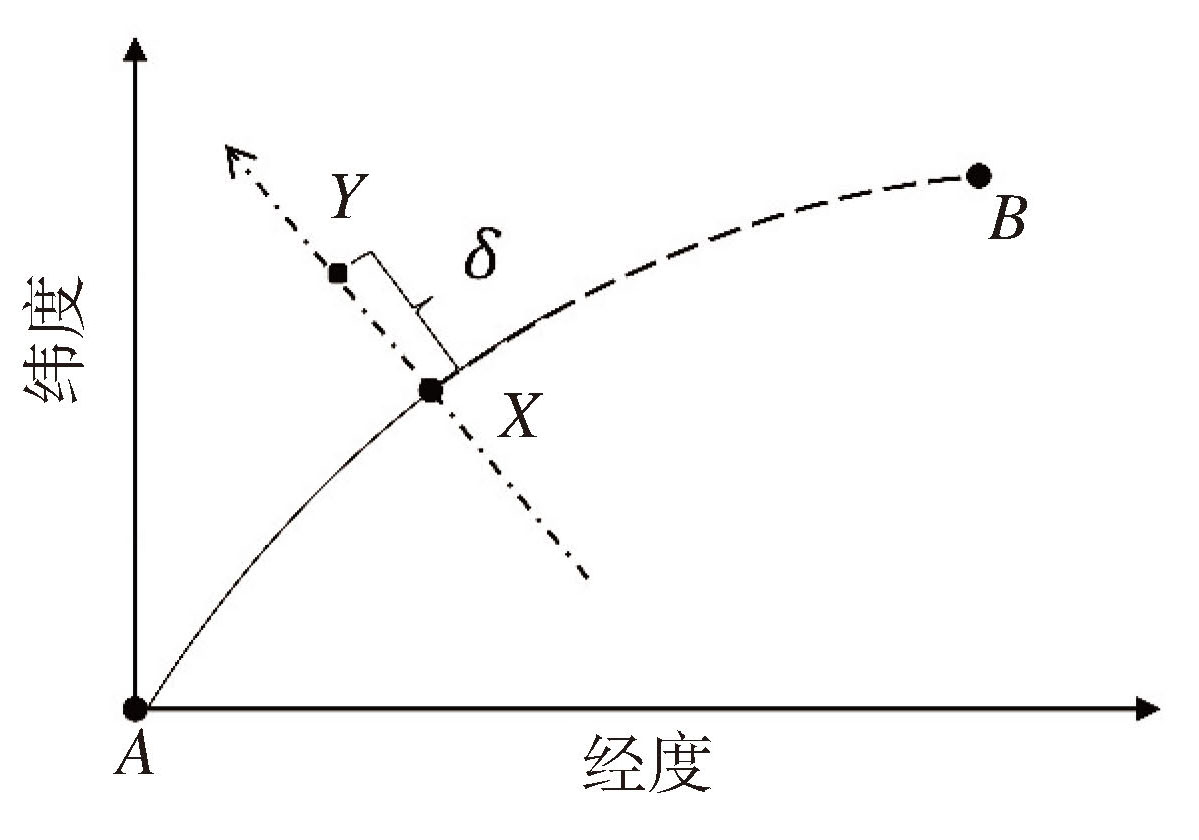
其中σ=1表示向东,σ=-1表示向西,图 3展示了公式(7)—(13)计算航路图中单个节点的经纬度。
|
图 3 航路点计算 Fig.3 Waypoint calculation |
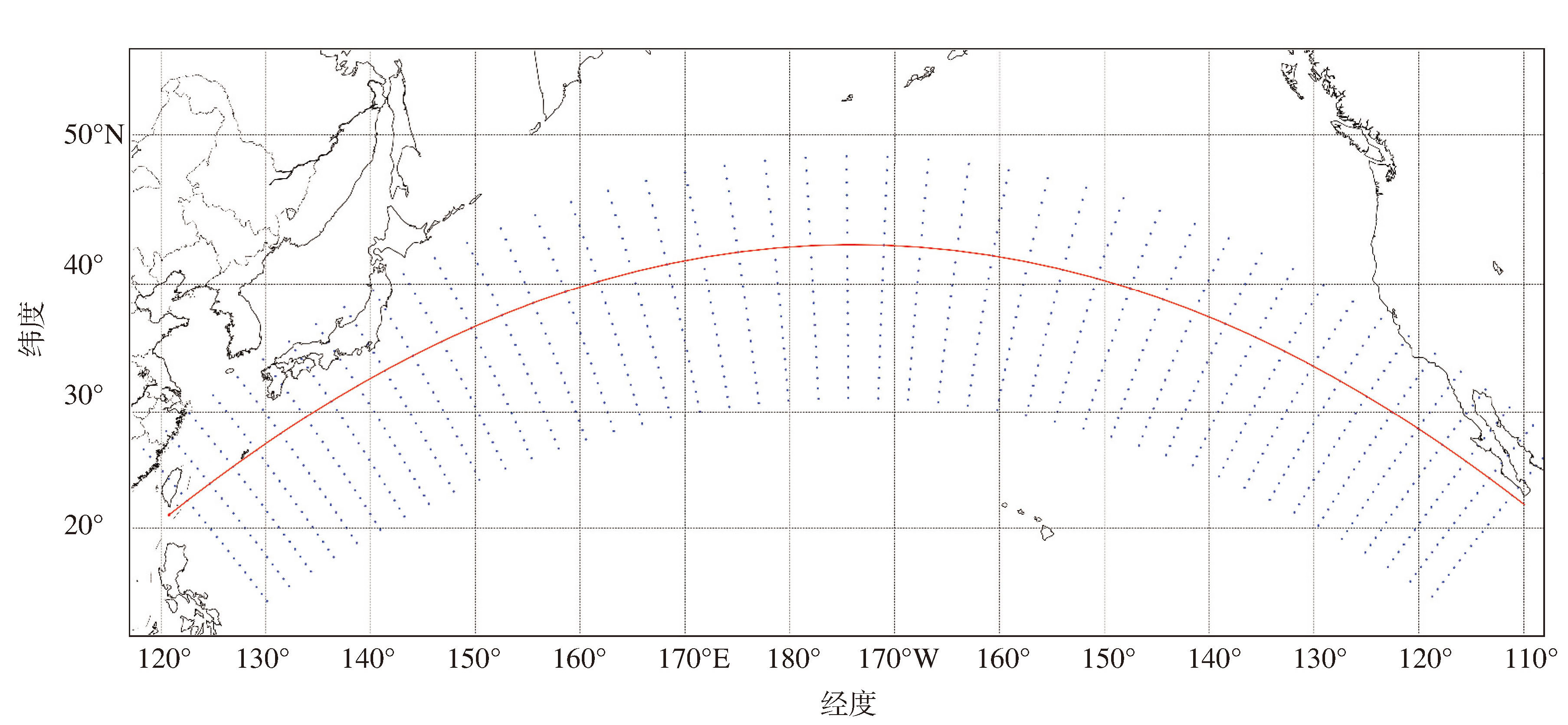
根据公式(7)—(13),在大圆航线上每隔m n mile,在垂直于大圆航线h n mile范围内,每隔δ n mile计算航路点,计算出来的所有航路点如图 4所示。
|
图 4 航路点集合 Fig.4 Waypoint set 红色弧线—大圆航线;蓝色圆点—航路点。 |
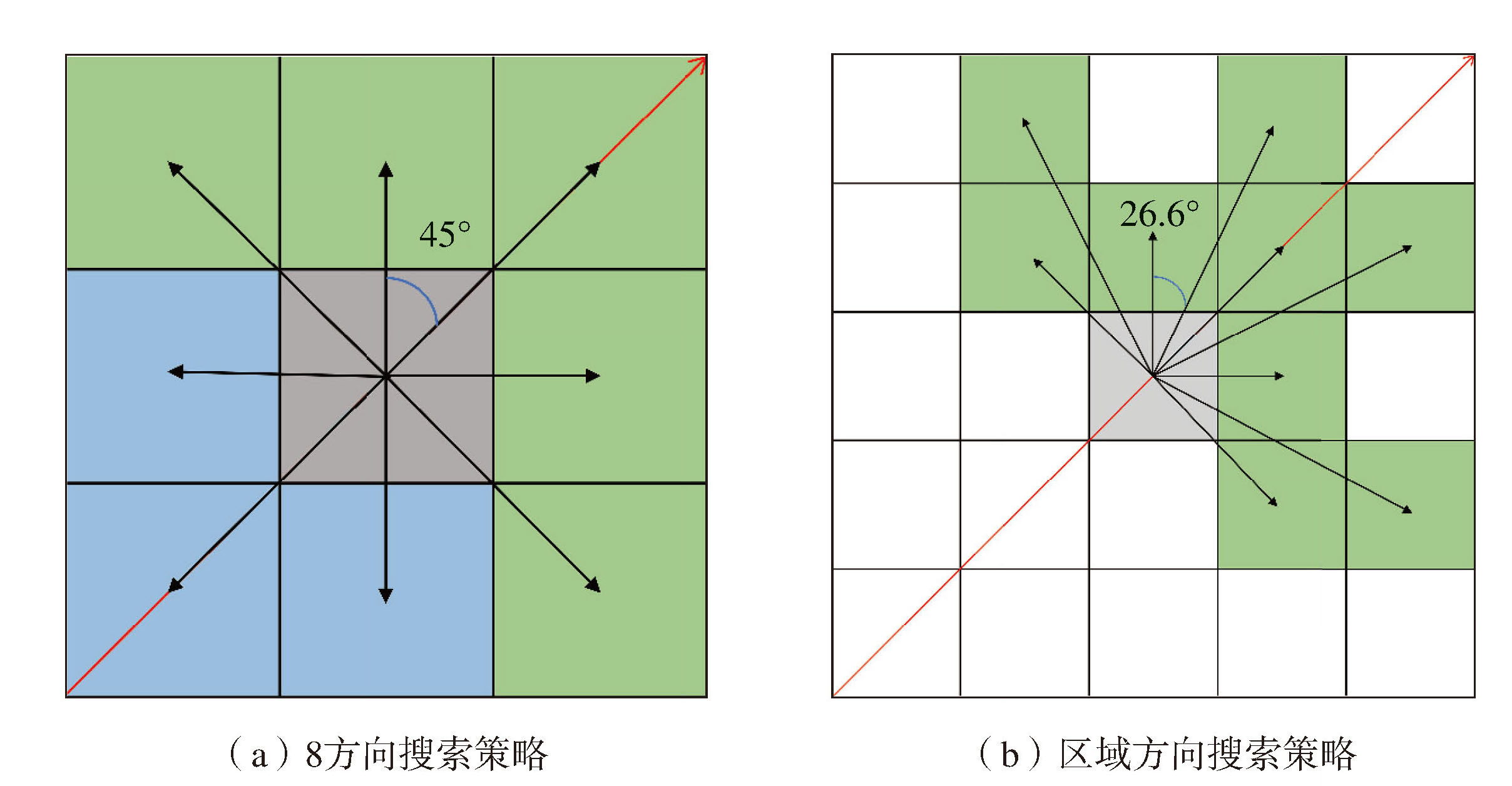
传统图搜索算法Dijkstra的8方向图搜索策略以45°为间隔,无法满足航线适航性的要求[20]。因此,提出了一种区域方向搜索策略,在计划航线的基础上,在船舶航行方向的区域内搜索,图 5为当m=δ时,8方向和区域方向搜索策略的示意图。
|
图 5 8方向和区域方向搜索策略示意图 Fig.5 Schematic of 8-way search method and regional directional search method 灰色区域—船舶当前位置所在网格;红色箭头—船舶计划航线;绿色区域—有效搜索网格;淡蓝色区域—无效搜索网格。 |
区域方向搜索策略能够在每个时间步长内探索更多有效节点,将图 4中的航路点利用区域方向搜索策略进行联通,每条边的权重为节点间的恒向线距离,航路点和所有边组成了一个完整的航路图。当航路图中的边穿过陆地时,则从航路图中删除该条边,最终的航路图如图 6所示。
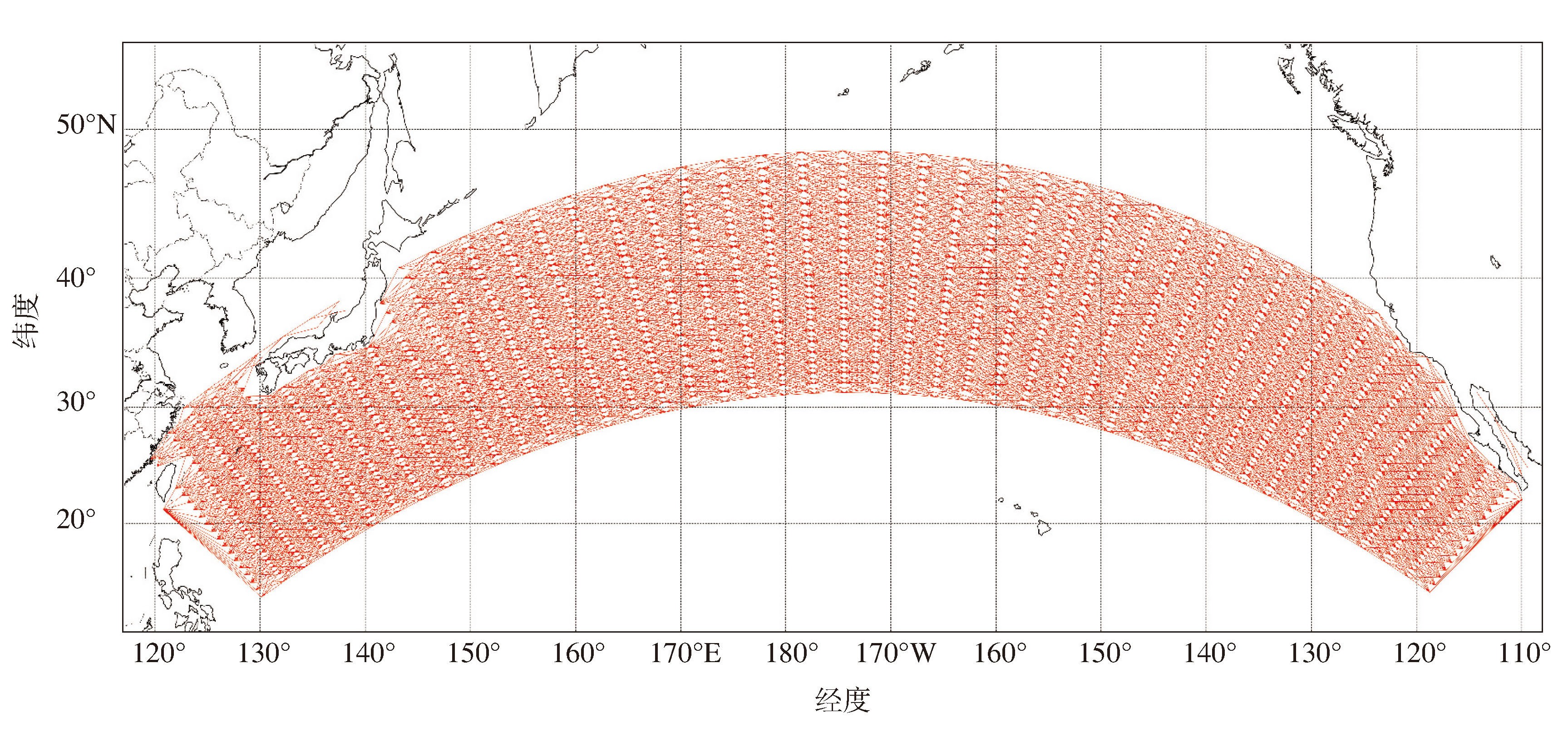
|
图 6 船舶航路图 Fig.6 Ship's route map |
在避台航线设计时,船舶需要进行降速、停车或绕航等措施相结合实现最优避台。本文提出一种新的边权重计算方法,新的权重考虑了船舶在大风浪下的船舶速度损失和船舶航速变化,计算每条边的航行时间et代替距离权重,计算方法如式(14)所示:
| $ e_t=\left\{\begin{array}{ll} \frac{e_d}{e_{v(\mathrm{~g})}}, & A(\text { risk })_t=0 \\ K, & A(\text { risk })_t=1 \end{array}\right. \text { 。} $ | (14) |
式(14)中:ed表示边的恒向线距离,ev(g)表示考虑船舶失速后的船舶对地航速,每条边遍历对水航速集合V(w)i=[vstop, veco, vmax],遍历计算航路图中每个初始节点的对水航速和图搜索方向,选取最快到达目标节点的航行方案,实现船舶变速与变向组合避台,K为值较大的惩罚系数,A(risk)t=0表示在t时刻推算船位未驶入危险区域,A(risk)t=1表示在t时刻推算船位已经驶入危险区域,惩罚函数使得最终规划的避台航线与台风路径保持安全距离。
3 案例分析为验证文中提出的避台航线规划方法的有效性,基于中国气象局气象导航中心的服务船舶COSCO SHIPPING WISDOM在满载状态航行时的数据,以台风“杜苏芮”为例,为了更贴近船舶气象导航实际业务中的应用场景,在实验过程中使用的气象/海洋格点场均为欧洲中期天气预报中心(European Centre for Medium-Range Weather Forecasts,ECMWF)预报场,空间分辨率为0.1°×0.1°,台风路径强度数据为中央气象台的主观预报数据,由于实验过程中的船位推算时间间隔为1 h,故将ECMWF预报场和台风路径强度预报数据插值为1 h间隔,具体实验参数见表 3。
|
|
表 3 实验相关参数设置 Table 3 Setting of experimental parameters |
台风“杜苏芮”于7月21日08:00(北京时,下同)生成,24日20:00加强为超强台风级,转向西北方向移动,经过巴士海峡强度减弱为强台风级,随后进入南海东北部海域再度加强,并于28日09:55登陆福建晋江,达到强台风级。我国沿海航线在遭遇台风“杜苏芮”时,利用本文提出的算法得到的避台航线在航行安全与航时优化方面的效果,起点与终点之间的计划航线作为比较对象。计划航线与避台航线在2023年7月28日11:00的浪高分布见图 7,可以看出:按照计划航线航行时,船舶将在2023年7月28日11:00遭遇6 m以上浪高,距离台风“杜苏芮”中心不足150 n mile。避台航线由于提前变向变速,使得船舶与台风中心始终保持在安全距离范围内,遭遇到的有效波高也始终低于6 m。

|
图 7 计划航线与避台航线 Fig.7 Predefined route and typhoon avoidance route 红色虚线—船舶开航前设定的计划航线;绿色虚线—利用本文算法生成的避台航线;黑色船标—2条航线在2023年7月28日11:00的推算船位。 |
表 4比较了原始航线和避台航线的仿真结果,虽然避台航线在距离上比原始航线多了19 n mile,但是由于避台航线船舶遭遇到的风浪较小,船舶失速与原始航线相比较小,使得避台航线的平均航速高于原始航线,最终节省了2.18 h。图 8展示了原始航线和避台航线在有效波高、船台距离、对地航速和风速的时序比较,由于避台航线所遭遇到的有效波高比原始航线低,船舶速度损失较小,避台航线始终维持在11 kn以上的航行速度。同时,避台航线上的船舶与台风的会遇距离也始终保持安全距离,实现了船舶的最优避台航线规划。
|
|
表 4 航线推算结果 Table 4 Route's calculation results |
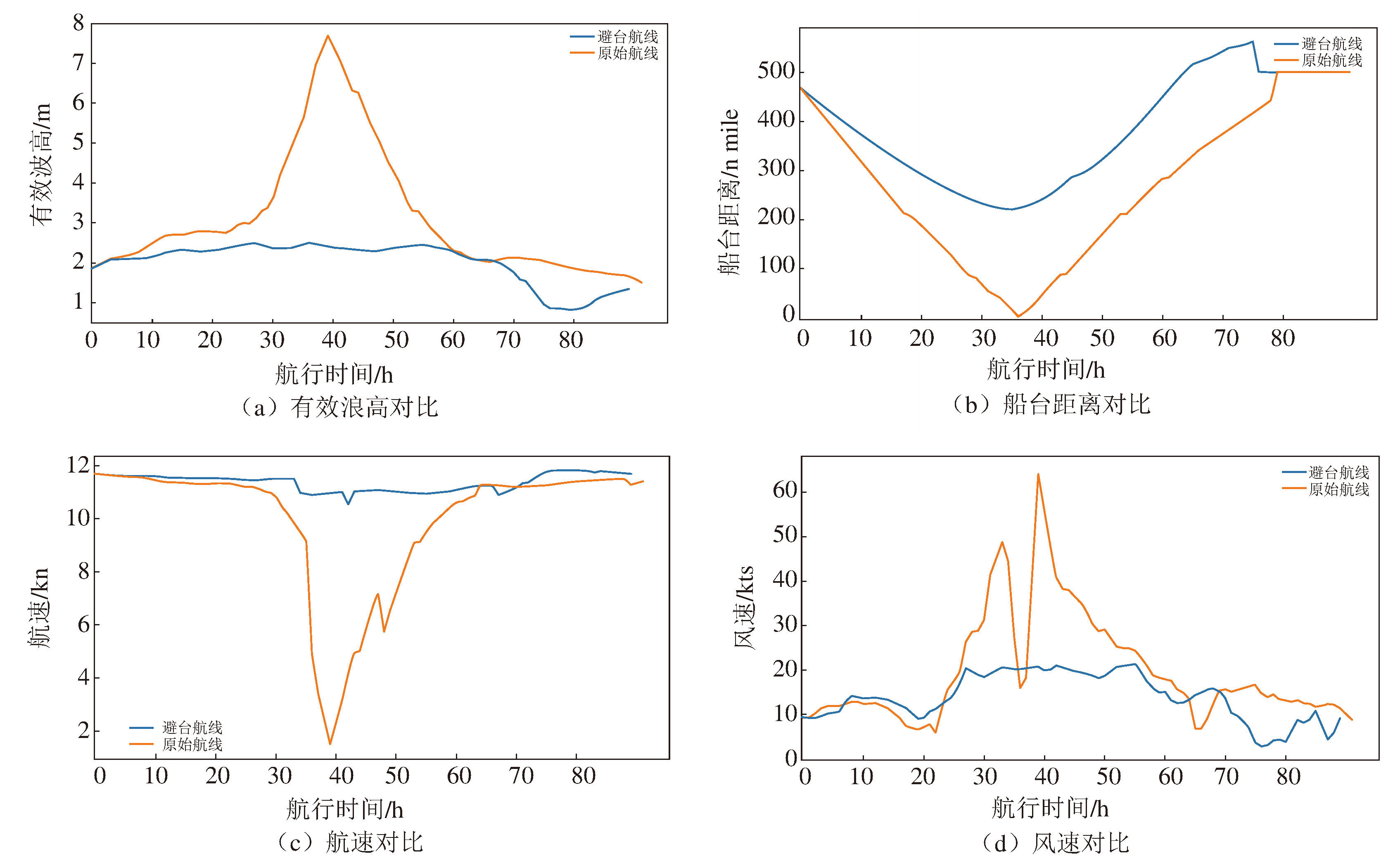
|
图 8 航线信息比较 Fig.8 Route's information comparison |
为解决船舶避台航线优化问题,以最短航时为优化目标,通过改进图搜索策略,引入有限变速集合,基于构建的船舶失速模型进行气象航线推算,以船舶与台风的逐小时会遇距离作为船舶在台风影响下的航行风险约束,提出了一种基于图搜索算法的避台航线规划算法。该算法在保证船舶航行安全的前提下,最小化避台航线的航行时间,最后以台风“杜苏芮”为例,进行船舶避台实验,证明了文中提出的算法通过改变船舶设计航线的航向和变速能够有效避台,优化航行时间。
在避台航线规划中受到台风风圈预报方法的限制,采用了固定船台距离的约束进行避台。在后续工作中,需要结合台风风圈预报数据,航行风险模型,同时也需要考虑洋流、浪高、风速和涌浪的影响。此外,由于研究的是航时最短的避台航线,本研究案例中船舶始终保持了最大对水航速进行航行以最小化航行时间,船舶的变速体现在最小化燃油消耗的避台航线设计中,需要构建航速-燃油消耗模型,以达到最小化燃油的避台航线要求。
| [1] |
王长青. 热带气旋探讨[C]//气象海洋环境与船舶航行安全论文集. 大连: 大连远洋运输有限公司, 2010: 45-49.
|
| [2] |
向纯怡, 高拴柱, 刘达. 2021年西北太平洋和南海台风活动概述[J]. 海洋气象学报, 2022, 42(1): 39-49. |
| [3] |
褚善东. 论台风对船舶航行和停泊安全的影响[J]. 浙江国际海运职业技术学院学报, 2020(2): 5-8. |
| [4] |
李丽芳, 任福民, 刘春霞, 等. 台风大风预报研究回顾[J]. 海洋气象学报, 2022, 42(1): 50-60. |
| [5] |
夏施敏. 台风对沿海船舶的影响及防抗措施研究[J]. 中国水运, 2008(9): 50-51. |
| [6] |
武强, 石磊, 宗锋, 等. 龙口至旅顺海上航线大风实况资料处理方法研究[J]. 海洋气象学报, 2017, 37(3): 102-108. |
| [7] |
王凤武, 郑中义, 吴兆麟. 大风浪船舶安全航行的研究综述[J]. 大连海事大学学报, 2002, 28(4): 60-63. |
| [8] |
张晓川, 崔建辉, 荣雷. 最优气象航线的设计与选择[J]. 天津航海, 2014(1): 4-5. |
| [9] |
刘大刚, 刘正江, 吴兆麟. 基于多源预报的热带气旋危险区域的确定方法[J]. 交通运输工程学报, 2008, 8(2): 80-84. |
| [10] |
杨多才, 艾万政. 中国沿海无动力船舶避台方法研究[J]. 中国水运, 2014, 14(7): 20-21, 29. |
| [11] |
于丰武. 船舶避台锚地选择及优化设计分析[J]. 中国水运, 2013, 13(8): 265-266. |
| [12] |
张进峰, 王晓鸥, 刘永森. 基于动态风浪环境的我国近海船舶避台航线优化[J]. 中国航海, 2016, 39(2): 45-49. |
| [13] |
WU L C, WEN Y Q, PENG S Q, et al. Optimizing the routing of ship's tropical cyclone avoidance based on the numerical forecasts[J]. Nat Hazards, 2013, 69(1): 781-792. |
| [14] |
王军, 朱芍颐, 王冠卓, 等. 气象不确定下的船舶避台路径优化[J]. 大连海事大学学报, 2021, 47(2): 56-62. |
| [15] |
LIU D G, WANG D Q, WU Z L. Quantitative analysis model of non-accident loss for tropical cyclone avoidance routing[C]//International Conference on Transportation Engineering 2007. Reston, VA: American Society of Civil Engineers, 2007: 1123-1128.
|
| [16] |
MANNARINI G, COPPINI G, ODDO P, et al. A prototype of ship routing decision support system for an operational oceanographic service[J]. TransNav-Int J Mar Navigation Safe Sea Transp, 2013, 7(1): 53-59. |
| [17] |
陈宏权, 黄立文, 邓健. 在航船舶基于气象分析的实用避台方法[J]. 武汉理工大学学报(交通科学与工程版), 2005, 29(3): 436-439. |
| [18] |
刘建美, 马寿峰, 马帅奇. 基于改进的Dijkstra算法的动态最短路计算方法[J]. 系统工程理论与实践, 2011, 31(6): 1153-1157. |
| [19] |
鲍培明. Dijkstra算法在动态权值系统中的应用[J]. 计算机工程, 2000, 26(4): 11-12, 23. |
| [20] |
SHIN Y W, ABEBE M, NOH Y, et al. Near-optimal weather routing by using improved A* algorithm[J]. ApplSci, 2020, 10(17): 6010. |
 2023, Vol. 43
2023, Vol. 43


