2. 国家卫星海洋应用中心,北京 100081;
3. 武汉大学测绘遥感信息工程国家重点实验室,湖北 武汉 430079
2. National Satellite Ocean Application Service, Beijing 100081, China;
3. State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University, Wuhan 430079, China
北京时间2018年9月7日11时15分,我国在太原卫星发射中心通过长征二号丙火箭成功发射海洋一号C卫星(HY-1C)[1],该星搭载的海岸带成像仪(coastal zone imager,CZI)作为其中一个对地成像载荷,波段范围覆盖可见光和近红外波段。HY-1C卫星可以实现对全球范围不同海域不同季节的海面温度、冷空气、气旋等天气过程的实时监测和预警[2-5],HY-1C/CZI在海岸带动态监测、海岸带资源开发和海洋灾害监测等领域有着重要意义[5]。海洋遥感典型的应用有沿海赤潮、突发溢油事件、极地冰川变化、洪涝灾情、台风监测、农作物变化、森林火灾监测等[1],这些都需要大幅宽、大数据量、高频次覆盖的影像进行高精度波段配准、时序化分析、场景变化检测、多传感器协同分析等处理,而高精度几何定位是这些技术的重要基础和保障。因此,几何定位精度是决定海洋带成像仪发挥海洋遥感服务质量好坏的关键。
受到卫星发射过程中各种扰动力干扰、在轨运行时的空间环境变化、成像器件的损坏和老化等影响,卫星发射之前地面标定的成像几何参数较在轨实际状态存在较大误差,若直接使用实验室参数影像平面定位精度仅为10 km左右,无法满足用户使用需求。在轨几何定标[6]通过对在轨成像系统的内外方位元素状态进行精确标定,来补偿卫星平台系统外部误差和相机系统内部误差,为影像的高精度几何处理提供高质量的几何成像参数,这是地面高精度数据处理的关键。
为实现高精度几何标定,国外知名的高分辨率卫星如IKONOS、GeoEye、Worldview、Advanced Land Observing Satellite(ALOS)、PLEIADES等[7-11]利用地面定标场对其进行了精确的在轨几何定标,影像内部几何畸变得到显著改善。世界上首颗高分辨率商业卫星IKONOS[8]通过凤凰城、澳大利亚等地的地面定标场进行定标,在无地面控制点的条件下,平面定位精度达到12 m;ALOS卫星[9]为了实现三视立体相机的精确标定,从地面参考影像数据中提取四千余个控制点,利用线性回归的方法获取相机各片电荷耦合光敏元器件(charge-coupled device,CCD)的内定标参数,使得相邻片影像拼接精度达到子像素级。
随着我国光学遥感卫星的蓬勃发展,嵩山、安阳、伊犁、东营等地的地面定标场也不断增多,这大大促进了相关研究者对几何定标工作的深入研究。李德仁等[12]利用河南嵩山检校场对资源三号卫星进行了在轨几何定标,其中下视相机影像的无控定位精度从1 500 m提高到15 m左右,并证实了资源三号卫星三线阵相机符合零畸变的设计要求。在此基础上,当前国内许多研究者利用地面高精度参考影像数据,将光学卫星在轨实际获取的影像数据与其进行密集控制点匹配,建立光学卫星影像像方坐标(描述像点的平面位置)与参考影像物方坐标(描述地面点的空间三维坐标位置)的映射关系,通过空间后方交会方法进行光学卫星内外定标参数的解算[13],对光学遥感卫星相机进行了严格检校,将影像几何内精度提升到优于一个像素。目前已经成功应用到“资源三号”“高分四号”“高分五号”“高分六号”“吉林一号”等卫星几何误差标定[12-18]。
不少学者对光学遥感影像在轨自主几何定标进行了一些探索研究,其主要思想是通过构建影像像对之间同名光线的相对约束条件来对相机几何内部畸变实现补偿。皮英东等[19]采用基于稀少控制点定标方法,不依赖于地面定标场,利用沿CCD方向两景重叠影像及覆盖区稀少控制点即可实现内外定标参数的解算,定标后可以达到与使用定标场数据同样的几何定位精度。但这一方法无法完全摆脱地面参考点的限制且对重叠影像选取有严格的要求。本文根据HY-1C/CZI相机成像特点,重点介绍一种基于探元指向角的在轨几何定标方法,主要分为几何定标模型构建、参考波段绝对几何定标和波段间相对几何定标,并对标定结果进行精度验证和分析。
1 海岸带成像仪相机成像特点海岸带成像仪(CZI)采用线阵推扫成像,光学系统光轴同视轴重合、与像面垂直,并搭载2台相机,每台相机焦面搭载2片CCD器件,每片CCD影像光谱覆盖范围为0.42~0.89 μm,分别为蓝波段、绿波段、红波段、近红外波段。表 1列出了海洋一号C卫星搭载的海岸带成像仪载荷的具体信息。
|
|
表 1 海岸带成像仪相关参数 Table 1 Relevant parameters of CZI |
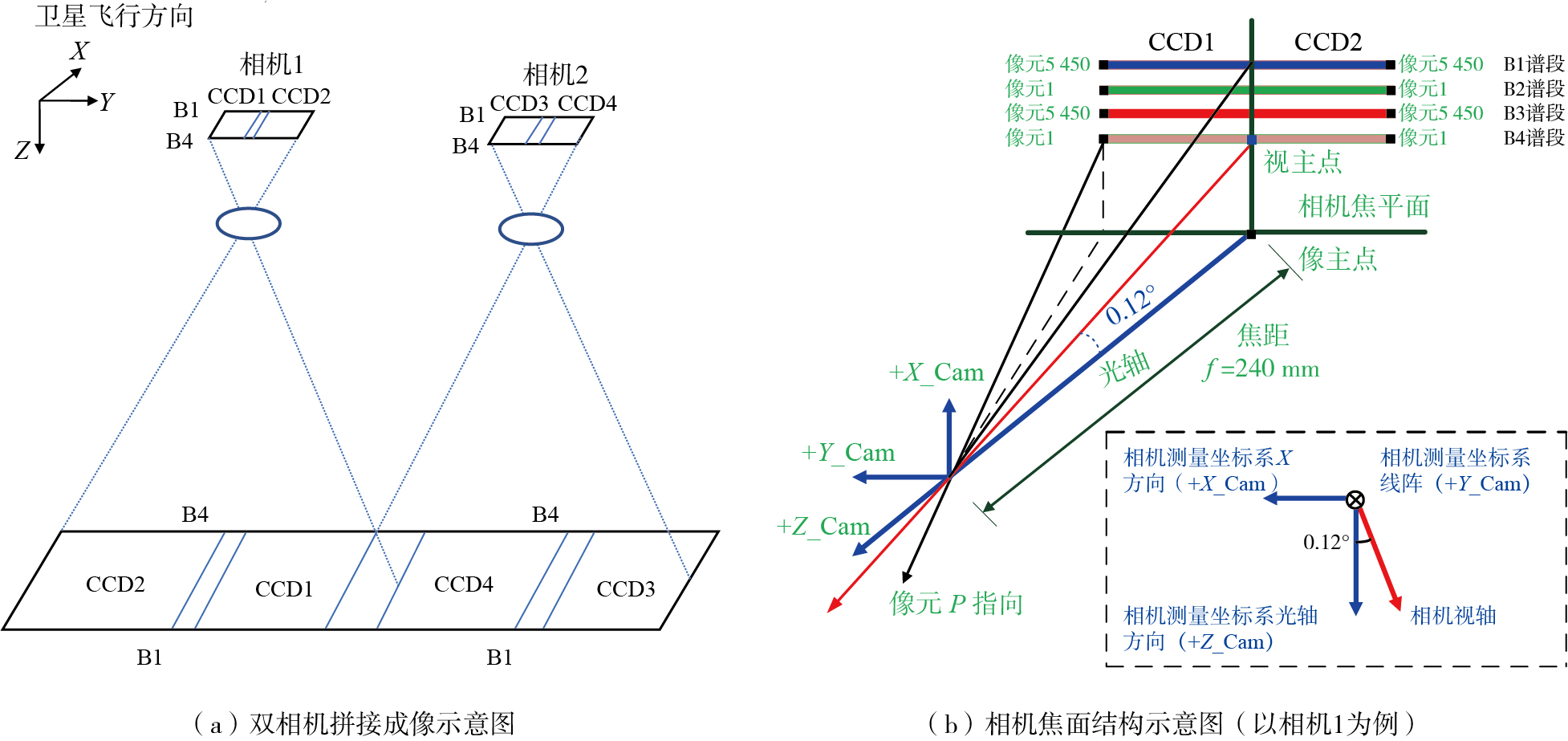
为满足大幅宽成像要求,CZI采用2台相机组合的成像模式(图 1a),2台相机具有同样的设计结构和成像方式,对地面成像时存在一定的重叠区域,在相机内部的2片CCD进行了全反全透棱镜的光学拼接,可以视为“一条扫描线”。由于制造及装配工艺的限制,平台和相机中各项参数与其设计值之间难免存在一定的偏差,这需要通过在轨几何定标对畸变进行补偿处理。
|
图 1 海岸带成像仪相机多片CCD成像示意图 Fig.1 Schematic diagram of CCD imaging of cameras in CZI |
卫星在发射前会对相机进行严格的实验室检校,但是在实际运行过程中由于空间物理环境因素的改变,实验室定标参数与实际在轨运行参数之间存在一定的偏差,因此,需要对存在的误差进行检校来改善影像处理的几何质量。其中,影响几何处理精度的误差主要来自两个方面:一是卫星搭载平台的外部系统误差(如相机安装角的改变、姿态与轨道的误差等),二是相机内部系统误差(如CCD物理畸变、相机光学畸变、相机主距误差等)。海岸带成像仪相机的视轴与光轴存在0.12°的差异(图 1b),这会导致光线通过相机镜头时偏离其理想成像位置,即像主点中心的指向角和探元的指向角会存在明显的角度偏差,从而造成相机内部几何畸变。
对于光学卫星,利用严格几何成像模型对各项系统误差进行补偿,在理论上具有严格的物理意义,但是主要存在两个关键问题。一方面是由于卫星成像过程中各探元成像光线之间接近平行,各项系统误差参数存在相关性,利用物方控制点信息进行平差解算时,会出现病态化难以收敛的问题,待解算的内外方位元素解算结果的可靠性无法保证。另一方面则是存在如姿态漂移误差的外方位元素非模型化误差的影响,这两个因素均会对可模型化误差参数的解算带来较大的困难。因此,在实际应用中,直接采用严格几何成像模型解算其中各项系统误差参数是不可行的,需要通过对其中各项系统误差参数依据其特性规律进行合理的优化,并建立适合于光学卫星影像在轨几何定标的几何成像模型。
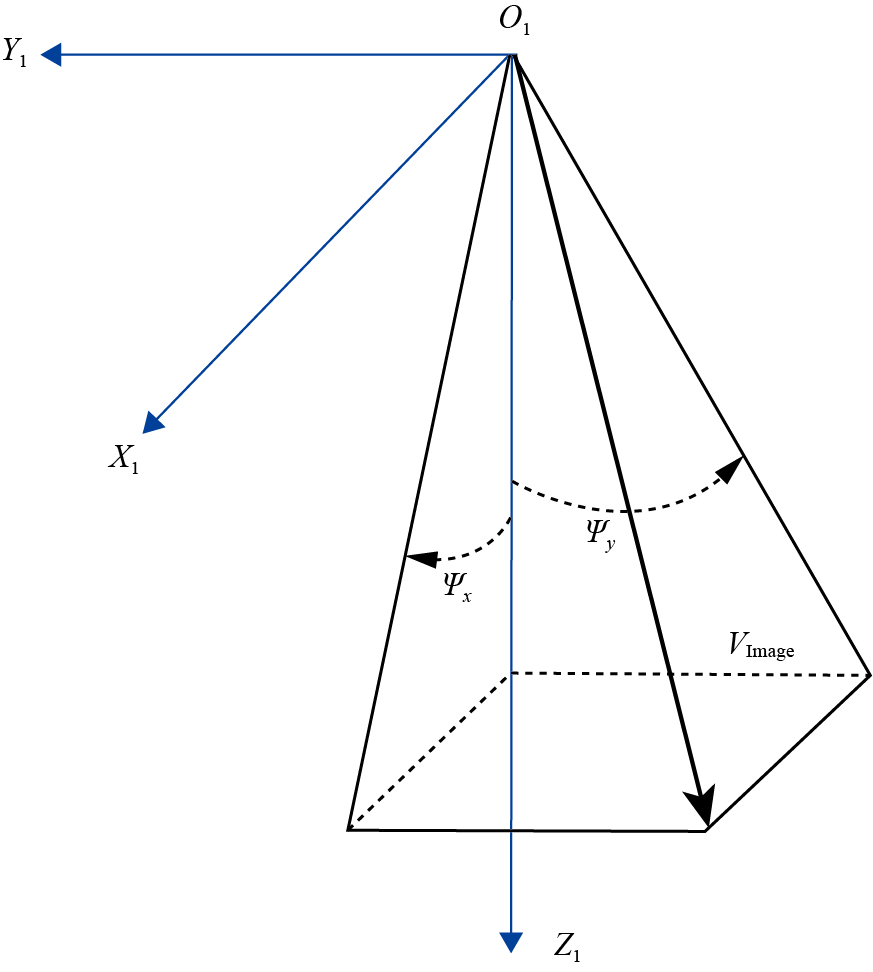
针对相机严格几何成像模型存在的问题,采用一种基于探元指向角的几何定标模型对CZI进行在轨定标(图 2)。通过相机安装矩阵来补偿相机安装误差的外部系统误差,并利用探元指向角参数来补偿主点、主距、镜头畸变等相机内部误差,最终恢复每个探元在空间中的精确指向,解决了相机严格几何成像模型无法准确标定的问题。
|
图 2 CCD探元指向角模型 Fig.2 Directional angle model of CCD probe |
由探元指向角的物理含义可知,对各探元指向角进行标定本质上是对相机主距进行归一化处理,确定各探元的指向角在单位主距下的相机焦平面投影坐标,即:
| $ \left(V_{\text {Image }}\right)_{\text {cam }}=\left(\begin{array}{l} x \\ y \\ f \end{array}\right)=\left(\begin{array}{c} \tan \left(\psi_x\right) \\ \tan \left(\psi_y\right) \\ 1 \end{array}\right) 。$ | (1) |
式(1)中:ψx和ψy为像元(x, y)在相机坐标系(O-X1Y1Z1)下的探元指向角,f为相机焦距。相机线阵CCD内定标模型实质上是一个多项式模型,本文采用三次多项式来对CCD上各探元在“广义”相机坐标系下进行拟合,以此确定每一个探元的指向角。
| $ \left\{\begin{array}{l} \psi_x(s)=a x_0+a x_1 \times s+a x_2 \times s^2+a x_3 \times s^3 \\ \psi_y(s)=a y_0+a y_1 \times s+a y_2 \times s^2+a y_3 \times s^3 \end{array}, \right. $ | (2) |
式(2)中:s为CCD的探元号,ax0、ax1、ax2、ax3、ay0、ay1、ay2、ay3为多项式的系数,用于描述CCD的内定标参数进而确定探元指向角。
因此,通过对探元指向角的准确标定,可以构建基于探元指向角的在轨几何定标模型,如式(3)所示:
| $\left(\begin{array}{c} \tan \left(\psi_x(s)\right) \\ \tan \left(\psi_y(s)\right) \\ 1 \end{array}\right)=\lambda \boldsymbol{R}_{\mathrm{body}}^{\mathrm{cam}} \boldsymbol{R}_{\mathrm{J} 2000}^{\mathrm{body}} \boldsymbol{R}_{\mathrm{WGS} 84}^{\mathrm{J} 2000}\left[\begin{array}{c} X-X_{\mathrm{gps}} \\ Y-Y_{\mathrm{gps}} \\ Z-Z_{\mathrm{gps}} \end{array}\right]_{\mathrm{WGS} 84}。$ | (3) |
式(3)中:
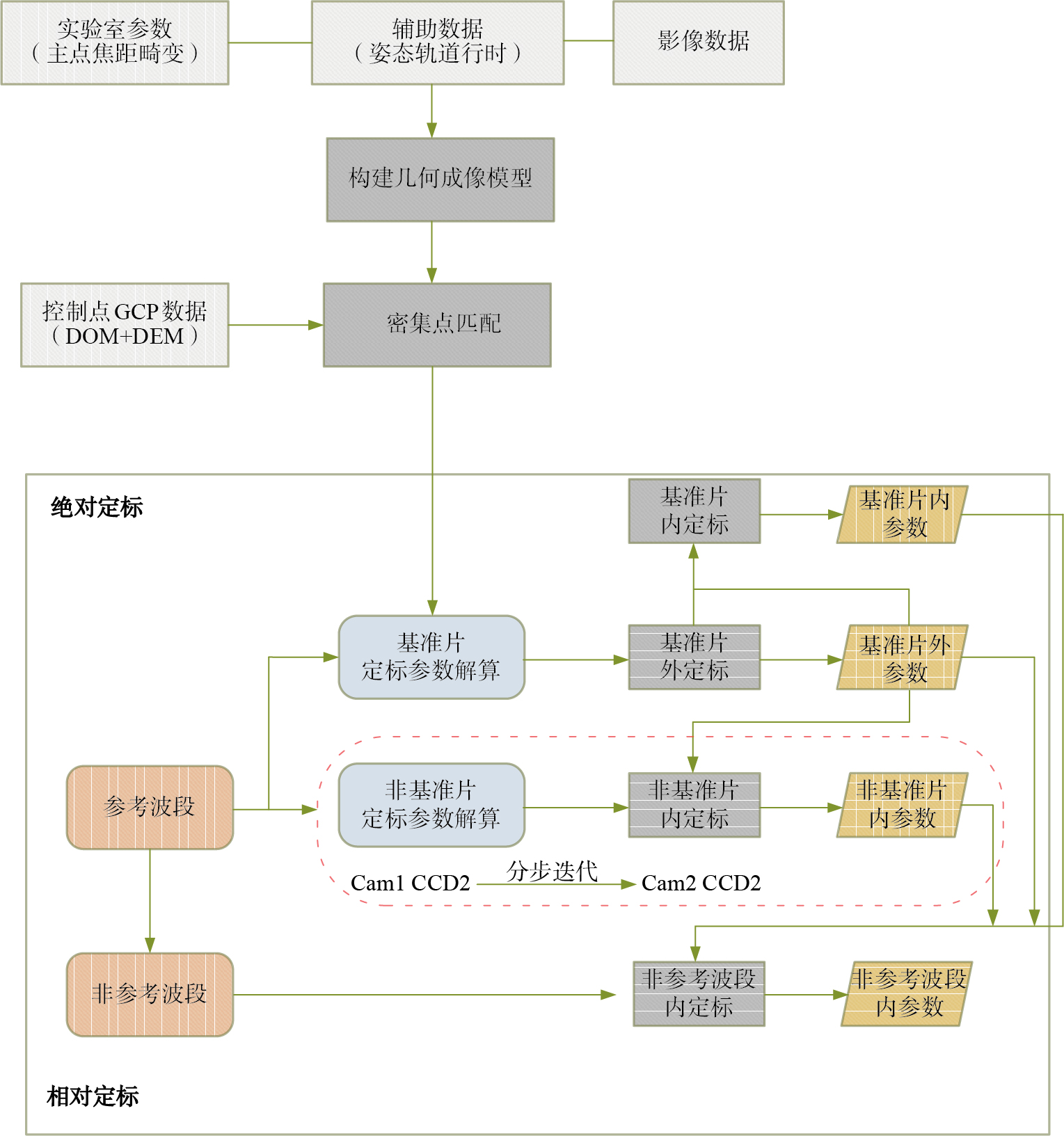
考虑到海岸带成像仪CZI相机设计特点和成像方式,采用了一种基于参考影像的绝对几何定标和基于波段间约束关系的相对几何定标方案,流程如图 3所示。
|
图 3 海岸带成像仪在轨几何定标流程 Fig.3 On-orbit geometric calibration process of CZI |
根据HY-1C/CZI在轨几何定标模型的特点,首先选择B2波段作为参考波段(中间波段为参考影像便于波段间相对定标),利用该波段影像作为待定标影像数据,构建探元指向角几何定标模型,将待定标影像与参考影像进行密集同名点匹配,选择出大量均匀分布的控制点,进行外定标参数解算;然后,利用外定标参数对2个相机4片CCD进行内定标,解算探元指向角参数。其中,内定标参数的解算是以外定标参数所确定的“广义”相机坐标系作为参考基准的。因此,采用分步定标的策略,即先解算外定标参数,再在外定标参数确定的情况下解算内定标参数。
2.2.2 波段间相对几何定标为了提高各波段影像之间的相对几何精度,采用一种波段间的相对几何定标方法,对各波段之间的相对几何畸变进行检校,从而提高各波段影像之间的相对几何精度,实现高精度的几何定位一致性配准。根据HY-1C/CZI选择B2影像为参考波段,以参考波段为基准,仅对非参考波段与参考波段之间的相对几何畸变进行在轨几何定标。选择B2波段作为参考波段,B1、B3和B4作为非参考波段,下面将以B1波段为例阐述具体技术流程:
(1) 将非参考波段B1影像与参考波段B2影像进行连接点匹配,在波段B2影像上,匹配的连接点应在沿轨方向上相同的一段较短区域内,垂轨方向上则要求均匀覆盖整片影像。
(2) 根据外定标获取的相机安装参数和参考波段B2的内定标参数(探元指向角参数)构建严格几何成像模型。对非参考波段B1影像与参考波段B2影像的每一个连接点对[p1(x1, y1), p2(x2, y2)],通过成像模型计算出参考波段B2的像平面坐标p2i(x, y)转换到物方空间的地理坐标P(B, L, H)。
(3) 将P(B, L, H)作为控制点,其在非参考波段B1影像上对应的像平面坐标即为p1(x1, y1),同2.2.1节进行B1影像的内定标参数解算。
3 几何定标试验与分析 3.1 实验数据针对CZI在轨几何定标实验,为了保证匹配控制点的均匀分布,要求研究区域内没有大面积云和水覆盖。实验数据选择的是覆盖于华北地区的单景CZI-1A影像产品(预处理辐射校正级产品),地理范围为108 °36 ′~118 °14 ′ E、34 °05 ′~39 °16 ′ N,包含山东、河北、河南、山西、陕西5省部分区域,区域地形主要是平原和山地。表 2列出了该定标景影像的具体信息。
|
|
表 2 海岸带成像仪定标景影像信息 Table 2 Calibration image information of CZI |
传统低轨道卫星定标主要是采用高精度几何定标场数据作为参考影像,但无法满足海岸带成像仪CZI这种大幅宽传感器的应用。选取的定标参考数据分别为Landsat 8卫星的全色波段正射影像(digital orthophoto map,DOM)和航天飞机雷达地形测绘任务(shuttle radar topography mission,STRM3)的数字高程影像(digital elevation model,DEM),通过影像拼接的方法来保证定标景影像区域实现全部覆盖。其中,DOM的地面几何分辨率(ground sampling distance, GSD)为15 m,平面精度优于2 m,DEM的地面几何分辨率GSD为90 m,其高程精度优于16 m,如图 4所示。

|
图 4 定标参考数据 Fig.4 Calibration reference data |
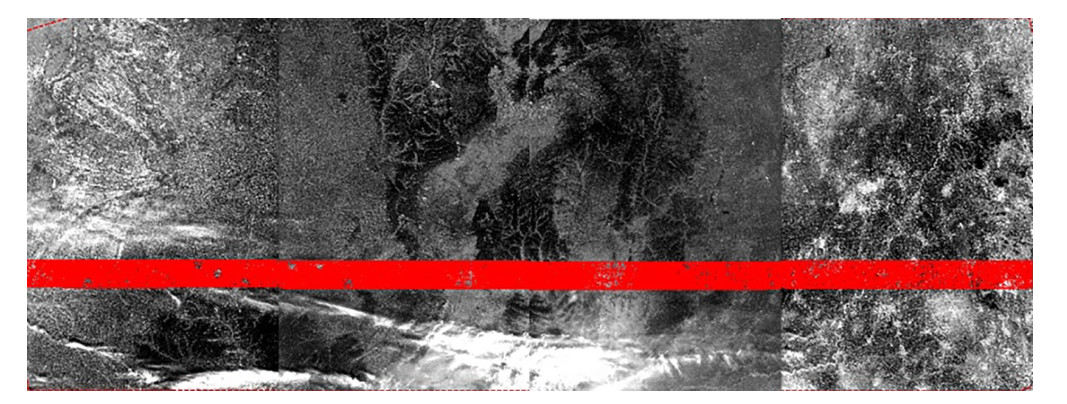
首先在基准波段B2影像沿轨方向上选取一段无云覆盖区域影像(便于进行匹配)作为定标区域,然后利用SIFT匹配算法在待定标影像区域和数字正射影像DOM进行密集匹配,将提取到的同名点作为内外定标参数解算的控制点。图 5为待定标片CCD影像与参考DOM影像密集控制点匹配结果,在待定标的4片CCD影像上分别得到了19 008、26 749、25 175和17 805个地面控制点。
|
图 5 定标影像与参考DOM密集控制点匹配 Fig.5 Matching of calibration image and reference DOM dense control point |
基于前面提出的定标模型及解算方法,利用3.2.1节中获取的密集控制点对海岸带成像仪CZI的4片CCD进行联合外定标,然后在此基础上对各片CCD分别进行内定标参数解算,表 3列出了外定标参数的解算结果以及实验室提供的初始检校值。
|
|
表 3 外定标参数结算结果 Table 3 Settlement results of external calibration parameters |
目前,常用的内定标参数的精度评价方法是用探测器畸变曲线来进行刻画。考虑到所采用的几何定标模型中内定标参数并没有直接的物理含义,本文在各片CCD每隔一定间隔选取一个探元作为样本探元,用探元号作为横坐标,用实验室检校值与在轨几何定标的内定标参数分别计算探元指向角的值,将其作为纵坐标,绘制各片CCD的几何定标前后的探元畸变曲线。该曲线可以准确直观的反映各片CCD在沿轨和垂轨方向上的几何畸变情况以及评判几何定标效果的质量好坏。由图 6可以看出,各片CCD内部在沿轨和垂轨方向上均存在明显的非线性畸变,经过内外定标后,相机内部畸变得到了有效的补偿。
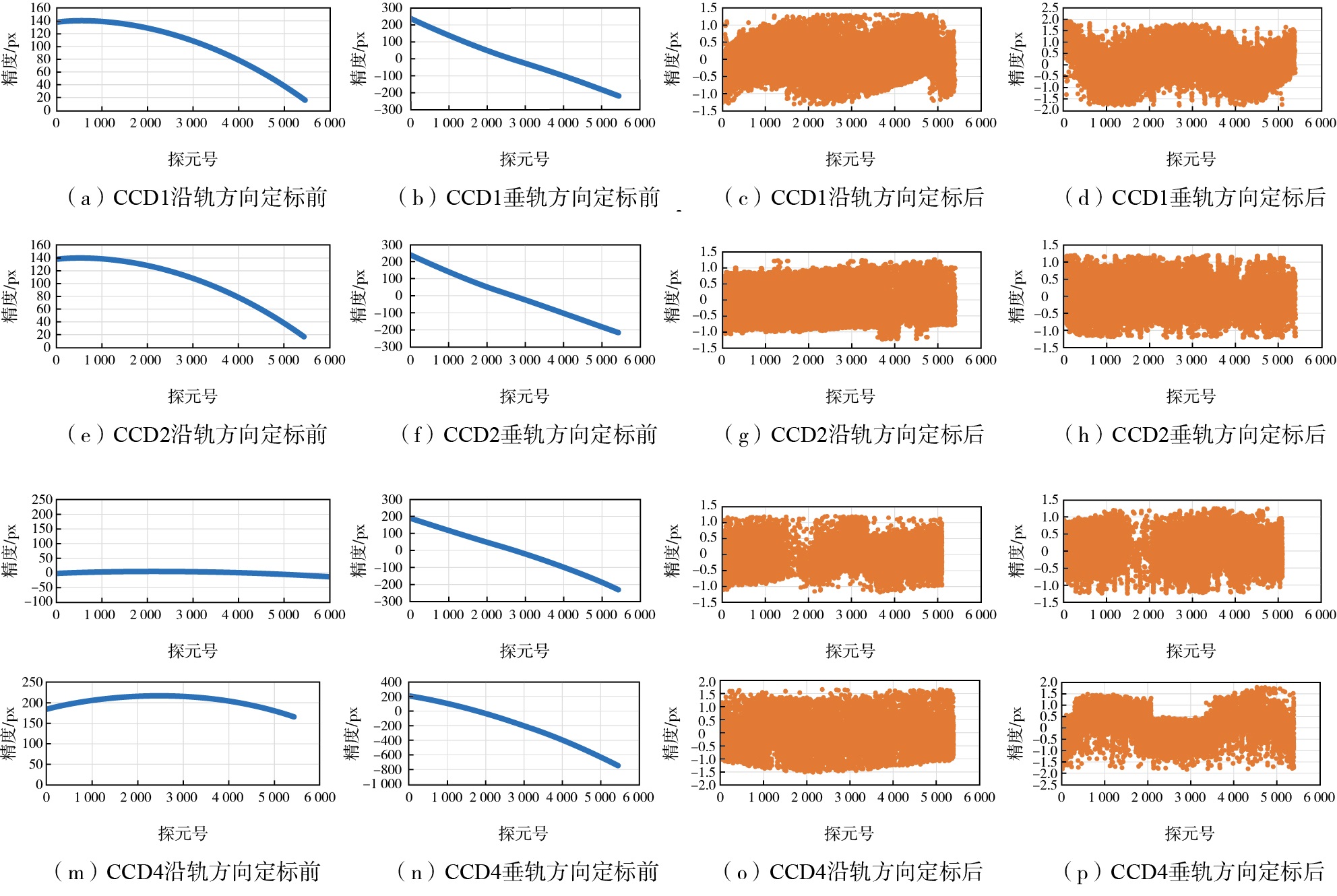
|
图 6 CZI相机定标前后各片CCD内部畸变曲线 Fig.6 Internal distortion curve of each CCD before and after CZI camera calibration |
影像平面定位精度可以用量测坐标(待评价影像控制点的地理坐标)与真实地理坐标(参考影像的实际地理坐标)残差的均方根误差来表示。假设待评价影像基准点在影像产品上的量测坐标为(Xo, Yo),在参考数据中的真实坐标为
| $ \left\{\begin{array}{l} X_{\mathrm{o} i}=X_i-X_{\mathrm{o}} \\ Y_{\mathrm{o} i}=Y_i-Y_{\mathrm{o}} \\ \widetilde{X}_{\mathrm{o} i}=\widetilde{X}_i-\widetilde{X}_{\mathrm{o}}, \\ \widetilde{Y}_{\mathrm{o} i}=\widetilde{Y}_i-\widetilde{Y}_{\mathrm{o}} \end{array}\right., $ | (4) |
量测坐标与真实地理坐标残差为
| $ \varDelta X_{\mathrm{o} i}=X_{\mathrm{o} i}-\widetilde{X}_{\mathrm{o} i}, \quad \Delta Y_{\mathrm{o} i}=Y_{\mathrm{o} i}-\widetilde{Y}_{\mathrm{o} i}, $ | (5) |
残差的均方根误差(root mean square error,RMSE)为
| $\begin{aligned} V(\operatorname{RMSE})_X & =\sqrt{\frac{1}{n-1} \sum\limits_{i=1}^{n-1}\left(\Delta X_{\mathrm{o} i}\right)^2}, \\ V(\operatorname{RMSE})_Y & =\sqrt{\frac{1}{n-1} \sum\limits_{i=1}^{n-1}\left(\Delta Y_{\mathrm{o} i}\right)^2} 。\end{aligned} $ | (6) |
根据定标前后各片CCD影像,分别选取对应区域的高精度数字正射影像DOM和数字高程影像DEM作为参考影像,利用影像匹配的方法自动选取出若干数量均匀分布的控制点,来评价影像的平面定位精度(表 4)。经过参考波段的绝对几何定标后,各片CCD影像的无控定位精度得到明显改善,各片影像几何定位精度均在0.5个像元左右。
|
|
表 4 定标前后各片CCD几何定位精度
Table 4 Geometric positioning accuracy of each CCD before and after calibration |
把参考基准波段B2影像与待配准B1、B3、B4波段影像分别进行连接点匹配,这些连接点的区域与绝对几何定标中的控制区域保持一致。根据2.2节提出的定标方案,利用与参考基准波段B2影像匹配得到的密集连接点,外定标参数可采用参考基准波段B2的外定标解算结果,然后通过波段间相对几何定标,对B1、B3、B4波段的4片CCD影像分别进行内定标参数解算。对于相对几何定标的结果精度可以从各波段各片CCD的几何定位精度以及波段配准精度两方面进行评价。图 7为相对定标后各片CCD的定位精度,通过波段间相对几何定标,4个波段的每片CCD定位精度均在0.5个像元左右,可以有效保证非参考波段的几何精度。
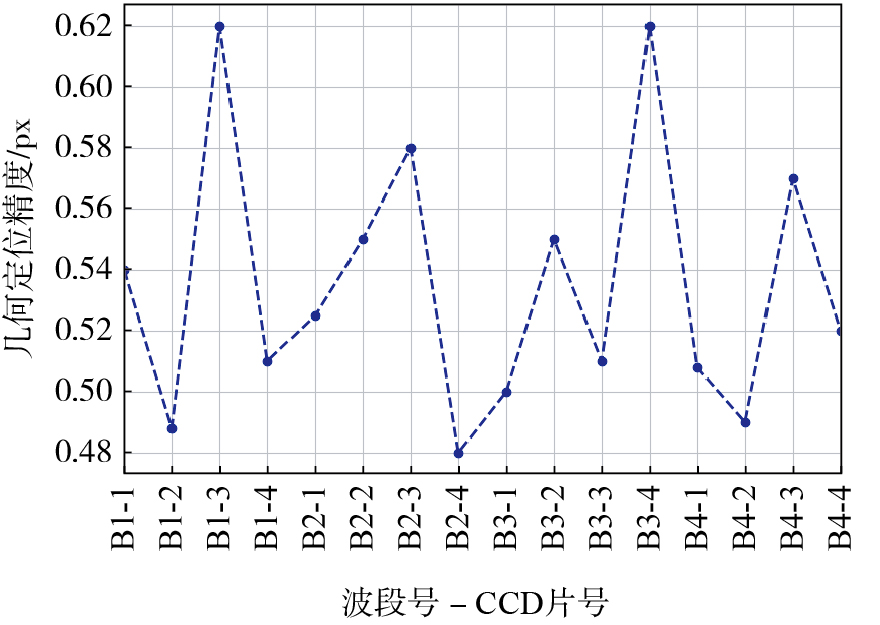
|
图 7 相对几何定标后各片CCD几何定位精度 Fig.7 Geometric positioning accuracy of each CCD after relative geometric calibration |
为了验证在轨几何定标后几何定位精度的可靠性,选取中心为河南郑州、北京怀柔、辽宁大连、内蒙古呼和浩特、印度西伯利亚、澳大利亚埃芒萨特等6个地区的海岸带成像仪影像,通过与参考影像DOM进行匹配,并计算影像平面定位精度,表 5给出了各验证景影像具体的几何定位精度信息,由表 5可得,选取多组影像试验,经在轨几何定标后,影像的无控定位精度平均约4.2个像元。
|
|
表 5 验证景影像几何定位精度统计
Table 5 Geometric positioning accuracy statistics of validation image |
根据海洋一号C卫星搭载的海岸带成像仪相机设计特点和成像特性,采用一种基于探元指向角的在轨几何定标模型,提出先开展参考波段的绝对几何定标,再通过波段间约束关系进行相对几何定标,最后获取定标模型参数的在轨几何定标方案。实验结果表明,尽管海岸带成像仪在发射前进行了实验室几何定标,但由于发射过程各种动力的影响、在轨运行空间环境的变化以及传感器的损耗等因素,相机在轨运行参数发生变化,影像产品的几何质量无法满足使用要求。通过在轨几何定标实验,相机内部畸变得到了很好的补偿,几何定位精度得明显改善。经多组影像产品精度测试验证,几何定位精度完全满足优于5个像元的指标要求,说明本文的定标模型与方案具有稳定性和可靠性的特点。
| [1] |
刘建强, 蒋兴伟, 王丽丽, 等. 海洋一号C、D卫星组网观测与应用[J]. 卫星应用, 2021(9): 19-26. |
| [2] |
刘达, 王慧, 黄彬, 等. 2021年春季海洋天气评述[J]. 海洋气象学报, 2021, 41(3): 11-23. |
| [3] |
王皘, 刘达, 董林, 等. 2021年夏季海洋天气评述[J]. 海洋气象学报, 2021, 41(4): 82-94. |
| [4] |
聂高臻, 黄彬. 2021年秋季海洋天气评述[J]. 海洋气象学报, 2022, 42(1): 74-82. |
| [5] |
刘建强, 曾韬, 梁超, 等. 海洋一号C卫星在自然灾害监测中的应用[J]. 卫星应用, 2020(6): 26-34. |
| [6] |
龚健雅, 王密, 杨博. 高分辨率光学卫星遥感影像高精度无地面控制精确处理的理论与方法[J]. 测绘学报, 2017, 46(10): 1255-1261. |
| [7] |
王密, 田原, 程宇峰. 高分辨率光学遥感卫星在轨几何定标现状与展望[J]. 武汉大学学报(信息科学版), 2017, 42(11): 1580-1588. |
| [8] |
FRASER C S, BALTSAVIAS E, GRUEN A. Processing of Ikonos imagery for submetre 3D positioning and building extraction[J]. ISPRS J Photogramm Remote Sens, 2002, 56(3): 177-194. |
| [9] |
TADONO T, SHIMADA M, MURAKAMI H, et al. Calibration of PRISM and AVNIR-2 onboard ALOS "Daichi"[J]. IEEE Trans Geosci Remote Sens, 2009, 47(12): 4042-4050. |
| [10] |
TAKAKU J, TADONO T. PRISM on-orbit geometric calibration and DSM performance[J]. IEEE Trans Geosci Remote Sens, 2009, 47(12): 4060-4073. |
| [11] |
DE LUSSY F, GRESLOU D, DECHOZ C, et al. Pleiades HR in flight geometrical calibration: location and mapping of the focal plane[J]. Int Arch Photogramm Remote Sens Spatial Inf Sci, 2012, XXXIX-B1: 519-523. |
| [12] |
李德仁, 王密. "资源三号"卫星在轨几何定标及精度评估[J]. 航天返回与遥感, 2012, 33(3): 1-6. |
| [13] |
曹金山, 袁修孝, 龚健雅, 等. 资源三号卫星成像在轨几何定标的探元指向角法[J]. 测绘学报, 2014, 43(10): 1039-1045. |
| [14] |
王密, 程宇峰, 常学立, 等. 高分四号静止轨道卫星高精度在轨几何定标[J]. 测绘学报, 2017, 46(1): 53-61. |
| [15] |
王密, 秦凯玲, 程宇峰, 等. 高分五号可见短波红外高光谱影像在轨几何定标及精度验证[J]. 遥感学报, 2020, 24(4): 345-351. |
| [16] |
秦凯玲, 程宇峰, 王密, 等. 高分五号卫星全谱段光谱成像仪在轨几何定标方法及精度验证[J]. 上海航天, 2019, 36(S2): 210-218. |
| [17] |
王密, 郭贝贝, 龙小祥, 等. 高分六号宽幅相机在轨几何定标及精度验证[J]. 测绘学报, 2020, 49(2): 171-180. |
| [18] |
武红宇, 白杨, 王灵丽, 等. 吉林一号宽幅01星宽幅相机在轨几何定标及精度验证[J]. 光学精密工程, 2021, 29(8): 1769-1781. |
| [19] |
皮英冬, 谢宝蓉, 杨博, 等. 利用稀少控制点的线阵推扫式光学卫星在轨几何定标方法[J]. 测绘学报, 2019, 48(2): 216-225. |
 2023, Vol. 43
2023, Vol. 43


