2. 山东省气象工程技术中心, 山东 济南 250031;
3. 长岛国家气侯观象台, 山东 长岛 265800
2. Shandong Meteorological Engineering Technology Center, Jinan 250031, China;
3. Changdao National Climatology Observatory, Changdao 265800, China
气象观测资料是辨别和解析区域与全球变化的重要条件[1],气象、气候学基础理论研究以及各类气象服务的开展都离不开气象观测资料[2]。其中,地面气象观测资料尤为重要,它不仅有更长的时间观测序列,而且还可以更精准地反映近地面的大气特征[3],对气象服务起着至关重要的作用。目前,自动气象站是地面气象观测资料的主要来源之一。在实际气象业务中,不仅需要台站所在区域的观测资料,而且还需要利用台站资料得到非台站位置的气象要素值[4-5]。地面气象观测站的站网密度及空间分布影响其监测能力[6],布局科学合理的观测站网能提高预报预测的准确率和精细化水平。
气象站网的布局设计,最早起源于苏联,1946年,Drozdov等[7]提出将结构函数作为观测站网设计的依据。1982年,Mooley等[8]将结构函数应用于热带站网雨量场设计中,建立了内插误差与距离的关系。2004年,Schneebeli等[9]利用模糊数学和概率统计,研究了测雪站网的布站间距。我国观测站网设计研究起步较晚,1985年,廖洞贤[10]最早提出最优相邻测站间距、最优垂直网格和观测时间间隔的公式。1989年,卢文芳等[11]研究表明,上海地区二类和三类站的最佳距离分别为50 km和30 km。赵瑞霞等[12]对北京地区站网布局进行研究,得到北京东南地区二类气象台站的最佳布站距离应不超过16 km。相关学者[13-15]也采用结构函数对气象站网布局开展研究,得到了陕北高原和陕南山地各要素站网合理间距以及四川降水量和气温要素的合理布站间距等,取得了一系列研究成果。Munn[16]研究发现,气象要素间具有空间协相关和时间自相关性,这使得利用气象要素的时空分布来确定站网密度成为可能。Drozdov等[7]提出气象要素的内插标准误差只与该要素的结构函数有关,结构函数被广泛应用于气象观测站网的布局研究中。
目前,山东已基本建成功能完善、质量稳健的综合气象观测系统,站网数量也得到明显提升。但是,地面气象观测站网的整体探测能力如何,缺乏科学的评估,这在一定程度上影响着观测站网布局规划的合理性。此文依据世界气象组织(World Meteorological Organization,WMO)滚动需求评估(Rolling Review of Requirements,RRR)的原则,对山东已建地面气象观测站网与WMO的观测系统能力分析和审查工具(Observation System Capability Analysis and Review,OSCAR)各应用领域的需求进行评估。利用山东国家级基准、基本及常规气象观测站资料,基于结构函数研究其气温、相对湿度、降水量的最佳布站方案与最佳布站距离。研究结果为山东站网布局的设计与优化提供科学依据。
1 资料山东地面气象观测站资料包括国家级基准、基本及常规气象观测站、国家气象观测站、区域气象观测站、农业小气候观测站和设施农业观测站(以下简称“应用气象观测站”)。各观测站具体信息见表 1。此文在对山东地面气象观测站网水平分辨率评估中用到了表 1所列的4类地面气象观测站中的台站数量,用于计算水平分辨率。在山东国家级基准、基本及常规气象观测站的最佳布站方式及站间距的研究中,用到了该类观测站1992—2021年的数据,因绝大多数台站海拔在200 m以下,泰山站海拔为1 533 m,其观测数据与其他台站差异明显,故未对泰山站的观测数据进行分析。地面气温、相对湿度的日均值以及降水量的日值由各要素的小时值计算得到,观测资料经过了空间一致性和时间连续性等数据质量控制。除降水量资料外,气温和相对湿度每间隔2 d选取1 d的数据作为筛选后的样本进行研究,这样可较好地避免相邻数据的过分相关。在所选的样本序列中,对于气温、相对湿度,选取1992—2021年的1、4、7、10月的资料分别代表冬、春、夏、秋季。对于降水量,选取1992—2021年的1—2月、4—5月、7—8月、10—11月分别代表冬、春、夏、秋季。
|
|
表 1 山东地面气象观测站信息 Table 1 Information of surface meteorological observing stations in Shandong |
RRR是WMO在2015年启动编制新的全球综合观测系统手册时被确定的重要原则,其流程被确定为WMO所有成员国和参与观测合作的网络应遵循的观测站网设计、规划发展和效果评价的规范[17]。OSCAR是全球综合观测系统的重要组成部分,它由4个组分构成:OSCAR/需求、OSCAR/分析、OSCAR/地面和OSCAR/空间。其中,OSCAR/分析将现有观测系统的能力与WMO的RRR过程提出的需求进行比对,使得专家和观测系统运行方找出差距并支持他们的规划。OSCAR将气象应用需求划分了14个领域,WMO按应用、变量、领域分别列出了各指标的观测用户需求,并给出了每种需求类型的门限值、目标值和突破值。在规划和设计观测系统时,从成本效益的角度出发,使观测系统达到突破值要求的水平是最适合的。
表 2给出了常用领域要素水平分辨率的目标值、突破值及门限值。由于不能获取到地面观测设备的各种完备数据,此文没有对全方位指标的需求差距分析评估,选取主要的评估指标水平分辨率,对山东已建的地面气象观测站网进行分析评估。
|
|
表 2 常用观测要素的OSCAR应用领域的水平分辨率指标值
Table 2 Horizontal resolution index values of common observing elements in application fields of OSCAR |
结构函数揭示了变量在空间不同点间的离散程度。Gandin[18]将其定义为:某个气象要素在A、B两点间的结构函数bf(A, B)为两个站点间要素距平差值平方的平均值。计算公式为
| $ b_f(A, B)=\overline{\left[f^{\prime}(A)-f^{\prime}(B)\right]^2} \text {, } $ | (1) |
其中:f′(A)和f′(B)分别代表要素f在A、B两点的距平值。为了表征结构函数与站点间距的关系,需要计算站点间的距离,见公式(2)。
| $ l=\rho\left[2-2 \sin \emptyset_A \sin \emptyset_B-2 \cos \emptyset_A \cos \emptyset_B \cos \left(\lambda_A-\lambda_B\right)\right]^{\frac{1}{2}}, $ | (2) |
其中:l代表A、B两点的站间距离,ρ为地球半径,ø、λ分别代表站点的纬度和经度。
2.3 观测随机误差及内插标准误差 2.3.1 观测随机误差气象要素的观测误差由系统误差和随机误差两部分组成[13]。其系统误差在采用偏差计算结构函数时已被消除。假设区域内气象要素在某点上的随机误差不与其他点的偏差和随机误差相关,且各点观测随机误差相等,则
| $ b_f^{\prime}(l)=b_f(l)+2 \sigma_f^2 \text { 。} $ | (3) |
其中:bf′(l)和bf(l)分别为实际和理论的结构函数,l和σf2分别代表A、B两点的距离和观测随机标准误差。由公式(3)可见,实际观测资料得到的结构函数要高于其理论值。若A、B两点重合时,即l=0,则bf(0)=0。因此
| $ \sigma_f^2=\frac{1}{2} b_f^{\prime}(0) \text { 。} $ | (4) |
将实际观测资料获得的结构函数推算至零距离,由公式(4)可得观测随机标准误差的估算值。
2.3.2 内插标准误差针对线段、正三角形、正方形3种内插情况进行讨论。气象要素插值其两点间的中点误差最大。A、B两点的中点C的内插标准误差E可表示为:
| $ E=b_f\left(\frac{l}{2}\right)-\frac{1}{4} b_f(l)+\frac{1}{2} \sigma_f^2 \text { 。} $ | (5) |
假设区域内满足各向同性和均匀性,由公式(3)、(4)可知,线段内插标准误差与结构函数的关系式如下:
| $ E=b_f{ }^{\prime}\left(\frac{l}{2}\right)-\frac{1}{4} b_f{ }^{\prime}(l)-\frac{1}{2} b_f{ }^{\prime}(0)\text { , } $ | (6) |
其中,bf′(0)是将结构函数与距离的关系曲线外推至距离零处而得到。
对平面正三角形和正方形的中心进行内插,其内插标准误差E分别见公式(7)、(8):
| $ E=b_f{ }^{\prime}\left(\frac{l}{\sqrt{3}}\right)-\frac{1}{3} b_f{ }^{\prime}(l)-\frac{1}{2} b_f{ }^{\prime}(0) \text{, } $ | (7) |
| $ E=b_f{ }^{\prime}\left(\frac{l}{\sqrt{2}}\right)-\frac{1}{4} b_f{ }^{\prime}(l)-\frac{1}{8} b_f{ }^{\prime}(\sqrt{2} l)-\frac{1}{2} b_f{ }^{\prime}(0) 。$ | (8) |
根据公式(6)、(7)、(8),由各观测要素结构函数便可计算不同距离下内插标准误差E值。
2.4 最大容许误差和最大容许距离Gandin[18]研究发现,对绝大多数气象要素而言,其点值内插的标准误差不应超过观测标准误差。最大容许误差可由公式(5)右边前两项的数值不超过观测标准误差来确定,因此
| $ E \leqslant \frac{3}{2} \sigma_f^2 \text{, } $ | (9) |
| $ E_{\max }=\frac{3}{2} \sigma_f^2=\frac{3}{4} b_f^{\prime}(0) \text { 。} $ | (10) |
公式(10)中Emax为最大容许误差,对应距离为最大容许距离。该距离为站间距合理布局的依据。
3 结果与讨论 3.1 山东地面气象观测站网水平分辨率评估观测站网水平分辨率由站网水平站间距计算公式[19]得到
| $ C=\sqrt{10000 \times S /\left(N_1+N_2+\ldots+N_i+\ldots+N_m\right)} \text{。} $ | (11) |
其中:C表示平均站间距,即水平分辨率,单位为km;S表示面积,单位为万km2;Ni表示第i种仪器的观测站数量;m表示观测目标要素的仪器种类数量。
山东4类地面气象观测站各要素水平分辨率见表 3。区域气象观测站最小,应用气象观测站最大。其中,区域气象观测站降水量要素水平分辨率最小,为10.36 km,应用气象观测站风向和风速及降水量要素水平分辨率最大,为58.59 km。国家气象观测站和区域气象观测站各要素水平分辨率由小到大依次为降水量、气温、风向和风速、相对湿度、气压,国家级基准、基本及常规气象观测站各要素水平分辨率相同,应用气象观测站气温与相对湿度水平分辨率小于风向和风速及降水量。
|
|
表 3 山东地面气象观测站网各要素水平分辨率 Table 3 Horizontal resolution of each element of surface meteorological observing station networks in Shandong |
山东各地市地面气象观测站各要素水平分辨率见表 4。各市地面气象观测站各要素水平分辨率大致为:气压最大,相对湿度次之,再次之为风向和风速,风向和风速水平分辨率略大于气温和降水量。除滨州、德州、东营、菏泽、济宁外,其他地市降水量要素的水平分辨率均最小。各地市地面观测站各要素水平分辨率分布趋势与全省的基本一致。山东各市地面气象观测站降水量、气温、风向和风速的水平分辨率优于相对湿度和气压的水平分辨率。
|
|
表 4 山东各市地面气象观测站网各要素水平分辨率 Table 4 Horizontal resolution of each element of surface meteorological observing station networks in cities of Shandong |
就各市观测要素水平分辨率而言,菏泽的相对湿度、气压、风向和风速水平分辨率全省最大,东营的气温、降水量要素的水平分辨率全省最大;济南的气温、降水量、风向和风速要素的水平分辨率全省最小,日照的相对湿度、气压要素的水平分辨率全省最小。综上,济南、青岛、淄博、日照地面观测站整体探测能力较强,临沂、菏泽、潍坊地面观测站整体探测能力较弱。
将山东4类地面气象观测站各要素水平分辨率与OSCAR各应用领域的指标值(门限值、突破值、目标值)进行对比分析(图 1—2)。可见,国家级基准、基本及常规气象观测站和国家气象观测站的气温、相对湿度、气压、风向和风速要素的水平分辨率仅优于全球数值天气预报的突破值,高于其门限值,降水量要素的水平分辨率达到了短时临近预报和全球数值天气预报的门限值;区域气象观测站的气温、风向和风速、降水量要素的水平分辨率基本达到了OSCAR各应用领域的门限值。其中,气温和降水量要素的水平分辨率分别优于全球数值天气预报的目标值和突破值,风向和风速要素的水平分辨率优于海洋应用领域突破值。相对湿度、气压要素水平分辨率略差,仅优于全球数值天气预报的突破值,与海洋应用领域门限值持平;应用气象观测站的气温、相对湿度要素的水平分辨率略优于全球数值天气预报突破值,风向和风速要素的水平分辨率优于海洋应用的门限值,降水量要素的水平分辨率最差,未达到任何常用应用领域的门限值。
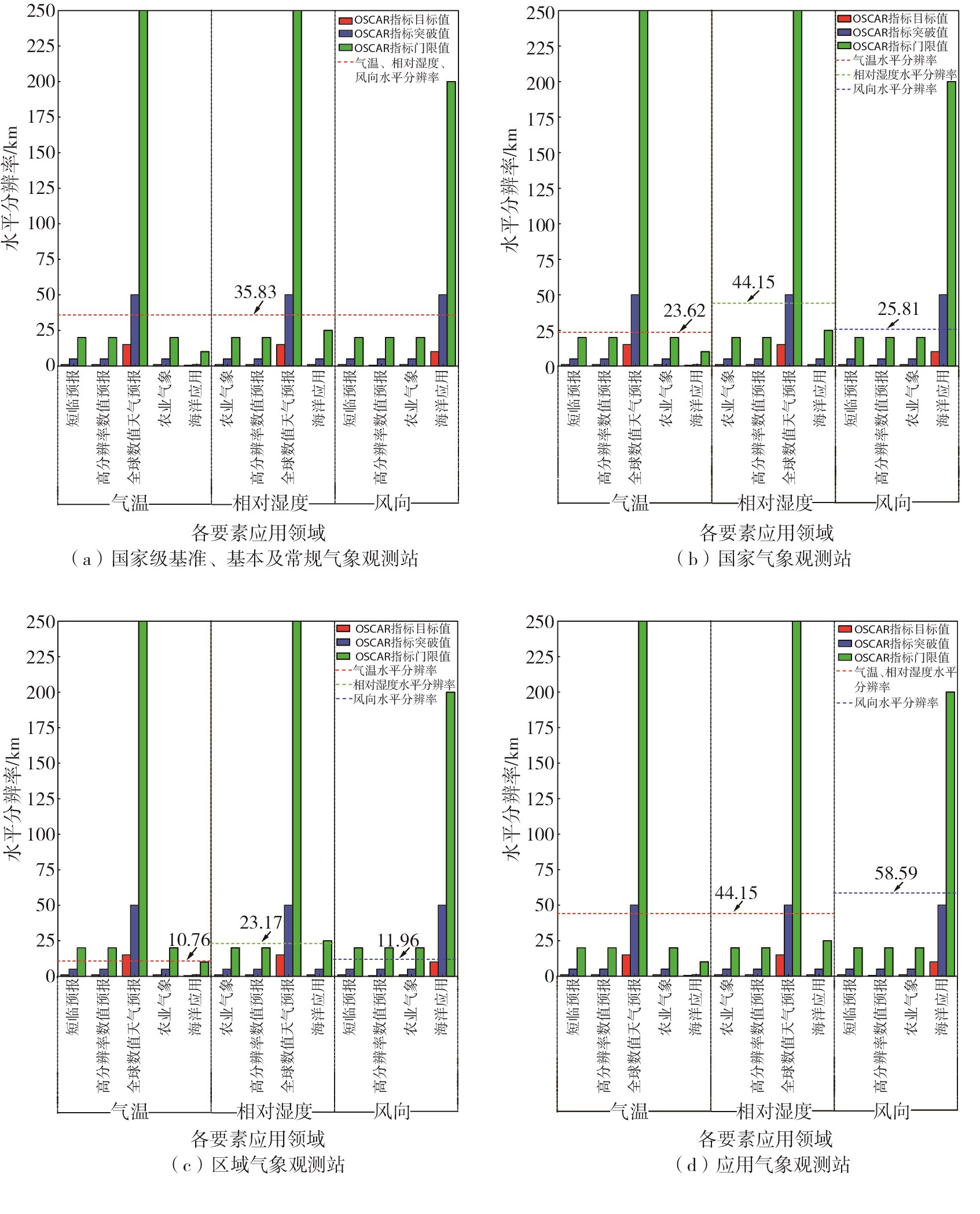
|
图 1 4类地面气象观测站气温、相对湿度、风向的水平分辨率与OSCAR各领域指标值对比 Fig.1 Comparison between horizontal resolution of temperature, relative humidity and wind direction of 4 types of surface meteorological observing stations and index values of various fields of OSCAR |
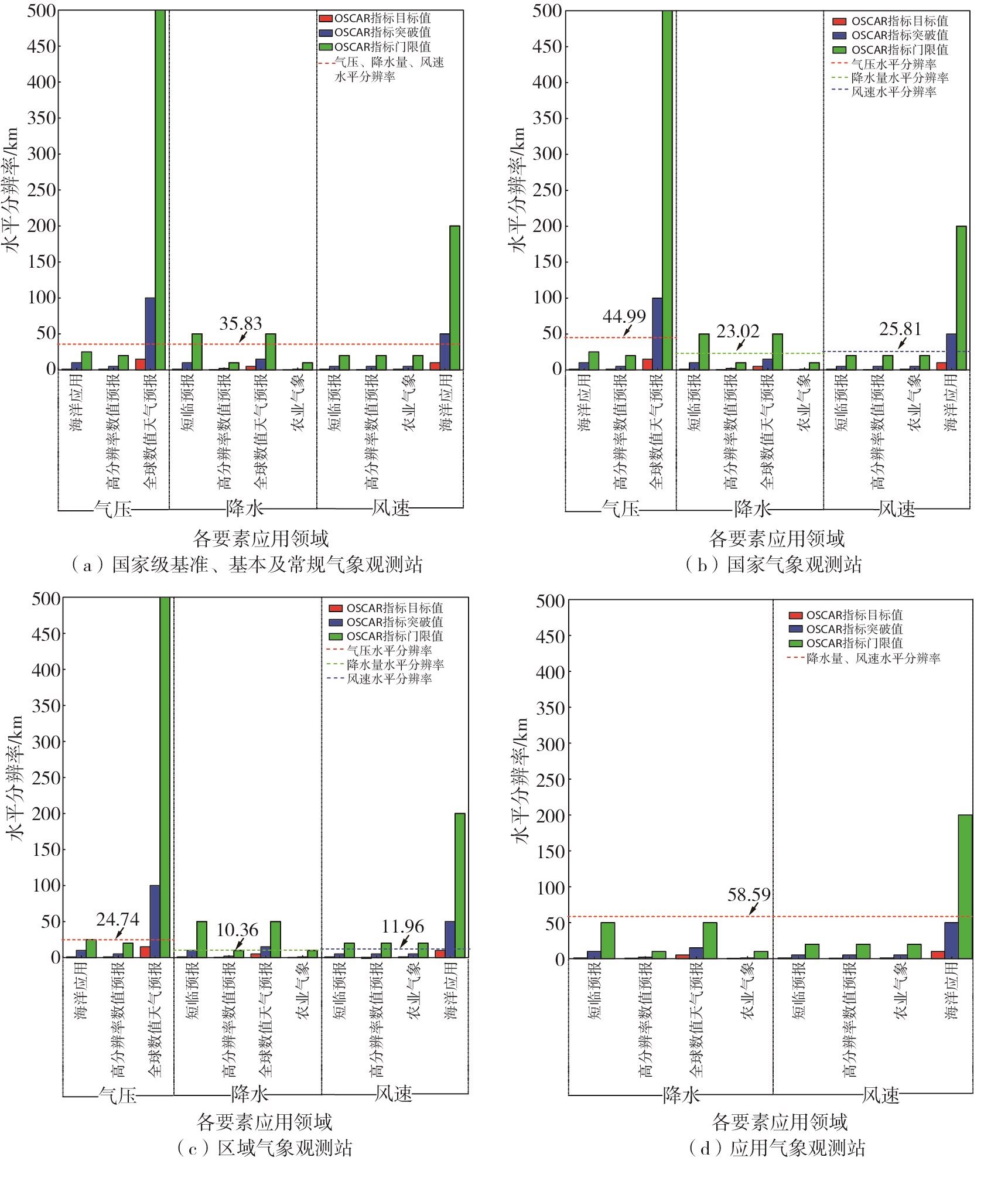
|
图 2 4类地面气象观测站气压、降水量、风速水平分辨率与OSCAR各领域指标值对比 Fig.2 Comparison between horizontal resolution of air pressure, precipitation and wind speed of 4 types of surface meteorological observing stations and index values of various fields of OSCAR |
综上,除全球数值天气预报和海洋应用领域外,4类地面气象观测站各要素水平分辨率相比OSCAR各应用领域突破值尚有较大差距。其中,区域气象观测站探测能力最好,应用气象观测站探测能力最弱。国家级基准、基本及常规气象观测站和国家气象观测站的气温、相对湿度、气压、风向和风速探测能力相当,降水量略优;区域气象观测站气温、降水量、风向和风速探测能力略优于气压和相对湿度;应用气象观测站气温、相对湿度探测能力优于风向和风速及降水量,降水量要素的探测能力最弱。
3.2 山东国家级基准、基本及常规气象观测站最佳布站方式和站间距 3.2.1 地面气温、相对湿度及降水量结构函数图 3a为山东国家级基准、基本及常规气象观测站日平均气温四季结构函数随距离变化特征。气温四季结构函数大致上随距离增加而增大,且随着距离的增加,结构函数的季节差异性也逐渐变大。其中,夏、秋、冬季结构函数差异不显著,春季结构函数明显大于其他3个季节,且结构函数随距离的变化
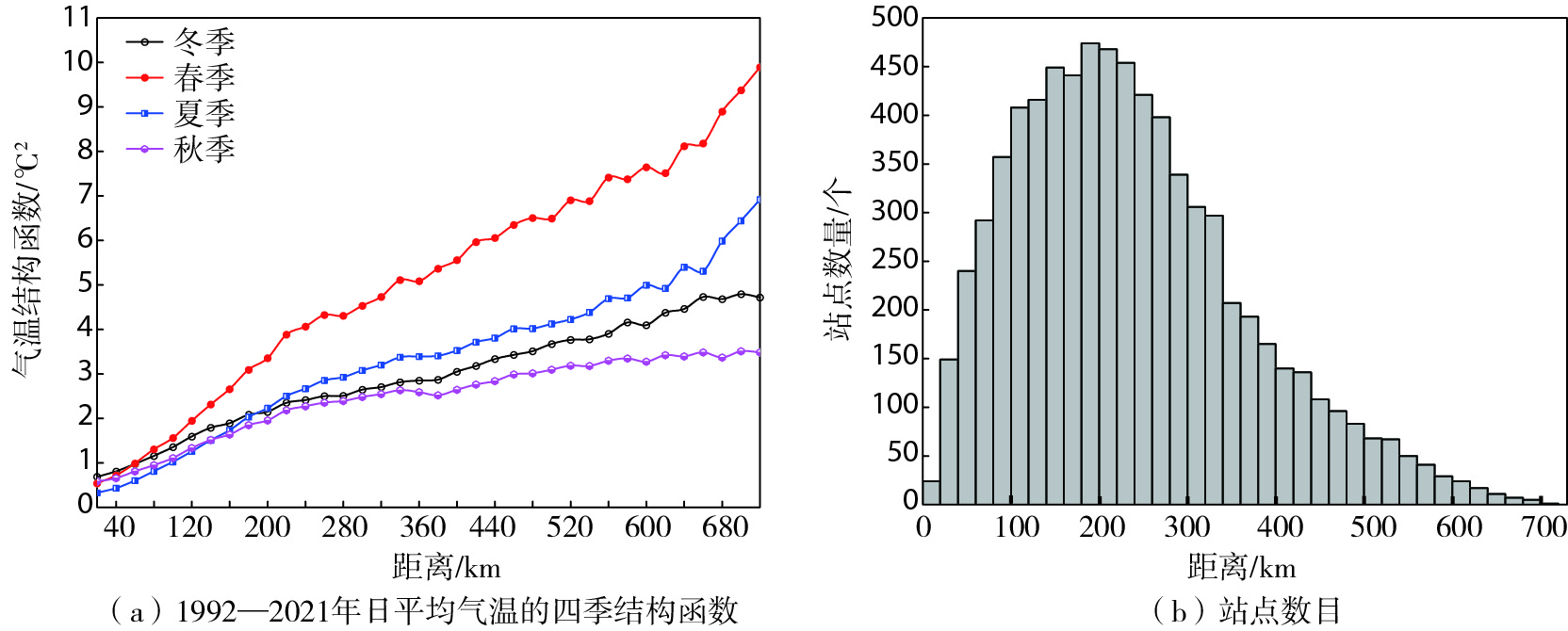
|
图 3 山东国家级基准、基本及常规气象观测站1992—2021年日平均气温四季结构函数及站点数目统计 Fig.3 Structure functions of 4 seasons' daily mean temperature of national reference, basic and conventional meteorological observing stations in Shandong from 1992 to 2021 and distribution of the number of stations |
更为剧烈一些。主要原因是山东春季处于冬、夏季风抗争的地带,冷暖气团进退不定,南北风交替十分频繁,导致气温变化幅度较大。距离小于600 km,气温四季结构函数变化较为平稳,近似线性,此后随着距离的增大,结构函数曲线波动较明显。由站点数量和距离的统计结果(图 3b)可见,600 km以后,随着距离的增加,站点数变得越来越少,站点样本数过少造成结构函数偏离度变大,出现较大的波动。
相对湿度四季结构函数基本随距离增加而增大,春季结构函数最大,夏季结构函数最小(图 4a)。其中,冬、春季相对湿度结构函数变化趋势基本一致,且其结构函数随距离的增加变化幅度明显,夏季相对湿度结构函数随距离的增大变化不明显。冬、春季冷空气影响频繁,空气干冷,地面相对湿度的空间变化率较大,而夏季空气相比冬春季要湿润一些,且气温相对高一些,因而其结构函数的分布也较为均匀。图 4b为降水量结构函数随距离的变化,夏季降水量结构函数较春、秋、冬季有明显差异,主要是由降水的随机性较大导致的。夏季降水量结构函数最大,冬季最小。夏季雨水丰沛,暴雨的小尺度特征明显,而冬季的降水量小且多为系统性降水,故其结构函数值也非常小,且结构函数随距离基本不变。相对湿度及降水量结构函数在远距离处出现的波动也是由于站点样本数过少,造成了结构函数偏离度变大。
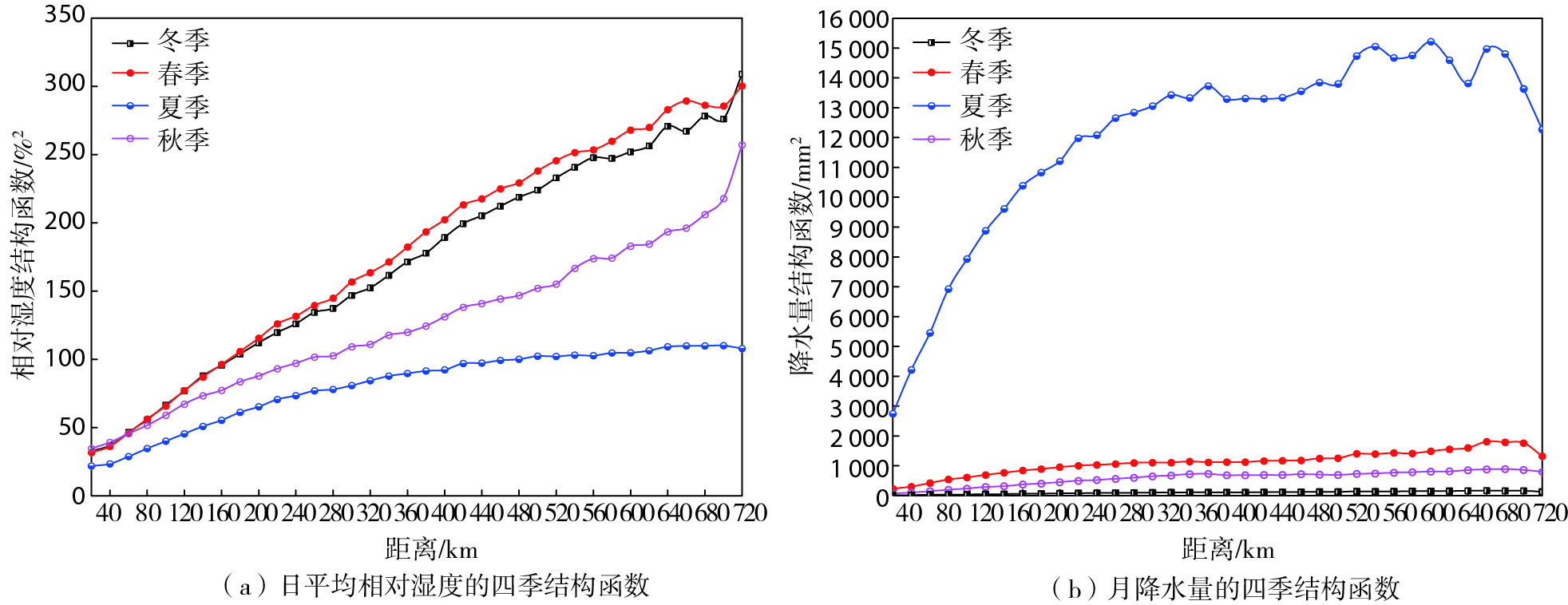
|
图 4 山东国家级基准、基本及常规气象观测站1992—2021年相对湿度和降水量的四季结构函数 Fig.4 Structure functions of 4 seasons' relative humidity and precipitation of national reference, basic and conventional meteorological observing stations in Shandong from 1992 to 2021 |
由于实际计算的结构函数为离散数据,为此需要对结构函数进行拟合。采用线性、二次多项式、三次多项式、指数4种函数对结构函数进行拟合,拟合结果(图略)显示,二次或三次多项式的拟合效果好。由公式(4)中bf′(0)>0的限制条件以及结构函数拟合要满足拟合精度高及拟合函数尽量简单等特点,故采用二次或三次多项式对气温、相对湿度及降水量的结构函数与距离的关系进行拟合,拟合后的回归方程见表 5。
|
|
表 5 山东国家级基准、基本及常规气象观测站1992—2021年日平均气温、日平均相对湿度及月降水量结构函数与距离的回归方程 Table 5 Regression equation of structure function and distance of daily mean temperature, daily mean relative humidity and monthly precipitation of national reference, basic and conventional meteorological observing stations in Shandong from 1992 to 2021 |
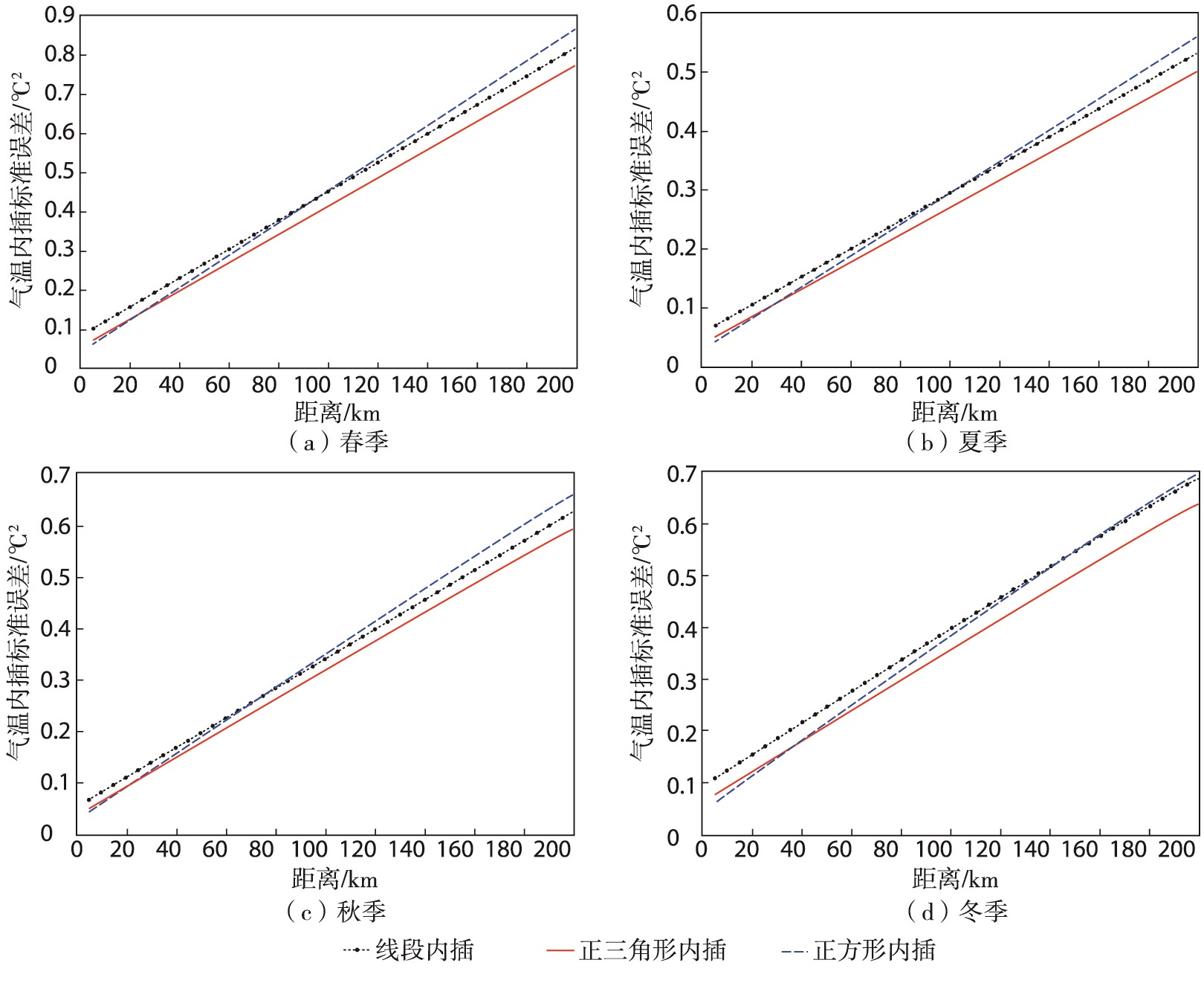
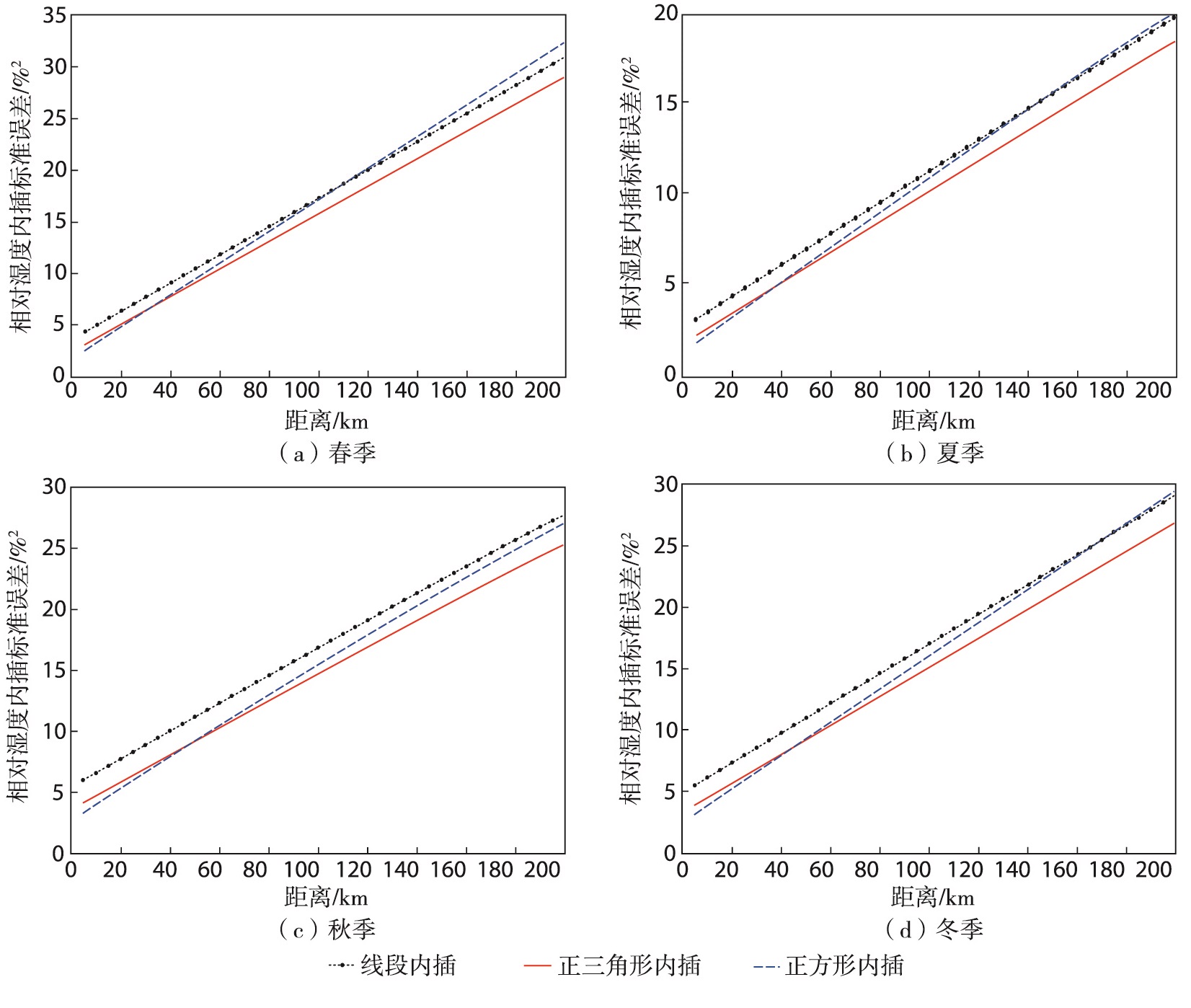
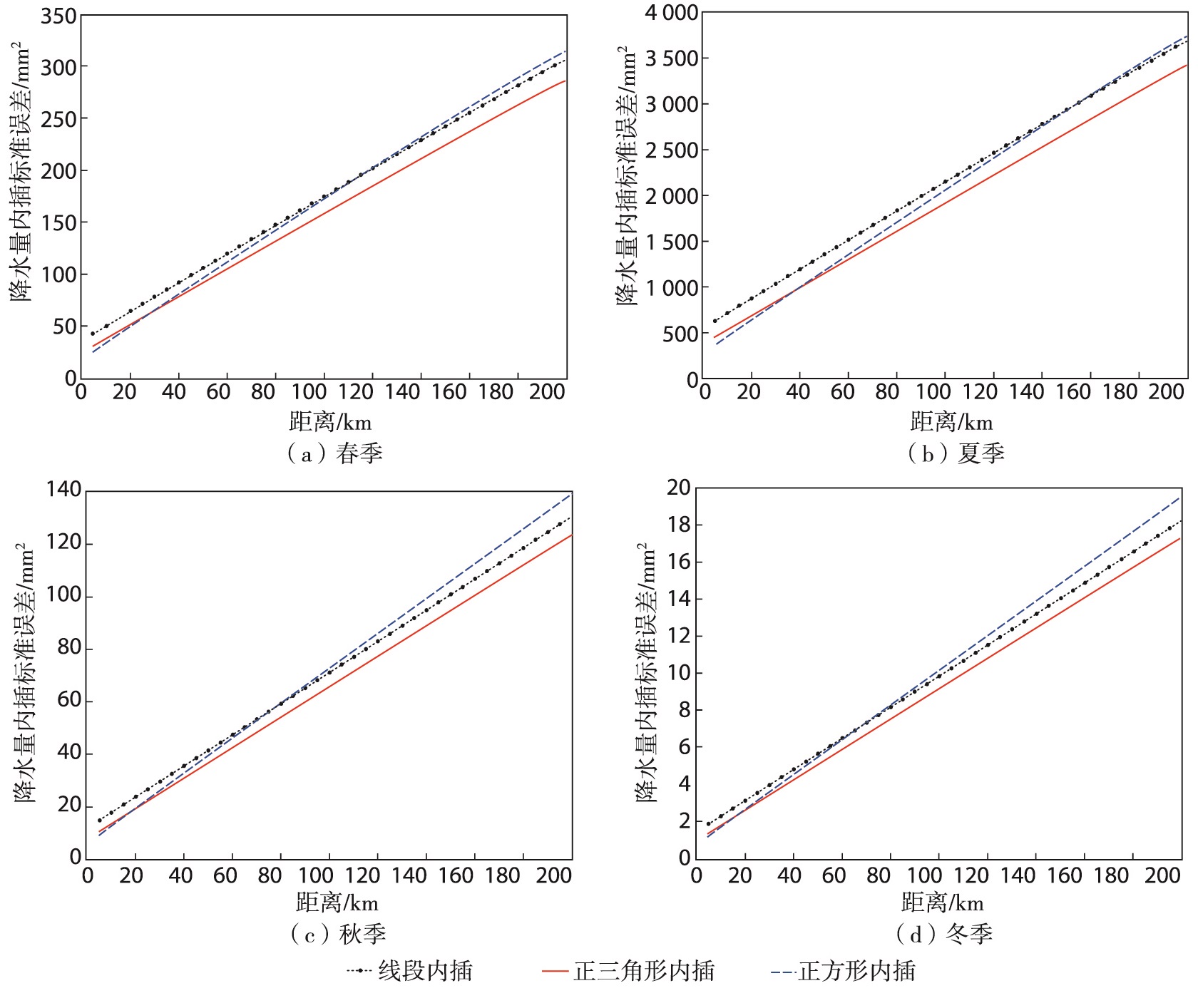
将表 5中各要素四季回归方程分别代入公式(6)—(8),即可得到气温、相对湿度及降水量在线段、正三角形、正方形3种内插方式下的内插标准误差与距离的关系式(式略)。由关系式绘制出日平均气温、日平均相对湿度及月降水量的内插标准误差与距离的关系曲线,见图 5—7。可见,四季的日平均气温、日平均相对湿度及月降水量在3种内插方式下的内插标准误差均随距离的增加而增大。对气温、相对湿度及降水而言,在距离越小的情形下,正方形内插精度最高,线段内插精度最低,而当距离超过某一临界距离阈值时,正三角形内插精度最高,正方形内插精度最低。且该临界距离阈值随观测要素和季节的不同而不同。
|
图 5 山东国家级基准、基本及常规气象观测站1992—2021年日平均气温在3种布站方案下的内插标准误差与距离的关系 Fig.5 Relationship between interpolation standard error and distance of daily mean temperature of national reference, basic and conventional meteorological observing stations in Shandong from 1992 to 2021 under three stationing schemes |
|
图 6 山东国家级基准、基本及常规气象观测站1992—2021年日平均相对湿度在3种布站方案下的内插标准误差与距离的关系 Fig.6 The same as Fig. 5, but for daily mean relative humidity |
|
图 7 山东国家级基准、基本及常规气象观测站1992—2021年月降水量在3种布站方案下的内插标准误差与距离的关系 Fig.7 The same as Fig. 5, but for monthly precipitation |
气温、相对湿度、降水量内插精度的季节性差异较大。气温内插标准误差由大到小的季节排序为春、冬、秋、夏;距离小于70 km,相对湿度内插标准误差由大到小的季节排序为秋、冬、春、夏,随距离变大,内插标准误差由大到小的季节排序为春、冬、秋、夏;降水量内插标准误差由大到小的季节排序为夏、春、秋、冬。春季气温内插误差最大,与春季结构函数最大相一致,主要是春季气温的时间变幅和空间梯度较大导致的;夏季相对湿度内插标准误差最小,与夏季结构函数最小是一致的;而冬季降水量的内插标准误差最小,与冬季的降水量相比其他季节都少有关。
3.2.3 最大容许内插标准误差及最大容许距离利用表 5各要素的回归方程分别求取其距离为零处的结构函数bf′(0),然后代入公式(10)即得到Emax。将Emax再分别代入到3.2.2节中得到的气温、相对湿度及降水量在线段、正三角形、正方形3种内插方式下的内插标准误差与距离的关系式中,即可得到各要素在线段、正三角形、正方形3种内插方式下的最大容许距离,结果见表 6。由最大容许距离,结合图 5—7,当距离满足点值内插标准误差小于观测标准误差时,气温、相对湿度和降水量均表现为正三角形内插精度最高,且正三角形内插的最大容许距离也最大。故对山东国家级基准、基本及常规气象观测站的气温、相对湿度和降水量,科学合理的布站方案均为正三角形布设。气温最佳布站距离应不超过43.6 km,相对湿度最佳布站距离应不超过63.4 km,降水量最佳布站距离应不超过40.3 km。
|
|
表 6 各观测要素在3种布站方案下的最大容许内插标准误差和最大容许距离 Table 6 The maximum allowable interpolation standard error and the maximum allowable distance of each observing element under three stationing schemes |
依据WMO的RRR原则,评估了山东4类地面观测站各要素的水平分辨率,与OSCAR不同气象应用领域的需求进行对比分析,评估了山东地面观测站网的探测能力。利用山东1992—2021年国家级基准、基本及常规气象观测站资料,基于结构函数研究了气温、相对湿度、降水量要素的最佳布站方案和最佳布站距离。主要结论如下:
(1) 就山东4类地面气象观测站各要素水平分辨率而言,区域气象观测站最小,应用气象观测站最大。国家气象观测站和区域气象观测站各要素水平分辨率由小到大依次为降水量、气温、风向和风速、相对湿度、气压,国家级基准、基本及常规气象观测站各要素的水平分辨率均相同,应用气象观测站气温与相对湿度要素的水平分辨率小于风向和风速及降水量。各地市地面观测网探测能力显示,济南、青岛、淄博、日照探测能力较强,临沂、菏泽、潍坊探测能力较弱。
(2) 除全球数值天气预报和海洋应用领域外,山东4类地面气象观测站各要素水平分辨率相比OSCAR各应用领域突破值尚有较大差距。区域气象观测站探测能力最好,应用气象观测站探测能力最弱。国家级基准、基本及常规气象观测站和国家气象观测站的气温、相对湿度、气压、风向和风速探测能力相当,降水量略优;区域气象观测站气温、降水量、风向和风速探测能力略优于气压和相对湿度;应用气象观测站气温、相对湿度探测能力优于风向和风速及降水量。
(3) 山东国家级基准、基本及常规气象观测站气温、相对湿度、降水量四季结构函数整体上随距离的增加而增大,结构函数的季节性差异明显。气温结构函数春季最大,秋季最小;相对湿度结构函数春季最大,夏季最小;降水量结构函数夏季最大,冬季最小。不同观测要素结构函数的季节性差异反映了各要素的时间变幅和空间梯度季节分布的不同。
(4) 山东国家级基准、基本及常规气象观测站气温、相对湿度、降水量的线段、正三角形、正方形内插标准误差与距离均呈线性关系,且随距离增加而增大。在距离满足点值内插标准误差小于观测标准误差时,气温、相对湿度和降水量均为正三角形内插精度最高。
(5) 山东国家级基准、基本及常规气象观测站的气温、相对湿度和降水量,最佳布站方案均为正三角形布设。气温最佳布站距离应不超过43.6 km,相对湿度最佳布站距离应不超过63.4 km,降水最佳布站距离应不超过40.3 km。
| [1] |
FENG S, HU Q, QIAN W H. Quality control of daily meteorological data in China, 1951-2000: a new dataset[J]. Int J Climatol, 2004, 24(7): 853-870. DOI:10.1002/joc.1047 |
| [2] |
高理, 刘焕彬. 1991—2021年山东省人体舒适度时空分布特征[J]. 海洋气象学报, 2023, 43(3): 71-79. DOI:10.19513/j.cnki.issn2096-3599.2023.03.007 |
| [3] |
ZHAO H, ZOU X L, QIN Z K. Quality control of specific humidity from surface stations based on EOF and FFT: case study[J]. Front Earth Sci, 2015, 9(3): 381-393. DOI:10.1007/s11707-014-0483-2 |
| [4] |
朱文刚, 李昌义, 车军辉. 基于统一高度Cressman方法的地面2 m气温客观分析[J]. 海洋气象学报, 2021, 41(2): 138-148. DOI:10.19513/j.cnki.issn2096-3599.2021.02.014 |
| [5] |
张茜茹, 陈益玲, 李长军, 等. 两种融合降水实况分析产品在山东地区的适用性评估[J]. 海洋气象学报, 2023, 43(2): 100-108. DOI:10.19513/j.cnki.issn2096-3599.2023.02.009 |
| [6] |
李伶杰, 胡庆芳, 黄勇, 等. 近实时卫星降水数据对南京"20170610" 极端性强降水过程的监测分析[J]. 高原气象, 2018, 37(3): 806-814. |
| [7] |
DROZDOV O A, SHEPELEVSKII A A. The theory of interpolation in a stochastic field of meteorological elements and its application to meteorological map and network rationalization problems[J]. Trudy Niu Gugms, 1946, Series 1: No.13. |
| [8] |
MOOLEY D A, ISMAIL M. Structure functions of rainfall field and their application to network design in the tropics[J]. Arch Meteor Geophys Bioclimatol Ser B, 1982, 30(1): 95-105. |
| [9] |
SCHNEEBELI M, LATERNSER M. A probabilistic model to evaluate the optimal density of stations measuring snowfall[J]. J Appl Meteor, 2004, 43(5): 711-719. |
| [10] |
廖洞贤. 最优测站距离、最优垂直分层和最优观测时间间隔的决定[J]. 气象学报, 1985, 43(2): 153-161. |
| [11] |
卢文芳, 王永华. 空间结构函数在上海地区气象站网设计中的应用[J]. 南京气象学院学报, 1989, 12(3): 325-332. |
| [12] |
赵瑞霞, 李伟, 王玉彬, 等. 空间结构函数在北京地区气象观测站网设计中的应用[J]. 应用气象学报, 2007, 18(1): 94-101. |
| [13] |
白光弼, 刘岳俊. 高原和山区气象站网的合理布局[J]. 陕西气象, 1992(3): 18-21. |
| [14] |
于杰, 曾文华, 王建刚. 中国东南地区气象要素场线性内插标准误差初步分析[J]. 解放军理工大学学报(自然科学版), 2003, 4(5): 95-99. |
| [15] |
岑思弦, 李跃清, 赖欣. 四川降水相关函数场的分析及其在气象观测站网布局中的应用[J]. 干旱气象, 2015, 33(5): 874-881. |
| [16] |
MUNN R E. The design of environmental monitoring systems[J]. Prog Phys Geog: Earth Environ, 1980, 4(4): 567-576. |
| [17] |
许小峰. 世界气象组织观测系统的需求与评估[EB/OL]. (2022-4-12)[2023-07-28]. https://blog.sciencenet.cn/blog-1310230-1333587.html.
|
| [18] |
GANDIN L S. The planning of meteorological station networks[R]. Geneva: WMO, 1970.
|
| [19] |
吴薇, 黄晓龙, 周春花, 等. 四川省地面雨量站站网现状分析[J]. 气象科技, 2023, 51(5): 639-647. |
 2024, Vol. 44
2024, Vol. 44

