2. 南京信息工程大学海洋科学学院, 南京 210044;
3. 自然资源部空间海洋遥感与应用重点实验室, 北京 100081
2. School of Marine Sciences, Nanjing University of Information Science & Technology, Nanjing 210044, China;
3. Key Laboratory of Space Ocean Remote Sensing and Applications, Ministry of Natural Resources, Beijing 100081, China
海浪谱又称海浪的能量谱,表示海浪的能量随不同频率(波数)、方向的分布,是随机海浪的一个重要统计性质,是研究海洋的重要物理量。利用海浪谱可以计算有效波高(significant wave height,SWH)和周期,再利用波高和波长的概率密度分布,即可推算出海洋内部由哪些组成波构成,不仅如此,海浪谱还可以给出海浪的外部特征[1]。
目前全球海浪谱信息的获取主要依靠海浪的数值模拟和卫星观测。数值模拟已经发展到第三代海浪模式,比如近岸波浪模式(Simulating WAves Nearshore,SWAN)、第三代波浪模式(WAVEWATCH Ⅲ,简记为“WW3”)等[2-3]。对于卫星观测,目前主要有合成孔径雷达[4-5]和星载波谱仪。合成孔径雷达探测全球海浪谱有自身的缺陷[6-8],并且该卫星数据资料昂贵,业务化生成全球海浪谱尚有困难。截至目前,全球范围内专门用于测量海浪谱的卫星仅有一颗,即2018年10月发射的中法海洋卫星(China-France Oceanography SATellite,CFOSAT)。
CFOSAT是一颗小型卫星,由法国国家空间研究中心(Centre National d'Études Spatiales,CNES)和中国国家航天局(China National Space Administration,CNSA)联合开发。其上搭载的SWIM(Surface Waves Investigation and Monitoring)波谱仪可以测量二维海浪谱。该雷达有6个旋转的波束,其中心入射角分别为0°、2°、4°、6°、8°和10°,孔径为2°×2°,旋转速度为5.7 r·min-1,可以进行360°全方位扫描[9-10]。SWIM从谱波束(6°、8°和10°)观测中得到海浪方向谱,进而计算主波波长(peak wave length, PWL)和主波波向(peak wave direction, PWD)等海浪信息,其测量的70~500 m波长范围内的海浪谱质量已经过较多验证[11-12]。星下点0°波束能提供有效波高和海面风速的信息,类似于高度计的功能,该有效波高的质量达到了高度计的水平,可以作为全球有效波高的新数据源[13]。
实际海浪谱的应用主要基于L2产品,该产品在CNES和中国国家卫星海洋应用中心(National Satellite Ocean Application Service,NSOAS)相关网站都可以下载。虽然双方网站提供数据使用的算法一致,但数据产品也有区别:(1)由于法方和中方卫星数据接收站不相同,卫星0级数据在下传地面后,中法双方的数据文件划分长度不一,因此就会产生不同的文件,最终海浪谱也有一定差异;(2)中法双方地面处理软件在L1A产品生成L2产品时,都需要输入辅助气象数据,该辅助气象数据包括模式风、波高、海面温度等信息,以进行初步的异常回波筛选。法方采用的是欧洲中期天气预报中心(European Centre for Medium-Range Weather Forecasts,ECMWF)提供的定制数据,中方则是自主研发的辅助气象产品,这也会导致两者最终海浪产品有一定区别。这两种区别对最终海浪谱影响程度如何,尚需探讨。为了明晰中法L2海浪谱数据的差异,文中将搜集到的中法双方L2海浪谱数据进行对比分析。
1 数据与方法 1.1 卫星数据CFOSAT SWIM L2数据来自法国CNES网站(https://www.aviso.altimetry.fr/home.html)和中国NSOAS网站(https://osdds.nsoas.org.cn)[14]。研究使用2024年3月1—31日收集的6.2.0版本的L2数据。
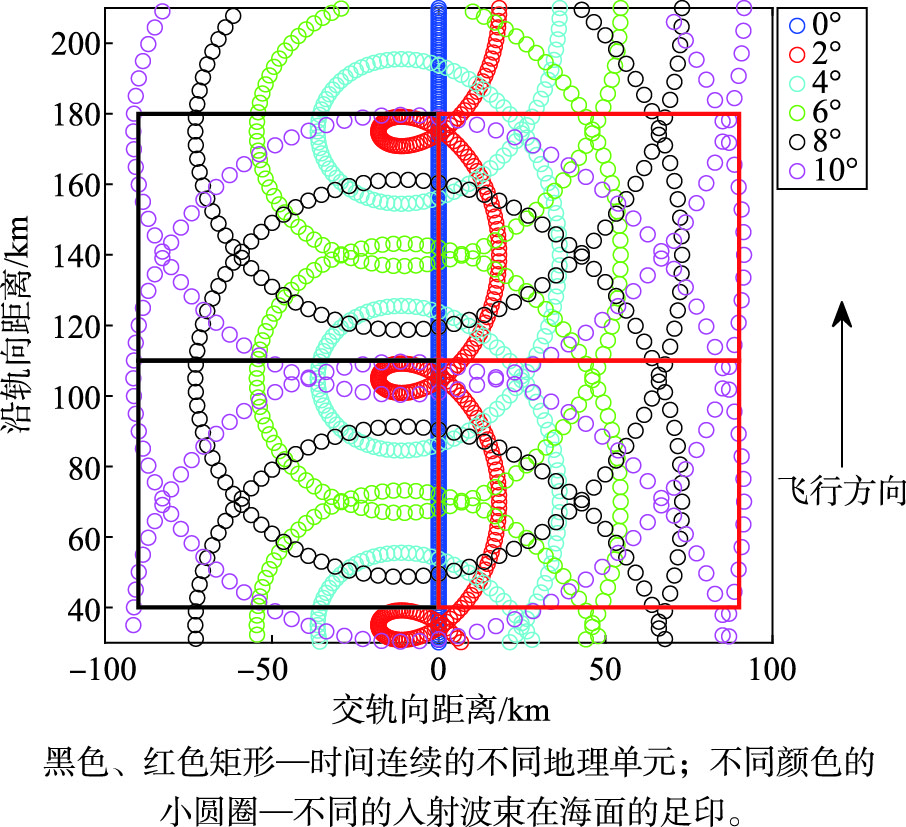
SWIM天线以接近6 r·min-1的速度绕轴旋转,旋转一圈的时间约为10 s。也就是说,海洋表面的大地理单元大小沿轨道约为70 km,横跨轨道约为180 km,如图 1所示。一个轨道数据约包含500×2个地理单元,即左地理单元和右地理单元,卫星飞行方向左侧黑色矩形为左地理单元,右侧红色矩形为右地理单元[15]。对于每个地理单元,SWIM L2产品都会获取一个二维海浪谱,但该二维海浪谱具有180°模糊,即只给出了0°~180°方位角范围的海浪谱信息。同时,每个谱波束(6°、8°和10°)实际上都可以单独获取一个二维海浪谱。相对应地,每个二维海浪谱可以获取3个主要的海浪参数,即有效波高、主波波长和主波波向。
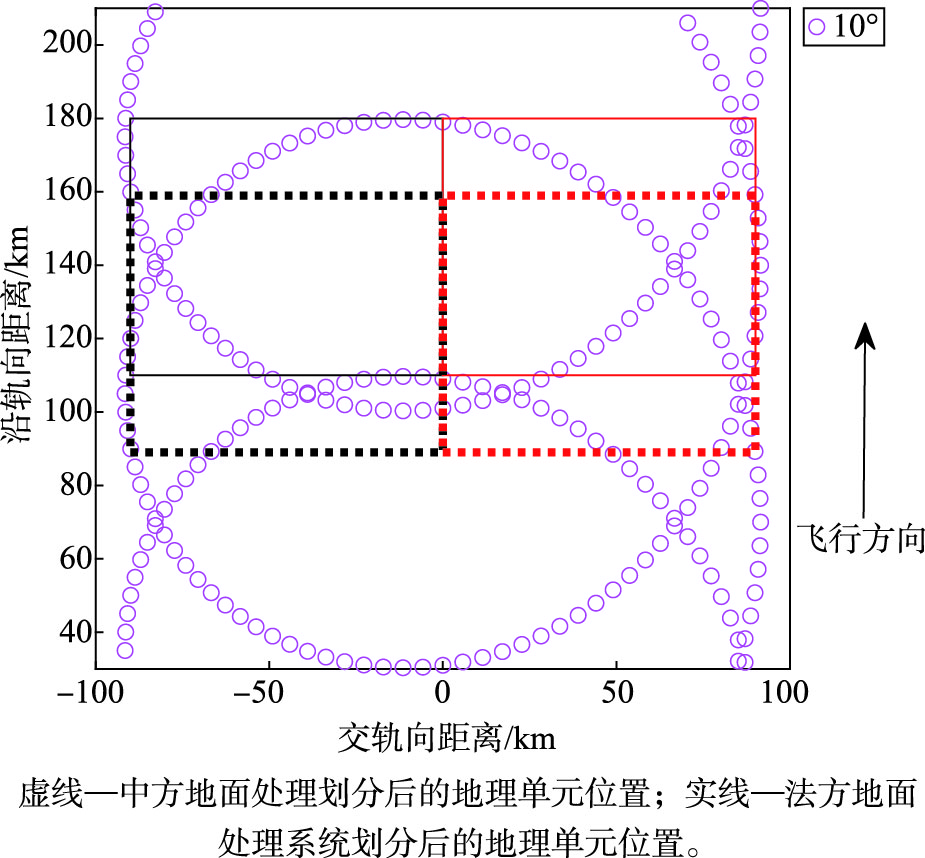
1.2 数据匹配方法中法数据卫星接收站的不同,会导致图 1中地理单元划分的差异。每个地理单元大概有48个宏周期(6个波束分别一次连续发射接收完回波所用的总时间,即为一个宏周期)对应的波形,即不同接收站接收的起始波形是不同的,导致不同地理单元中用来制作二维海浪谱所用到的48个波形就会有区别。由于每个地理单元覆盖海面的时间基本稳定在10 s,因此中法不同数据处理结果会导致地理单元最多有5 s的区别。图 2展示了两者差3 s导致的地理单元海面覆盖面积的区别(为了清晰显示,只画了10°波束的足印),卫星轨迹地面飞行速度约为7 km·s-1,故2个地理单元在飞行方向覆盖面积有约21 km的距离差别。由于接收起始数据存在一定的随机性,因此双方数据存在0~5 s,即0~35 km的距离差别。
|
图 1 SWIM的6个波束在海面上的足迹几何形状以及地理单元在海面的覆盖示意图[15] Fig.1 Footprint geometry of SWIM's 6 beams on the sea surface and schematic representation of the coverage of geographical boxes on the sea surface |
|
图 2 中方和法方SWIM地理单元划分区别 Fig.2 Difference between Chinese and French SWIM geographical box division |
不同地理单元覆盖海面的差别会导致二维海浪谱反演时输入的回波波形不同,所以二维海浪谱结果有差异。为了获取不同地理单元划分之后海浪谱产品的差异,文中对一个月的L2产品分别进行5.0 s、3.0 s、1.0 s和0.1 s的时间匹配,即分别将这4个时间差别的中方数据和法方数据认定为同一地理单元,以检验不同起始数据和不同辅助气象数据对海浪谱结果的影响。
在分析参数一致性时,采用的各指标计算公式[13]分别为:
| $ V_{\text {Bias }}=\frac{1}{N} \sum\limits_{i=1}^N\left(A_i-B_i\right), $ | (1) |
| $ V_{\mathrm{STD}}=\sqrt{\frac{1}{N-1} \sum\limits_{i=1}^N\left(A_i-B_i-V_{\mathrm{Bias}}\right)^2} \text {, } $ | (2) |
| $ V_{\mathrm{RMSE}}=\sqrt{\frac{1}{N} \sum\limits_{i=1}^N\left(A_i-B_i\right)^2}, $ | (3) |
| $ I_{\mathrm{S}}=\frac{\sqrt{\frac{1}{N} \sum\limits_{i=1}^N\left[\left(A_i-\bar{A}\right)-\left(B_i-\bar{B}\right)\right]^2}}{\bar{B}}, $ | (4) |
| $ R=\frac{\sum\limits_{i=1}^N(A-\bar{A})(B-\bar{B})}{\sqrt{\sum\limits_{i=1}^N\left(A_i-\bar{A}\right)^2\left(B_i-\bar{B}\right)^2}} $ | (5) |
其中:VBias为偏差值,A、B为卫星测得的SWH、主波波长或主波波向,N为匹配对的总数量,VSTD为标准偏差(standard deviation, STD)值,VRMSE为均方根误差(root mean square error, RMSE)值,IS为散点指数,A和B分别为A和B的平均值,R为相关系数。
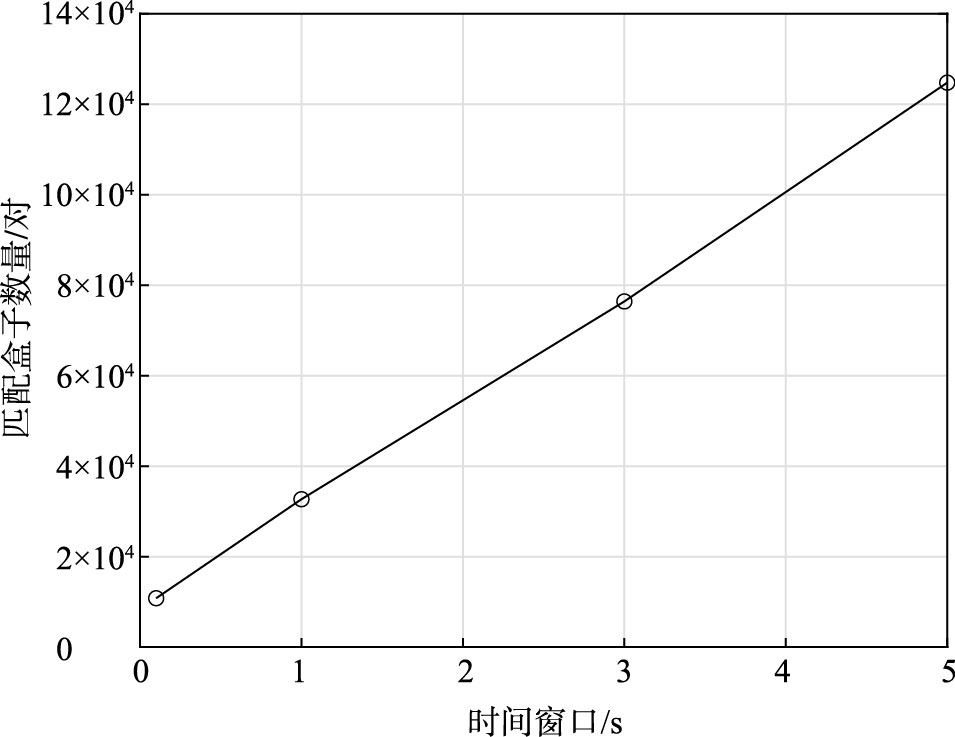
2 中法双方产品一致性分析根据中法双方发布的波谱仪产品,可以通过匹配不同时间差别来分析海浪谱主要参数的一致性特征。图 3给出了4个匹配时间获取的一个月的匹配地理单元数量。通过该图可以看出,两个产品的匹配地理单元数量与时间窗口成线性关系,时间窗口越小,匹配地理单元数量越少,时间窗口越大,匹配地理单元数量越多。数量基本与匹配时间成线性关系,说明中法两种地理单元内波形的起始时间差别是均匀随机分布。
|
图 3 匹配时间为5.0 s、3.0 s、1.0 s和0.1 s时对应的匹配数量 Fig.3 The number of collocations at the matching time of 5.0 s, 3.0 s, 1.0 s and 0.1 s, respectively |
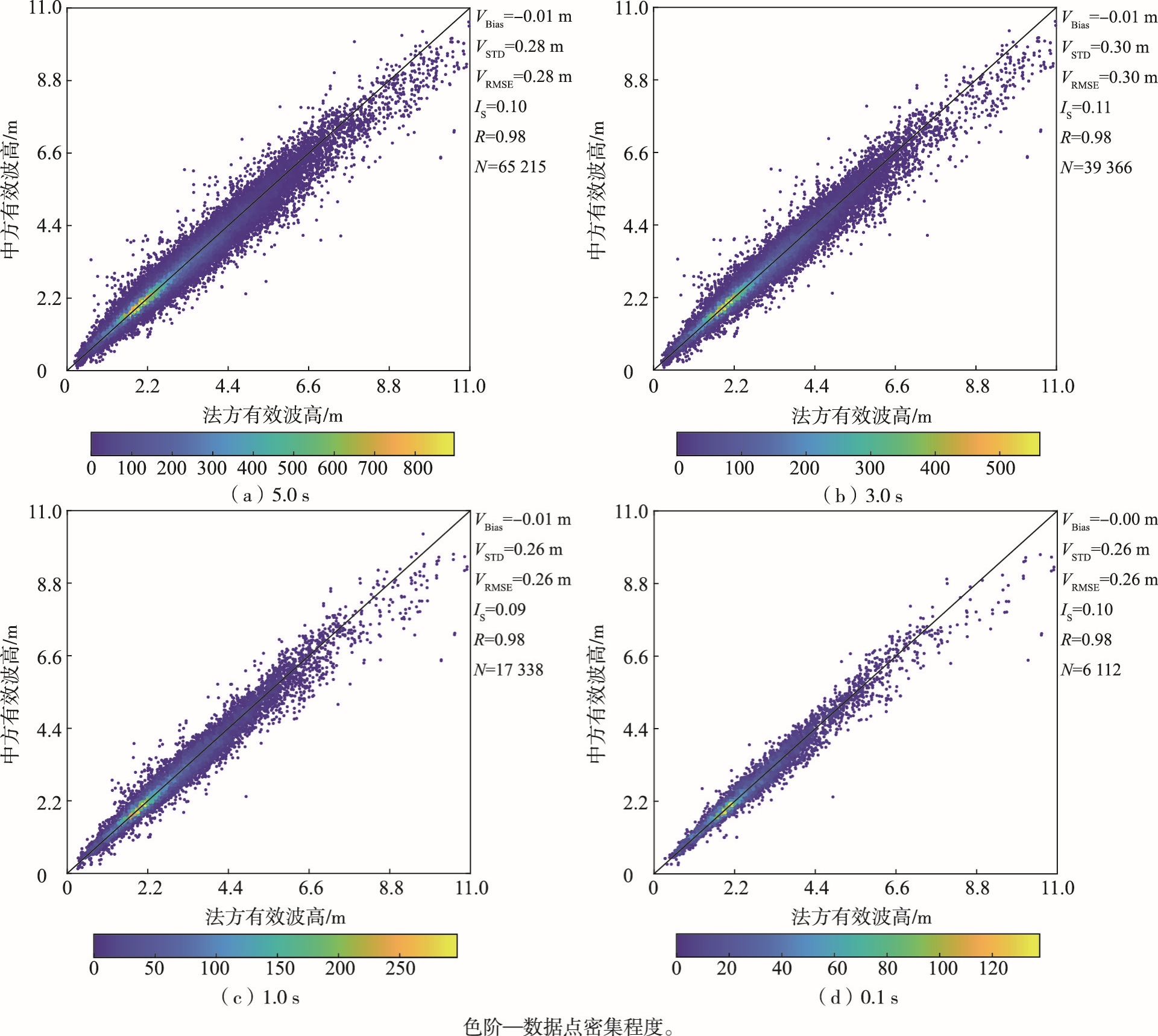
图 4、5、6分别给出了有效波高、主波波长和主波波向的中法产品在匹配时间为5.0 s、3.0 s、1.0 s和0.1 s时的对比图。
|
图 4 匹配时间为5.0 s、3.0 s、1.0 s和0.1 s时中法双方有效波高产品对比 Fig.4 Comparison between Chinese and French SWH at the matching time of 5.0 s, 3.0 s, 1.0 s and 0.1 s, respectively |
|
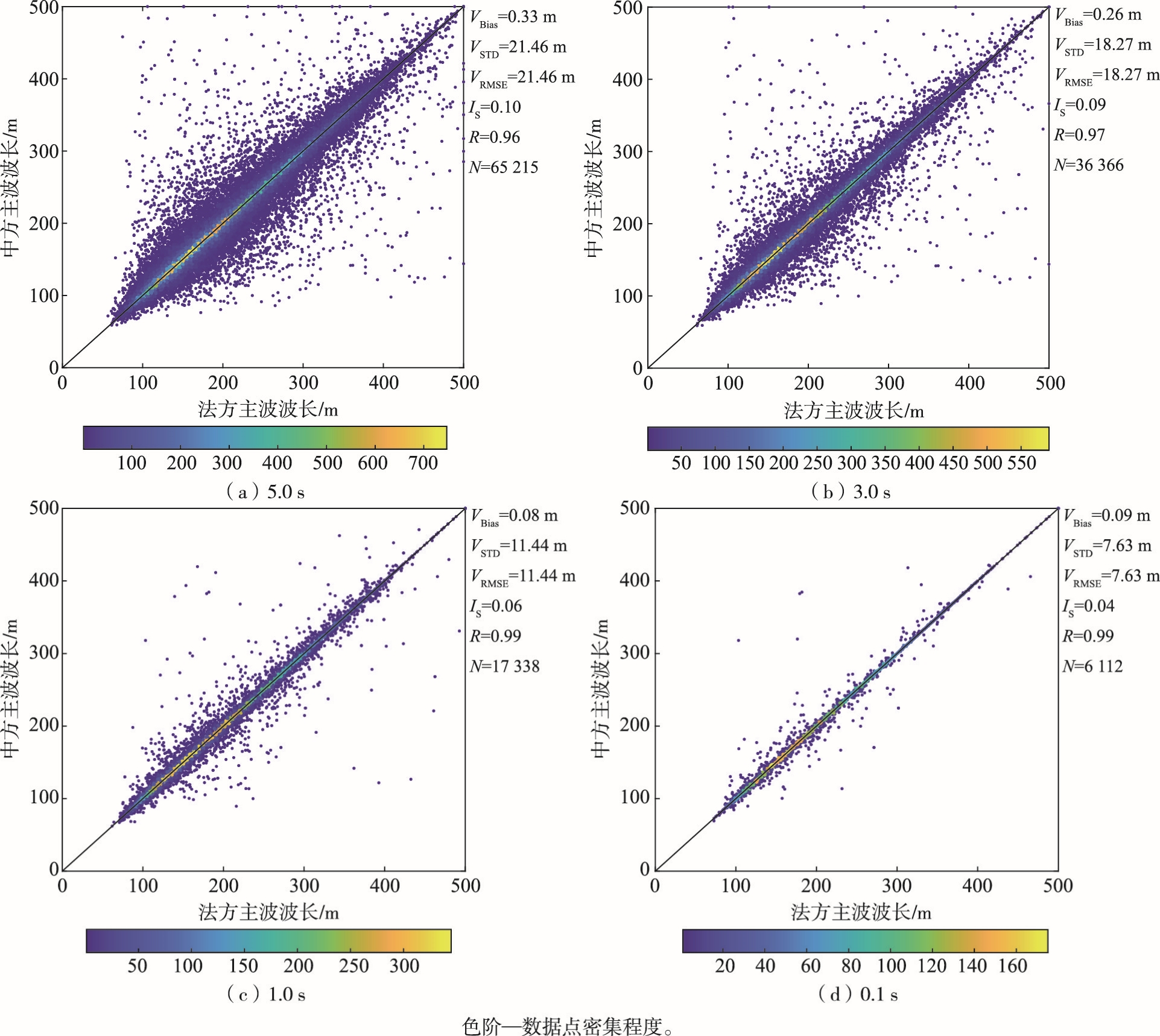
图 5 匹配时间为5.0 s、3.0 s、1.0 s和0.1 s时中法双方主波波长产品对比 Fig.5 Comparison between Chinese and French peak wave length at the matching time of 5.0 s, 3.0 s, 1.0 s and 0.1 s, respectively |
|
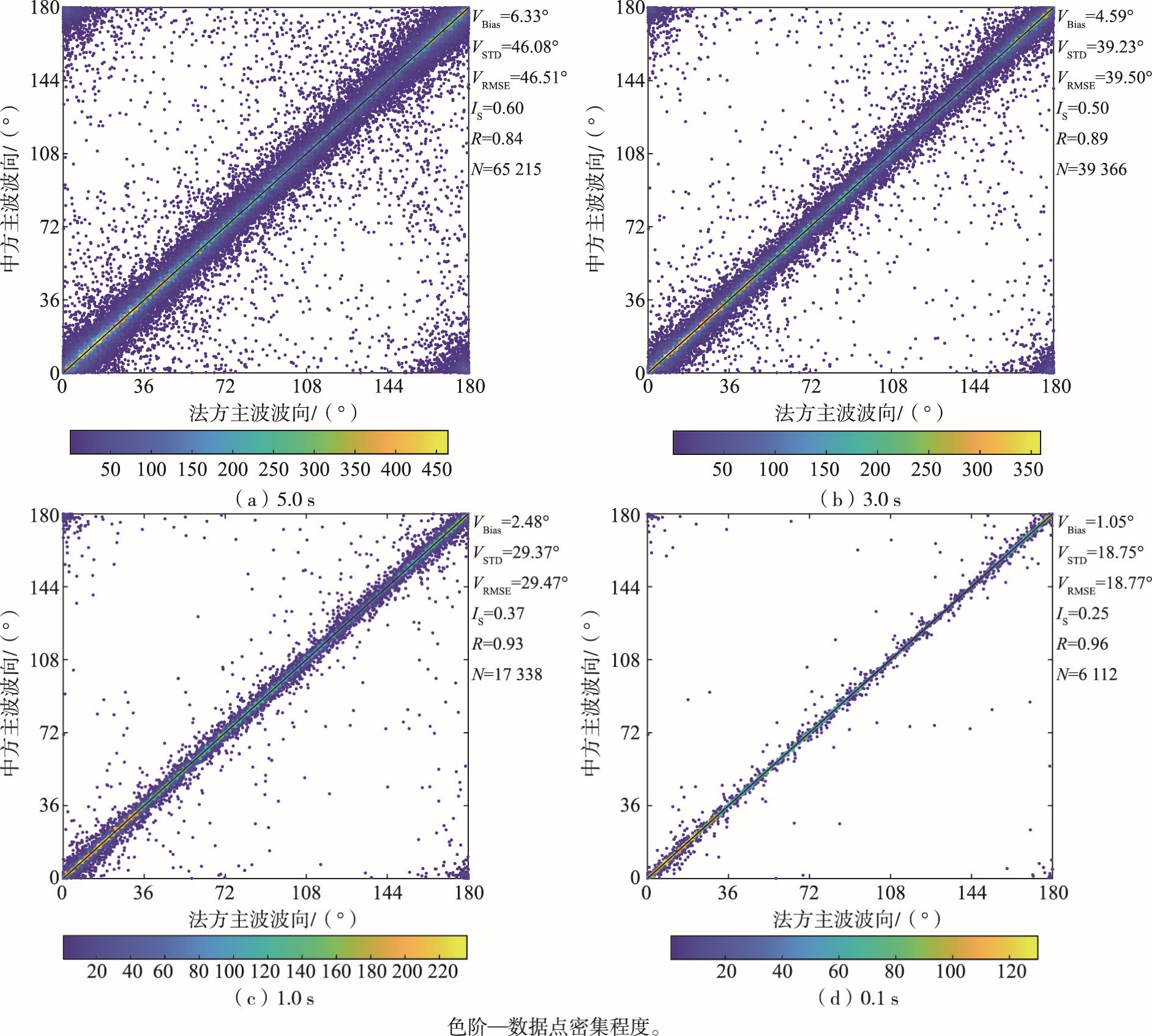
图 6 匹配时间为5.0 s、3.0 s、1.0 s和0.1 s时中法双方主波波向产品对比 Fig.6 Comparison between Chinese and French peak wave direction at the matching time of 5.0 s, 3.0 s, 1.0 s and 0.1 s, respectively |
由图 4中法有效波高RMSE在0.26~0.28 m范围的变化表明,有效波高产品在35 km左右的海面空间变化范围内,探测结果基本不变。实际上,有效波高产品目前是星下点观测结果,即该结果在35 km变化范围内,有效波高基本没有变化。另外,由于星下点有效波高观测精度原本就在0.5 m以内,因此RMSE在该范围之内变化符合产品设计指标[14]。
图 5中的主波波长时间窗口在0.1~5.0 s变化时RMSE逐渐增加,说明时间窗口越大,该参数相差越大,也就是主波波长变化相对有效波高来说更敏感。但5.0 s时间窗口差别最大,也不超过25 m,表明半个地理单元的窗口差距,最多会导致25 m的主波波长误差。而0.1 s时间窗口时,RMSE为7.63 m,两者几乎完全一致,表明当两者输入的波形接近时,得到的主波波长可认为没有变化,即说明由于中法输入的辅助气象数据的差异带来的主波波长差异可以忽略不计。标准偏差(STD)、散点指数(IS)和相关系数(R)的变化特征也表明了和RMSE一致的结果。
图 6表明主波波向和主波波长存在同样的结论,即半个地理单元(35 km)的空间差距可以造成主波波向不超过47°的差异,即中法双方产品由于不同辅助气象数据输入导致的主波波向差异很小。标准偏差(STD)、散点指数(IS)和相关系数(R)的变化特征也表明了和RMSE一致的结果。
综合图 4—6,中法产品主波波长和波向在时间窗口为5.0 s时差异最大,这种差异主要是由35 km的空间跨度导致的波长和波向的变化,并非是由双方地面处理导致的差异,因为时间窗口为0.1 s时差异非常小。也就是说,当每个地理单元输入波形相同时,波长波向基本一致,辅助气象数据不同引起的结果差异有限。有效波高由于其精度本身就在0.5 m以内,且在35 km范围内,其真值变化不大,故差异和匹配时间几乎没有关联性。
为了探讨中法双方二维海浪谱之间的差异,通过公式(6),计算得到不同时间窗口时差异随波数和方位角二维分布的平均态。
| $ \delta E(k, \varphi)=\overline{\left[E_{\mathrm{C}}(k, \varphi)-E_{\mathrm{F}}(k, \varphi)\right] / E_{\mathrm{F}}(k, \varphi)}, $ | (6) |
其中,δE(k, φ)为平均误差,EC(k, φ)为中方二维海浪斜率谱,EF(k, φ)为法方二维海浪斜率谱,k为波数,φ为方位角。
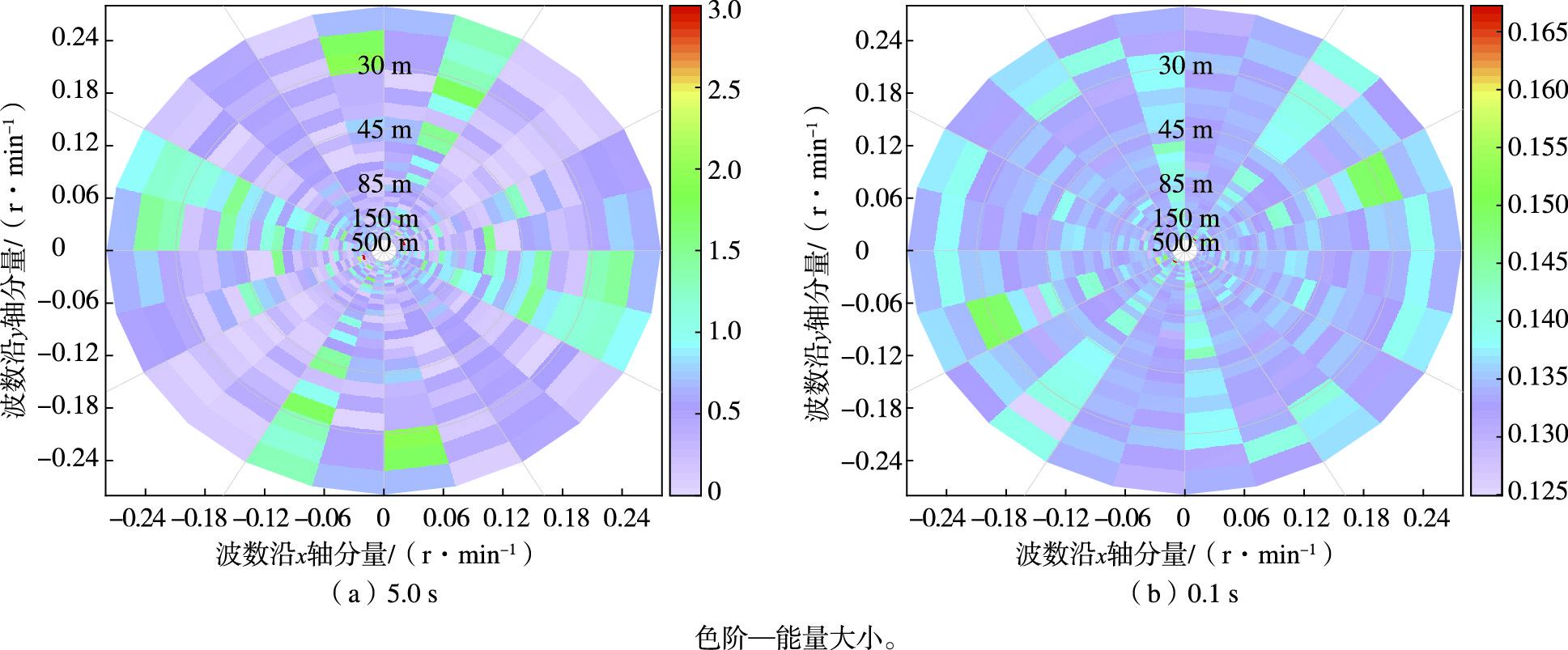
由图 7可以看出,随着匹配时间减小,相对差异逐渐减小,这与主波波长和波向参数结果是一致的。由色阶可以看出,在匹配时间为5.0 s时,差别明显大于0.1 s。0.1 s的相对差异在16.5%以内。这些差异随波数和方位角分布没有明显规律,具有一定随机性。
|
图 7 匹配时间为5.0 s和0.1 s时中法双方二维海浪斜率谱产品对比 Fig.7 Comparison between Chinese and French two-dimensional wave slope spectrum at the matching time of 5.0 s and 0.1 s, respectively |
CFOSAT SWIM波谱仪是世界上第一颗专门用于测量海浪谱的星载传感器,目前其数据产品由法方CNES和中方NSOAS提供分发服务。虽然两者提供的产品版本一致,但由于数据接收站差异和初始输入辅助气象数据差异,导致其产品有一定区别。分别收集2个机构提供的2024年3月1—31日的波谱仪L2产品,对其进行数据匹配,从而得到了产品一致性情况的分析,其结论如下:
(1) 2个波谱仪L2产品地理单元划分时输入的起始波形序号是均匀随机的,即2个产品匹配时,匹配时间窗口越长,匹配后的数据对越多。
(2) 有效波高比较稳定,在最大半个地理单元的空间差别下仍然保持几乎不变的精度。
(3) 随着匹配时间增加,主波波长和主波波向差异越来越大;匹配时间为5.0 s时,两者分别达到约21.5 m和46.5°的差异,这个差异是由波浪性质随海面空间变化引起,而非双方产品误差。
(4) 匹配时间为0.1 s时,主波波长和波向差异很小,即中法不同地面处理系统输入的气象辅助数据源差异而引起的产品差别可以忽略。
(5) 中法二维海浪斜率谱差异随波数和波向的分布具有一定随机性,在16.5%以内。
综上所述,中法双方产品可以被认为结果一致。中法双方目前已经提供了长达5年的海浪产品,在海浪数据同化等产品应用方面发挥着重要作用。随着数据处理方法的更新和改进,未来将在海浪预报等海洋环境信息和服务等方面发挥更积极的作用。
致谢: 感谢法方CNES和中方NSOAS提供的免费下载SWIM波谱仪数据服务。
| [1] |
文圣常, 余宙文. 海浪理论与计算原理: 科学出版社, 1984.
|
| [2] |
SHENG Y X, SHAO W Z, LI S Q, et al. Evaluation of typhoon waves simulated by WaveWatch-Ⅲ model in shallow waters around Zhoushan Islands[J]. J Ocean Univ China, 2019, 18(2): 365-375. DOI:10.1007/s11802-019-3829-2 |
| [3] |
ZHENG K W, SUN J, GUAN C L, et al. Analysis of the global swell and wind sea energy distribution using WAVEWATCH Ⅲ[J]. Adv Meteor, 2016, 8419580. |
| [4] |
SCHULZ-STELLENFLETH J, LEHNER S, HOJA D. A parametric scheme for the retrieval of two-dimensional ocean wave spectra from synthetic aperture radar look cross spectra[J]. J Geophys Res, 2005, 110: C05004. |
| [5] |
WANG H, MOUCHE A, HUSSON R, et al. Quantifying uncertainties in the partitioned swell heights observed from CFOSAT SWIM and sentinel-1 SAR via triple collocation[J]. IEEE Trans Geosci Remote Sens, 2022, 60: 4207716. |
| [6] |
ULABY F T, LONG D G. Microwave radar and radiometric remote sensing[M]. Ann Arbor: University of Michigan Press, 2015.
|
| [7] |
KERBAOL V, CHAPRON B, VACHON P W. Analysis of ERS-1/2 synthetic aperture radar wave mode imagettes[J]. J Geophys Res, 1998, 103(C4): 7833-7846. DOI:10.1029/97JC01579 |
| [8] |
HASSELMANN K, HASSELMANN S. On the nonlinear mapping of an ocean wave spectrum into a synthetic aperture radar image spectrum and its inversion[J]. J Geophys Res, 1991, 96(C6): 10713-10729. DOI:10.1029/91JC00302 |
| [9] |
HAUSER D, TOURAIN C, HERMOZO L, et al. New observations from the SWIM radar on-board CFOSAT: instrument validation and ocean wave measurement assessment[J]. IEEE Trans Geosci Remote Sens, 2021, 59(1): 5-26. DOI:10.1109/TGRS.2020.2994372 |
| [10] |
TISON C, HAUSER D. SWIM products users guide: product description and algorithm theoretical baseline description[EB/OL]. (2019-06-07)[2024-05-12]. https://mobile.aviso.altimetry.fr/fileadmin/documents/data/tools/SWIM_ProductUserGuide.pdf.
|
| [11] |
XU Y, LIU J Q, XIE L L, et al. China-France Oceanography Satellite (CFOSAT) simultaneously observes the typhoon-induced wind and wave fields[J]. Acta Oceanol Sin, 2019, 38(11): 158-161. DOI:10.1007/s13131-019-1506-3 |
| [12] |
HAUSER D, TOURAIN C, HERMOZO L. Synthesis of cal-val studies at mid_calval[EB/OL]. (2019-10-05)[2024-05-12]. https://ftpaccess.aviso.altimetry.fr.
|
| [13] |
LI X Z, XU Y, LIU B C, et al. Validation and calibration of nadir SWH products from CFOSAT and HY-2B with satellites and in situ observations[J]. J Geophys Res: Oceans, 2021, 126(2): e2020JC016689. DOI:10.1029/2020JC016689 |
| [14] |
郎姝燕, 孙从容, 鲁云飞, 等. 中法海洋卫星微波散射计近海岸产品在台风遥感监测中的应用[J]. 海洋气象学报, 2022, 42(2): 74-80. |
| [15] |
LI X Z, KARAEV V, PANFILOVA M, et al. Measurements of total sea surface mean square slope field based on SWIM data[J]. IEEE Trans Geosci Remote Sens, 2022, 60: 5114109. |
 2024, Vol. 44
2024, Vol. 44


