2. 中国科学院大学,北京 100190;
3. 南京信息工程大学海洋科学学院,江苏 南京 210044;
4. 国家卫星海洋应用中心,北京 100081;
5. 自然资源部空间海洋遥感与应用重点实验室,北京 100081
2. University of Chinese Academy of Sciences, Beijing 100190, China;
3. School of Marine Sciences, Nanjing University of Information Science & Technology, Nanjing 210044, China;
4. National Satellite Ocean Application Service, Beijing 100081, China;
5. Key Laboratory of Space Ocean Remote Sensing and Applications, Ministry of Natural Resources, Beijing 100081, China
中法海洋卫星(China-France Oceanography SATellite,CFOSAT)搭载的波谱仪和微波散射计能够获取全球的海浪谱、有效波高、海面风场等海洋动力学参数。同时,风场数据可用于台风结构分析,提供更精细的风力信息,支持气象预报和海洋防灾决策[1]。卫星获得的在轨数据涵盖海气相互作用、海冰监测等领域,并在宽刈幅有效波高、风浪关系、热带海洋环境预报和台风监测等方面发挥着至关重要的作用[2]。
卫星搭载的微波散射计(CFOSAT SCATterometer,CSCAT) 采用扇形波束旋转扫描系统,能够快速覆盖地球表面,并且在保持相对缓慢扫描速度的同时增加了测量样本数量,在短时间内实现对同一分辨单元多维度的观测[3]。在刈幅中间的大部分区域,观测的组合次数至少可以超过10次,有效提升了风场反演的准确性[4]。而在后向散射测量和风场反演过程中,难以避免噪声的影响。董楹等[5]的研究中分析了仪器噪声和地球物理噪声随观测角度、海况以及网格分辨率的变化,结果表明,在满足海面风场观测需求的同时,地球物理噪声在影响微波散射计测量后向散射系数方面具有关键作用,并为星载Ku波段微波散射计近海岸风场反演提供了重要指导意义。
文中对重新定标后的数据特性进行了分析,并对地球物理噪声的影响进行了评估。由于新版本数据的定标系数存在差异,导致对后向散射测量误差的估计不同。分析结果旨在量化测量过程中的不确定性,涵盖了系统热噪声及信号衰落导致的传输误差,以及海面风场非一致性(即地球物理噪声)的影响[6]。目前,针对地球物理噪声的研究重点在于提升卫星微波散射计在海面风场反演中的精度和可靠性,为地球物理模型的完善和风场反演精度的提升提供科学的参考依据。
1 原理与方法 1.1 海洋定标在进行回波信号的距离向处理时,以约10 km为单位划分连续条带,随后进行定标处理。基于数值天气预报(numerical weather prediction,NWP)的海洋定标法(NWP Ocean Calibration,NOC)[7],使用地球物理模型函数(geophysical model function,GMF)对测量的后向散射与NWP风场输入的仿真值进行比较,以评估测量数据和仿真数据之间的差异。GMF模型描述了仿真的后向散射系数和平均风矢量之间的相关性,该经验模型可用于估计给定风速、风向和入射角下的后向散射系数[8]。因此定标值为
| $ \varDelta \sigma^0(\theta)=B_0^{\text {scat }}(\theta)-B_0^{\mathrm{NWP}}(\theta)。$ | (1) |
其中:Δσ0(θ)为定标值,B0scat(θ)为散射计测量值,B0NWP(θ)为NWP风场仿真值,θ为入射角。
当定标值随着时间趋于稳定时,可以将其视为仪器固有偏差或校正因子。NOC的优点在于能在短时间内广泛应用于全球海洋数据,并获得较为精确的测量结果,详细的定标流程如图 1所示。
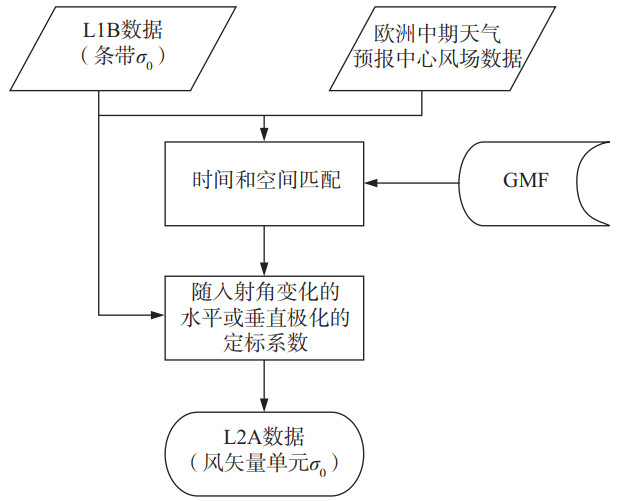
|
图 1 海洋定标数据处理流程 Fig.1 NOC processing flow |
基于CSCAT实际系统设计的特征,由于传输功率和信噪比相对较低,这将对后向散射的测量产生影响。测量的精度通常通过归一化标准差(Kp)来评估[9],参数值一般表述为
| $ K_{\mathrm{p}}=\frac{\sqrt{\delta\left[\sigma_{\text {meas }}^0\right]}}{\varepsilon\left[\sigma_{\text {meas }}^0\right]} $ | (2) |
其中:σmeas0为测量的后向散射系数,ε[σmeas0]为后向散射系数均值,δ[σmeas0]为后向散射系数方差,Kp数值越小则表示测量的后向散射系数越准确。通常,Kp被认为包含3个独立的变量,传输误差(Kpc)、定标误差(Kpr)和模型误差(Kpm)[10],即:
| $ K_{\mathrm{p}}=\sqrt{K_{\mathrm{pc}}^2+K_{\mathrm{pr}}^2+K_{\mathrm{pm}}^2}。$ | (3) |
定标误差Kpr是用于计算雷达方程中定标因子的误差。在数据处理中,雷达中所有关于定标因子的设备参数(如天线增益方向图、接收机增益、插入损耗)都应在发射前或发射后进行校准。发射、接收通道和星载处理时可能会产生漂移,通过在轨定标和地面定标结合的方式进行校准[11]。模型误差Kpm与目标固有的空间和时间可变性有关,如海洋的GMF模型中剔除了降雨情况下的风变化。通过选择高σ0稳定性的扩展目标,将Kpm降低到适当的值。
Kpc为由雷达固有的衰落效应和接收机热噪声的影响引起的σ0测量误差,与雷达的系统设计和测量几何有关,可以看成系统的固有偏差,不受定标影响。Kpc可以表示为信噪比(signal-to-noise ratio,SNR)的函数[4]:
| $ K_{\mathrm{pc}}=\sqrt{A+\frac{B}{V_{\mathrm{SNR}}}+\frac{C}{V_{\mathrm{SNR}}{ }^2}} 。$ | (4) |
其中:A、B和C为参数,已在发射前确定,表示与调制特性、滤波和信号带宽有复杂的相关性;VSNR为信噪比值。可以看到,Kpc与条带SNR密切相关。该表达式意味着,对于SNR较低的情况(例如低风速或大入射角),Kpc值会变大。对于给定的一组观测几何结构和微波散射计参数,SNR和Kpc被视为风速和入射角的函数。
对于L2A数据,剔除了陆地、降雨和海冰的影响,误差包括2个不同的误差源:仪器噪声(Kpc,代指由L1B传递到L2A的传递误差)和地球物理噪声(Kpg)。对于海面风单元来说,地球物理噪声主要是由风矢量单元(wind vector cell,WVC)内风的变化和雷达测量中空间不一致性导致的[12]。图 2中不同的椭圆代表了不同的波束足印被划分在同一个风单元内,因此不均一采样导致了所谓的空间误差。
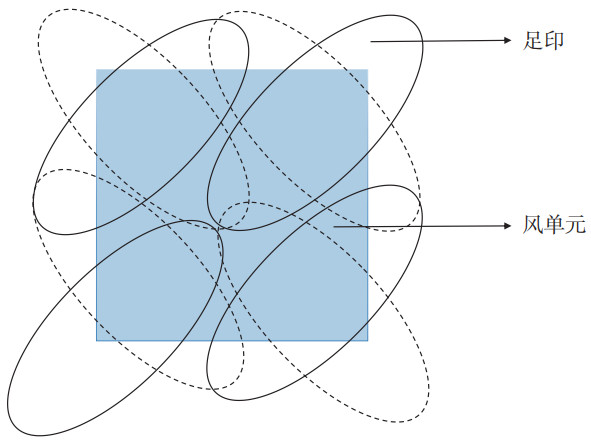
|
图 2 不同波束足印被划分在同一风矢量单元内的分布情况 Fig.2 Distribution of different beams' footprint divided into the same WVC |
风矢量反演过程采用最大似然估计对测量的后向散射系数估计最佳风场。反演利用一个风矢量单元中的一组视数和Kp值,并通过GMF搜索最佳的仿真后向散射系数。风场反演的代价函数(fMLE)[13]如下:
| $ f_{\mathrm{MLE}}=\frac{1}{N} \sum\limits_{i=1}^N \frac{\left(\sigma_{\mathrm{m}i}^0-\sigma_{\mathrm{s} i}^0\right)^2}{\left(K_{\mathrm{p} i} \times \sigma_{\mathrm{m} i}^0\right)^2} 。$ | (5) |
其中:N是具有不同入射角和方位角的观测数,σmi0是第i个视图的平均测量后向散射系数,σsi0是通过NSCAT-4模型的仿真值。Kpi是后向散射系数测量值的归一化标准差,计算公式[14]如下:
| $ K_{\mathrm{p} i}=\frac{\sqrt{\frac{1}{M} \sum\limits_{j=1}^M\left(\sigma_{\mathrm{m} i, j}^0-\sigma_{\mathrm{m} i}^0\right)^2}}{\sigma_{\mathrm{m} i}^0} 。$ | (6) |
其中:M是整合到第i个视数中的条带总数,σmi, j0是第j个条带的相应后向散射值。CSCAT结合多解方案(multiple solution scheme,MSS)进行风场反演,将风向细分,通过对代价函数求极小值计算得到与之相对应的风矢量[15]。通过Kpi,即获得某个视图的总Kp,并且通过
如图 3所示,卫星的轨道足迹被细分成网格,沿轨道方向形成一系列行信息,交轨向取得列信息。每一列包含42个风单元(25 km分辨率单元),从最左端到最右端(以卫星飞行方向为参考)分别标记为1~42。在L1B数据中,通过将信号回波划分为大约10 km间隔的条带,每个条带对应着一定数量的WVC。WVC可分为刈幅边缘风单元、最佳风单元和近星下点单元3个区域,随着卫星移动、天线旋转的变化,每个风单元网格中都会获得各种不同条带的入射角和方位角的测量组合(图 2)。在每个WVC中,将条带划分为多个不同视图,通过判断极化、方位角和入射角,然后将相似条件加权划分到同一视图(通常入射角小于2°、方位角小于6°)。在数据处理过程中,每个有效的风矢量单元包含2~16个视图(一个视图通常包括25~50个条带)[4]。由图 4可以看出最佳风矢量单元包含最多的视图,因为入射角和方位角分布有诸多组合方式,这有利于风场的反演。在近星下点位置,方位角主要分布在0°和180°左右,而入射角有所不同。刈幅边缘风矢量单元则在方位角上分布更为广泛,但入射角最大。
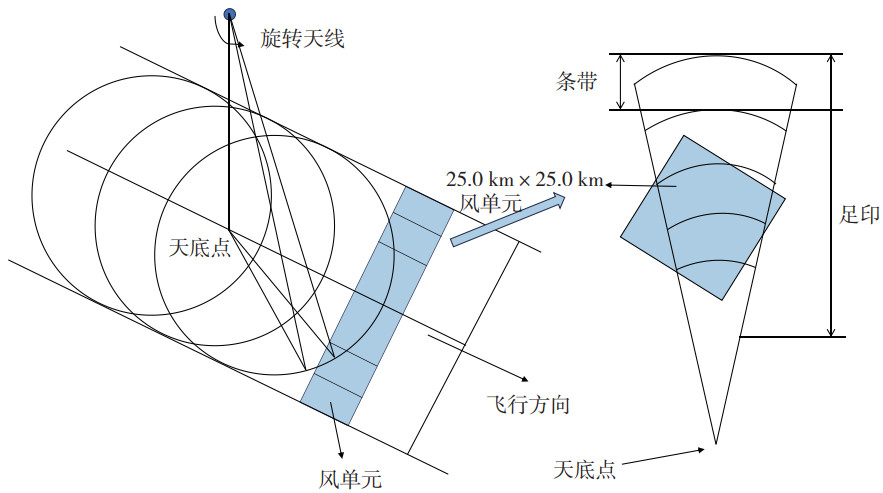
|
图 3 卫星观测刈幅内风单元和条带划分 Fig.3 WVC and slice division of satellite swath |
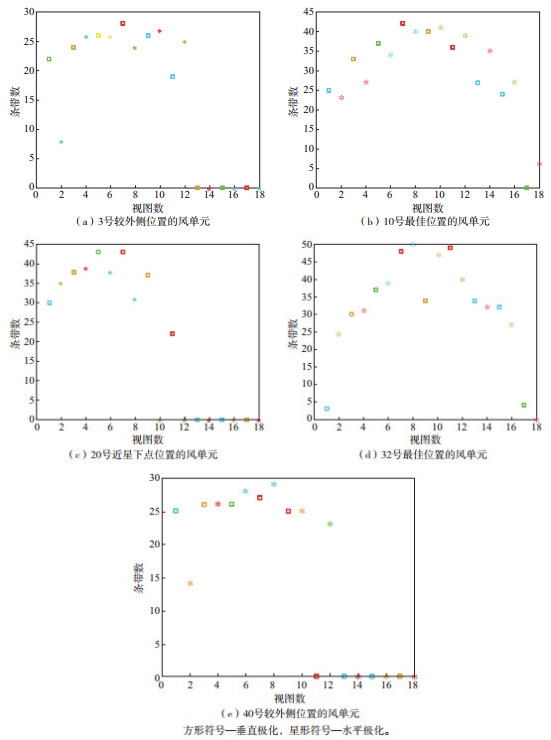
|
图 4 不同风单元位置每个视图被划分的条带个数 Fig.4 The number of slices of each view at different WVC locations |
图 4表示2019年3月1日第1 871轨数据的第700行(L2A一轨数据1 720行)每个风矢量单元中每个视图相对应的条带数量。与最低点风单元和刈幅较外侧风矢量单元相比,10号和32号附近代表了最佳风单元位置涵盖的视图更广泛。将这些充分观测到的后向散射系数组合应用到地球物理模型中,可获得高质量的海面风速和风向信息。对应于公式(6),即有更丰富的条带信息来计算L2A数据风单元的Kpi。
3 结果分析 3.1 NOC系数NOC方法通过比较测量的后向散射数据与欧洲中期天气预报中心(European Centre for Medium-Range Weather Forecasts,ECMWF)风场数据模拟的后向散射值,以消除系统偏差。定标中参考Mou等[16]对数据的一致性分析,选取2021年3月上旬3.0版较稳定的数据计算12.5 km和25.0 km的NOC系数,该系数随后被应用于L2A数据处理的流程。为保证数据的准确性,通过质量控制环节,排除陆地、海冰及降雨等因素的干扰。
根据上述部分的定标原理,NOC系数可以表示为入射角的函数,入射角范围为28°~51°,划分间隔为1°。如图 5所示,随着入射角的增加,水平和垂直极化校正的绝对值显著增大。与仿真的后向散射系数相比,微波散射计测量的后向散射系数偏差主要来自刈幅远端,且在水平极化条件下的偏差相比于垂直极化要大,差异范围为0~1.4 dB。造成这种现象的原因在于水平极化中信噪比偏低,尤其在低风速环境下,出现了较多的负σ0值。另外,对比不同分辨率的定标系数,发现存在细微偏差,这主要归因于不同分辨单元内部风的变异性。
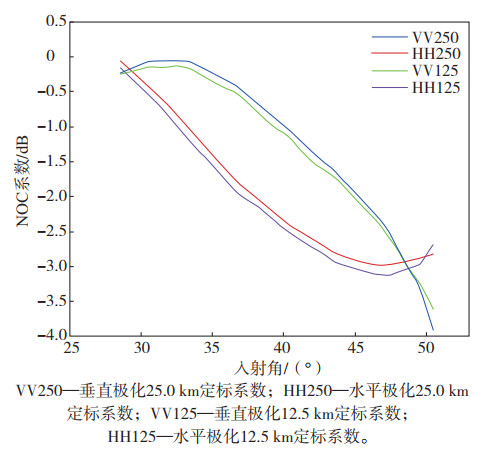
|
图 5 NOC系数随入射角、极化和空间分辨率的变化 Fig.5 Variation of NOC coefficient with incidence angle, polarization and spatial resolution |
原则上,条带σ0的精度由测量的SNR、条带带宽、脉冲时间和接收窗口决定。系统参数在发射前已经确定,σ0的精度取决于发射后的信噪比。鉴于L1B产品中并无真实的风,通过几何关系将风速插值到相应的位置。图 6展示了不同风速条件、入射角度和极化方式下条带信噪比的分布特性。结果表明,信噪比随着风速的增加而增大,而在低风速环境下(如风速小于5 m·s-1),所有观测的信噪比均小于0 dB;信噪比最大值出现在入射角约为39°处,角度与天线峰值增益角度一致。此外,对比不同极化情况,水平极化的信噪比普遍低于垂直极化。
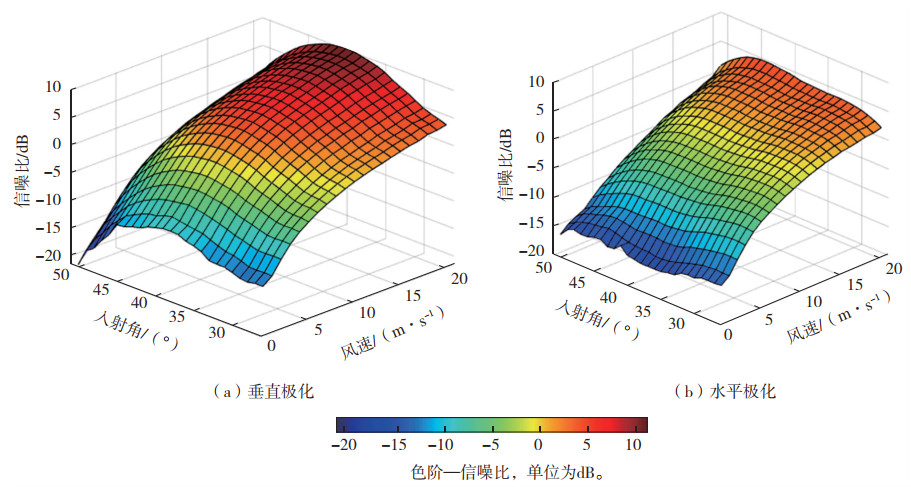
|
图 6 L1B数据中信噪比随入射角和风速的变化 Fig.6 Variation of SNR in L1B data with incidence angle and wind speed |
运用公式(4)可以计算出σ0的传递误差。总体而言,误差随着风速的增加呈逐渐减小的趋势。当风速较低(小于4 m·s-1)时,Kpc>20%;随着风速增加至8 m·s-1,Kpc集中在20%~30%;当风速大于15 m·s-1时,Kpc一般小于20%,且不再随着风速的增大明显变化。另外,近星下点风单元与刈幅远端风单元的Kpc有明显差异性,这与该区域的观测入射角或方位角信息较丰富有关,刈幅远端测量精度相对更低;除去风速较低的情况外,刈幅在±100~±400 km范围内时,Kpc较为稳定一致。另外,由于在定标环节已经采用不同的定标系数,针对不同空间分辨率的产品分别做了校正,且基于大量的数据统计分析Kpc随风速和入射角的变化,结果表明曲线几乎重合。因此,Kpc没有再区分分辨率的不同。
通过对L2A数据的分析,关于总的Kpi与风速及入射角之间的相关性,具体表现为图 7所示。整体来看,水平极化相较于垂直极化误差较大。特别是在风速较低的情况下,误差显著增加,这一现象被归因于地球物理噪声的显著影响。
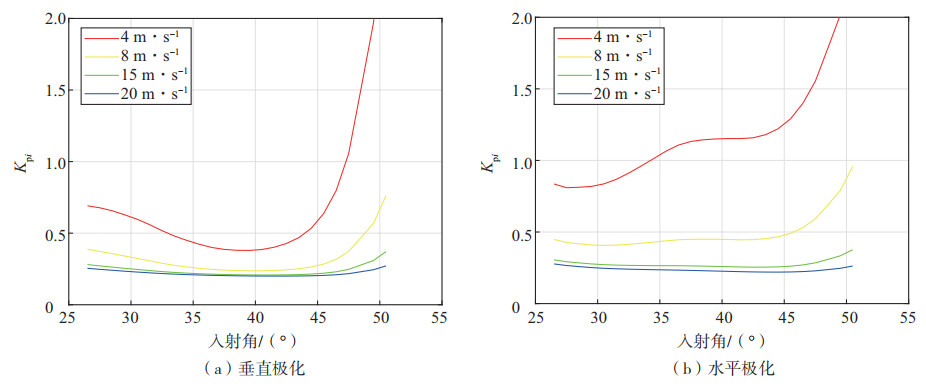
|
图 7 Kpi随典型风速和入射角的变化 Fig.7 Variation of Kpi with wind speed and incidence angle |
根据
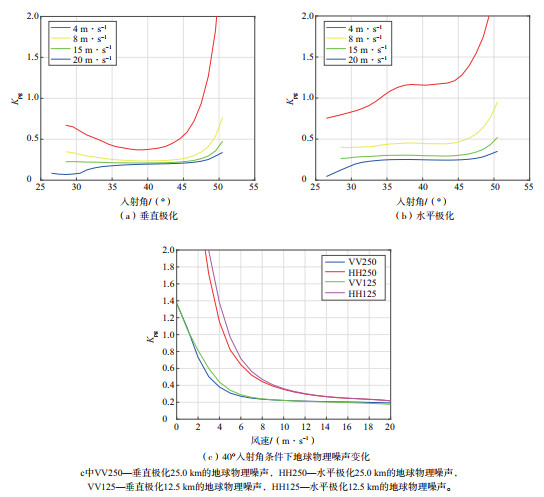
|
图 8 地球物理噪声随入射角变化及40°入射角条件下地球物理噪声随风速变化 Fig.8 Variation of geophysical noise with incidence angle and variation with wind speed at 40° incidence angle |
中法海洋卫星稳定运行的5年内,为海洋科学研究提供了大量高质量的数据资源。卫星所搭载的扇形波束旋转扫描微波散射计具备多样化的观测组合,极大地丰富了风场反演所需的数据信息。文中分析了CSCAT的基本性能及其数据特点,并指出海洋定标技术的优势在于能迅速获得较为可靠的校准系数,一方面对于实时风场监测至关重要,另一方面有效提升了后向散射系数σ0的测量准确性,从而显著提高了风场反演的精度。
进一步,对CSCAT系统的关键参数——归一化标准差(Kp)进行了评估。对L1B数据的信噪比及传输误差进行详细的统计分析,研究其随风速和入射角变化的规律。考虑到扇形扫描的独特性,L2A风场数据结合了丰富的测量信息。通过计算Kp值,能够对地球物理噪声进行合理估计。由于存在数据版本和定标系数的差异,导致对地理噪声估计不同。分析结果显示,在排除极低风速测量不确定性的影响后,对地球物理噪声的一致估计占比为20%~30%。
| [1] |
郎姝燕, 孙从容, 鲁云飞, 等. 中法海洋卫星微波散射计近海岸产品在台风遥感监测中的应用[J]. 海洋气象学报, 2022, 42(2): 74-80. |
| [2] |
TOURAIN C, HERMOZO L, HAUSER D, et al. CFOSAT: products reprocessing and contributions in oceanography[C]//2023 IEEE International Geoscience and Remote Sensing Symposium. Pasadena, California, USA: IEEE, 2023: 3958-3961.
|
| [3] |
林文明, 郎姝燕, 赵晓康, 等. 中法海洋卫星散射计近海岸海面风场反演研究[J]. 海洋学报, 2021, 43(10): 115-123. |
| [4] |
LIU J Q, LIN W M, DONG X L, et al. First results from the rotating fan beam scatterometer onboard CFOSAT[J]. IEEE Trans Geosci Remote Sens, 2020, 58(12): 8793-8806. DOI:10.1109/TGRS.2020.2990708 |
| [5] |
董楹, 林文明. CFOSAT散射计海面后向散射系数误差及影响[J]. 空间科学学报, 2024, 44(2): 326-334. |
| [6] |
ANDERSON C, BONEKAMP H, DUFF C, et al. Analysis of ASCAT ocean backscatter measurement noise[J]. IEEE Trans Geosci Remote Sens, 2012, 50(7): 2449-2457. DOI:10.1109/TGRS.2012.2190739 |
| [7] |
STOFFELEN A. A simple method for calibration of a scatterometer over the ocean[J]. J Atmos Oceanic Technol, 1999, 16(2): 275-282. DOI:10.1175/1520-0426(1999)016<0275:ASMFCO>2.0.CO;2 |
| [8] |
WENTZ F J, SMITH D K. A model function for the ocean-normalized radar cross section at 14 GHz derived from NSCAT observations[J]. J Geophys Res: Oceans, 1999, 104(C5): 11499-11514. DOI:10.1029/98JC02148 |
| [9] |
FISCHER R E. Standard deviation of scatterometer measurements from space[J]. IEEE Trans Geosci Electron, 1972, 10(2): 106-113. DOI:10.1109/TGE.1972.271276 |
| [10] |
LONG D G, SKOUSON G B. Calibration of spaceborne scatterometers using tropical rain forests[J]. IEEE Trans Geosci Remote Sens, 1996, 34(2): 413-424. DOI:10.1109/36.485119 |
| [11] |
YUN R, XU X G, DONG X L, et al. The processing and simulation of the CFOSAT RFSCAT[C]//2015 IEEE International Geoscience and Remote Sensing Symposium. Milan, Italy: IEEE, 2015: 5332-5335.
|
| [12] |
PORTABELLA M, STOFFELEN A. Scatterometer backscatter uncertainty due to wind variability[J]. IEEE Trans Geosci Remote Sens, 2006, 44(11): 3356-3362. DOI:10.1109/TGRS.2006.877952 |
| [13] |
STOFFELEN A, PORTABELLA M. On Bayesian scatterometer wind inversion[J]. IEEE Trans Geosci Remote Sens, 2006, 44(6): 1523-1533. DOI:10.1109/TGRS.2005.862502 |
| [14] |
ANDERSON C, BONEKAMP H, DUFF C, et al. Analysis of ASCAT ocean backscatter measurement noise[J]. IEEE Trans Geosci Remote Sens, 2012, 50(7): 2449-2457. DOI:10.1109/TGRS.2012.2190739 |
| [15] |
PORTABELLA M, STOFFELEN A. A probabilistic approach for SeaWinds data assimilation[J]. Quart J Royal Meteoro Soc, 2004, 130(596): 127-152. DOI:10.1256/qj.02.205 |
| [16] |
MOU X H, LIN W M, HE Y J. Towards a consistent wind data record for the CFOSAT scatterometer[J]. Remote Sens, 2023, 15(8): 2081. DOI:10.3390/rs15082081 |
 2024, Vol. 44
2024, Vol. 44


