2. 河海大学水文水资源学院,江苏 南京 210098;
3. 中国科学院空天信息创新研究院遥感与数字地球重点实验室,北京 100101;
4. 国家卫星海洋应用中心,北京 100081;
5. 自然资源部空间海洋遥感与应用重点实验室,北京 100081
2. College of Hydrology and Water Resources, Hohai University, Nanjing 210098, China;
3. Key Laboratory of Remote Sensing and Digital Earth, Aerospace Information Research Institute, Chinese Academy of Sciences, Beijing 100101, China;
4. National Satellite Ocean Application Service, Beijing 100081, China;
5. Key Laboratory of Space Ocean Remote Sensing and Applications, Ministry of Natural Resources, Beijing 100081, China
土壤水分是反映土壤状态的基本参数,对动植物的生长和土壤理化性质有直接影响,在蒸发下渗、地下水补给和地表径流等水循环和能量循环中发挥着重要作用[1]。土壤水分是青藏高原地区重要的地表参数之一,其在能量与水分循环过程中对亚洲季风、东亚大气环流及全球气候变化中有着重要影响[2],尤其是在地球气候系统各组分之间的相互作用过程中,土壤水分在陆气相互作用中对青藏高原地区大气环流和气候变化有着关键影响[3]。获取大尺度范围内准确的长时序微波土壤水分产品对于理解这一区域的陆气交互过程及其对周边地区的气候影响有重要意义。因此,文中选取青藏高原地区的土壤水分作为研究对象,并且准确持续地监测青藏高原地表土壤水分一直是科学研究的努力方向之一。
土壤水分遥感产品是监测土壤水分的最佳途径。目前主流的土壤水分产品如土壤湿度和海洋盐度(Soil Moisture and Ocean Salinity,SMOS)、主被动土壤湿度(Soil Moisture Active and Passive,SMAP)等是基于被动微波遥感数据获取的[4]。虽然被动微波遥感是探测地表土壤水分的有效途径,但也存在分辨率低、数据缺失严重等问题[5]。随着中法海洋卫星(China-France Oceanography SATellite,CFOSAT)搭载的国际首个扇形波束旋转扫描体制散射计(SCATterometer, 简记为“CSCAT”)的发射[6],其不仅提供了多角度测量,也有独特的扇形观测几何,为更高质量和更高空间分辨率的青藏高原土壤水分产品研发提供了新机遇[7-8]。土壤水分的准确监测不仅需要持续的CFOSAT卫星观测数据,还需要考虑在土壤水分反演过程中消除土壤粗糙度、植被(含水量与植被结构)、入射角等因素的影响[9],因此,如何消除这些影响是土壤水分反演过程中的关键问题。
随着土壤水分反演方法的发展,不同学者针对裸土地表提出了一系列模型,主要分为理论模型与经验、半经验模型[10]。理论模型包括基尔霍夫近似(Kirchhoff approach,KA)以及小扰动模型(small perturbation method,SPM),前者在不同粗糙度情况下可通过驻留相位近似法与标量近似法分别得到几何光学模型(geometrical optics model,GOM)和物理光学模型(physical optics model,POM)。Fung等[11]提出的以积分方程模型(integral equation model,IEM)为代表的随机粗糙面散射模型因具有更大的粗糙度适用范围而获得广泛应用。针对IEM模型在推导过程中做了不同程度的假设,导致某些情况下模拟结果与实测值仍然不一致的问题,Chen等[12]又对IEM模型进行了改进,提出改进模型AIEM(advanced IEM)。常见的经验模型有Oh模型[13]、Dubois模型[14]以及Shi模型[15]。这些模型在实际应用中因适用粗糙度范围较窄而受到限制。自然地表中很多区域都被植被覆盖,比如农田、草地和森林等。由于植被会对微波回波信号产生多种影响,例如植被介电特性(植被叶片和树干含水量)和植被结构对微波信号的散射或者衰减产生影响,导致以上模型不能直接应用于植被覆盖地表的土壤水分反演[16]。Attema等[17]以农作物为研究对象利用微波辐射传输模型生成估算农作物覆盖地表土壤水分的半经验模型,即水-云模型(water cloud model,WCM)。为进一步准确描述植被与微波信号的相互作用,Ulaby等[18]提出的密歇根微波植被散射(Michigan Microwave Canopy Scattering,MIMICS)模型,较完整地描述了森林冠层的散射特性。但上述模型参数较多难以在实际反演中进行应用,因此需要进一步发展更加具有普适性的土壤水分反演模型。
为了进一步提高模型的适用性,逐渐发展了查找表方法、迭代方法以及基于随机森林和深度学习方法等的一系列土壤水分反演方法[19]。查找表法虽然简单高效,但反演精度受限于所使用模型对地表后向散射系数的描述精度[20]。利用遗传算法、支持向量机、模拟退火等优化方法构建代价函数迭代反演土壤水分[21]。近年来,学者利用随机森林、深度学习在土壤水分反演中也取得了较好的效果[22],但以上方法大都需要大量的训练样本作为输入数据,同时地表参数的空间异质性以及模型的欠精确性使得大范围、高鲁棒性的反演结果仍然较难获取[23]。因此,提出一种更加简单有效的土壤水分反演方法。
由Wagner等[24]提出的变化检测方法为土壤水分反演提供了新的思路,以多时相观测数据为输入来解决土壤水分反演中的欠定问题。在自然环境中,地表粗糙度的变化相对于土壤水分的变化是缓慢的,假设在一定周期内粗糙度不变,利用散射计的高频次观测数据,土壤水分的变化则是引起后向散射系数变化的主导因素[25]。但对于植被区域,植被的快速变化严重影响了后向散射系数对土壤水分影响的敏感性[26]。Jiang等[27]利用水-云模型校正植被覆盖下的后向散射系数,Zribi等[28]基于散射计数据通过建立归一化植被指数(normalized differential vegetation index,NDVI)和后向散射系数差之间的经验关系,有效消除了植被带来的影响。Gao等[29]提出了2种有效的消除植被影响方法,一种是在观测周期内利用任意后向散射系数减去最干燥土壤对应的后向散射系数的差值,另一种是在连续观测周期的后向散射系数之间求差值。但由于其实验区域位于农田区域,植被可能处于快速变化状态。在青藏高原地区,需要发展更具普适性的变化检测算法。
为建立适用于青藏高原地区的土壤水分变化检测算法,文中以CFOSAT观测周期内的后向散射系数为变量,分别求解裸土和植被覆盖条件下的2种后向散射系数差。裸土情况下利用传统变化检测方法,即任意时刻后向散射系数与最小后向散射系数求差值。植被情况下则引入NDVI,将NDVI分为不同等级以此来消除植被物候的变化对土壤水分求解的影响,在不同NDVI等级下,即假设植被的状态保持稳定,然后计算经过NDVI校正后的后向散射系数差值。最后在青藏高原地区与土壤水分观测站点数据进行对比验证,并分析青藏高原地区的土壤水分时空分布特征。
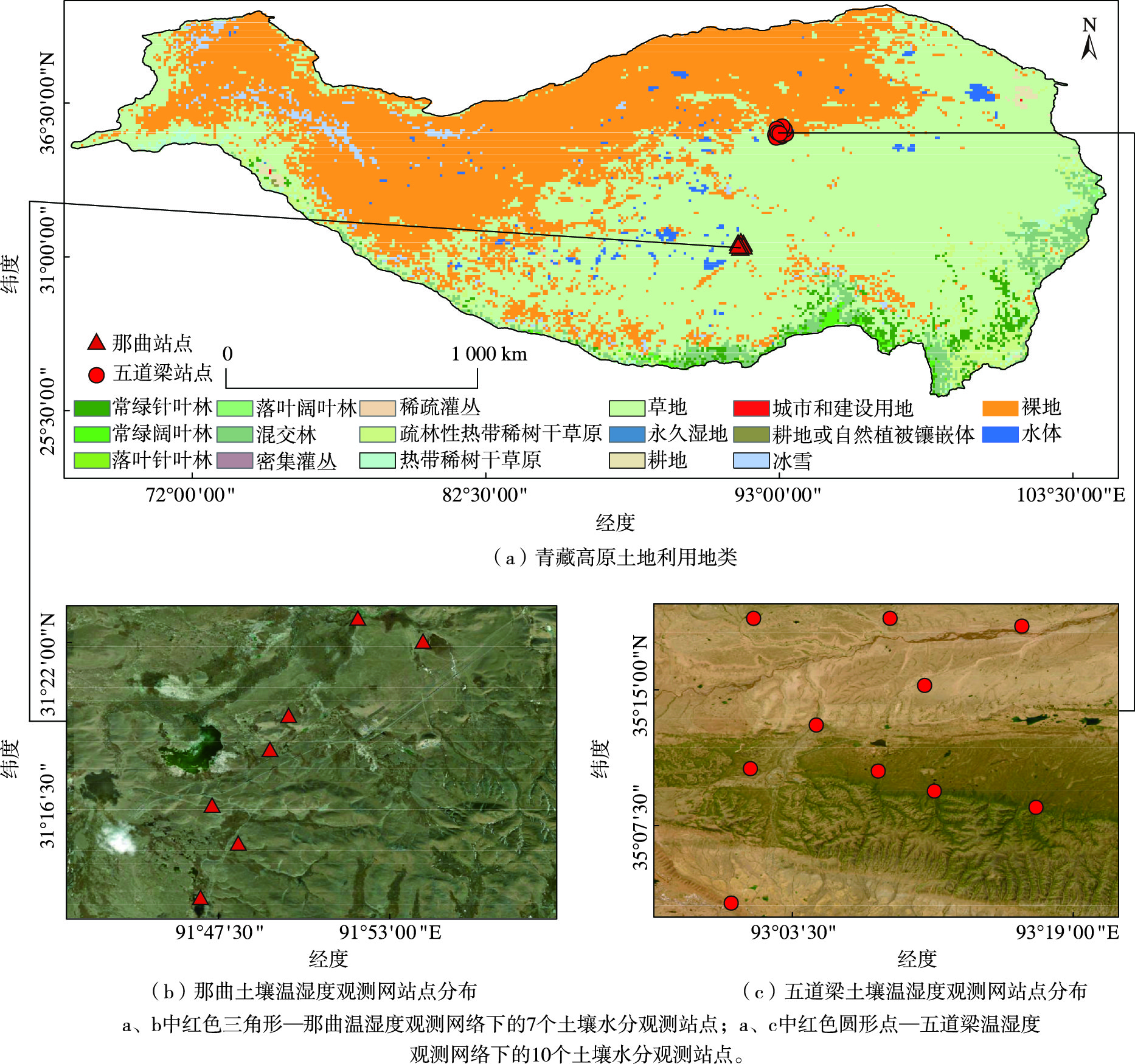
1 研究区与数据源 1.1 研究区概况青藏高原位于亚洲内陆,被称为世界“第三极”,平均海拔为4 000 m,是世界上平均海拔最高、面积最大、地形最为复杂的高原地区[30],是影响全球水汽和能量循环的关键区域,也是对全球气候变化最为敏感的地区之一[31]。青藏高原土壤类型多为冻土,高原草甸分布广泛。由图 1a可知,整个青藏高原地区植被类型丰富,植被覆盖呈现由东南部向西北部逐渐降低的空间分布特征。
|
图 1 研究区概况 Fig.1 Overview of the study area |
站点数据选取在国际土壤水分网络数据库(https://ismn.earth/en/)下载的那曲监测网,如图 1b所示。建立于2019年9月的五道梁土壤温湿度观测网络,如图 1c所示,包含五道梁温湿度观测网络下的10个土壤水分观测站点[32]。2个监测网络均属于多尺度网络,观测仪器每30 min获取不同土壤深度的土壤水分数据。考虑CFOSAT散射计的过境时间及Ku波段微波的穿透特性,此研究选取了地表表层5 cm的实测土壤水分数据,并将各观测网络所有站点的平均值作为验证数据。
1.3 星载微波散射计CFOSAT是由中法两国联合研发的新一代海洋卫星,发布了包含25 km和12.5 km分辨率的L2A产品(数据下载地址为 https://osdds.nsoas.org.cn/home)[33]。卫星搭载的Ku波段扇形波束扫描散射计不仅适用于海上风场监测,还可用于青藏高原地区土壤水分高频监测。
文中以25 km分辨率L2A的CFOSAT数据为研究基础,将CFOSAT的Ku波段垂直极化(vertical transmit,vertical receive,简记为“VV”)的后向散射数据角度归一化为40°,去除不同角度变化对土壤水分反演的影响。主要计算方法[28]如下:
| $ \sigma_{\theta_n}^0=\sigma_{40}^0+\beta\left(\theta_n-40\right)-\mu\left(\theta_n-40\right)^2 。$ | (1) |
式中:θ为入射角,σθn0为任意角度下的后向散射系数,σ400为40°时的后向散射系数,β为同一观测位置的n次观测拟合斜率(即一次项系数),μ为同一观测位置的n次观测拟合曲率(即二次项系数)。然后通过CFOSAT散射计数据在同一时刻观测的n次(n>2)入射角和对应的后向散射系数代入公式(1),利用最小二乘法求解未知参数结果[34]。
以多通道协同反演算法(multi-channel collaborative algorithm,MCCA)生产的9 km SMAP土壤水分产品作为文中土壤水分反演的辅助数据,即计算得到土壤水分最大值和最小值。MCCA利用参数间的自约束关系与通道间的理论转换关系进行地表参数反演,反演过程不依赖于其他辅助数据,并适用于多种不同载荷配置[35]。MCCA SMAP土壤水分产品经过19个土壤水分密集观测站网验证,精度优于其他SMAP产品(MCCA下载地址为 https://doi.org/10.11888/Terre.tpdc.300486)。同时使用风云三号D星(FY-3D)中分辨率光谱成像仪(medium resolution spectral imager,MERSI)生产的5 km NDVI产品作为植被影响校正的辅助参数(NDVI下载地址为 http://www.nsmc.org.cn/nsmc/cn/home/)[36]。为了便于计算,数据都采用统一的网格分辨率(25 km)。
2 研究方法 2.1 变化检测模型土壤水分反演方法裸土区的散射计后向散射系数主要受土壤水分和土壤表面粗糙度的影响,而散射计能够在大尺度上进行裸土的后向散射观测,当在大尺度上进行土壤水分反演时,裸土粗糙度变化较小,可以认为其对后向散射的贡献保持稳定。因此利用散射计对同一区域进行连续观测,可以忽略粗糙度对后向散射变化的影响,此时认为观测到的地表后向散射变化主要由土壤水分变化引起[25]。因此建立后向散射变化对土壤水分变化的响应关系可以实现对土壤水分的反演。
假设裸土条件下微波后向散射系数与土壤水分之间存在非线性响应关系,有如下公式:
| $ \sigma^{\text {soil }}=\ln (M+K)+{\mathrm{C}}。$ | (2) |
其中:σsoil为后向散射系数;M为体积土壤水分含量(单位为m3·m-3);K表示散射计信号对土壤水分的敏感性;C主要受土壤粗糙度、微波波长、入射角等的影响[24],在同一观测周期内利用同一传感器进行观测,因此在公式(2)中将C视为常数。
文中用MCCA作为青藏高原土壤水分的极大和极小值参考。因此,在重复观测周期内,当土壤水分达到最大值MmaxSMAP时,CFOSAT后向散射系数取最大值σmaxsoil,此时有:
| $ \sigma_{\max }^{\text {soil }}=\ln \left(M_{\max }^{\mathrm{SMAP}}+K\right)+\mathrm{C} 。$ | (3) |
而当土壤水分达到最小值MminSMAP时,CFOSAT后向散射系数取最小值σminsoil,则有:
| $ \sigma_{\min }^{\text {soil }}=\ln \left(M_{\min }^{\text {SMAP }}+K\right)+\mathrm{C}。$ | (4) |
因此观测周期内土壤水分最大变化量ΔMmax=MmaxSMAP-MminSMAP,根据公式(3)、(4),此时观测周期内CFOSAT后向散射系数的最大变化量可以表示为:
| $ \varDelta \sigma_{\max }^{\text {soil }}=\ln \left(M_{\max }^{\mathrm{SMAP}}+K\right)-\ln \left(M_{\min }^{\mathrm{SMAP}}+K\right)。$ | (5) |
其中:Δσmaxsoil为CFOSAT后向散射系数在观测周期内的最大变化量。
对于观测周期内第t天的土壤水分Mt以及对应的CFOSAT后向散射系数σtsoil,第t天土壤水分相对于最小土壤水分的变化量ΔMt=Mt-MminSMAP,此时有:
| $ \varDelta \sigma_t^{\text {soil }}=\ln \left(M_t+\mathrm{K}\right)-\ln \left(M_{\min }^{\mathrm{SMAP}}+K\right) 。$ | (6) |
其中:Δσtsoil为第t天的后向散射系数相对于观测周期内最小后向散射σminsoil的变化量。因此联合公式(5)、(6),根据CFOSAT后向散射系数的变化量可以获得裸土土壤水分的变化量。公式如下:
| $ \frac{\varDelta \sigma_t^{\text {soil }}}{\varDelta \sigma_{\max }^{\text {soil }}}=\frac{\ln \left(M_t+K\right)-\ln \left(M_{\min }^{\mathrm{SMAP}}+K\right)}{\ln \left(M_{\max }^{\mathrm{SMAP}}+K\right)-\ln \left(M_{\min }^{\mathrm{SMAP}}+K\right)} 。$ | (7) |
而在植被覆盖区,CFOSAT后向散射系数的变化不仅受到土壤水分变化的影响,也受到地表植被覆盖的影响。将总的后向散射变化量表示为裸土下CFOSAT后向散射系数的变化量与植被影响的和:
| $ \varDelta \sigma_t^{\mathrm{veg}}=\alpha \cdot I_{\mathrm{NDV}}+\varDelta \sigma_t^{\text {soil }}。$ | (8) |
其中:Δσtveg表示观测周期内第t天相对最干燥时刻的CFOSAT后向散射系数变化量;INDV表示植被指数;α为植被对CFOSAT后向散射系数变化量的影响系数,其大小主要跟散射计波段频率有关[37]。Δσtsoil为相对于裸土条件下的CFOSAT后向散射系数变化量。
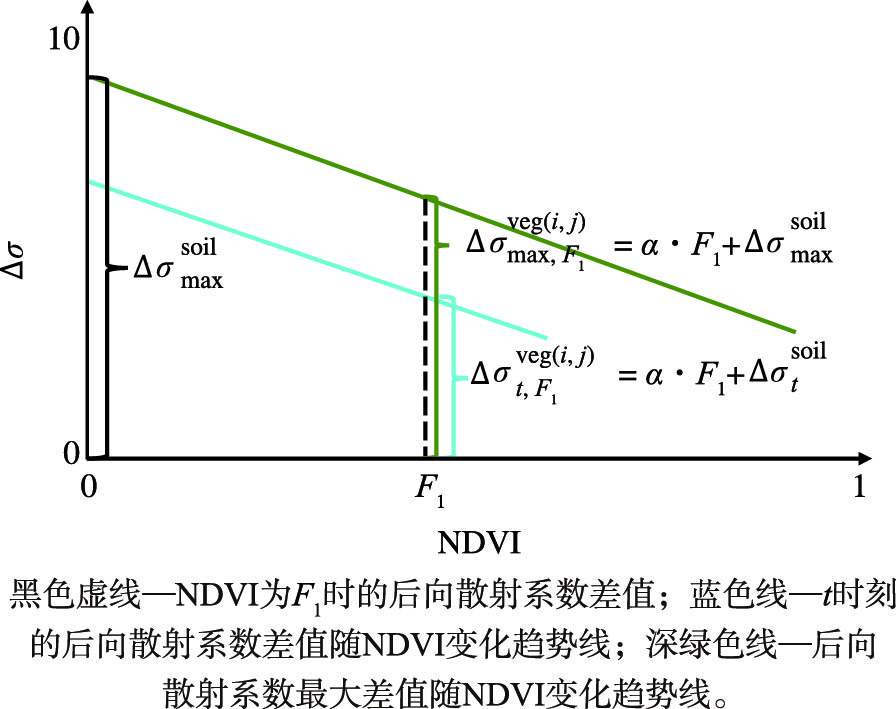
假设图 2成立,其中观测到的植被覆盖地表CFOSAT后向散射系数变化量可由CFOSAT观测数据计算得出,NDVI由MERSI计算得出。结合观测到的植被覆盖地表CFOSAT后向散射系数变化量及对应的植被指数,即可求得相对于裸土条件下的CFOSAT后向散射系数变化量。
|
图 2 NDVI对CFOSAT后向散射系数变化量的影响关系 Fig.2 Influence of NDVI on the variation of backscattering coefficient of CFOSAT |
因此,由图 2中观测周期内CFOSAT后向散射系数变化最大值Δσmax, F1veg(i, j)和t时刻CFOSAT后向散射系数变化量Δσt, F1veg(i, j)代入公式(7),可得植被条件下的土壤水分计算公式:
| $ \frac{\Delta \sigma_{t, F_1}^{\operatorname{veg}(i, j)}-\alpha \cdot F_1}{\Delta \sigma_{\max , F_1}^{\operatorname{veg}(i, j)}-\alpha \cdot F_1}=\frac{\ln \left(M_t+K\right)-\ln \left(M_{\min }^{\mathrm{SMAP}}+K\right)}{\ln \left(M_{\max }^{\mathrm{SMAP}}+K\right)-\ln \left(M_{\min }^{\mathrm{SMAP}}+K\right)} 。$ | (9) |
检验土壤水分反演模型的可靠性和反演能力是模型应用的前提,模型评估使用统计指标皮尔逊相关系数(R)、偏差(Bias)、均方根误差(root mean square error, RMSE)和无偏均方根误差(unbiased root mean square error, ubRMSE)。各评价指标计算公式如下:
| $ R=\sqrt{1-\frac{\sum\left(M_{\text {retrieve }}-M_{\text {insitu }}\right)^2}{\sum\left(M_{\text {retrieve }}-\overline{M_{\text {insitu }}}\right)^2}}, $ | (10) |
| $ V_{\text {Bias }}=\overline{M_{\text {retrieve }}}-\overline{M_{\text {insitu }}}, $ | (11) |
| $ V_{\text {RMSE }}=\sqrt{\overline{\left(M_{\text {retrieve }}-M_{\text {insitu }}\right)^2}}, $ | (12) |
| $ V_{\mathrm{ubRMSE}}=\sqrt{V_{\mathrm{RMSE}}{ }^2-V_{\text {Bias }}{ }^2}。$ | (13) |
其中:Mretrieve表示相应站点位置的反演土壤水分;Minsitu表示原位站点实测土壤水分;R表示土壤水分反演结果与实测土壤水分的一致性;VBias为偏差值,表示反演结果的偏离程度;VRMSE为均方根误差值,VubRMSE为无偏均方根误差值,两者均表示土壤水分反演的精度准确性,值越小则模型精度越高。
3 结果 3.1 植被指数拟合青藏高原的经验模型植被覆盖区土壤水分反演的难点在于植被和土壤水分对微波信号都有影响,如何将其信号进行分离是一个难点,而基于变化检测算法的思路为解决这一问题提供了新的方向。在拟合植被经验函数时,文中将NDVI按照(0,1,0.01)步长为0.01分为不同等级,在每个像元的基础上在相同NDVI等级下计算CFOSAT后向散射系数差,即在相同植被覆盖条件下计算土壤水分的变化量,这样可以避免植被对土壤水分反演的影响。
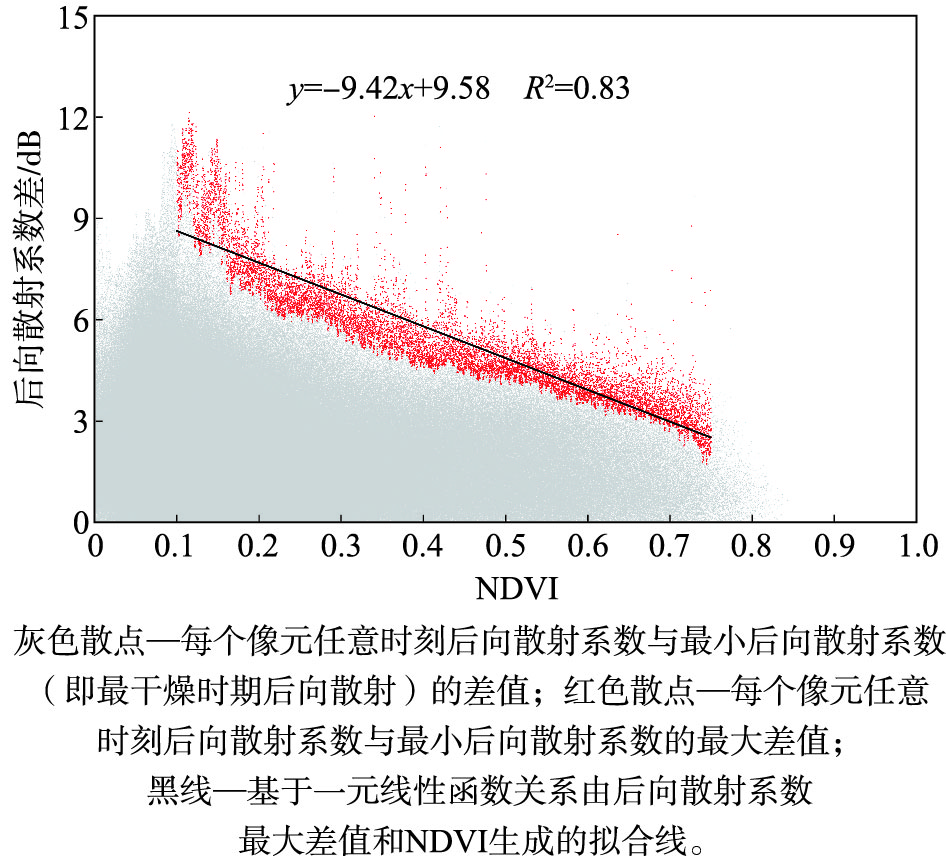
图 3展示了青藏高原分级NDVI下后向散射系数的变化趋势,图中每个点纵坐标代表研究区像元在任意一天观测到的后向散射系数相对于最小后向散射系数的差,横坐标代表任意一天观测到的NDVI。NDVI较小时植被对后向散射的影响可以忽略,NDVI大于0.75的像元明显减少,为了减小数据量少带来的误差,在计算植被拟合函数时将NDVI范围设置为0.10~0.75。随着NDVI(植被)的增加,CFOSAT后向散射系数最大差值(即后向散射系数的最大变化量)呈现逐渐减小的趋势,对最大变化量部分进行线性拟合,其拟合关系式已通过p < 0.01的显著性检验,R2为0.83。同时也印证了图 2的假设,在青藏高原地区,植被覆盖与后向散射系数变化量之间存在明显的线性函数关系。
|
图 3 青藏高原分级NDVI构建的经验模型 Fig.3 Empirical model constructed with graded NDVI over the Qinghai-Tibet Plateau |
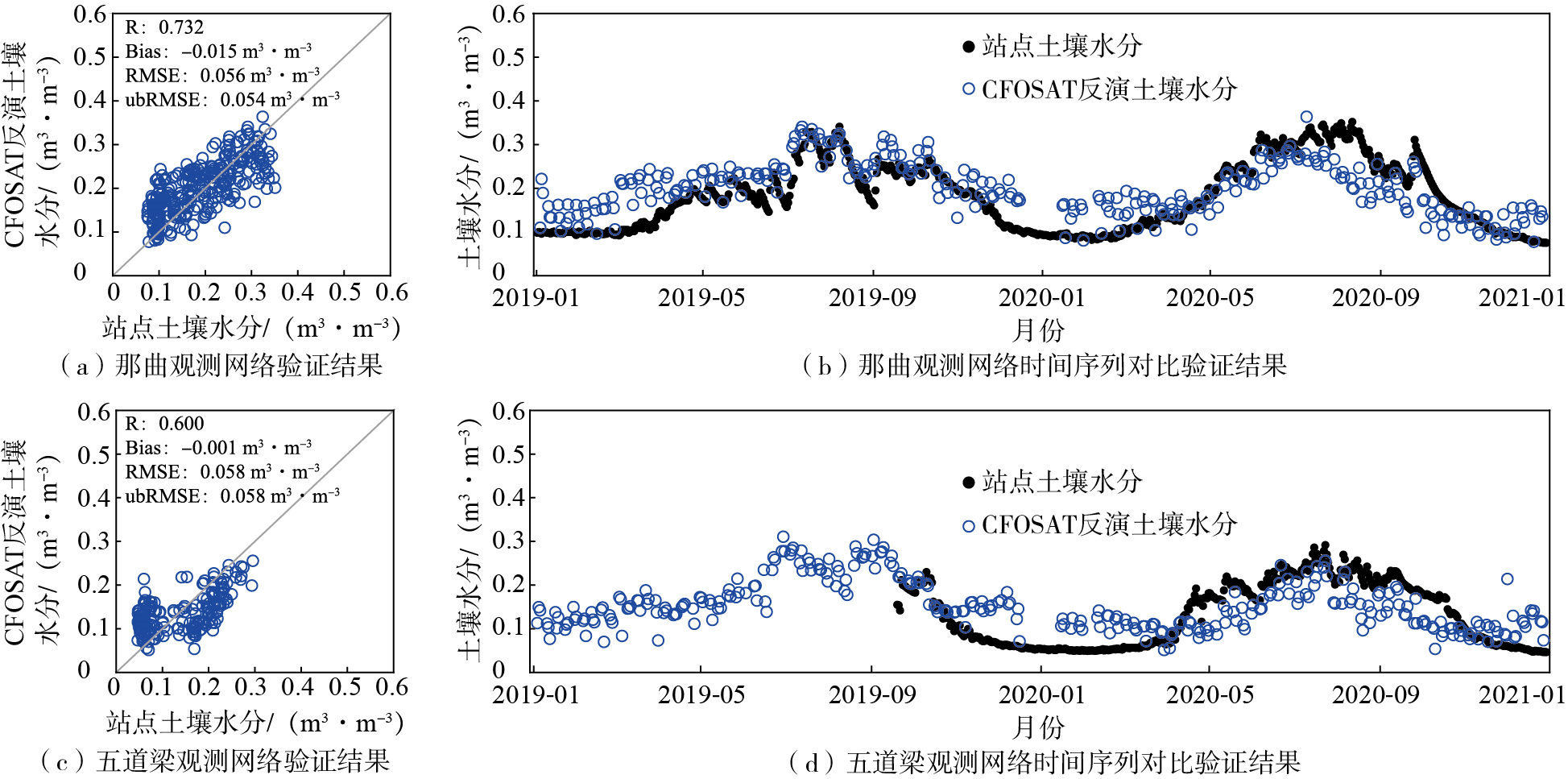
利用改进的长时序变化检测方法对青藏高原地区的土壤水分进行反演,有2个关键因素:一是2019—2021年长时间周期内在青藏高原地区受人为因素影响较小,大多数环境条件基本不变;二是更长的时间尺度可以更准确地确定土壤水分最干燥的情况(即后向散射系数最小值)以及土壤水分最大和最小参考值,以此得到更准确的土壤水分绝对值。在NDVI小于0.1时,采用裸土区变化检测算法,NDVI大于0.1时则采用植被覆盖区变化检测算法。结合MCCA土壤水分产品中计算出参考土壤水分最大值和最小值来得到土壤水分绝对值。再将那曲和五道梁土壤水分观测网络的站点进行平均,并与CFOSAT反演土壤水分格网数据进行对比。如图 4a、c所示,文中提出的变化检测算法表现出良好的性能,CFOSAT反演土壤水分与站点土壤水分相关系数为0.600和0.732,Bias均小于0.02 m3·m-3,RMSE和ubRMSE均小于0.06 m3·m-3。
|
图 4 CFOSAT反演土壤水分与站点土壤水分对比 Fig.4 Comparison between soil moisture retrieved by CFOSAT and measured soil moisture |
结合图 4b、d和图 1可知,由于那曲和五道梁观测网络位于多年冻土的高原草甸区,受不同季节的温度变化影响。因此,变化检测算法反演的CFOSAT土壤水分结果在多年时间序列上也表现出明显的季节性波动,这充分说明变化检测算法在青藏高原地区具有良好的适用性。但在土壤冻融期(一般为11月—次年3月),反演的土壤水分相对于站点土壤水分数据均出现了不同程度的高估,且土壤水分出现较为明显的异常波动。Ku波段容易受到降雪和降雨的影响,可能造成后向散射系数发生剧烈变化,从而使土壤水分反演结果产生一定的误差。同时,粗糙度变化也是影响土壤水分的一个因素,在青藏高原地区土壤冻融过程中地表粗糙度也会变化。尚伦宇等[38]计算青藏高原玛曲地区11月—次年3月土壤未冻结阶段、冻结阶段和融化后的地表粗糙度分别为3.23×10-3 m、2.27×10-3 m和1.92×10-3 m,地表粗糙度呈现逐渐减小的趋势。因此,土壤冻融过程、降雪和降雨等都会导致土壤水分反演结果出现较大的误差[39]。而文中的变化检测方法忽略了地表粗糙度的时间变化以及降雨和降雪的天气因素,可能是导致冻融期土壤水分波动较大且异常高估的原因。
在非冻融期,土壤水分对后向散射系数影响有着主导作用,这在那曲和五道梁两个观测网络都有明显的体现。冰川、积雪融化和降水等影响因素导致土壤水分含量上升,而后又缓慢下降。文中的变化检测算法可以很好地捕捉到土壤水分的变化。同时,由多年的土壤水分变化趋势可以发现,非冻融期的土壤水分明显高于冻融期,这可能是由夏季的降水增加以及青藏高原地区的冰川、积雪融化导致的。
3.3 青藏高原土壤水分时空分布为了进一步分析青藏高原地区的土壤水分时空变化,文中从2019—2021年的年平均土壤水分资料分析青藏高原地区土壤水分空间分布异质性,从2019—2021年的季节平均分析青藏高原地区土壤水分的时间变化规律。
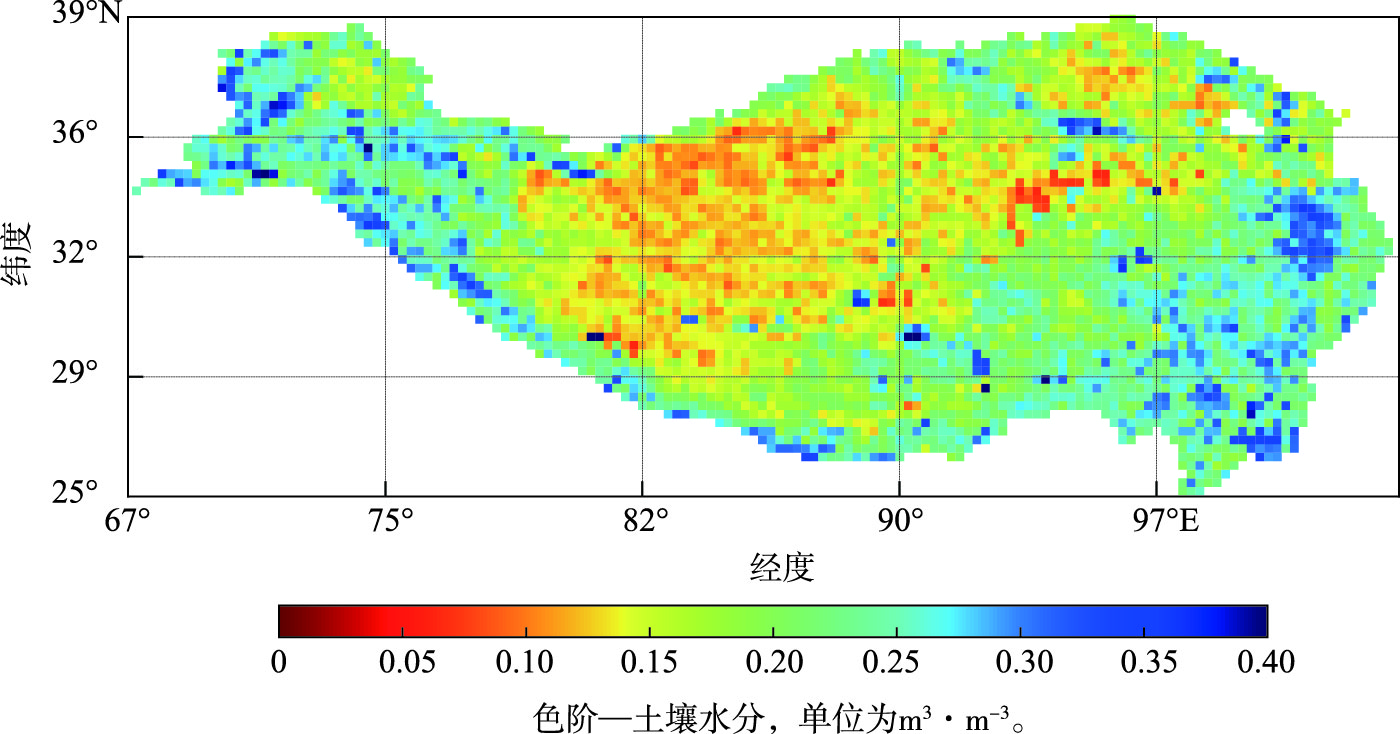
3.3.1 青藏高原土壤水分空间分布图 5为基于CFOSAT散射计数据反演得到的年平均地表土壤水分空间分布。从总体看,变化检测算法反演的土壤水分空间分布合理,土壤水分大多在青藏高原中北部偏干,西部和东南部偏湿,同时在局部区域存在复杂的空间特征。
|
图 5 2019—2021年青藏高原地区年平均CFOSAT反演土壤水分空间分布 Fig.5 Spatial distribution of annual mean soil moisture retrieved by CFOSAT in the Qinghai-Tibet Plateau from 2019 to 2021 |
从局部细节看,在青藏高原中部地区常年处于较干燥的状态,这是由于高原内陆地区远离海洋,水汽输送难以抵达。但在青藏高原最南边存在一个常年湿润的带状区域,这主要是由于喜马拉雅山阻挡了大气环流中的水汽,因而在南边形成降水,反之北边处于干燥的雨影区。从而形成了青藏高原地区土壤水分干湿分布的独特性,也使得青藏高原南部地区多森林植被,中部地区多草甸或裸土覆盖。
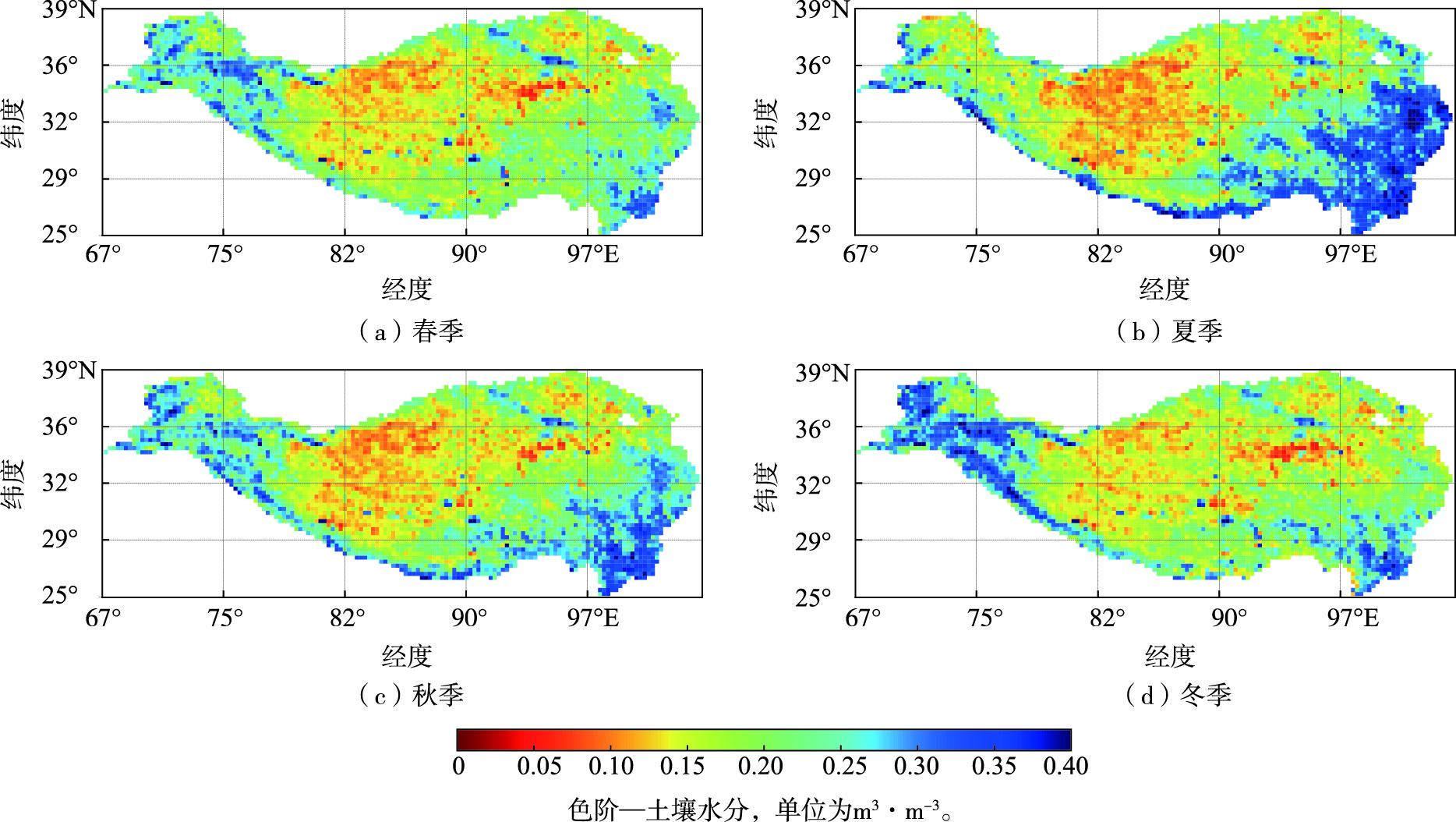
3.3.2 青藏高原土壤水分季节变化由图 6可知,青藏高原土壤水分季节性变化显著,该地区受到高原地区的大气环流影响,具体主要是印度季风和东亚季风。可以发现,不同季节下青藏高原土壤水分空间分布差异较大。夏季土壤水分是所有季节中最湿润的,其次是秋季,而春季和冬季都相对比较干燥。从具体空间细节上分析,土壤水分也呈现不同的差异性变化。
|
图 6 青藏高原地区CFOSAT反演土壤水分不同季节空间分布 Fig.6 Spatial distribution of soil moisture retrieved by CFOSAT in different seasons in the Qinghai-Tibet Plateau |
在西部地区,土壤水分整体较中部地区湿润,土壤水分变化呈现冬季大于春季和秋季,其中春季和秋季干湿程度相对一致,而夏季相对最干燥。在中部地区,春夏秋冬四个季节的土壤水分都非常干燥,其土壤水分含量大部分在0.05 m3·m-3左右,且变化相对不明显。在东部地区,土壤水分则有明显的季节变化,春季土壤水分呈现干燥的状态,夏季土壤水分增加,部分地区超过0.4 m3·m-3,秋季土壤水分稍微降低,而冬季土壤水分则达到了相对较干的程度。
4 小结此研究基于CFOSAT微波散射计数据以及MCCA土壤水分参考极值和MERSI植被产品构建变化检测算法,反演青藏高原地区土壤水分,并详细分析了青藏高原土壤水分时空分布特征。得到如下结论:利用分级NDVI计算后向散射系数差,并以后向散射系数差与NDVI拟合青藏高原地区的一元线性植被经验模型;将变化检测算法反演结果与地面实测结果比较,发现CFOSAT反演结果与实测结果有很好的一致性,其验证精度指标Bias均小于0.02 m3·m-3,RMSE和ubRMSE均小于0.06 m3·m-3;变化检测算法反演的土壤水分空间总体分布合理,青藏高原土壤水分中北部偏干,西部和东南部偏湿,在局部区域存在复杂的空间特征,且具有显著的季节性变化。
| [1] |
KANNENBERG S A, ANDEREGG W R L, BARNES M L, et al. Dominant role of soil moisture in mediating carbon and water fluxes in dryland ecosystems[J]. Nat Geosci, 2024, 17(1): 38-43. DOI:10.1038/s41561-023-01351-8 |
| [2] |
拉巴, 边巴次仁, 拉珍, 等. 青藏高原土壤水分时空变化特征及其与气候变化的关系研究[J]. 高原科学研究, 2023, 7(1): 1-8. |
| [3] |
王澄海, 杨凯, 张飞民, 等. 青藏高原土壤冻融过程的气候效应: 进展和展望[J]. 高原气象, 2021, 40(6): 1318-1336. |
| [4] |
杨娜, 汤燕杰, 张宁馨, 等. 基于SMOS、SMAP数据的青藏高原季风及植被生长季土壤水分长消特征研究[J]. 遥感技术与应用, 2022, 37(6): 1373-1384. |
| [5] |
姚盼盼. 微波遥感土壤水分时空扩展研究[D]. 北京: 中国科学院大学, 2018.
|
| [6] |
XU Y, LIU J Q, XIE L L, et al. China-France Oceanography Satellite (CFOSAT) simultaneously observes the typhoon-induced wind and wave fields[J]. Acta Oceanol Sin, 2019, 38(11): 158-161. DOI:10.1007/s13131-019-1506-3 |
| [7] |
林文明, 郎姝燕, 赵晓康, 等. 中法海洋卫星散射计近海岸海面风场反演研究[J]. 海洋学报, 2021, 43(10): 115-123. |
| [8] |
郎姝燕, 孙从容, 鲁云飞, 等. 中法海洋卫星微波散射计近海岸产品在台风遥感监测中的应用[J]. 海洋气象学报, 2022, 42(2): 74-80. |
| [9] |
王振. 植被覆盖地表土壤水分的雷达反演方法研究[D]. 北京: 中国矿业大学, 2021.
|
| [10] |
李俐, 王荻, 潘彩霞, 等. 土壤水分反演中的主动微波散射模型[J]. 国土资源遥感, 2016, 28(4): 1-9. |
| [11] |
FUNG A K, LI Z, CHEN K S. Backscattering from a randomly rough dielectric surface[J]. IEEE Trans Geosci Remote Sens, 1992, 30(2): 356-369. DOI:10.1109/36.134085 |
| [12] |
CHEN K S, WU T D, TSANG L, et al. Emission of rough surfaces calculated by the integral equation method with comparison to three-dimensional moment method simulations[J]. IEEE Trans Geosci Remote Sens, 2003, 41(1): 90-101. DOI:10.1109/TGRS.2002.807587 |
| [13] |
OH Y. Quantitative retrieval of soil moisture content and surface roughness from multipolarized radar observations of bare soil surfaces[J]. IEEE Trans Geosci Remote Sens, 2004, 42(3): 596-601. DOI:10.1109/TGRS.2003.821065 |
| [14] |
DUBOIS P C, VAN ZYL J, ENGMAN T. Measuring soil moisture with imaging radars[J]. IEEE Trans Geosci Remote Sens, 1995, 33(4): 915-926. DOI:10.1109/36.406677 |
| [15] |
SHI J C, WANG J, HSU A Y, et al. Estimation of bare surface soil moisture and surface roughness parameter using L-band SAR image data[J]. IEEE Trans Geosci Remote Sens, 1997, 35(5): 1254-1266. DOI:10.1109/36.628792 |
| [16] |
万幼川, 陈晶, 余凡, 等. 利用星载散射计反演地表土壤水分[J]. 农业工程学报, 2014, 30(3): 70-77. |
| [17] |
ATTEMA E P W, ULABY F T. Vegetation modeled as a water cloud[J]. Radio Sci, 1978, 13(2): 357-364. DOI:10.1029/RS013i002p00357 |
| [18] |
ULABY F T, McDONALD K, SARABANDI K, et al. Michigan microwave canopy scattering model[J]. Int J Remote Sens, 1990, 11(7): 1223-1253. DOI:10.1080/01431169008955090 |
| [19] |
蒋玲梅, 崔慧珍, 王功雪, 等. 积雪、土壤冻融与土壤水分遥感监测研究进展[J]. 遥感技术与应用, 2020, 35(6): 1237-1262. |
| [20] |
王建明. 基于ERS散射计数据的青藏高原土壤水分估算方法研究[D]. 北京: 中国科学院研究生院, 2005.
|
| [21] |
孙时雨, 宋承运, 周露. 基于优化BP神经网络ESA CCI土壤水分重建方法研究[J]. 无线电工程, 2023, 53(11): 2507-2514. |
| [22] |
石高松. 基于机器学习的高分辨率土壤湿度数据集生成研究[D]. 长春: 长春师范大学, 2023.
|
| [23] |
杜鑫. 基于Alpha变化检测模型的青藏高原地区土壤水分反演[D]. 淮南: 安徽理工大学, 2022.
|
| [24] |
WAGNER W, LEMOINE G, ROTT H. A method for estimating soil moisture from ERS scatterometer and soil data[J]. Remote Sens Environ, 1999, 70(2): 191-207. DOI:10.1016/S0034-4257(99)00036-X |
| [25] |
杜绍杰, 赵天杰, 施建成, 等. Sentinel-1和Sentinel-2协同反演地表土壤水分[J]. 遥感技术与应用, 2022, 37(6): 1404-1413. |
| [26] |
方西瑶, 蒋玲梅, 崔慧珍. 基于Sentinel-1雷达数据的青藏高原地区土壤水分反演研究[J]. 遥感技术与应用, 2022, 37(6): 1447-1459. |
| [27] |
JIANG L H, CHEN Y, CHEN Y P, et al. An improved change detection method for soil moisture retrieval using Sentinel-1 and Smap data[C]//2020 IEEE International Geoscience and Remote Sensing Symposium. Waikoloa: IEEE, 2020: 4466-4469.
|
| [28] |
ZRIBI M, ANDRÉ C, DECHARME B. A method for soil moisture estimation in western Africa based on the ERS scatterometer[J]. IEEE Trans Geosci Remote Sens, 2008, 46(2): 438-448. DOI:10.1109/TGRS.2007.904582 |
| [29] |
GAO Q, ZRIBI M, ESCORIHUELA M J, et al. Synergetic use of Sentinel-1 and Sentinel-2 data for soil moisture mapping at 100 m resolution[J]. Sensors, 2017, 17(9): 1966. |
| [30] |
袁源, 李璐含, 胡伟, 等. 青藏高原土壤湿度-气候相互影响研究进展[J]. 冰川冻土, 2023, 45(2): 341-354. |
| [31] |
吴小丽, 刘桂民, 李新星, 等. 青藏高原多年冻土和季节性冻土区土壤水分变化及其与降水的关系[J]. 水文, 2021, 41(1): 73-78. |
| [32] |
ZHENG J Y, ZHAO T J, LV H S, et al. Use of a new Tibetan Plateau network for permafrost to characterize satellite-based products errors: an application to soil moisture and freeze/thaw[J]. Remote Sens Environ, 2024, 300: 113899. |
| [33] |
BEINEKE L W, PIPPERT R E. The number of labeled k-dimensional trees[J]. J Comb Theory, 1969, 6(2): 200-205. |
| [34] |
BJÖRCK Å. Least squares methods[M]//CIARLET P G, LIONS J L. Handbook of Numerical Analysis. Amsterdam: Elsevier, 1990: 465-652.
|
| [35] |
PENG Z Q, ZHAO T J, SHI J C, et al. First mapping of polarization-dependent vegetation optical depth and soil moisture from SMAP L-band radiometry[J]. Remote Sens Environ, 2024, 302: 113970. |
| [36] |
王圆圆, 李贵才. 全球风云三号D星MERSI/NDVI产品质量评估[J]. 气象学报, 2022, 80(1): 124-135. |
| [37] |
WANG Z, ZHAO T J, SHI J C, et al. 1-km soil moisture retrieval using multi-temporal dual-channel SAR data from Sentinel-1 A/B satellites in a semi-arid watershed[J]. Remote Sens Environ, 2023, 284: 113334. |
| [38] |
尚伦宇, 吕世华, 张宇, 等. 青藏高原东部土壤冻融过程中地表粗糙度的确定[J]. 高原气象, 2010, 29(1): 17-22. |
| [39] |
武舒阳. 地表冻融过程微波辐射模拟[D]. 焦作: 河南理工大学, 2022.
|
 2024, Vol. 44
2024, Vol. 44


