2. 辽阳市气象局,辽宁 辽阳 111010;
3. 雅安市气象局,四川 雅安 625000
2. Liaoyang Meteorological Service, Liaoyang 111010, China;
3. Ya'an Meteorological Service, Ya'an 625000, China
厄尔尼诺-南方涛动(El Niño-Southern Oscillation,ENSO)事件是指发生在热带东太平洋海面温度(sea surface temperature, SST)持续异常升高或降低的现象,是影响全球的连续但不规则的大气和海洋循环变化的一种现象。虽然ENSO发生在热带,但其对全球天气的深远影响是不争的事实。热带海洋和全球大气(Tropical Ocean-Global Atmosphere,TOGA)研究计划的十年间,ENSO研究取得了长足的进展,关于ENSO的机制和不规则性有了丰富的理论解释,更有意义的是在此期间发展了各种复杂程度不一的数值模式来模拟并预测ENSO。然而,20世纪90年代以来,厄尔尼诺事件异常发生、发展导致对ENSO预报技巧的降低,引起学术界对已有的ENSO理论及其预测可信度的争议。这说明加深对海气相互作用物理机制的认识,寻找ENSO的不规则性原因仍是具有重要意义的课题。
20世纪60年代,Bjerknes[1]指出,海洋中的厄尔尼诺和南方涛动现象,是热带大尺度海气相互作用的一种表现,并通过沃克(Walker)环流和哈得来(Hadley)环流的调整来阐述ENSO循环的物理机制,开启了将热带海洋和全球大气作为一个耦合系统来研究的先河。McCreary等[2]在Walker环流和Hadley环流调整的基础上,结合暖性(冷性)开尔文(Kelvin)波的东传和暖性(冷性)罗斯贝(Rossby)波的西传提出了ENSO循环的物理机制。Schopf等[3]则利用热带海气耦合模式的计算结果,该模式通过赤道中太平洋的不稳定海气相互作用调整Kelvin波和Rossby波的冷暖特征来影响SST的变化,给出了一种令人信服的ENSO循环的物理机制。上述研究主要集中在热带海气相互作用的不稳定理论上,其主要途径包括对热带海气耦合赤道波的稳定性(线性稳定性和弱非线性)分析和非线性简化模式的模拟,这些结果通过热带海洋-大气间反馈机制可以产生不稳定的模态,并且输出类似ENSO的不规则时间序列。除了不稳定理论外,值得指出的是,Suarez等[4]使用一种比较另类的模式即时滞振子方程也可以较好地再现ENSO循环的基本过程。但其赖以建立的物理基础远不如直接由两种地球流体的运动及相互作用出发的经典方法坚实、明确。总体而言,上述的研究深化了对ENSO现象的认识,包括ENSO产生的物理机制及不规则性。但这些研究更多的是采用数值计算,对于热带海气耦合系统如何作用、不规则性是怎样产生的,缺乏详细的动力分析。
除了ENSO自身循环的自激振荡外,外场环境对其发展也具有影响。李崇银[5]指出大气季节内振荡对厄尔尼诺的激发作用。黄荣辉等[6]提出ENSO循环可能是亚洲季风区与Hadley环流区之间存在的低频振荡的产物,并进一步指出了赤道附近西风异常是ENSO发生的必要条件。李崇银等[7]分析东亚大气环流与ENSO相互影响时指出,在厄尔尼诺年夏季,由于遥相关机制,东亚及西太平洋中纬度地区出现地面气压及高度场负距平,西太平洋副热带高压位置持续偏南,而拉尼娜(La Niña)年副热带高压则偏北。张人禾等[8]概述了副热带太平洋海气异常影响ENSO研究方面的科学背景及研究进展,综述了前人提出的副热带太平洋大气海洋异常通过经向风应力以及北太平洋和南太平洋经向模态,影响ENSO发展演变的途径及相关物理机制。李晓惠等[9]用经验正交函数分析法以及小波分析方法研究西太平洋暖池与ENSO循环过程之间的作用机制。张萍等[10]从南海降水异常的角度探讨了在ENSO期间,Walker环流异常对南海海面温度异常(SST anomaly,SSTA)的影响过程。林婷婷等[11]研究了ENSO与南海SST关系的年代际变化。薛德强等[12]分析了两类厄尔尼诺事件期间的SST异常,发现东部型和中部型厄尔尼诺期间海洋和大气加热场不是赤道对称,赤道以南热源强度大于赤道以北。
观测事实[13-14]表明,ENSO现象的基本特征之一是其准周期性,因此,不应将ENSO看作是孤立的、偶尔发生的事件,而应该看作是连续的准周期循环。文中将研究这种准周期循环现象的物理机制,从而说明ENSO现象是热带海气耦合系统中的一种固有振荡现象。关于线性的自由Kelvin波和自由Rossby波的存在性,Matsuno[15]已经做了深入的研究。对于海气耦合系统而言,还需要解决海气的耦合可行性、耦合波的相互作用和非线性效应以及海气的相互作用(热力和风应力)对耦合波的影响等问题。Domaracki等[16]从能量的角度分析Kelvin波和自由Rossby波的非线性特征,但要深入地认识ENSO的振荡特征,还需要从海气流场结构的演变来进一步分析。
为此,通过海气耦合系统的Kelvin波和Rossby波的相互作用来研究ENSO循环的物理机制。首先,从尺度分析的角度研究海气耦合的可行性,并得到无量纲的海气耦合方程;其次,结合多尺度分析和摄动近似,对无量纲的海气耦合模式进行简化,得到大气和海洋Kelvin波和Rossby波波幅的准周期变化特征;最后,结合两者的经向结构,分析ENSO循环的物理机制。
1 赤道海气耦合方程Chao等[17]对热带海洋和大气的尺度分析认为,虽然大气运动的变化比海洋的运动快得多,大气的经圈尺度比海洋的经圈尺度大得多,但是海洋以其时间尺度加热于大气经圈尺度上的大气运动,而大气以其时间尺度作用于海洋经圈尺度上的海洋运动,这样的加热和风应力作用是一致的,因此热带海洋和大气的耦合是协调的。
下面,通过近似地转效应的浅水方程来分析热带海气耦合系统的非线性Kelvin波和Rossby波的运动情况。
海洋浅水波模式如下。
| $ \left\{\begin{array}{l} \left(\frac{\partial}{\partial t}+u_{\mathrm{s}} \frac{\partial}{\partial x}+v_{\mathrm{s}} \frac{\partial}{\partial y}\right) u_{\mathrm{s}}-\beta y v_{\mathrm{s}}=-\frac{\partial {\mathit{\emptyset}}_{\mathrm{s}}}{\partial x}+\tau_x \\ \left(\frac{\partial}{\partial t}+u_{\mathrm{s}} \frac{\partial}{\partial x}+v_{\mathrm{s}} \frac{\partial}{\partial y}\right) v_{\mathrm{s}}+\beta y u_{\mathrm{s}}=-\frac{\partial {\mathit{\emptyset}}_{\mathrm{s}}}{\partial y} \\ \left(\frac{\partial}{\partial t}+u_{\mathrm{s}} \frac{\partial}{\partial x}+v_{\mathrm{s}} \frac{\partial}{\partial y}\right) {\mathit{\emptyset}}_{\mathrm{s}}+C_{\mathrm{s}}^2\left(\frac{\partial u_{\mathrm{s}}}{\partial x}+\frac{\partial v_{\mathrm{s}}}{\partial y}\right)=0 \end{array}\right. $ | (1) |
其中:t为时间;us为海洋纬向速度;vs为海洋经向速度;x为纬向距离;y为经向距离;
房佳蓓等[18]的研究结果表明,纬向风应力在海气耦合中起绝对主导作用,所以在研究热带太平洋海气耦合动力学对ENSO不稳定发展的贡献时,采用忽略经向风应力作用的近似是合理可行的。为此,在海洋浅水波模式中,仅考虑纬向风应力,而忽略经向风应力。
大气线性模式如下。
| $ \left\{\begin{array}{l} \frac{\partial u_{\mathrm{a}}}{\partial t}-\beta y v_{\mathrm{a}}=-\frac{\partial {\mathit{\emptyset}}_{\mathrm{a}}}{\partial x} \\ \beta y u_{\mathrm{a}}=-\frac{\partial {\mathit{\emptyset}}_{\mathrm{a}}}{\partial y} \\ C_{\mathrm{a}}^2\left(\frac{\partial u_{\mathrm{a}}}{\partial x}+\frac{\partial v_{\mathrm{a}}}{\partial y}\right)=Q \end{array}\right. $ | (2) |
其中:ua为大气纬向速度;va为大气经向速度;Øa=
根据Bjerknes[1]关于Walker环流调整阐述ENSO循环的物理机制的假设,这里的海洋浅水模式主要考虑了纬向风应力,而略去经向风应力。由于Philander等[13]考虑海洋斜温层深度的变化影响SST,后者再加热给大气,因此,可设大气热源和海洋斜温层深度成正比,即
| $ Q=\lambda {\mathit{\emptyset}}_{\mathrm{s}} $ | (3) |
再设洋面的风应力与大气风速成正比,即
| $ \tau_x=r u_{\mathrm{a}} $ | (4) |
其中:λ=10-2 s-1,为热源加热系数;r=5×10-7 s-1,为风应力系数。假定风应力为定常,则根据大气线性模式,可知
| $ \left\{\begin{array}{l} \left(\frac{\partial}{\partial t}+u_{\mathrm{s}} \frac{\partial}{\partial x}+v_{\mathrm{s}} \frac{\partial}{\partial y}\right) u_{\mathrm{s}}-\beta y v_{\mathrm{s}}=-\frac{\partial {\mathit{\emptyset}}_{\mathrm{s}}}{\partial x}+\frac{r \lambda}{C_{\mathrm{a}}^2} \int_0^{L_{\mathrm{s}}}\left(2 {\mathit{\emptyset}}_{\mathrm{s}}+y \frac{\partial {\mathit{\emptyset}}_{\mathrm{s}}}{\partial y}\right) \mathrm{d} x \\ \beta y u_{\mathrm{s}}=-\frac{\partial {\mathit{\emptyset}}_{\mathrm{s}}}{\partial y} \\ \left(\frac{\partial}{\partial t}+u_{\mathrm{s}} \frac{\partial}{\partial x}+v_{\mathrm{s}} \frac{\partial}{\partial y}\right) {\mathit{\emptyset}}_{\mathrm{s}}+C_{\mathrm{s}}{ }^2\left(\frac{\partial u_{\mathrm{s}}}{\partial x}+\frac{\partial v_{\mathrm{s}}}{\partial y}\right)=0 \end{array}\right. $ | (5) |
对上述方程进行无量纲分析,令
| $ \begin{array}{l} \left(u_{\mathrm{a}}, v_{\mathrm{a}}\right) \sim O\left(U_{\mathrm{a}}\right)\left(u_{\mathrm{a}}^{\prime}, v_{\mathrm{a}}^{\prime}\right), (t) \sim O\left(1 / \beta L_{\mathrm{a}}\right) t^{\prime}, (x, y) \sim O\left(L_{\mathrm{a}}\right)\left(x^{\prime}, y^{\prime}\right), \left({\mathit{\emptyset}}_{\mathrm{a}}\right) \sim O\left(\beta L_{\mathrm{a}}^{2} U_{\mathrm{a}}\right) {\mathit{\emptyset}}_{\mathrm{a}}^{\prime} \\ \left(u_{\mathrm{s}}, v_{\mathrm{s}}\right) \sim O\left(U_{\mathrm{s}}\right)\left(u_{\mathrm{s}}^{\prime}, v_{\mathrm{s}}^{\prime}\right), (t) \sim O\left(1 / \beta L_{\mathrm{s}}\right) t^{\prime}, (x, y) \sim O\left(L_{\mathrm{s}}\right)\left(x^{\prime}, y^{\prime}\right), \left({\mathit{\emptyset}}_{\mathrm{s}}\right) \sim O\left(\beta L_{\mathrm{s}}^{2} U_{\mathrm{s}}\right) {\mathit{\emptyset}}_{\mathrm{s}}^{\prime} \end{array} $ | (6) |
其中:O表示函数阶数;
| $ \left\{\begin{array}{l} \frac{\partial u_{\mathrm{s}}}{\partial t}+\varepsilon\left(u_{\mathrm{s}} \frac{\partial}{\partial x}+v_{\mathrm{s}} \frac{\partial}{\partial y}\right) u_{\mathrm{s}}-y v_{\mathrm{s}}=-\frac{\partial {\mathit{\emptyset}}_{\mathrm{s}}}{\partial x}+\varepsilon \kappa \int_{0}^{L_{\mathrm{s}}}\left(2 {\mathit{\emptyset}}_{\mathrm{s}}+y \frac{\partial {\mathit{\emptyset}}_{\mathrm{s}}}{\partial y}\right) \mathrm{d} x \\ \frac{\partial v_{\mathrm{s}}}{\partial t}+\varepsilon\left(u_{\mathrm{s}} \frac{\partial}{\partial x}+v_{\mathrm{s}} \frac{\partial}{\partial y}\right) v_{\mathrm{s}}+y u_{\mathrm{s}}=-\frac{\partial {\mathit{\emptyset}}_{\mathrm{s}}}{\partial y} \\ \frac{\partial {\mathit{\emptyset}}_{\mathrm{s}}}{\partial t}+\varepsilon\left(u_{\mathrm{s}} \frac{\partial}{\partial x}+v_{\mathrm{s}} \frac{\partial}{\partial y}\right) {\mathit{\emptyset}}_{\mathrm{s}}+\left(\frac{\partial u_{\mathrm{s}}}{\partial x}+\frac{\partial v_{\mathrm{s}}}{\partial y}\right)=0 \end{array}\right. $ | (7) |
其中:
假设赤道太平洋范围为-R≤y≤R,0≤x≤D,其中R=4 500 km,D=10 000 km,又设耦合模式运动在该范围关于赤道是对称的。由于太平洋西海岸为非刚性边界,在此研究中,考虑通道流,对应的耦合模式非刚性边界条件如下。
| $ \begin{equation*} \frac{\partial u_{\mathrm{s}}}{\partial y}=\frac{\partial {\mathit{\emptyset}}_{\mathrm{s}}}{\partial y}=v_{\mathrm{s}}=0, \quad y= \pm R \end{equation*} $ | (8) |
下面,根据公式(7)和边界条件(8),分析耦合模式的Kelvin波和Rossby波的运动,在此基础上,讨论ENSO准周期运动的物理机制。
2 非线性赤道海气耦合Kelvin波与Rossby波将赤道海气耦合运动做如此分解:海洋运动为具有水平切变的基本流和扰动流(大气运动不分解,直接通过线性模式求解)。
| $ \begin{equation*} u_{\mathrm{s}}=\bar{U}_{\mathrm{s}}(y)+u_{\mathrm{s}}^{\prime}, v_{\mathrm{s}}=v_{\mathrm{s}}^{\prime}, {\mathit{\emptyset}}_{\mathrm{s}}=\bar{\varPhi}_{\mathrm{s}}(y)+{\mathit{\emptyset}}_{\mathrm{s}}^{\prime} \end{equation*} $ | (9) |
其中:
| $ \left\{\begin{array}{l}\left(\frac{\partial}{\partial t}+\varepsilon \bar{U}_{\mathrm{s}} \frac{\partial}{\partial x}\right) u_{\mathrm{s}}+\varepsilon\left(u_{\mathrm{s}} \frac{\partial}{\partial x}+v_{\mathrm{s}} \frac{\partial}{\partial y}\right) u_{\mathrm{s}}-\left(y-\varepsilon \frac{\mathrm{d} \bar{U}_{\mathrm{s}}}{\mathrm{d} y}\right) v_{\mathrm{s}}=-\frac{\partial {\mathit{\emptyset}}_{\mathrm{s}}}{\partial x}+\varepsilon \kappa \int_{0}^{L_{\mathrm{s}}}\left(2\left(\bar{\varPhi}_{\mathrm{s}}+{\mathit{\emptyset}}_{\mathrm{s}}\right)+y \frac{\partial\left(\bar{\varPhi}_{\mathrm{s}}+{\mathit{\emptyset}}_{\mathrm{s}}\right)}{\partial y}\right) \mathrm{d} x \\ y u_{\mathrm{s}}+\frac{\partial {\mathit{\emptyset}}_{\mathrm{s}}}{\partial y}=0 \\ \left(\frac{\partial}{\partial t}+\varepsilon \bar{U}_{\mathrm{s}} \frac{\partial}{\partial x}\right) {\mathit{\emptyset}}_{\mathrm{s}}+\varepsilon\left(u_{\mathrm{s}} \frac{\partial}{\partial x}+v_{\mathrm{s}} \frac{\partial}{\partial y}\right) {\mathit{\emptyset}}_{\mathrm{s}}+\varepsilon \frac{\mathrm{d} \bar{\varPhi}_{\mathrm{s}}}{\mathrm{d} y} v_{\mathrm{s}}+\left(\frac{\partial u_{\mathrm{s}}}{\partial x}+\frac{\partial v_{\mathrm{s}}}{\partial y}\right)=0\end{array}\right. $ | (10) |
扰动流场的边界条件为
| $ \begin{equation*} u_{\mathrm{s}}={\mathit{\emptyset}}_{\mathrm{s}}=v_{\mathrm{s}}=0, y= \pm R \end{equation*} $ | (11) |
由于ENSO属于年际变化,其过程既包含了快运动,又包含了慢运动。因此,对公式(10)中的小参数ε(0<ε≪1),采用多重尺度分析法,引入缓变的时间与空间变量:
| $ \left\{\begin{array} { l } { \tau = \varepsilon t } \\ { \xi = \varepsilon x } \end{array} \quad \left\{\begin{array}{l} T=\varepsilon^{2} t \\ X=\varepsilon^{2} x \end{array}\right.\right. $ | (12) |
且在y方向上仍为快变的,则
| $ \begin{equation*} \frac{\partial}{\partial t} \rightarrow \varepsilon \frac{\partial}{\partial \tau}+\varepsilon^{2} \frac{\partial}{\partial T}, \quad \frac{\partial}{\partial x} \rightarrow \varepsilon \frac{\partial}{\partial \xi}+\varepsilon^{2} \frac{\partial}{\partial X} \end{equation*} $ | (13) |
将扰动函数展开为
| $ \left\{\begin{array}{l} u_{\mathrm{s}}=u_{\mathrm{s} 0}+\varepsilon u_{\mathrm{s} 1}+\varepsilon^{2} u_{\mathrm{s} 2}+\cdots \cdots \\ v_{\mathrm{s}}=v_{\mathrm{s} 0}+\varepsilon v_{\mathrm{s} 1}+\varepsilon^{2} v_{\mathrm{s} 2}+\cdots \cdots \\ {\mathit{\emptyset}}_{\mathrm{s}}={\mathit{\emptyset}}_{\mathrm{s} 0}+\varepsilon {\mathit{\emptyset}}_{\mathrm{s} 1}+\varepsilon^{2} {\mathit{\emptyset}}_{\mathrm{s} 2}+\cdots \cdots \end{array}\right. $ | (14) |
将公式(12)、(13)和(14)带入到公式(10)中,得到关于Øs的ε-各阶问题。
O(ε0)阶问题:
| $ \left\{\begin{array}{l} \frac{\partial u_{\mathrm{s} 0}}{\partial t}+\frac{\partial {\mathit{\emptyset}}_{\mathrm{s} 0}}{\partial x}-y v_{\mathrm{s} 0}=0 \\ y u_{\mathrm{s} 0}+\frac{\partial {\mathit{\emptyset}}_{\mathrm{s} 0}}{\partial y}=0 \\ \frac{\partial {\mathit{\emptyset}}_{\mathrm{s} 0}}{\partial t}+\left(\frac{\partial u_{\mathrm{s} 0}}{\partial x}+\frac{\partial v_{\mathrm{s} 0}}{\partial y}\right)=0 \end{array}\right. $ | (15) |
可以看出,O(ε0)阶问题即为线性模式。根据Matsuno[15]的研究,线性低纬大气方程可以激发出东行的Kelvin波和西行的Rossby波。因此可以设
| $ \begin{equation*} {\mathit{\emptyset}}_{\mathrm{s} 0}={\mathit{\emptyset}}_{\mathrm{s} 01}+{\mathit{\emptyset}}_{\mathrm{s} 02} \end{equation*} $ | (16) |
其中:
简化方程(15),得到关于Øs0的方程。
| $ \begin{equation*} \mathscr{L}\left({\mathit{\emptyset}}_{\mathrm{s} 0}\right)=0 \end{equation*} $ | (17) |
其中:
| $ \begin{equation*} \frac{\mathrm{d}^{2} \varphi_{j}^{(0)}}{\mathrm{d} y^{2}}-\frac{2}{y} \frac{\mathrm{~d} \varphi_{j}^{(0)}}{\mathrm{d} y}-\left(\frac{1}{c_{j}}+y^{2}\right) \varphi_{j}^{(0)}=0 \end{equation*} $ | (18) |
根据扰动流场的边界条件(11),可以认为
| $ \begin{equation*} \left.\varphi_{j}^{(0)}(y)\right|_{y \rightarrow \pm \infty} \rightarrow 0 \end{equation*} $ | (19) |
此时,方程(18)在边界条件(19)下的解为
| $ \begin{equation*} \varphi_{j}^{(0)}=\frac{1}{2}\left(\omega_{j}-k\right) \psi_{n+1}-n\left(\omega_{j}+k\right) \psi_{n-1}, j=1, 2 \end{equation*} $ | (20) |
其中:
O(ε1)阶问题:
| $ \left\{\begin{array}{l} \frac{\partial u_{\mathrm{s} 1}}{\partial t}+\frac{\partial {\mathit{\emptyset}}_{\mathrm{s} 1}}{\partial x}-y v_{\mathrm{s} 1}=F_{1} \\ y u_{\mathrm{s} 1}+\frac{\partial {\mathit{\emptyset}}_{\mathrm{s} 1}}{\partial y}=0 \\ \frac{\partial {\mathit{\emptyset}}_{\mathrm{s} 1}}{\partial t}+\frac{\partial u_{\mathrm{s} 1}}{\partial x}+\left(\frac{\partial v_{\mathrm{s} 1}}{\partial y}\right)=F_{2} \end{array}\right. $ | (21) |
其中
| $ \begin{array}{l} F_{1}=-\left( \begin{array}{l} {\frac{\partial u_{\mathrm{s} 0}}{\partial \tau}+\frac{\partial {\mathit{\emptyset}}_{\mathrm{s} 0}}{\partial \xi}+u_{\mathrm{s} 0} \frac{\partial u_{\mathrm{s} 0}}{\partial x}+\bar{U}_{\mathrm{s}} \frac{\partial u_{\mathrm{s} 0}}{\partial x}+v_{\mathrm{s} 0} \frac{\partial u_{\mathrm{s} 0}}{\partial y}+\frac{\mathrm{d} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y} v_{\mathrm{s} 0}+}\\{\kappa \int_{0}^{x}\left(2\left(\bar{\varPhi}_{\mathrm{s}}+{\mathit{\emptyset}}_{\mathrm{s}}\right)+y \frac{\partial\left(\bar{\varPhi}_{\mathrm{s}}+{\mathit{\emptyset}}_{\mathrm{s}}\right)}{\partial y}\right) \mathrm{d} x} \end{array} \right)\\ F_{2}=-\left(\frac{\partial {\mathit{\emptyset}}_{\mathrm{s} 0}}{\partial \tau}+\frac{\partial u_{\mathrm{s} 0}}{\partial \xi}-y \bar{U}_{\mathrm{s}} v_{\mathrm{s} 0}+u_{\mathrm{s} 0} \frac{\partial {\mathit{\emptyset}}_{\mathrm{s} 0}}{\partial x}+\bar{U}_{\mathrm{s}} \frac{\partial {\mathit{\emptyset}}_{\mathrm{s} 0}}{\partial x}+v_{\mathrm{s} 0} \frac{\partial {\mathit{\emptyset}}_{\mathrm{s} 0}}{\partial y}\right) \end{array} $ |
通过公式(15),将O(ε1)阶问题化为关于海洋偏差的一阶近似Ø1的方程
| $ \begin{equation*} \mathscr{L}\left({\mathit{\emptyset}}_{1}\right)=F=F_{2}+\frac{\partial}{\partial y}\left(\frac{1}{y} F_{1}\right) \end{equation*} $ | (22) |
将公式(16)带入到公式(22),并考虑到公式(20),得到
| $ \begin{array}{l} \mathscr{L}\left({\mathit{\emptyset}}_{1}\right)=-\sum\limits_{j=1}^{2} \mathrm{e}^{\mathrm{i} k\left(x-c_{j}t\right)} f_{1 j}-\sum\limits_{j=1}^{2} \mathrm{i} k A_{j}^{2} \mathrm{e}^{2 {\rm{i}} k\left(x-c_{j}t\right)} f_{2 j}-\\ \mathrm{i} k A_{1} A_{2} \mathrm{e}^{\mathrm{i} k\left[2 x-\left(c_{1}+c_{2}\right) t\right]} f_{3}-\mathrm{i} k A_{1} \bar{A}_{2} \mathrm{e}^{-\left(c_{1}-c_{2}\right) t} f_{4}-\\ \mathrm{i} k \bar{A}_{1} A_{2} \mathrm{e}^{\left(c_{1}-c_{2}\right) t} f_{5}-\frac{\kappa}{\mathrm{i} k} A_{1} \mathrm{e}^{\mathrm{i} k\left(-c_{1}\right) t} f_{6}-\frac{\kappa}{\mathrm{i} k} A_{2} \mathrm{e}^{\mathrm{i} k\left(-c_{2}\right) t} f_{7}-\\ \kappa \frac{2 x}{y^{2}} \bar{\varPhi}_{\mathrm{s}}+\kappa \frac{2 x}{y} \frac{\mathrm{~d} \bar{\varPhi}_{\mathrm{s}}}{\mathrm{d} y}-\kappa x \frac{\mathrm{~d}^{2} \bar{\varPhi}_{\mathrm{s}}}{\mathrm{d} y^{2}}+C . C \end{array} $ | (23) |
f1j、f2j、f3、f4、f5、f6、f7的表达式见附录A。由于
| $ \begin{align*} & \left(\frac{1}{y^{2}} \varphi_{j}^{(0)}+\frac{1}{y} \frac{\mathrm{~d} \varphi_{j}^{(0)}}{\mathrm{d} y}\right) \frac{\partial A_{j}}{\partial \xi}-\left(\varphi_{j}^{(0)}+\frac{2}{y^{3}} \frac{\mathrm{~d} \varphi_{j}^{(0)}}{\mathrm{d} y}-\frac{1}{y^{2}} \frac{\mathrm{~d}^{2} \varphi_{j}^{(0)}}{\mathrm{d} y^{2}}\right) \frac{\partial A_{j}}{\partial \tau}=\frac{1}{y}\left[\frac{\mathrm{~d}^{2} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y^{2}}\left(\varphi_{j}^{(0)}+c_{j} \frac{1}{y} \frac{\mathrm{~d} \varphi_{j}^{(0)}}{\mathrm{d} y}\right)+\right. \\ & \left.\frac{c_{j}}{y^{2}} \frac{\mathrm{~d} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y}\left(\frac{\mathrm{~d}^{2} \varphi_{j}^{(0)}}{\mathrm{d} y^{2}}-\frac{1}{y} \frac{\mathrm{~d} \varphi_{j}^{(0)}}{\mathrm{d} y}\right)-\bar{U}_{\mathrm{s}}\left(c_{j} \frac{\mathrm{~d} \varphi_{j}^{(0)}}{\mathrm{d} y}-\frac{1}{y} \frac{\mathrm{~d}^{2} \varphi_{j}^{(0)}}{\mathrm{d} y^{2}}\right)+\frac{1}{k^{2}}\left(\frac{1}{y} \varphi_{j}^{(0)}-\frac{\mathrm{d} \varphi_{j}^{(0)}}{\mathrm{d} y}\right)\right] \mathrm{i} k A_{j} \end{align*} $ | (24) |
不妨设
| $ \begin{align*} & \varphi_{1}=\sum\limits_{j=1}^{2} A_{j}^{2} \varphi_{j}^{(1)}(y) \mathrm{e}^{2 {\rm{i}} k\left(x-c_{j} t\right)}+A_{1} A_{2} \varphi_{3}{ }^{(1)}(y) \mathrm{e}^{\mathrm{i} k\left[2 x-\left(c_{1}+c_{2}\right) t\right]}+A_{1} \bar{A}_{2} \varphi_{4}{ }^{(1)}(y) \mathrm{e}^{-\mathrm{i} k\left(c_{1}-c_{2}\right) t}+\bar{A}_{1} A_{2} \varphi_{5}{ }^{(1)}(y) \mathrm{e}^{\mathrm{i} k\left(c_{1}-c_{2}\right) t}+ \\ & \frac{\kappa}{\mathrm{i} k} A_{1} \varphi_{6}{ }^{(1)}(y) \mathrm{e}^{\mathrm{i} k\left(-c_{1}\right) t}+\frac{\kappa}{\mathrm{i} k} A_{2} \varphi_{7}{ }^{(1)}(y) \mathrm{e}^{\mathrm{i} k\left(-c_{2}\right) t}+\kappa x^{2} \bar{\varPhi}_{\mathrm{s}}-\kappa x^{2} y \frac{\mathrm{~d} \bar{\varPhi}_{\mathrm{s}}}{\mathrm{~d} y}+\kappa x y^{2} \frac{\mathrm{~d}^{2} \bar{\varPhi}_{\mathrm{s}}}{\mathrm{~d} y^{2}}+C . C \end{align*} $ | (25) |
为进一步得到关于振幅Aj的条件,需进一步考虑O(ε2)阶问题。
O(ε2)阶问题(由于扰动Øs也是按ε展开的,因此强迫项将从两个方面影响O(ε2)阶问题):
| $ \left\{\begin{array}{l} \frac{\partial u_{\mathrm{s} 2}}{\partial t}+\frac{\partial {\mathit{\emptyset}}_{\mathrm{s} 2}}{\partial x}-y v_{\mathrm{s} 2}=G_{1} \\ y u_{\mathrm{s} 2}+\frac{\partial {\mathit{\emptyset}}_{\mathrm{s} 2}}{\partial y}=0 \\ \frac{\partial {\mathit{\emptyset}}_{\mathrm{s} 2}}{\partial t}+\left(\frac{\partial u_{\mathrm{s} 2}}{\partial x}+\frac{\partial v_{\mathrm{s} 2}}{\partial y}\right)=G_{2} \end{array}\right. $ | (26) |
其中
| $ \begin{aligned} & G_{1}=-\frac{\partial u_{\mathrm{s} 1}}{\partial \tau}-u_{\mathrm{s} 0} \frac{\partial u_{\mathrm{s} 1}}{\partial x}-u_{\mathrm{s} 1} \frac{\partial u_{\mathrm{s} 0}}{\partial x}-v_{\mathrm{s} 0} \frac{\partial u_{\mathrm{s} 1}}{\partial y}-v_{\mathrm{s} 1} \frac{\partial u_{\mathrm{s} 0}}{\partial y}-\bar{U} \frac{\partial u_{\mathrm{s} 1}}{\partial x}- \\ & \frac{\partial {\mathit{\emptyset}}_{\mathrm{s} 1}}{\partial \xi}-\frac{\mathrm{d} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y} v_{\mathrm{s} 1}-u_{\mathrm{s} 0} \frac{\partial u_{\mathrm{s} 0}}{\partial \xi}-\frac{\partial u_{\mathrm{s} 0}}{\partial T}-\frac{\partial {\mathit{\emptyset}}_{\mathrm{s} 0}}{\partial X}-\kappa \int_{0}^{x} {\mathit{\emptyset}}_{\mathrm{s} 1} \mathrm{~d} x, \end{aligned} $ |
| $ \begin{aligned} & G_{2}=-\frac{\partial u_{\mathrm{s} 1}}{\partial \xi}-u_{\mathrm{s} 0} \frac{\partial {\mathit{\emptyset}}_{\mathrm{s} 1}}{\partial x}-u_{\mathrm{s} 1} \frac{\partial {\mathit{\emptyset}}_{\mathrm{s} 0}}{\partial x}-v_{\mathrm{s} 0} \frac{\partial {\mathit{\emptyset}}_{\mathrm{s} 1}}{\partial y}-v_{\mathrm{s} 1} \frac{\partial {\mathit{\emptyset}}_{\mathrm{s} 0}}{\partial y}- \\ & \frac{\partial {\mathit{\emptyset}}_{\mathrm{s} 1}}{\partial \tau}+y \bar{U}_{\mathrm{s}} v_{\mathrm{s} 1}-\bar{U}_{\mathrm{s}} \frac{\partial {\mathit{\emptyset}}_{\mathrm{s} 1}}{\partial x}-u_{\mathrm{s} 0} \frac{\partial {\mathit{\emptyset}}_{\mathrm{s} 0}}{\partial \xi}-\frac{\partial {\mathit{\emptyset}}_{\mathrm{s} 0}}{\partial T}-\frac{\partial u_{\mathrm{s} 0}}{\partial X}{ }。\end{aligned} $ |
通过公式(15)、(21),将O(ε2)阶问题化为关于海洋偏差的二阶近似Ø2的方程
| $ \begin{equation*} \mathscr{L}\left({\mathit{\emptyset}}_{2}\right)=G=G_{2}+\frac{\partial}{\partial y}\left(\frac{1}{y} G_{1}\right) \end{equation*} $ | (27) |
将公式(16)、(25)带入公式(27),得到
| $ \begin{align*} & \mathscr{L}\left({\mathit{\emptyset}}_{2}\right)=\left\{\frac{y^{4}}{4} \varphi_{1}^{(1)} \frac{\partial A_{1}}{\partial X}-\frac{y^{2}}{4}\left(-y \frac{\mathrm{~d} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y} \frac{\mathrm{~d}^{2} \varphi_{1}^{(1)}}{\mathrm{d} y^{2}}+\left(y^{3} \bar{U}_{\mathrm{s}}-y \frac{\mathrm{~d}^{2} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y^{2}}+3 \frac{\mathrm{~d} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y}\right) \frac{\mathrm{d} \varphi_{1}^{(1)}}{\mathrm{d} y}\right) \frac{\partial A_{1}}{\partial \tau}-\right. \\ & \frac{y^{3}}{4}\left(y^{3} \varphi_{1}^{(1)}-y \frac{\mathrm{~d}^{2} \varphi_{1}^{(1)}}{\mathrm{d} y^{2}}+2 \frac{\mathrm{~d} \varphi_{1}^{(1)}}{\mathrm{d} y}\right) \frac{\partial A_{1}}{\partial T}+\frac{y^{3}}{4}\left(-y \frac{\mathrm{~d}^{2} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y^{2}} \varphi_{1}^{(1)}-y \frac{\mathrm{~d} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y} \frac{\mathrm{~d} \varphi_{1}^{(1)}}{\mathrm{d} y}+\left(y^{3} \bar{U}_{\mathrm{s}}+2 \frac{\mathrm{~d} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y}\right) \varphi_{1}^{(1)}\right) \frac{\partial A_{1}}{\partial \xi}+ \\ & \kappa\left[\frac{x y^{3}}{4}\left(-y \frac{\mathrm{~d} \bar{\varPhi}_{\mathrm{s}}}{\mathrm{~d} y}+\bar{\varPhi}_{\mathrm{s}}\right) \frac{\mathrm{d}^{3} \varphi_{1}^{(1)}}{\mathrm{d} y^{3}}+\frac{x y^{4}}{4} \frac{\mathrm{~d}^{3} \bar{\varPhi}_{\mathrm{s}}}{\mathrm{~d} y^{3}} \frac{\mathrm{~d} \varphi_{1}^{(1)}}{\mathrm{d} y}-x y^{2}\left(-y \frac{\mathrm{~d} \bar{\varPhi}_{\mathrm{s}}}{\mathrm{~d} y}+\bar{\varPhi}_{\mathrm{s}}\right) \frac{\mathrm{d}^{2} \varphi_{1}^{(1)}}{\mathrm{d} y^{2}}-\frac{x y^{3}}{4} \frac{\mathrm{~d}^{2} \bar{\varPhi}_{\mathrm{s}}}{\mathrm{~d} y^{2}} \frac{\mathrm{~d} \varphi_{1}^{(1)}}{\mathrm{d} y}+\right. \\ & \left.x y\left(-y \frac{\mathrm{~d} \bar{\varPhi}_{\mathrm{s}}}{\mathrm{~d} y}+\bar{\varPhi}_{\mathrm{s}}\right) \frac{\mathrm{d} \varphi_{1}^{(1)}}{\mathrm{d} y}\right] A_{1}+\left[\frac{k y}{4} \frac{\mathrm{~d}^{2} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y^{2}}\left(\left(y_{U_{\mathrm{s}}}-2 c_{1} \frac{\mathrm{~d} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y}\right) \frac{\mathrm{d} \varphi_{1}^{(1)}}{\mathrm{d} y}-2 y \frac{\mathrm{~d} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y} \varphi_{1}^{(1)}\right)-\right. \\ & \frac{\kappa k x^{2} y^{3}}{8} \frac{\mathrm{~d}^{4} \bar{\varPhi}_{\mathrm{s}}}{\mathrm{~d} y^{4}}\left(y \varphi_{1}^{(1)}+c_{1} \frac{\mathrm{~d} \varphi_{1}^{(1)}}{\mathrm{d} y}\right)+\frac{\kappa x y^{2}}{4} \frac{\mathrm{~d}^{3} \bar{\varPhi}_{\mathrm{s}}}{\mathrm{~d} y^{3}}\left(-\frac{k c_{1} x y}{2} \frac{\mathrm{~d}^{2} \varphi_{1}^{(1)}}{\mathrm{d} y^{2}}+\left(-\frac{k x y^{2}}{2}+\frac{3 k c_{1} x}{2}\right) \frac{\mathrm{d} \varphi_{1}^{(1)}}{\mathrm{d} y}+k x y \varphi_{1}^{(1)}\right)+ \\ & y\left(-y\left(\frac{k c_{1}}{4}\left(\frac{\mathrm{~d} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y}\right)^{2}-\frac{k y}{4} \bar{U}_{\mathrm{s}} \frac{\mathrm{~d} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y}\right) \frac{\mathrm{d}^{2} \varphi_{1}^{(1)}}{\mathrm{d} y^{2}}+\frac{\kappa k c_{1} x^{2} y^{4}}{8} \frac{\mathrm{~d}^{2} \bar{\varPhi}_{\mathrm{s}}}{\mathrm{~d} y^{2}} \frac{\mathrm{~d} \varphi_{1}^{(1)}}{\mathrm{d} y}+\frac{k y}{4}\left(y^{3} \bar{U}_{\mathrm{s}}+3 \frac{\mathrm{~d} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y}\right) \frac{\mathrm{d} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y} \varphi_{1}^{(1)}+\right. \\ & \left.\left.\left(k c_{1}\left(\frac{\mathrm{~d} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y}\right)^{2}+\frac{k y}{4}\left(c_{1} y^{2}-3\right) \bar{U}_{\mathrm{s}} \frac{\mathrm{~d} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y}-\frac{k y^{4}}{4} \bar{U}_{\mathrm{s}}^{2}\right) \frac{\mathrm{d} \varphi_{1}^{(1)}}{\mathrm{d} y}\right)\right] \mathrm{i} A_{1}+\left[\frac{k\left(c_{1}-c_{2}\right) y^{2}}{4} \frac{\mathrm{~d}^{3} \varphi_{2}^{(1)}}{\mathrm{d} y^{3}} \frac{\mathrm{~d} \varphi_{5}^{(1)}}{\mathrm{d} y}+y \varphi_{2}^{(1)} \frac{\mathrm{d} \varphi_{5}^{(1)}}{\mathrm{d} y}+\right.\end{align*} $ |
| $ \begin{align*} & \frac{k y^{2}}{4}\left(y \varphi_{2}^{(1)}+c_{2} \frac{\mathrm{~d} \varphi_{2}^{(1)}}{\mathrm{d} y}\right) \frac{\mathrm{d}^{3} \varphi_{5}^{(1)}}{\mathrm{d} y^{3}}-\frac{5 k y}{4} \frac{\mathrm{~d}^{2} \varphi_{2}^{(1)}}{\mathrm{d} y^{2}}\left(-\frac{c_{1} y}{5} \frac{\mathrm{~d}^{2} \varphi_{5}^{(1)}}{\mathrm{d} y^{2}}+\left(c_{1}-\frac{4 c_{2}}{5}\right) \frac{\mathrm{d} \varphi_{5}^{(1)}}{\mathrm{d} y}\right)-k y^{2} \varphi_{2}^{(1)} \frac{\mathrm{d}^{2} \varphi_{5}^{(1)}}{\mathrm{d} y^{2}}- \\ & \left.\left.k y\left(\left(-\frac{y^{2}}{4}+\frac{c_{1}}{4}+c_{2}\right) \frac{\mathrm{d} \varphi_{2}^{(1)}}{\mathrm{d} y}\right) \frac{\mathrm{d}^{2} \varphi_{5}^{(1)}}{\mathrm{d} y^{2}}+\left(\left(\frac{5 c_{1}}{4}-\frac{c_{1} y^{4}}{4}-\frac{y^{2}}{4}\right) \frac{\mathrm{d} \varphi_{2}^{(1)}}{\mathrm{d} y}\right) \frac{\mathrm{d} \varphi_{5}^{(1)}}{\mathrm{d} y}\right] \mathrm{i} A_{1}\left|A_{2}\right|^{2}\right\} \mathrm{e}^{\mathrm{i} k\left(x-c_{1} t\right)}+ \\ & \left\{\frac{y^{4}}{4} {\varphi}_{2}^{(1)} \frac{\partial A_{2}}{\partial X}-\frac{y^{2}}{4}\left(-y \frac{\mathrm{~d} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y} \frac{\mathrm{~d}^{2} {\varphi}_{2}^{(1)}}{\mathrm{d} y^{2}}+\left(y^{3} \bar{U}_{\mathrm{s}}-y \frac{\mathrm{~d}^{2} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y^{2}}+3 \frac{\mathrm{~d} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y}\right) \frac{\mathrm{d} \varphi_{2}^{(1)}}{\mathrm{d} y}\right) \frac{\partial A_{2}}{\partial \tau}-\right. \\ & \frac{y^{3}}{4}\left(y^{3} \varphi_{2}^{(1)}-y \frac{\mathrm{~d}^{2} {\varphi}_{2}^{(1)}}{\mathrm{d} y^{2}}+2 \frac{\mathrm{~d} \varphi_{2}^{(1)}}{\mathrm{d} y}\right) \frac{\partial A_{2}}{\partial T}+\frac{y^{3}}{4}\left(-y \frac{\mathrm{~d}^{2} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y^{2}} {\varphi}_{2}^{(1)}-y \frac{\mathrm{~d} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y} \frac{\mathrm{~d} \varphi_{2}^{(1)}}{\mathrm{d} y}+\left(y^{3} \bar{U}_{\mathrm{s}}+2 \frac{\mathrm{~d} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y}\right) {\varphi}_{2}^{(1)}\right) \frac{\partial A_{2}}{\partial \xi}+ \\ & \kappa\left[\frac{x y^{3}}{4}\left(-y \frac{\mathrm{~d} \bar{\varPhi}_{\mathrm{s}}}{\mathrm{~d} y}+\bar{\varPhi}_{\mathrm{s}}\right) \frac{\mathrm{d}^{3} \varphi_{2}^{(1)}}{\mathrm{d} y^{3}}+\frac{x y^{4}}{4} \frac{\mathrm{~d}^{3} \bar{\varPhi}_{\mathrm{s}}}{\mathrm{~d} y^{3}} \frac{\mathrm{~d} \varphi_{2}^{(1)}}{\mathrm{d} y}-x y^{2}\left(-y \frac{\mathrm{~d} \bar{\varPhi}_{\mathrm{s}}}{\mathrm{~d} y}+\bar{\varPhi}_{\mathrm{s}}\right) \frac{\mathrm{d}^{2} \varphi_{2}^{(1)}}{\mathrm{d} y^{2}}-\frac{x y^{3}}{4} \frac{\mathrm{~d}^{2} \bar{\varPhi}_{\mathrm{s}}}{\mathrm{~d} y^{2}} \frac{\mathrm{~d} \varphi_{2}^{(1)}}{\mathrm{d} y}+\right. \\ & \left.x y\left(-y \frac{\mathrm{~d} \bar{\varPhi}_{\mathrm{s}}}{\mathrm{~d} y}+\bar{\varPhi}_{\mathrm{s}}\right) \frac{\mathrm{d} \varphi_{2}^{(1)}}{\mathrm{d} y}\right] A_{2}+\left[\frac{k y}{4} \frac{\mathrm{~d}^{2} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y^{2}}\left(\left(y \bar{U}_{\mathrm{s}}-2 c_{2} \frac{\mathrm{~d} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y}\right) \frac{\mathrm{d} \varphi_{2}^{(1)}}{\mathrm{d} y}-2 y \frac{\mathrm{~d} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y} \varphi_{2}^{(1)}\right)-\right. \\ & \frac{\kappa k x^{2} y^{3}}{8} \frac{\mathrm{~d}^{4} \bar{\varPhi}_{\mathrm{s}}}{\mathrm{~d} y^{4}}\left(y \varphi_{2}^{(1)}+c_{2} \frac{\mathrm{~d} \varphi_{2}^{(1)}}{\mathrm{d} y}\right)+\frac{\kappa x y^{2}}{4} \frac{\mathrm{~d}^{3} \bar{\varPhi}_{\mathrm{s}}}{\mathrm{~d} y^{3}}\left(-\frac{k c_{2} x y}{2} \frac{\mathrm{~d}^{2} \varphi_{2}^{(1)}}{\mathrm{d} y^{2}}+\left(-\frac{k x y^{2}}{2}+\frac{3 k c_{2} x}{2}\right) \frac{\mathrm{d} \varphi_{2}^{(1)}}{\mathrm{d} y}+k x y \varphi_{2}^{(1)}\right)+ \\ & y\left(-y\left(\frac{k c_{2}}{4}\left(\frac{\mathrm{~d} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y}\right)^{2}-\frac{k y}{4} \bar{U}_{\mathrm{s}} \frac{\mathrm{~d} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y}\right) \frac{\mathrm{d}^{2} \varphi_{2}^{(1)}}{\mathrm{d} y^{2}}+\frac{\kappa k c_{2} x^{2} y^{4}}{8} \frac{\mathrm{~d}^{2} \bar{\varPhi}_{\mathrm{s}}}{\mathrm{~d} y^{2}} \frac{\mathrm{~d} \varphi_{2}^{(1)}}{\mathrm{d} y}+\frac{k y}{4}\left(y^{3} \bar{U}_{\mathrm{s}}+3 \frac{\mathrm{~d} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y}\right) \frac{\mathrm{d} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y} \varphi_{2}^{(1)}+\right. \\ & \left.\left.\left(k c_{2}\left(\frac{\mathrm{~d} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y}\right)^{2}+\frac{k y}{4}\left(c_{2} y^{2}-3\right) \bar{U}_{\mathrm{s}} \frac{\mathrm{~d} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y}-\frac{k y^{4}}{4} \bar{U}_{\mathrm{s}}^{2}\right) \frac{\mathrm{d} \varphi_{2}^{(1)}}{\mathrm{d} y}\right)\right] \mathrm{i} A_{2}+\left[\frac{k\left(c_{2}-c_{1}\right) y^{2}}{4} \frac{\mathrm{~d}^{3} \varphi_{1}^{(1)}}{\mathrm{d} y^{3}} \frac{\mathrm{~d} \varphi_{5}^{(1)}}{\mathrm{d} y}+y \varphi_{1}^{(1)} \frac{\mathrm{d} \varphi_{5}^{(1)}}{\mathrm{d} y}+\right. \\ & \frac{k y^{2}}{4}\left(y \varphi_{1}^{(1)}+c_{1} \frac{\mathrm{~d} \varphi_{1}^{(1)}}{\mathrm{d} y}\right) \frac{\mathrm{d}^{3} \varphi_{5}^{(1)}}{\mathrm{d} y^{3}}-\frac{5 k y}{4} \frac{\mathrm{~d}^{2} \varphi_{1}^{(1)}}{\mathrm{d} y^{2}}\left(-\frac{c_{2} y}{5} \frac{\mathrm{~d}^{2} \varphi_{5}^{(1)}}{\mathrm{d} y^{2}}+\left(c_{2}-\frac{4 c_{1}}{5}\right) \frac{\mathrm{d} \varphi_{5}^{(1)}}{\mathrm{d} y}\right)-k y^{2} \varphi_{1}^{(1)} \frac{\mathrm{d}^{2} \varphi_{5}^{(1)}}{\mathrm{d} y^{2}}- \\ & \left.\left.k y\left(\left(-\frac{y^{2}}{4}+\frac{c_{2}}{4}+c_{1}\right) \frac{\mathrm{d} \varphi_{1}^{(1)}}{\mathrm{d} y}\right) \frac{\mathrm{d}^{2} \varphi_{5}^{(1)}}{\mathrm{d} y^{2}}+\left(\left(\frac{5 c_{2}}{4}-\frac{c_{2} y^{4}}{4}-\frac{y^{2}}{4}\right) \frac{\mathrm{d} \varphi_{1}^{(1)}}{\mathrm{d} y}\right) \frac{\mathrm{d} \varphi_{5}^{(1)}}{\mathrm{d} y}\right] \mathrm{i} A_{2}\left|A_{1}\right|^{2}\right\} \mathrm{e}^{\mathrm{i} k\left(x-c_{2} t\right)}+\text { 其他项 } \end{align*} $ | (28) |
消除久期项,并在经向方向积分,得到赤道海洋和大气的耦合Kelvin波和Rossby波的振幅方程
| $ \left\{\begin{array}{l} \frac{\partial A_{1}}{\partial T}+\alpha_{1} \frac{\partial A_{1}}{\partial X}+\beta_{1} \frac{\partial A_{1}}{\partial \xi}+\gamma_{1} \frac{\partial A_{1}}{\partial \tau}+\kappa \delta_{1} A_{1}+\mathrm{i} \eta_{1} A_{1}+\mathrm{i} \sigma_{12} A_{1}\left|A_{2}\right|^{2}=0 \\ \frac{\partial A_{2}}{\partial T}+\alpha_{2} \frac{\partial A_{2}}{\partial X}+\beta_{2} \frac{\partial A_{2}}{\partial \xi}+\gamma_{2} \frac{\partial A_{2}}{\partial \tau}+\kappa \delta_{2} A_{2}+\mathrm{i} \eta_{2} A_{2}+\mathrm{i} \sigma_{21} A_{2}\left|A_{1}\right|^{2}=0 \end{array}\right. $ | (29) |
其中
| $ \begin{aligned} & \alpha_{1}=\frac{I_{11}}{I_{1}}, \beta_{1}=\frac{I_{12}}{I_{1}}, \gamma_{1}=\frac{I_{13}}{I_{1}}, \delta_{1}=\frac{I_{14}}{I_{1}}, \eta_{1}=\frac{I_{15}}{I_{1}}, \sigma_{1}=\frac{I_{16}}{I_{1}} \\ & \alpha_{2}=\frac{I_{21}}{I_{2}}, \beta_{2}=\frac{I_{22}}{I_{2}}, \gamma_{2}=\frac{I_{23}}{I_{2}}, \delta_{2}=\frac{I_{24}}{I_{2}}, \eta_{2}=\frac{I_{25}}{I_{2}}, \sigma_{2}=\frac{I_{26}}{I_{2}} \end{aligned} $ |
方程中的各参数表达式见附录B。
3 耦合模式中的风应力强迫作用通过WKB方法,已得到赤道海洋和大气的耦合Kelvin波和Rossby波的振幅方程。根据海洋和大气波动理论,其耦合波运动主要依赖于振幅的调制。然而,振幅方程(29)是非线性的复偏微分方程,无法对其求解析解,为了更清楚地了解耦合波运动的物理机制,需要对方程(29)进行进一步分析。为此,对振幅方程(29)的时间和空间做如下变换:
| $ \begin{align*} & \zeta=\left(\xi-\frac{\beta_{1}}{\gamma_{1}} \tau\right)-\gamma_{1}\left(X-\alpha_{1} T\right)= \\ & \mathrm{K}\left[\left(\xi-\frac{\beta_{2}}{\gamma_{2}} \tau\right)-\gamma_{2}\left(X-\alpha_{2} T\right)\right] \end{align*} $ | (30) |
得到如下复方程形式:
| $ \left\{\begin{array}{l} \frac{\mathrm{d} A_{1}}{\mathrm{~d} \zeta}=\kappa \delta_{1}^{\prime} A_{1}+\mathrm{i} \eta_{1}^{\prime} A_{1}+\mathrm{i} \sigma_{12}^{\prime} A_{1}\left|A_{2}\right|^{2} \\ \frac{\mathrm{~d} A_{2}}{\mathrm{~d} \zeta}=\kappa \delta_{2}^{\prime} A_{2}+\mathrm{i} \eta_{2}^{\prime} A_{2}+\mathrm{i} \sigma_{21}^{\prime} A_{2}\left|A_{1}\right|^{2} \end{array}\right. $ | (31) |
由于Aj(j=1, 2)为复数,则设
| $ \begin{equation*} A_{1}=A_{1 R}+\mathrm{i} A_{1 I}, A_{2}=A_{2 R}+\mathrm{i} A_{2 I} \end{equation*} $ | (32) |
则方程可以化为如下实方程:
| $ \left\{\begin{array}{l} \frac{\mathrm{d} A_{1 R}}{\mathrm{~d} \zeta}=\kappa \delta_{1}^{\prime} A_{1 R}-\eta_{1}^{\prime} A_{1 I}-\sigma_{12}^{\prime} A_{1 I}\left(A_{2 R}{ }^{2}-A_{2 I}{ }^{2}\right) \\ \frac{\mathrm{d} A_{1 I}}{\mathrm{~d} \zeta}=\kappa \delta_{1}^{\prime} A_{1 I}+\eta_{1}^{\prime} A_{1 R}+\sigma_{12}^{\prime} A_{1 R}\left(A_{2 R}{ }^{2}-A_{2 I}{ }^{2}\right) \\ \frac{\mathrm{d} A_{2 R}}{\mathrm{~d} \zeta}=\kappa \delta_{2}^{\prime} A_{2 R}-\eta_{2}^{\prime} A_{2 I}-\sigma_{21}^{\prime} A_{2 I}\left(A_{1 R}{ }^{2}-A_{1 I}{ }^{2}\right) \\ \frac{\mathrm{d} A_{2 I}}{\mathrm{~d} \zeta}=\kappa \delta_{2}^{\prime} A_{2 I}+\eta_{2}^{\prime} A_{2 R}+\sigma_{21}^{\prime} A_{2 R}\left(A_{1 R}{ }^{2}-A_{1 I}{ }^{2}\right) \end{array}\right. $ | (33) |
变换后的振幅方程(33)是四维的非线性常微分方程组,无法直接求出解析解,但可采用定性理论对其进行分析。根据复方程形式(31)可知,方程右边各项系数为实数,或者为纯虚数,而实系数主要由外源强迫引起,即大气风应力和海洋热力强迫。
下面的分析将会表明,纯虚系数项在系统(31)中起着重要作用,将单独考虑。为此,假设耦合运动无外源强迫,即没有风应力和热力强迫作用。令κ=0,此时方程(33)线性部分的拓扑结构为环,其对应的时序解为周期解,在非线性作用下,Kelvin波和Rossby波的振幅呈准周期变化。由方程(33)可以看出,出现这种准周期变化的原因主要在于两点:一是线性扭结作用,即复方程(31)中的纯虚数项经过复数分解(32),构成了方程(33)的线性系统的双环结构,这种双环结构将造成Kelvin波和Rossby波各自独立地做周期运动,是耦合波做准周期运动的基础;二是非线性作用,方程(33)的非线性项中含有|A3-j|2,该项即为Kelvin波与Rossby波的相互作用,通过自身的变化来引起对方的变化,使得二者的振幅呈准周期振荡,而不是周期性振荡。
取k=2, n=1,[y1, y2]=(-∞, ∞),初值(A1R, A1I, A2R, A2I)|ζ=0=(0.7, 1.0, 1.5, 2.0),Ø(y)=0.5y,根据计算,α1=0.264 1, α2=0.421 0,β1=0.083, β2=0.170。γ1=1.57, γ2=2.06,η′1=0.71, η′2=0.64,σ′12=2.61, σ′21=3.17。同时,考虑到无量纲变换公式(2),得到如下Kelvin波和Rossby波波幅的相图(图 1)和时序图(图 2)。
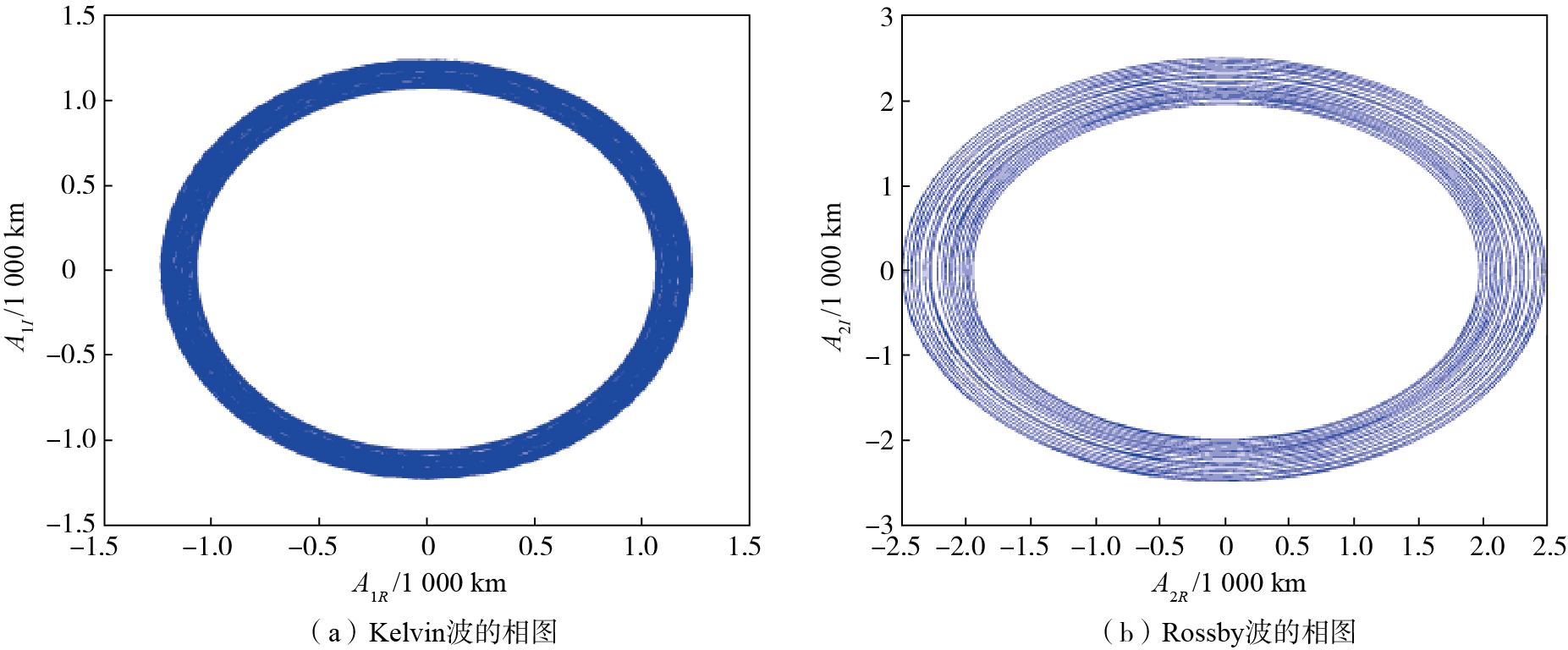
|
图 1 κ=0时Kelvin波和Rossby波的相图 Fig.1 Phase diagram of Kelvin and Rossby waves in the condition of κ=0 |
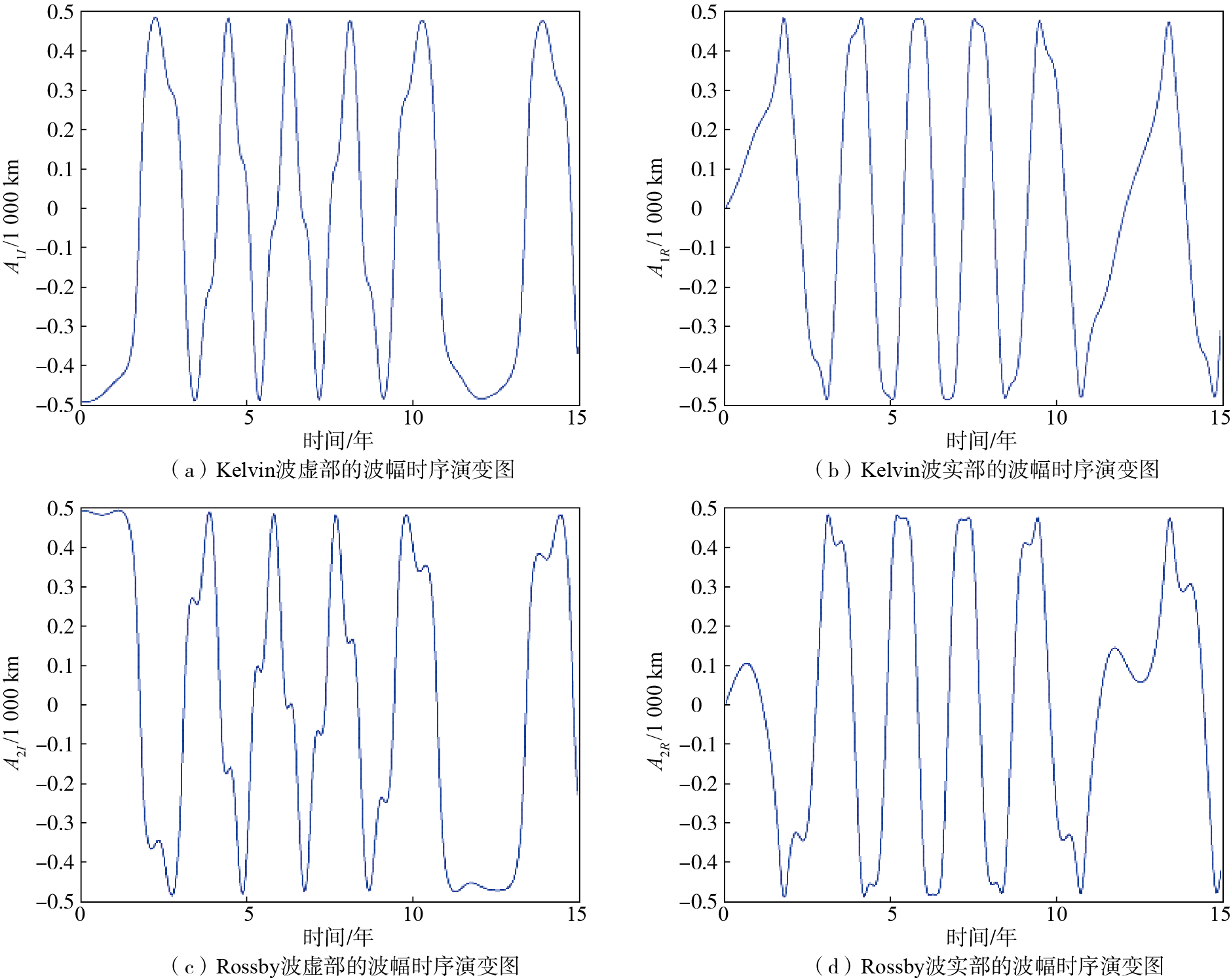
|
图 2 κ=0时Kelvin波和Rossby波的波幅时序演变图 Fig.2 Time series of amplitude of Kelvin and Rossby waves in the condition of κ=0 |
进一步地,分析κ≠0的情况。此时,线性系统不再是环结构,而是不稳定焦点结构。这意味着系统(33)在初始阶段,主要由线性项控制,受不稳定焦点结构影响,Kelvin波和Rossby波的振幅将呈指数型螺旋振荡增大;时间达到一定时长后,主要由非线性项驱动,而非线性项具有准周期振荡特征。注意,Rossby波的波幅出现了混沌现象。
根据上面的取值,可得κ=0.026,η″1=0.86,η″2=0.73,其他值不变。同时,考虑到无量纲变换公式(2),得到如下Kelvin波和Rossby波波幅的相图(图 3)和时序图(图 4)。
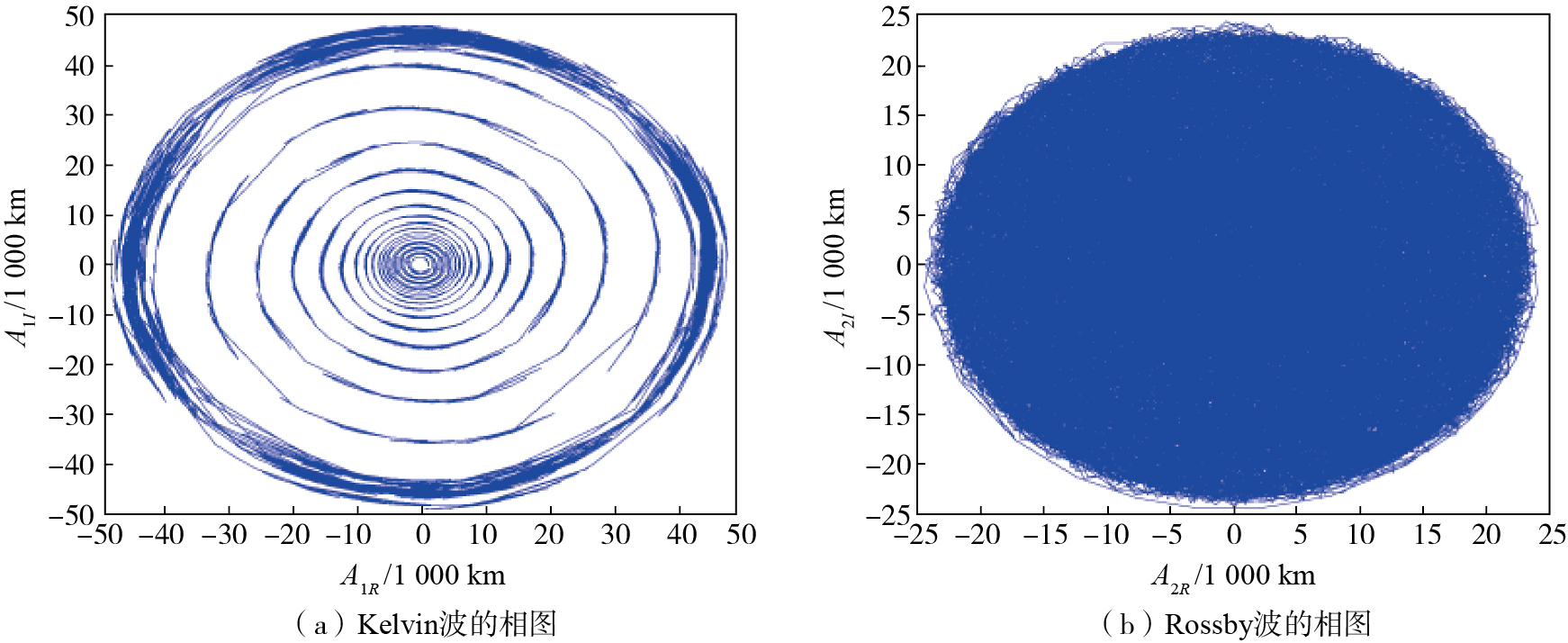
|
图 3 κ≠0时Kelvin波和Rossby波的相图 Fig.3 Phase diagram of Kelvin and Rossby waves in the condition of κ≠0 |
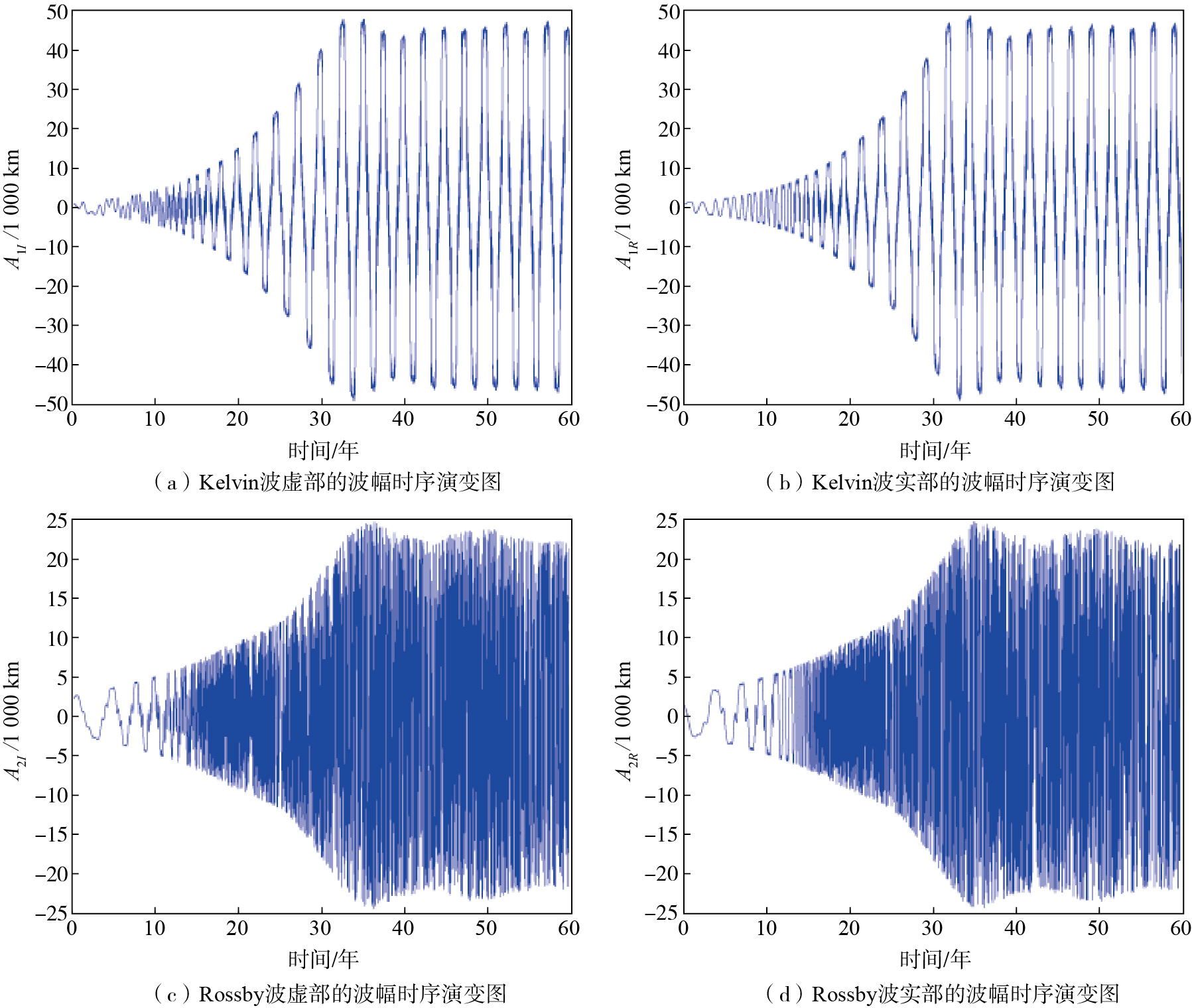
|
图 4 κ≠0时Kelvin波和Rossby波的波幅时序演变图 Fig.4 Time series of amplitude of Kelvin and Rossby waves in the condition of κ≠0 |
由上述分析可以看出,海洋自身具有Kelvin波和Rossby波的非线性准周期振荡的自驱动力,但是这种自驱动力较弱,而风应力以及海洋热源强迫对风应力的反馈作用(下面简称“反馈作用”),促进了海洋Kelvin波和Rossby波振幅增大;同时,风应力及反馈作用也进一步加强了海洋Kelvin波和Rossby波的非线性效应,在上述参数下,Rossby波出现明显的混沌现象。这种准周期与非周期振荡的叠加效应,体现了ENSO不规则性的特征。
4 ENSO准周期振荡模拟对赤道海洋和大气的耦合Kelvin波和Rossby波的相互作用进行分析,为了获得赤道太平洋运动的物理机制,根据一阶近似表达式(25),还需求出耦合波的经向结构,因此,需要求出φ1(1)、φ2(1)、φ3(1)、φ4(1)、φ5(1)、φ6(1)、φ7(1)的特征值问题。
| $ \left\{\begin{array}{l} \frac{\mathrm{d}^2 \varphi_1^{(1)}}{\mathrm{d} y^2}-\frac{2}{y} \frac{\mathrm{~d} \varphi_1^{(1)}}{\mathrm{d} y}-\left(\frac{1}{c_1}+y^2\right) \varphi_1^{(1)}=-\frac{f_{21} y^2}{2 c_1} \\ \frac{\mathrm{~d}^2 \varphi_2^{(1)}}{\mathrm{d} y^2}-\frac{2}{y} \frac{\mathrm{~d} \varphi_2^{(1)}}{\mathrm{d} y}-\left(\frac{1}{c_2}+y^2\right) \varphi_2^{(1)}=-\frac{f_{22} y^2}{2 c_2} \\ \frac{\mathrm{~d}^2 \varphi_3^{(1)}}{\mathrm{d} y^2}-\frac{2}{y} \frac{\mathrm{~d} \varphi_3^{(1)}}{\mathrm{d} y}-\left(\frac{1}{c_1+c_2}+y^2\right) \varphi_3^{(1)}=-\frac{f_3 y^2}{2\left(c_1+c_2\right)} \\ \frac{\mathrm{d}^2 \varphi_4^{(1)}}{\mathrm{d} y^2}-\frac{2}{y} \frac{\mathrm{~d} \varphi_4^{(1)}}{\mathrm{d} y}-y^2 \varphi_4^{(1)}=-\frac{f_4 y^2}{\left(c_1-c_2\right)} \\ \frac{\mathrm{d}^2 \varphi_5^{(1)}}{\mathrm{d} y^2}-\frac{2}{y} \frac{\mathrm{~d} \varphi_5^{(1)}}{\mathrm{d} y}-y^2 \varphi_5^{(1)}=-\frac{f_5 y^2}{\left(c_2-c_1\right)} \\ \frac{\mathrm{d}^2 \varphi_6^{(1)}}{\mathrm{d} y^2}-\frac{2}{y} \frac{\mathrm{~d} \varphi_6^{(1)}}{\mathrm{d} y}-y^2 \varphi_5^{(1)}=\frac{f_6 y^2}{c_1} \\ \frac{\mathrm{~d}^2 \varphi_7^{(1)}}{\mathrm{d} y^2}-\frac{2}{y} \frac{\mathrm{~d} \varphi_7^{(1)}}{\mathrm{d} y}-y^2 \varphi_7^{(1)}=\frac{f_7 y^2}{c_2} \end{array}\right. $ | (34) |
根据附录A,公式(34)的右边为φ1(0)、φ2(0)的函数。因此,将解(23)带入到公式(34)中,得到
| $ \left\{ \begin{array}{l} & \frac{\mathrm{d}^{2} {\varphi}_{1}^{(1)}}{\mathrm{d} y^{2}}-\frac{2}{y} \frac{\mathrm{~d} \varphi_{1}^{(1)}}{\mathrm{d} y}-\left(\frac{1}{c_{1}}+y^{2}\right) \varphi_{1}^{(1)}=\chi_{1}(y) \mathrm{e}^{-\frac{1}{2} y^{2}}+\delta_{1}(y) \mathrm{e}^{-y^{2}} \\ & \frac{\mathrm{~d}^{2} {\varphi}_{2}^{(1)}}{\mathrm{d} y^{2}}-\frac{2}{y} \frac{\mathrm{~d} \varphi_{2}^{(1)}}{\mathrm{d} y}-\left(\frac{1}{c_{2}}+y^{2}\right) \varphi_{2}^{(1)}=\chi_{2}(y) \mathrm{e}^{-\frac{1}{2} y^{2}}+\delta_{2}(y) \mathrm{e}^{-y^{2}} \\ & \frac{\mathrm{~d}^{2} {\varphi}_{3}^{(1)}}{\mathrm{d} y^{2}}-\frac{2}{y} \frac{\mathrm{~d} \varphi_{3}^{(1)}}{\mathrm{d} y}-\left(\frac{1}{c_{1}+c_{2}}+y^{2}\right) \varphi_{3}^{(1)}=\delta_{3}(y) \mathrm{e}^{-y^{2}} \\ & \frac{\mathrm{~d}^{2} {\varphi}_{4}^{(1)}}{\mathrm{d} y^{2}}-\frac{2}{y} \frac{\mathrm{~d} \varphi_{4}^{(1)}}{\mathrm{d} y}-\left(\frac{1}{c_{1}-c_{2}}+y^{2}\right) \varphi_{4}^{(1)}=\chi_{4}(y) \mathrm{e}^{-\frac{1}{2} y^{2}}+\delta_{4}(y) \mathrm{e}^{-y^{2}} \\ & \frac{\mathrm{~d}^{2} \varphi_{5}^{(1)}}{\mathrm{d} y^{2}}-\frac{2}{y} \frac{\mathrm{~d} \varphi_{5}^{(1)}}{\mathrm{d} y}-\left(\frac{1}{c_{2}-c_{1}}+y^{2}\right) \varphi_{5}^{(1)}=\delta_{5}(y) \mathrm{e}^{-y^{2}} \\ & \frac{\mathrm{~d}^{2} \varphi_{6}^{(1)}}{\mathrm{d} y^{2}}-\frac{2}{y} \frac{\mathrm{~d} \varphi_{6}^{(1)}}{\mathrm{d} y}-y^{2} {\varphi}_{6}^{(1)}=\delta_{6}(y) \mathrm{e}^{-y^{2}} \\ & \frac{\mathrm{~d}^{2} {\varphi}_{7}^{(1)}}{\mathrm{d} y^{2}} -\frac{2}{y} \frac{\mathrm{~d} \varphi_{7}^{(1)}}{\mathrm{d} y}-y^{2} {\varphi}_{7}^{(1)}=\delta_{7}(y) \mathrm{e}^{-y^{2}} \end{array} \right. $ | (35) |
方程(35)为Sturm-Liouville方程形式,χm(m =1, 2, 3, ……), δm(m=1, 2, 3, ……)为多项式函数,其表达式见附录C。由χm(m=1, 2, 3, ……), δm(m=1, 2, 3, ……)为多项式函数,因此,在边界条件(11)下,方程(35)有形式如下的解:
| $ \left\{\begin{array}{l} {\varphi}_{1}^{(1)}=r_{1}(y) \mathrm{e}^{-\frac{1}{2} y^{2}}+s_{1}(y) \mathrm{e}^{-y^{2}} \\ {\varphi}_{2}^{(1)}=r_{2}(y) \mathrm{e}^{-\frac{1}{2} y^{2}}+s_{2}(y) \mathrm{e}^{-y^{2}} \\ {\varphi}_{3}^{(1)}=r_{3}(y) \mathrm{e}^{-\frac{1}{2} y^{2}}+s_{3}(y) \mathrm{e}^{-y^{2}} \\ {\varphi}_{4}^{(1)}=r_{4}(y) \mathrm{e}^{-\frac{1}{2} y^{2}}+s_{4}(y) \mathrm{e}^{-y^{2}} \\ {\varphi}_{5}^{(1)}=r_{5}(y) \mathrm{e}^{-\frac{1}{2} y^{2}}+s_{5}(y) \mathrm{e}^{-y^{2}} \\ {\varphi}_{6}^{(1)}=r_{6}(y) \mathrm{e}^{-\frac{1}{2} y^{2}}+s_{6}(y) \mathrm{e}^{-y^{2}} \\ {\varphi}_{7}^{(1)}=r_{7}(y) \mathrm{e}^{-\frac{1}{2} y^{2}}+s_{7}(y) \mathrm{e}^{-y^{2}} \end{array}\right. $ | (36) |
其中,rm(y) (m=1, 2, ……,5)和sm(y) (m=1, 2, ……, 5)为复杂的多项式函数,此处略去。将海洋流场分解公式(9)、一阶近似表达式(25)、振幅的空间和时间变换公式(30)带入到级数分解公式(14)中,得到关于海洋重力势φs的一阶近似
| $ \begin{align*} & \varphi_{\mathrm{s}}=\bar{\varPhi}_{\mathrm{s}}(y)+\varphi_{\mathrm{s} 0}+\varepsilon \varphi_{\mathrm{s} 1}=A_{1}(\tau, T, \xi, X) \varphi_{1}{ }^{(0)}(y) \mathrm{e}^{\mathrm{i} k\left(x-c_{1} t\right)}+A_{2}(\tau, T, \xi, X) \varphi_{2}{ }^{(0)}(y) \mathrm{e}^{\mathrm{i} k\left(x-c_{2} t\right)}+ \\ & \varepsilon\left(\sum\limits_{j=1}^{2} A_{j}{ }^{2} \varphi_{j}^{(1)}(y) \mathrm{e}^{2 {\rm{i}} k\left(x-c_{{j}}t\right)}+A_{1} A_{2} \varphi_{3}{ }^{(1)}(y) \mathrm{e}^{\mathrm{i} k\left[2 x-\left(c_{1}+c_{2}\right) t\right]}+A_{1} \bar{A}_{2} \varphi_{4}{ }^{(1)}(y) \mathrm{e}^{-\mathrm{i} k\left(c_{1}-c_{2}\right) t}+\bar{A}_{1} A_{2} \varphi_{5}{ }^{(1)}(y) \mathrm{e}^{\mathrm{i} k\left(c_{1}-c_{2}\right) t}+\right. \\ & \left.\frac{1}{\mathrm{i} k} A_{1} \varphi_{6}{ }^{(1)}(y) \mathrm{e}^{\mathrm{i} k\left(-c_{1}\right) t}+\frac{1}{\mathrm{i} k} A_{2} \varphi_{7}{ }^{(1)}(y) \mathrm{e}^{\mathrm{i} k\left(-c_{2}\right) t}+\kappa x^{2} \bar{\varPhi}_{\mathrm{s}}-\kappa x^{2} y \frac{\mathrm{~d} \bar{\varPhi}_{\mathrm{s}}}{\mathrm{~d} y}+\kappa x y^{2} \frac{\mathrm{~d}^{2} \bar{\varPhi}_{\mathrm{s}}}{\mathrm{~d} y^{2}}\right)+C . C \end{align*} $ | (37) |
取上述参数,可得到60个月的海洋Kelvin波和Rossby波的准周期运动。
根据图 5可知,在ENSO运动中,Kelvin波和Rossby波是一直都存在的,由于相互的非线性作用,二者在不同阶段体现出不同的状态,总体为:蛰伏(酝酿)→增长→衰减→蛰伏(酝酿),而耦合波波包效应的正负变换,对应了赤道太平洋温跃层的高低变换。ENSO正是赤道太平洋在Kelvin波东移和Rossby波西移过程中,通过耦合波状态的循环与波包效应的正负变换,形成的不规则的准周期运动。具体表现如下。

|
图 5 Kelvin波和Rossby波在一个典型ENSO周期内的运动 Fig.5 Motion of Kelvin and Rossby waves in a typical ENSO cycle |
在El Niño位相前兆期,赤道波导区低空的西风应力,在赤道激发出暖的Kelvin波,它从西太平洋到达东太平洋的时间为2~3个月。西风产生的气旋性风应力旋度使东太平洋表层海水辐散,致使温跃层变浅,海面温度变冷,有弱的冷Rossby波存在,其蛰伏时间为暖Kelvin波运动时间。当暖的Kelvin波到达东太平洋后,使该处海面温度升高,温跃层变深,形成El Niño位相,此时赤道两边的辐散作用增强,冷的Rossby波开始增强并缓慢向西运动,它通过热带海盆所需的时间为1~2年,随后逐渐衰减。此时,暖的Kelvin波在东海岸维持少动并逐渐衰减。随着冷的Rossby波到达西太平洋,使得原来的暖池变冷,形成La Niña位相前兆期。随后,在赤道波导区低空西风应力的作用下,赤道激发出冷的Kelvin波,它从西太平洋到达东太平洋的时间为2~3个月。西风产生的反气旋风应力旋度使该处表层海水辐合,致使温跃层变深,海面温度变高,有弱的暖Rossby波存在,其蛰伏时间为冷的Kelvin波运动时间。当冷的Kelvin波到达东太平洋后,使该处海面温度变低,温跃层变浅,形成La Niña位相,此时赤道两边的辐散作用增强,暖的Rossby波开始增强并缓慢向西运动,它通过热带海盆所需的时间为1~2年,随后逐渐衰减。此时,暖的Kelvin波在东海岸维持少动并逐渐衰减。随着暖的Rossby波到达西太平洋,使得暖池恢复,再次形成El Niño位相前兆期。
5 结论与讨论基于微软公司开发的符号计算系统Maple,以一阶近似地转效应的浅水方程为基础,通过多尺度和摄动近似的方法,分析了低纬海气耦合系统的非线性Kelvin波和Rossby波的相互作用。首先,给出了无风应力条件下自激耦合系统的运动特征,这种自激运动振幅较小且呈准周期变化,分析发现自激耦合运动的准周期变化是Kelvin波和Rossby波各自的扭结效应和二者的非线性效应共同作用的结果。其次,研究分析了在有风应力条件下耦合系统的运动特征,即耦合波振幅在指数型螺旋振荡增大后,Kelvin波呈准周期振荡,Rossby波呈非周期振荡,这种准周期与非周期振荡的叠加效应,使得ENSO准周期运动呈显著的不规则性。最后,通过简化流场的近似模拟得出,在ENSO运动中,Kelvin波和Rossby波是一直都存在的,由于相互的非线性作用,二者在不同阶段体现出不同的状态,总体为:蛰伏(酝酿)→增长→衰减→蛰伏(酝酿)。
此研究仅考虑了定常的大气运动,没有体现出Walker环流的变化特征。因此,下一步将研究非定常风应力在低纬海气耦合的作用,以进一步揭示ENSO准周期振荡的物理机制。
附录A方程(23)的各项系数如下:
| $ \begin{aligned} & f_{1 j}=\left(\frac{1}{y^{2}} \varphi_{j}^{(0)}+\frac{1}{y} \frac{\mathrm{~d} \varphi_{j}^{(0)}}{\mathrm{d} y}\right) \frac{\partial A_{j}}{\partial \xi}-\left(\varphi_{j}^{(0)}+\frac{2}{y^{3}} \frac{\mathrm{~d} \varphi_{j}^{(0)}}{\mathrm{d} y}-\frac{1}{y^{2}} \frac{\mathrm{~d}^{2} \varphi_{j}^{(0)}}{\mathrm{d} y^{2}}\right) \frac{\partial A_{j}}{\partial \tau}-\frac{1}{y}\left[\frac{\mathrm{~d}^{2} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y^{2}}\left(\varphi_{j}^{(0)}+c_{j} \frac{1}{y} \frac{\mathrm{~d} \varphi_{j}^{(0)}}{\mathrm{d} y}\right)-\right. \\ & \left.\frac{1}{y} \frac{1}{y} \frac{\mathrm{~d} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y}\left(c_{j} \frac{1}{y} \frac{\mathrm{~d}^{2} \varphi_{j}^{(0)}}{\mathrm{d} y^{2}}-c_{j} \frac{1}{y^{2}} \frac{\mathrm{~d} \varphi_{j}^{(0)}}{\mathrm{d} y}\right)-\bar{U}_{\mathrm{s}}\left(c_{j} \frac{\mathrm{~d} \varphi_{j}^{(0)}}{\mathrm{d} y}-\frac{1}{y} \frac{\mathrm{~d}^{2} \varphi_{j}^{(0)}}{\mathrm{d} y^{2}}\right)+\frac{1}{k^{2}}\left(\frac{1}{y} \varphi_{j}^{(0)}-\frac{\mathrm{d} \varphi_{j}^{(0)}}{\mathrm{d} y}\right)\right] \mathrm{i} k A_{j}, \\ & f_{2 j}=\left[-\left(\frac{1}{y^{4}}+\frac{2}{y^{3}}\right)\left(\frac{\mathrm{d} \varphi_{j}^{(0)}}{\mathrm{d} y}\right)^{2}+\frac{2}{y^{3}} \frac{\mathrm{~d}^{2} \varphi_{j}^{(0)}}{\mathrm{d} y^{2}} \frac{\mathrm{~d} \varphi_{j}^{(0)}}{\mathrm{d} y}-\frac{1}{y} \frac{\mathrm{~d} \varphi_{j}^{(0)}}{\mathrm{d} y}\right]+\frac{1}{y^{2}}\left(c_{j} \frac{1}{y} \frac{\mathrm{~d}^{2} \varphi_{j}^{(0)}}{\mathrm{d} y^{2}}+\frac{\mathrm{d} \varphi_{j}^{(0)}}{\mathrm{d} y}-c_{j} \frac{1}{y^{2}} \frac{\mathrm{~d} \varphi_{j}^{(0)}}{\mathrm{d} y}\right) \times \\ & \left(\frac{1}{y^{2}} \frac{\mathrm{~d} \varphi_{j}^{(0)}}{\mathrm{d} y}-\frac{1}{y} \frac{\mathrm{~d}^{2} \varphi_{j}^{(0)}}{\mathrm{d} y^{2}}\right)+\left(\varphi_{j}^{(0)}+c_{j} \frac{1}{y} \frac{\mathrm{~d} \varphi_{j}^{(0)}}{\mathrm{d} y}\right)\left(\frac{1}{y} \frac{\mathrm{~d} \varphi_{j}^{(0)}}{\mathrm{d} y}-\frac{4}{y^{5}} \frac{\mathrm{~d} \varphi_{j}^{(0)}}{\mathrm{d} y}+\frac{4}{y^{4}} \frac{\mathrm{~d}^{2} \varphi_{j}^{(0)}}{\mathrm{d} y^{2}}-\frac{1}{y^{3}} \frac{\mathrm{~d}^{3} \varphi_{j}^{(0)}}{\mathrm{d} y^{3}}\right), \\ & f_{3}=-\left(\frac{1}{y} \varphi_{1}^{(0)} \frac{\mathrm{d} \varphi_{2}^{(0)}}{\mathrm{d} y}-\frac{1}{y} \frac{\mathrm{~d} \varphi_{1}^{(0)}}{\mathrm{d} y} \varphi_{2}^{(0)}+\frac{2}{y^{4}} \frac{\mathrm{~d} \varphi_{1}^{(0)}}{\mathrm{d} y} \frac{\mathrm{~d} \varphi_{2}^{(0)}}{\mathrm{d} y}\right)+\frac{2}{y^{3}}\left(\frac{\mathrm{~d} \varphi_{1}^{(0)}}{\mathrm{d} y} \frac{\mathrm{~d}^{2} \varphi_{2}^{(0)}}{\mathrm{d} y^{2}}+\frac{\mathrm{d}^{2} \varphi_{1}^{(0)}}{\mathrm{d} y^{2}} \frac{\mathrm{~d} \varphi_{2}^{(0)}}{\mathrm{d} y}\right)+ \\ & \frac{1}{y}\left[\left(\varphi_{2}^{(0)}+c_{2} \frac{1}{y} \frac{\mathrm{~d} \varphi_{2}^{(0)}}{\mathrm{d} y}\right) \frac{\mathrm{d} \varphi_{1}^{(0)}}{\mathrm{d} y}+\left(\varphi_{1}^{(0)}+c_{1} \frac{1}{y} \frac{\mathrm{~d} \varphi_{1}^{(0)}}{\mathrm{d} y}\right) \frac{\mathrm{d} \varphi_{2}^{(0)}}{\mathrm{d} y}\right]-\frac{4}{y^{4}} \frac{\mathrm{~d} \varphi_{1}^{(0)}}{\mathrm{d} y} \frac{\mathrm{~d} \varphi_{2}^{(0)}}{\mathrm{d} y}+ \\ & \frac{1}{y^{2}}\left(\varphi_{2}^{(0)}+c_{2} \frac{1}{y} \frac{\mathrm{~d} \varphi_{2}^{(0)}}{\mathrm{d} y}\right)\left(-\frac{4}{y^{3}} \frac{\mathrm{~d} \varphi_{1}^{(0)}}{\mathrm{d} y}+\frac{4}{y^{2}} \frac{\mathrm{~d}^{2} \varphi_{1}^{(0)}}{\mathrm{d} y^{2}}-\frac{1}{y} \frac{\mathrm{~d}^{3} \varphi_{1}^{(0)}}{\mathrm{d} y^{3}}\right)+\frac{1}{y^{2}}\left(\varphi_{1}^{(0)}+c_{1} \frac{1}{y} \frac{\mathrm{~d} \varphi_{1}^{(0)}}{\mathrm{d} y}\right) \times \\ & \frac{1}{y^{2}}\left(c_{2} \frac{1}{y} \frac{\mathrm{~d}^{2} \varphi_{2}^{(0)}}{\mathrm{d} y^{2}}+\frac{\mathrm{d} \varphi_{2}^{(0)}}{\mathrm{d} y}-c_{2} \frac{1}{y^{2}} \frac{\mathrm{~d} \varphi_{2}^{(0)}}{\mathrm{d} y}\right)\left(\frac{1}{y^{2}} \frac{\mathrm{~d} \varphi_{1}^{(0)}}{\mathrm{d} y}-\frac{1}{y} \frac{\mathrm{~d}^{2} \varphi_{1}^{(0)}}{\mathrm{d} y^{2}}\right)+ \end{aligned} $ |
| $ \begin{aligned} & \frac{1}{y^{2}}\left(c_{1} \frac{1}{y} \frac{\mathrm{~d}^{2} \varphi_{1}^{(0)}}{\mathrm{d} y^{2}}+\frac{\mathrm{d} \varphi_{1}^{(0)}}{\mathrm{d} y}-c_{1} \frac{1}{y^{2}} \frac{\mathrm{~d} \varphi_{1}^{(0)}}{\mathrm{d} y}\right)\left(\frac{1}{y^{2}} \frac{\mathrm{~d} \varphi_{2}^{(0)}}{\mathrm{d} y}-\frac{1}{y} \frac{\mathrm{~d}^{2} \varphi_{2}^{(0)}}{\mathrm{d} y^{2}}\right), \\ & f_{4}=-\left(\frac{1}{y} \varphi_{1}^{(0)} \frac{\mathrm{d} \bar{\varphi}_{2}^{(0)}}{\mathrm{d} y}-\frac{1}{y} \frac{\mathrm{~d} \varphi_{1}^{(0)}}{\mathrm{d} y} \bar{\varphi}_{2}^{(0)}+\frac{2}{y^{4}} \frac{\mathrm{~d} \varphi_{1}^{(0)}}{\mathrm{d} y} \frac{\mathrm{~d} \bar{\varphi}_{2}^{(0)}}{\mathrm{d} y}\right)+\frac{2}{y^{3}}\left(\frac{\mathrm{~d} \varphi_{1}^{(0)}}{\mathrm{d} y} \frac{\mathrm{~d}^{2} \bar{\varphi}_{2}^{(0)}}{\mathrm{d} y^{2}}+\frac{\mathrm{d}^{2} \varphi_{1}^{(0)}}{\mathrm{d} y^{2}} \frac{\mathrm{~d} \bar{\varphi}_{2}^{(0)}}{\mathrm{d} y}\right)+ \\ & \frac{1}{y}\left[\left(\bar{\varphi}_{2}^{(0)}+c_{2} \frac{1}{y} \frac{\mathrm{~d} \bar{\varphi}_{2}^{(0)}}{\mathrm{d} y}\right) \frac{\mathrm{d} \varphi_{1}^{(0)}}{\mathrm{d} y}+\left(\varphi_{1}^{(0)}+c_{1} \frac{1}{y} \frac{\mathrm{~d} \varphi_{1}^{(0)}}{\mathrm{d} y}\right) \frac{\mathrm{d} \bar{\varphi}_{2}^{(0)}}{\mathrm{d} y}\right]-\frac{4}{y^{4}} \frac{\mathrm{~d} \varphi_{1}^{(0)}}{\mathrm{d} y} \frac{\mathrm{~d} \bar{\varphi}_{2}^{(0)}}{\mathrm{d} y}+ \\ & \frac{1}{y^{2}}\left(\bar{\varphi}_{2}^{(0)}+c_{2} \frac{1}{y} \frac{\mathrm{~d} \bar{\varphi}_{2}^{(0)}}{\mathrm{d} y}\right)\left(-\frac{4}{y^{3}} \frac{\mathrm{~d} \varphi_{1}^{(0)}}{\mathrm{d} y}+\frac{4}{y^{2}} \frac{\mathrm{~d}^{2} \varphi_{1}^{(0)}}{\mathrm{d} y^{2}}-\frac{1}{y} \frac{\mathrm{~d}^{3} \varphi_{1}^{(0)}}{\mathrm{d} y^{3}}\right)+\frac{1}{y^{2}}\left(\varphi_{1}^{(0)}+c_{1} \frac{1}{y} \frac{\mathrm{~d} \varphi_{1}^{(0)}}{\mathrm{d} y}\right) \times \\ & \left(-\frac{4}{y^{3}} \frac{\mathrm{~d} \bar{\varphi}_{2}^{(0)}}{\mathrm{d} y}+\frac{4}{y^{2}} \frac{\mathrm{~d}^{2} \bar{\varphi}_{2}^{(0)}}{\mathrm{d} y^{2}}-\frac{1}{y} \frac{\mathrm{~d}^{3} \bar{\varphi}_{2}^{(0)}}{\mathrm{d} y^{3}}\right)+\frac{1}{y^{2}}\left(c_{2} \frac{1}{y} \frac{\mathrm{~d}^{2} \bar{\varphi}_{2}^{(0)}}{\mathrm{d} y^{2}}+\frac{\mathrm{d} \bar{\varphi}_{2}^{(0)}}{\mathrm{d} y}-c_{2} \frac{1}{y^{2}} \frac{\mathrm{~d} \bar{\varphi}_{2}^{(0)}}{\mathrm{d} y}\right) \times \\ & \left(\frac{1}{y^{2}} \frac{\mathrm{~d} \varphi_{1}^{(0)}}{\mathrm{d} y}-\frac{1}{y} \frac{\mathrm{~d}^{2} \varphi_{1}^{(0)}}{\mathrm{d} y^{2}}\right)+\frac{1}{y^{2}}\left(c_{1} \frac{1}{y} \frac{\mathrm{~d}^{2} \varphi_{1}^{(0)}}{\mathrm{d} y^{2}}+\frac{\mathrm{d} \varphi_{1}^{(0)}}{\mathrm{d} y}-c_{1} \frac{1}{y^{2}} \frac{\mathrm{~d} \varphi_{1}^{(0)}}{\mathrm{d} y}\right)\left(\frac{1}{y^{2}} \frac{\mathrm{~d} \bar{\varphi}_{2}^{(0)}}{\mathrm{d} y}-\frac{1}{y} \frac{\mathrm{~d}^{2} \bar{\varphi}_{2}^{(0)}}{\mathrm{d} y^{2}}\right), \\ & f_{5}=-\left(\frac{1}{y} \varphi_{2}^{(0)} \frac{\mathrm{d} \bar{\varphi}_{1}^{(0)}}{\mathrm{d} y}-\frac{1}{y} \frac{\mathrm{~d} \varphi_{2}^{(0)}}{\mathrm{d} y} \bar{\varphi}_{1}^{(0)}+\frac{2}{y^{4}} \frac{\mathrm{~d} \varphi_{2}^{(0)}}{\mathrm{d} y} \frac{\mathrm{~d} \bar{\varphi}_{1}^{(0)}}{\mathrm{d} y}\right)+\frac{2}{y^{3}}\left(\frac{\mathrm{~d} \varphi_{2}^{(0)}}{\mathrm{d} y} \frac{\mathrm{~d}^{2} \bar{\varphi}_{1}^{(0)}}{\mathrm{d} y^{2}}+\frac{\mathrm{d}^{2} \varphi_{2}^{(0)}}{\mathrm{d} y^{2}} \frac{\mathrm{~d} \bar{\varphi}_{1}^{(0)}}{\mathrm{d} y}\right)+ \\ & \frac{1}{y}\left[\left(\bar{\varphi}_{1}^{(0)}+c_{1} \frac{1}{y} \frac{\mathrm{~d} \bar{\varphi}_{1}^{(0)}}{\mathrm{d} y}\right) \frac{\mathrm{d} \varphi_{2}^{(0)}}{\mathrm{d} y}+\left(\varphi_{2}^{(0)}+c_{2} \frac{1}{y} \frac{\mathrm{~d} \varphi_{2}^{(0)}}{\mathrm{d} y}\right) \frac{\mathrm{d} \bar{\varphi}_{1}^{(0)}}{\mathrm{d} y}\right]-\frac{4}{y^{4}} \frac{\mathrm{~d} \varphi_{2}^{(0)}}{\mathrm{d} y} \frac{\mathrm{~d} \bar{\varphi}_{1}^{(0)}}{\mathrm{d} y}+ \\ & \frac{1}{y^{2}}\left(\bar{\varphi}_{1}^{(0)}+c_{1} \frac{1}{y} \frac{\mathrm{~d} \bar{\varphi}_{1}^{(0)}}{\mathrm{d} y}\right)\left(-\frac{4}{y^{3}} \frac{\mathrm{~d} \varphi_{2}^{(0)}}{\mathrm{d} y}+\frac{4}{y^{2}} \frac{\mathrm{~d}^{2} \varphi_{2}^{(0)}}{\mathrm{d} y^{2}}-\frac{1}{y} \frac{\mathrm{~d}^{3} \varphi_{2}^{(0)}}{\mathrm{d} y^{3}}\right)+\frac{1}{y^{2}}\left(\varphi_{2}^{(0)}+c_{2} \frac{1}{y} \frac{\mathrm{~d} \varphi_{2}^{(0)}}{\mathrm{d} y}\right) \times \\ & \left(-\frac{4}{y^{3}} \frac{\mathrm{~d} \bar{\varphi}_{1}^{(0)}}{\mathrm{d} y}+\frac{4}{y^{2}} \frac{\mathrm{~d}^{2} \bar{\varphi}_{1}^{(0)}}{\mathrm{d} y^{2}}-\frac{1}{y} \frac{\mathrm{~d}^{3} \bar{\varphi}_{1}^{(0)}}{\mathrm{d} y^{3}}\right)+\frac{1}{y^{2}}\left(c_{1} \frac{1}{y} \frac{\mathrm{~d}^{2} \bar{\varphi}_{1}^{(0)}}{\mathrm{d} y^{2}}+\frac{\mathrm{d} \bar{\varphi}_{1}^{(0)}}{\mathrm{d} y}-c_{1} \frac{1}{y^{2}} \frac{\mathrm{~d} \bar{\varphi}_{1}^{(0)}}{\mathrm{d} y}\right) \times \\ & \left(\frac{1}{y^{2}} \frac{\mathrm{~d} \varphi_{2}^{(0)}}{\mathrm{d} y}-\frac{1}{y} \frac{\mathrm{~d}^{2} \varphi_{2}^{(0)}}{\mathrm{d} y^{2}}\right)+\frac{1}{y^{2}}\left(c_{2} \frac{1}{y} \frac{\mathrm{~d}^{2} \varphi_{2}^{(0)}}{\mathrm{d} y^{2}}+\frac{\mathrm{d} \varphi_{2}^{(0)}}{\mathrm{d} y}-c_{2} \frac{1}{y^{2}} \frac{\mathrm{~d} \varphi_{2}^{(0)}}{\mathrm{d} y}\right)\left(\frac{1}{y^{2}} \frac{\mathrm{~d} \bar{\varphi}_{1}^{(0)}}{\mathrm{d} y}-\frac{1}{y} \frac{\mathrm{~d}^{2} \bar{\varphi}_{1}^{(0)}}{\mathrm{d} y^{2}}\right), \\ & f_{6}=\frac{2}{y} \frac{\mathrm{~d} \varphi_{1}^{(0)}}{\mathrm{d} y}-\frac{2}{y^{2}} \varphi_{1}^{(0)}+\frac{\mathrm{d}^{2} \varphi_{1}^{(0)}}{\mathrm{d} y^{2}}, \\ & f_{7}=\frac{2}{y} \frac{\mathrm{~d} \varphi_{2}^{(0)}}{\mathrm{d} y}-\frac{2}{y^{2}} \varphi_{2}^{(0)}+\frac{\mathrm{d}^{2} \varphi_{2}^{(0)}}{\mathrm{d} y^{2}} \text { 。} \end{aligned} $ |
振幅方程(29)中的各项系数构成如下:
| $ \begin{aligned} & I_{1}=\int_{y_{1}}^{y_{2}}\left[-\frac{y^{3}}{4}\left(y^{3} \varphi_{1}^{(1)}-y \frac{\mathrm{~d}^{2} \varphi_{1}^{(1)}}{\mathrm{d} y^{2}}+2 \frac{\mathrm{~d} \varphi_{1}^{(1)}}{\mathrm{d} y}\right)\right] \mathrm{d} y, \\ & I_{11}=\int_{y_{1}}^{y_{2}}\left(\frac{y^{4}}{4} \varphi_{1}^{(1)}\right) \mathrm{d} y, \\ & I_{12}=\int_{y_{1}}^{y_{2}}\left\{\frac{y^{3}}{4}\left[-y \frac{\mathrm{~d}^{2} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y^{2}} \varphi_{1}^{(1)}-y \frac{\mathrm{~d} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y} \frac{\mathrm{~d} \varphi_{1}^{(1)}}{\mathrm{d} y}+\left(y^{3} \bar{U}_{\mathrm{s}}+2 \frac{\mathrm{~d} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y}\right) \varphi_{1}^{(1)}\right]\right\} \mathrm{d} y, \\ & I_{13}=\int_{y_{1}}^{y_{2}}\left\{-\frac{y^{2}}{4}\left[-y \frac{\mathrm{~d} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y} \frac{\mathrm{~d}^{2} \varphi_{1}^{(1)}}{\mathrm{d} y^{2}}+\left(y^{3} \bar{U}_{\mathrm{s}}-y \frac{\mathrm{~d}^{2} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y^{2}}+3 \frac{\mathrm{~d} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y}\right) \frac{\mathrm{d} \varphi_{1}^{(1)}}{\mathrm{d} y}\right]\right\} \mathrm{d} y, \end{aligned} $ |
| $ \begin{aligned} & I_{14}=\int_{y_{1}}^{y_{2}}\left[\frac{x y^{3}}{4}\left(-y \frac{\mathrm{~d} \bar{\varPhi}_{\mathrm{s}}}{\mathrm{~d} y}+\bar{\varPhi}_{\mathrm{s}}\right) \frac{\mathrm{d}^{3} \varphi_{1}^{(1)}}{\mathrm{d} y^{3}}-x y^{2}\left(-y \frac{\mathrm{~d} \bar{\varPhi}_{\mathrm{s}}}{\mathrm{~d} y}+\bar{\varPhi}_{\mathrm{s}}\right) \frac{\mathrm{d}^{2} \varphi_{1}^{(1)}}{\mathrm{d} y^{2}}+\right. \\ & \left.\frac{x y^{4}}{4} \frac{\mathrm{~d}^{3} \bar{\varPhi}_{\mathrm{s}}}{\mathrm{~d} y^{3}} \frac{\mathrm{~d} \varphi_{1}^{(1)}}{\mathrm{d} y}-\frac{x y^{3}}{4} \frac{\mathrm{~d}^{2} \bar{\varPhi}_{\mathrm{s}}}{\mathrm{~d} y^{2}} \frac{\mathrm{~d} \varphi_{1}^{(1)}}{\mathrm{d} y}+x y\left(-y \frac{\mathrm{~d} \bar{\varPhi}_{\mathrm{s}}}{\mathrm{~d} y}+\bar{\varPhi}_{\mathrm{s}}\right) \frac{\mathrm{d} \varphi_{1}^{(1)}}{\mathrm{d} y}\right] \mathrm{d} y, \\ & I_{15}=\int_{y_{1}}^{y_{2}}\left\{\frac{k y}{4} \frac{\mathrm{~d}^{2} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y^{2}}\left[\left(y \bar{U}_{\mathrm{s}}-2 c_{1} \frac{\mathrm{~d} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y}\right) \frac{\mathrm{d} \varphi_{1}^{(1)}}{\mathrm{d} y}-2 y \frac{\mathrm{~d} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y} \varphi_{1}^{(1)}\right]-\right. \\ & \frac{\kappa k x^{2} y^{3}}{8} \frac{\mathrm{~d}^{4} \bar{\varPhi}_{\mathrm{s}}}{\mathrm{~d} y^{4}}\left(y \varphi_{1}^{(1)}+c_{1} \frac{\mathrm{~d} \varphi_{1}^{(1)}}{\mathrm{d} y}\right)+\frac{k y^{2}}{4}\left(y^{3} \bar{U}_{\mathrm{s}}+3 \frac{\mathrm{~d} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y}\right) \frac{\mathrm{d} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y} \varphi_{1}^{(1)}+ \\ & \frac{\kappa x y^{2}}{4} \frac{\mathrm{~d}^{3} \bar{\varPhi}_{\mathrm{s}}}{\mathrm{~d} y^{3}}\left[-\frac{k c_{1} x y}{2} \frac{\mathrm{~d}^{2} \varphi_{1}^{(1)}}{\mathrm{d} y^{2}}+\left(-\frac{k x y^{2}}{2}+\frac{3 k c_{1} x}{2}\right) \frac{\mathrm{d} \varphi_{1}^{(1)}}{\mathrm{d} y}+k x y \varphi_{1}^{(1)}\right]+ \\ & y\left[-y\left(\frac{k c_{1}}{4}\left(\frac{\mathrm{~d} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y}\right)^{2}-\frac{k y}{4} \bar{U}_{\mathrm{s}} \frac{\mathrm{~d} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y}\right) \frac{\mathrm{d}^{2} \varphi_{1}^{(1)}}{\mathrm{d} y^{2}}+\frac{\kappa k c_{1} x^{2} y^{4}}{8} \frac{\mathrm{~d}^{2} \bar{\varPhi}_{\mathrm{s}}}{\mathrm{~d} y^{2}} \frac{\mathrm{~d} \varphi_{1}^{(1)}}{\mathrm{d} y}+\right. \\ & \left.\left.\left(k c_{1}\left(\frac{\mathrm{~d} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y}\right)^{2}+\frac{k y}{4}\left(c_{1} y^{2}-3\right) \bar{U}_{\mathrm{s}} \frac{\mathrm{~d} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y}-\frac{k y^{4}}{4} \bar{U}_{\mathrm{s}}{ }^{2}\right) \frac{\mathrm{d} \varphi_{1}^{(1)}}{\mathrm{d} y}\right]\right\} \mathrm{d} y, \\ & I_{16}=\int_{y_{1}}^{y_{2}}\left\{\frac{k\left(c_{1}-c_{2}\right) y^{2}}{4} \frac{\mathrm{~d}^{3} {\varphi}_{2}^{(1)}}{\mathrm{d} y^{3}} \frac{\mathrm{~d} \varphi_{5}^{(1)}}{\mathrm{d} y}+y \varphi_{2}^{(1)} \frac{\mathrm{d} \varphi_{5}^{(1)}}{\mathrm{d} y}-k y^{2} \varphi_{2}^{(1)} \frac{\mathrm{d}^{2} {\varphi}_{5}^{(1)}}{\mathrm{d} y^{2}}+\right. \\ & \frac{k y^{2}}{4}\left(y \varphi_{2}^{(1)}+c_{2} \frac{\mathrm{~d} \varphi_{2}^{(1)}}{\mathrm{d} y}\right) \frac{\mathrm{d}^{3} \varphi_{5}^{(1)}}{\mathrm{d} y^{3}}-\frac{5 k y}{4} \frac{\mathrm{~d}^{2} \varphi_{2}^{(1)}}{\mathrm{d} y^{2}}\left[-\frac{c_{1} y}{5} \frac{\mathrm{~d}^{2} \varphi_{5}^{(1)}}{\mathrm{d} y^{2}}+\left(c_{1}-\frac{4 c_{2}}{5}\right) \frac{\mathrm{d} \varphi_{5}^{(1)}}{\mathrm{d} y}\right]- \\ & \left.k y\left[\left(-\frac{y^{2}}{4}+\frac{c_{1}}{4}+c_{2}\right) \frac{\mathrm{d} \varphi_{2}^{(1)}}{\mathrm{d} y}\right] \frac{\mathrm{d}^{2} \varphi_{5}^{(1)}}{\mathrm{d} y^{2}}+\left[\left(\frac{5 c_{1}}{4}-\frac{c_{1} y^{4}}{4}-\frac{y^{2}}{4}\right) \frac{\mathrm{d} \varphi_{2}^{(1)}}{\mathrm{d} y}\right] \frac{\mathrm{d} \varphi_{5}^{(1)}}{\mathrm{d} y}\right\} \mathrm{d} y 。\\ & I_{2}=\int_{y_{1}}^{y_{2}}\left[-\frac{y^{3}}{4}\left(y^{3} {\varphi}_{2}^{(1)}-y \frac{\mathrm{~d}^{2} {\varphi}_{2}^{(1)}}{\mathrm{d} y^{2}}+2 \frac{\mathrm{~d} {\varphi}_{2}^{(1)}}{\mathrm{d} y}\right)\right] \mathrm{d} y, \\ & I_{21}=\int_{y_{1}}^{y_{2}}\left(\frac{y^{4}}{4} \varphi_{2}^{(1)}\right) \mathrm{d} y, \\ & I_{22}=\int_{y_{1}}^{y_{2}}\left\{\frac{y^{3}}{4}\left[-y \frac{\mathrm{~d}^{2} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y^{2}} \varphi_{2}^{(1)}-y \frac{\mathrm{~d} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y} \frac{\mathrm{~d} \varphi_{2}^{(1)}}{\mathrm{d} y}+\left(y^{3} \bar{U}_{\mathrm{s}}+2 \frac{\mathrm{~d} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y}\right) \varphi_{2}^{(1)}\right]\right\} \mathrm{d} y, \end{aligned} $ |
| $ \begin{aligned} & I_{23}=\int_{y_{1}}^{y_{2}}\left\{-\frac{y^{2}}{4}\left[-y \frac{\mathrm{~d} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y} \frac{\mathrm{~d}^{2} \varphi_{2}^{(1)}}{\mathrm{d} y^{2}}+\left(y^{3} \bar{U}_{\mathrm{s}}-y \frac{\mathrm{~d}^{2} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y^{2}}+3 \frac{\mathrm{~d} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y}\right) \frac{\mathrm{d} \varphi_{2}^{(1)}}{\mathrm{d} y}\right]\right\} \mathrm{d} y, \\ & I_{24}=\int_{y_{1}}^{y_{2}}\left[\frac{x y^{3}}{4}\left(-y \frac{\mathrm{~d} \bar{\varPhi}_{\mathrm{s}}}{\mathrm{~d} y}+\bar{\varPhi}_{\mathrm{s}}\right) \frac{\mathrm{d}^{3} {\varphi}_{2}^{(1)}}{\mathrm{d} y^{3}}-x y^{2}\left(-y \frac{\mathrm{~d} \bar{\varPhi}_{\mathrm{s}}}{\mathrm{~d} y}+\bar{\varPhi}_{\mathrm{s}}\right) \frac{\mathrm{d}^{2} \varphi_{2}^{(1)}}{\mathrm{d} y^{2}}+\right. \\ & \left.\frac{x y^{4}}{4} \frac{\mathrm{~d}^{3} \bar{\varPhi}_{\mathrm{s}}}{\mathrm{~d} y^{3}} \frac{\mathrm{~d} \varphi_{2}^{(1)}}{\mathrm{d} y}-\frac{x y^{3}}{4} \frac{\mathrm{~d}^{2} \bar{\varPhi}_{\mathrm{s}}}{\mathrm{~d} y^{2}} \frac{\mathrm{~d} \varphi_{2}^{(1)}}{\mathrm{d} y}+x y\left(-y \frac{\mathrm{~d} \bar{\varPhi}_{\mathrm{s}}}{\mathrm{~d} y}+\bar{\varPhi}_{\mathrm{s}}\right) \frac{\mathrm{d} \varphi_{2}^{(1)}}{\mathrm{d} y}\right] \mathrm{d} y, \\ & I_{25}=\int_{y_{1}}^{y_{2}}\left\{\frac{k y}{4} \frac{\mathrm{~d}^{2} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y^{2}}\left[\left(y \bar{U}_{\mathrm{s}}-2 c_{2} \frac{\mathrm{~d} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y}\right) \frac{\mathrm{d} \varphi_{2}^{(1)}}{\mathrm{d} y}-2 y \frac{\mathrm{~d} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y} \varphi_{2}^{(1)}\right]-\right. \\ & \frac{\kappa k x^{2} y^{3}}{8} \frac{\mathrm{~d}^{4} \bar{\varPhi}_{\mathrm{s}}}{\mathrm{~d} y^{4}}\left(y \varphi_{2}^{(1)}+c_{2} \frac{\mathrm{~d} \varphi_{2}^{(1)}}{\mathrm{d} y}\right)+\frac{k y^{2}}{4}\left(y^{3} \bar{U}_{\mathrm{s}}+3 \frac{\mathrm{~d} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y}\right) \frac{\mathrm{d} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y} {\varphi}_{2}^{(1)}+ \end{aligned} $ |
| $ \begin{aligned} & \frac{\kappa x y^{2}}{4} \frac{\mathrm{~d}^{3} \bar{\varPhi}_{\mathrm{s}}}{\mathrm{~d} y^{3}}\left[-\frac{k c_{2} x y}{2} \frac{\mathrm{~d}^{2} \varphi_{2}^{(1)}}{\mathrm{d} y^{2}}+\left(-\frac{k x y^{2}}{2}+\frac{3 k c_{2} x}{2}\right) \frac{\mathrm{d} \varphi_{2}^{(1)}}{\mathrm{d} y}+k x y \varphi_{2}^{(1)}\right]+ \\ & y\left[-y\left(\frac{k c_{2}}{4}\left(\frac{\mathrm{~d} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y}\right)^{2}-\frac{k y}{4} \bar{U}_{\mathrm{s}} \frac{\mathrm{~d} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y}\right) \frac{\mathrm{d}^{2} \varphi_{2}^{(1)}}{\mathrm{d} y^{2}}+\frac{\kappa k c_{2} x^{2} y^{4}}{8} \frac{\mathrm{~d}^{2} \bar{\varPhi}_{\mathrm{s}}}{\mathrm{~d} y^{2}} \frac{\mathrm{~d} \varphi_{2}^{(1)}}{\mathrm{d} y}+\right. \\ & \left.\left.\left(k c_{2}\left(\frac{\mathrm{~d} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y}\right)^{2}+\frac{k y}{4}\left(c_{2} y^{2}-3\right) \bar{U}_{\mathrm{s}} \frac{\mathrm{~d} \bar{U}_{\mathrm{s}}}{\mathrm{~d} y}-\frac{k y^{4}}{4} \bar{U}_{\mathrm{s}}^{2}\right) \frac{\mathrm{d} \varphi_{2}^{(1)}}{\mathrm{d} y}\right]\right\} \mathrm{d} y, \\ & I_{26}=\int_{y_{1}}^{y_{2}}\left\{\frac{k\left(c_{2}-c_{1}\right) y^{2}}{4} \frac{\mathrm{~d}^{3} \varphi_{1}^{(1)}}{\mathrm{d} y^{3}} \frac{\mathrm{~d} \varphi_{5}^{(1)}}{\mathrm{d} y}+y \varphi_{1}^{(1)} \frac{\mathrm{d} \varphi_{5}^{(1)}}{\mathrm{d} y}-k y^{2} \varphi_{1}^{(1)} \frac{\mathrm{d}^{2} \varphi_{5}^{(1)}}{\mathrm{d} y^{2}}+\right. \\ & \frac{k y^{2}}{4}\left(y \varphi_{1}^{(1)}+c_{1} \frac{\mathrm{~d} \varphi_{2}^{(1)}}{\mathrm{d} y}\right) \frac{\mathrm{d}^{3} \varphi_{5}^{(1)}}{\mathrm{d} y^{3}}-\frac{5 k y}{4} \frac{\mathrm{~d}^{2} \varphi_{1}^{(1)}}{\mathrm{d} y^{2}}\left[-\frac{c_{2} y}{5} \frac{\mathrm{~d}^{2} \varphi_{5}^{(1)}}{\mathrm{d} y^{2}}+\left(c_{2}-\frac{4 c_{1}}{5}\right) \frac{\mathrm{d} \varphi_{5}^{(1)}}{\mathrm{d} y}\right]- \\ & \left.k y\left[\left(-\frac{y^{2}}{4}+\frac{c_{2}}{4}+c_{1}\right) \frac{\mathrm{d} \varphi_{1}^{(1)}}{\mathrm{d} y}\right] \frac{\mathrm{d}^{2} \varphi_{5}^{(1)}}{\mathrm{d} y^{2}}+\left[\left(\frac{5 c_{2}}{4}-\frac{c_{2} y^{4}}{4}-\frac{y^{2}}{4}\right) \frac{\mathrm{d} \varphi_{1}^{(1)}}{\mathrm{d} y}\right] \frac{\mathrm{d} \varphi_{5}^{(1)}}{\mathrm{d} y}\right\} \mathrm{d} y_{\circ} \end{aligned} $ |
方程(35)的各项系数如下:
| $ \begin{aligned} & \chi_{1}(y)=-k, \\ & \delta_{1}(y)=-\frac{k^{2}}{y^{2}}\left(c_{1} y^{2}+y^{2}+c_{1}+2 y-2\right), \\ & \chi_{2}(y)=2\left(\omega_{2}-k\right) y^{2}-n\left(\omega_{2}+k\right)-5\left(\omega_{2}-k\right), \\ & \delta_{2}(y)=-\frac{1}{y^{2}}\left[-4\left(\omega_{2}-k\right) n\left(\omega_{2}+k\right) c_{2} y^{4}+36\left(\omega_{2}-k\right) n\left(\omega_{2}+k\right) c_{2} y^{2}+4\left(\omega_{2}-k\right)^{2} c_{2} y^{6}-\right. \\ & 48\left(\omega_{2}-k\right)^{2} c_{2} y^{4}-4\left(\omega_{2}-k\right) n\left(\omega_{2}+k\right) y^{4}+93\left(\omega_{2}-k\right)^{2} c_{2} y^{2}+n^{2}\left(\omega_{2}+k\right)^{2} c_{2} y^{2}- \\ & 8\left(\omega_{2}-k\right) n\left(\omega_{2}+k\right) y^{3}+14\left(\omega_{2}-k\right) n\left(\omega_{2}+k\right) y^{2}-34\left(\omega_{2}-k\right)^{2}- \\ & 2 n^{2}\left(\omega_{2}+k\right)^{2}+4\left(\omega_{2}-k\right)^{2} y^{6}+8\left(\omega_{2}-k\right)^{2} y^{5}-20\left(\omega_{2}-k\right)^{2} y^{4}-40\left(\omega_{2}-k\right)^{2} y^{3}+77\left(\omega_{2}-k\right)^{2} y^{2}+ \\ & \left.n^{2}\left(\omega_{2}+k\right)^{2} y^{2}+45\left(\omega_{2}-k\right)^{2} c_{2}+n^{2}\left(\omega_{2}+k\right)^{2} c_{2}+50\left(\omega_{2}-k\right)^{2} y+2 n^{2}\left(\omega_{2}+k\right)^{2} y-20\left(\omega_{2}-k\right) n\left(\omega_{2}+k\right)\right], \\ & \delta_{3}(y)=\frac{k}{y^{2}}\left[2\left(\omega_{2}-k\right)\left(c_{1}+c_{2}\right) y^{4}+4\left(\omega_{2}-k\right) y^{4}-17\left(\omega_{2}-k\right) c_{1} y^{2}-n\left(\omega_{2}+k\right)\left(c_{1}+c_{2}\right) y^{2}-\right. \\ & \left.5\left(\omega_{2}-k\right) c_{2} y^{2}-2\left(\omega_{2}-k\right) y^{2}-2 n\left(\omega_{2}+k\right) y^{2}-14\left(\omega_{2}-k\right) c_{2}-2 n\left(\omega_{2}+k\right) c_{2}\right], \\ & \chi_{4}(y)=-2\left[2\left(\omega_{2}-k\right)\left(c_{2}-c_{1}\right) y^{2}-9\left(\omega_{2}-k\right)\left(c_{2}-c_{1}\right)-n\left(\omega_{2}+k\right)\left(c_{2}-c_{1}\right)-4\left(\omega_{2}-k\right)\right], \\ & \delta_{4}(y)=-\frac{2}{y}\left[16\left(\omega_{2}-k\right) y^{4}-12\left(\omega_{2}-k\right) c_{1} y^{2}+4\left(\omega_{2}-k\right) c_{2} y^{2}-64\left(\omega_{2}-k\right) y^{2}+8 n\left(\omega_{2}+k\right) y^{2}-\right. \\ & \left.18\left(\omega_{2}-k\right) c_{1}-2 n\left(\omega_{2}+k\right) c_{1}-20\left(\omega_{2}-k\right) c_{2}-2 n\left(\omega_{2}+k\right) c_{2}+80\left(\omega_{2}-k\right)+8 n\left(\omega_{2}+k\right)\right], \\ & \delta_{5}(y)=\frac{k}{y^{2}}\left[2\left(\omega_{2}-k\right)\left(c_{1}+c_{2}\right) y^{4}+4\left(\omega_{2}-k\right) y^{4}-15\left(\omega_{2}-k\right) c_{1} y^{2}-n\left(\omega_{2}+k\right)\left(c_{1}+c_{2}\right) y^{2}-\right. \\ & \left.7\left(\omega_{2}-k\right) c_{2} y^{2}-10\left(\omega_{2}-k\right) y^{2}-2 n\left(\omega_{2}+k\right) y^{2}-9\left(\omega_{2}-k\right) c_{1}-n\left(\omega_{2}+k\right)\left(c_{1}+c_{2}\right)-5\left(\omega_{2}-k\right) c_{2}\right] 。\end{aligned} $ |
| [1] |
BJERKNES J. A possible response of the atmospheric Hadley circulation to equatorial anomalies of ocean temperature[J]. Tellus, 1966, 18(4): 820-829. DOI:10.3402/tellusa.v18i4.9712 |
| [2] |
McCREARY J P Jr, ANDERSON D L T. A simple model of El Niño and the Southern Oscillation[J]. Mon Wea Rev, 1984, 112(5): 934-946. DOI:10.1175/1520-0493(1984)112<0934:ASMOEN>2.0.CO;2 |
| [3] |
SCHOPF P S, SUAREZ M J. Vacillations in a coupled ocean-atmosphere model[J]. J Atmos Sci, 1988, 45(3): 549-566. DOI:10.1175/1520-0469(1988)045<0549:VIACOM>2.0.CO;2 |
| [4] |
SUAREZ M J, SCHOPF P S. A delayed action oscillator for ENSO[J]. J Atmos Sci, 1988, 45(21): 3283-3287. DOI:10.1175/1520-0469(1988)045<3283:ADAOFE>2.0.CO;2 |
| [5] |
李崇银. 大气季节内振荡研究的新进展[J]. 自然科学进展, 2004, 14(7): 734-741. |
| [6] |
黄荣辉, 傅云飞, 臧晓云. 亚洲季风与ENSO循环的相互作用[J]. 气候与环境研究, 1996, 1(1): 38-54. DOI:10.3878/j.issn.1006-9585.1996.01.05 |
| [7] |
李崇银, 胡季. 东亚大气环流与埃尔尼诺相互影响的一个分析研究[J]. 大气科学, 1987, 11(4): 359-364. |
| [8] |
张人禾, 闵庆烨, 苏京志. 有关副热带太平洋对ENSO影响研究的综述[J]. 海洋气象学报, 2017, 37(1): 1-9. DOI:10.19513/j.cnki.issn2096-3599.2017.01.001 |
| [9] |
李晓惠, 徐峰, 陈虹颖, 等. 1980—2016年西太平洋暖池与ENSO循环过程的相关分析[J]. 海洋气象学报, 2017, 37(3): 85-94. DOI:10.19513/j.cnki.issn2096-3599.2017.03.010 |
| [10] |
张萍, 徐峰, 涂石飞, 等. 1979—2017年南海SSTA时空特征及其与沃克环流异常的相关[J]. 海洋气象学报, 2019, 39(1): 15-25. DOI:10.19513/j.cnki.issn2096-3599.2019.01.002 |
| [11] |
林婷婷, 李春. ENSO与南海SST关系的年代际变化[J]. 海洋气象学报, 2019, 39(2): 68-75. DOI:10.19513/j.cnki.issn2096-3599.2019.02.007 |
| [12] |
薛德强, 徐建军. 两类厄尔尼诺事件期间热带大气GILL响应分析[J]. 海洋气象学报, 2021, 41(1): 82-91. DOI:10.19513/j.cnki.issn2096-3599.2021.01.008 |
| [13] |
PHILANDER S G H, YAMAGATA T, PACANOWSKI R C. Unstable air-sea interactions in the tropics[J]. J Atmos Sci, 1984, 41(4): 604-613. |
| [14] |
CANE M A, ZEBIAK S E. A theory for El Niño and the Southern Oscillation[J]. Science, 1985, 228(4703): 1085-1087. |
| [15] |
MATSUNO T. Quasi-geostrophic motions in the equatorial area[J]. J Meteor Soc Japan, 1966, 44(1): 25-43. |
| [16] |
DOMARACKI A, LOSSCH A Z. Nonlinear interactions among equatorial waves[J]. J Atmos Sci, 1977, 34(3): 486-498. |
| [17] |
CHAO J P, ZHANG R H. The air-sea interaction waves in the tropics and their instabilities[J]. Acta Meteor Sin, 1988, 2(3): 275-287. |
| [18] |
房佳蓓, 杨修群. 经向风应力在热带不稳定海气相互作用中的角色[J]. 热带气象学报, 2003, 19(1): 43-52. |
 2025, Vol. 45
2025, Vol. 45


