2. 山东省气象台,山东 济南 250031
2. Shandong Meteorological Observatory, Jinan 250031, China
根据SMULL and HOUZE[1]的定义,拖曳型飑线的典型雷达回波特征包括三部分:前导对流带、尾随层状区和反射率槽区。对流带(区域)被定义为深对流的前线,表现出有组织的多细胞结构。层状区是一个广泛的回波区域,主要特征是存在融化层亮带。反射率槽被定义为弱反射率的窄带,它分离了对流带和拖曳的层状区域。BIGGERSTAFF and HOUZE[2]提出的飑线概念模型是基于详细的双多普勒雷达分析,指出,层状云区域有一个“次最大降水区”,其特征是对流层上部的中尺度上升气流和低空中尺度下沉气流。反射率槽(或过渡区)是前导对流带和拖曳层状云区之间的最小雷达反射率区域,它与中至上层观测到的深厚沉降有关,另外,ATLAS et al.[3]还利用中值体积直径D0的变化来确定过渡区。
由于对流带、过渡区和尾随层状云具有明显不同的微物理降水形成机制,所以拖曳型飑线成为研究不同降水机制雨滴谱特征,以及研究层状云和对流云降水分类标准的最佳对象[4-8]。垂直穿过飑线对流带,雨强增大过程雨滴谱特征大多是多峰模态、低雨滴浓度和高反射率因子,而在雨强减弱过程逐渐转为单峰、较高的雨滴浓度和较低反射率因子[6, 9]。王俊等[10]利用多台雨滴谱仪观测资料进行研究,揭示了雨滴谱在飑线对流带纵向的不同特征,最大雨强可以出现在对流云降水的开始,也可以出现在对流云降水的结束阶段,不同的降水演变对应明显不同的雨滴谱分布特征。除此之外,在飑线的不同发展阶段,雨滴谱特征也存在明显的差异性。WEN et al.[11]利用C波段偏振多普勒雷达反演的雨滴谱参数分析表明,当飑线从形成阶段发展到成熟阶段时,其对流区的雨滴谱特征由大陆性对流演变为更似海洋性的对流,与以前的研究不同,对流带的雨滴谱特征可能不是简单地由地理位置决定,而是在其整个生命周期中广泛地变化。
WALDVOGEL[12]分析雨滴谱指数分布的截距参数N0时发现,当降水类型从均匀变为对流时,同一雨强的参数N0存在跳跃现象。利用三参数的Gamma谱分布[13]拟合雨滴谱时,TOKAY and SHORT[4]发现热带海洋降水的雨滴谱参数N0、λ(斜率参数)有明显的分层现象,即在相同雨强时,层状云的雨滴谱参数N0、λ比对流云的数值要小,两者之间明显分离。随后许多研究表明N0、λ随着雨强的变化,分层特征并不确定,有时出现分层现象,有时没有分层现象。MAKI et al.[5]分析澳大利亚达尔文地区大陆性拖曳型飑线的雨滴谱特征,对流和层状区域的N0-R有明显的分层特征,经过调整的N0-R关系可以区分对流中心和层状区域的雨滴谱。THURAI et al.[7]利用达尔文的双偏振雷达反演资料显示,TOKAY and SHORT[4]给出的分离线很好地分离了层状云和对流云降水,相同雨强时对流云降水的N0比层状云降水大。CARACCIOLO et al.[14]则发现中纬度大陆性降水的N0、λ随着雨强的增大而减小,变化过程是连续的,没有出现分层现象。YOU et al.[15]利用韩国釜山和昌源的Parsivel雨滴谱仪观测资料显示N0和λ随雨强变化在不同的观测地点有差别,釜山有较明显的分层特征,而昌源分层特征不明显。ZHANG et al.[8]分析中国中东部大陆型飑线,层状云降水与对流云降水之间也存在分层特征,但TOKAY and SHORT[4]给出的分离线只能区分飑线对流中心和层状区域的雨滴谱。
由于归一化Gamma谱分布消除了N0与μ之间的依赖,使得不同含水量的雨滴谱可以很容易进行对比[16]。LEE et al.[17]认为归一化Gamma雨滴谱方法可以提供更多区分对流云和层状云降水类型的证据。BRINGI et al.[18]利用赤道附近, 以及海洋到陆地的不同气候区归一化Gamma谱的数浓度和中值体积直径(NW和D0)的分布特征,发现海洋性和大陆性, 以及对流云和层状云降水之间存在差别。BRINGI et al.[19]和THURAI et al.[7]利用达尔文地区双频廓线仪反演的归一化Gamma谱参数NW、D0,给出了log10NW与D0之间的分离线:
| $ {\log _{10}}{N_{\rm{W}}} = {C_1}{D_0} + {C_2} $ | (1) |
式中,C1在-1.6~-1.7之间,C2在6.3~6.4之间;D0,单位:mm;NW,单位:m-3·mm-1。
层状云降水数据点位于分离线以下,而对流云则在分离线之上,过渡区数据看起来跨坐分离线上。YOU et al.[15]利用韩国Parsivel雨滴谱仪观测分析表明,分离线(1)不能准确分类两个观测点的层状-对流云降水,但新的分离线也具有公式(1)的形式,只是C1要小一些。公式(1)也可以区分中国中东部大陆型飑线的层状-对流云降水[8],以及中国北部夏季的对流云和层状云降水[20],但系数C1明显要小一些,接近-1.0。
山东中西部是飑线等中尺度对流系统的多发区[21-22],许多研究者利用雷达、卫星、数值模拟和常规观测资料开展了研究[23-32],近几年,利用雨滴谱仪观测资料分析飑线微物理特征的研究开始增多[10]。2017年7月18日,一次拖曳型飑线过程影响山东省中西部,发展加强阶段经过安装在东阿的激光雨滴谱仪(DE),而减弱阶段经过山东省气象局雨滴谱仪观测点(简称省局,SJ),本文利用雨滴谱仪观测资料,结合新一代多普勒雷达资料,分析了飑线不同发展阶段的雨滴谱演变特征,这有助于加深理解降水系统微物理过程的发展演变规律,促进雨滴谱资料在人工影响天气、数值天气预报、云演变模式和雷达估计降水中的应用。
1 资料与方法Thies激光雨滴谱仪2011年11月安装在省局和东阿,该设备主要特点参见有关文献[33],王俊等[10]分析表明Thies激光雨滴谱仪观测资料采用FRIEDRICH et al.[34]给出的方法进行质量控制后,雨强和累计雨量与自动站符合得很好,本研究也采用这一方法对观测资料进行质量控制。新一代多普勒天气雷达(CINRAD/SA)位于齐河(36°48′10″N,116°46′51″E)、滨州(37°21′00″N,117°58′40″E),省局激光雨滴谱仪距离齐河、滨州雷达站的距离分别为22.3 km、115.2 km,东阿激光雨滴谱仪距离齐河、滨州雷达站的距离分别为55.2 km、187.4 km(图 2a)。
|
图 2 济南雷达不同时次组合反射率(a.04:38,b.06:12,c.06:42,d.06:59,e.07:46,f.08:04,g.08:33,h.09:32)以及东阿(DE)(i)和省局(SJ)(j)雨滴谱仪站点雷达反射率因子(填色,单位:dBz)高度-时间剖面 Fig.2 Composite reflectivity (a. 04:38 BST, b. 06:12 BST, c. 06:42 BST, d. 06:59 BST, e. 07:46 BST, f. 08:04 BST, g. 08:33 BST, h. 09:32 BST) of Jinan radar and height-time cross section (colored, units: dBz) of radar reflectivity factor of disdrometers located at Donge (DE) and Shengju (SJ, Jinan) |
利用雨滴谱仪观测资料,雨滴尺度谱可以用以下公式计算得到:
| $ N\left( {{D_j}} \right) = \sum\limits_{i = 1}^{20} {\frac{{{n_{ij}}}}{{A \cdot \mathit{\Delta }t \cdot {V_i} \cdot \mathit{\Delta }{D_j}}}} $ | (2) |
A(单位:m2)和Δt(单位:s)分别是Thies激光雨滴谱仪取样面积和取样时间,分别为45.6×10-4 m2和60 s,nij(单位:个/min)是第j个直径通道、第i个速度通道的雨滴浓度,Vi (单位:m·s-1)是第j个直径通道、第i个速度通道对应的雨滴落速,ΔDj(单位:mm)是第j个直径通道的宽度,N(Dj)(单位:m-3·mm-1)是第j个直径通道Dj至Dj+ΔDj之间的雨滴数浓度。
目前,常用三参数的Gamma分布[13]来拟合雨滴谱分布,Gamma分布函数为:
| $ N(D) = {N_0}{D^\mu }\exp ( - \lambda D) $ | (3) |
其中N(D)(单位:m-3·mm-1)为单位体积单位尺度间隔的雨滴数浓度,N0是截距参数(单位:m-3·mm-1-μ),μ是形状因子(无量纲参数),λ是斜率参数(单位:mm-1)。公式(3)中系数N0包含形状因子μ,不同雨强时μ不同,所以N0之间没有可比性,而归一化的Gamma谱分布公式[16, 35]为:
| $ N(D) = {N_{\rm{w}}}f(\mu )\left( {\frac{D}{{{D_{\rm{m}}}}}} \right)\exp \left[ { - (4 + \mu )\frac{D}{{{D_{\rm{m}}}}}} \right] $ | (4) |
其中
| $ {N_{\rm{w}}} = \frac{{{4^4}}}{{{\rm{ \mathsf{ π} }}{\rho _{\rm{w}}}}}\frac{W}{{D_m^4}} $ | (5) |
| $ f(\mu ) = \frac{6}{{{4^4}}}\frac{{{{(4 + \mu )}^{\mu + 4}}}}{{\mathit{\Gamma }(4 + \mu )}} $ | (6) |
| $ \frac{{\rm{ \mathsf{ π} }}}{{\rm{6}}}\mathop \smallint \limits_{{D_{\min }}}^{{D_0}} {D^3}N(D){\rm{d}}D = \frac{1}{2}\frac{{\rm{ \mathsf{ π} }}}{6}\mathop \smallint \limits_{{D_{\min }}}^{{D_{\max }}} {D^3}N(D){\rm{d}}D $ | (7) |
| $ W = \frac{{{\rm{ \mathsf{ π} }}\rho }}{6}\int_{{D_{\min }}}^{{D_{\max }}} N (D){D^3}{\rm{d}}D $ | (8) |
W是雨水含量(单位:g·m-3),Dmin、Dmax分别是雨滴的最小和最大直径。Nw的单位是m-3·mm-1,不同雨强的Nw之间具有可比性,Γ(x)是Gamma函数。参考有关研究[7, 19],利用中值体积直径D0代替体积权重平均直径Dm(volume-weighted mean diameter)。Nw的计算公式改为[36]:
| $ {N_{\rm{w}}} = \frac{{{{3.67}^4}}}{{{\rm{ \mathsf{ π} }}{\rho _{\rm{w}}}}}\left( {\frac{{{{10}^3}W}}{{D_0^4}}} \right) $ | (9) |
近年来,阶矩法被广泛应用于估计Gamma谱分布参数[13, 14],该方法的优点在于云微物理量与各阶矩量有一定的对应关系,如雨滴浓度NT等于0阶矩,含水量与3阶矩成正比,雷达反射率因子与6阶矩成正比等。第n阶矩定义为:
| $ {M_n} = \mathop \smallint \limits_0^\infty N(D){D^n}{\rm{d}}D $ | (10) |
N(D)为(3)式所示的Gamma分布时,n阶矩等于:
| $ {M_n} = \frac{{{N_0}\mathit{\Gamma }(n + \mu + 1)}}{{{\lambda ^{n + \mu + 1}}}} $ | (11) |
一般来说,三参数可以利用任意三个矩计算出,但实际应用中需要根据不同设备性能和雨滴谱特征来确定具体采用几阶矩计算雨滴谱参数。本文采用3、4、6阶矩计算三参数[4],计算公式为:
| $ {N_0} = \frac{{{\lambda ^{\mu + 4}}{M_3}}}{{\mathit{\Gamma }(\mu + 4)}} $ | (12) |
| $ \lambda = \frac{{\mu + 4}}{{{D_m}}} $ | (13) |
| $ \mu = \frac{{11G - 8 + {{[G(G + 8)]}^{0.5}}}}{{2(1 - G)}} $ | (14) |
其中
| $ G = \frac{{M_4^3}}{{M_3^2{M_6}}} $ | (15) |
| $ {D_m} = \frac{{{M_4}}}{{{M_3}}} $ | (16) |
另外,雨滴总浓度NT、雨强R、雷达反射率因子Z可以利用N(Dj)分别计算得出。
| $ {N_{\rm{T}}} = \mathop \smallint \limits_0^\infty N(D){\rm{d}}D $ | (17) |
| $ R = \mathop \smallint \limits_0^\infty A\mathit{\Delta }tN(D){D^3}V{\rm{d}}D $ | (18) |
| $ \mathit{Z} = \mathop \smallint \limits_0^\infty N(D){D^6}{\rm{d}}D $ | (19) |
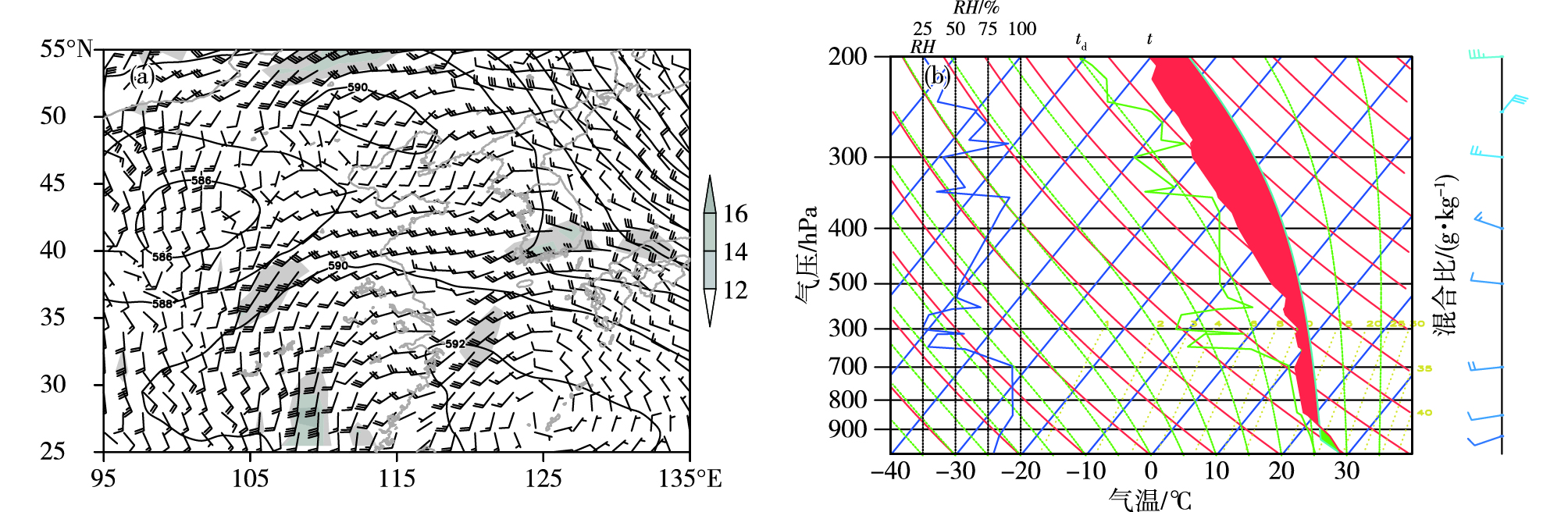
2017年7月16日08:00—20:00(北京时,下同),在大陆高压588 dagpm和海上副热带高压(以下简称“副高”)588 dagpm趋于合并过程中(图略),“两高”之间存留下了位势高度低于588 dagpm的低值中心,配合以温度小于-4 ℃的冷中心。18日08:00,大陆高压和海上副高继续合并,控制我国大陆,副高592 dagpm线控制江南地区,位势高度低于588 dagpm的低值区域位于西北地区东部—华北南部上空,最低位势高度值出现在延安站,为585 dagpm(图 1a)。山东位于此低值中心与副高592 dagpm线之间。从850 hPa至500 hPa,山东西部处于低值系统前部切变线的控制(图 1a)。此次飑线过程即发生在强盛副高边缘切变线的天气背景下。17日20时,东亚地区海平面气压场表现为鞍型场特征(图略),大陆高压中心位于贝加尔湖附近,高压前部冷锋位于我国内蒙古和蒙古国交界处;海上高压中心位于台湾岛以东洋面,黄淮地区地面为弱南风控制。自17日20:00至18日08:00,500 hPa低值中心略有东移,与海上副高之间位势梯度加大,表现为二者之间南风增强,以郑州站和南阳站探空为代表,17日20:00 850 hPa西南风速为4 m·s-1,到18日08:00风速已增强为14 m·s-1,天气系统演变趋势有利于强对流天气发生。以章丘站为例(图 1b),17日20:00其CAPE为2 304 J·kg-1(图 1b),850 hPa比湿达到15 g·kg-1,抬升凝结高度低于925 hPa,18日05:00山东内陆地区露点温度为24~26 ℃,表明大气具备较高的对流不稳定能量和丰富的低层水汽,是产生此次飑线天气过程的有利环境条件。需要说明的是,此次飑线发生时对流发生地及周边区域水平风垂直风切变不大,这是由副高控制这一环流背景特征决定的。
|
图 1 2017年7月18日08:00天气形势(a;黑色实线:500 hPa等位势高度线,单位:dagpm,风矢:850 hPa风场,单位:m·s-1,阴影部分风速≥12 m·s-1)和章丘站探空t-lnp图(b) Fig.1 Synoptic situation (a; dark contour line for geopotential height at 500 hPa, units: dagpm; barb for wind at 850 hPa, units: m·s-1, the wind speed in shaded area is equal to or greater than 12 m·s-1) and t-lnp diagram (b) of Zhangqiu station at 08:00 BST on 18 July 2017 |
2017年7月18日04:38,自河南东移的雷达回波逐渐发展成线状中尺度对流系统L1(图 2a),而在鲁西南局地发展起来的对流回波L2也发展得比较强盛,同时,两者之间不断有对流回波生成。至05:25,L1与L2尚未连接(图略),两者靠近部位的最大反射率因子都稍有减弱,特别是在L2的前侧又有对流回波带L3产生。以后L2逐渐减弱成积层混合云,而L3和L1都逐渐发展加强并互相靠近,至06:12(图 2b),L1与L3大于40 dBz的强回波仍未连接,此时在L3之前又有对流带L4产生。06:42(图 2c),L1与L4完全连接在一起,形成新的线状中尺度对流带L,大于40 dBz的强回波带呈反弓形, 最大反射率因子大于55 dBz,回波顶高超过12 km。此时,在L之前又有新对流带L5生成。
反弓形L的中部发展加强,移动速度加快并与L5合并,形成的对流带的前沿具有强回波中心,06:59(图 2d)成熟对流带顶点的左侧强回波前沿经过东阿雨滴谱仪。07:46(图 2e)回波发展成正常的弓形回波,此时回波具有典型拖曳型飑线结构:强对流带、弱回波的过渡区和尾随层状云。08:04(图 2f)弓形回波顶点的右侧对流带经过省局雨滴谱仪,此时回波强度减弱,最大反射率因子小于50 dBz。08:33(图 2g)对流带继续减弱,省局雨滴谱仪处在过渡区,东阿雨滴谱仪位于层状云区。随后对流带继续减弱并快速前冲,过渡区增大(图 2h),雨滴谱仪位于层状云区,降水逐渐结束。
东阿雨滴谱仪观测站上空反射率因子的高度-时间剖面(图 2i,利用济南雷达观测资料绘制)显示,对流云18 dBz回波顶高约为13.0 km,38 dBz的强回波顶高约为8.0 km。大于50 dBz的强回波分布不连续,分别出现在3.0~4.0 km和4.0~5.0 km,出现时间很短暂;过渡区回波较弱,近地层低于5 dBz。高空回波也很弱,18 dBz回波顶高6.0 km左右,存在强度小于1 dBz的弱空洞;层状云回波主要特征之一是5.0 km以下存在0 ℃层亮带,08:30左右亮带强度大于38 dBz。大于10 dBz(或者5 dBz)回波顶高度有明显起伏,而18 dBz回波顶高变化不大。另外,近地层的回波强度也有较为明显的变化,08:20—09:10近地层具有较强的反射率因子。图 2j是省局雨滴谱仪观测站上空反射率因子的高度-时间剖面(利用滨州雷达观测资料绘制),垂直结果显示,对流回波强度明显减弱,最大回波强度只有43.6 dBz,并且18 dBz回波顶高低于10.0 km,38 dBz回波顶高低于4.0 km;过渡区回波较弱,但过渡区18 dBz回波顶高较高;层状云回波较为稳定,云顶高度(18 dBz)是逐渐较低的,但0 ℃层亮带较强,大于38 dBz的较强回波区水平和垂直范围较大。
成熟弓状回波具有中纬度典型拖曳层状中尺度对流系统[37-38]的雷达回波特征,但本次过程弓状回波的发展具有较为复杂的演变特征,右侧对流回波的前面不断有新对流带产生,而旧回波减弱成层状云回波。左右对流带逐渐靠近、两者之间有对流回波产生发展,最后,合并的回波发展的比较强盛,形成反弓形的对流带。反弓形回波的顶点具有较快的移动速度,逐渐发展成弓状回波。而弓状回波阶段(反弓形和弓形)对流带前侧也不断有对流带生成并合并到主对流带的前侧,使得对流带的前沿具有强的反射率因子。
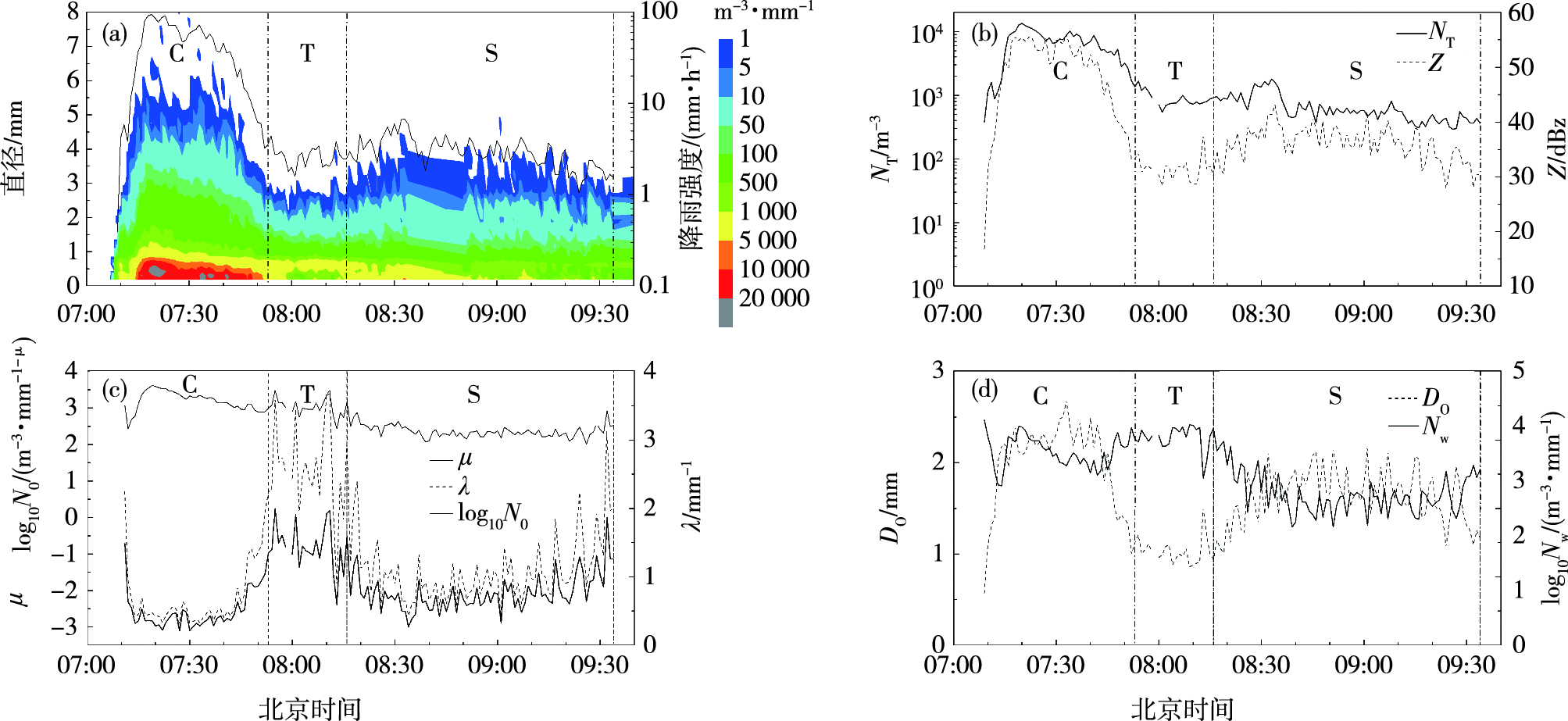
3 单站雨滴谱资料时间序列分析 3.1 东阿雨滴谱积分参数时间序列分析下面较为详细地分析东阿雨滴谱N(D)和积分参数随时间的演变(图 3),综合雷达回波和雨滴谱演变特征,07:09—07:52为对流云降水,07:19和07:33分别对应两个较为明显的雨强极值中心。07:53—08:16是过渡区,雨强在2.0~4.5 mm·h-1之间。08:17—09:34为层状云降水,雨强在1.0~7.0 mm·h-1之间。
|
图 3 2017年7月18日东阿(DE)雨滴谱和积分参数演变(a.雨滴谱和降雨强度,填色:雨滴数浓度N(D),单位:m-3·mm-1,黑实线:降雨强度R,单位:mm·h-1;b.雨滴浓度和反射率因子,实线:雨滴浓度NT,单位:m-3,虚线:反射率因子Z,单位:dBz;c.截距参数log10N0、斜率参数λ和形状因子μ,细实线:log10N0,单位:m-3·mm-1-μ,点划线:λ,单位:mm-1,粗实线:μ;d.归一化截距参数log10Nw和中值体积直径D0,实线:log10Nw,单位:m-3·mm-1,虚线:D0,单位:mm) Fig.3 Temporal evolution of raindrop size distribution and integral parameters of the disdrometer located at DE on 18 July 2017 (a. raindrop size distribution and rainfall intensity, colored for raindrop number concentration N(D), units: m-3·mm-1, black solid line for rainfall intensity R, units: mm·h-1; b. raindrop concentration and reflectivity factor, solid line for raindrop concentration NT, units: m-3, dashed line for reflectivity factor Z, units: dBz; c. intercept parameter log10N0, slope parameter λ, and form factor μ, thin solid line for log10N0, units: m-3·mm-1-μ, dotted line for λ, units: mm-1, thick solid line for μ; d. normalized intercept parameter log10Nw and median volume diameter D0, solid line for log10Nw, units: m-3·mm-1, dashed line for D0, units: mm) |
对流云降水过程,07:09—07:19、07:28—07:33分别是雨强增加时段,随着雨强很快增大,粒子数密度也很快增大,但雨强减弱阶段是直径小于1 mm的小尺寸粒子的数密度极值中心,直径0.44 mm对应最大粒子数密度大于20 000 m-3·mm-1(图 3a)。直径在1.0~3.0 mm的中等尺寸粒子的数密度减小的很快,在50~2 000 m-3·mm-1之间,雨强增大、减弱阶段没有较明显的差别。直径在3.0~5.0 mm的大尺寸粒子的数密度在1~90 m-3·mm-1之间,最大雨强07:19前后具有较多的3 mm粒子,而雨强第二极值中心07:33前后具有更多5 mm的大粒子。直径大于5 mm的特大粒子分布不连续,数密度小于5 m-3·mm-1,07:33前后粒子数密度比最大雨强稍大一些;过渡区粒子谱宽很窄,只有小和中等尺寸的降水粒子,粒子数密度小于3 000 m-3·mm-1,最大数密度对应粒子直径0.63 mm,比对流云0.44 mm要大;层状云降水的雨滴谱有比较明显的差别,08:17—08:35雨强逐渐增大,雨滴谱特征是小尺寸粒子的密度变化不大,中等尺寸和大粒子的数密度逐渐增大。08:45—09:05雨强变化不大,粒子数密度变化也不大。层状云存在少量(小于5 m-3·mm-1)直径3.0~4.0 mm的大粒子。
受雨滴谱分布特征的影响,雨滴浓度NT和反射率因子Z有不一样的演变特征(图 3b)。在对流云降水阶段,NT的最大浓度出现在最大雨强之后,07:20时最大雨滴浓度为13 435 m-3,而07:19最大雨强时雨滴浓度为12 670 m-3。同样,07:34时雨滴浓度10 220 m-3,也比07:33时8 814 m-3大得多。很明显,雨强减弱阶段雨滴浓度比雨强增大阶段相同雨强时要大,这主要是因为雨强减弱阶段具有更多小尺寸粒子。反射率因子Z基本是在极大雨强或者雨强增大阶段对应极大的Z值,最大Z值56.0 dBz出现在07:33,即第二雨强极值中心,主要原因是雨滴谱中存在较多大和特大粒子;过渡区中,有较多的降水粒子,但反射率因子Z最小,主要原因是雨滴谱宽最小;层状云降水阶段,08:17—08:35随着雨强逐渐增大,雨滴浓度NT和反射率因子Z都是逐渐增大的,而后期雨滴浓度NT稍有减小,反射率因子Z减弱的更明显。
Gamma谱三参数N0、λ、μ随时间的演变(图 3c)表明,对流云降水阶段,μ在-1.0~-3.1之间,λ值在0.32~2.3 mm-1之间,log10N0数值在2.4~3.6 m-3·mm-1-μ之间。但λ、μ和log10N0随着雨强变化的趋势不同,λ、μ随着雨强增大基本是逐渐减小的,而log10N0则相反,是随着雨强增大逐渐增大。λ、μ的最小值出现在07:30,是第二极大雨强的雨强增大阶段,log10N0的最大值出现在最大雨强时(07:19);在过渡区,λ、μ有很大的起伏变化,μ可以是负值,也可以是正值。log10N0变化不大,但数值较大;层状云降水阶段,μ在-1.0~-2.9之间,λ在0.6~2.4 mm-1之间,log10N0数值在2.0~2.9 m-3·mm-1-μ之间。
归一化谱参数log10Nw、D0随时间的演变(图 3d)显示,对流云降水阶段,07:13—07:30,D0和log10Nw较稳定,变化不大,D0在2.1~2.3 mm之间,log10Nw在3.3~4.1 m-3·mm-1之间。07:31—07:45,D0和log10Nw有较大变化,D0在2.1~2.7 mm之间,log10Nw则是逐渐减少;过渡区具有较大的log10Nw和较小的D0;层状云降水D0与雨强具有一致的变化趋势,基本在1.0~2.0 mm之间。log10Nw则比对流和过渡区的数值都要小,基本在2.7~3.6 m-3·mm-1之间。
3.2 济南雨滴谱积分参数时间序列分析分析省局雨滴谱N(D)和积分参数随时间的演变(图 4)特征,08:10—08:46为对流云降水,08:18—08:29是雨强大于10 mm·h-1的强降水时段,只持续了12 min,08:22最大雨强45.6 mm·h-1。08:47—09:04是过渡区,雨强在0.8~2.9 mm·h-1之间。09:05—10:45为层状云降水,雨强在1.0~6.0 mm·h-1之间。

|
图 4 2017年7月18日省局(SJ)雨滴谱和积分参数演变(a.雨滴谱和降雨强度,填色:雨滴数浓度N(D),单位:m-3·mm-1,黑实线:降雨强度R,单位:mm·h-1;b.雨滴浓度和反射率因子,实线:雨滴浓度NT,单位:m-3,虚线:反射率因子Z,单位:dBz;c.截距参数log10N0、斜率参数λ和形状因子μ,细实线:log10N0,单位:m-3·mm-1-μ,点划线:λ,单位:mm-1,粗实线:μ;d.归一化截距参数log10Nw和中值体积直径D0,实线:log10Nw,单位:m-3·mm-1,虚线:D0,单位:mm) Fig.4 The same as Fig. 3, but for the disdrometer located at SJ, Jinan |
省局雨滴谱N(D)和雨强R随时间的演变(图 4a)显示,对流云降水阶段,强对流云降水雨滴谱的主要特征之一也是雨强增大阶段小尺寸粒子具有较小的数密度,雨强减弱阶段则有较大的粒子数密度,并且最大粒子数密度对应的粒子直径为0.19 mm,而东阿最大粒子数密度对应的粒子直径为0.44 mm,表明此处降水包含更多的小尺寸粒子。直径在1.0~3.0 mm的中等尺寸粒子的数密度较小,在10~1 000 m-3·mm-1之间。直径在3~4.25 mm的大尺寸粒子的数密度在1~20 m-3·mm-1之间,仔细分析发现雨强减弱阶段大粒子的数密度更多一些;过渡区粒子谱也是最窄的,只有小和中等尺寸的降水粒子,粒子数密度一般小于3 000 m-3·mm-1。但雨滴谱最主要的特征是双峰谱,0.19 mm和0.63 mm分别对应数密度的极大值中心;层状云降水的雨滴谱也较窄,主要是小和中等尺寸的粒子。小尺寸粒子数密度在100~6 000 m-3·mm-1之间,09:10—09:30小尺寸粒子的数密度有较大的起伏,其他时间变化不大。中等尺寸粒子数密度在1~500 m-3·mm-1之间,大于3 mm的大粒子的数密度只有几个,并且分布不连续。
雨滴浓度NT和反射率因子Z随时间的分布(图 4b)表明,在强对流云降水时段,随着雨强增大,NT逐渐增大,最大浓度出现在最大雨强时。随着雨强减小,NT逐渐减小,但比增大阶段相同雨强时明显要大。反射率因子Z也有类似的演变特征,即在雨强减弱阶段有较大的反射率因子,最大雨强时反射率因子为50.1 dBz,08:29时Z有最大值50.2 dBz,此时雨强只有14.9 mm·h-1,主要原因是雨滴谱中存在少量直径6.75 mm的特大粒子,导致大的反射率因子;过渡区具有最小的Z和较低的NT,层状云区NT和Z稍大一些,总的来看,过渡区和层状云区NT和Z具有一致的变化特征。
Gamma谱三参数N0、λ、μ随时间的演变(图 4c)表明,强对流云降水时段,μ在-2.0~-3.3之间,λ在0.28~1.10 mm-1之间,具有较低的值。而log10N0数值较大,在2.9~3.5 m-3·mm-1-μ之间。对流云降水后期,μ、λ增大,μ在-1.0~0.0之间,λ在2.5 mm-1左右,而log10N0数值基本在3.3 m-3·mm-1-μ左右;在过渡区,N0、λ、μ都有很大的起伏变化,μ可以是负值,也可以是正值,λ和log10N0数值变化也较大;层状云降水阶段,μ在-1.0~-2.6之间,λ在0.7~2.4 mm-1之间,log10N0数值在2.1~2.8 m-3·mm-1-μ之间。
图 4d是归一化谱参数log10Nw、D0随时间的演变,强对流云降水时段D0约为1.7 mm,log10Nw约为4.2 m-3·mm-1,对流云降水后期D0减小,而log10Nw稍有增大;过渡区具有较大的log10Nw和最小的D0,D0小于1.0 mm;层状云降水D0也是与雨强有一致的变化趋势,基本在1.0~2.0 mm之间。log10Nw则比较稳定,基本在3.0~3.8 m-3·mm-1之间。
4 雨滴谱统计特征分析 4.1 不同类型降水平均雨滴谱特征分析为了更好地认识飑线降水的雨滴谱分布规律,进一步分析不同类型降水的平均雨滴谱特征。对流带降水分成4部分,对流前沿LE和对流后沿TE(雨强小于10 mm·h-1)、对流增强阶段LC和对流减弱阶段TC(雨强大于10 mm·h-1)。过渡区、层状云降水则分析总的平均雨滴谱特征。不同观测点的分类情况见表 1。
|
|
表 1 东阿(DE)和省局(SJ)不同降水类型平均雨滴谱特征 Table 1 Characteristics of average raindrop size distribution at DE and SJ for different types of precipitatio |
对流降水的平均雨滴谱(图 5a)显示,对流前沿LE是雨强小于10 mm·h-1的弱降水,雨滴谱窄、数密度小。对流后沿TE也是窄谱,并且比LE的谱稍窄一些。另外,东阿的雨滴谱比省局的谱稍窄,小粒子的数密度也偏小;两个观测点对流增强阶段LC和减弱阶段TC的雨滴谱特征类似,只有小的差异,TC的谱较宽一些,如省局降水的雨滴谱连续宽度最大为5.0 mm,增强阶段在5.75 mm有少量大雨滴,但减弱阶段在6.0~7.0 mm之间存在一定浓度的大粒子。所以东阿LC和TC平均谱的斜率λ和形状因子μ很接近,截距参数N0有明显差别(表 1)。而省局TC有较多大粒子,其平均谱的有较小的斜率λ和较小的负形状因子μ。东阿和省局的降水雨滴谱存在明显差别,第一个不同是省局的雨滴谱是单峰谱,雨滴最小直径对应最大粒子数密度,而东阿的雨滴谱则不同,LE和TE的最大粒子数密度分别出现在0.44 mm和0.31 mm。第二是雨滴谱的最大谱宽有明显差异,省局对流降水雨滴谱的最大谱宽小于7.0 mm,而东阿约为8.0 mm。第三,雨滴直径大于2.0 mm时,随着直径增大,两个观测点雨滴谱的数密度之间的差异逐渐增大。这些不同表明东阿对流降水的雨滴谱有较多的大雨滴,而省局对流降水有更多的小粒子。

|
图 5 平均雨滴谱(a.对流降水,b.层状云和过渡区) Fig.5 Average raindrop size distribution (a. convective precipitation, b. stratiform cloud and transition zone) |
层状云的平均雨滴谱基本是单调递减的(图 5b),两个观测点之间类似,较明显的差别出现在小和较大粒子端,省局的层状云降水有较多的小于0.5 mm的小雨滴,东阿的层状云降水有较多直径大于2.5 mm的较大粒子。另外,东阿层状云降水的平均雨滴谱比省局稍宽一些。Gamma谱三参数显示(表 1),层状云的平均雨滴谱接近指数谱,形状因子μ接近0;过渡区降水的平均雨滴谱是双峰谱(图 5b),东阿的平均谱在雨滴直径0.625 mm有最大的粒子数密度,省局则是第二峰值。两者比较明显的区别是粒子直径大于1.5 mm时,东阿的平均谱有较大的粒子数密度和较大的粒子谱宽。所以两个观测点的平均谱都有正的形状因子,并且东阿平均谱有较小的斜率和较小的形状因子。
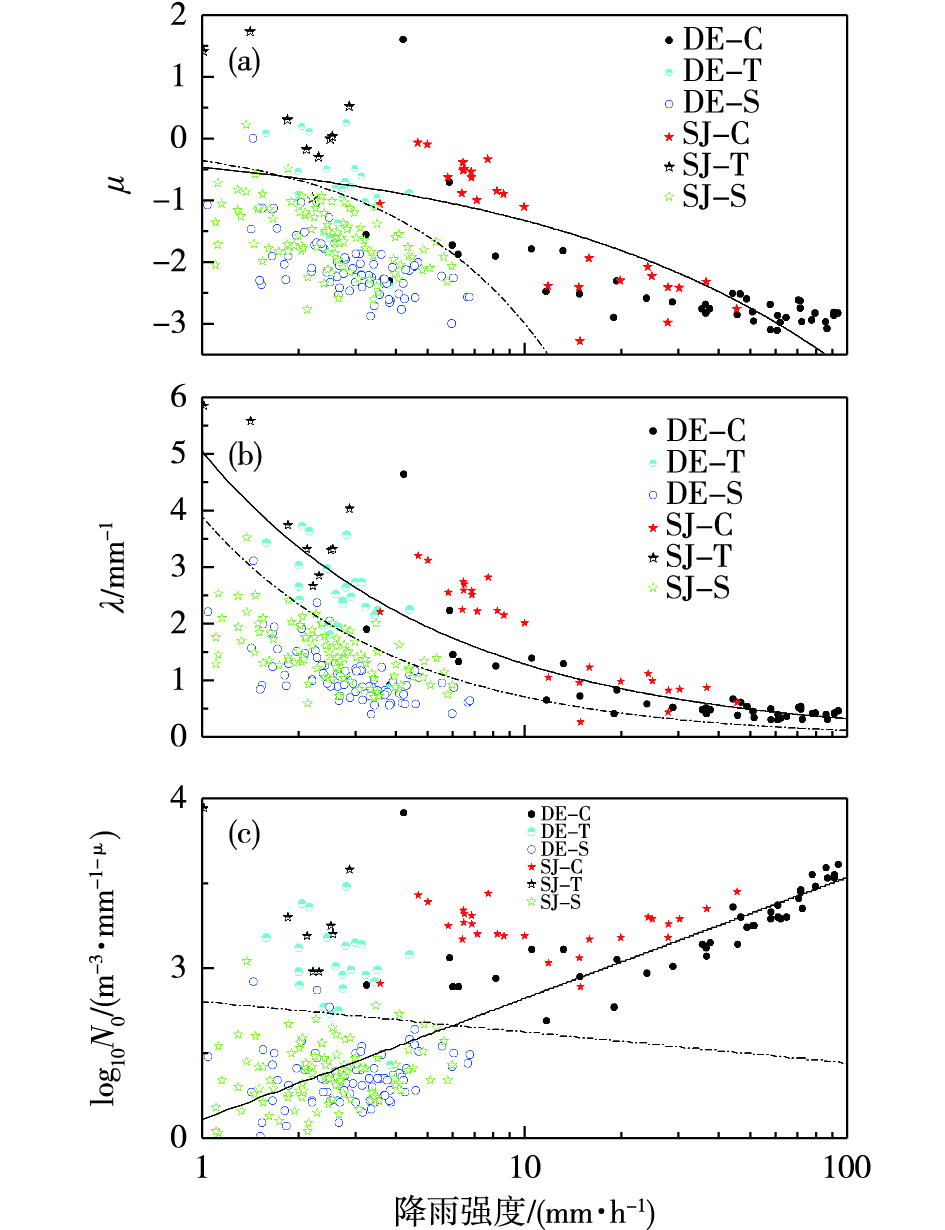
4.2 Gamma谱三参数特征分析Gamma谱三参数与雨强之间的散点图(图 6)表明,对流云降水的雨滴谱参数λ、μ随着雨强增大而逐渐减小,拟合方程分别为μ=-0.472 5R0.145、λ=5.045 8R-0.587 3,μ与R是正指数关系,λ与R是负指数关系。雨强大于10 mm·h-1时N0随雨强增大而增大,可以用幂函数关系拟合,N0=129.1R-0.711 6;过渡区Gamma谱参数λ、μ的数据点基本在对流数据点向后的延长线附近,但参数N0的数据点位于对流线之上,具有较大的数值;层状云的λ、μ也是随着雨强增大而逐渐减小,N0随雨强增大而增大,但明显比对流云和过渡区相同雨强的数值要小,两者具有明显的分层现象。图中点划线是对流和层状之间的分离线,分别为μ=-0.36R0.92,λ=3.9R-0.73,N0=637.2R-0.18。
|
图 6 Gamma谱三参数μ(a)、λ(b)、log10 N0(c)与降雨强度之间的散点图(圆点和五角星分别代表东阿和省局,实心代表对流、空心代表层状云、半空心代表过渡区数据, 粗实线:对流雨滴谱参数与降雨强度之间的拟合线,点划线:对流和层状之间的分离线) Fig.6 Scatter plot between R and μ (a), λ (b), and log10N0 (c) (dot and star for DE and SJ, respectively, solid dot for convective cloud data, hollow dot for stratiform cloud data, semi-hollow dot for transition zone data, thick solid line for the fitting line of convective raindrop size distribution parameter and R, dot-dash line for separation line between convective cloud and stratiform cloud precipitation) |
对比分析东阿和省局观测点Gamma谱三参数随着雨强变化的变化趋势,不同观测点的数据分布有一定的差别。省局观测点的Gamma谱三参数偏大一些,对流和过渡区的N0、λ数据点基本在对流拟合线之上,层状云的数据点更靠近分离线一些。说明弓状回波不同发展阶段雨滴谱演变特征的差异可以导致谱参数的一些统计关系有一定的差别。另外,本次过程λ、μ随着雨强增大减小,而N0随着雨强增大而增大(雨强大于10 mm·h-1),三参数变化特征与TOKAY and SHORT[4]、CARACCIOLO et al.[14]给出的三参数的变化趋势明显不同,TOKAY and SHORT[4]给出的对流—层状分离线不能区分本次过程的对流和层状云降水雨滴谱。
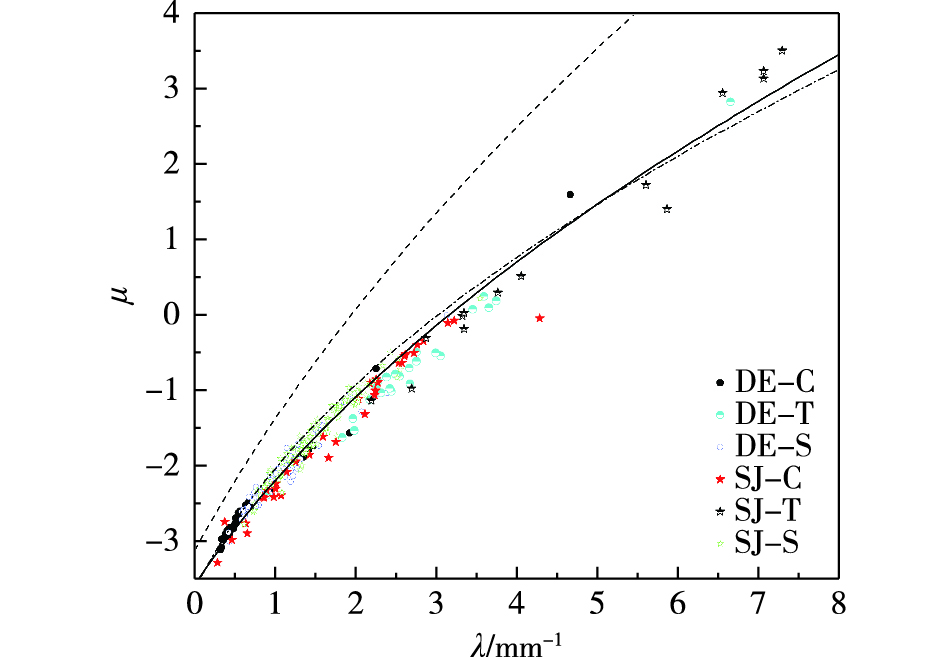
另外,研究结果表明,Gamma谱的三个参数并非相互独立的[13],参数之间的相关性有助于减少未知数,从而促进雨滴谱观测结果的应用,如利用双偏振雷达的水平和垂直反射率来反演雨滴谱。ZHANG et al.[39]研究认为λ-μ之间存在着很好的二次多项式关系。CHU and SU[40]利用二维雨滴谱资料从理论和试验两方面分析了μ和λ之间的关系,认为λ-μ关系与几阶矩计算参数无关。THURAI et al.[41]也发现利用不同方法评估的λ-μ关系是一致的。图 7是雨强大于0.5 mm·h-1时的μ-λ散点图,图中还给出了ZHANG et al.[39]和王俊等[10]的λ-μ拟合曲线。本次过程λ-μ拟合公式为:λ=0.073 6μ2+1.144 9μ+3.151。与ZHANG et al.[39]结果相比,二次多项式各项的系数有明显的的差别。与王俊等[10]的结果相比,拟合曲线很相近,常数和一次项的系数非常接近,二次项的系数差别稍大一些,可能的原因是以前的个例只是对流带降水,λ、μ数值范围较小,而本次过程包含对流带、层状云和过渡区降水,λ、μ具有较大范围的数值,利用最小二乘法计算拟合曲线时存在小的差别是可以理解的。总的来看,两者之间的差别很小,不同降水个例之间倾向于具有一致的λ-μ关系。
|
图 7 降雨强度大于0.5 mm·h-1的λ-μ散点图(虚线:ZHANG et al.的拟合线,点划线:王俊等的拟合线,实线:本次过程拟合线) Fig.7 Scatter plot of λ and μ when R is greater than 0.5 mm·h-1 (dashed line for fitting line by ZHANG et al., dotted line for fitting line by WANG et al., solid line for fitting line of the process on 18 July 2017) |
不同观测点和不同降水类型的数据分布有小的差异(图 7),东阿的对流和层状降水的数据很靠近拟合线,而过渡区降水有较大的λ值,数据点都在拟合线之下。省局的对流和层状降水的数据也比较靠近拟合线,但两者的分布有不同,对流降水基本在拟合线之下,而层状降水在拟合线之上。省局过渡区降水一部分点在拟合线之下,而有较大λ值的部分点在拟合线之下。表明不同降水阶段、不同降水类型的λ-μ关系只有小的差别,倾向于具有一致的λ-μ关系。
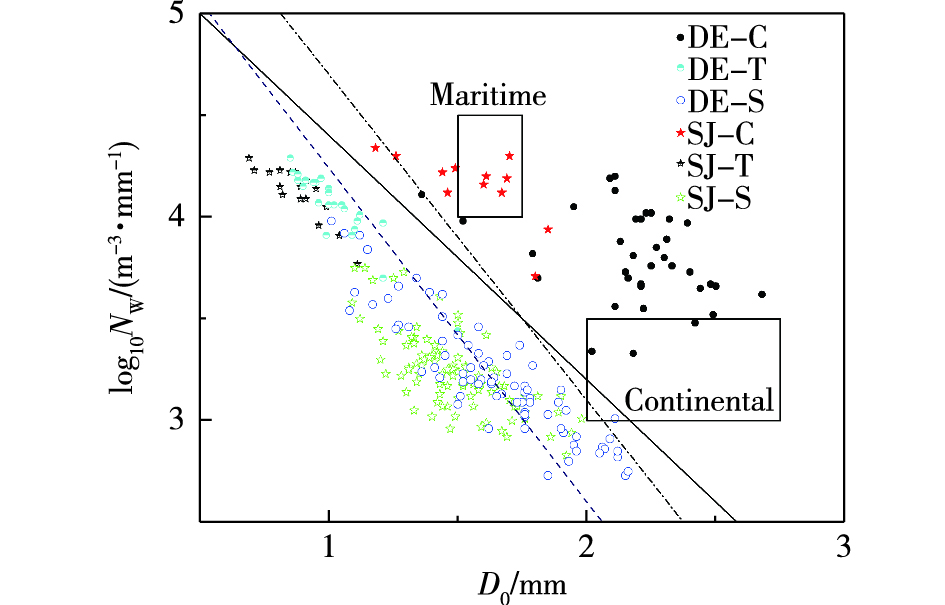
4.3 归一化参数Nw、D0分布特征不同观测点log10Nw-D0平面图(图 8)显示,东阿和省局对流云降水的分布有非常明显的差别,东阿雨滴谱具有较大的D0,主要在2.0~2.5 mm之间,而log10Nw在3.5~4.0 m-3·mm-1之间,与BRINGI et al.[18]给出的大陆性对流云降水分布区相比,log10Nw偏大,而直径相当;省局雨滴谱的D0偏小,一般在1.4~1.7 mm之间,而log10Nw较大,在4.0~4.4 m-3·mm-1之间,很明显,省局对流云降水的数据点位于BRINGI et al.[18]给出的海洋性对流云降水分布区。过渡区雨滴谱数据点分布得比较集中,D0较小,一般小于1.2 mm,log10Nw较大,在4.0左右,对比来看,东阿雨滴谱D0要稍大一些。层状云数据点有较大的分布范围,东阿雨滴谱有较大D0,一般在1.1~2.2 mm之间,log10Nw在2.7~3.9 m-3·mm-1之间;省局雨滴谱D0稍小,一般在1.1~2.0 mm之间,log10Nw在2.9~3.9 m-3·mm-1之间。图中虚线是BRINGI et al.[18]给出的层状云降水的平均分布,本次过程层状云降水雨滴谱分布在虚线附近,东阿数据点在虚线之上,而省局数据点大部分在虚线之下。
|
图 8 log10Nw-D0散点图(圆点和五角星分别代表东阿和省局,实心代表对流、空心代表层状云、半空心代表过渡区数据;粗实线:对流与层状云降水之间的分离线,点划线:BRINGI et al.分离线,虚线: BRINGI et al.层状分布,黑色矩形框:BRINGI et al.给出的海洋性和大陆性对流分布) Fig.8 Scatter plot of log10Nw and D0(dot and star for DE and SJ, respectively, solid dot for convective cloud data, hollow dot for stratiform cloud data, semi-hollow dot for transition zone data, thick solid line for separation line between convective cloud and stratiform cloud precipitation, dotted line for separation line by BRINGI et al., dashed line for distribution of stratiform by BRINGI et al., black rectangle for distribution of maritime and continental convection by BRINGI et al.) |
BRINGI et al.[19]给出的对流、层状分离线(公式(1)),基本可以区分本次过程的对流和层状云降水的雨滴谱(图 8中点划线),层状云只有一个数据点位于分离线之上,有3个强对流云降水的数据点位于分离线上和之下。过渡区数据位于分离线之下,没有跨坐在分离线上。但这一分离线的斜率较大,而层状云和对流云log10Nw随着D0分布的斜率较小,新的分离线为:
| $ {\log _{10}}{N_{\rm{w}}} = - 1.2{D_0} + 5.6 $ | (20) |
公式(20)可以更好地分离本次过程的对流和层状云降水雨滴谱。BRINGI et al.[19]给出的分离线具有较大的斜率,但他们认为强烈的大陆风暴含有旺盛的混合相过程和大量的蒸发,导致分界线向低的log10Nw和大的D0方向倾斜。中国北部夏季的对流和层状云降水[20]、以及YOU et al.[15]的研究结果显示分离线具有较小的斜率,数值约为1.0,这说明不同气候区降水形成的微物理过程存在差异,导致分离线的斜率出现一定的差别。
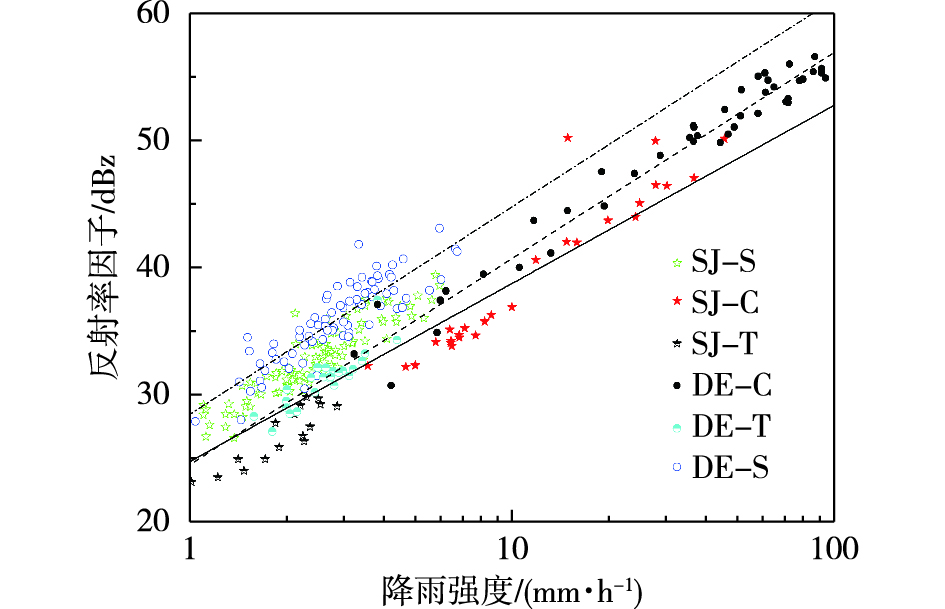
4.4 Z-R关系分析图 9是雨滴谱计算的雷达反射率Z与雨强R(大于1 mm·h-1)的散点图,图中虚线是对流云降水的拟合方程,Z=283.9R1.65。点划线是层状云降水的拟合方程,Z=706.6R1.63。实线是新一代多普勒雷达对流云降水Z-R关系[42]。东阿对流云降水的雨滴谱数据在拟合线附近稍稍偏上,而省局对流云降水的雨滴谱数据在拟合线之下(只有2个点在拟合线之上)。过渡区的数据分布差别更明显,东阿观测数据大部分在对流拟合线之上,而省局观测数据基本在拟合线之下。层状云也是这一特征,东阿雨滴谱具有较大的反射率因子,位于层状拟合线附近,而省局层状云降水雨滴谱具有较小的反射率因子,数据位于拟合线之下。由于两个观测点处于飑线不同的发展阶段,雨滴谱特在差异,东阿降水的雨滴谱有较多的大粒子,所以有较大的反射率因子。
|
图 9 雨滴谱计算的雷达反射率因子Z与雨强R(大于1 mm·h-1)的散点图(圆点和五角星分别代表东阿和省局,实心代表对流、空心代表层状云、半空心代表过渡区数据;虚线:对流云降水的拟合方程,点划线:层状云降水的拟合方程,实线:FULTON et al.的对流云降水Z-R关系) Fig.9 Scatter plot of Z and R (greater than 1 mm·h-1) calculated by raindrop size distribution (dot and star for DE and SJ, respectively, solid dot for convective cloud data, hollow dot for stratiform cloud data, semi-hollow dot for transition zone data; dashed line for fitting equation of convective cloud precipitation, dotted line for fitting equation of stratiform cloud precipitation, solid line for Z-R relationship in convective cloud precipitation by FULTON et al.) |
UIJLENHOET et al.[43]分析拖曳型飑线的Z-R关系,发现对流和过渡区数据点在一条直线,而层状云数据点在线之上,三者之间几乎没有重叠。本次过程不同类型降水雨滴谱数据的分布也具有类似的特点,不同之处是省局层状云降水与东阿过渡区和部分对流云降水的观测数据存在重叠。另外,研究[44]表明,当雨滴浓度是影响雨滴谱的主要因素时,Z-R关系中的指数接近1.0,而系数较大。而当雨滴直径是影响雨滴谱的主要因素时,Z-R关系中的指数较大,超过1.5。本次过程对流云降水Z-R关系中的指数为1.65,这属于典型的尺寸控制的雨滴谱特征。而层状云的系数和指数都较大,表明雨滴浓度和尺寸共同控制雨滴谱特征。
5 结论利用Thies激光雨滴谱仪观测资料和CINRAD/SA多普勒雷达观测资料,分析了一次拖曳型飑线不同发展阶段雨滴谱和积分参数的演变特征,以及Gamma谱拟合参数、归一化Gamma谱参数Nw和D0的统计特征,主要结果为:
1) 本次过程受强盛副高边缘切变线影响,具有较高的对流不稳定能量和丰富的低层水汽,是此次飑线天气过程产生的有利环境条件。雷达资料显示,成熟弓状回波具有中纬度拖曳型飑线的典型回波特征:对流带、过渡区和拖曳层状云区,对流带前侧不断有对流带生成并合并到主对流带中,使得对流带的前沿具有强的反射率因子,并且有多个雨强中心。过渡区回波弱,层状云回波典型特征是有较强的0 ℃层亮带。
2) 垂直穿过对流带,雨强增加阶段有较少的直径小于1 mm的小粒子和直径大于5 mm的特大粒子,而雨强减弱阶段有较多的小尺寸粒子和特大粒子。因此在雨强增大过程大多是较低的雨滴浓度和反射率因子,而在雨强减弱过程是较高的雨滴浓度和反射率因子。本次过程雨强减弱时段有较多的大和特大粒子,这是与以往研究不同之处。
过渡区雨滴谱最窄,但雨滴谱的峰值直径较大(0.63 mm),后期转变为双峰谱。另外,过渡区的Gamma谱三参数N0、μ、λ起伏变化大,这也是识别过渡区的一个判据。
飑线发展加强阶段,雨滴谱中小粒子的峰值直径较大(0.44 mm),有较多的大和特大粒子。而在飑线减弱阶段,滴谱中小粒子的峰值直径小(0.19 mm),有较少的大粒子,几乎没有特大粒子。
3) 对流、过渡区和层状云降水雨滴谱的Gamma谱三参数N0、μ、λ有明显的分层特征,相同雨强时,对流和过渡区降水的Gamma谱三参数N0、μ、λ比层状云降水的参数的数值大,但TOKAY and SHORT[4]以前给出的对流-层状分离线不能分离本次过程的对流和层状云降水雨滴谱。
二次多项式可以拟合λ-μ关系,飑线不同发展阶段、不同降水类型的λ-μ关系只有小的差别,倾向于具有一致的λ-μ关系。
4) Z-R关系分析显示,对流和过渡区降水的数据点基本分布在一条直线上,而层状云降水的数据明显偏离这一直线。另外,飑线不同发展阶段的Z-R关系稍有差别,主要原因是不同发展阶段的雨滴谱中大雨滴存在差异。
5) log10Nw-D0平面图中对流-层状数据具有明显分层特征,方程log10NW=-1.2D0+5.6可以将对流云和层状云区分开来。飑线发展阶段雨滴谱具有大陆性对流云降水的特征,只是log10Nw偏大一些。而减弱阶段雨滴谱具有典型的海洋性对流云降水的特征,这说明飑线演变过程降水形成的微物理机制发生变化,前期冷云过程有重要影响,而后期暖云过程起主导作用。
| [1] |
SMULL B F, HOUZE R A JR. Dual-Doppler radar analysis of a midlatitude squall line with a trailing region of stratiform rain[J]. J Atmos Sci, 1987, 44(15): 2128-2149. DOI:10.1175/1520-0469(1987)044<2128:DDRAOA>2.0.CO;2 |
| [2] |
BIGGERSTAFF M I, HOUZE R A JR. Kinematic and precipitation structure of the 10—11 June 1985 squall line[J]. Mon Wea Rev, 1991, 119(12): 3034-3065. DOI:10.1175/1520-0493(1991)119<3034:KAPSOT>2.0.CO;2 |
| [3] |
ATLAS D, ULBRICH C W, MARKS F D JR, et al. Systematic variation of drop size and radar-rainfall relations[J]. J Geophys Res, 1999, 104(D6): 6155-6169. DOI:10.1029/1998JD200098 |
| [4] |
TOKAY A, SHORT D A. Evidence from tropical raindrop spectra of the origin of rain from stratiform versus convective clouds[J]. J Appl Meteor, 1996, 35(3): 355-371. DOI:10.1175/1520-0450(1996)035<0355:EFTRSO>2.0.CO;2 |
| [5] |
MAKI M, KEENAN T D, SASAKI Y, et al. Characteristics of the raindrop size distribution in tropical continental squall lines observed in Darwin, Australia[J]. J Appl Meteor, 2001, 40(8): 1393-1412. DOI:10.1175/1520-0450(2001)040<1393:COTRSD>2.0.CO;2 |
| [6] |
NZEUKOU A, SAUVAGEOT H, OCHOU A D, et al. Raindrop size distribution and radar parameters at cape verde[J]. J Appl Meteor, 2004, 43(1): 90-105. DOI:10.1175/1520-0450(2004)043<0090:RSDARP>2.0.CO;2 |
| [7] |
THURAI M, BRINGI V N, MAY P T. CPOL radar-derived drop size distribution statistics of stratiform and convective rain for two regimes in Darwin, Australia[J]. J Atmos Oceanic Technol, 2010, 27(5): 932-942. DOI:10.1175/2010JTECHA1349.1 |
| [8] |
ZHANG H S, ZHANG Y, HE H R, et al. Comparison of raindrop size distributions in a midlatitude continental squall line during different stages as measured by parsivel over East China[J]. J Appl Meteor Climatol, 2017, 56(7): 2097-2111. DOI:10.1175/JAMC-D-16-0336.1 |
| [9] |
SAUVAGEOT H, KOFFI M. Multimodal raindrop size distributions[J]. J Atmos Sci, 2000, 57(15): 2480-2492. DOI:10.1175/1520-0469(2000)057<2480:MRSD>2.0.CO;2 |
| [10] |
王俊, 姚展予, 侯淑梅, 等. 一次飑线过程的雨滴谱特征研究[J]. 气象学报, 2016, 74(3): 450-464. |
| [11] |
WEN J, ZHAO K, HUANG H, et al. Evolution of microphysical structure of a subtropical squall line observed by a polarimetric radar and a disdrometer during OPACC in eastern China[J]. J Geophys Res, 2017, 122(15): 8033-8050. |
| [12] |
WALDVOGEL A. The N0 jump of raindrop spectra[J]. J Atmos Sci, 1974, 31(4): 1067-1078. DOI:10.1175/1520-0469(1974)031<1067:TJORS>2.0.CO;2 |
| [13] |
ULBRICH C W. Natural variations in the analytical form of the raindrop size distribution[J]. J Climate Appl Meteor, 1983, 22(10): 1764-1775. DOI:10.1175/1520-0450(1983)022<1764:NVITAF>2.0.CO;2 |
| [14] |
CARACCIOLO C, PRODI F, BATTAGLIA A., et al. Analysis of the moments and parameters of a gamma DSD to infer precipitation properties: A convective stratiform discrimination algorithm[J]. Atmos Res, 2006, 80(2/3): 165-186. |
| [15] |
YOU C H, LEE D I, KANG M Y, et al. Classification of rain types using drop size distributions and polarimetric radar: Case study of a 2014 flooding event in Korea[J]. Atmos Res, 2016, 181: 211-219. DOI:10.1016/j.atmosres.2016.06.024 |
| [16] |
WILLIS P T. Functional fits to some observed drop size distributions and parameterization of rain[J]. J Atmos Sci, 1984, 41(9): 1648-1661. DOI:10.1175/1520-0469(1984)041<1648:FFTSOD>2.0.CO;2 |
| [17] |
LEE G W, ZAWADZKI I, SZYRMER W, et al. A general approach to double-moment normalization of drop size distributions[J]. J Appl Meteor, 2004, 43(2): 264-281. DOI:10.1175/1520-0450(2004)043<0264:AGATDN>2.0.CO;2 |
| [18] |
BRINGI V N, CHANDRASEKAR V, HUBBERT J, et al. Raindrop size distribution in different climatic regimes from disdrometer and dual-polarized radar analysis[J]. J Atmos Sci, 2003, 60(2): 354-365. DOI:10.1175/1520-0469(2003)060<0354:RSDIDC>2.0.CO;2 |
| [19] |
BRINGI V N, WILLIAMS C R, THURAI M, et al. Using dual-polarized radar and dual-frequency profiler for DSD characterization: a case study from Darwin, Australia[J]. J Atmos Oceanic Technol, 2009, 26(10): 2107-2122. DOI:10.1175/2009JTECHA1258.1 |
| [20] |
WEN G, XIAO H, YANG H L, et al. Characteristics of summer and winter precipitation over northern China[J]. Atmos Res, 2017, 197: 390-406. DOI:10.1016/j.atmosres.2017.07.023 |
| [21] |
MENG Z Y, YAN D C, ZHANG, Y J. General features of squall lines in East China[J]. Mon Wea Rev, 2013, 141(5): 1629-1647. DOI:10.1175/MWR-D-12-00208.1 |
| [22] |
王俊. 线状中尺度对流系统的多普勒雷达统计特征分析[J]. 海洋气象学报, 2017, 37(4): 25-33. |
| [23] |
龚佃利, 吴增茂, 傅刚. 一次华北强对流风暴的中尺度特征分析[J]. 大气科学, 2005, 29(3): 453-464. DOI:10.3878/j.issn.1006-9895.2005.03.13 |
| [24] |
朱君鉴, 刁秀广, 曲军, 等. 4.28临沂强对流灾害性大风多普勒天气雷达产品分析[J]. 气象, 2008, 34(12): 21-26. DOI:10.7519/j.issn.1000-0526.2008.12.003 |
| [25] |
卓鸿, 赵平, 任健, 等. 2007年济南"7.18"大暴雨的持续拉长状对流系统研究[J]. 气象学报, 2011, 69(2): 263-276. |
| [26] |
王俊, 龚佃利, 刁秀广, 等. 一次弓状回波、强对流风暴及合并过程研究Ⅰ:以单多普勒雷达资料为主的综合分析[J]. 高原气象, 2011, 30(4): 1067-1077. |
| [27] |
张婷婷, 王培涛, 王凤娇. 一次长寿命超级单体风暴雷达回波特征分析[J]. 海洋气象学报, 2017, 37(1): 98-103. |
| [28] |
高帆, 张永婧, 李瑞, 等. 2015年8月3日山东西北部暴雨过程的中尺度特征分析[J]. 海洋气象学报, 2017, 37(2): 96-101. |
| [29] |
高晓梅, 王世杰, 王文波, 等. 2016年山东一次阵风锋触发的强对流天气分析[J]. 海洋气象学报, 2018, 38(2): 67-75. |
| [30] |
万夫敬, 江敦双, 赵传湖. 2017年8月6日山东罕见雷暴大风成因分析[J]. 海洋气象学报, 2018, 38(2): 60-66. |
| [31] |
刁秀广. 阵风锋、海风锋和冷锋等触发局地强对流风暴实例分析[J]. 海洋气象学报, 2018, 38(4): 45-57. |
| [32] |
侯淑梅, 孙鹏程, 杨璐瑛, 等. 环境场条件对雷暴传播运动影响实例分析[J]. 海洋气象学报, 2018, 38(4): 58-70. |
| [33] |
DE MORAES FRASSON R P, DA CUNHA L K, KRAJEWSKI W F. Assessment of the thies optical disdrometer performance[J]. Atmos Res, 2011, 101(1/2): 237-255. |
| [34] |
FRIEDRICH K, KALINA E A, MASTERS F J, et al. Drop-Size distributions in thunderstorms measured by optical disdrometers during VORTEX2[J]. Mon Wea Rev, 2013, 141(4): 1182-1203. DOI:10.1175/MWR-D-12-00116.1 |
| [35] |
TESTUD J, OURY S, BLACK R A, et al. The concept of "normalized" distribution to describe raindrop spectra: A tool for cloud physics and cloud remote sensing[J]. J Appl Meteor, 2001, 40(6): 1118-1140. DOI:10.1175/1520-0450(2001)040<1118:TCONDT>2.0.CO;2 |
| [36] |
THOMPSON E J, RUTLEDGE S A, DOLAN B, et al. Drop size distributions and radar observations of convective and stratiform rain over the equatorial Indian and West Pacific Oceans[J]. J Atmos Sci, 2015, 72(11): 4091-4125. DOI:10.1175/JAS-D-14-0206.1 |
| [37] |
PARKER M D, JOHNSON R H. Organizational modes of midlatitude mesoscale convective systems[J]. Mon Wea Rev, 2000, 128(10): 3413-3436. DOI:10.1175/1520-0493(2001)129<3413:OMOMMC>2.0.CO;2 |
| [38] |
ZHENG L L, SUN J H, ZHANG X L, et al. Organizational modes of mesoscale convective systems over central East China[J]. Wea Forecasting, 2013, 28(5): 1081-1098. DOI:10.1175/WAF-D-12-00088.1 |
| [39] |
ZHANG G F, VIVEKANANDAN J, BRANDES E A, et al. The shape-slope relation in observed gamma raindrop size distributions: statistical error or useful information?[J]. J Atmos Ocean Technol, 2003, 20(8): 1106-1119. DOI:10.1175/1520-0426(2003)020<1106:TSRIOG>2.0.CO;2 |
| [40] |
CHU Y H, SU C L. An investigation of the slope-shape relation for gamma raindrop size distribution[J]. J Appl Meteor Climatol, 2008, 47(10): 2531-2544. DOI:10.1175/2008JAMC1755.1 |
| [41] |
THURAI M, WILLIAMS C R, BRINGI V N. Examining the correlations between drop size distribution parameters using data from two side-by-side 2D-video disdrometers[J]. Atmos Res, 2014, 144: 95-110. DOI:10.1016/j.atmosres.2014.01.002 |
| [42] |
FULTON R A, BREIDENBACH J P, SEO D J, et al. The WSR-88D rainfall algorithm[J]. Wea Forecasting, 1998, 13(2): 377-395. DOI:10.1175/1520-0434(1998)013<0377:TWRA>2.0.CO;2 |
| [43] |
UIJLENHOET R, STEINER M, SMITH J A. Variability of raindrop size distributions in a squall line and implications for radar rainfall estimation[J]. J Hydrometeorol, 2003, 4(1): 43-61. DOI:10.1175/1525-7541(2003)004<0043:VORSDI>2.0.CO;2 |
| [44] |
UIJLENHOET R, SMITH J A, STEINER M. The microphysical structure of extreme precipitation as inferred from ground-based raindrop spectra[J]. J Atmos Sci, 2003, 60(10): 1220-1238. DOI:10.1175/1520-0469(2003)60<1220:TMSOEP>2.0.CO;2 |
 2019, Vol. 39
2019, Vol. 39

