2. 山东省气象局机关服务中心,山东 济南 250031
2. Service Center of Shandong Meteorological Bureau, Jinan 250031, China
近年来,随着社会的发展和科学技术的突飞猛进,现代化大气探测设施建设也获得迅猛发展,天、地、空一体化观测体系正显著提升大气探测水平,提高对灾害性天气的应对能力。其中,多普勒天气雷达在我国已经完成整体布网和全面应用。多普勒天气雷达对云雨等的高时空分辨率立体探测能力使其在龙卷、大风、暴雨、台风等灾害性天气的监测预警以及科学研究中发挥重要作用,多普勒天气雷达可有效提升对灾害性天气的深入理解和预报服务能力[1-5]。
多年来,国内外多普勒天气雷达质控领域已经进行了大量的研究,包括模糊逻辑[6]、神经网络[7]等技术已经很好地应用到业务中。尽管如此,多普勒天气雷达在探测和预报业务实践中仍存在一些问题和不足,其中复杂电磁环境下干扰回波就是其中重要的一个。随着通信技术和应用领域不断发展,频谱利用范围也显著增加,在复杂的电磁环境下,多普勒天气雷达回波会受到相应的干扰,造成异常回波。其中,径向杂波是天气雷达回波中常见的一种异常回波,存在于山东多个雷达站点的回波中。它在径向上呈条辐状分布,通常情况下和降水回波在很多区域重叠,影响较大。径向干扰回波是影响天气雷达回波资料准确性不可忽视的因素之一,特别是它对雷达资料的定量应用产生严重的影响。了解这类回波特征并对它们进行实时的有效识别是准确剔除这些干扰杂波的基础,也是获取高质量雷达基数据及各类雷达产品的重要保证。
海洋气象学报第39卷第4期周雪松等:一种基于快速傅里叶变换的多普勒天气雷达弱杂波识别方法近年来,针对这类有源干扰杂波类似的径向杂波的识别,气象科学工作者进行了大量的研究,也取得了较为显著的成果。中国气象科学研究院研发的地物回波及电磁干扰回波质控算法在“新一代天气雷达建设业务软件系统开发及应用(ROSE)”系统中的业务试应用,干扰回波的识别成功率为94.39%,能有效识别小于5个径向的窄条辐状干扰回波[8]。杜言霞等[9]使用同一距离库上相邻方位回波强度差与单一方位上回波强度的方差,黄勤等[10]使用相邻径向比较方法等,开展了对新一代天气雷达数据质量控制,并取得了较好的效果。近期,黄小玉等[11]提出反射率因子径向能量以及径向能量一阶差分的概念,并使用径向能量一阶差分识别有源干扰回波所在的方位。
尽管以上干扰回波的识别算法在大多数情况下可以对该类回波进行识别并进行消除,但是,各类算法都存在一定的适应范围,且对某些强度较弱的干扰回波识别能力有限。如ROSE中质控算法仍需改进以便完成对麻点状、螺旋状和大面积径向干扰回波的自动识别[8],功率法等在去除较弱的干扰回波时效果也受到限制。大多数径向干扰回波识别算法是基于相邻方位角径向回波对比,因此,需要整个仰角扫描数据,甚至整个体扫数据。随着人们对灾害性天气预报服务时间、空间和及时性要求的日益提高,多普勒天气雷达实时数据质控和产品处理也日益迫切,但基于径向对比的算法限制了实时处理时效的进一步提升。本文针对多普勒天气雷达有源干扰回波,提出了一种基于快速傅里叶变换(fast Fourier transform, FFT)的干扰回波识别算法,可较好地应对干扰回波较弱时对干扰回波的识别问题。通过本文研究和对质控算法的改进,以期提供一种新的质控技术,补充和完善多普勒天气雷达数据质量控制中干扰回波的识别工作,进一步推进雷达数据质控水平的提高。
1 干扰回波的特征分析当多普勒天气雷达回波受外界同频或临近频率设备发出的电磁波干扰时,就会出现干扰回波。当出现这种现象时一般表现为螺旋带回波、干扰麻点和一条直线[12]。近距离干扰, 一直存在满屏干扰麻点;远距离干扰时, 一般在某个方向上存在固定的干扰[13]。通常情况下,山东出现的干扰回波以若干径向上线性干扰较多。一些较明显的干扰回波或回波强度较强的电磁回波可以通过径向能量等方法[11]给予很好的识别并剔除,但是一些较弱的干扰回波相对较难识别。另外,一些其他原因也可能造成类似的弱径向杂波。
2019年8月23日09:23(北京时间,下同), 在山东滨州多普勒天气雷达0.5°仰角西北偏西方向出现了一系列的径向干扰回波。其中既有回波较为连续的线性回波,也有回波较为零散的散点回波(图 1a)。研究分析发现,都存在较为明显的周期规律性,即强度在径向方向上存在强弱规律性变化。对上述极坐标上的干扰回波在方位角方向展开后(图 1b),可以更加明显地看到在275°~290°方位上,径向距离360 km范围内都存在规律的回波信号,且回波强度差别较大,但是总体强度较弱;而在其他方位角上,是较为典型的晴空回波或无回波。

|
图 1 滨州多普勒天气雷达2019年8月23日09:23电磁杂波(a)及极坐标展开后(b) Fig.1 Electromagnetic clutter (a) and electromagnetic clutter after polar coordinate expansion (b) at 09:23 on 23 August 2019 from Binzhou Doppler weather radar |
针对以上干扰回波规律性特征的分析,发现其回波在空间上具有较强的周期性强弱波动。因此,在径向回波识别时,使用相关算法将径向上数据转换到频域上进行处理。其中,利用了离散傅里叶变换(discrete Fourier transform, DFT),把径向数据从空间域变换到频率域,进而研究数据的频谱结构和变化规律。为更加快速地实现该算法,使用了快速傅里叶变换算法,这是一种利用计算机计算离散傅里叶变换的高效、快速计算方法,可更好地实现计算量的节省。该方法在气象上多个领域都有很好的应用,除雷达I/Q信号处理[14]等核心应用外,在暴雨激发重力波研究[15]、气候态研究[16]和遥感反演海浪波长[17]等研究方面都取得了较好的效果。本研究使用该方法主要是实现频谱能量分布特征的提取。
2.2 数据与质控方法 2.2.1 应用的数据本方法研究中,使用了多普勒天气雷达流传输生成的逐仰角数据和FY-4静止卫星数据。选择流传输逐仰角数据作为本研究使用的雷达数据,一方面是该数据具有更好的更新频次和传输时效,另一方面针对当前和未来双偏振雷达可以获得更高分辨率的数据,从而便于更好的业务应用和研究。
2.2.2 数据预处理与分析目前,基于流传输技术的逐仰角雷达观测数据可以通过全国气象传输系统CTS2及时获得,每部天气雷达,可以在逐仰角扫描完毕后及时得到。由于雷达扫描模式为连续性扫描模式,为便于进一步处理,对雷达扫描数据进行预处理,逐方位重新整理从而形成0°~359°共360个方位角的连续数据,即形成由雷达反射率因子组成的二维矩阵。为便于理解,将2019年8月23日09:23山东滨州多普勒天气雷达0.5°仰角数据作为示例进行分析和方法研究。
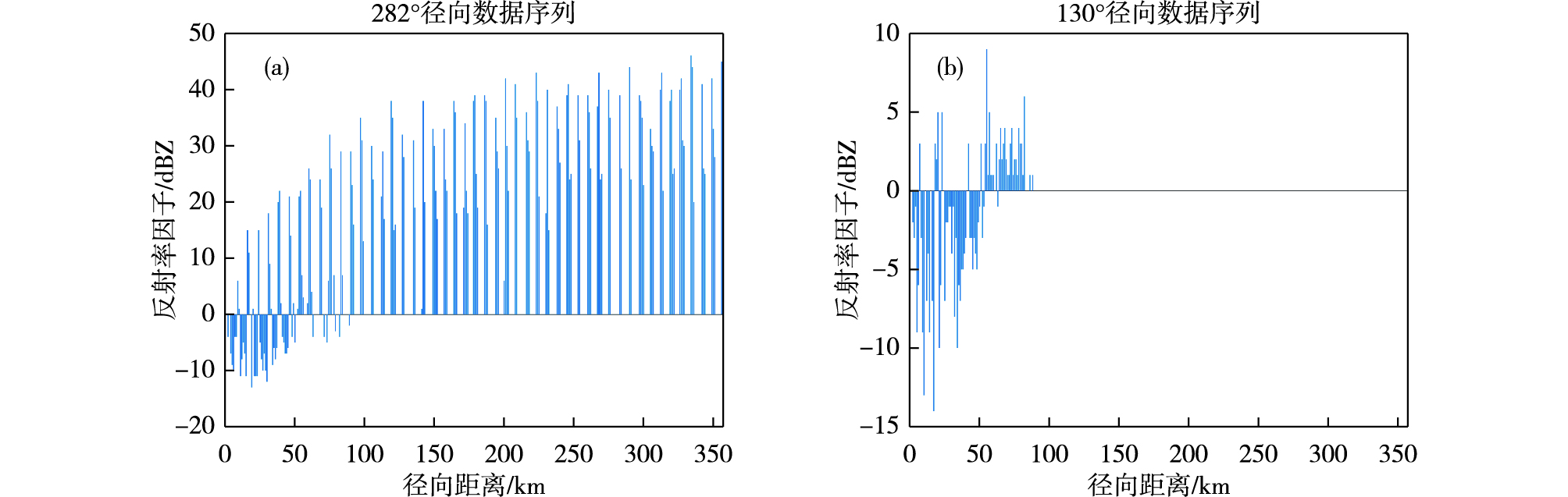
前述分析已表明干扰杂波在径向上具有明显的规律性。图 2分别给出了干扰较严重的282°方位上和无干扰的130°方位上反射率因子随径向距离的分布图。由图 2a可以看到,存在干扰杂波的范围在-12~45 dBZ,且具有非常明显的周期规律性,即具有相同频率的数据起伏变换。而非干扰径向杂波则无此特征,仅包含10 dBZ相对较弱反射率因子(图 2b)。这些差异性特征为进一步研究识别算法提供了很好的基础,可以通过反射率因子的分布特征进行杂波识别,而不是前人研究较多的基于具体反射率因子总功率等方法进行识别。
|
图 2 282°方位(a)和130°方位(b)反射率因子分布 Fig.2 Distribution of reflectivity factor at azimuth of 282° (a) and 130° (b) |
为更好地对前面分析的反射率因子的周期性变化特征进行分析,本研究中使用快速傅里叶变换方法(FFT,使用了Matlab相关函数)对径向上反射率因子数据进行了处理,从而获得频率能量分布密度,其中在该径向上无回波数据使用0.0进行替换以便进行FFT处理。
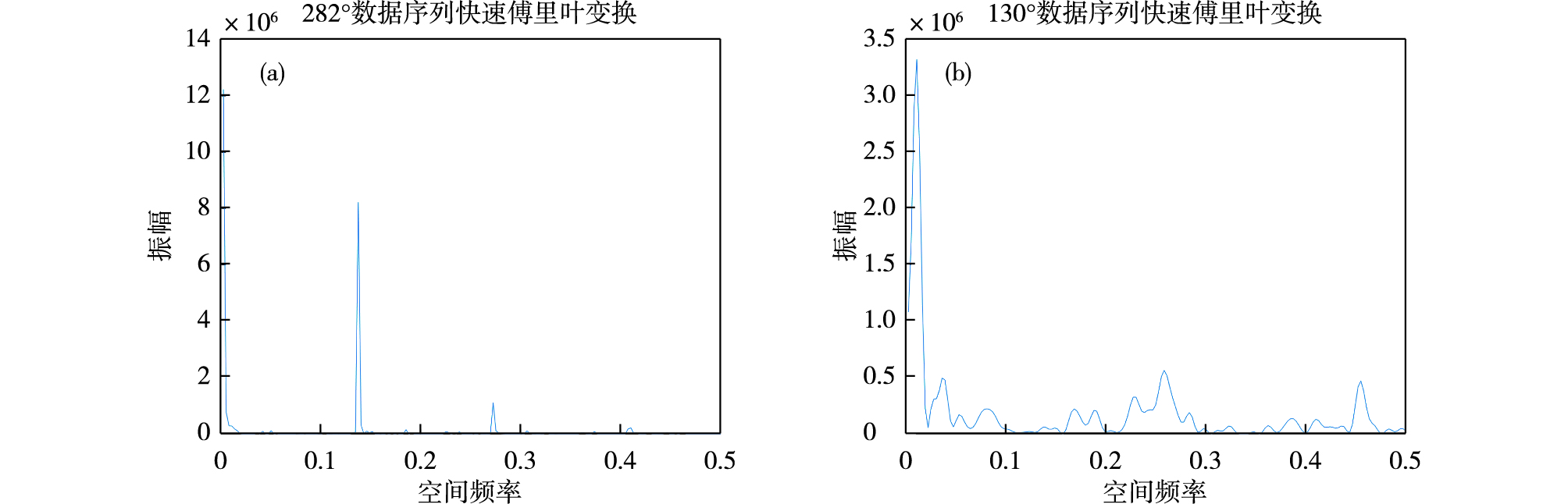
对转换后的结果分析可见,在干扰杂波较明显的典型方位上(282°,图 3a),存在三个能量峰值,分别为0附近区域,0.14附近达8.2×106,以及0.27附近为1.1×106,结合图 2a反射率周期性变化的径向距离分析,其中第二个位置能量高峰与前述分析的规律性有很好的对应关系。而在非干扰杂波的典型方位(130°,图 3b)上,除0附近高值外不存在明显的高能量区。由频域分析来看,这两类回波的差异较为明显。通过这些特征可以很好地对干扰杂波进行区分。
|
图 3 282°方位(a)和130°方位(b)方位角频谱能量密度 Fig.3 Energy density spectrum at azimuth of 282° (a) and 130° (b) |
从前面经过FFT变换后的频域能量分布来看,在0.1~0.2范围内的能量对是否存在干扰回波具有很好的指示作用。为此,逐方位角对上述范围内的能量进行统计分析(图 4a)。从图上分析可以看出,在270°~290°方位范围内,存在着明显的由于周期性特征造成的高能量区,这一区域正是干扰回波所在的范围。FFT变换后可以很好地识别异常回波出现的方位角,从而实现对干扰回波的准确识别。

|
图 4 各方位频谱能量分布(a)和质控后的回波分布(b) Fig.4 Distribution of energy spectrum at varied azimuths (a) and distribution of reflectivity factor after quality control (b) |
通过使用频域变换的方法,对干扰杂波识别并剔除后,原来周期性变化的异常回波已经被识别并剔除。最终,经过本方法处理后的雷达图像得到了很好的质量控制(图 4b)。
3 天气实例算法应用上述方法结果表明,该方法对径向上离散性分布的杂波具有较好的识别能力。但其适用性如何还需要进一步的研究讨论。为更好地检验该方法在不同类型的实际天气过程中的效果,本文在雷达局地降雨和大范围降雨个例雷达杂波识别中进行应用,以进一步分析该算法的应用效果,同时还探讨了在其他非气象杂波识别中的作用。
3.1 局地降水个例杂波识别2018年第18号台风“温比亚”给山东带来严重的灾害,既有龙卷灾害,又有大范围强降雨。在台风影响前期,8月17日临沂雷达出现了较大范围的径向干扰回波,干扰回波既出现在17日上午局地降水期间,也出现在下午开始的大范围降雨期间。
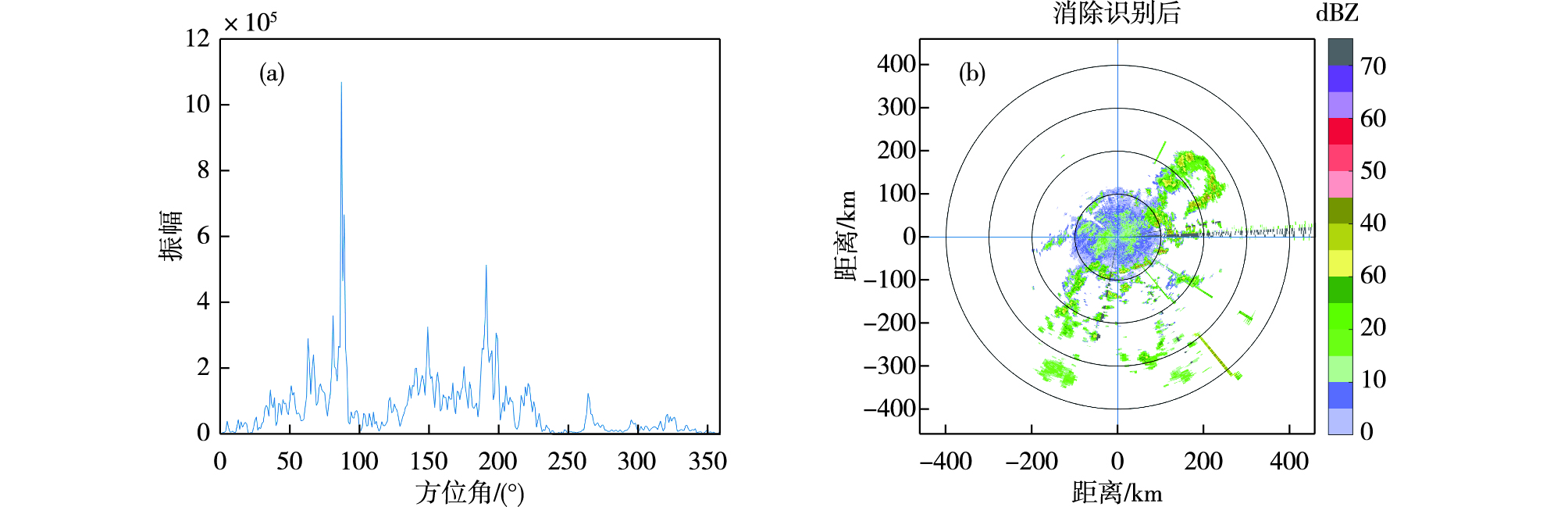
通过对2018年8月17日09:05临沂雷达回波分析,在85°方位方向有明显的频域能量大值区(图 5a),达1.1×106,这与雷达回波图(图 5b)中位于该方位角处较为零散但周期规律明显的干扰回波相一致,该处干扰回波(图 5b中灰色回波)被准确识别,但是其他两处在120°和150°附近相对均匀的干扰回波并没有很好地被识别出来。由此也可以看出,该方法还是侧重于周期规律性干扰回波,而对缺乏周期性规律的均匀和密集干扰回波识别能力较弱。
|
图 5 临沂雷达2018年8月17日09:05 0.5°仰角频谱能量分布(a)及杂波识别结果(b) Fig.5 Distribution (a) of energy spectrum at 0.5° elevation and clutter identification results (b) at 09:05 on 17 August 2018 from Linyi radar |
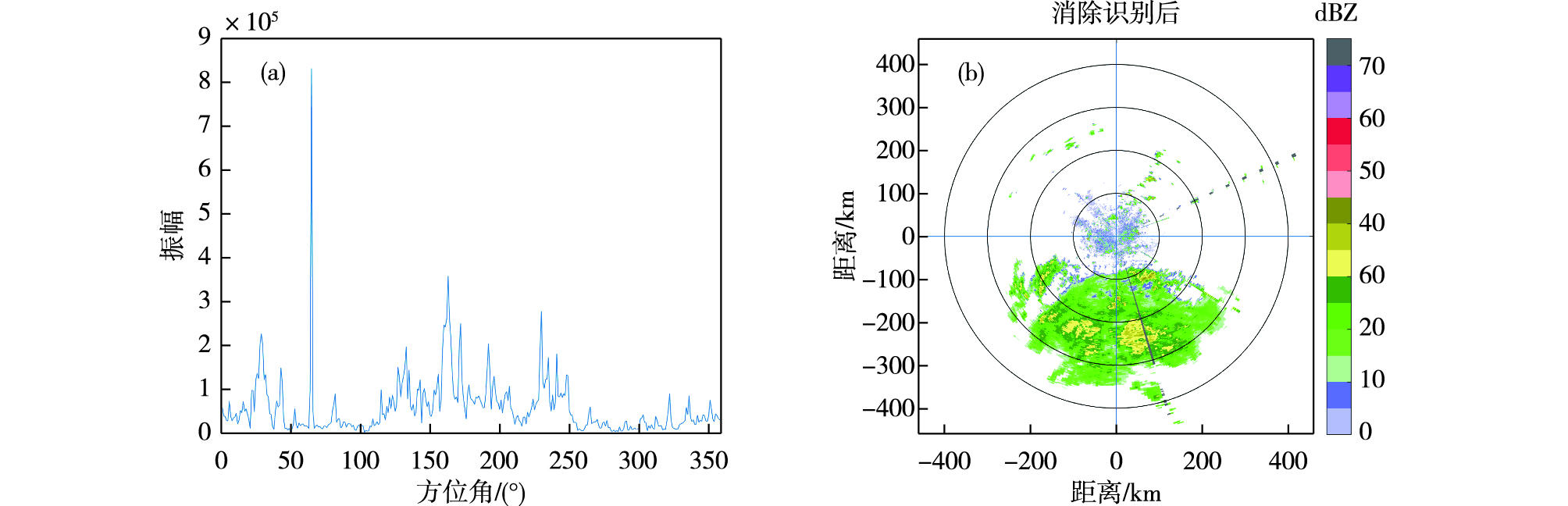
针对大范围降水中出现的干扰回波,该方法同样可以有效地进行识别和处理。2018年8月17日18:12临沂雷达干扰产生时,正处于雷达探测到大范围降雨阶段。由频域能量分析(图 6a),在65°左右方位范围内存在大值区,在雷达反射率因子回波图上同样存在间断性干扰回波,该干扰回波被准确识别出来(图 6b,灰色回波),但是在160°附近的降雨回波被错误地识别为干扰回波,这也表明该算法存在一定程度的过度识别问题。
|
图 6 临沂雷达2018年8月17日18:12频谱能量分布(a)及杂波识别结果(b) Fig.6 Distribution (a) of energy spectrum and clutter identification results (b) at 18:12 on 17 August 2018 from Linyi radar |
研究过程中,为进一步分析该算法的适用范围,还针对存在超折射残余的复杂的晴空回波情况下,研究了该杂波识别算法对杂波的识别问题,以研究该算法的适应能力。
2019年8月31日08:30前后,山东省大部分范围内以晴好天气为主,通过FY-4可见光云图可以较好地看到,除鲁东南部分区域有少量云覆盖外,其他区域基本以晴到少云天气为主(图 7)。这一阶段滨州多普勒天气雷达探测到的0.5°仰角上基本反射率回波以晴空回波为主,强度在10 dBZ以下;在滨州雷达的西北部则存在一些超折射残余回波(图 8),且部分区域反射率因子较强,达到40 dBZ以上,这些复杂回波的存在给雷达产品应用带来很多不便。

|
图 7 FY-4静止卫星2019年8月31日08:31的可见光云图 Fig.7 Visible cloud imagery of geostationary satellite FY-4 at 08:31 on 31 August 2019 |

|
图 8 滨州雷达2019年8月31日08:27—08:57 0.5°仰角反射率因子(a-f) Fig.8 Reflectivity factor at 0.5° elevation from 08:27 to 08:57 on 31 August 2019 from Binzhou radar (a-f) |
针对该时段0.5°仰角基本反射率因子,应用本方法进行分析研究。研究发现,在290°附近频域能量存在大值区(图 9),其中08:33能量出现最大值达2.5×106(图 9b);期间,最小值出现在08:57,但也达5.3×105(图 9f),且该时段该能量大值区域都比较集中。

|
图 9 滨州雷达2019年8月31日08:27—08:57 0.5°仰角各方位角频谱能量分布(a-f) Fig.9 Distribution of energy spectrum at 0.5° elevation at varied azimuths from 08:27 to 08:57 on 31 August 2019 from Binzhou radar (a-f) |
通过对最终识别结果(图 10)分析发现,该时段基本反射率因子中大部分超折射残余回波都已经有效识别,而且较好地保留了正常的晴空回波,取得了相对较好的效果。但是,也应该看到,在08:27,滨州北部个别回波还没有被很好地识别出来,存在一些不足。

|
图 10 滨州雷达2019年8月31日08:27—08:57 0.5°仰角干扰回波识别结果(a-f) Fig.10 Clutter identification results (a-f) at 0.5° elevation from 08:27 to 08:57 on 31 August 2019 from Binzhou radar (a-f) |
通过使用基于快速傅里叶变换的杂波识别方法,对包括局地降雨、大范围降雨和超折射残余回波三类实际天气过程个例进行分析,发现该算法可以在一定程度上较好地识别出弱径向干扰回波和部分超折射残余回波。但是,也可以看到该方法存在对连续性均匀密实的径向干扰回波识别能力弱的问题。
同时,当前该方法是采用对每个方位角上整个雷达径向数据一起处理的方式,因此识别时是以整个方位角数据作为一个整体处理和识别的。因此,本算法无法很好地区分径向上不同距离弱干扰回波存在较大差异时的回波识别问题,这些都在一定程度限制了方法的应用范围和效果。
4 结论与讨论本文针对多普勒天气雷达回波中径向干扰回波问题,提出了一种基于快速傅里叶变换的天气雷达弱径向杂波识别方法,并对局地降水、大范围降水和超折射残余回波三种典型环境下干扰回波进行了应用和分析研究。研究分析了该类干扰回波有别于常规天气回波的特征差异,使用快速傅里叶变换(FFT)的方法对雷达干扰回波径向数据进行变换,从而利用频域能量分布特征实现对该类回波的识别,研究表明:
1) 部分雷达径向干扰回波强度较弱且较为松散,常规识别算法较难识别,但具有与常规天气回波不同的径向周期性特征。
2) 通过对径向雷达基本反射率因子数据进行快速傅里叶变换,在得到的频域上雷达干扰回波在某些区域上具有明显的能量大值区,通过这些大值区可以有效地对径向干扰回波进行识别。
3) 该方法对局地性降水、大范围降水和超折射残余回波三类天气过程中存在的异常回波均有一定的识别能力。
4) 该方法存在一定的薄弱环节,对缺乏周期性特征,同时相对均匀和密实的径向干扰回波识别能力较弱。
从研究和业务实际来看,多普勒天气雷达杂波识别和消除既是一个理论发展的过程,也是一个与业务实践不断磨合的过程,本文提出的基于快速傅里叶变换的径向杂波识别方法仅是针对其中一类干扰回波的识别,还比较初步。并且,该方法存在对均匀密实径向干扰回波识别能力较弱,无法区分和识别单一方位角上不同径向距离干扰回波和天气回波共存的问题。同时,该方法与其他干扰回波识别算法类似,也存在过度抑制问题。尽管如此,该方法可以作为一个有效的雷达质控技术补充,给常规径向干扰回波质控方法提供差异性质控增强能力。今后,将进一步加强该类方法的研究和改进,以便更好地推进多普勒天气雷达数据质量控制方法研究和业务的开展。
| [1] |
刁秀广, 孟宪贵, 张立, 等. 台风"摩羯"与"温比亚"环流中龙卷小尺度涡旋特征及可预警性分析[J]. 海洋气象学报, 2019, 39(3): 19-28. |
| [2] |
龚佃利, 庞华基, 王俊, 等. 2006年4月28日山东强飑线过程中尺度结构和动力机制分析[J]. 海洋气象学报, 2019, 39(3): 64-73. |
| [3] |
万夫敬, 江敦双, 赵传湖. 2017年8月6日山东罕见雷暴大风成因分析[J]. 海洋气象学报, 2018, 38(2): 60-66. |
| [4] |
赵海军, 李柏, 潘玲, 等. 暴雨过程中逆风区特征及应用判据研究[J]. 海洋气象学报, 2019, 39(2): 126-133. |
| [5] |
郑怡, 杨晓霞, 孙晶. 台风"温比亚"(1818)造成山东极端强降水的成因分析[J]. 海洋气象学报, 2019, 39(1): 106-115. |
| [6] |
BERENGUER M, SEMPERE-TORRES D, CORRAL C, et al. A fuzzy logic technique for identifying nonprecipitating echoes in radar scans[J]. J Atmos Oceanic Technol, 2006, 23(9): 1157-1180. |
| [7] |
GRECU M, KRAJEWSKI W F. Detection of anomalous propagation echoes in weather radar data using neural networks[J]. IEEE Trans Geosci Remote Sens, 1999, 37(1): 287-296. |
| [8] |
文浩, 刘黎平, 张持岸, 等. 新一代天气雷达地物回波及电磁干扰质控算法业务试运行评估[J]. 气象科学, 2016, 36(6): 789-799. |
| [9] |
杜言霞, 陈斯智, 陈州川, 等. 天气雷达远距离单频点电磁径向干扰回波的特征分析及识别[J]. 气象研究与应用, 2017, 38(4): 65-68. |
| [10] |
黄勤, 龙亚星, 任芳. 陕西新一代天气雷达数据质量控制[J]. 陕西气象, 2016(1): 43-47. |
| [11] |
黄小玉, 彭洁, 毛紫阳, 等. 多普勒天气雷达有源干扰回波识别算法研究[J]. 气象, 2019, 45(3): 371-380. |
| [12] |
江源.天气雷达观测资料质量控制方法研究及其应用[D].北京: 中国气象科学研究院, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10300-1013340789.htm
|
| [13] |
周红根, 柴秀梅, 胡帆, 等. 新一代天气雷达回波异常情况分析[J]. 气象, 2008, 34(6): 112-115. |
| [14] |
步志超, 李柏, 邵楠, 等. CINRAD/SA天气雷达双PRF技术I/Q信号仿真及算法对比验证[J]. 北京理工大学学报, 2016, 36(12): 1289-1293. |
| [15] |
孙睿, 姚志刚, 韩志刚, 等. 一次暴雨激发平流层重力波的卫星观测与数值模拟[J]. 空间科学学报, 2018, 38(4): 469-481. |
| [16] |
梁驹, 梁骏, 雍阳阳. 广西极端降水事件气候态及其对ENSO的潜在响应[J]. 气候变化研究进展, 2017, 13(2): 117-127. |
| [17] |
沈斯敏, 朱首贤, 康彦彦, 等. 基于快速傅里叶变换方法遥感反演海浪波长和水深的仿真分析[J]. 华东师范大学学报(自然科学版), 2019(2): 184-194. |
 2019, Vol. 39
2019, Vol. 39

