2. 广西北部湾海洋灾害研究重点实验室,广西 钦州 535000
2. Guangxi Key Laboratory of Marine Disaster in the Beibu Gulf, Qinzhou 535000, China
台风是我国发生频率较高、影响较严重的一种自然灾害,登陆的台风不仅会带来狂风暴雨,还会造成泥石流及山体滑坡等次生灾害,特别是在我国的华南沿海地区,登陆的台风最为频繁,其造成的损失也更为严重[1]。如2015年的台风“彩虹”造成的华南地区直接经济损失达288.088 7亿元,以及2016年的台风“莎莉嘉”、2017年的台风“天鸽”和2018年的台风“山竹”都对华南地区造成了严重的危害。
在我国,已有许多专家及学者对登陆的台风进行形成机理、灾害评估等各方面的研究[2-5]。而针对华南地区的台风灾害研究,也有一些专家及学者通过模型的建立,来对华南台风进行分析。如刘合香和徐庆娟[6]利用模糊数学、灰色理论和信息扩散技术,构造中国华南地区热带气旋灾害风险评估模型和灾变年预测模型;谭金凯等[7]通过构造灾情指数与致灾源指数,建立基于模糊聚类下的灾害风险熵模型,结果表明,灾害风险熵与致灾因子、灾情具有较高的负相关性。
模糊时间序列模型是在模糊理论的基础上建立的预测模型,该模型成功应用于多个领域。如廖民生等[8]通过对三亚市历年的旅游总收入,建立模糊时间序列模型,进行历史数据模拟预测以及未知年预测,并与GM模型(灰色预测模型)进行对比。结果表明,模糊时间序列模型计算方便且预测误差率较小;王炎林等[9]基于改进的一种模糊时间序列模型,对全国的农用拖拉机总数量进行预测;华逸群和曹健[10]利用模糊时间序列对36条航线的最低机票价格数据进行预测,并利用绝对平均误差对实验结果进行评估,最后与AR模型(自回归模型)进行对比。结果表明,模糊时间序列模型可提高预测的准确率。但是利用模糊时间序列模型对台风风速进行预测,目前还没有相关学者涉及。台风风速极值受天气、测量仪器误差等客观因素影响,导致台风风速极值具有不确定性和模糊性,而模糊时间序列在处理数据的不确定性和模糊性方面具有明显优势。因此,本文尝试通过建立模糊时间序列模型,对登陆华南地区的台风登陆时最大风速极值进行预测试验,并与传统时间序列模型进行对比,探讨模糊时间序列在台风登陆时最大风速极值预测上的优势。
1 模糊时间序列模型的构建模糊时间序列最初是由SONG and CHISSOM[11-13]提出的,经过各个学者加以改进,成功应用于实践中[14-15],其建模过程主要包括以下4个步骤。
1.1 确定论域及划分子区间首先,根据时间序列数据具体数值确定论域,记为U=(Dmin, Dmax),其中Dmin,Dmax分别表示论域的下界和上界,这里可分别代指样本数据集的最小值和最大值。接着,将论域U划分为k个子区间,则论域也可表示为U=(u1, u2, …, uk)。最后,可通过聚类中心值来定义子区间的边界值,确定每个子区间的范围。
对于子区间的划分,常用层次分析法(AHP)、K均值算法(K-means)和模糊聚类算法(FCM)等通过聚类来进行划分。在这些方法中,FCM是目前应用最为广泛的一种聚类算法[16-18]。由于台风登陆时最大风速极值具有一定的模糊性,因此,本文利用FCM算法将论域划分为k个子区间,并且用FCM来确定聚类中心ci, 其中i表示聚为i类(i=1, 2, …, k)。
将子区间的边界值定义为di(i=1, 2, …, k),其计算过程如下:
| $ \left\{\begin{array}{l} {d_{1}=\left(c_{1}+c_{2}\right) / 2} \\ {\cdots} \\ {d_{j}=\left(c_{j}+c_{j+1}\right) / 2} \\ {\cdots} \\ {d_{k-1}=\left(c_{k-1}+c_{k}\right) / 2} \end{array}\right. $ | (1) |
由公式(1)可得到子区间为:u1=(Dmin, d1),u2=(d1, d2),...,uk=(dk-1, Dmax)。
1.2 建立模糊集合将样本数据记为xm(m=1, 2, …, n),通过隶属度函数,对其进行模糊化处理,得到其隶属度值,确定模糊集合Am。对于子区间u1, u2, …, uk,根据以下公式(2),计算其隶属度。
| $ \left\{\begin{array}{l} {u_{1 m}=\frac{d_{1}-D_{\min }}{\left|x_{m}-D_{\min }\right|+\left|d_{1}-x_{m}\right|}} \\ {\cdots} \\ {u_{j m}=\frac{d_{j}-d_{j-1}}{\left|x_{m}-d_{j-1}\right|+\left|d_{j}-x_{m}\right|}} \\ {\cdots} \\ {u_{k m}=\frac{D_{\max }-d_{k-1}}{\left|x_{m}-d_{k-1}\right|+\left|D_{\max }-x_{m}\right|}} \end{array}\right. $ | (2) |
则模糊集合Am可定义为:
| $ A_{m}=\frac{u_{1 m}}{u_{1}}+\frac{u_{2 m}}{u_{2}}+\dots+\frac{u_{k m}}{u_{k}} $ | (3) |
利用前t-1个的数据作为训练集,对第t个数据进行预测,将第t-1个的数据模糊化成一个标准矩阵,记为:
| $ \boldsymbol{F}_{t}=\boldsymbol{f}_{t-1}=\left[\begin{array}{llll} {u_{1 t-1}} & {u_{2 t-1}} & {\cdots} & {u_{k t-1}} \end{array}\right] $ | (4) |
其中,0≤uit-1≤1。
再将前t-2个的数据模糊化成一个计算矩阵,记为:
| $ \boldsymbol{B}_{t}^{t-2}=\left[\begin{array}{c} {f_{1}} \\ {\vdots} \\ {f_{t-2}} \end{array}\right] $ | (5) |
定义模糊关系矩阵为Rt,具体表达式如下:
| $ \boldsymbol{R}_{t}=\boldsymbol{F}_{t} \cdot \boldsymbol{B}_{t}^{t-2}=\left[\begin{array}{ccc} {r_{11}} & {\cdots} & {r_{1 k}} \\ {\vdots} & {\ddots} & {\vdots} \\ {r_{t-21}} & {\cdots} & {r_{t-2 k}} \end{array}\right] $ | (6) |
这里的Rt定义了时间序列的模糊关系,通过公式(6)的运算方法将模糊关系合成,从而可计算得到第t个预测的变化值ft,其计算过程为:
| $ \begin{array}{l} {f_t} = \left[ {\max \left( {{r_{11}}, {r_{21}}, {r_{t - 11}}} \right)} \right.\left. { \cdots \quad \max \left( {{r_{1k}}, {r_{2k}}, {r_{t - 1k}}} \right)} \right] = \\ \left[ {{f_{t1}}\quad {f_{t2}}} \right.\quad\left. { \cdots \quad {f_{tk}}} \right] \end{array} $ | (7) |
对求出的预测变化值ft,采用重心法实现去模糊化:
| $ {f_t} = \frac{{\sum\limits_{i = 1}^k {{c_i}} {f_{ti}}}}{{\sum\limits_{i = 1}^k {{f_{ti}}} }} $ | (8) |
其中,ci表示聚类中心,fti表示隶属度。
最后,根据公式(9)求得第t个的预测值G(t);
| $ G(t)=g(t-1)-f_{t} $ | (9) |
其中,g(t-1)表示第t-1数据的观测值。
2 实例应用 2.1 数据来源选取了1995—2017年登陆华南地区的33个台风样本,对登陆时最大风速极值进行预测,数据来源于中国热带气旋年鉴(1995—2014年)[19]和中国天气台风网(2015—2017年,网址:http://typhoon.weather.com.cn)。
2.2 数据预处理将33个台风样本的登陆时最大风速极值记为序列集,记为X=(x1, x2, …, x33)。首先做出登陆时最大风速极值时序图,如图 1a所示。

|
图 1 原始数据的平稳化处理(a.原始数据时序图,b.原始数据一阶差分处理后的时序图) Fig.1 Smoothing of raw data (a. sequence diagram of raw data, b. sequence diagram after first order differential processing of raw data) |
由图 1a可以看出,这33个台风样本登陆时最大风速极值呈现出上升的趋势,且图像波动幅度较大,即原始序列很可能为非平稳序列,对该序列进行平稳性检验,其P值(即显著性概率)为0.433,大于0.05。则说明在0.05的显著水平下,不能拒绝原假设,即认为该序列为非平稳序列。通过原始序列进行一阶差分处理以消除趋势性,图 1b为经一阶差分处理后的新序列,由图可知,图像波动幅度比较平缓,通过对其进行平稳性检验,其P值为0.013,小于0.05。说明在0.05的显著水平下,不能接受原假设,即认为一阶差分后序列为平稳序列;接着对一阶差分后序列进行白噪声检验,其P值为0.014,小于0.05。说明在0.05的显著水平下,不能接受原假设,即一阶差分后序列为平稳非白噪声序列。
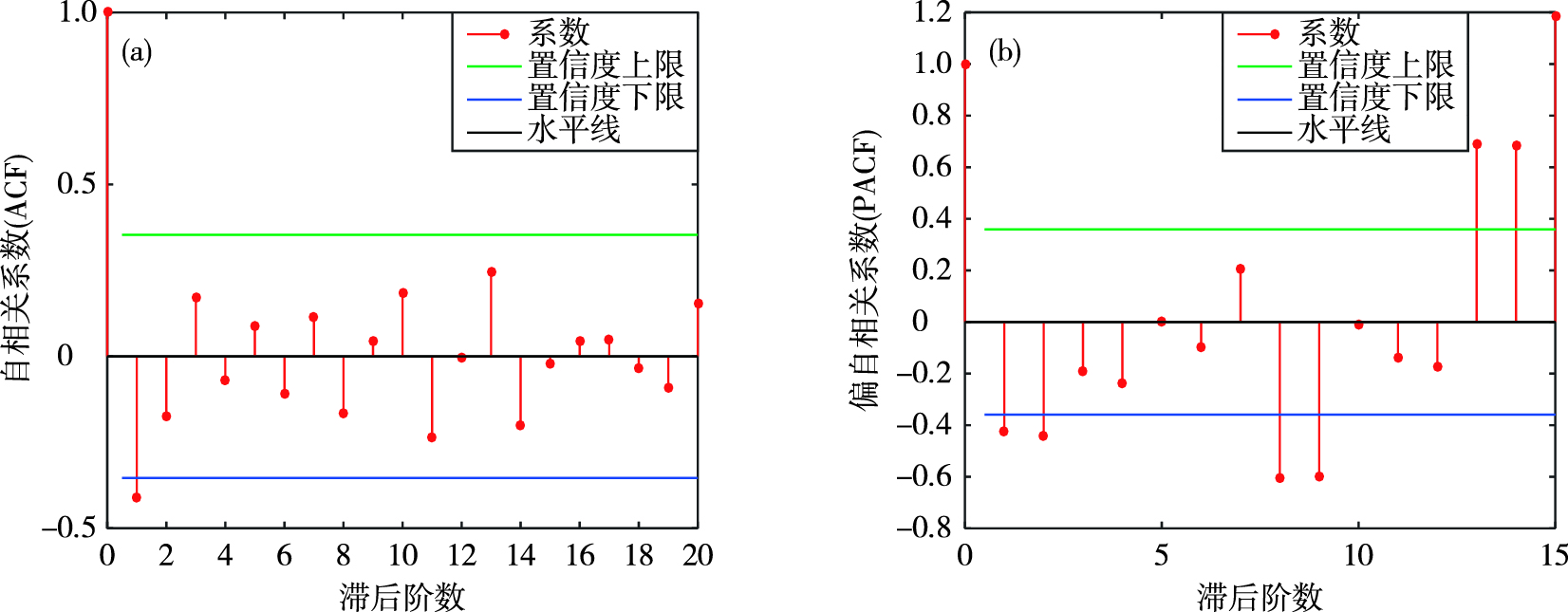
2.3 平稳非白噪声序列的传统时间序列建模与预测ARIMA模型(自回归差分移动平均模型),是传统时间序列模型的一种[20]。在ARIMA(p, d, q)模型中,AR代表自回归,I代表差分,MA代表移动平均,p为自回归项数,q为移动平均项数,d为使原序列成为平稳序列所做的差分阶数。本文利用台风登陆时最大风速极值数据,构建传统时间序列ARIMA模型进行训练。根据ARIMA的建模步骤,接下来对模型进行定阶。首先计算台风样本登陆时最大风速极值的自相关系数(ACF)和偏自相关系数(PACF),具体如图 2所示。
|
图 2 台风登陆时最大风速极值的自相关系数(a)与偏自相关系数(b) Fig.2 Autocorrelation coefficients (a) and partial autocorrelation coefficients (b) of extreme values of the maximum wind speed when typhoon makes landfall |
根据p取落入置信区间外的自相关系数的个数或与0有显著差异的自相关系数,q取落入置信区间之外的偏自相关系数的个数或与0有显著差异的偏自相关系数的原则,对p和q进行取值。由图 2a可以看出,在滞后期K=1的自相关系数超过置信区间,其值为-0.385,则表明在K=1后截尾;在图 2b中,滞后期K=1和K=2的偏自相关系数与0存在显著差异,分别为-0.426和-0.442,而其他并没有明显趋向于0,可认为在K=2后拖尾。因此,在这里选取p=2和q=3。并且根据图 1b可知,登陆时最大风速极值序列在一阶差分后趋于平稳,所以可定为ARIMA(2, 1, 3)模型。
选取1995—2015年28个台风样本的登陆时最大风速极值作为训练集,利用ARIMA(2, 1, 3)模型进行训练,将训练好的模型对2016—2017年5个台风的登陆时最大风速极值进行预测,得到5个台风测试样本的登陆时最大风速极值的预测值,并使用绝对误差、相对误差以及RMSE(均方根误差)来评估模型的预测效果,其结果见表 1。
|
|
表 1 台风登陆时最大风速极值的传统时间序列预测结果与误差值 Table 1 Prediction results and error values of extreme values of the maximum wind speed when typhoon makes landfall based on traditional time series |
从表 1中可以发现,在前4个台风样本预测值与观测值的比较中,预测值较为接近观测值,但在第5个台风样本的预测中,预测值与观测值差距较大,说明传统时间序列对于异常点的预测效果较差。并且由表 1可知,RMSE值为6.358 m·s-1,反映了登陆时最大风速极值的预测值偏离其观测值的程度较大,同时也表明用传统时间序列模型预测登陆时最大风速极值存有较大误差。
2.4 平稳化序列的模糊时间序列建模与预测首先,同样选取1995—2015年28个台风样本作为训练集,对其进行差分,得到平稳化序列,将平稳化序列记为ym,m=1, 2, …, 27。然后,确定论域的上下界,为Dmin(ym)=-28和Dmax(ym)=25,因此论域范围可记为U=(-28, 25)。最后,采用FCM算法计算,并设定聚类数k=5,得到5个聚类中心分别为-28,-10.50,0.35,14.75,25。再根据公式(1)计算边界值,求得结果为(d1, d2, d3, d4)=(-19.25, -5.075, 7.55, 19.875)。因此,论域可由5个子空间构成,表示为U=(u1, u2, u3, u4, u5),5个子空间也可分别记为u1=(-28, -19.25),u2=(-19.25, -5.075),u3=(-5.075, 7.55),u4=(7.55, 19.875)和u5=(19.875, 25)。
使用隶属度的计算方法计算各样本点对各模糊集的隶属度,从而将时间序列数据模糊化为论域上的模糊时间序列数据,根据公式(2)和公式(3)求得以下结果:
| $ \begin{aligned} &A_{1}=\frac{0.082}{u_{1}}+\frac{0.168}{u_{2}}+\frac{0.220}{u_{3}}+\frac{0.139}{u_{4}}+\frac{0.339}{u_{5}}, \\ &A_{2}=\frac{0.077}{u_{1}}+\frac{0.157}{u_{2}}+\frac{0.200}{u_{3}}+\frac{0.130}{u_{4}}+\frac{0.243}{u_{5}}, \\ &A_{28}=\frac{0.059}{u_{1}}+\frac{0.114}{u_{2}}+\frac{0.130}{u_{3}}+\frac{0.096}{u_{4}}+\frac{0.093}{u_{5}}。\end{aligned} $ |
再利用登陆华南地区的1311号至1522号台风的6个登陆时最大风速极值来预测第7个台风(1604号)登陆时最大风速极值。首先,选取这6个台风样本中的前5个模糊数据作计算矩阵,把第6个1117号台风的模糊数据作为计算向量;再利用公式(4)、公式(5)和公式(6)进行计算;最后,可求得第7个台风,即1604号台风的登陆时最大风速极值模糊化数据。
其中,求得计算矩阵为:
| $ \boldsymbol{B}_{7}^{5}=\left[\begin{array}{ccccc} {0.067} & {0.131} & {0.155} & {0.109} & {0.131} \\ {0.064} & {0.124} & {0.145} & {0.104} & {0.114} \\ {0.047} & {0.086} & {0.092} & {0.073} & {0.054} \\ {0.067} & {0.131} & {0.155} & {0.109} & {0.131} \\ {0.075} & {0.150} & {0.188} & {0.125} & {0.204} \end{array}\right] $ |
计算向量为:
| $ \boldsymbol{F}_{7}=\boldsymbol{f}_{6}=\left[\begin{array}{lllll} {0.059} & {0.114} & {0.130} & {0.096} & {0.093} \end{array}\right] $ |
其计算的模糊矩阵R7为:
| $ \boldsymbol{R}_{7}=\boldsymbol{F}_{7} \cdot \boldsymbol{B}_{7}^{5}= \\ \left[\begin{array}{ccccc}{0.004} & {0.015} & {0.020} & {0.011} & {0.012} \\ {0.004} & {0.014} & {0.019} & {0.010} & {0.011} \\ {0.003} & {0.010} & {0.012} & {0.007} & {0.005} \\ {0.004} & {0.015} & {0.020} & {0.011} & {0.012} \\ {0.004} & {0.017} & {0.024} & {0.012} & {0.019}\end{array}\right] $ |
再根据公式(7)可计算得:
| $ \boldsymbol{f}_{7}=\left[\begin{array}{llllll} {0.004} & {0.017} & {0.024} & {0.012} & {0.019} \end{array}\right] $ |
最后根据公式(8)和公式(9)可求出1604号台风登陆时最大风速极值的预测值为45.4 m·s-1,而该台风实际登陆时最大风速极值为42.0 m·s-1,预测值与观测值间误差不大,其预测的相对误差为0.080,预测的精确度较高。
同理可求出2016—2017年登陆华南地区的5个台风登陆时最大风速极值的预测值,并用绝对误差,相对误差以及RMSE(均方根误差)来评估模型的预测效果,其计算结果见表 2。
|
|
表 2 台风登陆时最大风速极值的模糊时间序列预测结果与误差值 Table 2 The same as Table 1, but for fuzzy time series |
由表 2可知,5个台风个例登陆时最大风速极值的模糊时间序列预测值与其观测值结果较为接近,特别是在预测1714号台风登陆时最大风速极值中,其预测值比传统时间序列的预测值更接近观测值,能够较好地反映未来的变化趋势。通过计算可知,登陆时最大风速极值的预测值与观测值的平均相对误差为0.066,表明建立的模糊时间序列模型对台风登陆时最大风速极值的预测精度较高。又由表 2知,其RMSE的计算结果为2.727 m·s-1,反映了登陆时最大风速极值的预测值偏离其观测值的程度较小。对比表 1与表 2,模糊时间序列对登陆时最大风速极值预测的平均绝对误差、平均相对误差和均方根误差都低于传统时间序列,表明模糊时间序列模型在对台风登陆时最大风速极值的预测精度上要优于传统时间序列模型。
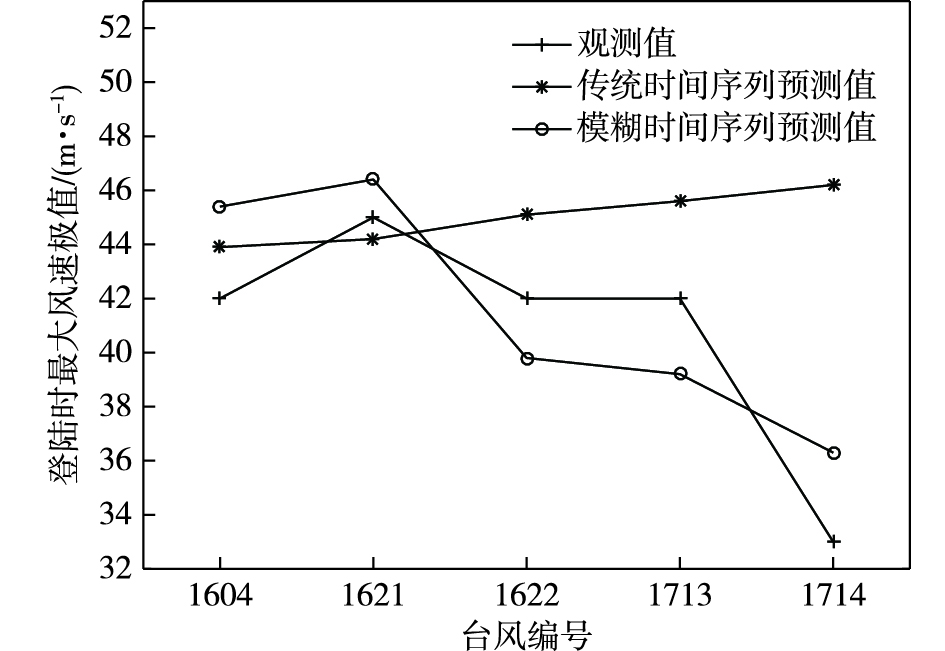
为了更好反映模糊时间序列模型对华南台风登陆时最大风速极值的预测效果,绘制了其预测值与观测值的趋势图,如图 3所示。由图 3可知,通过登陆时最大风速极值的预测值与观测值比较可看出,模糊时间序列预测值与观测值的趋势大致一致,而传统时间序列的预测值呈不明显的直线上升趋势,与登陆时最大风速极值的实际观测值曲线相比,无法反映出其变化趋势,并结合表 1和表 2中不同评判标准的预测精度情况,可得模糊时间序列预测模型优于传统时间序列预测模型。因此,在对华南台风的登陆时最大风速极值预测上,模糊时间序列模型比传统时间序列模型表现出更好的性能。
|
图 3 台风登陆时最大风速极值的预测值与观测值趋势图 Fig.3 Tendency chart of predicted and observed extreme values of the maximum wind speed when typhoon makes landfall |
本文依据模糊时间序列理论,利用华南台风登陆时最大风速极值数据,建立模糊时间序列模型,对台风登陆时最大风速极值进行预测,并与传统时间序列模型作对比。通过模型建立及应用,得到以下结论,并针对该模型作出讨论。
1) 在模糊时间序列的理论基础上建立模糊时间序列模型,预测台风登陆时最大风速极值,经过实证分析与检验,可取得较好的预测结果。与传统时间序列模型对比,发现模糊时间序列预测的平均绝对误差、平均相对误差和均方根误差值都小于传统时间序列,计算值分别为2.621 m·s-1、0.066和2.727 m·s-1,表明模糊时间序列模型对台风登陆时最大风速极值的预测精度优于传统时间序列。
2) 影响台风风速的因素诸多,比如气候、地域环境等因素,这些因素也具有不确定性以及模糊性。因此,应用模糊时间序列理论对登陆华南台风登陆时最大风速极值进行预测,更具有客观性及科学性。但模糊时间序列模型也具有一定的局限性,该模型只能做中短期的预测,无法进行长期预测。
3) 本文对于子区间的划分,采用的是FCM算法。其他一些机器学习算法,如人工神经网络及遗传算法等方法,也可用来划分模型区间。以后,还可以将建立的模糊时间序列模型应用于台风灾害的其他致灾因子以及灾情因子的分析,进一步加强对台风灾害的研究。
| [1] |
廖永丰, 赵飞, 王志强, 等. 2000—2011年中国自然灾害灾情空间分布格局分析[J]. 灾害学, 2013, 28(4): 55-60. DOI:10.3969/j.issn.1000-811X.2013.04.011 |
| [2] |
张守峰, 钱奇峰. 台湾岛对登陆台风的影响特征[J]. 海洋气象学报, 2018, 38(2): 45-49. |
| [3] |
肖辉, 万齐林, 刘显通, 等. 台风"妮妲"(1604)登陆期间近地层风特性分析[J]. 海洋气象学报, 2017, 37(2): 42-50. |
| [4] |
刘少军, 张京红, 何政伟, 等. 改进的物元可拓模型在台风灾害预评估中的应用[J]. 自然灾害学报, 2012, 21(2): 135-141. |
| [5] |
张悦, 李珊珊, 陈灏, 等. 广东省台风灾害风险综合评估[J]. 热带气象学报, 2017, 33(2): 281-288. |
| [6] |
刘合香, 徐庆娟. 基于r维正态扩散的区域热带气旋灾害模糊风险分析[J]. 数学的实践与认识, 2011, 41(3): 150-159. |
| [7] |
谭金凯, 刘合香, 倪增华, 等. 台风致洪灾害的广义模糊熵模型研究[J]. 模糊系统与数学, 2016, 30(1): 182-190. |
| [8] |
廖民生, 张鲲, 王鸿绪, 等. 基于模糊时间序列模型预测三亚旅游总收入[J]. 经济研究导刊, 2015(4): 237-242. DOI:10.3969/j.issn.1673-291X.2015.04.107 |
| [9] |
王炎林, 陈建, 王卓, 等. 基于模糊时间序列的农用拖拉机总数量预测[J]. 农机化研究, 2019, 41(4): 251-256. DOI:10.3969/j.issn.1003-188X.2019.04.048 |
| [10] |
华逸群, 曹健. 机票价格预测的模糊时间序列方法[J]. 小型微型计算机系统, 2016, 37(11): 2547-2551. DOI:10.3969/j.issn.1000-1220.2016.11.031 |
| [11] |
SONG Q, CHISSOM B S. Forecasting enrollments with fuzzy time series: Part Ⅰ[J]. Fuzzy Set Syst, 1993, 54(1): 1-9. DOI:10.1016/0165-0114(93)90355-L |
| [12] |
SONG Q, CHISSOM B S. Fuzzy time series and its models[J]. Fuzzy Set Syst, 1993, 54(3): 269-277. DOI:10.1016/0165-0114(93)90372-O |
| [13] |
SONG Q, CHISSOM B S. Forecasting enrollments with fuzzy time series: Part Ⅱ[J]. Fuzzy Set Syst, 1994, 62(1): 1-8. DOI:10.1016/0165-0114(94)90067-1 |
| [14] |
胡世前, 姜倩雯, 王博. 模糊时间序列在中国汽车产业规划中的应用[J]. 东北财经大学学报, 2017(5): 40-45. DOI:10.3969/j.issn.1008-4096.2017.05.006 |
| [15] |
李博群, 贾政权, 刘利平. 基于模糊时间序列的空气质量指数预测[J]. 华北理工大学学报(自然科学版), 2018, 40(3): 78-86. DOI:10.3969/j.issn.2095-2716.2018.03.013 |
| [16] |
余文利, 方建文, 廖建平. 一种新的基于模糊C均值算法的模糊时间序列确定性预测模型[J]. 计算机工程与科学, 2010, 32(7): 112-116. DOI:10.3969/j.issn.1007-130X.2010.07.031 |
| [17] |
朱林, 王士同, 邓赵红. 改进模糊划分的FCM聚类算法的一般化研究[J]. 计算机研究与发展, 2009, 46(5): 814-822. |
| [18] |
宫改云, 高新波, 伍忠东. FCM聚类算法中模糊加权指数m的优选方法[J]. 模糊系统与数学, 2005, 19(1): 143-148. DOI:10.3969/j.issn.1001-7402.2005.01.025 |
| [19] |
中国气象局. 热带气旋年鉴1995—2014年[M]. 北京: 气象出版社, 1996.
|
| [20] |
何书元. 应用时间序列分析[M]. 北京: 北京大学出版社, 2003.
|
 2019, Vol. 39
2019, Vol. 39


