2. 山东省气象台,山东 济南 250031
2. Shandong Meteorological Observatory, Jinan 250031, China
青藏高原(the Tibetan Plateau, TP)是中国最大、世界海拔最高的高原,被称为“世界屋脊”和“第三极”,其平均海拔在4 000 m以上,为东亚、东南亚和南亚许多大河流的发源地[1-3]。在全球变化的大背景下,青藏高原不仅是最为敏感的区域之一,其同时也可以对全球气候变化产生重要影响,成为气候变化的启张器和调节器。该区域的气候变化不仅可以直接驱动中国东部和西南部地区气候的变化,而且对北半球具有巨大的影响,甚至对全球的气候变化也具有明显的敏感性、超前性和调节性[4-6]。尤其是占全年降水量60%~70%的青藏高原区域夏季降水[7],会影响该区域的热力状况以及全球水循环,这会直接影响到亚洲夏季风系统的强弱,进而对东亚和南亚地区的夏季降水变化产生影响。因此对青藏高原区域夏季降水时空变化的研究具有重要意义。
由于青藏高原区域复杂的地理条件,对该区域降水的准确观测十分困难,气候模式成为研究青藏高原气候变化的重要工具之一[8-10],因此需要准确评估气候模式对该区域降水的模拟能力,这对模式模拟的误差归因以及进一步的模式改进工作具有重要意义。目前我国学者在评估气候模式对降水的模拟效果时,研究区域大多集中在东亚或者整个中国[11-14],而对青藏高原区域降水时空变化模拟效果的评估较少,仅有部分学者评估耦合模式对青藏高原东南部降水[15-17]或将90°E以东的青藏高原东部降水作为一个整体[18]的模拟效果,或在耦合模式对全球降水的评估中仅少量提及对青藏高原区域降水的模拟效果[13, 19-21]。结果[22]表明,由于模式分辨率的限制以及物理参数化方案的不准确等原因,目前数值模式对该区域的降水模拟存在很大的偏差。
值得注意的是,青藏高原东北部和东南部夏季降水大致以唐古拉山脉(35°N)为界,表现为东北部和东南部降水存在反位相的双极型变化关系[23],而这种反位相的时空差异也体现在青藏高原区域夏季降水经验正交函数(empirical orthogonal function, EOF)分解的前两个主模态,可以明显反映出青藏高原中东部夏季降水的局地变化特征[24]。并且,这种反位相的变化关系十分稳定,是年际尺度上青藏高原夏季降水的主要模态,即偶极振荡的跷跷板结构[25-26]。从物理机制上来看,在耦合的气候系统模式中,青藏高原中东部夏季降水的双极型特征与春季北大西洋地区三极型海温具有很好的相关性,北大西洋地区的海温异常通过激发定常波传播E-P(Eliassen-Palm)通量对下游青藏高原地区的夏季降水产生影响[27]。因此对青藏高原区域降水的评估工作需要综合考虑该区域降水的南北差异,而青藏高原单一子区域的降水评估工作或全区统一的评估工作无法全面展示模式对该区域降水的综合模拟效果。另外,目前对青藏高原中东部夏季降水双极型模拟效果的模式评估工作尚属空白。
基于此,本文综合评估47个参与第五次耦合模式比较计划(Coupled Model Intercomparison Project Phase 5,CMIP5)的耦合模式对青藏高原中东部夏季降水双极型的模拟效果,评估工作主要针对EOF分解的前两个主模态。首先对用于评估的耦合模式以及观测数据进行简要说明,并对评估方法进行简要介绍,然后给出47个CMIP5模式的主要评估结果,最后对评估结果进行总结和讨论。
1 数据和方法 1.1 数据降水观测数据来自于“中国国家级地面气象站基本气象要素日值数据集”,该套数据集包含了国家基本气象站、国家基准气候站、一般气象站在内的主要2 474个站点1951年1月以来地面基本气象要素逐日观测数据。从2 474个站点中选取青藏高原区域海拔高度在1 500 m以上,且1961—2005年记录连续的130个国家标准气象站的夏季(6—8月)站点观测值,剔除明显异常值且将逐日数据转化为逐月数据。由于青藏高原西部的站点观测稀少,因此本文的评估工作集中在88°E以东的青藏高原中东部地区。用于比较的数据来自于提交CMIP5历史模拟试验的47个耦合模式1961—2005年的模拟结果,模式结果来自于http://www.ipcc-data.org/sim/gcm_monthly/AR5/Reference-Archive.html,评估时选取这些模式所有集合成员平均的结果。47个模式的基本信息如表 1所示。由于这47个模式的水平分辨率不同,为了便于评估,将47个模式的模拟结果统一插值到1°×1°分辨率的网格上。并且,由于青藏高原中东部夏季降水的双极型特征与春季北大西洋地区三极型海温具有很好的相关性,模式对北大西洋地区三极型海温的模拟效果越好,则该模式对青藏高原中东部夏季降水双极型特征的模拟效果也越好。因此,本文在表 1的第四列中给出了CMIP5各模式与HadISST分析资料[28]中北大西洋三极型海温的相关系数。
|
|
表 1 用于评估的47个CMIP5模式的基本信息 Table 1 Basic information of 47 CMIP5 models used for evaluation |
由于本文研究的青藏高原东南部和东北部的夏季降水为EOF分解的结果,站点观测中EOF分解第一模态(EOF1)的方差贡献为23.49%,第二模态(EOF2)的方差贡献为14.01%,而第三模态(EOF3)的方差贡献仅为8.95%且并不表现为双极型分布型态,因此主要关注分解后前两个主模态的空间型态、时间系数以及方差贡献这三个方面,并采用多种指标来评估模式的模拟效果。TAYLOR[29]在2001年提出了一种基于相关系数和标准差进行评估的综合指标S评分,其定义形式为:
| $ S \equiv \frac{{{{\left( {1 + R} \right)}^4}}}{{4{{\left( {SDR + 1/SDR} \right)}^2}}} $ | (1) |
式(1)中R表示模式和观测的相关系数,SDR表示模式与观测的标准差的比值[30]。该综合指标S评分的范围在0~1之间,并且数值越接近于1,说明模式的模拟效果越好。
对于EOF1和EOF2的空间型态而言,
| $ {S_{{\rm{sp}}}} = \frac{{{{\left( {1 + {R_{{\rm{sp}}}}} \right)}^4}}}{{4{{\left( {SD{R_{{\rm{sp}}}} + 1/SD{R_{{\rm{sp}}}}} \right)}^2}}} $ | (2) |
式(2)中Ssp表示空间型态的综合指标S评分,Rsp表示模式与观测的空间相关系数,SDRsp表示模式与观测的空间标准差的比值。Ssp数值越接近于1,说明该模式对空间型态的综合模拟效果越好。
同理,对于EOF1和EOF2的时间系数而言,
| $ {S_{{\rm{ts}}}} = \frac{{{{\left( {1 + {R_{{\rm{ts}}}}} \right)}^4}}}{{4{{\left( {SD{R_{{\rm{ts}}}} + 1/SD{R_{{\rm{ts}}}}} \right)}^2}}} $ | (3) |
式(3)中Sts表示时间系数的综合指标S评分,Rts表示模式与观测的时间相关系数,SDRts表示模式与观测的时间标准差的比值。Sts数值越接近于1,说明该模式对时间系数的综合模拟效果越好。而对于EOF1和EOF2的方差贡献而言,模式的方差贡献Dmod与观测的方差贡献Dobs的差值的绝对值越小,表示该模式对方差贡献的模拟效果越好。
在综合指标Ssp和Sts评分的基础上定义了一个新的指标Snew来进一步定量评估47个CMIP5模式对空间型态、时间系数和方差贡献的综合模拟能力,其具体定义形式为:
| $ {S_{{\rm{new}}}} = \sqrt {{{\left( {1 - {S_{{\rm{sp}}}}} \right)}^2} + {{\left( {1 - {S_{{\rm{ts}}}}} \right)}^2} + {{\left( {1 - \frac{{{D_{{\rm{mod}}}}}}{{{D_{{\rm{obs}}}}}}} \right)}^2}} $ | (4) |
在该定义下,式(4)结果越接近于0,表示该模式对空间型态、时间系数和方差贡献的综合模拟效果越好。
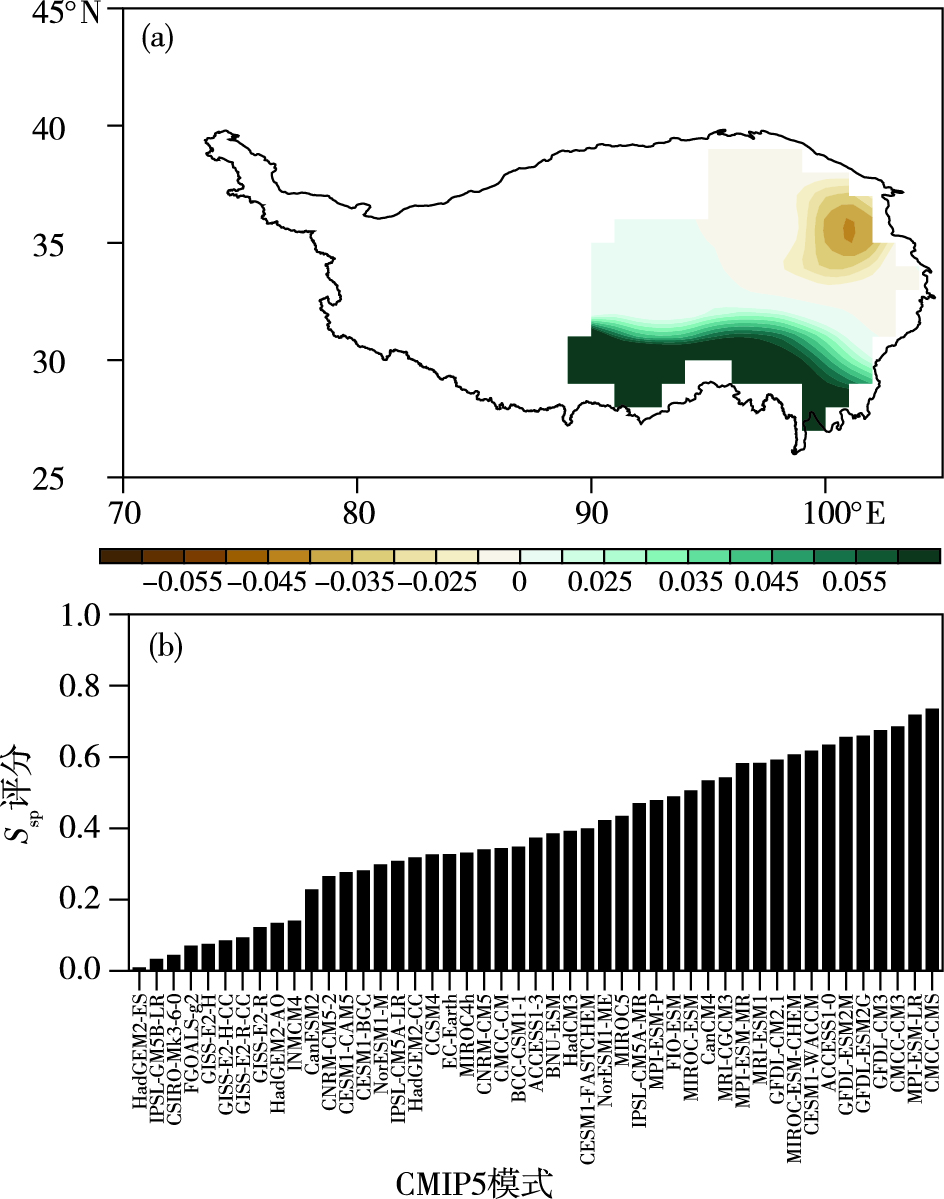
2 结果 2.1 EOF1降水“北少南多”时空特征的模拟效果图 1给出了观测的1961—2005年青藏高原中东部夏季降水EOF1的空间型态以及47个CMIP5模式EOF1的综合指标Ssp评分。观测主要表现为大致以35°N为界的东北部和东南部降水反位相的变化特征(图 1a)。大多数模式可以分解出这种反位相的空间分布型态,尤其是对青藏高原东南部夏季降水的模拟效果优于东北部。47个CMIP5模式EOF1的空间相关系数在0.162~0.850之间,其中空间相关系数最大的是CMCC-CMS模式,最低的是HadGEM2-ES模式,大约有70%(32/47)的CMIP5模式EOF1的空间相关系数高于0.3。由综合指标Ssp评分(图 1b)来看,得到的Ssp评分的排名情况与空间相关系数基本一致,CMCC-CMS和MPI-ESM-LR模式对EOF1空间型态的综合模拟效果较好,HadGEM2-ES和IPSL-CM5B-LR模式对EOF1空间型态的综合模拟效果较差。
|
图 1 1961—2005年青藏高原中东部站点观测夏季降水的EOF1空间型态(a;色阶表示EOF分解得到的特征向量值,下同)以及47个CMIP5模式EOF1空间型态的综合指标Ssp评分(b) Fig.1 Spatial pattern of EOF1 mode of summer precipitation observation at stations over the central and eastern TP from 1961 to 2005 (a; the color scale represents the eigenvector using the EOF technique, the same hereafter) and corresponding Ssp with 47 CMIP5 models (b) |
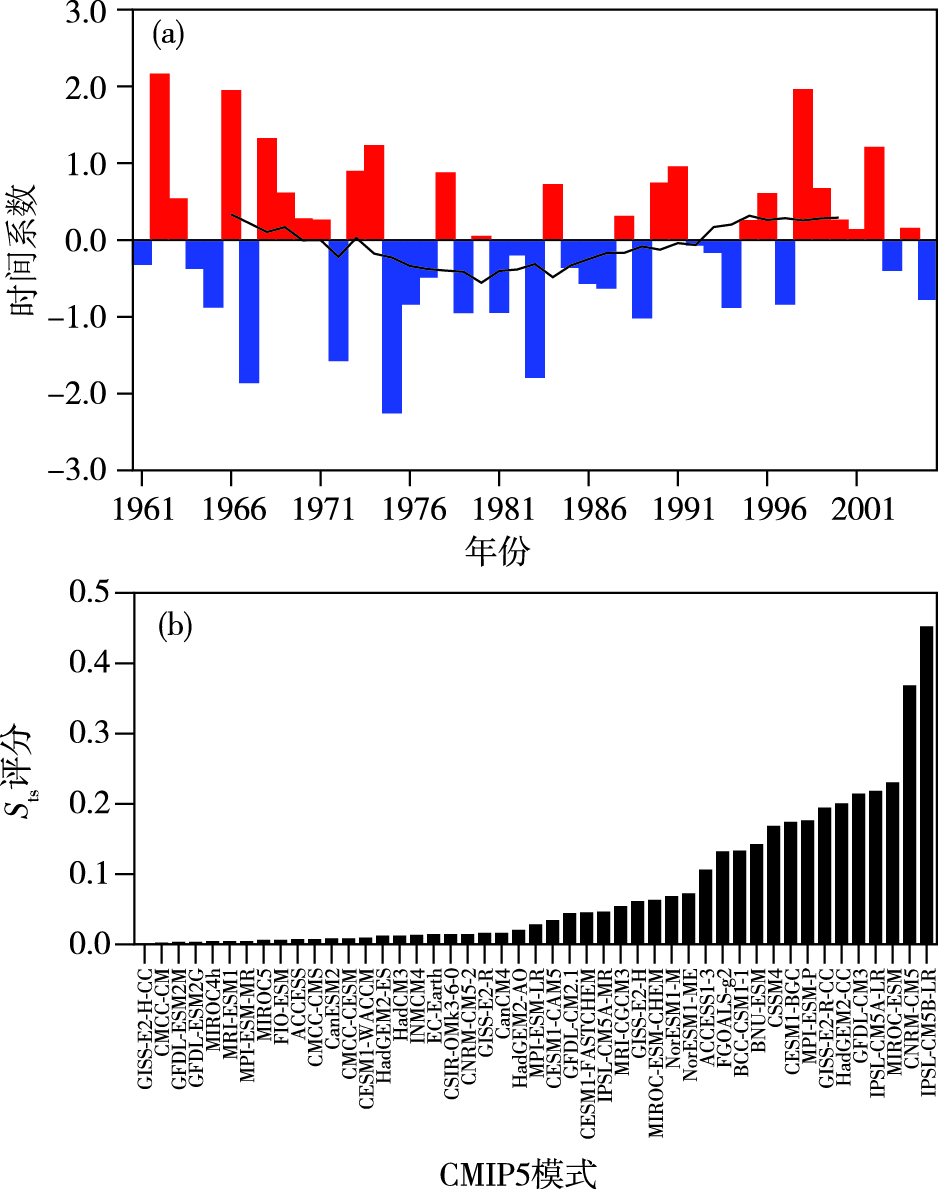
由EOF1的时间系数(图 2)来看,观测主要表现为20世纪70年代初期的下降趋势以及20世纪90年代初期的上升趋势(图 2a)。但是,大多数模式无法表现出这种明显的年代际转折的变化趋势,47个CMIP5模式与观测时间系数的相关系数在-0.691(GISS-E2-H-CC)~0.719(CNRM-CM5)之间,只有28%(13/47)的CMIP5模式EOF1时间系数的相关系数通过了95%的信度检验,接近64%(30/47)的CMIP5模式时间序列的相关系数为负值。由相应的综合指标Sts评分(图 2b)来看,IPSL-CM5B-LR模式对EOF1时间系数的综合模拟效果最好,但是其对EOF1空间型态的综合模拟效果却较差,而GISS-E2-H-CC和CMCC-CM模式对EOF1的时间系数几乎没有模拟技巧。
|
图 2 1961—2005年青藏高原中东部站点观测夏季降水的EOF1时间系数(a,黑线表示11 a滑动平均)以及47个CMIP5模式EOF1时间系数的综合指标Sts评分(b) Fig.2 Time coefficients of EOF1 mode of summer precipitation observation at stations over the central and eastern TP from 1961 to 2005 (a, the black line represents 11-year running average) and corresponding Sts with 47 CMIP5 models (b) |
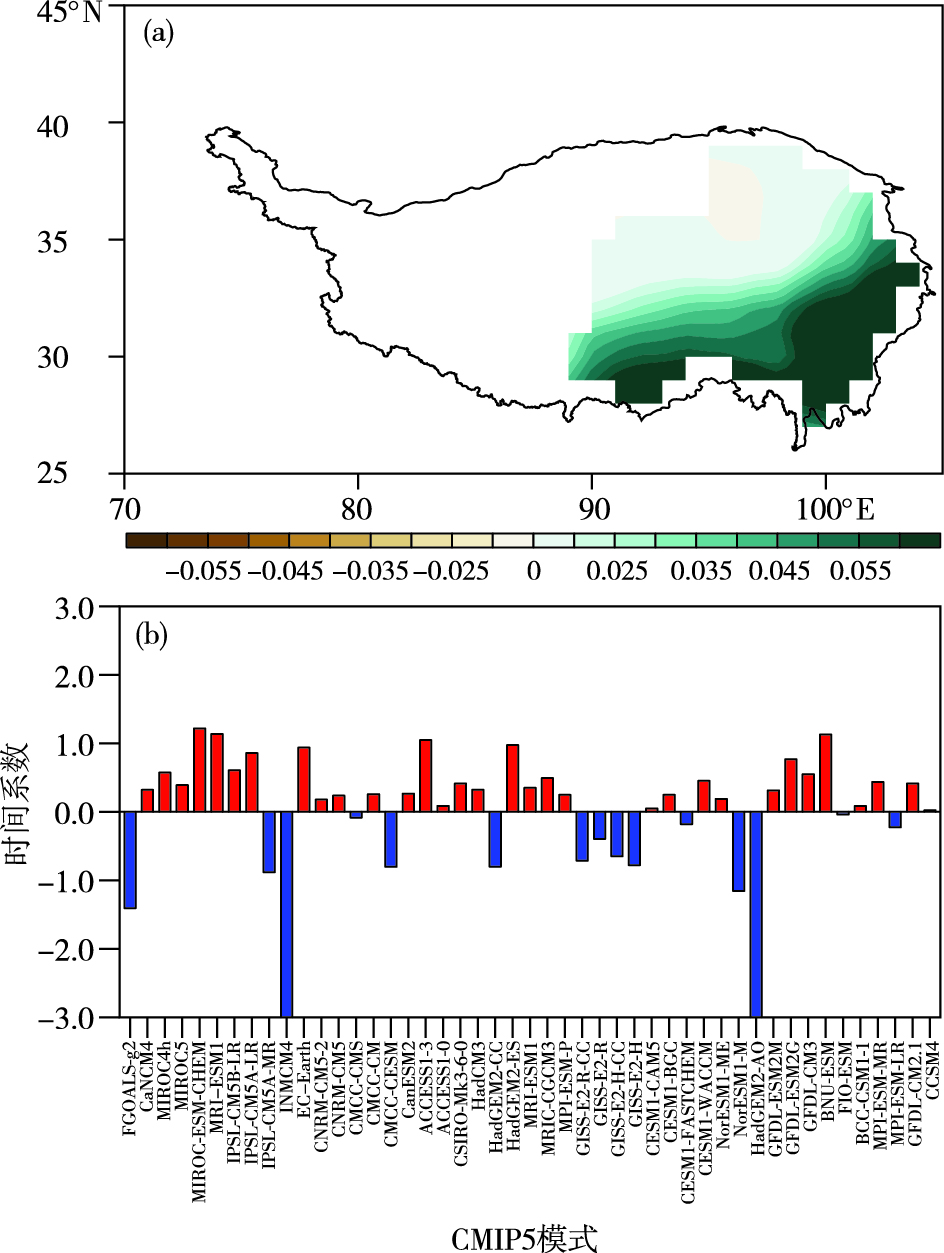
为了得到47个CMIP5模式对EOF1的主要模拟偏差,本文采用模式间EOF分析方法。模式间EOF分析方法与传统EOF时空分解方法不同,其主要关注CMIP5各模式间具有最大贡献的模拟偏差[31-32],模式间EOF分析的第一主模态和第二主模态的分解结果如图 3和图 4所示。第一主模态的方差贡献为31.979%,从中可以看出,主要表现为在32°N以南的东西向模拟偏差(图 3a)。从相应的时间系数中可以看出,NorESM1-M、IPSL-CM5A-MR和GISS系列模式得到的这种东西向模拟偏差最为明显;相反,CanCM4、MIROC-ESM-CHEM、MPI-ESM-P和MRI-CGCM3得到的这种东西向模拟偏差较小(图 3b)。模式间EOF分析的第二主模态(方差贡献为22.473%)表现为47个CMIP5模式间较为一致的全区模拟偏差(图 4a),并且这种模拟偏差主要集中在35°N以南。从相应的时间系数中可以看出,INMCM4、HadGEM2-AO、FGOALS-g2和NorESM1-M模式表现为较大的负模拟偏差;MIROC-ESM-CHEM、MIROC-ESM、ACCESS1-3和BNU-ESM模式表现为较大的正模拟偏差(图 4b)。然而,CCSM4、FIO-ESM、BCC-CSM1-1、CESM1-CAM5、CMCC-CMS和ACCESS1-0得到的这种全区一致的模拟偏差较小。

|
图 3 模式与观测之间1961—2005年青藏高原中东部夏季降水EOF1空间型态偏差的模式间EOF分析第一模态的空间型态(a)及其时间系数(b) Fig.3 Spatial pattern (a) and corresponding time coefficient (b) of the first inter-model EOF mode of deviations of summer precipitation EOF1 spatial pattern over the central and eastern TP from 1961 to 2005 between models and station observation |
|
图 4 模式与观测之间1961—2005年青藏高原中东部夏季降水EOF1空间型态偏差的模式间EOF分析第二模态的空间型态(a)及其时间系数(b) Fig.4 The same as Fig. 3, but for the second mode |
可以看出,选择不同指标进行模式评估时得到的评估结论不同,因此需要采用一个综合指标来评估模式对空间型态、时间系数以及方差贡献的综合模拟效果。从综合评估指标Snew中得到的评分排名前15和后15名的模式如表 2所示,其中MIROC-ESM、HadGEM2-CC、ACCESS1-0、MIROC-ESM-CHEM和IPSL-CM5A-MR模式的综合模拟效果较好,但是GISS系列模式、CESM1-CAM5和MPI-ESM-LR模式的综合模拟效果较差。并且,从表 1中可以看出,对青藏高原中东部夏季降水EOF1综合模拟效果较好(较差)的模式其春季北大西洋地区三极型海温的模拟相关系数也相对较高(较低),尤其是GISS系列模式,其得到的春季北大西洋地区三极型海温的相关系数基本为负值。
|
|
表 2 根据模式在模拟1961—2005年青藏高原中东部夏季降水EOF1时的综合评估指标Snew得到的排名前15名和后15名的模式排名情况 Table 2 Ranking of the top (left)/bottom (right) 15 models according to the comprehensive evaluation index Snew of the models in simulating summer precipitation EOF1 over the central and eastern TP from 1961 to 2005 |
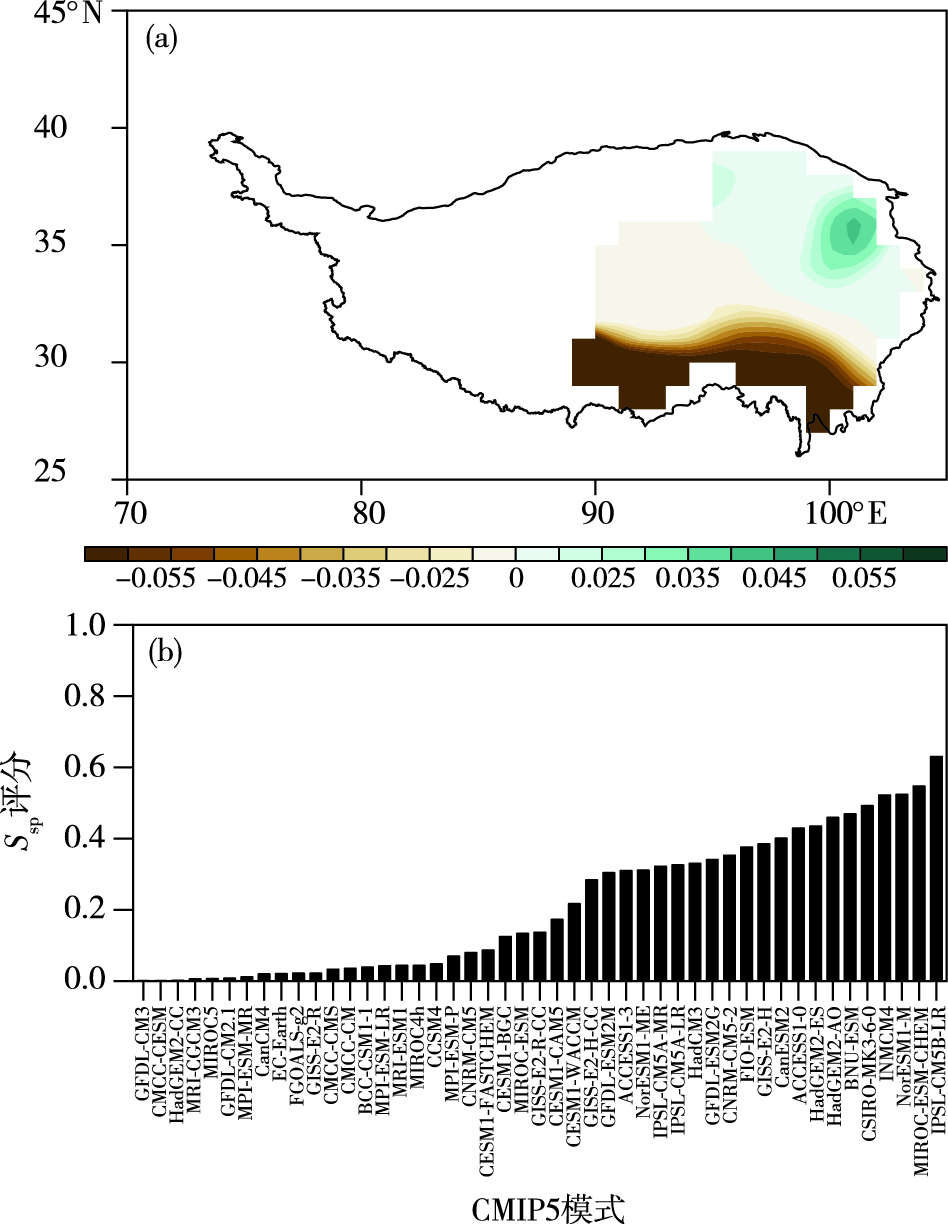
图 5给出了观测的1961—2005年青藏高原中东部夏季降水EOF2的空间型态(图 5a)以及47个CMIP5模式对EOF2空间型态的综合指标Ssp评分(图 5b)。观测中EOF2的空间型态也表现为该区域夏季降水东北部和东南部反位相的变化特征,但是位相与EOF1正好相反,表现为大致在35°N以南的负位相以及以北的正位相。整体来看,模式对EOF2空间型态的整体模拟效果差于EOF1。例如,MIROC4h、MIROC5、EC-Earth、CNRM-CM5-2和GISS系列模式几乎无法表现出EOF2反位相的变化型态;MIROC-ESM、ACCESS1-3、CMCC-CM和CESM1-CAM5模式模拟得到的青藏高原东南部的负位相范围小于观测,而MPI-ESM-P却显著高估了东南部负位相的范围和强度;对于东北部,INMCM4、IPSL-CM5A-LR、IPSL-CM5A-MR和HadGEM2-CC模式明显高估了降水的强度,MIROC-ESM、ACCESS1-3、ACCESS1-0和HadGEM2-ES表现出明显的位置和强度的模拟偏差(图略)。由空间相关系数来看,空间相关系数在-0.569~0.745之间,其中IPSL-CM5B-LR的空间相关系数最大,GFDL-CM3的空间相关系数最小。由EOF2空间型态的综合评估指标Ssp来看,评估结论与空间相关系数也基本一致,IPSL-CM5B-LR和MIROC-ESM-CHEM模式对EOF2空间型态的综合模拟效果较好,GFDL-CM3和CMCC-CESM模式对EOF2空间型态的综合模拟效果较差。
|
图 5 1961—2005年青藏高原中东部站点观测夏季降水的EOF2空间型态(a)以及47个CMIP5模式EOF2空间型态的综合指标Ssp评分(b) Fig.5 The same as Fig. 1, but for EOF2 mode |
图 6给出了EOF2相应的时间系数,其变化趋势与EOF1的时间系数相反,表现为20世纪70年代初期的上升趋势和20世纪90年代初期的下降趋势(图 6a)。但是大多数模式无法很好地抓住这种变化特征,MIROC、IPSL和MRI系列模式甚至无法表现出明显的变率特征,而INMCM4、CMCC-CESM、ACCESS1-0、CSIRO-Mk3-6-0、HadCM3、HadGEM2-CC、GISS-E2-H-CC、CESM1-WACCM、NorESM1-ME、BNU-ESM、MPI-ESM-MR和CCSM4模式表现出相反的变化趋势。FGOALS-g2模式可以大致表现出这种变化趋势,但是转折点落后观测大约5 a。由47个CMIP5模式的时间系数与观测的相关系数来看,其中只有11个模式的相关系数通过了95%的信度检验,其中FIO-ESM的相关系数最高。由EOF2时间系数的综合评估指标Sts(图 6b)来看,有近乎一半的模式对EOF2的时间系数几乎没有模拟能力,其Sts的数值几乎为0,但是FIO-ESM模式对EOF2时间系数的综合模拟效果具有明显优势,其综合评估指标Sts评分很高。

|
图 6 1961—2005年青藏高原中东部站点观测夏季降水的EOF2时间系数(a,黑线表示11 a滑动平均)以及47个CMIP5模式EOF2时间系数的综合指标Sts评分(b) Fig.6 The same as Fig. 2, but for EOF2 mode |
利用模式间EOF分析方法,从其得到的EOF1(图 7)可以看出,青藏高原中东部夏季降水的第二主模态也主要表现为在35°N以南的东西向模拟偏差,由相应的时间系数可以看出,GISS-E2-R、IPSL-CM5A-LR、ACCESS1-3和HadGEM2-ES模式的该种模拟偏差相对较小,而MIROC-ESM-CHEM、CanESM2、CMCC-CESM、CanCM4和MIROC5的该种模拟偏差相对较大。由其得到的EOF2(图 8)可以看出,第二种主要的模拟偏差位于青藏高原的中东部地区,并集中在30°~35°N之间。从相应的时间系数中可以看出,CanCM4、IPSL-CM5B-LR、CMCC-CMS和CESM1-FASTCHEM的该种模拟偏差相对较小,而MPI-ESM-P、EC-Earth、ACCESS1-3和GFDL-CM2.1的该种模拟偏差相对较大。
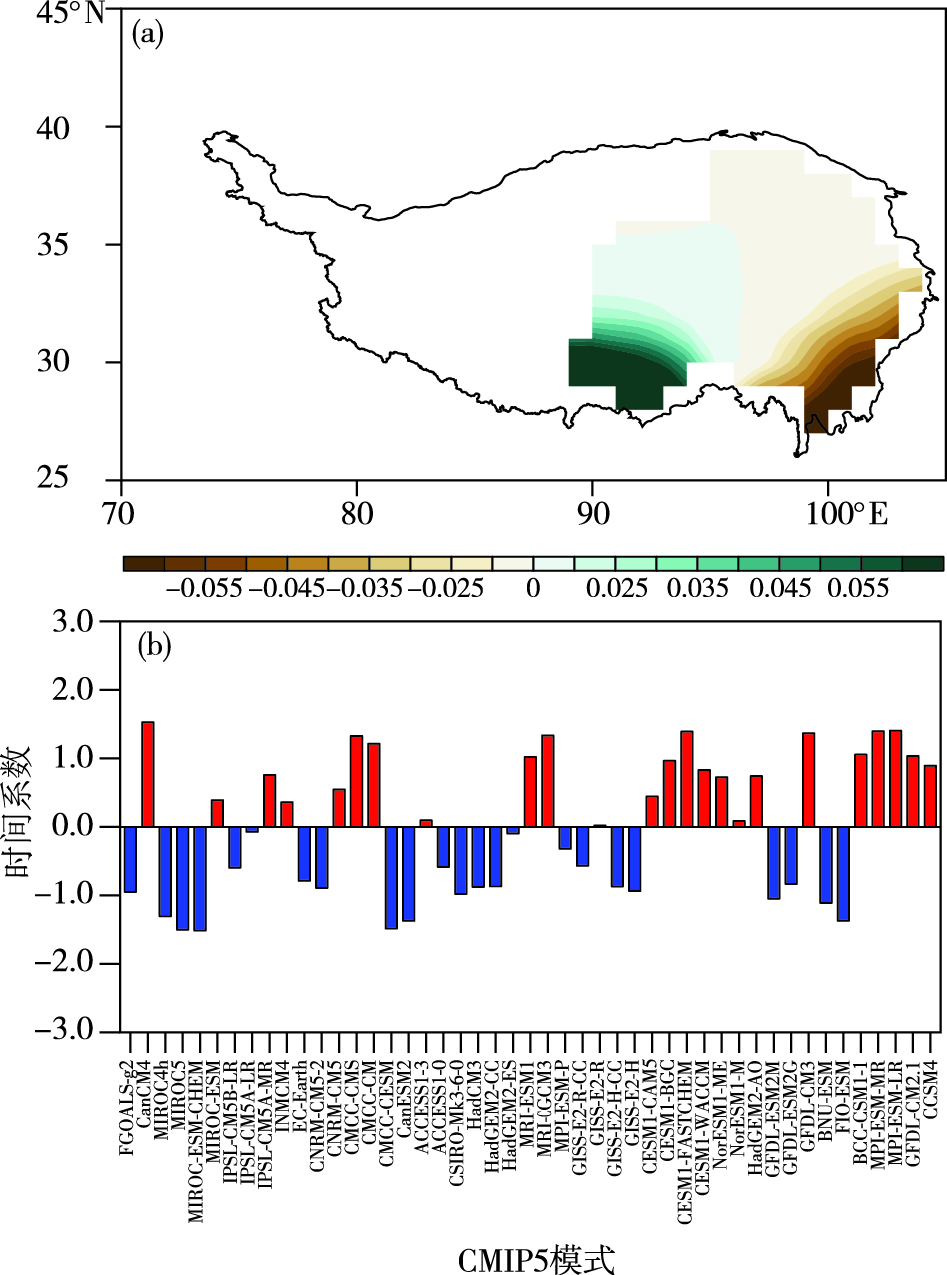
|
图 7 模式与观测之间1961—2005年青藏高原中东部夏季降水EOF2空间型态偏差的模式间EOF分析第一模态的空间型态(a)及其时间系数(b) Fig.7 Spatial pattern (a) and corresponding time coefficient (b) of the first inter-model EOF mode of deviations of summer precipitation EOF2 spatial pattern over the central and eastern TP from 1961 to 2005 between models and station observation |

|
图 8 模式与观测之间1961—2005年青藏高原中东部夏季降水EOF2空间型态偏差的模式间EOF分析第二模态的空间型态(a)及其时间系数(b) Fig.8 The same as Fig. 7, but for the second mode |
从综合评估指标Snew中得到的EOF2评分排名前15名和后15名的模式如表 3所示,从中可以看出,FIO-ESM、HadGEM2-AO和MIROC-ESM-CHEM模式的综合模拟能力相对较好,而CMCC-CESM、MPI-ESM-MR和GFDL-CM3的综合模拟能力相对较差。结合EOF1的综合评估结果,MIROC-ESM-CHEM模式对EOF1和EOF2的综合模拟效果较好,GISS-E2-R模式对EOF1和EOF2的综合模拟效果较差。MIROC-ESM-CHEM模式的分辨率虽然不是最高的,但是其模拟效果在本文的评估指标中表现最佳,其原因可能为该模式是跨行业影响模式国际比较计划(ISI-MIP)中用于气候变化与极端气候研究的全球模式之一,其参数符合各种影响模型需求[33-34],其对北大西洋地区三极型海温的模拟效果也相对较好,并且MIROC-ESM-CHEM模式对肯尼亚[35]和中国黄河流域[36]降水的模拟效果也较好。GISS-E2-R模式的EOF1和EOF2的综合评估指标Ssp和Sts均较低且对EOF1方差贡献的模拟结果(64.40%)明显偏离观测,且其对北大西洋地区三极型海温的模拟效果也相对较差,导致其在本文的评估指标中综合模拟效果较差。
|
|
表 3 根据模式在模拟1961—2005年青藏高原中东部夏季降水EOF2时的综合评估指标Snew得到的排名前15名和后15名的模式排名情况 Table 3 Ranking of the top (left)/bottom (right) 15 models according to the comprehensive evaluation index Snew of the models in simulating summer precipitation EOF2 over the central and eastern TP from 1961 to 2005 |
本文评估了参与CMIP5历史模拟试验的47个模式对青藏高原中东部夏季降水EOF分解前两个模态的模拟效果,并定义了一个新的评估指标Snew来定量评估模式对EOF分解前两个模态的空间型态、时间系数以及方差贡献的综合模拟效果。
评估结果表明,由空间型态来看,大多数模式可以表现出大致以35°N为界的EOF1“北少南多”以及EOF2“北多南少”的空间型态,但是存在降水强度和位相的模拟偏差。由模式间EOF分析的结果来看,在35°N以南的东西向模拟偏差是最主要的模拟偏差,其次表现为全区一致的模拟偏差,但是EOF1的全区一致的模拟偏差主要集中在35°N以南,EOF2的主要集中在30°~35°N之间。由时间系数来看,大多数模式对时间系数的模拟效果差于空间型态,不能表现出观测中降水模态在20世纪70年代和20世纪90年代的年代际转折。在47个模式中,只有13(11)个模式的EOF1(EOF2)时间系数的相关系数通过了95%的信度检验。从不同方面进行评估得到的评估结论不同,因此本文接着定义了一个同时考虑空间型态、时间系数以及方差贡献的综合指标Snew来评估模式对EOF1和EOF2的综合模拟效果。对于EOF1,MIROC-ESM、HadGEM2-CC、ACCESS1-0、MIROC-ESM-CHEM和IPSL-CM5A-MR模式的综合模拟效果较好,但是GISS系列模式、CESM1-CAM5和MPI-ESM-LR模式的综合模拟效果较差。对于EOF2,FIO-ESM、HadGEM2-AO和MIROC-ESM-CHEM模式的综合模拟能力相对较好,而CMCC-CESM、MPI-ESM-MR和GFDL-CM3模式的综合模拟能力相对较差。由EOF1和EOF2的综合评估结果来看,MIROC-ESM-CHEM模式对EOF1和EOF2的综合模拟效果较好,GISS-E2-R模式对EOF1和EOF2的综合模拟效果较差。
但是,本文也有三点主要不足。首先,定义的综合评估指标Snew基于等权重的空间型态、时间系数以及方差贡献,如果要着重考虑其中的某一方面,应加入权重。其次,仅从该模式对春季北大西洋地区三极型海温的模拟效果的角度来分析其对青藏高原中东部双极型降水模拟效果的好坏,未来可以通过例如增加模式分辨率以及耦合资料同化等方式,改进耦合模式对北大西洋地区海温的模拟效果,进而提升该模式对青藏高原中东部夏季降水的模拟效果。最后,由于青藏高原西部观测资料匮乏,本评估工作仅限于青藏高原中东部地区,随着未来气象观测站数量的增加,如果青藏高原西部地区有足够的观测站点,未来应进一步将青藏高原西部地区纳入评估工作之中。
| [1] |
KUKULIES J, CHEN D L, WANG M H. Temporal and spatial variations of convection, clouds and precipitation over the Tibetan Plateau from recent satellite observations. Part Ⅱ: precipitation climatology derived from global precipitation measurement mission[J]. Int J Climatol, 2020, 40(11): 4858-4875. DOI:10.1002/joc.6493 |
| [2] |
LI M, SHAO Q X. An improved statistical approach to merge satellite rainfall estimates and raingauge data[J]. J Hydrol, 2010, 385(1/2/3/4): 51-64. |
| [3] |
WU C, CHEN J M. The use of precipitation intensity in estimating gross primary production in four northern grasslands[J]. J Arid Environ, 2012, 82: 11-18. DOI:10.1016/j.jaridenv.2012.02.014 |
| [4] |
刘珂, 杨明祥, 徐艳红. 青藏高原春季地表感热加热特征及其对黄河源区汛期降水的影响[J]. 水文, 2020, 40(2): 72-79. |
| [5] |
MANABE S, BROCCOLI A J. Mountains and arid climates of middle latitudes[J]. Science, 1990, 247(4939): 192-195. DOI:10.1126/science.247.4939.192 |
| [6] |
KUTZBACH J E, PRELL W L, RUDDIMAN W F. Sensitivity of Eurasian climate to surface uplift of the Tibetan Plateau[J]. J Geol, 1993, 101(2): 177-190. DOI:10.1086/648215 |
| [7] |
LU H L, SHAO Q Q, LIU J Y, et al. Cluster analysis on summer precipitation field over Qinghai-Tibet Plateau from 1961 to 2004[J]. J Geogr Sci, 2008, 18(3): 295-307. DOI:10.1007/s11442-008-0295-y |
| [8] |
JOHN V O, SODEN B J. Temperature and humidity biases in global climate models and their impact on climate feedbacks[J]. Geophys Res Lett, 2007, 34(18): L18704. DOI:10.1029/2007GL030429 |
| [9] |
FU Y H, GAO X J, ZHU Y M, et al. Climate change projection over the Tibetan Plateau based on a set of RCM simulations[J]. Adv Climate Change Res, 2021, 12(3): 313-321. DOI:10.1016/j.accre.2021.01.004 |
| [10] |
王超. GFDL模式不同类型试验模拟海洋中CFC-11分布结果的评估[J]. 海洋气象学报, 2020, 40(2): 40-51. |
| [11] |
刘敏, 江志红. 13个IPCC AR4模式对中国区域近40 a气候模拟能力的评估[J]. 南京气象学院学报, 2009, 32(2): 256-268. DOI:10.3969/j.issn.1674-7097.2009.02.013 |
| [12] |
OU T H, CHEN D L, LINDERHOLM H W, et al. Evaluation of global climate models in simulating extreme precipitation in China[J]. Tellus A, 2013, 65: 19799. DOI:10.3402/tellusa.v65i0.19799 |
| [13] |
CHEN L, FRAUENFELD O W. A comprehensive evaluation of precipitation simulations over China based on CMIP5 multimodel ensemble projections[J]. J Geophys Res: Atmos, 2014, 119(10): 5767-5786. DOI:10.1002/2013JD021190 |
| [14] |
KAN M Y, HUANG A N, ZHAO Y, et al. Evaluation of the summer precipitation over China simulated by BCC_CSM model with different horizontal resolutions during the recent half century[J]. J Geophys Res: Atmos, 2015, 120(10): 4657-4670. DOI:10.1002/2015JD023131 |
| [15] |
姜大膀, 王会军, 郎咸梅. 全球变暖背景下东亚气候变化的最新情景预测[J]. 地球物理学报, 2004, 47(4): 590-596. DOI:10.3321/j.issn:0001-5733.2004.04.007 |
| [16] |
许崇海, 沈新勇, 徐影. IPCC AR4模式对东亚地区气候模拟能力的分析[J]. 气候变化研究进展, 2007, 3(5): 287-292. DOI:10.3969/j.issn.1673-1719.2007.05.008 |
| [17] |
FENG L, ZH OU, T J, WU B, et al. Projection of future precipitation change over China with a high-resolution global atmospheric model[J]. Adv Atmos Sci, 2011, 28(2): 464-476. DOI:10.1007/s00376-010-0016-1 |
| [18] |
SU F G, DUAN X L, CHEN D L, et al. Evaluation of the global climate models in the CMIP5 over the Tibetan Plateau[J]. J Climate, 2013, 26(10): 3187-3208. DOI:10.1175/JCLI-D-12-00321.1 |
| [19] |
WANG X C, WU G X. The analysis of the relationship between the spatial modes of summer precipitation anomalies over China and the general circulation[J]. Chinese J Atmos Sci, 1997, 21(2): 133-142. |
| [20] |
WENG H Y, LAU K M, XUE Y K. Multi-scale summer rainfall variability over China and its long-term link to global sea surface temperature variability[J]. J Meteor Soc Japan, 1999, 77(4): 845-857. DOI:10.2151/jmsj1965.77.4_845 |
| [21] |
NITTA T, HU Z Z. Summer climate variability in China and its association with 500 hPa height and tropical convection[J]. J Meteor Soc Japan, 1996, 74(4): 425-445. DOI:10.2151/jmsj1965.74.4_425 |
| [22] |
CHEN X Y, YOU Q L, SIELMANN F, et al. Climate change scenarios for Tibetan Plateau summer precipitation based on canonical correlation analysis[J]. Int J Climatol, 2017, 37(3): 1310-1321. DOI:10.1002/joc.4778 |
| [23] |
JIANG X W, TING M F. A dipole pattern of summertime rainfall across the Indian subcontinent and the Tibetan Plateau[J]. J Climate, 2017, 30(23): 9607-9620. DOI:10.1175/JCLI-D-16-0914.1 |
| [24] |
刘焕才, 李曼, 石培宏, 等. NAO对青藏高原中东部夏季降水双极振荡模态影响的时间尺度厘定[J]. 高原气象, 2015, 34(3): 633-641. |
| [25] |
LIU X D, YIN Z Y. Spatial and temporal variation of summer precipitation over the eastern Tibetan Plateau and the North Atlantic oscillation[J]. J Climate, 2001, 14(13): 2896-2909. DOI:10.1175/1520-0442(2001)014<2896:SATVOS>2.0.CO;2 |
| [26] |
LIU H C, DUAN K Q, LI M, et al. Impact of the North Atlantic Oscillation on the Dipole Oscillation of summer precipitation over the central and eastern Tibetan Plateau[J]. Int J Climatol, 2015, 35(15): 4539-4546. DOI:10.1002/joc.4304 |
| [27] |
LI F F, WANG B, HE Y J, et al. Important role of North Atlantic air-sea coupling in the interannual predictability of summer precipitation over the eastern Tibetan Plateau[J]. Climate Dyn, 2021, 56(5/6): 1433-1448. |
| [28] |
RAYNER N A, PARKER D E, HORTON E B, et al. Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century[J]. J Geophys Res, 2003, 108(D14): 4407. DOI:10.1029/2002JD002670 |
| [29] |
TAYLOR K E. Summarizing multiple aspects of model performance in a single diagram[J]. J Geophys Res: Atmos, 2001, 106(D7): 7183-7192. DOI:10.1029/2000JD900719 |
| [30] |
HIROTA N, TAKAYABU Y N. Reproducibility of precipitation distribution over the tropical oceans in CMIP5 multi-climate models compared to CMIP3[J]. Climate Dyn, 2013, 41(11/12): 2909-2920. |
| [31] |
LI G, XIE S P. Origins of tropical-wide SST biases in CMIP multi-model ensembles[J]. Geophys Res Lett, 2012, 39(22): L22703. |
| [32] |
LI G, XIE S P. Tropical biases in CMIP5 multimodel ensemble: the excessive equatorial Pacific cold tongue and double ITCZ problems[J]. J Climate, 2014, 27(4): 1765-1780. DOI:10.1175/JCLI-D-13-00337.1 |
| [33] |
查芊郁, 高超, 杨茹, 等. 全球升温1.5 ℃和2.0 ℃情景下淮河上游干流径流量研究[J]. 气候变化研究进展, 2018, 14(6): 583-592. |
| [34] |
王艳君, 刘俸霞, 翟建青, 等. 全球升温1.5 ℃与2.0 ℃目标下长江流域极端降水的变化特征[J]. 气象科学, 2019, 39(4): 540-547. |
| [35] |
MUMO L, YU J H. Gauging the performance of CMIP5 historical simulation in reproducing observed gauge rainfall over Kenya[J]. Atmos Res, 2020, 236: 104808. DOI:10.1016/j.atmosres.2019.104808 |
| [36] |
周文翀, 韩振宇. CMIP5全球气候模式对中国黄河流域气候模拟能力的评估[J]. 气象与环境学报, 2018, 34(6): 42-55. DOI:10.3969/j.issn.1673-503X.2018.06.005 |
 2022, Vol. 42
2022, Vol. 42


