2. 中国海洋大学深海圈层与地球系统前沿科学中心,山东 青岛 266100;
3. 中国海洋大学物理海洋教育部重点实验室,山东 青岛 266100;
4. 中国海洋大学未来海洋学院,山东 青岛 266100;
5. 崂山实验室,山东 青岛 266237
2. Frontiers Science Center for Deep Ocean Multispheres and Earth System, Ocean University of China, Qingdao 266100, China;
3. Key Laboratory of Physical Oceanography of Ministry of Education, Ocean University of China, Qingdao 266100, China;
4. Academy of the Future Ocean, Ocean University of China, Qingdao 266100, China;
5. Laoshan Laboratory, Qingdao 266237, China
海面温度半球间偶极子(sea surface temperature inter-hemispheric dipole,SSTID)是全球海面温度(sea surface temperature,SST)异常的主导变率模态之一,表现为南、北两半球间SST异常在年代际至多年代际尺度上的“跷跷板”变化[1-2]。前人研究发现,虽然SSTID与大西洋多年代际涛动(Atlantic multidecadal oscillation,AMO)在时间序列上存在相关性[3-4],但二者空间型表现显著不同[1, 5]。在季节特征方面,SSTID对应的半球间偶极子型海面温度异常结构在北半球(Northern Hemisphere,NH)夏、秋、冬3个季节的强度比春季偏强[6]。观测分析和模式模拟结果表明,SSTID有广泛的气候影响[5]。SSTID对热带降水有显著的影响,造成了热带降水在多年代际时间尺度上的南、北半球非对称性特征[1]。此外,研究发现,SSTID调控了北半球夏季风的年代际变化,SSTID正、负位相分别对应北半球夏季风的增强和减弱,从而调控夏季风环流和季风降水的年代际变化[7]。
热带气旋(tropical cyclone,TC)是地球上最具危害性的自然灾害之一[8],全球60%~70%的TC发生在北半球。观测到的近几十年TC强度呈现出上升趋势,但其发生频率和持续时间减少[9-10]。除了气候变化会对TC强度产生影响[11-12]之外,气候内部变率也会对TC活动产生影响。比如,西北太平洋热带气旋的活动展现出显著的年际变率,研究表明厄尔尼诺-南方涛动事件是对TC年际变率产生重要影响的因子之一[13-16]。此外,印度洋偶极子[17]、西北太平洋副热带高压[18]及其他海洋和大气环境也对影响TC活动起重要作用[19-20]。除年际变率外,TC活动还表现出显著的年代际变化[21]。前人发现,AMO对西北太平洋TC强度具有遥控作用[22],AMO通过跨海盆影响西北太平洋SST及其上空大气环流条件,进而调控TC强度。然而,当前对于TC年代际变率的认识还不充分。
普遍认为,SST是影响TC活动的重要环境条件[23-24]。SSTID作为全球SST的主导变率模态之一,且在北半球夏季和秋季这一TC频发的时期信号显著,其对TC强度的影响是值得探究的。SSTID是一个年代际变率信号,所以SSTID可能对TC强度在年代际尺度上的变化具有调控作用。另外,由于海气相互作用的存在,下垫面SST的变化可以影响局地上空的大气环流,如风场、湿度等。这些大气因子也会对TC发展和TC增强产生影响[25]。因此,探究SSTID是否会对TC强度的年代际变率产生影响是可行且有重要意义的。
本文关注北半球TC活动的年代际变化,用7—11月北半球平均TC强度来表征北半球TC活动和TC强度,强调了7—11月SSTID对7—11月北半球平均TC强度提前9 a的调制作用,以期帮助更好地理解北半球平均TC强度的年代际变率和可预测性。
1 数据与方法 1.1 数据TC观测数据在20世纪70年代中期之后被认为是可信的[26],因此本文的研究时段为1976—2020年。由于南、北半球季节相反,本研究聚焦北半球TC变化,所以数据选择的季节为北半球TC活跃季(7—11月)。使用的数据如下:(1)美国国家海洋和大气管理局(National Oceanic and Atmospheric Administration,NOAA)提供的1854—2022年空间分辨率为2°×2°(经度×纬度)的全球范围扩展重建海面温度资料第5版本(Extended Reconstructed SST version 5, ERSSTv5;https://www.ncei.noaa.gov/products/extended-reconstructed-sst)[27];(2)NOAA提供的1842—2022年全球范围热带气旋最佳路径数据集资料第4版本(International Best Track Archive for Climate Stewardship version 4,IBTrACSv4;https://www.ncei.noaa.gov/products/international-best-track-archive)[28-29];(3)NCEP/NCAR提供的1948—2022年空间分辨率为2.5°×2.5°(经度×纬度)的月平均全球范围风速(u风速和v风速)、2 m气温、海平面气压、相对湿度和涡度数据[30]。
1.2 方法 1.2.1 指数定义本文用北半球与南半球空间平均SST异常之差来表征SSTID,可以很好地表征全球SST异常关于赤道反对称的物理模态[1, 5, 7]。此处SST异常为1976—2020年平均SST作为气候态的SST异常,考虑了纬度权重进行半球空间平均。SSTID模态表明海面温度存在南、北两半球间“跷跷板”式的反向变化:SSTID正指数表现为北半球SST偏暖,同时南半球SST偏冷;SSTID负指数表现为北半球SST偏冷,同时南半球SST偏暖。为研究SSTID对北半球TC强度的影响,选取的月份处于北半球TC活跃季,即7—11月,因此使用的SSTID时间序列为7—11月平均的SSTID。文中TC定义为中心最大持续风速超过34 kn (1 kn≈0.514 m·s-1),即IBTrACSv4数据集中强度小于34 kn的数据均不计入平均强度的计算。7—11月北半球平均TC强度定义为每年7—11月北半球出现的每一个TC生命周期中平均强度的平均值[31, 22],其中强度用6 h观测的中心最大风速表征。
1.2.2 统计学方法为了研究年代际尺度上SSTID对7—11月北半球平均TC强度的影响,对所有时间序列进行预处理,包括去除线性趋势和低通滤波,以扣除长期趋势和年际信号。
在去除线性趋势前,使用Mann-Kendall趋势检验[32-33]来检验年平均序列是否存在显著(通过置信水平为90%的显著性检验)的上升或下降趋势。如果时间序列X存在显著的线性趋势,则去趋势的序列X*为
| $ X^*=X-(a X+b) \text {, } $ | (1) |
其中,a和b分别为序列X线性回归的斜率和截距。
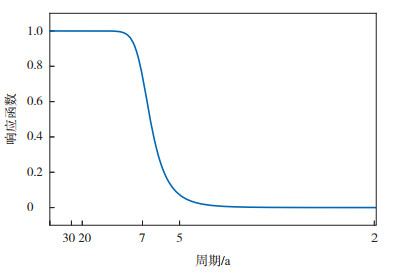
对无显著趋势的序列X*进行低通滤波,以提取年代际变率信号。本文使用阶数为8、截止频率为0.29的Butterworth滤波器,响应函数如图 1所示。可以看到,周期低于7 a的信号基本被去除,高于7 a的信号得以保留。
|
图 1 Butterworth低通滤波器的响应函数(滤波器的阶数为8、截止频率为0.29) Fig.1 Response function of Butterworth low-pass filter (the order of the filter is 8, and the cut-off frequency is 0.29) |
所使用的数据经过低通滤波之后存在较大的自相关,会对数据的自由度产生影响。在进行超前滞后分析时,两个自相关较强的时间序列的相关统计显著性使用有效自由度Neff进行双边t检验。有效自由度Neff由下式进行估计[7, 22, 34-36]:
| $ \frac{1}{N^{\mathrm{eff}}} \approx \frac{1}{N}+\frac{2}{N} \sum\limits_{j=1}^N \frac{N-j}{N} \rho_{X X}(j) \rho_{Y Y}(j), $ | (2) |
其中,N为样本长度,ρXX(j)和ρYY(j)分别为时间序列X和Y在滞后时刻j处的自相关。
使用多元线性回归理论建立基于超前9 a的7—11月SSTID的北半球平均TC强度年代际预测模型,并对该模型的模拟、后报和预测结果进行了显著性检验。假设多元线性回归模型为
| $ \widehat{y}=b_0+b_1 x_1+b_2 x_2+\cdots+b_m x_m, $ | (3) |
其中,
| $ \widehat{\sigma^2}=\frac{S_{y y}-\sum\limits_{i=1}^m \frac{S_{x_i y}{ }^2}{S_{x_i x_i}}}{n-m-1}, $ | (4) |
其中,Syy为变量y序列的方差,Sxiy为因子xi(i=1, 2, …, m)序列与变量y序列的协方差,Sxixi为因子xi(i=1, 2, …, m)序列的方差,n为序列长度。那么,对回归模型进行区间估计的范围为[37-39]
| $ \left(\widehat{y} \pm 2 t _{\frac{1+p}{2}} \sqrt{\widehat{\boldsymbol{\sigma}^2}\left(1+\boldsymbol{x}_j^T\left(\boldsymbol{X}^T \boldsymbol{X}\right)^{-1} \boldsymbol{x}_j\right)}\right), $ | (5) |
其中,p为置信水平,xj=[1, x1, x2, …, xm]T为第j个时刻的因子向量(j=1, 2, …, n),X=[x1, x2, …, xn]T为因子向量矩阵。
除以上方法外,本文还用到了回归分析来探究SSTID影响7—11月北半球平均TC强度年代际变化中可能的物理机制。
1.2.3 潜在生成指数为了探究SSTID影响7—11月北半球平均TC强度年代际变化的物理机制,除SST异常外,本文还分析了与TC生成和TC强度密切相关的TC潜在生成指数(genesis potential index,GPI)。GPI被广泛用于诊断和检验年代际尺度上大尺度环流对TC活动的影响[40-42]。GPI定义[43]为:
| $ I_{\mathrm{GP}}=\left(1+0.1 V_{\mathrm{VWS}}\right)^{-2.0}\left(\frac{H_{\mathrm{R}}}{50}\right)^{3.0}\left(\frac{V_{\mathrm{MPI}}}{70}\right)^{3.0}\left|10^5 \zeta_a\right|^{1.5}, $ | (6) |
其中,IGP为潜在生成指数值,垂直风切变(vertical wind shear,VWS)指标VVWS表征为850 hPa与200 hPa两层的风速矢量差(单位:m·s-1),HR为600 hPa相对湿度(单位:%),ζa为850 hPa绝对涡度(单位:s-1),最大潜在强度(maximum potential intensity,MPI)值VMPI由下式计算得出[44-45]:
| $ V_{\mathrm{MPI}}^2=\frac{C_{\mathrm{k}}}{C_{\mathrm{D}}} \frac{T_{\mathrm{s}}-T_{\mathrm{o}}}{T_{\mathrm{o}}}\left(h_{\mathrm{o}}^*-h^*\right), $ | (7) |
其中,Ck和CD分别为表面焓交换系数和动量交换系数,Ts和To分别为表面温度和出流温度,ho*和h*分别为海表面和自由大气的饱和湿静能。在实际计算中,使用了Gilford[46]提供的MPI计算代码。
Ck与CD在计算中以Ck/CD形式参与计算。Ck/CD是一个不确定常数,与海面状况有关。在计算MPI时通常取0.9[46-48]。基于公式(7),Bister等[49]给定条件将VMPI计算公式进行了简化:
| $ V_{\mathrm{MPI}}^2=\left.\frac{C_{\mathrm{k}}}{C_{\mathrm{D}}} \frac{T_{\mathrm{s}}}{T_{\mathrm{o}}}\left(V_{\mathrm{CAPE}}^*-V_{\mathrm{CAPE}_{\mathrm{env}}}\right)\right|_{\mathrm{RMW}}, $ | (8) |
其中,VCAPE*为饱和空气从海平面上升到流出层的对流有效势能,VCAPEenv是环境的对流有效势能,MPI在最大风半径(radius of maximum wind,RMW)处出现。式(7)中的饱和湿静能在简化后不参与计算,与之相关的部分由计算VCAPE取代,
| $ \begin{aligned} & V_{\mathrm{CAPE}}=+\int_{p_{H_2}}^{p_{H_1}} R_{\mathrm{d}}\left(T_\rho-T_{\rho, \mathrm{env}}\right) \mathrm{d} \log (p)- \\ & \;\;\;\;\;\;\;\;\int_{p_{H_1}}^{p_{j=0}} R_{\mathrm{d}}\left(T_\rho-T_{\rho, \text { env }}\right) \mathrm{d} \log (p), \\ & \end{aligned} $ | (9) |
其中,Rd为干空气气体常数,计算中取287.04 J·kg-1·K-1,pH2为中性浮力高度(level of neutral buoyancy,LNB)处的气压,pH1为自由对流高度(level of free convection,LFC)处的气压,pj=0为海平面气压,Tρ和Tρ, env分别为空气块提升和环境的密度温度,由下式确定:
| $ T_\rho=T \times\left(\frac{1+\frac{r}{\varepsilon}}{1+r_{\mathrm{T}}}\right), $ | (10) |
其中:T为温度(单位:K);r为混合比;ε为水汽气体常数和干空气气体常数的比值,计算中取0.62;rT为净水混合比,其值在抬升凝结高度以下与同高度处的气块混合比r相等。
在计算MPI时,流出层高度及出流温度To分别定义为LNB及该高度处的温度TLNB。LNB表示浮力为正的最高层所在的高度,即Tρ-Tρ, env>0时的最高层。由此,出流温度To即可确定。其他与MPI计算相关的公式和参数细节可见文献[46]以及文献[49]。
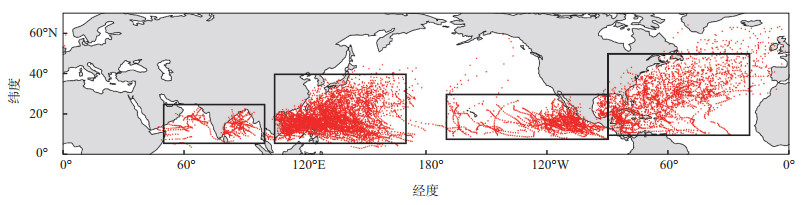
1.2.4 7—11月北半球TC活跃区为了探究7—11月SSTID对7—11月北半球平均TC强度的物理机制并量化分析该过程,图 2展示了1976—2020年7—11月强度超过34 kn的北半球TC每隔6 h观测的位置和以此划定的北半球TC活跃区,分别是北印度洋(50°~100°E,6°~25°N)、西北太平洋(105°~170°E,6°~40°N)、东北太平洋(170°~90°W,8°~30°N)和北大西洋(90°~20°W,10°~50°N)。北半球TC活跃区内TC事件个数占北半球TC总个数的96.63%,总强度占97.24%,累积气旋能量占97.87%。因此,本文定义的7—11月北半球TC活跃区内的TC可以代表北半球TC活动的总体情况。使用该定义对7—11月北半球TC活动进行研究是可行的。
|
图 2 1976—2020年7—11月北半球TC事件(红色点)和7—11月北半球TC活跃区(黑色框,下同) Fig.2 NH July-November TC cases (red dot) during the period of 1976-2020 and NH July-November TC active region (black box, the same below) |
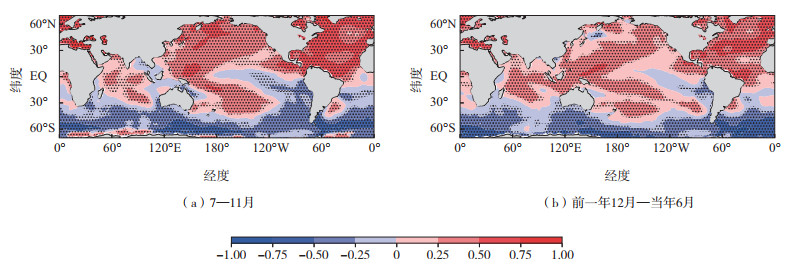
7—11月SSTID的空间型可以从7—11月SSTID与全球SST异常的相关场上得出,如图 3所示。在北半球TC活跃的7—11月,SSTID表现出显著的南、北半球间偶极子空间型(图 3a)。总体来看,两半球间的SST异常与SSTID相关性符号相反。在北半球,SSTID与7—11月SST正相关显著的区域主要位于西北太平洋、热带东北太平洋和北大西洋以及北印度洋的北部,均为北半球TC活跃的海域。因此,在年代际尺度上,由SSTID主导的SST异常模态可能对TC活动和TC强度产生显著影响。对比二者的相关系数在前一年12月—当年6月的表现(图 3b),在北半球TC活跃季节即7—11月,SSTID与SST的正相关在强度上更显著且在空间范围上更广泛。因此,SSTID主导的海面温度变率模态在北半球TC活跃的7—11月表现出了显著的半球间偶极子特征,并显著强于非北半球TC活跃季。由于下垫面SST展现出SSTID模态的空间特征,7—11月SSTID可能对会对北半球TC活动产生影响。
|
图 3 SSTID与全球SST异常的相关场(色阶)(点表示相关系数通过置信水平为95%的显著性检验) Fig.3 Correlation map (color scale) between SSTID and global SST anomalies (the dotted shading indicates correlation coefficients above the 95% confidence level) |
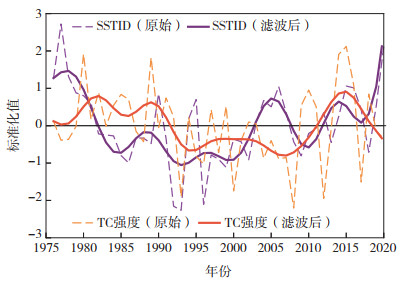
图 4给出了7—11月SSTID和北半球平均TC强度的年序列。除年际变率外,7—11月SSTID和北半球平均TC强度还表现出明显的年代际变化特征。1976年以来,7—11月SSTID在1976—1982年处在正位相,即北半球SST正异常,南半球SST负异常。1982—2003年,7—11月SSTID进入负位相,即南半球SST正异常,北半球SST负异常。在负位相期间SSTID出现3个谷值,分别在1985、1993和2000年前后。2003年之后,SSTID转为正位相,在2010年前后短暂下降后波动上升,并在2018年之后不断增强。
|
图 4 7—11月SSTID和7—11月北半球平均TC强度的时间序列(1976—2020年)(虚线和实线分别是原始序列和7 a Butterworth低通滤波的时间序列) Fig.4 Time series of July-November SSTID and NH July-November average TC intensity during the period of 1976-2020 (the dashed and solid lines are the raw time series and the corresponding 7-year Butterworth low-pass filtered time series, respectively) |
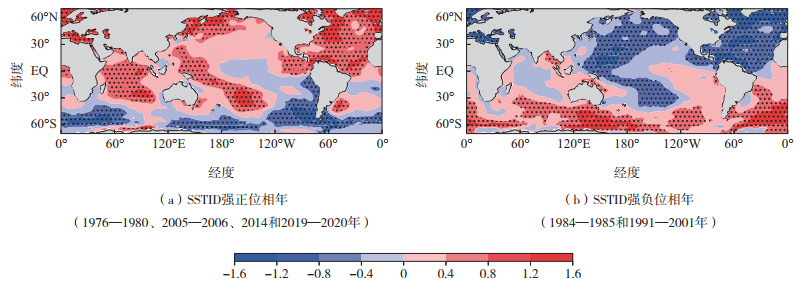
为了直观展现SSTID正、负异常时对应的空间模态,图 5展示了1976—2020年间SSTID强正、负位相的SST异常合成场。本文定义标准化的7—11月SSTID指数大于0.8(小于-0.8)为强正(负)位相年。7—11月SSTID强正位相年为1976—1980、2005—2006、2014和2019—2020年,强负位相年为1984—1985和1991—2001年。当SSTID处于强正位相时,其对应的全球SST异常呈现出北半球以正异常为主、南半球以负异常为主的特征(图 5a)。北半球SST正异常在西北太平洋和北大西洋西部较为显著。南半球SST负异常在南大洋中高纬度海域较为显著。与之相反,当SSTID处于强负位相时,北半球SST呈显著一致的负异常,负异常信号在西北太平洋和北大西洋较为显著(图 5b)。南半球SST在中高纬度的南大洋海域,呈现出纬向上较为一致的显著SST正异常。
|
图 5 7—11月全球SST异常场合成图(色阶,单位:℃)(在合成分析前,扣除SST数据的长期趋势并进行了7 a Butterworth低通滤波;点代表合成通过置信水平为95%的显著性检验) Fig.5 Composite map of July-November global SST anomalies (color scale, units: ℃) (the long-term linear trends in the SST data set are removed and the SST data set is 7-year Butterworth low-pass filtered before the composition analysis; the dots indicate the composites significant at the 95% confidence level) |
与7—11月SSTID相似,1976年以来,7—11月北半球平均TC强度也有明显的年代际变率特征(图 4)。1976—1992年,7—11月北半球平均TC强度偏强。1992—2012年,北半球平均TC强度偏弱。2012年之后,北半球平均TC强度偏强。北半球平均TC强度在2015年前后出现峰值,其后减弱。1976年以来有两个北半球平均TC强度较强的时期:1976—1992年和2010—2020年。
7—11月,SSTID和北半球平均TC强度可能表现出超过40 a的年代际变率,但受观测资料长度的限制,暂时无法对可靠的观测资料进行功率谱分析来验证SSTID和7—11月北半球平均TC强度变化的周期性。但值得注意的是,根据现有资料分析,7—11月SSTID可能超前北半球平均TC强度10 a左右进行位相转换。1980年左右,7—11月SSTID由正位相转为负位相,其后,1990年前后,7—11月北半球平均TC强度由正异常转为负异常。类似地,2002年前后,SSTID由负位相转为正位相,其后,2012年前后,7—11月北半球平均TC强度由负异常转为正异常。因此,采用考虑了序列自相关的有效自由度进行超前滞后相关分析,来探究SSTID与7—11月北半球平均TC强度的相关关系。
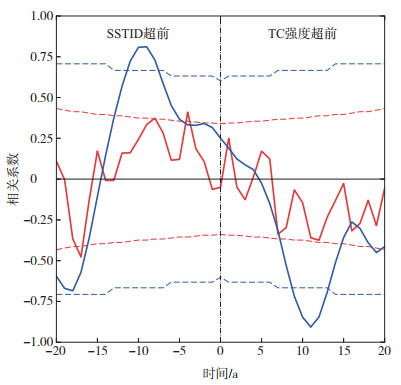
SSTID和7—11月北半球平均TC强度的低频分量有相似的年代际变率,并且前者超前后者约10 a。去趋势的7—11月SSTID在2000年以前经历了波动下降,2000年后表现出波动上升,并在2020年左右达到极大值,在北半球为TC增强提供了更加有利的背景场环境。对原始的和滤波后的SSTID与7—11月北半球平均TC强度分别进行超前滞后分析(图 6),结果表明,7—11月,SSTID超前北半球平均TC强度年代际变化分量8~11 a,在其提前9 a时达到最大正相关(相关系数为0.81,通过置信水平为95%的显著性检验)。这表明,超前9 a的SSTID可以解释7—11月北半球平均TC强度在年代际时间尺度上约66%的方差。关注到7—11月北半球SST和TC的变化:当北半球SST处于暖异常时,约9 a后,7—11月北半球平均TC强度较强;当北半球SST处于冷异常时,约9 a后,7—11月北半球平均TC强度较弱。
|
图 6 去趋势的7—11月SSTID与7—11月北半球平均TC强度(1976—2020年)超前滞后相关(红、蓝实线分别为原始时间序列和7 a Butterworth低通滤波后的序列的相关系数,负(正)轴表示7—11月SSTID超前(落后)北半球7—11月平均TC强度,红、蓝虚线分别表示对原始(滤波后) 时间序列采用有效自由度的置信水平为95%的临界相关系数) Fig.6 Lead-lag correlation between the detrended July-November SSTID and NH July-November average TC intensity (1976-2020) (the red and blue solid lines are correlation coefficients of the raw and 7-year Butterworth low-pass filtered time series, respectively; the negative and positive axises denote that the detrended July-November SSTID leads and lags NH July-November average TC intensity, respectively; the red and blue dashed lines indicate the 95% confidence levels for the raw and filtered time series using the effective number of degrees of freedom, respectively) |
SSTID与7—11月北半球平均TC强度时间序列无论在年际变率还是年代际尺度上,同期相关系数均小于0.3且不显著(图 6)。这说明在年代际尺度上,SSTID与7—11月北半球平均TC强度变化几乎不存在显著的同期相关。而在SSTID超前7—11月北半球平均TC强度9 a左右时,二者存在的最大正相关表明,SSTID对北半球平均TC强度的调控存在时间上的延迟,这与SST强大的信号存储和记忆能力有关。
3 海面温度半球间偶极子模态调控7—11月北半球平均TC强度年代际变化的物理过程本节探究了超前9 a的SSTID对7—11月北半球平均TC强度年代际变率调控可能的物理过程。由于SSTID对7—11月北半球平均TC强度的影响存在时间上的延迟,因此SSTID作为一个海洋信号可能会对9 a后的SST异常产生影响,将SSTID信号存储在TC活跃区的海水中,进而对TC活动产生影响。此外,SSTID并不能直接作用于TC强度,因此SSTID可能需要借助一个大气桥,将海洋的信号传递到大气中,进而影响TC强度。研究发现,北半球TC活跃区大气可以作为该大气桥,以GPI为表征来连接超前9 a的SSTID和当年的北半球平均TC强度。因此,本节从北半球TC活跃区海洋以SST的形式作为海洋桥存储SSTID信息、北半球TC活跃区大气作为大气桥以GPI为表征将SSTID信号传递给北半球平均TC强度,以及北半球TC活跃区SST和GPI的综合影响3个方面,应用海洋-大气耦合桥理论[38, 50-51]来解释7—11月SSTID调控7—11月北半球平均TC强度年代际变化的物理过程。
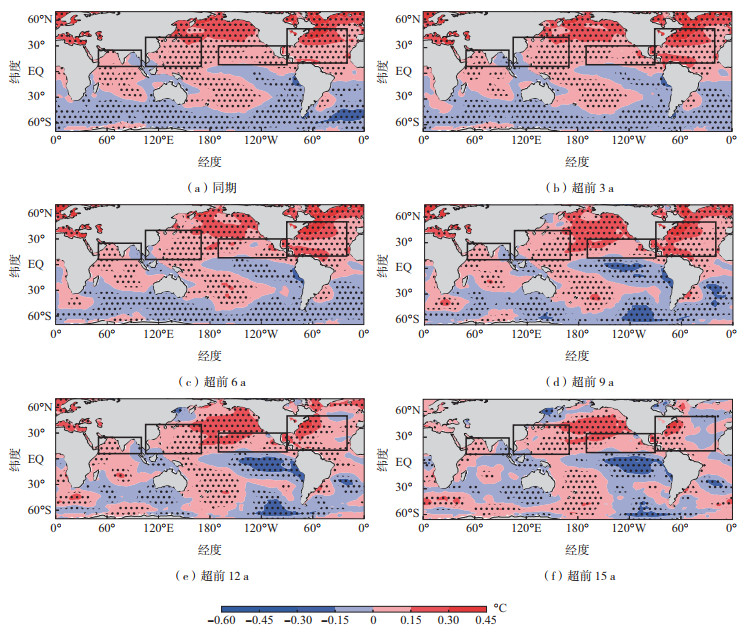
3.1 北半球TC活跃区海洋作为海洋桥存储SSTID信息将7 a低通滤波后的观测SST异常分别回归到同期及超前3~15 a归一化的7—11月SSTID序列上(图 7)。总体来说,与同期和超前3~15 a的7—11月SSTID相关的全球SST异常呈现出南、北两半球反向变化的特征。从演变的角度来看,随着SSTID超前时间的增加,其对北半球SST异常产生持续的正影响。在北半球中高纬海域,SST异常持续出现正异常的响应。值得注意的是,当SSTID超前3 a时,SST正异常的响应开始向热带海域发展,信号在热带北大西洋率先出现。当SSTID超前6 a时,北半球中东太平洋也出现了SST正异常响应。在SSTID超前6~9 a时,热带海域出现的与超前的SSTID相关的SST正异常响应有利于增强TC活动和TC发展。当SSTID超前12 a时,热带北大西洋的SST正异常响应范围开始缩小,强度开始减弱。直到SSTID超前15 a时,SST正异常响应范围在热带东北太平洋和北大西洋均缩小,对北半球TC的调控作用减弱。
|
图 7 SST异常(色阶)分别回归到归一化的同期和超前3、6、9、12和15 a的7—11月SSTID指数(1976—2020年)(在回归分析前,扣除SST数据的长期趋势并进行7 a Butterworth低通滤波;点代表回归系数通过置信水平为95%的显著性检验) Fig.7 Regression map of SST anomalies (color scale) onto the normalized July-November SSTID index (leading 0, 3, 6, 9, 12, and 15 years) based on the data during the period of 1976-2020 (the long-term linear trends in the SST data set are removed and the SST data set is 7-year Butterworth low-pass filtered before the regression analysis; the dots indicate the regression coefficients significant at the 95% confidence level) |
当SSTID超前时间大于9 a时,随着SSTID超前时间的增加,北半球SST正异常响应范围减小,负异常响应范围增加。南半球则相反,南半球SST负异常响应范围减小,正异常响应范围增加。这说明当SSTID超前时间大于9 a时,其在全球范围内对SST异常的影响在不断减弱,直至消失。全球SST的回归场可以更直观地展现和说明SSTID对全球SST影响的滞后性。
已有研究阐明了海洋下边界是影响TC强度的重要物理因子[52]。北半球暖SST有利于北半球TC增强。当7—11月SSTID超前SST异常9 a时,在北半球TC活跃区有显著的SST正异常。也就是说,北半球TC活跃区海水存储了超前9 a左右的SSTID信号。其中,显著的SST正异常主要出现在北印度洋西部、西北太平洋东部、东北太平洋西部以及北大西洋西部。特别地,在北大西洋TC活跃区海域出现了整个北半球SST正异常最广泛的极大值区。7—11月,北半球广泛的较暖SST下垫面为北半球TC强度发展提供了暖下垫面条件和能量来源。
前人研究已发现在年代际时间尺度上,局地SST变化对TC强度有调控作用[53-54]。在本研究中,北半球TC活跃区海洋以SST的形式作为海洋桥,存储了超前9 a的年代际SSTID信号。因此,超前9 a影响北半球TC活跃区内的SST正异常可以支持TC增强。除了在北半球一致的SST异常增暖外,7—11月SSTID引起的北半球SST异常也存在一定的海域间的强度差异。这表明SSTID通过引起北半球SST正异常而造成北半球TC增强这一物理过程也存在一定的空间差异。对东北太平洋和北大西洋TC的增强作用要显著强于北印度洋和西北太平洋的TC。
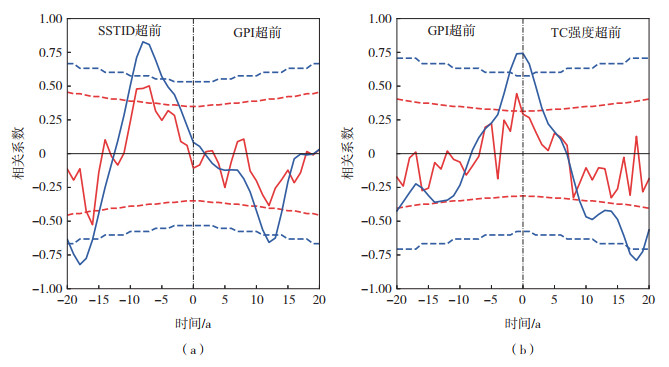
3.2 北半球TC活跃区大气作为大气桥将SSTID的影响传递给北半球平均TC强度对原始的和滤波后的7—11月SSTID与北半球TC活跃区的GPI分别进行超前滞后分析(图 8a),结果表明,7—11月SSTID超前GPI年代际变化分量7~9 a,在提前时间为8 a时达到最大正相关(相关系数为0.82,通过置信水平为95%的显著性检验)。这表明,超前8 a的SSTID可以解释7—11月北半球TC活跃区GPI在年代际时间尺度上约67%的方差。超前9 a的7—11月SSTID与GPI在年代际尺度上的相关系数为0.71。关注到7—11月SSTID和GPI的变化:当北半球SSTID处于正位相时,7~9 a后,7—11月北半球TC活跃区GPI较强;当北半球SSTID处于负位相时,7~9 a后,7—11月北半球TC活跃区GPI较弱。
|
图 8 同图 6,但表示去趋势的7—11月SSTID与7—11月北半球TC活跃区GPI的超前滞后相关以及去趋势的7—11月北半球TC活跃区GPI和7—11月北半球平均TC强度的超前滞后相关 Fig.8 The same as Fig. 6, but for the lead-lag correlation between the detrended July-November SSTID and NH July-November GPI over TC active regions and for the lead-lag correlation between the detrended NH July-November GPI over TC active regions and NH July-November average TC intensity |
图 8b展示了7—11月北半球TC活跃区的GPI和北半球平均TC强度的超前滞后相关。二者的同期相关最强,相关系数为0.74(通过置信水平为95%的显著性检验)。在年代际尺度上,7—11月北半球TC活跃区的GPI和北半球平均TC强度存在同位相的变化关系,并且GPI可以解释北半球平均TC强度约55%的方差。该结果表明,在年代际尺度上,当北半球TC活跃区GPI较强时,受其影响,北半球平均TC强度较强;当GPI较弱时,北半球平均TC强度也较弱。
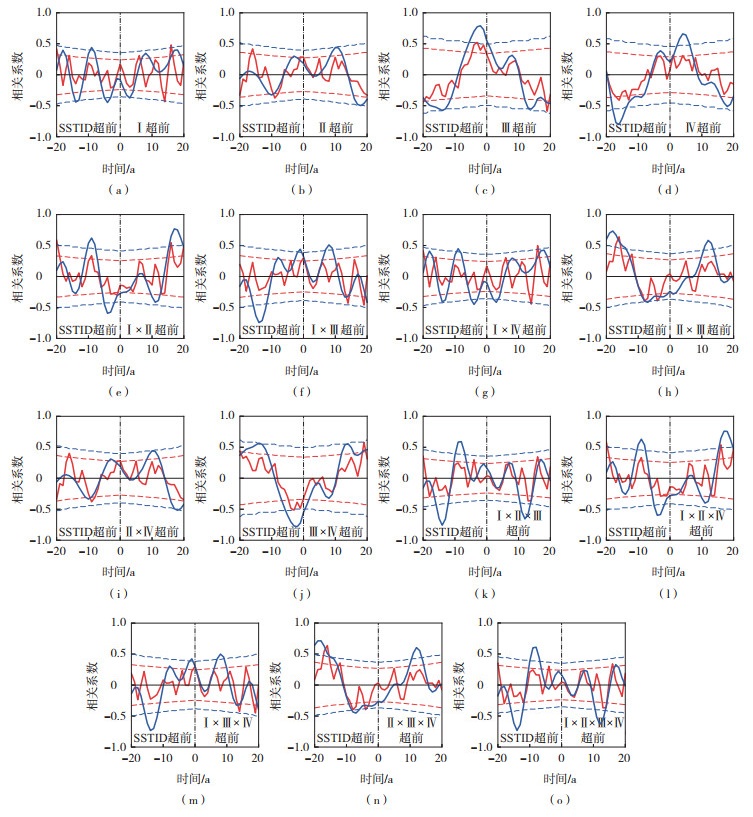
由图 8可知,超前9 a的7—11月SSTID可能通过作用于7—11月GPI进而同期影响7—11月北半球平均TC强度。北半球TC活跃区大气起到了传递SSTID信号到TC活动的大气桥作用,这个过程可由GPI对SSTID的响应来表征。由GPI的定义(式(6))可知,GPI的变化和VWS、600 hPa相对湿度、MPI、850 hPa绝对涡度这4个变量有关。为了进一步探究7—11月SSTID对7—11月GPI超前9 a的调控作用,分别对7—11月SSTID和上述4个变量及其变量组合进行了超前滞后相关分析,如图 9所示。7—11月SSTID和构成GPI的4个单因子并没有显著的超前9 a左右的相关关系(图 9a—d)。因此,SSTID对GPI的超前影响可能不是通过分别影响单因子来实现的。
|
图 9 同图 6,但分别表示去趋势的SSTID与7—11月北半球TC活跃区GPI有关的单变量以及多变量组合的超前滞后相关 Fig.9 The same as Fig. 6, but for the lead-lag correlation between the detrended July-November SSTID and single variables/multi-variable combinations related to GPI in the NH TC active regions |
由7—11月SSTID和各变量组合的超前滞后相关结果来看,SSTID仅对4组变量组合有超前9 a左右的显著正相关,分别是VWS与600 hPa相对湿度组合(图 9e),VWS、600 hPa相对湿度和MPI组合(图 9k),VWS、600 hPa相对湿度和850 hPa绝对涡度组合(图 9l)以及VWS、600 hPa相对湿度、MPI和850 hPa绝对涡度这4个组成GPI变量的组合(图 9o)。由该结果可以看出,7—11月SSTID对VWS与相对湿度的共同作用可能是其影响7—11月GPI的关键。SSTID对包含VWS与相对湿度因子的变量组合均表现出超前9 a左右的正相关。而且,对没有包含这2个因子的变量组合均没有显著的超前9 a左右的正相关。因此,SSTID可能会综合作用于与GPI相关的4个因子,并且VWS和相对湿度可能在该过程中起到关键作用。
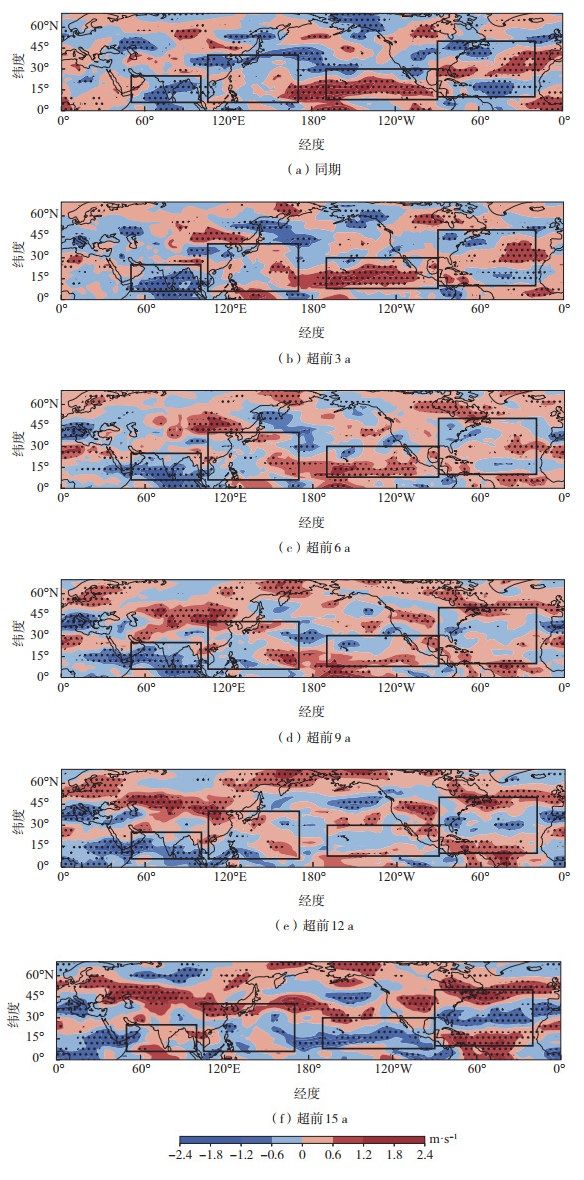
为了进一步分析7—11月SSTID对VWS和相对湿度的超前影响,图 10、11分别给出了7—11月北半球VWS和相对湿度对超前0~15 a的7—11月SSTID的回归场。7—11月VWS对7—11月SSTID正位相的同期响应主要表现为印度洋TC活跃区负异常、东北太平洋正异常和北大西洋从南到北的负-正-负异常响应。随着7—11月SSTID正位相超前时间从3 a增加至9 a,印度洋TC活跃区VWS持续出现负异常响应。西北太平洋TC活跃区中部和南部逐渐出现VWS负异常响应。东北太平洋TC活跃区VWS正异常响应减弱并向赤道移动,逐渐被负异常响应取代。北大西洋TC活跃区中部的VWS强正异常响应逐渐转变为弱的负异常响应。总体来看,当7—11月SSTID超前VWS 9 a左右时,SSTID引起的VWS变化在TC活跃区内以负异常为主。负的垂直风切变异常可以为TC发展提供稳定的动力背景,有助于TC发展和TC增强。
|
图 10 同图 7,但表示垂直风切变异常(色阶) Fig.10 The same as Fig. 7, but for vertical wind shear anomalies (color scale) |
|
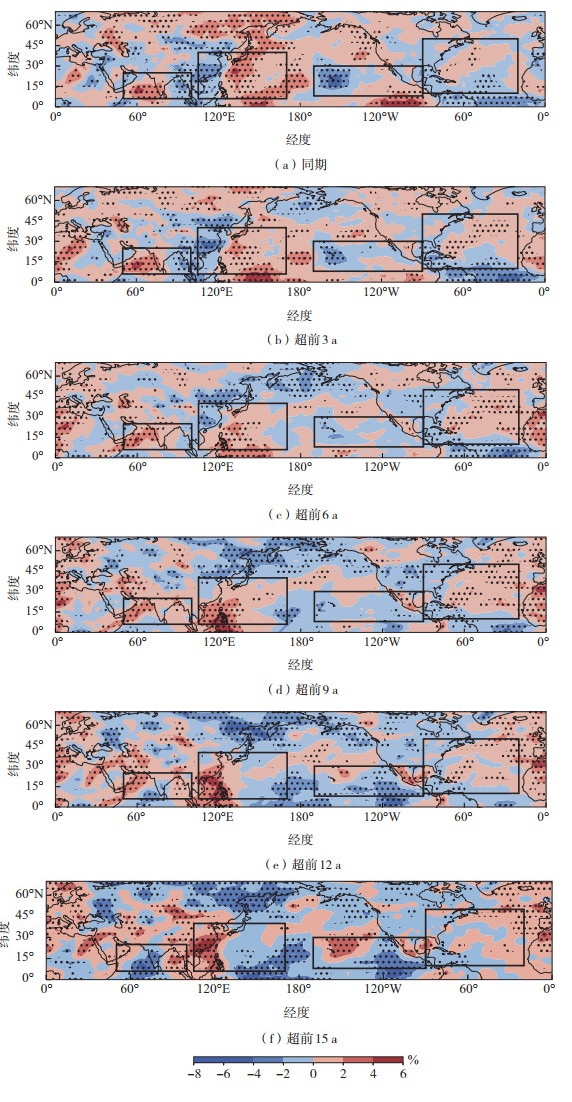
图 11 同图 7,但表示600 hPa相对湿度异常(色阶) Fig.11 The same as Fig. 7, but for relative humidity anomalies at 600 hPa (color scale) |
当7—11月SSTID正位相超前时间从9 a增加至15 a,总体上,VWS对SSTID的负异常响应区域从印度洋和西北太平洋转移到东北太平洋和北大西洋。印度洋TC活跃区VWS由负异常响应转变为正异常。西北太平洋TC活跃区北部出现显著的VWS正异常响应,南部有较弱的负异常。东北太平洋VWS以强的负异常响应为主。北大西洋VWS出现与同期时相反的自南向北的正-负-正异常响应。SSTID正位相可以对至少15 a后的VWS年代际变化产生调控作用,并存在一定的海域间的差异和传播特征。出现海域间差异的原因值得在未来的研究工作中进一步探究。
北半球TC活跃区内600 hPa相对湿度作为另一个SSTID调控GPI变化的关键因子,其对超前0~15 a SSTID正位相的响应也存在随时间的演变(图 11)。随着SSTID超前时间从同期增加到9 a,印度洋TC活跃区西部持续表现为偏湿响应,并且印度洋东部由偏干转变为偏湿。在西北太平洋TC活跃区,相对湿度由同期时“西干-东湿”响应转变为滞后9 a时一致的偏湿响应。在东北太平洋的偏干异常响应逐渐减弱。在北大西洋TC活跃区,偏湿异常逐渐增强。而随着SSTID超前时间继续增加至15 a,印度洋、西北太平洋东部和东北太平洋东部均出现了显著的偏干异常响应,不利于GPI增强和TC活动的发展。
因此,超前的7—11月SSTID正位相引起的北半球TC活跃区内600 hPa相对湿度偏湿异常响应在9 a左右达到最强。在超前9 a的7—11月SSTID的影响下,有更多的水汽得以进入对流层上层并释放凝结潜热。前人研究指出,空气湿度增大会增强对流活动,比如TC生成[55-56]。中低层湿度正异常可以增强大气不稳定性,加强潜热释放,配合TC生成所必须的低压扰动,有利于空气块提升到自由凝结高度,进而从大气中获取能量增强对流。与超前9 a的7—11月SSTID有关的北半球对流层空气变湿加速了对流增长的过程,有利于7—11月GPI增强,进而有助于北半球TC发展和增强。
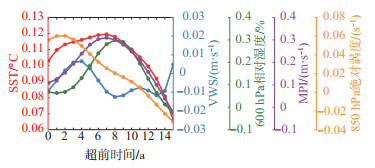
3.3 北半球TC活跃区SST与GPI的综合影响为了进一步解释SSTID对7—11月北半球平均TC强度的超前影响在9 a左右达到最强的原因,图 12给出了7—11月北半球TC活跃区内空间平均的SST、VWS、600 hPa相对湿度、MPI和850 hPa绝对涡度对SSTID的响应随SSTID超前年份的变化。在北半球TC活跃区内,7—11月SST、相对湿度和MPI对SSTID的响应随SSTID超前时间呈现出先增大后减小的变化,在7~9 a前后达到最强。VWS对SSTID的响应出现波动特征,在SSTID超前8 a前后VWS负异常响应最强。由于VWS出现负异常响应时有利于TC强度发展,因此与SSTID有关的VWS异常在滞后时间为8 a左右时对增强TC活动有最大贡献。绝对涡度的响应随着SSTID超前时间增加而不断减弱,但在滞后7~9 a前后依然为正异常响应,有助于气旋式扰动的发展。
|
图 12 7—11月北半球TC活跃区内空间平均的SST(红色线)、VWS(蓝色线)、600 hPa相对湿度(绿色线)、MPI (紫色线)和850 hPa绝对涡度(橙色线)对超前0~15 a归一化的7—11月SSTID的回归 Fig.12 Regression of spatially averaged SST (red line), VWS (blue line), relative humidity at 600 hPa (green line), MPI (purple line), and absolute vorticity (orange line) at 850 hPa during the period of July-November over the NH TC active regions onto the normalized July-November SSTID leading 0-15 years |
综合来看,北半球TC活跃区内的SST正异常在滞后SSTID 9 a前后达到较强的状态,从而对TC活动和TC发展产生影响。与7—11月GPI相关的4个因子对7—11月SSTID的综合响应导致SSTID对GPI有9 a左右的超前影响,GPI进而同期影响北半球平均TC强度。
上文分析了与7—11月SSTID有关的SST、GPI及其相关因子分量与7—11月北半球平均TC强度的显著相关关系。7—11月,与SSTID有关的SST变暖有利于降低北半球TC的最低中心气压,并为上升运动提供有利的背景条件。因此,有更多的能量从海洋释放到大气,并对TC活动增强有直接贡献。另外,SST变暖会增加空气中的水汽含量,增强对流层的湿度不稳定。北半球SST变暖可以引起大气柱垂直稳定性的变化,调控TC发展。TC强度与眼墙区域的上升运动密切相关,空气块需要从海洋和大气中获得能量来对抗重力作用。与7—11月SSTID有关的SST变暖、对流层空气变湿、垂直风切变减弱导致了北半球TC活跃区GPI的增加,并为TC增强提供了有利的环境。因此,海洋表面和大气低层的相互作用增强了深对流,并为TC发展提供了能量。基于此,超前9 a的SSTID和7—11月北半球平均TC强度之间的强正相关关系得以解释。
4 7—11月北半球平均TC强度年代际预测模型基于7—11月SSTID对7—11月北半球平均TC强度年代际变率超前9 a的调控作用,可以建立对7—11月北半球平均TC强度预测的物理模型,即
| $ \widetilde{\operatorname{Int}}(T)=a+b \operatorname{SSTID}(T-9)+c T, $ | (11) |
其中:
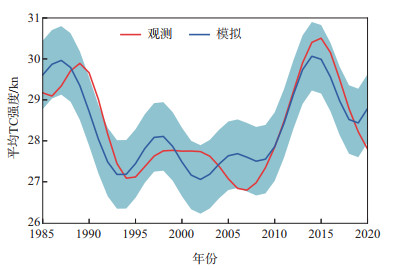
图 13展示了观测和模拟的1985—2020年7—11月北半球平均TC强度年代际分量。模拟值基于1976—2011年7—11月SSTID。在基于7—11月SSTID的年代际预测模型中,系数a=33.37,b=14.87,c=4.13×10-2。模型模拟的7—11月北半球平均TC强度能够复现其观测。特别地,模型能够模拟出7—11月北半球平均TC强度在1990年代快速下降、2010年代快速上升,以及在1990—2005年间的波动特征。这与7—11月SSTID在1980年代快速下降、2000年代快速上升和在1985—2005年间的波动特征是吻合的(图 4)。观测与模式模拟的7—11月北半球平均TC强度序列相关系数为0.88,通过了置信水平为95%的显著性检验,均方根误差为0.52。这表明7—11月SSTID和北半球平均TC强度变化的年代际变率在低频变化上表现出了较高的可预报性。7—11月SSTID与北半球平均TC强度之间稳健的超前滞后相关关系意味着7—11月北半球平均TC强度在年代际时间尺度上的变化可以由7—11月SSTID较好地预测。
|
图 13 观测和模拟的7—11月北半球平均TC强度年代际变化(1985—2020年)(观测为7 a Butterworth低通滤波后的序列,模型为基于7—11月SSTID(1976—2011年)的年代际预测模型(式(11));浅蓝色阴影区域表示模拟值的2-sigma不确定性区间) Fig.13 Observed and modeled variation of NH July-November average TC intensity during the period of 1985-2020 (the observation is from a 7-year Butterworth low-pass filtering, and the model is from the decadal prediction model (Formula 11) based on July-November SSTID (1976-2011); the light blue shaded area indicates the 2-sigma uncertainty range of the modeled values) |
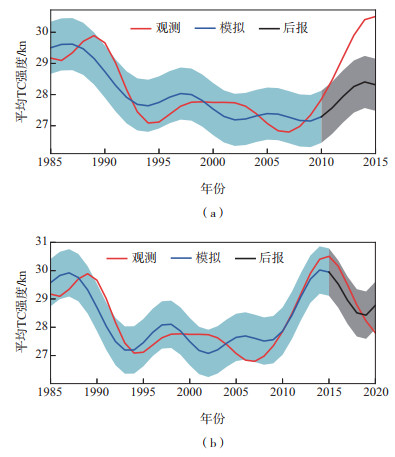
为了表现基于7—11月SSTID年代际预测模型的高性能,对7—11月北半球平均TC强度年代际变化进行了两组后报试验,分别是基于2002—2006年7—11月SSTID对2011—2015年7—11月北半球平均TC强度的后报(图 14a)和基于2007—2011年7—11月SSTID对2016—2020年7—11月北半球平均TC强度的后报试验(图 14b)。两组后报试验能够很好地捕捉到7—11月北半球平均TC强度在2015年之前的增强和2016年之后的减弱。因此,后报试验表明:一方面,7—11月SSTID的确是理解7—11月北半球平均TC强度年代际变化的有效因子;另一方面,基于7—11月SSTID的年代际预测是可靠的,模型可以被用来进行7—11月北半球平均TC强度的年代际预测。
|
图 14 观测、模拟和后报的7—11月北半球平均TC强度年代际变化(图a中观测是7 a Butterworth低通滤波后的序列(1985—2015年),模拟和后报分别基于1976—2001和2002—2006年7—11月SSTID,图b中观测时间段为1985—2020年,模拟和后报分别为基于1976—2006年和2007—2011年7—11月SSTID;浅蓝色和灰色阴影区域分别表示模拟和后报值的2-sigma不确定性区间) Fig.14 Observed, modeled, and hindcasted variation of NH July-November average TC intensity (in Fig. 14a, the observation (1985-2015) is from a 7-year Butterworth low-pass filtering, the model and the hindcast are based on July-November SSTID during the periods of 1976-2001 and 2002-2006, respectively; in Fig. 14b, the observation period is 1985-2020, the model and the hindcast are based on July-November SSTID during the periods of 1976-2006 and 2007-2011, respectively; the light blue and gray shaded areas indicate the 2-sigma uncertainty range of the modeled and hindcasted values, respectively) |
但必须指出,基于SSTID对7—11月北半球平均TC强度的模型在后报试验的表现上存在一定缺陷。后报试验能够捕捉到7—11月北半球平均TC强度增强和减弱的波动特征,但在增强和减弱的振幅上存在一定偏差。由于该模型是一个简单的线性回归模型,7—11月SSTID仅是调控7—11月北半球平均TC强度年代际变化的众多因子之一。所以在实际的预测工作中,有必要考虑基于多因子的非线性模型,来增强预测结果的准确性。但基于7—11月SSTID对7—11月北半球平均TC强度的年代际预测模型的较好表现是值得肯定的。
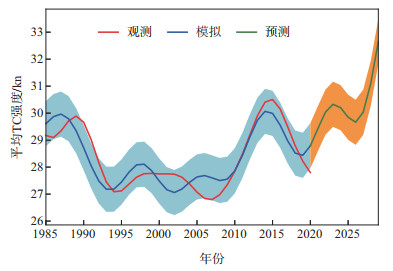
用基于SSTID的模型对7—11月北半球平均TC强度进行未来9 a(2021—2029年)的年代际预测(图 15)。模型使用了1976—2020年的历史数据。年代际预测结果表明在未来9 a,7—11月北半球平均TC强度总体上呈现出增强的趋势,在2023—2026年出现短暂下降。由于7—11月SSTID在2012—2020年进入正位相后总体上持续增强,北半球有不断增强的SST正异常,导致基于SSTID对7—11月北半球平均TC强度的年代际预测模型呈现出TC总体上不断增强的结果。同时,7—11月SSTID在2014—2017年短暂下降,导致该模型预测的北半球平均TC强度在2023—2026年也出现了短暂下降。二者是互相对应的。另一方面,年代际预测模型也考虑了全球变暖的线性增暖趋势。在7—11月SSTID进入正位相并不断增强和全球变暖的线性部分叠加作用下,未来7—11月北半球平均TC强度将不断增强。这与前人对全球变暖背景下TC强度继续增强这一预测相吻合[9, 57]。值得关注的是,TC强度在2020年代末可能会增强到近45 a来破纪录的强度。
|
图 15 观测、模拟和预测的7—11月北半球平均TC强度年代际变化(观测是7 a Butterworth低通滤波后的序列(1985—2020年),模拟和预测分别基于1976—2011和2012—2020年7—11月SSTID;浅蓝色和黄色阴影区域分别表示模拟和预测值的2-sigma不确定性区间) Fig.15 Observed, modeled, and predicted variation of NH July-November average TC intensity (the observation (1985-2020) is from a 7-year Butterworth low-pass filtering, the model and the prediction are baseds on July-November SSTID during the periods of 1976-2011 and 2012-2020, respectively; the light blue and yellow shaded areas indicate the 2-sigma uncertainty range of the modeled and predicted values, respectively) |
本文探究了7—11月SSTID对北半球平均TC强度年代际变率的影响,并通过7—11月SSTID对北半球平均TC强度进行了年代际预测。通过对观测资料的分析,发现SSTID与7—11月北半球TC平均强度存在较强的位相间关系。结果表明,7—11月,SSTID是北半球TC平均强度年代际变化的主要影响因子之一。在年代际时间尺度上,7—11月SSTID正位相超前北半球TC平均强度9 a左右时达到最大正相关,即SSTID超前北半球TC平均强度约9 a进行位相转换。
观测分析表明,与7—11月SSTID正位相相关的北半球SST异常增暖信号在9 a后移动到热带海域。北半球TC活跃区海洋作为海洋桥以SST的形式存储了超前9 a的SSTID信号,其正异常响应对北半球平均TC强度增强起到调控作用。同时,北半球TC活跃区大气作为大气桥,可以将超前9 a的SSTID信号传递到大气中,进而作用于北半球平均TC强度,该大气过程可以GPI对SSTID的响应作为表征。与7—11月GPI相联系的VWS、600 hPa相对湿度、MPI和850 hPa绝对涡度等大气条件的综合作用提供了有利于北半球TC增强的背景环境。垂直风切变和600 hPa相对湿度的综合影响在其中起关键作用。7—11月,北半球SST变暖,对流层空气变湿,增强了大气不稳定性,为深对流发展和北半球TC增强提供了更多能量。同时,7—11月SSTID引起的北半球TC活跃区对流层垂直风切变减小,有利于初始气旋式扰动发展成为较强TC。
基于SSTID的线性模型对7—11月北半球TC平均强度的年代际变化模拟表现出良好的性能。后报试验进一步证明了模型能够捕捉到观测中的波动特征。7—11月SSTID在进入2010年代后持续增强,北半球SST异常持续增强,因此基于7—11月SSTID对下个年代的预测表明北半球TC平均强度呈现出总体增强的趋势,甚至在2020年代末出现破记录的增强。
针对本文研究的主题,尚有不少重要研究工作有待进一步开展。比如,受限于观测手段,目前有效的TC强度观测数据长度受到限制。因此,在未来的工作中,需要等待更长的可靠的数据集来进一步验证SSTID与北半球TC平均强度关系的稳健性。另外,模式模拟也可以帮助验证在观测数据中寻找到的相关关系和作用机制。因此,在未来工作中有必要通过模式模拟的手段帮助深入理解和验证SSTID对北半球TC平均强度的作用过程。同时,虽然SSTID总体上表现为北半球SST一致的变化,但SSTID对北半球TC活跃区SST和对大气环境场的影响都存在着一定的海域间差异,探究造成其海域间差异的原因和海域间差异造成的海洋和大气响应,有助于进一步揭示SSTID的形成原因及其对海洋、大气的影响。
值得注意的是,超前滞后分析(图 6)显示,除了SSTID超前7—11月北半球平均TC强度9 a左右时二者达到最大正相关之外,7—11月北半球平均TC强度超前SSTID 11 a左右时二者达到最大负相关(相关系数为-0.91,通过置信水平为95%的显著性检验)。这意味着,超前11 a的7—11月北半球平均TC强度可以解释7—11月SSTID约83%的方差。当7—11月北半球平均TC强度偏强时,约11 a后,7—11月SSTID负异常,即北半球SST负异常,南半球SST正异常;同理,当7—11月北半球平均TC强度偏弱时,约11 a后,7—11月SSTID正异常,即北半球SST正异常,南半球SST负异常。该现象表明,除了7—11月SSTID会超前影响北半球平均TC强度外,7—11月北半球平均TC强度可能也会对SSTID产生影响。SSTID是南北半球间热量差异的表征,因此北半球平均TC强度会影响到南北两半球的热量再分配。前人研究发现,AMO作为SSTID在大西洋的表现形式,与海洋经向翻转环流带来的海水热输送有关[58-59],并且TC活动与北大西洋翻转环流关系密切[36]。7—11月北半球平均TC强度超前影响一个年代后的SSTID位相转变,可能为解释海洋热量在南北半球间的输送提供新的思路。但是,探究7—11月北半球平均TC强度经过11 a影响SST的过程是一个复杂的问题。这涉及到北半球TC活动如何跨时间尺度和跨空间尺度影响全球性的年代际信号的问题。对该问题的探究不仅需要建立跨尺度海气相互作用的理论,还需要通过观测数据和模式模拟来探究其动力过程。因此,在未来的工作中需要进一步探究该问题。
| [1] |
SUN C, LI J P, JIN F F, et al. Sea surface temperature inter-hemispheric dipole and its relation to tropical precipitation[J]. Environ Res Lett, 2013, 8(4): 044006. DOI:10.1088/1748-9326/8/4/044006 |
| [2] |
FOLLAND C K, PARKER D E, COLMAN A W, et al. Large scale modes of ocean surface temperature since the late nineteenth century[M]//NAVARRA A. Beyond El Niño: decadal and interdecadal climate variability. Berlin/Heidelberg: Springer, 1999: 73-102.
|
| [3] |
ENFIELD D B, MESTAS-NUÑEZ A M. Multiscale variabilities in global sea surface temperatures and their relationships with tropospheric climate patterns[J]. J Climate, 1999, 12(9): 2719-2733. DOI:10.1175/1520-0442(1999)012<2719:MVIGSS>2.0.CO;2 |
| [4] |
PARKER D, FOLLAND C, SCAIFE A, et al. Decadal to multidecadal variability and the climate change background[J]. J Geophys Res: Atmos, 2007, 112(D18): D18115. DOI:10.1029/2007JD008411 |
| [5] |
XUE J Q, SUN C, LI J P, et al. Divergent responses of extratropical atmospheric circulation to interhemispheric dipolar SST forcing over the two hemispheres in boreal winter[J]. J Climate, 2018, 31(18): 7599-7619. DOI:10.1175/JCLI-D-17-0817.1 |
| [6] |
薛佳庆. 海温半球间偶极子模态的时空特征及其全球气候影响[D]. 北京: 中国科学院大学, 2019.
|
| [7] |
XUE J Q, WANG B C, YU Y K, et al. Multidecadal variation of northern hemisphere summer monsoon forced by the SST inter-hemispheric dipole[J]. Environ Res Lett, 2022, 17(4): 044033. DOI:10.1088/1748-9326/ac5a65 |
| [8] |
吴彩铭, 任福民, 朱婧. 热带气旋灾害预评估模型研究回顾[J]. 海洋气象学报, 2022, 42(3): 13-22. |
| [9] |
EMANUEL K. Increasing destructiveness of tropical cyclones over the past 30 years[J]. Nature, 2005, 436(7051): 686-688. DOI:10.1038/nature03906 |
| [10] |
LIU K S, CHAN J C L. Inactive period of western North Pacific tropical cyclone activity in 1998-2011[J]. J Climate, 2013, 26(8): 2614-2630. DOI:10.1175/JCLI-D-12-00053.1 |
| [11] |
KNUTSON T, CAMARGO S J, CHAN J C L, et al. Tropical cyclones and climate change assessment. Part I: detection and attribution[J]. Bull Amer Meteor Soc, 2019, 100(10): 1987-2007. DOI:10.1175/BAMS-D-18-0189.1 |
| [12] |
KNUTSON T, CAMARGO S J, CHAN J C L, et al. Tropical cyclones and climate change cssessment. Part Ⅱ: projected response to anthropogenic warming[J]. Bull Amer Meteor Soc, 2020, 101(3): E303-E322. DOI:10.1175/BAMS-D-18-0194.1 |
| [13] |
WANG X, ZHOU W, LI C Y, et al. Comparison of the impact of two types of El Niño on tropical cyclone genesis over the South China Sea[J]. Int J Climatol, 2014, 34(8): 2651-2660. DOI:10.1002/joc.3865 |
| [14] |
LIU Y, CHEN G H. Intensified influence of the ENSO Modoki on boreal summer tropical cyclone genesis over the western North Pacific since the early 1990s[J]. Int J Climatol, 2018, 38(s1): e1258-e1265. |
| [15] |
PATRICOLA C M, CAMARGO S J, KLOTZBACH P J, et al. The influence of ENSO flavors on western North Pacific tropical cyclone activity[J]. J Climate, 2018, 31(14): 5395-5416. DOI:10.1175/JCLI-D-17-0678.1 |
| [16] |
孔蕴淇, 范伶俐, 李俊杰. 两类厄尔尼诺事件对登陆中国热带气旋的影响[J]. 海洋气象学报, 2020, 40(4): 77-88. |
| [17] |
ZHOU Q, WEI L X, ZHANG R Y. Influence of Indian Ocean Dipole on tropical cyclone activity over western North Pacific in boreal autumn[J]. J Ocean Univ China, 2019, 18(4): 795-802. DOI:10.1007/s11802-019-3965-8 |
| [18] |
WU Q, WANG X C, TAO L. Interannual and interdecadal impact of Western North Pacific Subtropical High on tropical cyclone activity[J]. Climate Dyn, 2020, 54(3/4): 2237-2248. |
| [19] |
周磊, 陈大可, 雷小途, 等. 海洋与台风相互作用研究进展[J]. 科学通报, 2019, 64(1): 60-72. |
| [20] |
邓孟珂, 田鹏飞, 杨华栋, 等. 印度洋海温异常对西北太平洋台风的影响及机制研究[J]. 海洋气象学报, 2021, 41(3): 60-68. |
| [21] |
陈光华, 黄荣辉. 西北太平洋低频振荡对热带气旋生成的动力作用及其物理机制[J]. 大气科学, 2009, 33(2): 205-214. DOI:10.3878/j.issn.1006-9895.2009.02.01 |
| [22] |
SUN C, LIU Y S, GONG Z Q, et al. The footprint of Atlantic Multidecadal Oscillation on the intensity of tropical cyclones over the western North Pacific[J]. Front Earth Sci, 2020, 8: 604807. DOI:10.3389/feart.2020.604807 |
| [23] |
LANDSEA C W. Hurricanes and global warming[J]. Nature, 2005, 438(7071): E11-E12. |
| [24] |
刘贝, 周倩莹, 付东洋. 海面温度对南海台风强度的影响[J]. 广东海洋大学学报, 2019, 39(1): 97-104. |
| [25] |
李畅, 姜霞, 沈新勇. 阿拉伯海热带气旋生成特征分析[J]. 海洋气象学报, 2021, 41(4): 62-72. |
| [26] |
KOSSIN J P, OLANDER T L, KNAPP K R. Trend analysis with a new global record of tropical cyclone intensity[J]. J Climate, 2013, 26(24): 9960-9976. DOI:10.1175/JCLI-D-13-00262.1 |
| [27] |
HUANG B Y, THORNE P W, BANZON V F, et al. Extended Reconstructed Sea Surface Temperature, version 5 (ERSSTv5): upgrades, validations, and intercomparisons[J]. J Climate, 2017, 30(20): 8179-8205. DOI:10.1175/JCLI-D-16-0836.1 |
| [28] |
KNAPP K R, KRUK M C, LEVINSON D H, et al. The International Best Track Archive for Climate Stewardship (IBTrACS): unifying tropical cyclone data[J]. Bull Amer Meteor Soc, 2010, 91(3): 363-376. DOI:10.1175/2009BAMS2755.1 |
| [29] |
KRUK M C, KNAPP K R, LEVINSON D H. A technique for combining global tropical cyclone best track data[J]. J Atmos Oceanic Technol, 2010, 27(4): 680-692. DOI:10.1175/2009JTECHA1267.1 |
| [30] |
KALNAY E, KANAMITSU M, KISTLER R, et al. The NCEP/NCAR 40-year reanalysis project[J]. Bull Amer Meteor Soc, 1996, 77(3): 437-472. DOI:10.1175/1520-0477(1996)077<0437:TNYRP>2.0.CO;2 |
| [31] |
WU L G, WANG B, BRAUN S A. Implications of tropical cyclone power dissipation index[J]. Int J Climatol, 2008, 28(6): 727-731. DOI:10.1002/joc.1573 |
| [32] |
MANN H B. Nonparametric tests against trend[J]. Econometrica, 1945, 13(3): 245-259. DOI:10.2307/1907187 |
| [33] |
MARDEN J I, KENDALL M G, GIBBONS J D. Rank correlation methods (5th ed)[J]. J Am Stat Assoc, 1992, 87(417): 249. DOI:10.2307/2290477 |
| [34] |
PYPER B J, PETERMAN R M. Comparison of methods to account for autocorrelation in correlation analyses of fish data[J]. Can J Fish Aquat Sci, 1998, 55(9): 2127-2140. DOI:10.1139/f98-104 |
| [35] |
XIE F, LI J P, TIAN W S, et al. The relative impacts of El Niño Modoki, canonical El Niño, and QBO on tropical ozone changes since the 1980s[J]. Environ Res Lett, 2014, 9(6): 064020. DOI:10.1088/1748-9326/9/6/064020 |
| [36] |
GONG Z Q, LIU Y S, SUN C, et al. Linking AMOC variations with the multidecadal seesaw in tropical cyclone activity between eastern North Pacific and Atlantic[J]. J Geophys Res: Oceans, 2021, 126(8): e2021JC017308. |
| [37] |
VON STORCH H, ZWIERS F W. Statistical analysis in climate research[M]. Cambridge: Cambridge University Press, 1999.
|
| [38] |
LI J P, SUN C, JIN F F. NAO implicated as a predictor of Northern Hemisphere mean temperature multidecadal variability[J]. Geophys Res Lett, 2013, 40(20): 5497-5502. DOI:10.1002/2013GL057877 |
| [39] |
LI J P, XIE T J, TANG X X, et al. Influence of the NAO on wintertime surface air temperature over East Asia: multidecadal variability and decadal prediction[J]. Adv Atmos Sci, 2022, 39(4): 625-642. DOI:10.1007/s00376-021-1075-1 |
| [40] |
ZHAO J W, ZHAN R F, WANG Y Q, et al. A multiscale-model-based near-term prediction of tropical cyclone genesis frequency in the Northern Hemisphere[J]. J Geophys Res: Atmos, 2022, 127(22): e2022JD037267. |
| [41] |
LAKSHANI W A E, ZHOU W. Observed decadal shifts and trends in global tropical cyclone activities from 1980 to 2021[J]. Atmos Ocean Sci Lett, 2022, 16(2): 100321. |
| [42] |
SONG K X, ZHAO J W, ZHAN R F, et al. Confidence and uncertainty in simulating tropical cyclone long-term variability using the CMIP6-HighResMIP[J]. J Climate, 2022, 35(19): 2829-2849. |
| [43] |
EMANUEL K A, NOLAN D S. Tropical cyclone activity and the global climate system[C]//American Meteorology Society. Preprints, 26th Conference on Hurricanes and Tropical Meteorology. Miami: American Meteorology Society, 2004: 240-241.
|
| [44] |
BISTER M, EMANUEL K A. Dissipative heating and hurricane intensity[J]. Meteor Atmos Phys, 1998, 65(3): 233-240. |
| [45] |
EMANUEL K A. Sensitivity of tropical cyclones to surface exchange coefficients and a revised steady-state model incorporating eye dynamics[J]. J Atmos Sci, 1995, 52(22): 3969-3976. DOI:10.1175/1520-0469(1995)052<3969:SOTCTS>2.0.CO;2 |
| [46] |
GILFORD D M. pyPI (v1.3): tropical cyclone potential intensity calculations in Python[J]. Geosci Model Dev, 2021, 14(5): 2351-2369. |
| [47] |
WANG S G, CAMARGO S J, SOBEL A H, et al. Impact of the tropopause temperature on the intensity of tropical cyclones: an idealized study using a mesoscale model[J]. J Atmos Sci, 2014, 71(11): 4333-4348. |
| [48] |
WING A A, EMANUEL K, SOLOMON S. On the factors affecting trends and variability in tropical cyclone potential intensity[J]. Geophys Res Lett, 2015, 42(20): 8669-8677. |
| [49] |
BISTER M, EMANUEL K A. Low frequency variability of tropical cyclone potential intensity 1: interannual to interdecadal variability[J]. J Geophys Res: Atmos, 2002, 107(D24): 4801. |
| [50] |
LI J P, ZHENG F, SUN C, et al. Pathways of influence of the Northern Hemisphere mid-high latitudes on East Asian climate: a review[J]. Adv Atmos Sci, 2019, 36(9): 902-921. |
| [51] |
LI J P. Impacts of annular modes on extreme climate events over the East Asian monsoon region[M]//LI J P, SWINBANK R, GROTJAHN R, et al. Dynamics and predictability of large-scale high-impact weather and climate events. Cambridge: Cambridge University Press, 2015: 343-353.
|
| [52] |
CHAN J C L, SHI J E, LIU K S. Improvements in the seasonal forecasting of tropical cyclone activity over the western North Pacific[J]. Wea Forecasting, 2001, 16(4): 491-498. |
| [53] |
MEI W, XIE S P, PRIMEAU F, et al. Northwestern Pacific typhoon intensity controlled by changes in ocean temperatures[J]. Sci Adv, 2015, 1(4): e1500014. |
| [54] |
WU L G, ZHAO H K. Dynamically derived tropical cyclone intensity changes over the western North Pacific[J]. J Climate, 2012, 25(1): 89-98. |
| [55] |
GETTELMAN A, SEIDEL D J, WHEELER M C, et al. Multidecadal trends in tropical convective available potential energy[J]. J Geophys Res: Atmos, 2002, 107(D21): 4606. |
| [56] |
CHEN X M, ZHANG J A, MARKS F D. A thermodynamic pathway leading to rapid intensification of tropical cyclones in shear[J]. Geophys Res Lett, 2019, 46(15): 9241-9251. |
| [57] |
EMANUEL K. 100 years of progress in tropical cyclone research[J]. Meteor Monogr, 2018, 59(1): 15.1-15.68. |
| [58] |
LATIF M, BÖNING C, WILLEBRAND J, et al. Is the thermohaline circulation changing?[J]. J Climate, 2006, 19(18): 4631-4637. |
| [59] |
KEENLYSIDE N S, LATIF M, JUNGCLAUS J, et al. Advancing decadal-scale climate prediction in the North Atlantic sector[J]. Nature, 2008, 453(7191): 84-88. |
 2023, Vol. 43
2023, Vol. 43


