海洋表面因受天体运动产生的引潮力的作用,海水会出现周期性涨落的现象,称此现象为潮汐[1]。潮流的变化会影响海上船舶的进出、货物的进出口作业和施工计划的制定等。青岛港口涉及到运输、系泊和沉放等相关业务,都与潮汐直接相关。
青岛港位于黄海西海岸,半岛南岸西部的胶州湾口附近,港内水域宽阔,为我国著名的天然良港。对潮汐的调和分析即找出影响某地潮汐的若干主要分潮,从而分析该处潮汐特性,或对该处潮汐变化进行预报。近代海洋潮汐学产生于17世纪后半叶,其任务是研究海洋潮汐的成因,分析潮汐特征及其随时间的变化规律,并作出预报[2-5]。平衡潮理论于1687年由牛顿提出。1868年,开尔文设计了用于预报的调和分析法,并发明潮汐预报机。DARWIN[6]最早采用调和分析法预报潮汐,之后DOODSON[7-8]改进了调和分析法,提高了计算精度。HORN[9]最早用计算机进行潮汐调和分析,并在1960年第一个运用计算机进行潮汐调和分析的计算。近年来,我国学者改进原有理论方法,并应用到本国实际情况中。郑有任等[10]采用T_TIDE程序对南海北部进行调和分析,总结海域潮汐特征,并利用结果预测潮高,比较全年和分季节的结果,统计分析预测结果与实测数据的残差。程诚和郑小萌[11]应用潮汐资料分析T_TIDE程序,对比连云港站点的调和分析结果与实测数据的误差,并根据计算的调和常数进行潮位预测分析。尹朝晖等[12]对工程施工海域的潮汐资料进行调和分析,并探究不同分潮个数对预报精度的影响。
本文对青岛港2019年全年逐时潮位资料进行调和分析,之后从2019年逐时潮高的调和分析结果中选择不同分潮建立调和预报模型,进而对2019年1月的潮高进行预测,通过对相对误差、判定系数结果进行分析,确定最优调和预报模型。
1 分析原理与数据 1.1 调和分析法潮汐静力理论(或称平衡潮理论)[13]是研究海水在引潮力作用下产生潮汐过程的理论,仅分析潮汐现象变化的基本规律和特点,不能获得具体的潮汐变化规律。为研究青岛港口潮汐的规律,据观测的实时潮汐水位数据进行调和分析,得到其主要分潮的调和常数,然后进行潮汐预测。
调和分析法[14]是根据实测潮位数据计算各分潮的调和常数,即分潮振幅和分潮迟角,然后应用两者预测潮位。为降低调和分析模型预报产生的偏差,研究人员常选取振幅较大的分潮进行预测。根据潮汐周期性运动的特点,调和分析法将潮汐视为若干个余弦函数的叠加,故潮汐水位可由下式表示:
| $ h(t)=\sum\limits_{k=1}^{n} f_{k} H_{k} \cos \left(\sigma_{k} t+v_{k}+u_{k}-g_{k}\right)+H_{0} $ | (1) |
式中:n为分潮数量,fk为交点因子,Hk为分潮振幅,σk为分潮角速度,vk为分潮初相位角,uk为天文相角的交角订正角,gk为迟角,H0为海平面,故每个分潮为f H cos(σt+v+u-g)。其中f、σ、(v+u)均已知,故只需求出每个分潮的H和g,则此分潮便可求出。H和g称为调和常数。
传统的潮汐调和分析常采用FOREMAN and NEUFELD[15]基于FORTRAN程序编写的软件进行,但古典潮汐计算理论忽略了对近日点的调制。2002年,PAWLOWICZ et al.[16]在FOREMAN and NEUFELD[15]程序的基础上进行改进,发表了T_TIDE潮汐处理软件包。相比于FOREMAN and NEUFELD[15]的程序,T_TIDE程序可对整年或较短的潮汐资料进行调和分析,还可解释未确定的潮汐成分,所得分析结果包含置信区间[17-20]。此外,T_TIDE程序也允许少量的缺测存在。t_predic.m利用t_tide.m得到的调和常数预测未来某时刻的潮汐水位。本文利用T_TIDE工具箱对青岛港口区域进行潮汐的调和分析。
1.2 资料来源与处理方法文中收集了2019年1月1日—12月31日青岛港验潮站逐小时的潮位观测资料。青岛港验潮站位于胶州湾口东北方,座落于青岛大港一号码头,即36.08°N,120.32°E,港池由防波堤环抱而成,其入口呈喇叭形向西南敞开,最窄处宽约270 m,港池内水深一般为5~13 m。该港池为大型固定码头,此次仿真实验数据来源于中国港口网(http://www.chinaports.com/tidal)
使用T_TIDE程序包执行带有节点校正、推理的古典调和分析,选择传统的最小平方法求解青岛港的调和常数值,并用Matlab加载和分析时间序列,对青岛港每日不同时刻的潮位情况数据进行分析。其中t_tide.m用于分析,t_predic.m用于潮汐预报。具体步骤如下:
(1) 数据预处理。对原始资料的奇异点进行滤波处理,去掉毛刺。在处理极少部分缺测资料时,利用GIL and DE TORO[21]介绍的最小二乘插值法进行插值,并使用格林尼治标准时。
(2) 程序实现。首先,读取原始潮位数据。接着,使用t_tide分析逐时的潮位资料,得到输出参数分潮的符号(name)、振幅(amp)、迟角(pha)、信噪比(snr)、回报的潮位(xout)等。一般认为信噪比Vsnr>2的分潮是显著的。
(3) 潮汐预报。调和分析结束后,用t_predic进行潮汐的预报,得到不含计算数据平均值的预报潮位。
2 结果与分析采用PAWLOWICZ et al.[16]编写的T_TIDE软件包进行验潮站潮位资料的调和分析和预报。首先,分析青岛验潮站一号码头2019年全年潮汐水位数据的性质。其次,为研究潮位资料长度与分潮振幅、平均海平面的关系,将全年资料分成不同的时间长度,对比分析仿真结果的变化。之后,选择不同分潮建立调和预报模型,通过2019年1月潮位的回报检验模型可靠性,确定最优调和预报模型。最后,用改进的模型预报五号码头2019年8月的潮位变化,结合观测资料检验调和预报效果。
2.1 调和分析潮汐的性质选用青岛港验潮站2019年1月1日—12月31日全年间隔1 h的潮位资料进行调和分析,T_TIDE中设置开始时间为2019年1月1日,纬度为36.08°N,信噪比为2,并添加M10分潮(太阴浅水1/10日分潮)。各观测站利用所有的逐时观测节点,用K1分潮(太阴-太阳赤纬全日分潮)推P1分潮(太阳赤纬全日分潮),用S2分潮(太阳主要半日分潮)推K2分潮(太阴-太阳赤纬半日分潮),置信度为95%。而其他参数按文献[16]中确定的取值不变,计算出该站点处的调和常数。使用青岛港1 a长时间序列数据能够消除各个主要分潮的相互影响,故能得到代表性良好的调和常数。最终得到67个分潮的振幅、迟角、信噪比以及年平均海平面(239 cm),主要分潮的振幅贡献如图 1所示。
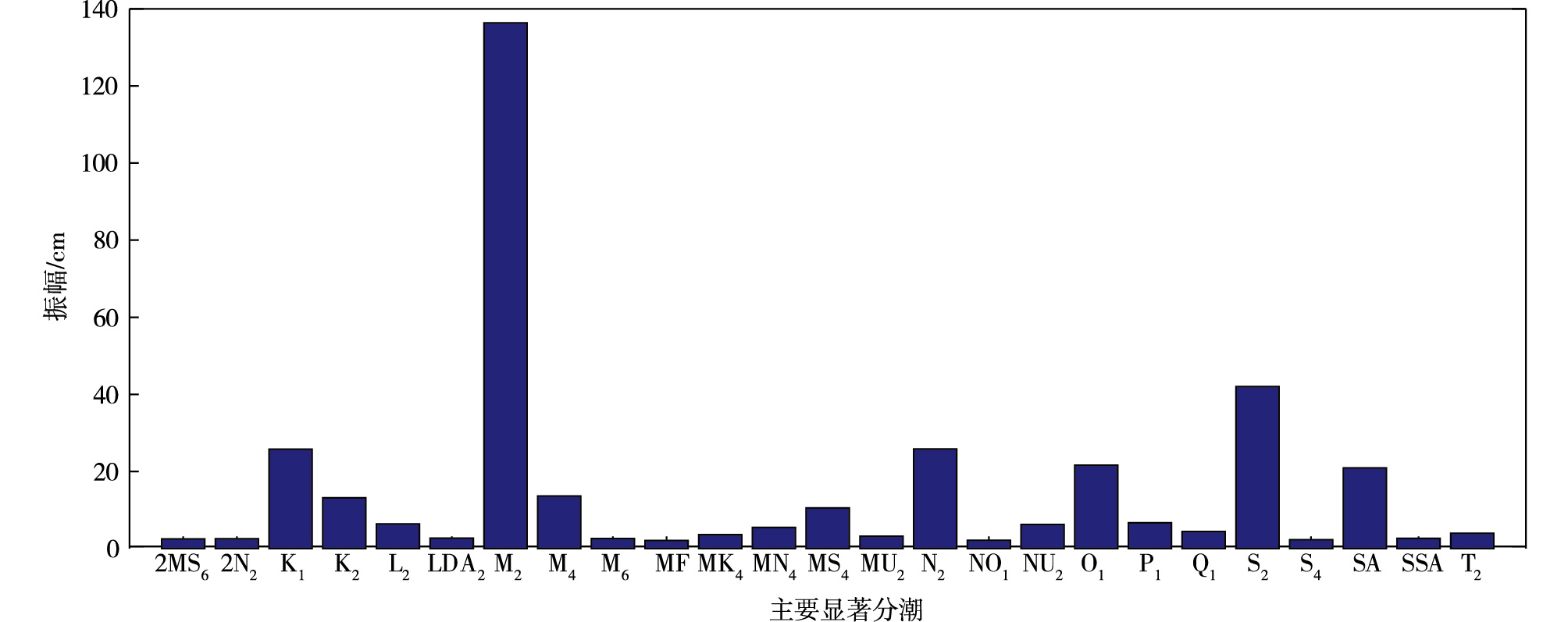
|
图 1 青岛港主要显著分潮振幅 Fig.1 Amplitude of main significant tidal components in Qingdao Port |
由图 1可以看出,青岛港潮汐以M2 分潮(太阴主要半日分潮)为主,其振幅高达136.4 cm。其次是S2分潮和N2分潮(太阴主要椭率半日分潮),振幅分别为42.0 cm和25.9 cm。K1分潮和O1分潮(太阴赤纬全日分潮)的振幅分别为25.8 cm和21.6 cm;SA分潮(太阳年周潮)的振幅为20.1 cm;M4 分潮(太阴浅水1/4日分潮)和MS4分潮(太阴-太阳浅水1/4日分潮)的振幅为13.6 cm和10.6 cm。
潮汐是各分潮叠加而形成的,实际中常用振幅较大的分潮M2、S2、K1、O1作为潮汐类型的判据[18]。潮汐类型的判别公式如下[22]:
| $ 规则半日潮:0 < \frac{{{H_{{{\rm{K}}_1}}} + {H_{{{\rm{O}}_1}}}}}{{{H_{{{\rm{M}}_2}}}}} \le 0.5 $ | (2) |
| $ 不规则半日潮 : 0.5<\frac{H_{\mathrm{K}_{1}}+H_{\mathrm{O}_{1}}}{H_{\mathrm{M}_{2}}} \leqslant 2.0 $ | (3) |
| $ 不规则全日潮: 2.0<\frac{H_{\mathrm{K}_{1}}+H_{0_{1}}}{H_{\mathrm{M}_{2}}} \leqslant 4.0 $ | (4) |
| $ 规则全日潮: \frac{H_{\mathrm{K}_{1}}+H_{0_{1}}}{H_{\mathrm{M}_{2}}}>4.0 $ | (5) |
其中,HK1、HO1和HM2,分别为分潮K1、O1和M2的平均振幅。在青岛港口中,分潮S2的振幅小于M2,故可用此划分标准。
通过公式(2)—(5)可以得到,该海域潮型数约为0.35,潮汐特征为规则半日潮,符合青岛港属于正规半日潮港的事实。
2.2 不同时段数据的调和分析利用T_TIDE的调和分析程序,研究不同潮位资料长度与分潮振幅、平均海平面的关系。为探究月资料和季节资料(即时间段长度为3个月)调和分析结果的关系,将2019年的潮汐水位数据逐时资料分成12个月和3个季节(春季:3月1日—5月31日;夏季:6月1日—8月31日;秋季:9月1日—11月30日)。同时,进一步探究季节资料和整年资料调和分析结果的关系。由Matlab仿真实验数据结果,绘制出12个月、3个季节资料长度的主要分潮对比图(图 2、3)以及各月平均海平面高度对比图(图 4)。此外,还得到了3个季节资料长度的平均海平面高度,分别为236 cm、257 cm、245 cm。
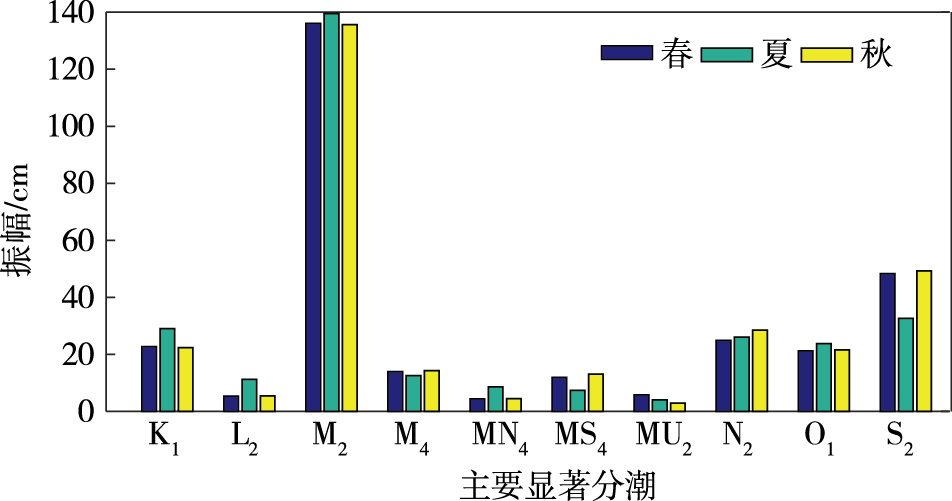
|
图 2 青岛港各季节主要显著分潮振幅比较 Fig.2 Comparison of amplitude of main significant tidal components in each season in Qingdao Port |

|
图 3 青岛港各月主要显著分潮振幅比较 Fig.3 Comparison of amplitude of main significant tidal components in each month in Qingdao Port |
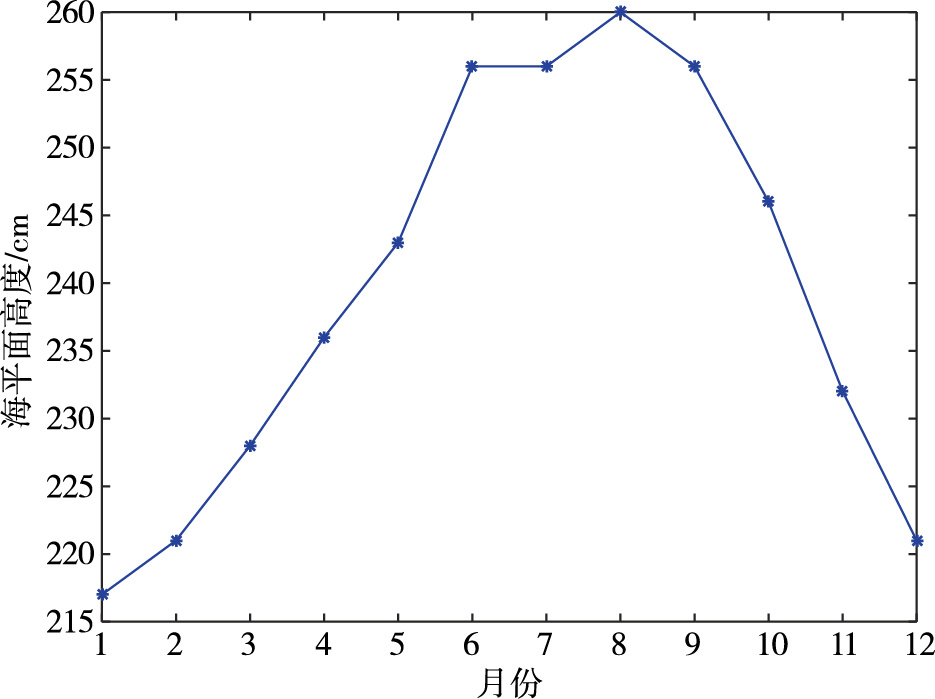
|
图 4 青岛港各月平均海平面比较 Fig.4 Comparison of monthly average sea level in each month in Qingdao Port |
由图 2和图 3知,3—11月和3个季节资料长度的仿真结果都主要受半日分潮M2的影响,其次受分潮S2、N2、K1和O1影响。其中M2分潮振幅在3月、4月、5月和春季分别为134.33 cm、136.43 cm、138.25 cm和136.04 cm,将3—5月结果与春季对比知,M2分潮振幅的平均差值为1.44 cm,其余分潮振幅的差值均在2.55 cm上下波动,其中存在2个较大差值,即在3月N2分潮处的7.77 cm和在5月S2分潮处的6.83 cm。对比6—8月和夏季的结果,其中M2分潮振幅在6月、7月、8月和夏季分别为144.97 cm、135.44 cm、136.09 cm和139.53 cm,其余分潮振幅差值的平均值为4.51 cm,同时也出现了2个较大差值,即在6月N2分潮处的9.92 cm和在8月S2分潮处的10.30 cm。对比9—11月和秋季的结果,在N2分潮处出现了1个较大差值。由图 1、2可知,3个季节和整年资料长度的结果也主要受分潮M2、S2的影响。对比其分潮振幅结果发现,其振幅的最大差值均出现在半日分潮S2处。由此可见,不同潮位资料长度对半日分潮S2、N2的振幅影响较大,但差值均小于11 cm,故所选取潮位资料长度对分潮振幅的影响较小。
青岛港逐月平均海平面高度如图 4所示,3个季节资料长度的平均海平面高度分别为236 cm、257 cm、245 cm,年平均海平面高度为239 cm。逐月海平面高度表现为“偏峰型”特征,峰值出现在8月,与季节海平面高度峰值出现在夏季(6—8月)相契合,而此时正值青岛地区的台风期。9号台风“利奇马”于2019年8月11日17时在青岛市南偏西方向约10 km的海面上(35.2°N,120.1°E)登陆,致使外围最大风力有9级(风速达23 m ·s-1)[23]。正是因为受台风影响,不同潮位资料长度的平均海平面的最大差值出现在8月和夏季。
对比1个月、3个月和整年的分潮振幅及平均海平面高度数据可知,仿真结果与所选取潮位资料长度几乎无关。但为建立最优的预报模型,下文使用由整年潮位资料长度得到的仿真结果进行分析预报。
2.3 潮汐调和分析效果检验理论上,在进行潮汐调和预报时选取的分潮个数越多,预测的精度越高。但实际应用中发现大部分分潮的振幅很小,因此可以忽略不计。为了定量分析分潮个数对调和回归效果的影响,选取由2019年全年调和分析所得的不同分潮个数,通过分析2019年1月的预测结果,确定最优的调和预报模型。
为评价不同预报模型仿真测试结果的性能,引入2个指标:(1)相对误差(E),指测量的绝对误差(即预测潮水位与实测潮水位的差值)与实测的潮水位之比,它能更好地反映测量的可信程度;(2)判定系数(R2),指统计学中“相关系数”的平方,用以表征两个变量的相关程度。其具体结果由公式(6)和公式(7)计算所得。
| $ {E_i} = \frac{{\left| {{{\hat y}_i} - {y_i}} \right|}}{{{y_i}}}, i = 1, 2, \cdots , n $ | (6) |
| $ {R^2} = \frac{{{{\left( {n\sum\limits_{i = 1}^n {{{\hat y}_i}} {y_i} - \sum\limits_{i = 1}^n {{y_i}} } \right)}^2}}}{{\left[ {n\sum\limits_{i = 1}^n {\hat y_i^2} - {{\left( {\sum\limits_{i = 1}^n {{{\hat y}_i}} } \right)}^2}} \right]\left[ {n\sum\limits_{i = 1}^n {y_i^2} - {{\left( {n\sum\limits_{i = 1}^n {{y_i}} } \right)}^2}} \right]}} $ | (7) |
式中:n为采集的数据数量,
采用增加、减少分潮数的方法建立最优回归模型,先将平均振幅从大到小进行排列,然后依次选取分潮数(5,10,15,……)进行仿真实验。选取5个分潮时,调和预报相对误差为0.205 8,判定系数为0.872 5;增加到25个分潮之后,调和预报相对误差降到0.106 6,判定系数增至0.969 4,预报效果可以得到明显提高;但是从25个分潮增加到50个时,则几乎没有改进(表 1)。
|
|
表 1 不同分潮个数调和预报的性能评价指标 Table 1 Performance evaluation index of harmonic forecast with different numbers of tidal components |
但是,对于量化研究而言,时间序列数据中存在异常值,故必须要对相对误差数据作预处理,使仿真数据更加客观,以便于更好地探究潮水位的规律。本文采取去极值的方法,用以降低极值对相对误差的影响,提升数据结论的准确性。选取5个分潮时,于1月25日15时出现一个极大值,数值为5.710 5, 剔除后的相对误差为0.155 0;当增加到25个分潮之后,同样于1月25日15时出现一个极大值,数值为2.945 5,剔除后的相对误差为0.089 6;但是从25个分潮增加到50个时,由去极值方法得到的相对误差波动幅度很小。
为确切地得到最优的调和预报模型,接着选取21、22、23和24个分潮进行调和预报,绘制出当分潮数为21、22、23和24个时的青岛港潮汐预测图(图 5)。由图 5可见,仿真结果和青岛港口的实际潮位基本一致。对比其相对误差,都在0附近上下起伏,但在16 h、40 h和132 h起伏较大。而16 h和40 h分别对应1月25日15时和26日15时,此时青岛的风力达到5级,温度日变量为7 ℃[24],故潮汐预测精度可能受大风、涌浪等非潮汐因素的影响。
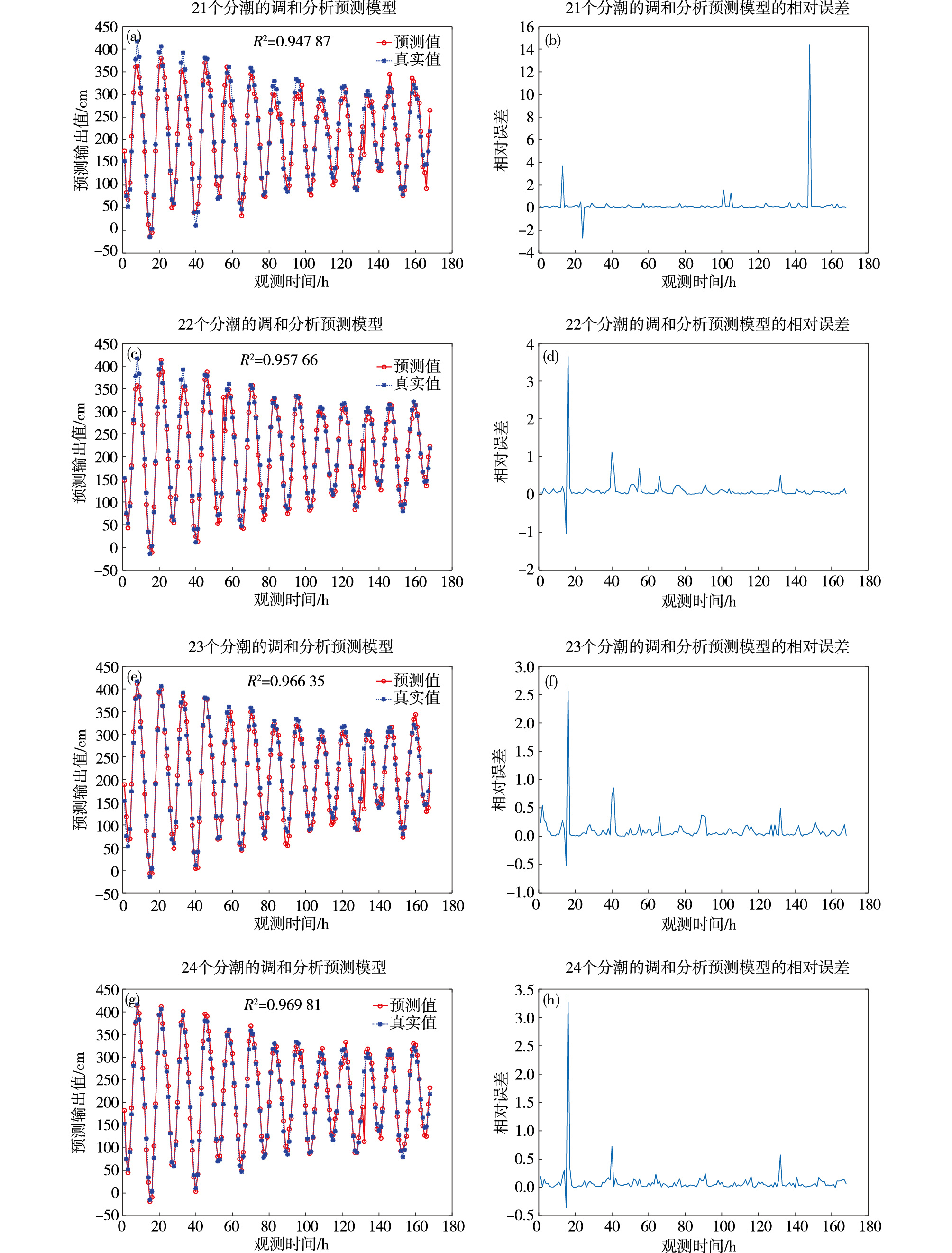
|
图 5 取21、22、23和24个分潮时的调和预报模型(a、c、e、g)及其相对误差(b、d、f、h) Fig.5 Harmonic forecast models (a/c/e/g) with 21, 22, 23, and 24 tidal components and their relative errors (b/d/f/h) |
为更加直观地对比数据,将图 5汇总成表 2。其中,选取21个分潮时,由图 4可见,于148 h(1月31日03时)出现一个极大值,为14.404 1,剔除后的相对误差为0.112 5;当增加到22、23、24个分潮之后,由图 5可知,均于16 h (1月25日15时)出现一个极大值,分别为3.787 6、2.661 6、3.394 3,剔除后的相对误差分别为0.078 2、0.084 4、0.068 3。
|
|
表 2 取21、22、23和24个分潮时的调和预报的性能评价指标 Table 2 Performance evaluation index of harmonic forecast with 21, 22, 23, and 24 tidal components |
由表 2可知,当分潮个数由21个增加至24个时,调和预报模型的判定系数提高了0.021 9,相对误差降低了0.109 5,去极值的相对误差降低了0.044 2。但其由24个进行增加时,判定系数、相对误差和去极值的相对误差值几乎不变。由此可见,使用24个分潮足以包含绝大部分的分潮信号,可以满足调和预报的需求。由2019年1月的观测潮位、调和预报潮位及其相对误差曲线可知:建立模型时,应选取24个分潮(即M2、S2、N2、K1、O1、SA、M4、K2、MS4、P1、L2、NU2、MN4、Q1、T2、MK4、MU2、LDA2、SSA、M6、2N2、2MS6、S4、NO1),其精确的振幅数值可见图 1。
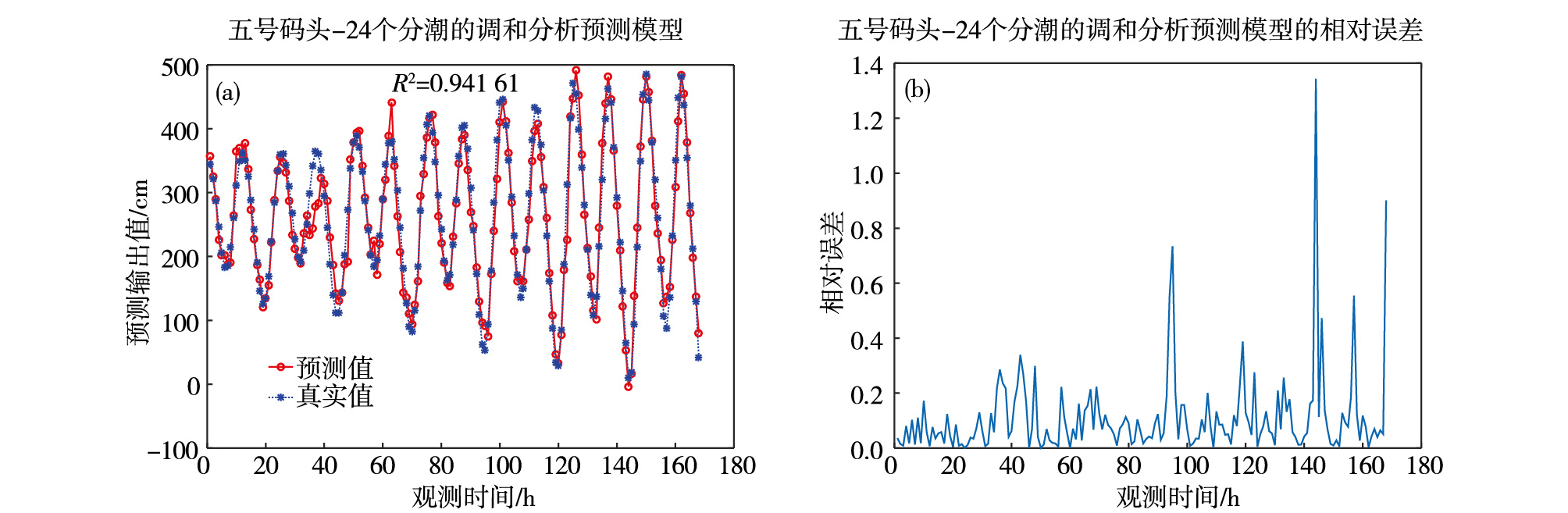
2.4 潮汐预报效果对比五号码头坐落于青岛港一号码头的西北方向,由东北向西南伸展共12个顺岸泊位,五号码头线总长约2 174 m,水深约8 m。同上节分析,选择24个分潮建立潮汐调和预报模型,分析预报五号码头2019年8月的潮位变化。使用相对误差和判定系数来检验回报精度,回报结果及相对误差见图 6。仿真结果(图 6)显示,潮位的回报精度为0.941 6,相对误差仅为0.082 7。这表明本文建立的模型可以较好地回报青岛港附近海域的潮汐变化情况。
|
图 6 五号码头的调和预报模型(a)及其相对误差(b) Fig.6 Harmonic forecast model (a) for Pier 5 and its relative error (b) |
对青岛港口潮汐进行调和分析,使用T_TIDE潮汐调和分析预报程序计算其调和常数,进而对其进行分析和预报。青岛港口潮汐性质为:潮汐为正规半日潮港,主要分潮有M2、S2、N2、K1、O1、M4、K2、MS4和P1,其中M2分潮尤其显著。对比潮位资料长度为1个月、3个月及整年的调和分析结果,可知各分潮的振幅、平均海表面高度与用于调和分析的潮位资料长度几乎无关。选择不同分潮数会在一定程度上影响调和预报精度,对比实验发现,选择24个分潮的预报潮位和实测潮位的相对误差为0.088 1,判定系数为0.969 8,此时为最优选择。
利用上述结果建立调和预测模型,分析五号码头2019年8月的潮位。仿真结果显示,预测的潮位与真实的潮位基本一致,可较好地预报青岛港附近海域的潮汐变化。由仿真结果分析知,潮汐预测误差较大的情况大多是由于风、海浪、风暴潮等高频自然因素运动造成的,故在潮汐预报时考虑非潮汐和自然等因素是值得研究的方向。
| [1] |
邱志雄. 航海概论[M]. 北京: 人民交通出版社, 1999: 86-95.
|
| [2] |
张洪欣, 唐声全, 刘祥宇, 等. 基于潜标资料的中南半岛外海水文特征分析[J]. 海洋气象学报, 2017, 37(1): 54-66. |
| [3] |
刘达, 王慧, 黄彬, 等. 2021年春季海洋天气评述[J]. 海洋气象学报, 2021, 41(3): 11-23. |
| [4] |
王楠喻, 王雪, 娄盼星, 等. 台风"利奇马"引发山东强降水成因分析[J]. 海洋气象学报, 2021, 41(1): 119-128. |
| [5] |
张泽国, 尹建川, 柳成. 基于Grey-GMDH的模块化实时潮汐预报[J]. 中国海洋大学学报(自然科学版), 2018, 48(11): 140-146. |
| [6] |
DARWIN G H. The scientific papers of Sir George Darwin: tidal friction and cosmogony[M/OL]. New York: Cambridge University Press, 2009[2021-11-11]. http://www.cambridge.org/9781108004435.
|
| [7] |
DOODSON A T. The analysis of tidal observations[J]. Philos Trans Roy Soc London, 1928, 227: 223-279. DOI:10.1098/rsta.1928.0006 |
| [8] |
DOODSON A T. The harmonic development of the tide-generating potential[J]. Proc Roy Soc London, 1921, 100(704): 305-329. |
| [9] |
HORN W. Some recent approaches to tidal problems[J]. Int Hydrogr Rev, 1960, 37(2): 65-84. |
| [10] |
郑有任, 张娟, 吴日升. 南海北部沿岸海域潮汐的调和分析[J]. 台湾海峡, 2012, 31(4): 549-556. DOI:10.3969/J.ISSN.1000-8160.2012.04.015 |
| [11] |
程诚, 郑小萌. 连云港站潮汐调和分析与预报[J]. 治淮, 2016(2): 28-29. |
| [12] |
尹朝晖, 巢纪平, 王彰贵, 等. 港珠澳大桥岛隧工程施工海域潮汐调和分析与预报[J]. 海洋预报, 2020, 37(3): 1-5. |
| [13] |
冯士筰, 李凤岐, 李少菁. 海洋科学导论[M]. 北京: 高等教育出版社, 1999: 87-137.
|
| [14] |
方国洪, 郑文振, 陈宗镛, 等. 潮汐和潮流的分析和预报[M]. 北京: 海洋出版社, 1986: 58-100.
|
| [15] |
FOREMAN M G G, NEUFELD E T. Harmonic tidal analyses of long time series[J]. Int Hydrogr Rev, 1991, 68(1): 85-108. |
| [16] |
PAWLOWICZ R, BEARDSLEY B, LENTZ S. Classical tidal harmonic analysis including error estimates in MATLAB using T_TIDE[J]. Comput Geosci, 2002, 28(8): 929-937. |
| [17] |
何佩东, 邬惠明, 曹兵, 等. 江苏近岸海域水位变化特征分析[J]. 海洋预报, 2020, 37(2): 54-59. |
| [18] |
陈耀祖, 高磊, 刘子洲, 等. 山东半岛海洋牧场潮汐特征分析[J]. 海洋与湖沼, 2019, 50(4): 719-727. |
| [19] |
沈欢欢, 李大刚. 黄浦江干流水域潮汐特征分析[J]. 中国水运, 2019(8): 119-120. |
| [20] |
朱巧云, 张志林, 乔红杰. 三峡工程蓄水前后长江河口段潮汐特征变化分析[J]. 水文, 2019, 39(3): 75-79. |
| [21] |
GIL E, DE TORO C. Improving tide-gauge data processing: a method involving tidal frequencies and inverted barometer effect[J]. Comput Geosci, 2005, 31(8): 1048-1058. |
| [22] |
陈宗镛. 潮汐学[M]. 北京: 科学出版社, 1980: 127-234.
|
| [23] |
柳龙生, 黄彬, 吕爱民, 等. 2019年夏季海洋天气评述[J]. 海洋气象学报, 2019, 39(4): 97-107. |
| [24] |
王皘, 黄彬, 聂高臻, 等. 2018年冬季海洋天气评述[J]. 海洋气象学报, 2019, 39(2): 94-105. |
 2022, Vol. 42
2022, Vol. 42


